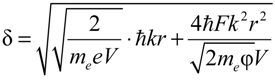1. Introduction
The problem of structure-properties connection is not solved yet for metallic glasses (MG), in part for bulk metallic glasses (BMGs), mostly because a clear understanding of their atomic structure is still questionable [
1,
2,
3]. In spite of the fact the structure translational invariance is absent in metallic glasses, a short- and medium-range order in form of the regular arrangement of adjacent polyhedra is established [
4,
5,
6,
7,
8,
9,
10], providing a basis for extending a structural description beyond the nearest neighbor shell. According to the polycluster model [
5,
6,
7] of amorphous solids, metallic glasses consist of locally regular clusters, whose atomic structure can be incompatible with the translational invariance. Existence of narrow topologically disordered intercluster boundaries in polyclusters is a logical corollary of this model. For this reason, the dislocationless slip at intercluster boundaries, formation and motion of dislocationlike defects are the main mechanism of the inhomogeneous plastic deformation of the polycluster MG. As a consequence, strain-induced softening of MG at deformation (unlike to the typically observed hardening of deformed crystalline metals) is explained under assumption that MG is consisting of “hard” amorphous grains (clusters) surrounded by soft intercluster boundaries, similarly to nanocrystalline materials [
11,
12,
13]. A functional form for deformation-induced softening is obtained assuming that the dislocationless slip at intercluster boundaries is the main mode of the low-temperature plastic deformation [
7].
Worth to note is that idea on the structural heterogeneities of glasses (more ordered amorphous grains surrounded by soft intercluster boundaries was already formulated by Lebedev at the first half of the past century [
5] and was reincarnated in many publications. One of the recent papers devoted to this problem is [
14]. Nevertheless, structural features of the intercluster layers are still not studied properly and debated. While in the covalently bonded glasses they are believed to be continuously disordered layers [
5], in the metallic glasses they are assumed to be topologically disordered intercluster boundaries with structure similar to that of large angle boundaries in crystals. One can expect that in the multicomponent BMGs compositionally differing from the cluster body amorphous boundary layers are forming along with existence of the narrow topologically disordered boundaries. In this case compositional heterogeneities are accompanying the topological disorder.
Presence of inner boundaries in MG essentially impacts diffusional transport, crystallization kinetics, electric resistivity, phonon scattering and localization, low-temperature anomalies of specific heat capacity and thermal conductivity, etc.
In this paper, the combined methods of field emission microscopy (FEM) in the field ion and electron modes and low-field ion microscopy (LFIM) are applied for investigation of the fine structure of the Zr41Ti14Cu12.5Ni10Be22.5 and Zr52.5Ti5Cu17.9Ni14.6Al10 BMGs. The investigations are focused on finding of the intercluster boundaries and studies of their features.
2. Results and Discussion
A typical FIM image of a Zr
41Ti
14Cu
12.5Ni
10Be
22.5 alloy formed by low-temperature field evaporation in high vacuum to a depth of about 50 nm is shown in
Figure 1. The FIM images of this alloy are characterized by an isotropic uncorrelated distribution of bright emission centers. Each of the emission centers corresponds to an isolated surface atom or a small group of atoms. In both investigated zirconium-based BMGs no compositional peculiarities of the structure were found in the FIM images.
Figure 1.
The FIM image of a Zr41Ti14Cu12.5Ni10Be22.5 alloy formed by low-temperature field evaporation in high vacuum to a depth of about 50nm. The scale bar is 5 nm.
In
Figure 2 typical LFIM images of Zr
41Ti
14Cu
12.5Ni
10Be
22.5 BMG at 17.0 kV (a) and 18.5 kV (b) are shown. The LFIM image in
Figure 2b was obtained after additional field evaporation of the surface layer of thickness up to 100 nm. In the both images the nanometer-scale heterogeneities of the structure of Zr
41Ti
14Cu
12.5Ni
10Be
22.5 BMG are clearly seen. The morphology of these surface layers is characterized by a cellular structure. The cells had an irregular elongated polygonal shape with transverse dimensions ranging from 2 nm to 20 nm. The mean diameter of the surface cell, stereologically determined by counting of the number of intersections of a line of known length with (
Figure 1) boundaries [
15], were 7 ± 2 nm and 14.9 ± 4 nm in the small and large cross-sections, respectively. The stereological relationships are based on assumption that the cell structure is isotropic, uniform and random so that all portions of the structure are equally represented.
Figure 2.
LFIM images of Zr41Ti14Cu12.5Ni10Be22.5 BMG at (a) 17.0 kV and (b) 18.5kV. The cellular morphology and nanometer-scale heterogeneities of the structure of are observed. Scale bar is 20nm.
The LFIM images of Zr
41Ti
14Cu
12.5Ni
10Be
22.5 BMG show that the alloy is locally anisotropic. The level of statistical significance for locally anisotropic structures is larger for the dimensionless ratio of mean diameters of the surface cells in the small and large cross-sections. This aspect ratio of the cells in the LFIM images of this alloy (
Figure 2) reaches the value of 2.1.
The LFIM images of Zr
52.5Ti
5Cu
17.9Ni
14.6Al
10 BMG also clearly revealed the nanometer-scale cellular topographic heterogeneities (
Figure 3). The cells have an irregular polygonal shape with transverse dimensions ranging from 3 nm to 15 nm. However, unlike to the Zr
41Ti
14Cu
12.5Ni
10Be
22.5 BMG, the cell structure is isotropic and the mean diameter of the surface cells is 9.2 ±2 nm in all directions on the surface. This value is obtained by stereological analysis of several cross-sections normal to specimen axis during the process of chemically induced field evaporation, two of which are presented in
Figure 3.
Figure 3.
Typical LFIM images of Zr52.5Ti5Cu17.9Ni14.6Al10 BMG (a)before and (b) after chemically induced field evaporation at a depth of about 100nm. Scale bar is 10 nm.
Field electron images of both BMGs also reveal substantial nanometer-scale heterogeneities of field emission from the surface formed by low-temperature field evaporation in high vacuum at 53–77 K (
Figure 4a). The contour plot of constant brightness levels of the image is presented in
Figure 4b. Difference between local energies of field evaporation in sample sites, which correspond to the neighbouring numbered contour lines of constant brightness in
Figure 4b, is equal to
![Metals 02 00441 i004]()
. Distances between centers of increased brightness in the investigated samples are changing within the range 5–20 nm.
Figure 4.
(a) Field electron image and (b) contour diagram of constant brightness levels for the Zr41Ti14Cu12.5Ni10Be22.5 BMG. An intercluster boundary is shown by arrow. Scale bar is 5nm.
The method of field emission microscopy allows determining local values of field evaporation energy
Qn. In a model of the image forces [
16]
where
n is the multiplicity of ionization of the evaporated atoms;
e is the electron charge. Variation of field evaporation energy was determined by shifts of contours of constant brightness levels in the field
Figure 2. From Fowler-Nordheim relationship [
17] for a field emission one can directly derive
where χ is the coefficient of the field sensitivity of electronic emission;
F is the local intensity of a field emission. In a mode of electron emission the field,
F changed within the range 2–4 V nm
−1 and the value of χ was in the range of 14–20 [
6,
18].
Heterogeneity of the local evaporation field strength distribution in the mode of electron emission is caused by peculiarities of the surface microrelief formed at field evaporation in the field ion mode. It reflects heterogeneity of the field evaporation energy determined by Equation 1. Thus, the contour lines of constant brightness for electron emission image correspond to the evaporation energy isolines. Calculation of the absolute values of field evaporation energy
Qn is complicate due to complexity of the charge spectrum of ions in a multicomponent alloy. But deviations of evaporation energy from the maximum value
![Metals 02 00441 i005]()
can be calculated directly using Equations 1 and 2. The energy values shown in
Figure 4 correspond to the difference of field evaporation energy, Δ
Q0, in the cluster center and at isoenergetic contours, calculated from Equation 1 for the series of evaporation voltages.
According to these observations, variance of the local energy of field evaporation is ~5% within cells of characteristic scale ~10 nm. The energy of evaporation decreases towards the cluster periphery, reaching a minimum value at the intercluster triple junctions (with ΔQ0 up to 1.30 eV). A local minimum energy, presumably at the intercluster boundary corresponds to ΔQ0 = 0.8 eV.
The mean width of such boundaries determined by a local decrease in brightness due to the effect of preferred field evaporation is 2.5 ± 1.0 nm. This value is rather higher than that generally determined by the FIM method of field etching [
6,
19]. Obviously, one of the reasons for this difference may be relatively low lateral resolution of the FEM in the electron mode. The FEM pattern on the screen is not very sharp, because emitted electrons have a transverse velocity, which results in a scattering disk on the phosphor screen. The resolution limit of the FEM can be characterized by a parameter
δ, which is defined as the minimal diameter of the image disk divided by the image magnification. There is a general trend toward an increase of the FEM and FIM spatial resolution
δ by miniaturization of pointed specimens [
16,
20]. Most of the calculations of this quantity were performed in the micron and submicron ranges of the specimen lateral dimension. The dependence of
δ on the curvature radius of the top of needlelike specimen
ρ in the nanometer-scale range can be calculated using the following formula [
20]:
with elementary charge
e, electron mass
me, Planck constant
ħ, image compression factor
k, emitter radius of curvature
r, potential
V and work function φ. Typically
k ≈ 1.5. With that Equation 3 gives estimation of the FEM resolution δ
≈ 1.1–1.5 nm. This value is considerably larger than that for a FIM (0.3 nm) [
16] and may be responsible for the broadening of the intercluster boundary image.
Performed analysis of the evaporation field distribution on the surface of partially evaporated samples clearly show presence of inner interfaces (intercluster boundaries) and their triple joints in the BMGs investigated. The used tools do not allow to investigate details of microscopic structure of the interfaces including the local toplogical and compositional order but our studies allow to estimate, at least qualitatively, the role of the topological and compositional order in formation of the interfaces. The width of the boundary layer, in which the field evaporation energy is steeply decreasing, is not small, up to 2.5 nm, as it is seen from the contour diagrams (
Figure 4). This feature can be attributed to gradual changes of the composition in the boundary layer. Decomposition of Zr
41Ti
14Cu
12.5Ni
10Be
22.5 glass and two-phase (Ti-reach and Be-reach) glass formation as result of liquid state aging (at
T >
Tg) was revealed in [
21,
22]. Therefore compositional stratification of this glass is an expected property. Even without special aging at
T >
Tg, partial decomposition of the glass occurs during the glass transition when solid-like amorphous germs separated by a liquid-like substance of a different composition are forming.
From the other hand, the measured minimal value of the field evaporation energy in the boundary layer (Δ
Q0 ≈ 0.8 eV) is comparable with decrease of the atom binding energy within the disordered boundaries in polycrystals [
23]. Of this evidence, one can conclude that a narrow topologically disordered intercluster boundary exists at the Δ
Q0 maximum location. Apparently this boundary appears when the solid clusters (with compositionally inhomogeneous periphery) are contacting and the structure relaxation processes are frozen because of low temperature. It can be assumed that the peculiarities of the revealed heterogeneities of the field evaporation energy are evidence of narrow topologically disordered intercluster boundaries surrounded by compositionally inhomogeneous layers.
3. Experimental Procedure
Measurements of the nanometer-scale structural heterogeneities of zirconium based bulk metallic glasses were performed using a two-chamber field ion microscope (FIM) at the specimens’ temperature 53–77 K [
24]. Image was formed by using neon under a pressure of 2 × 10
−3–2 × 10
−2 Pa. The working chamber of the microscope was evacuated by cryogenic pumps to a residual gas pressure of 10
−6 Pa. In order to use the microscope in both the field electron and ion modes, a constant positive voltage of 3–25 kV, and alternating voltage of amplitude 4–28 kV and frequency 50 Hz was supplied to specimens. The total voltage supplied to the specimen was of the pulse type with the ratio of the amplitudes of positive and negative voltages varied from 6 to 10. The negative voltage pulses of duration (2–3) × 10
−3 s was sufficient for creating on the specimen tip a field strength required for an electron current density of 10
2–10
3 A cm
−2.
Amorphous rods with a diameter of 12 mm and 50 mm length were smelted in a sealed quartz pipe in a pure argon atmosphere with subsequent quenching in water. By X-ray and electronic difractometry it was shown that the obtained material was completely amorphous and microscopically homogeneous. Thin disks 0.2 mm thick were cut from the rods. Then columns with sizes 10 mm× 0.2 mm× 0.2 mm were cut with the help of a diamond wire saw. Needlelike specimens with a curvature of 10 –100 nm at the top were prepared by electrochemical etching at a constant voltage 3–10 V in a 15% solution of chloric acid in ethyl alcohol at room temperature.
The surface of the specimens after mounting in the microscope was cleaned by field desorption [
16]. Then formation of the surface was carried out at 53–77 K by field evaporation to a depth not less than 10 nm. Thus not only adsorbed layers and surface layers contaminated during electrochemical processing were removed, but also a specific surface microtopography of samples was created.
The prepared surface relief represents the distribution of local threshold values of evaporation field strength Fe. The observed contrast of FEM images is determined mainly by this distributions formed during the process of preliminary surface polishing by field evaporation. The value of Fe was determined by comparison with the threshold field strength of ionization for atoms of imaging gas. The contour configuration for constant values of current density was determined by means of photometry with use of computer processing of brightness distribution in the field emission image.
The structure of the amorphous alloys was also studied by means of low-field ion microscopy using the phenomenon of field etching of the specimen surface under the action of water vapor accompanied by the emission of positive ions in electric fields of 2 V nm
−1 [
25]. Consecutive dissociation of water molecules with the formation (in the intermediate state) of the OH–radical bound to the metal surface followed by the formation of the oxide subsequently removed by the electric field was used to get specific FIM images. The products of chemical reactions occurring at the specimen surface during field etching ensure the formation of low-field ion images. Experiments were performed using the same FIM with the samples at room temperatures. The required concentration of water vapor in the chamber was attained by evacuation to a residual gas pressure of 10
−1 Pa. Since the image is formed by the flows of the material being evaporated and the products of chemical reactions occurring at the surface of the metal, this regime is dynamic and is accompanied by a continuous increase in the radius of the tip of the point sample. Gradual evaporation of micrometer-size samples to a large depth with continuous image recording forms the basis of the 3D nanometallography of BMGs.



 . Distances between centers of increased brightness in the investigated samples are changing within the range 5–20 nm.
. Distances between centers of increased brightness in the investigated samples are changing within the range 5–20 nm. 
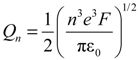
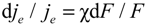
 can be calculated directly using Equations 1 and 2. The energy values shown in Figure 4 correspond to the difference of field evaporation energy, ΔQ0, in the cluster center and at isoenergetic contours, calculated from Equation 1 for the series of evaporation voltages.
can be calculated directly using Equations 1 and 2. The energy values shown in Figure 4 correspond to the difference of field evaporation energy, ΔQ0, in the cluster center and at isoenergetic contours, calculated from Equation 1 for the series of evaporation voltages.