1. Introduction
Metal foams (
Figure 1), which have an attractive combination of physical and mechanical properties, such as low density and high specific stiffness in relation to their weight, are extremely important for many branches of modern industry. Their behavior under mechanical loading mainly depends on relative density and base material, with other influential factors being morphology (open or closed cell), geometry and topology (regular or irregular structure) of the cellular structure [
1,
2,
3,
4,
5,
6].
Although metal foams were a subject of some intensive research studies in past years, there is still a lack of their mechanical characterization data, especially under dynamic loading conditions. The shock wave propagation through the cellular material structure due to impact loading has a significant effect on its deformation mechanism and is therefore imperative to understand its effects thoroughly. The strain rate dependence (up to 1,000 s
−1) of material properties of open cell magnesium foams (AZ91) under compressive loading conditions were examined by Mukai
et al. [
7]. Their research results show, that the amount of absorbed mechanical energy through cellular structure deformation heavily depends on the applied strain rate, since the energy absorption at a strain rate of 1,400 s
−1 is approximately 100% higher than at the quasi-static loading conditions. Christ
et al. [
8] examined the mechanical properties of closed-cell cellular materials subjected to compressive loading (up to the strain of 80%) under different strain rates, ranging from 0.0002 s
−1 to 2 s
−1. The authors concluded that with increased strain rate closed-cell materials lose their characteristic deformation behavior under compressive loading conditions (stress plateau in stress-strain diagram), because increased strain rates also increase the material stiffness, which results in the increase of absorbed mechanical energy.
Figure 1.
Open-cell metal foam.
Existing constitutive models of cellular materials, incorporated in some engineering computer simulation software systems, do not take into account the effects of geometric irregularity and strain rate effects under dynamic loading and thus cannot properly simulate the macroscopic behavior of cellular materials. This prompted development of new lattice computational model of irregular open-cell material [
9], which is able to account for the effects of structural irregularity and effects of different strain rates on the properties of open-cell materials under large deformations.
This paper presents the research results of experimental and computational study of open-cell aluminum foam behavior under underwater shock wave impact loading. The material and structural properties of water submerged open-cell aluminum foam sample under shock wave loading due to water-surface explosive detonation have been examined.
2. Experimental Procedure
The experimental tests of the aluminum foams samples have been performed at the Shock Wave and Condensed Matter Research Center, Kumamoto University, Japan [
10]. The aluminum specimens were submerged in a water container with clear PMMA walls to observe and visualize the effects of the shock wave loading. The container had the following dimensions: 200 mm × 200 mm × 135 mm, and was filled with water. Aluminum foam specimens, measuring 40 mm × 40 mm × 40 mm, were positioned at the bottom of water container. The specimens were made from the open-cell aluminum foam produced by m.pore GmbH with a relative density of 6.1% and a cell size of 20 ppi (mean cell diameter equals 3.8 mm) and pure aluminum EN AW-1070 as the base material. The nitrocellulose based (SEP) explosive set (pentaerythritol tetranitrate—PETN 65 wt% and paraffin wt. 35%; mass: 50 g, density: 1,310 kg/m
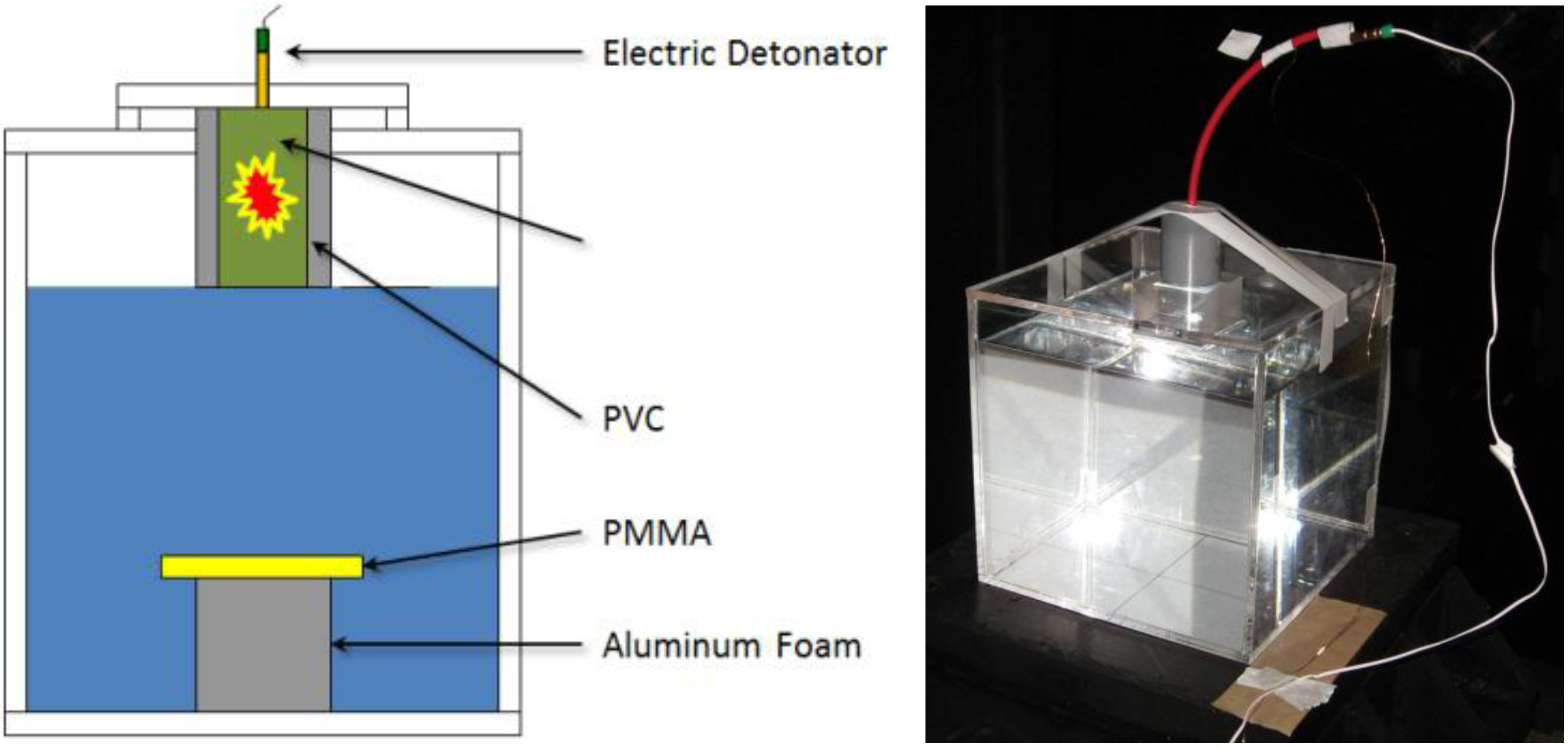
3, detonation velocity: 7,000 m/s, detonation pressure: 15.9 GPa) in the PVC pipe was positioned 110 mm above the foam specimen at the water surface. The SEP is an acronym of the Safety ExPlosive, fabricated and provided by Asani Chem. Industry Co., Japan. It was used as booster explosive for shock wave generation and was initiated by an electric detonator. A PMMA plate was placed on the top of the metal foam to assure its uniform deformation during the loading. The experimental setup is shown in
Figure 2 [
10].
Figure 2.
Experimental setup.
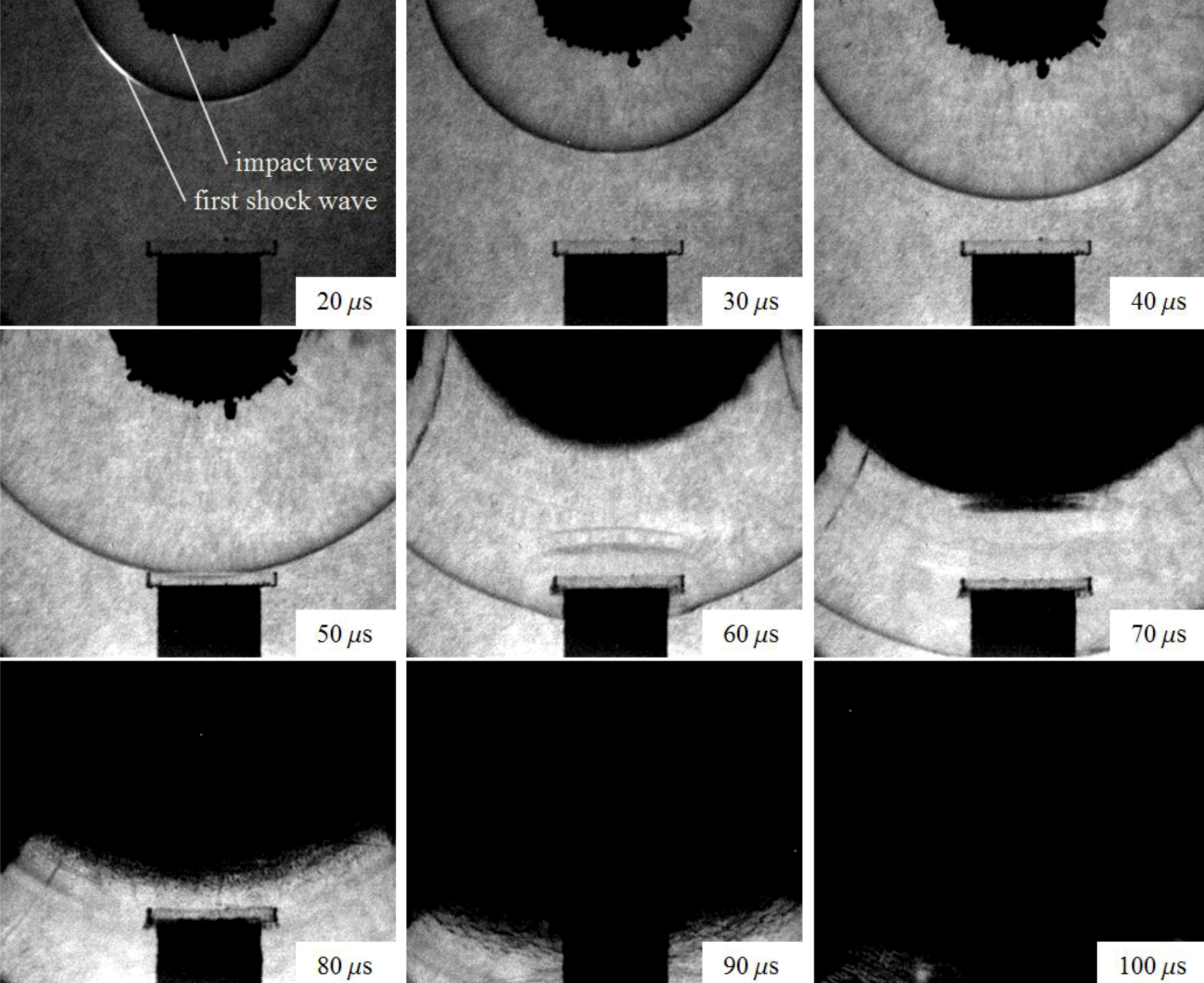
The shadowgraph method was used to observe the generation of shock wave and its influence on the aluminum foam. This method is used to observe and project the shadow of the light by density change on a screen or the film of a camera, and it is also called the direct projective technique. For this purpose the short arc power flashlight SA-200F with an exposure time of approximate 250 ms and the high speed digital video camera HPV-1 (Shimadzu Corporation) with a frame rate of 500,000 FPS and an image resolution of 320 × 260 pixels were used to visualize the shock wave propagation and its effects during the experiment (
Figure 3). From the figure it can be observed that the first shock wave is not strong enough to compress the metal foam, but it reflects back at approx. t = 50 ms. The impact wave (with the expanding gases) follows the first shock wave with a lower velocity v = 1660 m/s. When the impact wave reaches the metal foam specimen, it completely compresses it. After the experiment only small fractals of the specimen are possible to recover due to the massive deformation.
The shock wave velocity (shown later in
Figure 4) was determined by analyzing digital images taken during the experiment (
Figure 3). The maximum observed shock wave velocity was approximately 2,700 m/s, with accuracy ±250 m/s. From the figure it can be observed that the shock wave velocity decreases due to the pressure decay associated to spherical propagation. Since the shock wave front is spreading over a spherical surface area, the energy per unit area of the expanding spherical shock wave decreases affecting its velocity.
The deformation behavior of aluminum foam sample could not be studied in detail due to insufficient imaging resolution used in experimental testing.
Figure 3.
Shock wave propagation.
3. Computational Simulations
Computational simulations were used to further investigate the behavior of open-cell aluminum foams under shock wave loading conditions [
11,
12]. The explicit finite elements LS-DYNA software system was used for this purpose [
13].
First a simulation of the shock wave propagation through water without a foam specimen model was performed to computationally validate experimental shock wave observations. Due to the double symmetry only a quarter of the water container volume was modeled [
14]. The computational model (
Figure 6) consisted of parts modeled with an Eulerian mesh (the SEP explosive, the air and the water) while the PVC pipe was modeled with the Lagrangian mesh. The SEP explosive (r = 1,310 kg/m
3) behavior was modeled with the Jones-Wilkins-Lee (JWL) equation of state, the water (r = 998 kg/m
3) with the Mie Gruneisen equation of state, the air (r = 1.25 kg/m
3) with the linear polynomial equation of state and the PVC pipe was modeled with a piecewise-linear plasticity constitutive model with failure (r = 1,380 kg/m
3). The values of used equations of state are given in
Table 1.
Table 1.
Parameters of the equations of state.
| Equation of State | EOS | Parameters with units: [m], [kg], [s] |
|---|
| Air | Linear polynomial | c0 = c1 = c2 = c3 = 0, c4 = c5 = 0.4, e0 = 2.5e5, v0 = 1 |
| Water | Mie Gruneisen | c = 1647, s1 = 1.92, gama = 0.35, e0 = 2.9e5, v0 = 1 |
| SEP | Jones-Wilkins-Lee | a = 3.65e11, b = 2.3e9, r1 = 4.3, omeg = 0.28, e0 = 0.7e10, v0 = 1 |
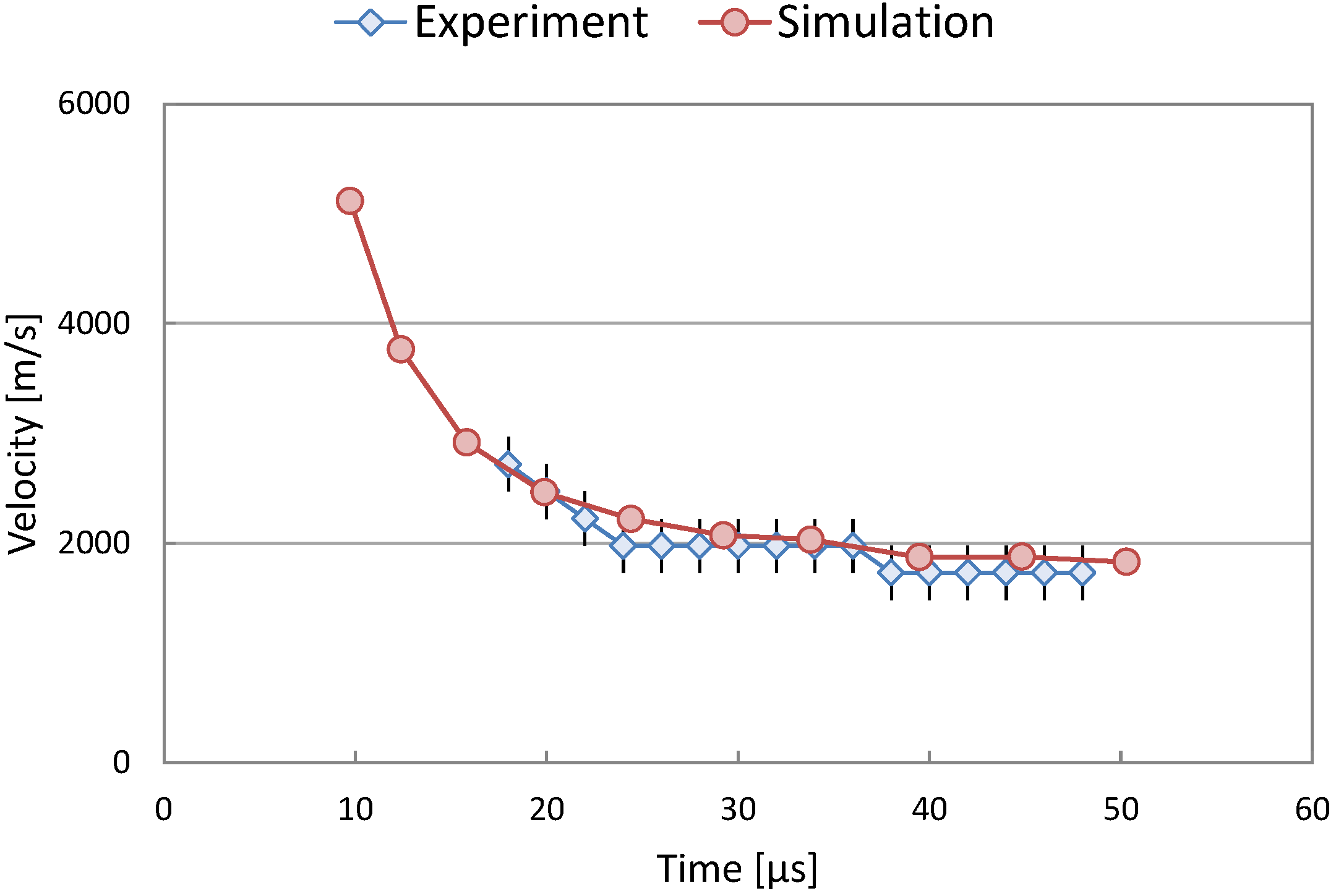
The fluid-structure interaction interface was defined on the boundaries of the PVC mesh. The shock wave velocity in the computer simulation (
Figure 4) was determined from the position of the pressure measurement points (defined every 10 mm from the water surface to the bottom) by observing their maximum pressure. The accuracy of this calculation was limited by the time sampling interval which equaled to 0.15 µs but was much higher than by the experiment. From the figure an excellent comparison between the shock wave velocity obtained by the experimental and computational results can been observed.
Figure 4.
Shock wave velocity comparison of the experimental and computational results.
In the second set of computational simulations homogenized foam specimen model was added to computationally observe the generated shock wave effects on the deformation behavior of the open-cell aluminum foam. Material properties of the analyzed metal foam that were obtained by additional experimental testing are given in the
Table 2.
Table 2.
Material properties of the metal foam.
| | Density | Young’s modulus | Poisson’s ration | Yield stress | Tangent modulus |
|---|
| Al Foam | 185 kg/m3 | 30 MPa | 0.3 | 0.25 MPa | 0.64 MPa |
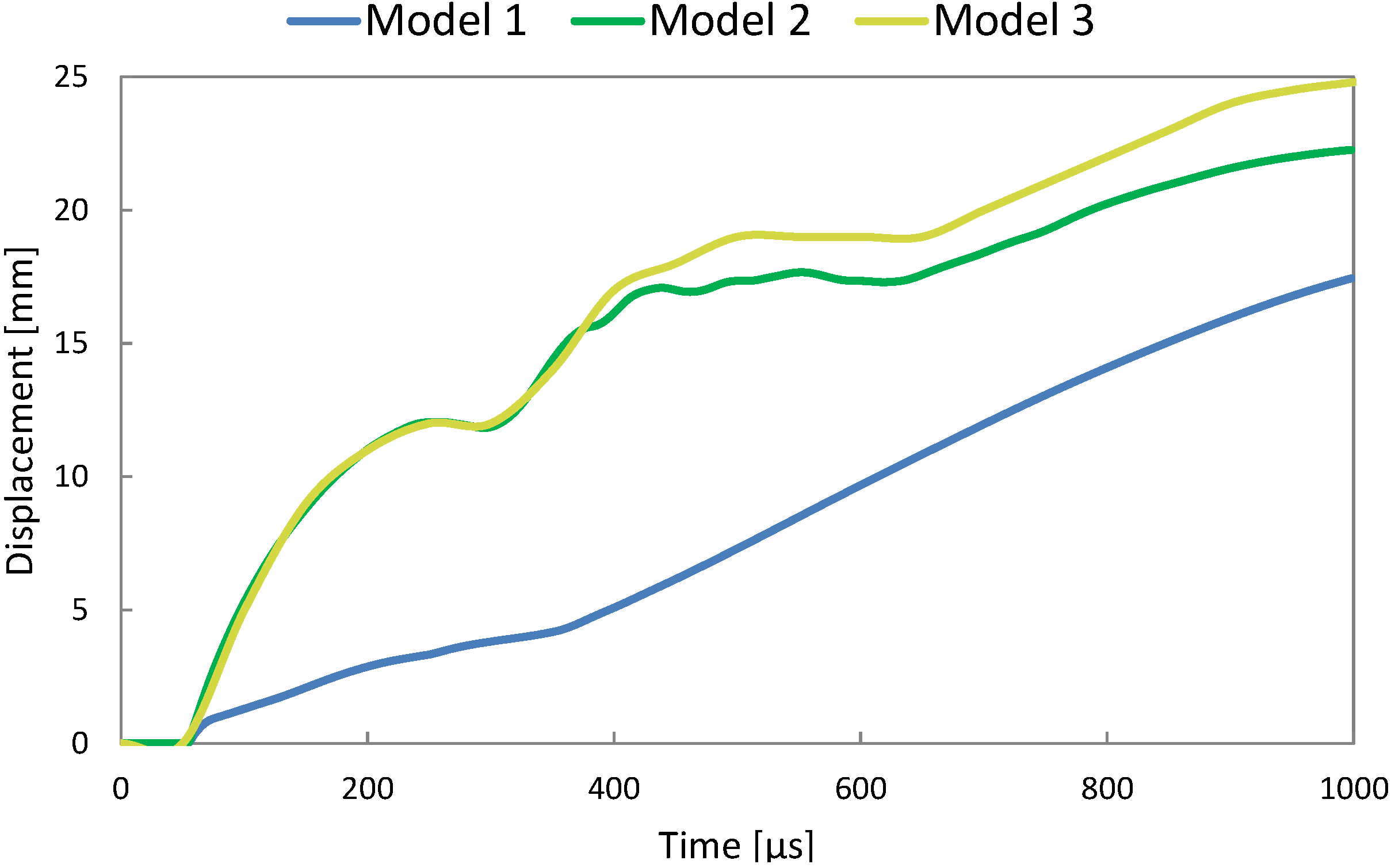
Three different foam sample modeling approaches were evaluated: (i) model 1: the foam sample was modeled with Lagrangian mesh and bilinear constitutive model; the water domain was modeled inside the foam; (ii) model 2: the foam sample was modeled with Lagrangian mesh and bilinear constitutive model; the air domain was modeled inside the foam; (iii) model 3: the foam sample was modeled with Eulerian mesh and bilinear constitutive model. Deformation behavior of all three different sample models is shown in
Figure 5.
Figure 6 shows the average top surface displacement of the aluminum foam sample for all three computational models employed. For the Lagrangian models (1 and 2) the average of all nodes on the top surface was taken into account while for the Eulerian model only averaging of 4 characteristic positions on the top surface was utilized. As it can be observed, the model 3 (Eulerian foam model) exhibits the lowest stiffness while the highest stiffness was observed for model 1 (Lagrangian mesh filled with water).
Figure 5.
Deformation of the homogenized foam model.
Figure 6.
Average vertical displacement of the top surface of the aluminum foam.
4. Conclusions
The paper presents the results of experimental and computational study of shock wave loading effects on water submerged aluminum foam. The shadowgraph method was used to observe the underwater shock wave formation, propagation and its effects on submerged aluminum foam sample. The average shock wave velocity was determined to be approximately 2,700 m/s. The deformation behavior of submerged aluminum foam sample could not be studied in detail due to insufficient imaging resolution used in experimental testing.
Computational simulations were used to further investigate the behavior of open-cell aluminum foams under shock wave loading conditions with use of the explicit finite elements LS-DYNA software system. The first computational model without considering the foam sample was used to validate experimental shock wave observations. In the following simulations three different foam sample modeling approaches were studied to determine their usefulness. The final foam sample model selection is yet to be determined by validating computational results with a new set of experiments to be performed with better recording equipment.