Gas Atomization of Aluminium Melts: Comparison of Analytical Models
Abstract
:1. Introduction
2. Break Up Models
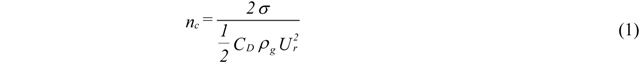





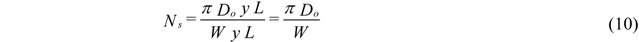


- Atomization Pressure : 150 psi (1.03 MPa);
- Ambient Pressure : 14 psi (0.096 MPa);
- Initial Melt Column Radius : 0.001 m;
- Initial Melt Exit Velocity : 1 m/s;
- End of break up calculations 0.4 m downstream of atomizer.
3. Results and Discussion
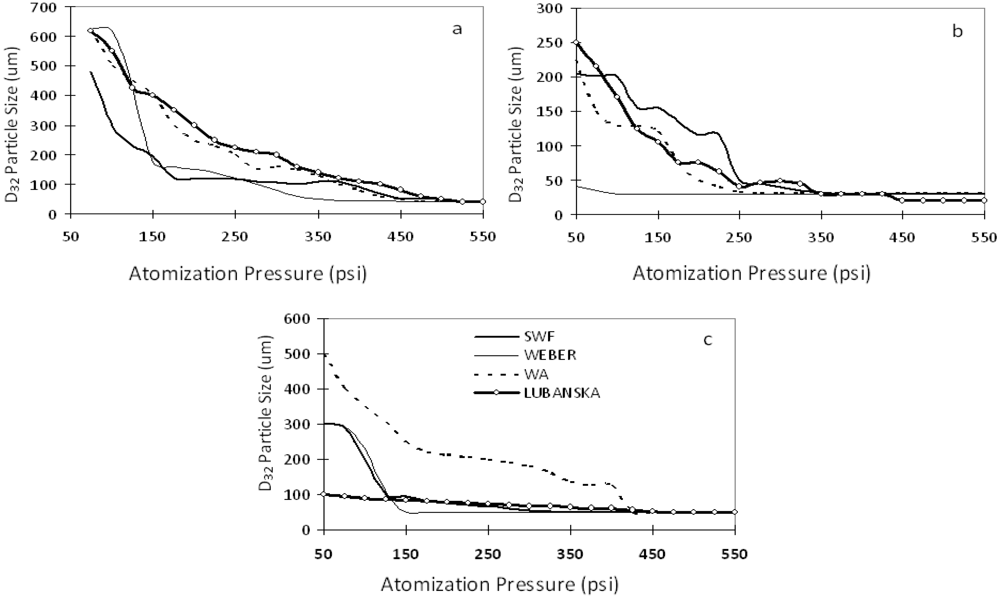
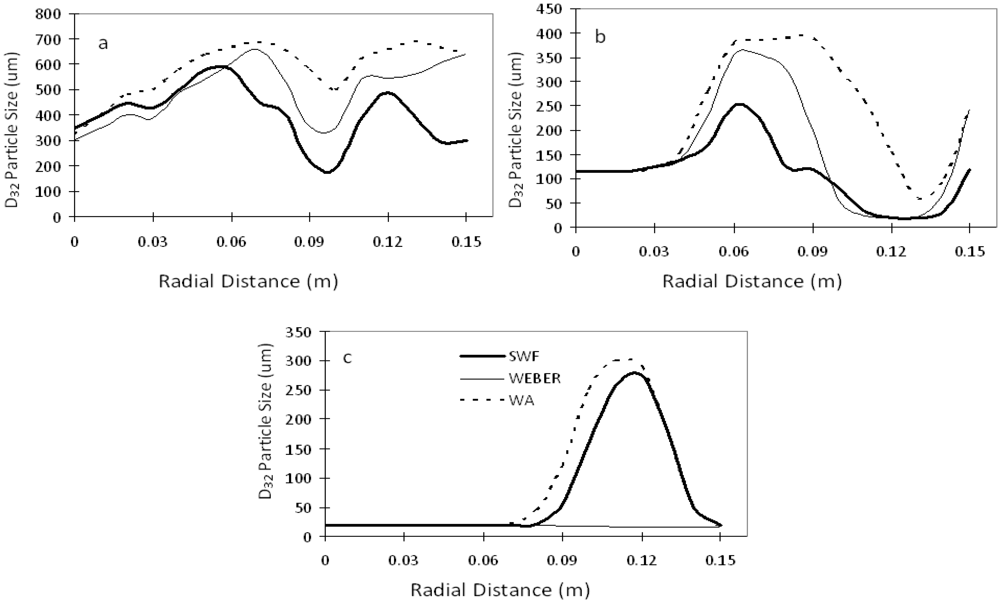

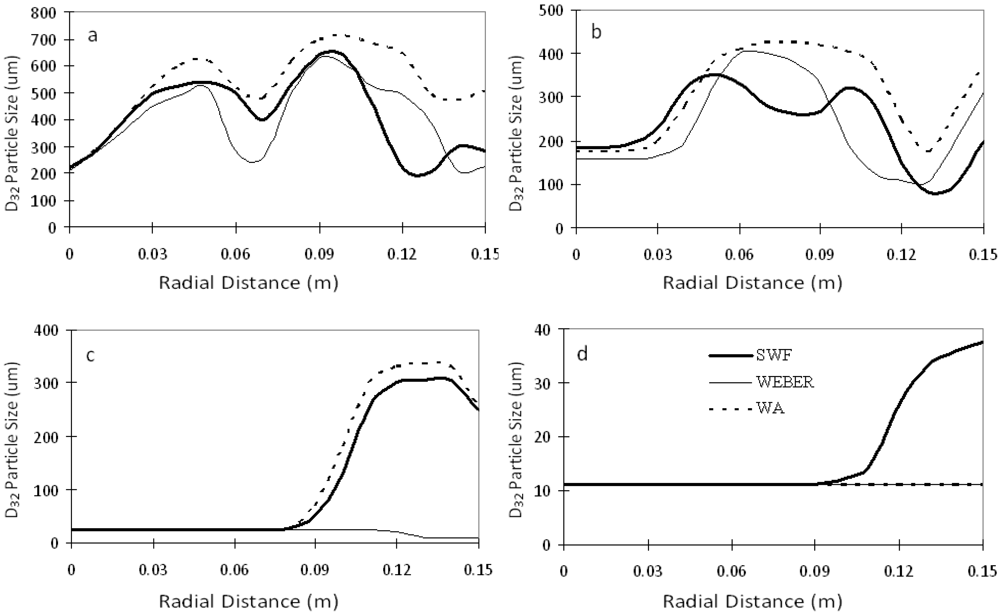
4. Conclusions
Rerefernces
- Dumouchel, C.; Cousin, J.; Triballier, K. Experimental analysis of liquid-gas interface at low weber number: Interface length and fractal dimension. Exp. Fluids 2005, 39, 651–666. [Google Scholar] [CrossRef]
- Fei, L.S.; Xu, S.L.; Wang, C.J.; Li, Q.; Huang, S.H. Experimental study on atomization phenomena of kerosene in supersonic cold flow. Sci. China E Technol. Sci. 2008, 51, 145–152. [Google Scholar]
- Shinjo, J.; Umemura, A. Simulation of liquid jet primary breakup: Dynamics of ligament and droplet formation. Int. J. Multiph. Flow 2010, 36, 513–532. [Google Scholar] [CrossRef]
- Ng, C.L.; Sankarakrishnana, R.; Sallam, K.A. Bag breakup of nonturbulent liquid jets in crossflow. Int. J. Multiph. Flow 2008, 34, 241–259. [Google Scholar] [CrossRef]
- Guildenbecher, D.R.; López-Rivera, C.; Sojka, P.E. Secondary atomization. Exp. Fluids 2009, 46, 371–402. [Google Scholar] [CrossRef]
- See, J.; Johnston, G. Interactions between nitrogen jets and liquid lead and tin streams. Powder Technol. 1978, 21, 119–133. [Google Scholar] [CrossRef]
- Kim, M.; Jones, H. Effect of process variables in gas-jet atomization and production of multilayer deposits. In Proceedings of the 4th International Conference on Rapidly Quenched Metal, Sendi, Japan, 22–24 August 1988.
- Hiroyasu, H.; Shimizu, M.; Arai, M. The breakup of a high speed jet in a high pressure gaseous atmosphere. In Proceedings of the 2nd International Conference on Liquid Atomization and Spray Systems, Madison, WI, USA, 20–24 June 1982.
- Pai, B.; Nijaguna, B. The charecterization of sprays. In Proceedings of the 2nd International Conference on Liquid Atomization and Spray Systems, Madison, WI, USA, 20–24 June 1982.
- Reitz, R. Modelling atomization processes in high-pressure vaporizing sprays. At. Spray Technol. 1987, 3, 309–337. [Google Scholar]
- Arai, M.; Shimizu, M.; Hiroyasu, H. Break-up length and spray formation mechanism of a high speed liquid jet. In Proceedings of the 4th International Conference on Liquid Atomization and Spray Systems, Sendai, Japan, 22–24 August 1988.
- Ünal, A. Effect of processing variables on particle size in gas atomization of rapidly solidified aluminium powders. Mater. Sci. Technol. 1987, 3, 1029–1039. [Google Scholar] [CrossRef]
- Ingebo, R. Experimental and theoretical effects of nitrogen gas flow rate on liquid jet atomization. J. Propuls. Power 1988, 4, 406–411. [Google Scholar] [CrossRef]
- Zanelli, S. Behaviour of a liquid jet near the nozzle. In Proceedings of the 4th International Conference on Liquid Atomization and Spray Systems, Sendai, Japan, 22–24 August 1988.
- Vahedi, T.H.; Pourdeyhimi, B. The effects of nozzle geometry on water jet breakup at high reynolds numbers. Exp. Fluids 2003, 35, 364–371. [Google Scholar] [CrossRef]
- Vukasinovic, B.; Smith, M.K.; Glezer, A. Mechanisms of free-surface breakup in vibration-induced liquid atomization. Phys. Fluids 2007, 19, 012104:1–012104:15. [Google Scholar]
- Dumouchel, C. On the experimental investigation on primary atomization of liquid streams. Exp. Fluids 2008, 45, 371–422. [Google Scholar] [CrossRef]
- Lubanska, H. Correction of spray ring data for gas atomization of liquid metals february. J. Metals 1970, 22, 45–49. [Google Scholar]
- Hinze, J. Fundamentals of the hydrodynamic mechanism of splitting in dispersion processes. AICHE J. 1955, 1, 289–295. [Google Scholar] [CrossRef]
- Gordon, G. Mechanism and speed of breakup of drops. J. App. Phys. 1959, 30, 1759–1761. [Google Scholar] [CrossRef]
- Mehrota, S. Mathematical modelling of gas atomization process for metal powder production. Powder Metall. Int. 1988, 13, 80–84. [Google Scholar]
- Haas, F. Stability of droplets suddenly exposed to a high velocity gas stream. AICHE J. 1964, 10, 920–924. [Google Scholar] [CrossRef]
- Gorokhovski, M.; Herrmann, M. Modeling primary atomization. Annu. Rev. Fluid Mech. 2008, 40, 343–366. [Google Scholar] [CrossRef]
- Ishimoto, J.; Ohira, K.; Okabayashi, K.; Chitose, K. Integrated numerical prediction of atomization process of liquid hydrogen jet. Cryogenics 2008, 48, 238–247. [Google Scholar] [CrossRef]
- Trinh, H.P.; Chen, C.P.; Balasubramanyam, M.S. Numerical simulation of liquid jet atomization including turbulence effects. J. Eng. Gas Turb. Power 2007, 129, 920–928. [Google Scholar] [CrossRef]
- Pougatcha, K.; Salcudeana, M.; Chanb, E.; Knapper, B. A two-fluid model of gas-assisted atomization including flow through the nozzle, phase inversion, and spray dispersion. Int. J. Multiph. Flow 2009, 35, 661–675. [Google Scholar] [CrossRef]
- Kumar, A.; Ghosh, S.; Dhindaw, B.K. Simulation of cooling of liquid Al-33 wt.% Cu droplet impinging on a metallic substrate and its experimental validation. Acta Mater. 2010, 58, 122–133. [Google Scholar] [CrossRef]
- Antipas, G.S.E. Spray forming of Al alloys: Experiment and theory. Mater. Res. 2012, 15, 131–135. [Google Scholar] [CrossRef]
- Antipas, G.S.E. Modelling of the break up mechanism in gas atomization of liquid metals, Part II. The gas flow model. Comput. Mater. Sci. 2009, 46, 955–959. [Google Scholar]
- Antipas, G.S.E. Modelling of the break up mechanism in gas atomization of liquid metals, Part I. The surface wave formation model. Comput. Mater. Sci. 2006, 35, 416–422. [Google Scholar] [CrossRef]
- Hinze, J.O. Fundamentals of the hydrodynamic mechanism of splitting in dispersion process. AICHE J. 1955, 1, 289–295. [Google Scholar] [CrossRef]
- Wolf, H.E.; Andersen, W.H. Aerodynamic break-up of liquid drops. In Proceedings of the 5th International Shock Tube Symposium, Berkely, CA, USA, 28–30 April 1965.
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Antipas, G. Gas Atomization of Aluminium Melts: Comparison of Analytical Models. Metals 2012, 2, 202-210. https://doi.org/10.3390/met2020202
Antipas G. Gas Atomization of Aluminium Melts: Comparison of Analytical Models. Metals. 2012; 2(2):202-210. https://doi.org/10.3390/met2020202
Chicago/Turabian StyleAntipas, Georgios. 2012. "Gas Atomization of Aluminium Melts: Comparison of Analytical Models" Metals 2, no. 2: 202-210. https://doi.org/10.3390/met2020202
APA StyleAntipas, G. (2012). Gas Atomization of Aluminium Melts: Comparison of Analytical Models. Metals, 2(2), 202-210. https://doi.org/10.3390/met2020202



