Error Uncertainty Analysis in Planar Closed-Loop Structure with Joint Clearances
Abstract
:1. Introduction
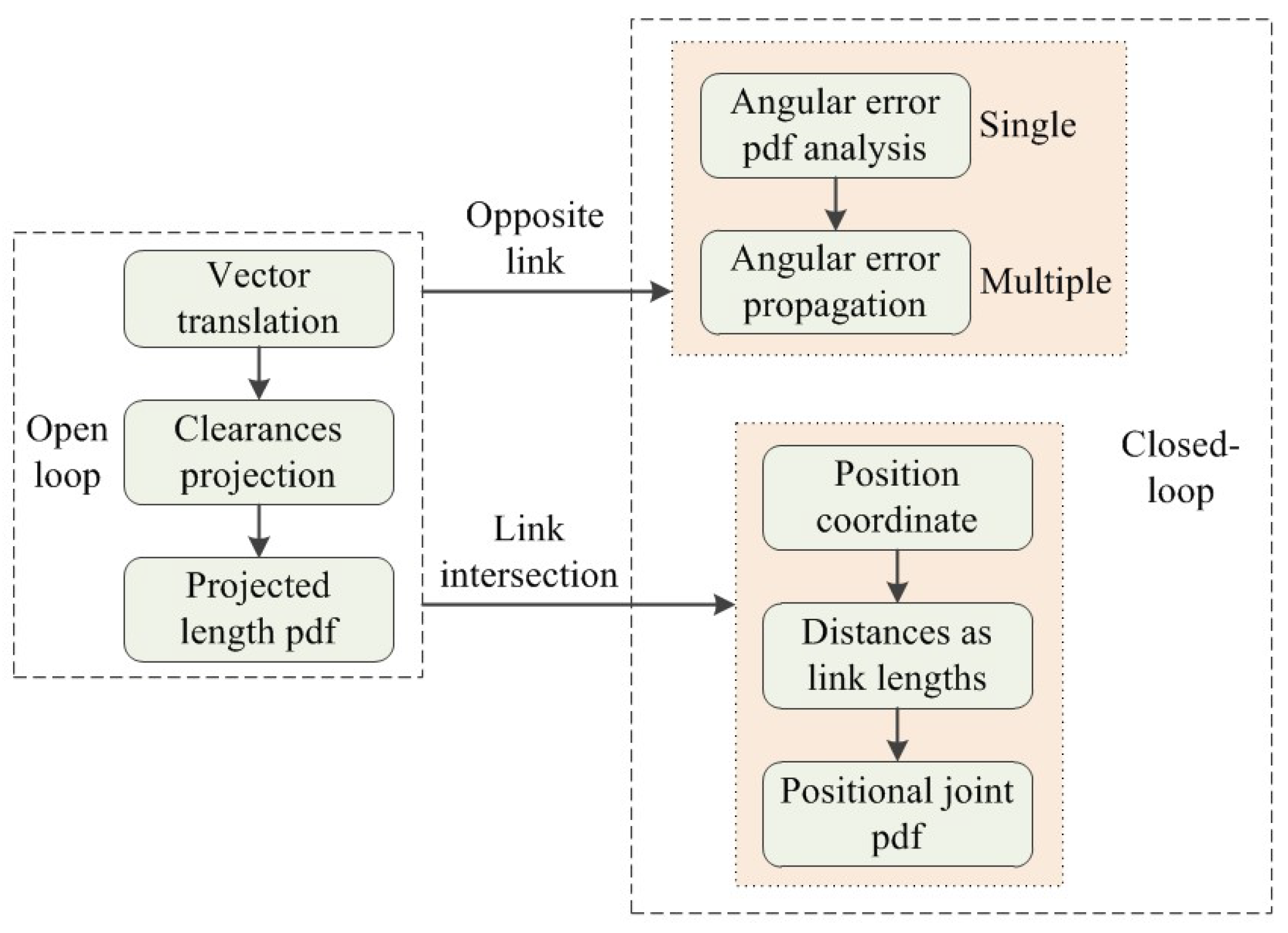
2. Closed-Loop Error Model Analysis
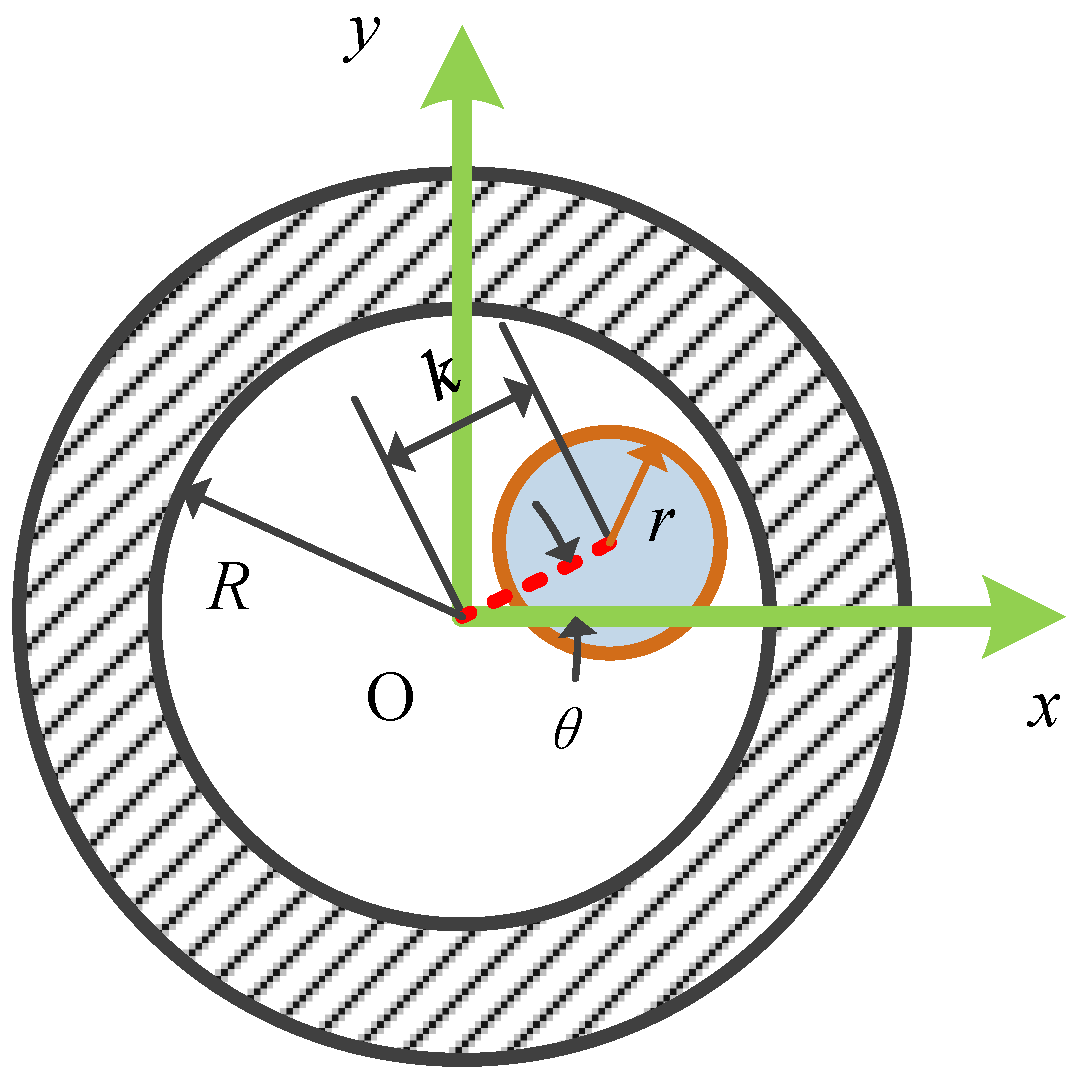
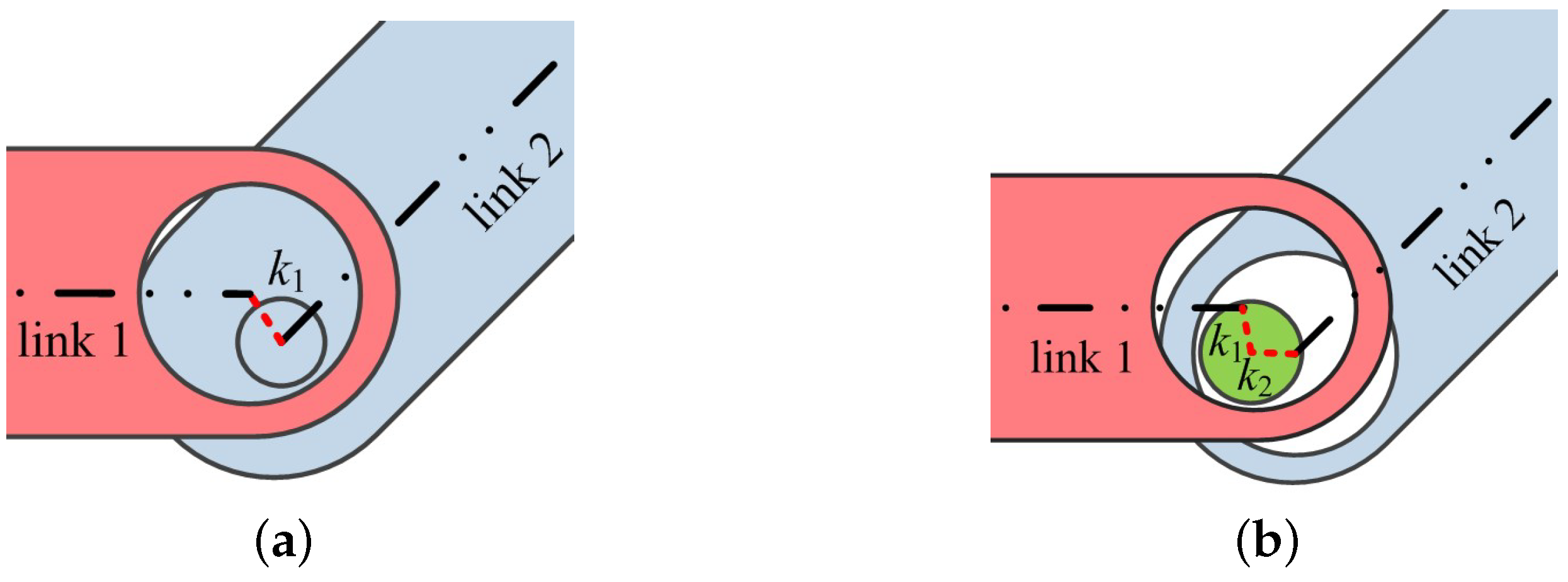
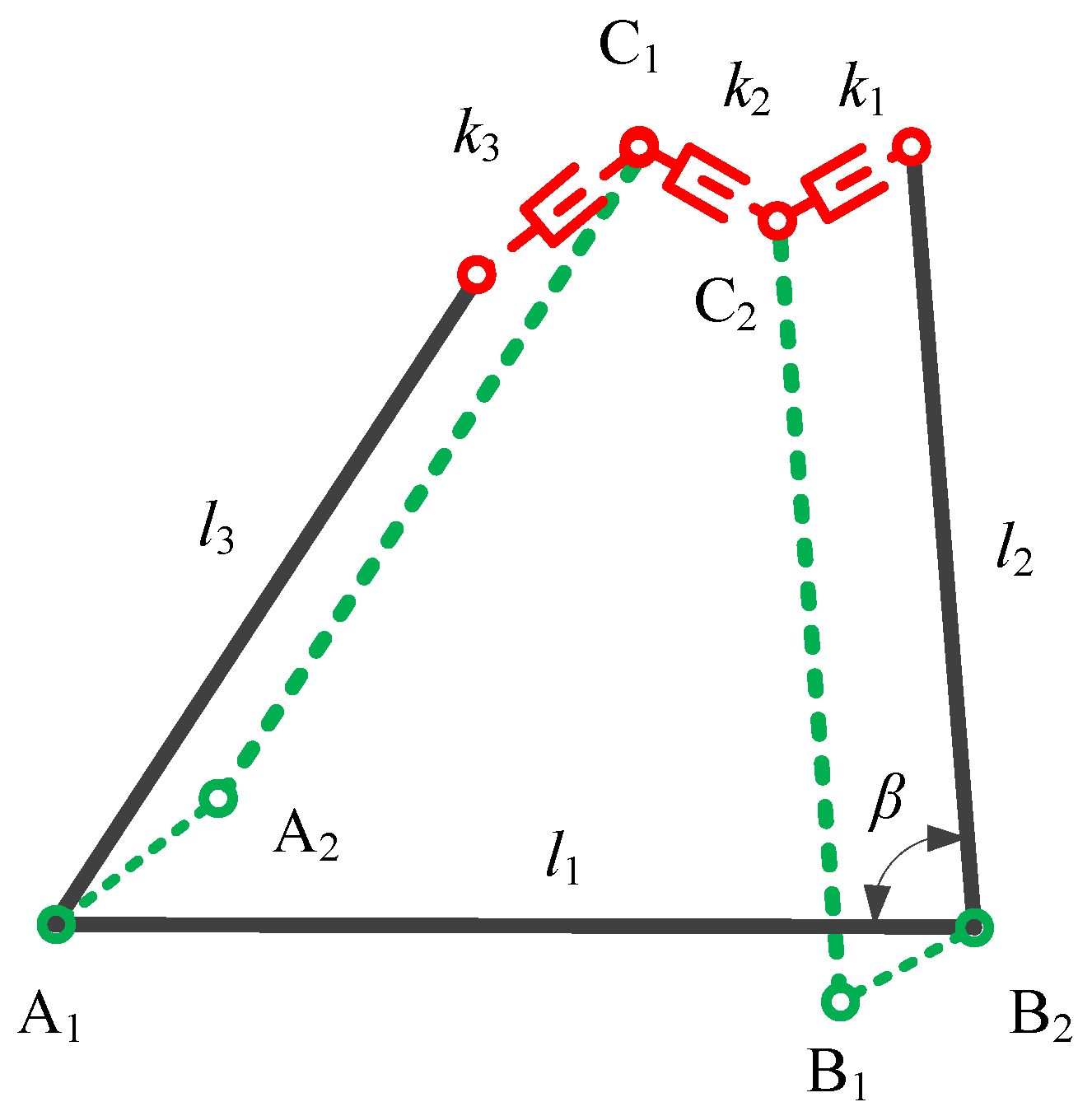
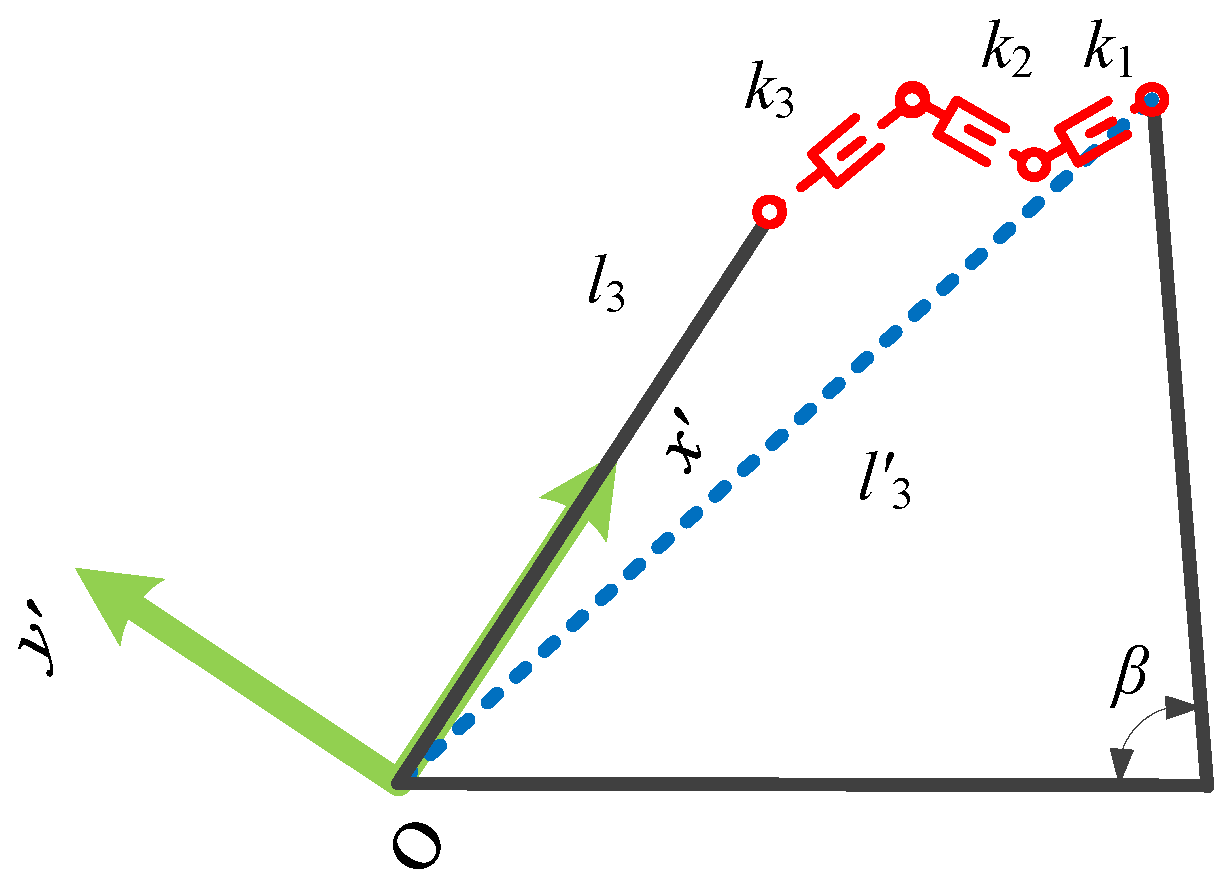
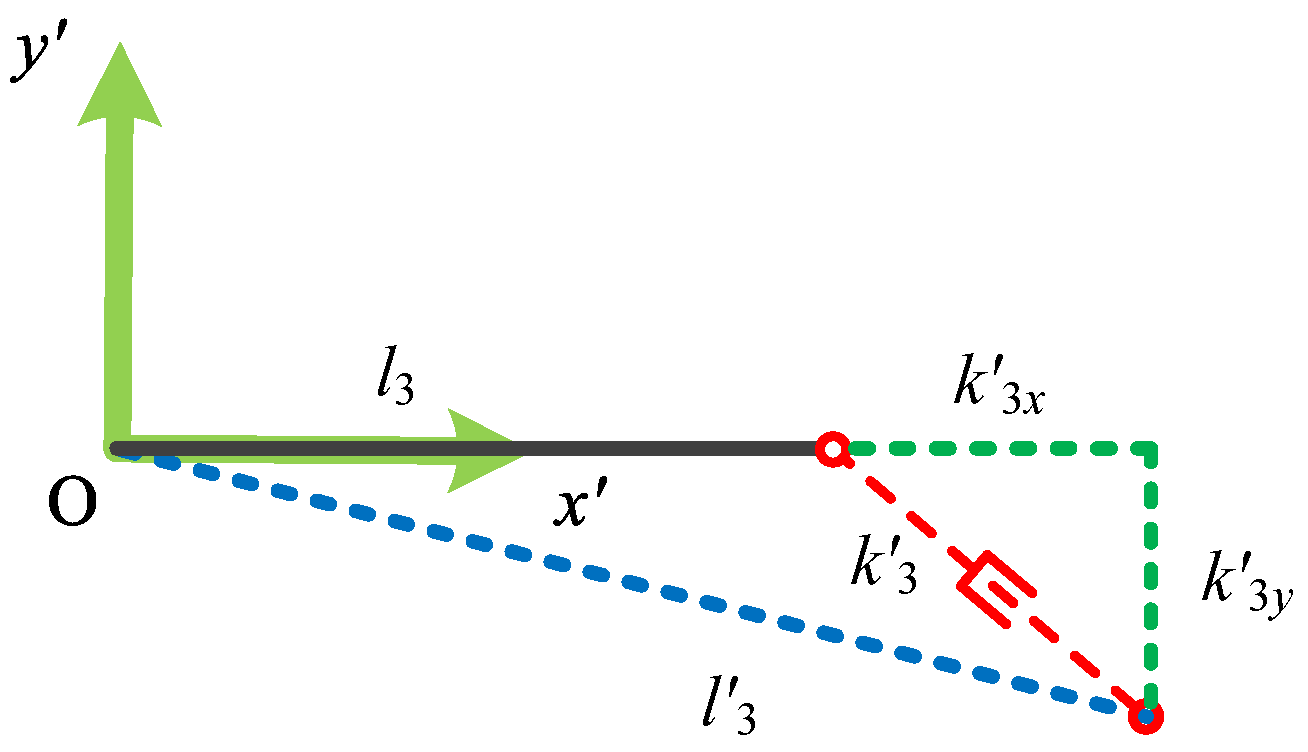
2.1. Modelling Method
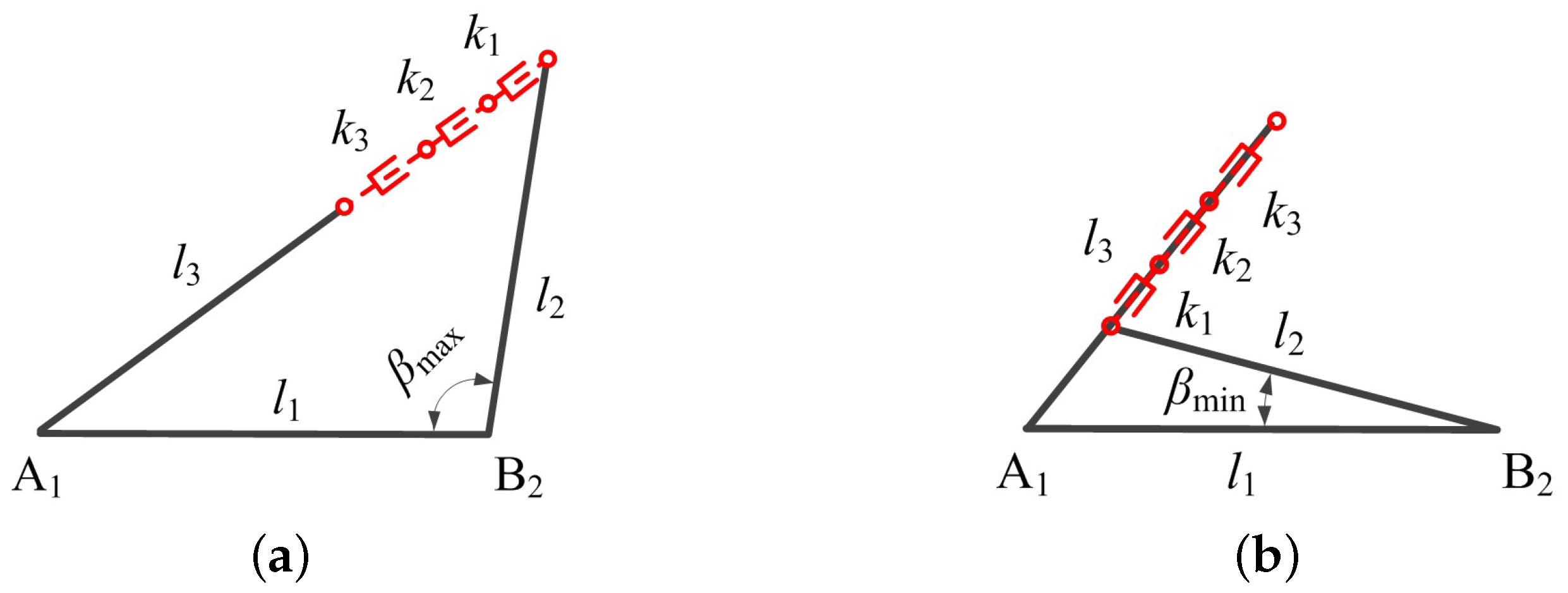
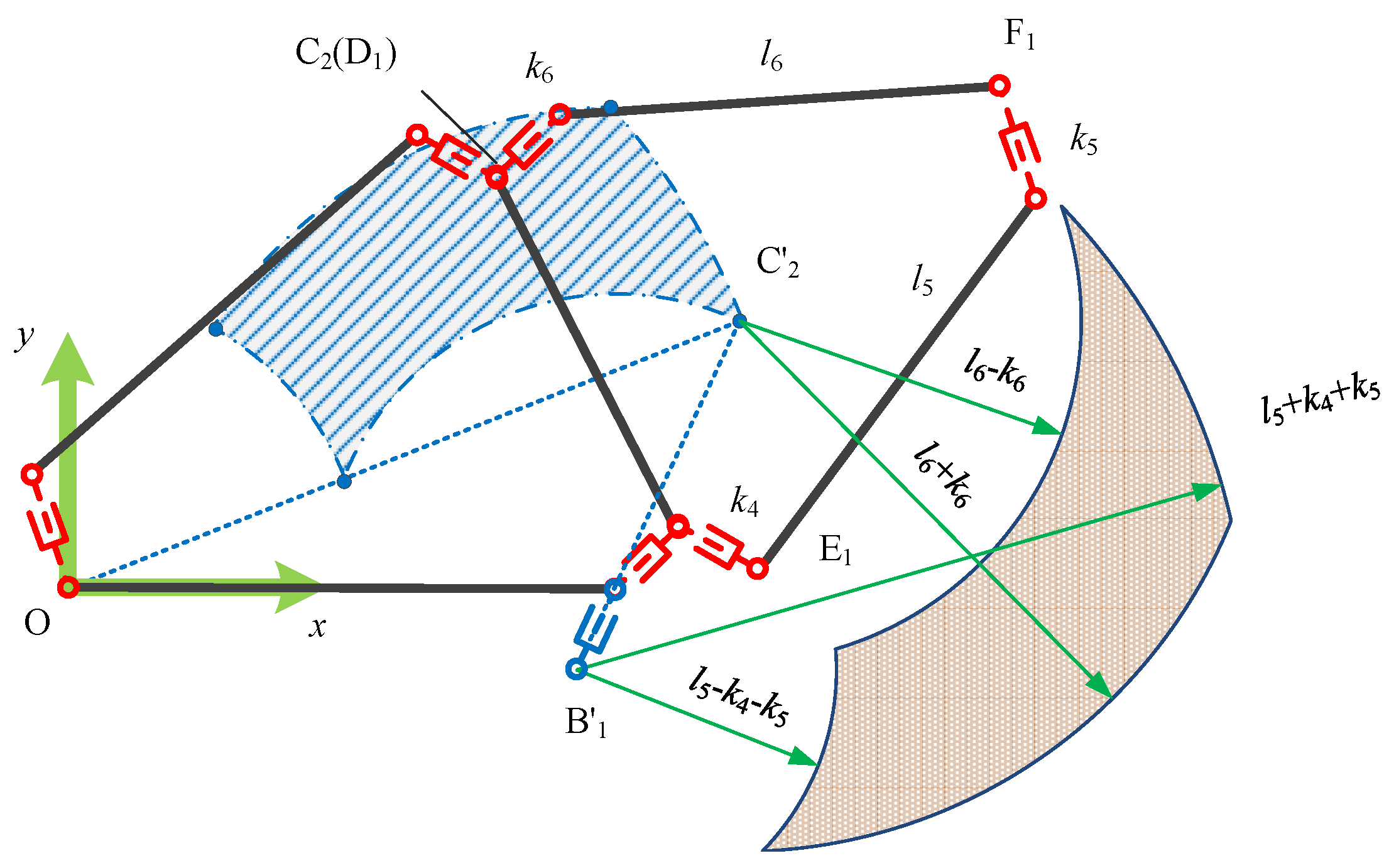
2.2. The Angular Error and Positional Error Boundaries
3. Error PDF Analysis and Simulation Method
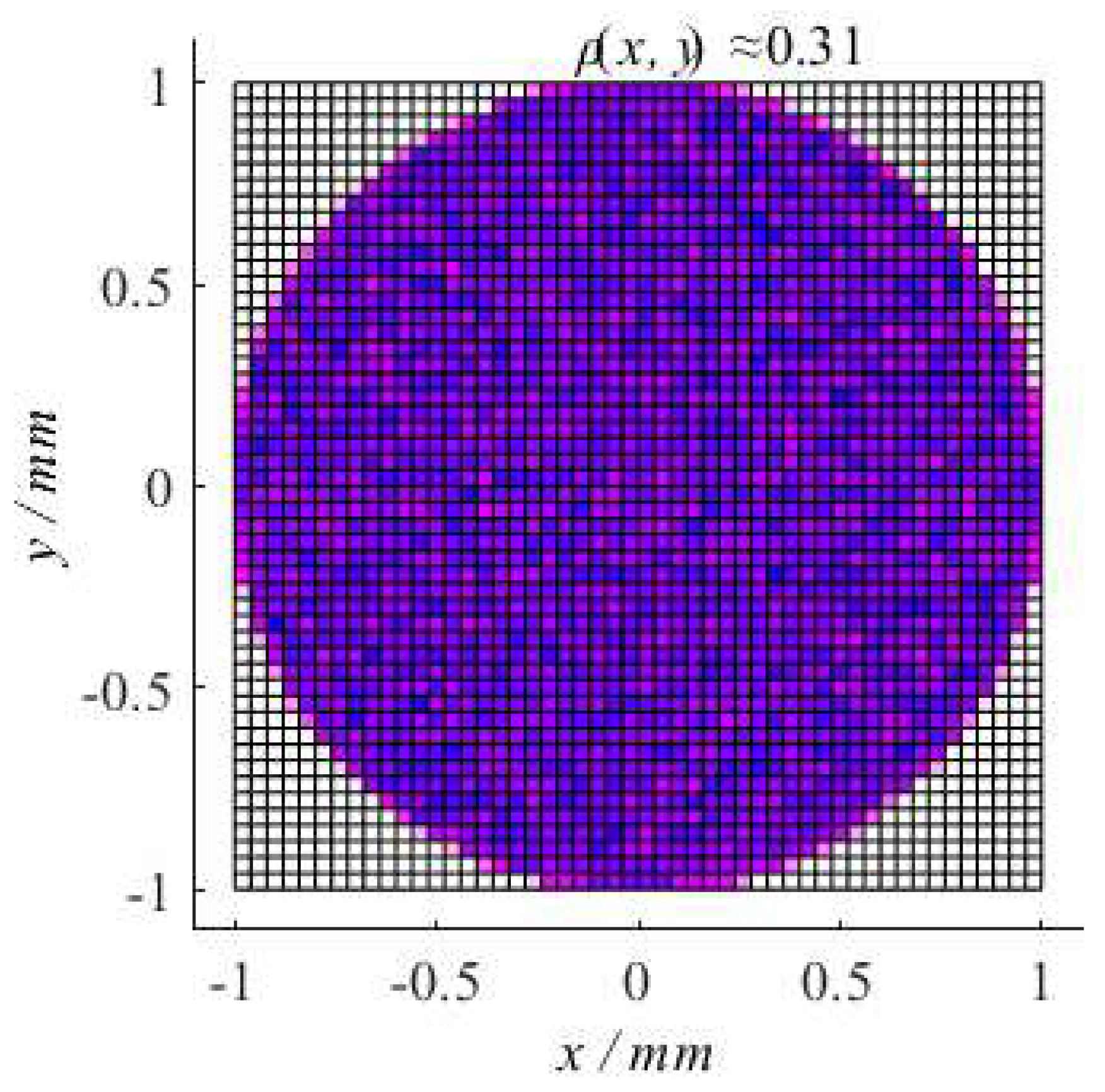
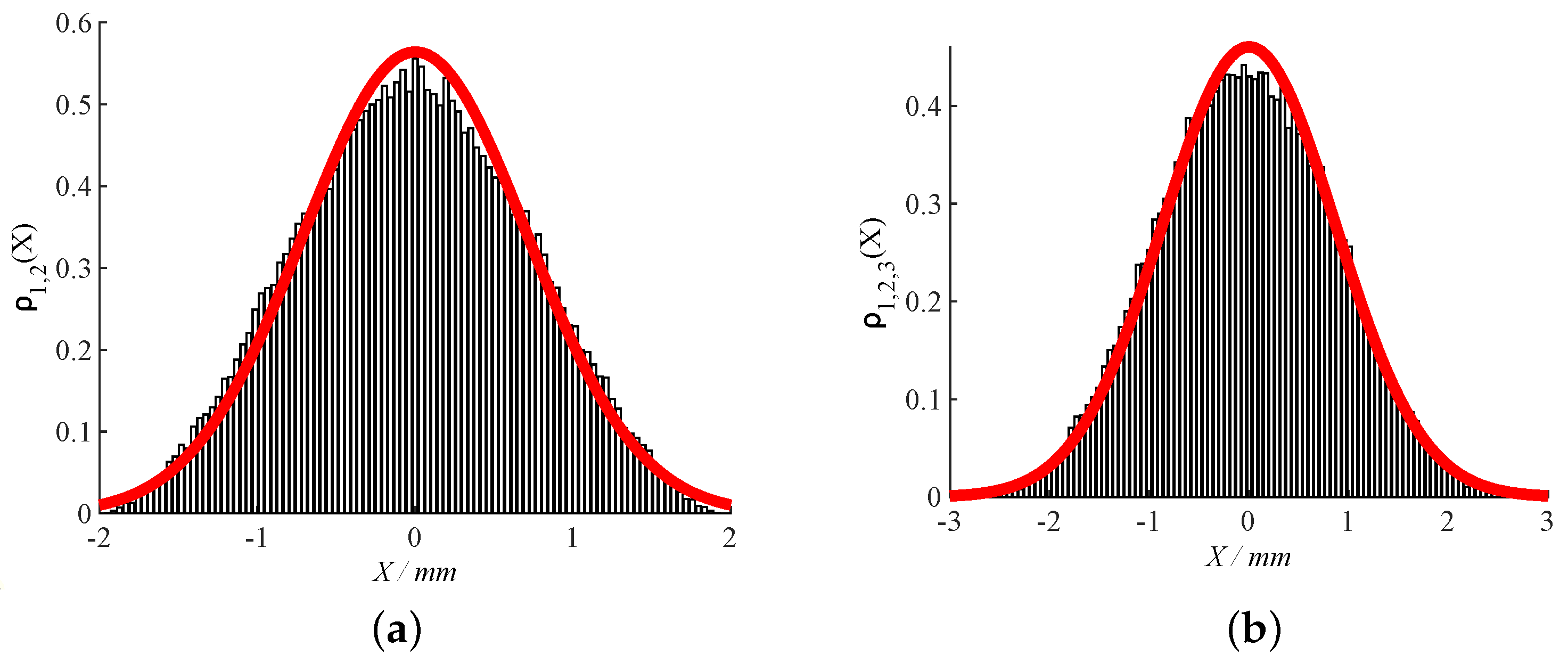
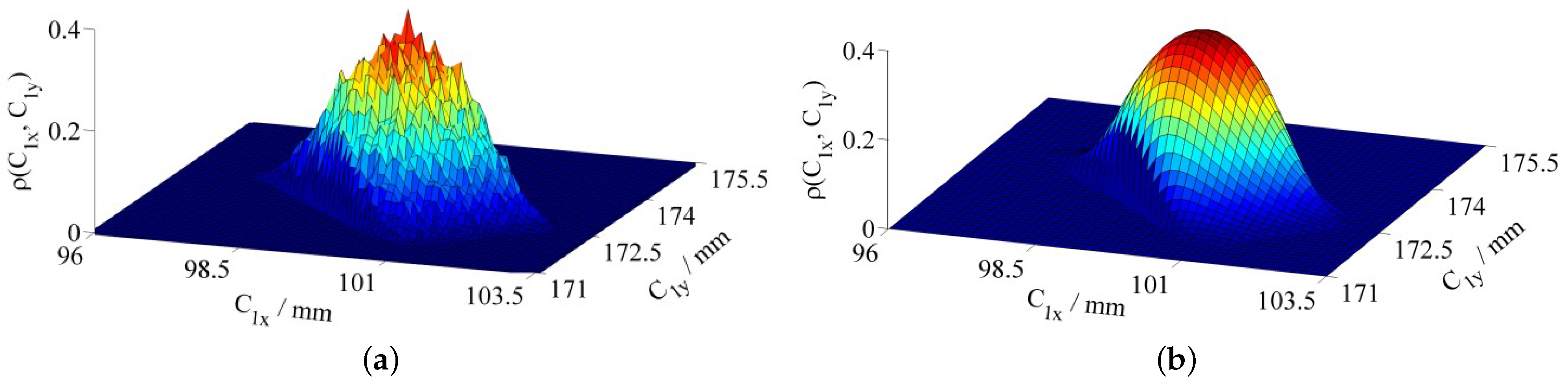
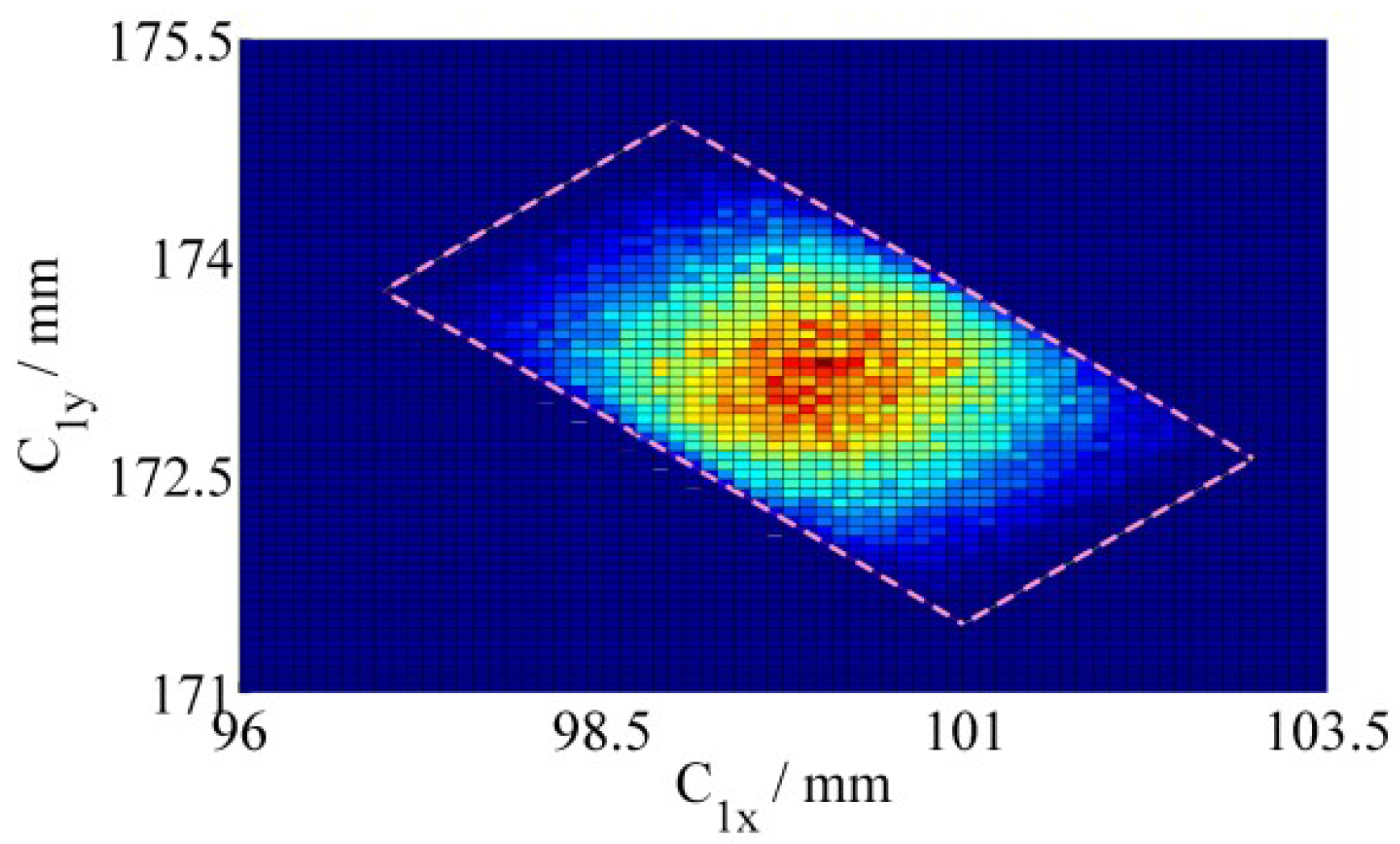
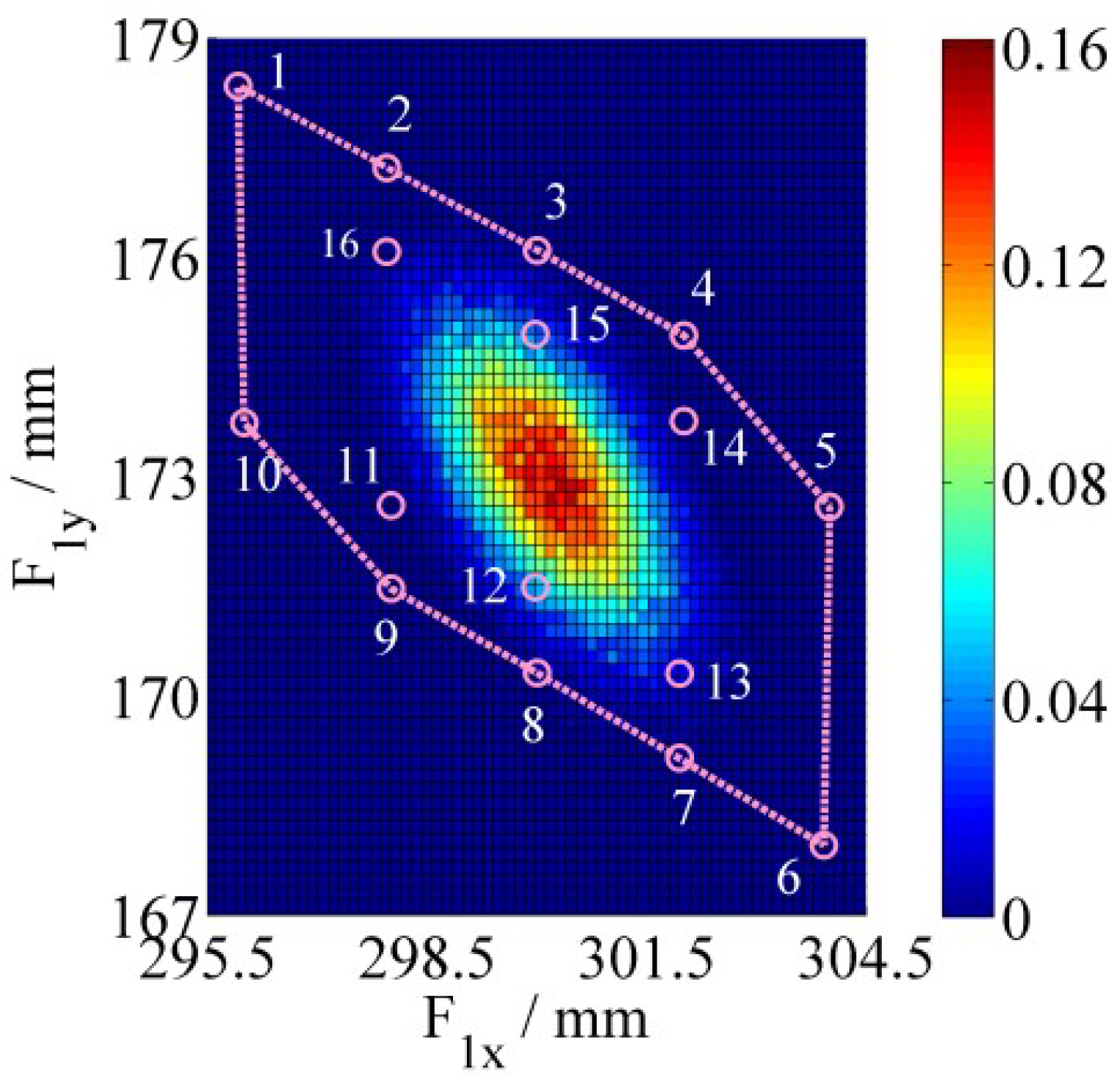
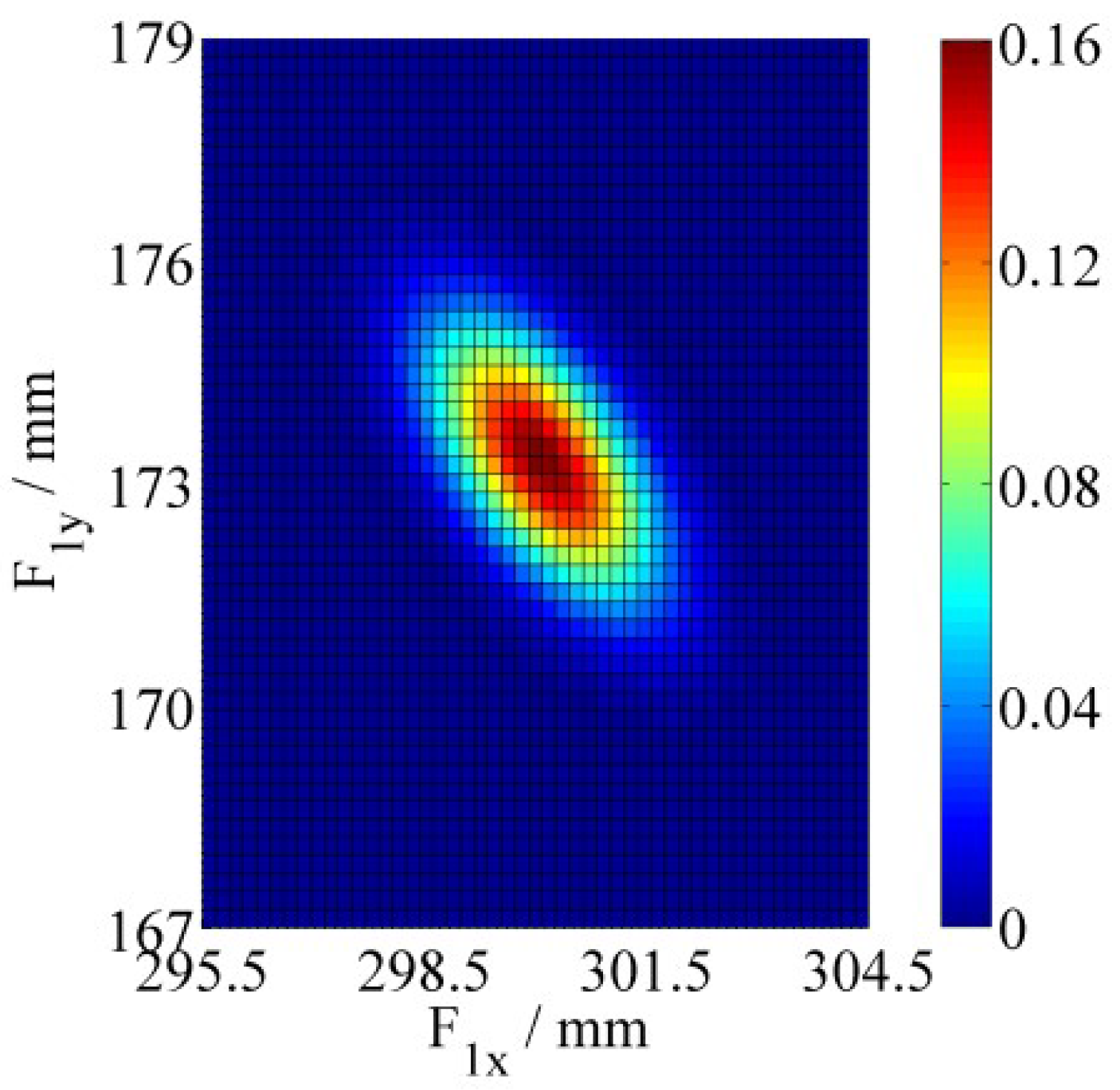
4. Numerical Simulations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pandey, M.D.; Zhang, X. System reliability analysis of the robotic manipulator with random joint clearances. Mech. Mach. Theory 2012, 58, 137–152. [Google Scholar] [CrossRef]
- Briot, S.; Bonev, I.A. Accuracy analysis of 3-DOF planar parallel robots. Mech. Mach. Theory 2008, 43, 445–458. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Song, W.J.; Kang, B.S. Stochastic approach to kinematic reliability of open-loop mechanism with dimensional tolerance. Appl. Math. Model. 2010, 34, 1225–1237. [Google Scholar] [CrossRef]
- Jawale, H.P.; Thorat, H.T. Investigation of Positional Error in Two Degree of Freedom Mechanism With Joint Clearance. J. Mech. Robot. 2012, 4, 011002. Available online: https://asmedigitalcollection.asme.org/mechanismsrobotics/article-pdf/4/1/011002/5522911/011002_1.pdf (accessed on 11 October 2021). [CrossRef]
- Jawale, H.P.; Thorat, H.T. Positional Error Estimation in Serial Link Manipulator Under Joint Clearances and Backlash. J. Mech. Robot. 2013, 5, 021003. Available online: https://asmedigitalcollection.asme.org/mechanismsrobotics/article-pdf/5/2/021003/6249812/jmr_5_2_021003.pdf (accessed on 11 October 2021). [CrossRef]
- Jawale, H.P.; Thorat, H.T. Comparison of Open Chain and Closed Chain Planar Two Degree of Freedom Manipulator for Positional Error. J. Mech. Robot. 2014, 6, 024501. Available online: https://asmedigitalcollection.asme.org/mechanismsrobotics/article-pdf/6/2/024501/6251721/jmr_006_02_024501.pdf (accessed on 11 October 2021). [CrossRef]
- Wang, J.; Zhang, J.; Du, X. Hybrid dimension reduction for mechanism reliability analysis with random joint clearances. Mech. Mach. Theory 2011, 46, 1396–1410. [Google Scholar] [CrossRef]
- Rao, S.; Bhatti, P. Probabilistic approach to manipulator kinematics and dynamics. Reliab. Eng. Syst. Saf. 2001, 72, 47–58. [Google Scholar] [CrossRef]
- Lai, X.; Duan, J. Probabilistic approach to mechanism reliability with multi-influencing factors. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2011, 225, 2991–2996. [Google Scholar] [CrossRef]
- Flores, P.; Lankarani, H.M. Dynamic Response of Multibody Systems with Multiple Clearance Joints. J. Comput. Nonlinear Dyn. 2012, 7, 031003. Available online: https://asmedigitalcollection.asme.org/computationalnonlinear/article-pdf/7/3/031003/5777007/031003_1.pdf (accessed on 11 October 2021). [CrossRef]
- Koshy, C.; Flores, P.; Lankarani, H. Study of the effect of contact force model on the dynamic response of mechanical systems with dry clearance joints: Computational and experimental approaches. Nonlinear Dyn. 2013, 73, 325–338. [Google Scholar] [CrossRef]
- Machado, M.; Costa, J.; Seabra, E.; Flores, P. The effect of the lubricated revolute joint parameters and hydrodynamic force models on the dynamic response of planar multibody systems. Nonlinear Dyn. 2012, 69, 635–654. [Google Scholar] [CrossRef] [Green Version]
- Tian, Q.; Sun, Y.; Liu, C.; Hu, H.; Flores, P. ElastoHydroDynamic lubricated cylindrical joints for rigid-flexible multibody dynamics. Comput. Struct. 2013, 114–115, 106–120. [Google Scholar] [CrossRef]
- Flores, P.; Lankarani, H. Spatial rigid-multibody systems with lubricated spherical clearance joints: Modeling and simulation. Nonlinear Dyn. 2010, 60, 99–114. [Google Scholar] [CrossRef]
- Muvengei, O.; Kihiu, J.; Ikua, B. Numerical study of parametric effects on the dynamic response of planar multi-body systems with differently located frictionless revolute clearance joints. Mech. Mach. Theory 2012, 53, 30–49. [Google Scholar] [CrossRef]
- Liu, C.; Tian, Q.; Hu, H. Dynamics and control of a spatial rigid-flexible multibody system with multiple cylindrical clearance joints. Mech. Mach. Theory 2012, 52, 106–129. [Google Scholar] [CrossRef]
- Erkaya, S.; Uzmay, I. Modeling and simulation of joint clearance effects on mechanisms having rigid and flexible links. Nonlinear Dyn. 2014, 28, 2979–2986. [Google Scholar] [CrossRef]
- Yao, X.; Guo, X.; Feng, Y.; Yu, C.; Ma, C. Dynamic analysis for planar beam with clearance joint. J. Sound Vib. 2015, 339, 324–341. [Google Scholar] [CrossRef]
- Yan, S.; Guo, P. Kinematic accuracy analysis of flexible mechanisms with uncertain link lengths and joint clearances. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2011, 225, 1973–1983. [Google Scholar] [CrossRef]
- Tsai, M.J.; Lai, T.H. Accuracy analysis of a multi-loop linkage with joint clearances. Mech. Mach. Theory 2008, 43, 1141–1157. [Google Scholar] [CrossRef]
- Tsai, M.J.; Lai, T.H. Kinematic sensitivity analysis of linkage with joint clearance based on transmission quality. Mech. Mach. Theory 2004, 39, 1189–1206. [Google Scholar] [CrossRef]
- Frisoli, A.; Solazzi, M.; Pellegrinetti, D.; Bergamasco, M. A new screw theory method for the estimation of position accuracy in spatial parallel manipulators with revolute joint clearances. Mech. Mach. Theory 2011, 46, 1929–1949. [Google Scholar] [CrossRef]
- Innocenti, C. Kinematic Clearance Sensitivity Analysis of Spatial Structures With Revolute Joints. J. Mech. Des. 1999, 124, 52–57. Available online: https://asmedigitalcollection.asme.org/mechanicaldesign/article-pdf/124/1/52/5697515/52_1.pdf (accessed on 11 October 2021). [CrossRef]
- Chebbi, A.H.; Affi, Z.; Romdhane, L. Prediction of the pose errors produced by joints clearance for a 3-UPU parallel robot. Mech. Mach. Theory 2009, 44, 1768–1783. [Google Scholar] [CrossRef]
- Venanzi, S.; Parenti-Castelli, V. A New Technique for Clearance Influence Analysis in Spatial Mechanisms. J. Mech. Des. 2004, 127, 446–455. Available online: https://asmedigitalcollection.asme.org/mechanicaldesign/article-pdf/127/3/446/5602606/446_1.pdf (accessed on 11 October 2021). [CrossRef]
- Ting, K.L.; Zhu, J.; Watkins, D. The effects of joint clearance on position and orientation deviation of linkages and manipulators. Mech. Mach. Theory 2000, 35, 391–401. [Google Scholar] [CrossRef]
- Wu, W.; Rao, S.S. Interval Approach for the Modeling of Tolerances and Clearances in Mechanism Analysis. J. Mech. Des. 2004, 126, 581–592. Available online: https://asmedigitalcollection.asme.org/mechanicaldesign/article-pdf/126/4/581/5488684/581_1.pdf (accessed on 11 October 2021). [CrossRef]
- Meng, J.; Zhang, D.; Zhang, T.; Wang, H.; Li, Z. Accuracy Analysis of General Parallel Manipulators with Joint Clearance. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Rome, Italy, 10–14 April 2007; pp. 889–894. [Google Scholar] [CrossRef]
- Wittwer, J.W.; Chase, K.W.; Howell, L.L. The direct linearization method applied to position error in kinematic linkages. Mech. Mach. Theory 2004, 39, 681–693. [Google Scholar] [CrossRef]
- Chen, G.; Wang, H.; Lin, Z. Generalized kinematic mapping of constrained plane motions and its application to the accuracy analysis of general planar parallel robots. Mech. Mach. Theory 2012, 50, 29–47. [Google Scholar] [CrossRef]
- Chen, G.; Wang, H.; Lin, Z. A unified approach to the accuracy analysis of planar parallel manipulators both with input uncertainties and joint clearance. Mech. Mach. Theory 2013, 64, 1–17. [Google Scholar] [CrossRef]
- Li, X.; Ding, X.; Chirikjian, G.S. Analysis of angular-error uncertainty in planar multiple-loop structures with joint clearances. Mech. Mach. Theory 2015, 91, 69–85. [Google Scholar] [CrossRef]
- Plitea, N.; Hesselbach, J.; Pisla, D.; Raatz, A.; Vaida, C.; Wrege, J.; Burisch, A. Innovative development of parallel robots and microrobots. Acta Teh. Napoc. Ser. Appl. Math. Mech. 2006, 49, 5–26. [Google Scholar]









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Y.; Li, J.; Li, X.; Yang, Y. Error Uncertainty Analysis in Planar Closed-Loop Structure with Joint Clearances. Metals 2021, 11, 1872. https://doi.org/10.3390/met11111872
Yu Y, Li J, Li X, Yang Y. Error Uncertainty Analysis in Planar Closed-Loop Structure with Joint Clearances. Metals. 2021; 11(11):1872. https://doi.org/10.3390/met11111872
Chicago/Turabian StyleYu, Yushu, Jinglin Li, Xin Li, and Yi Yang. 2021. "Error Uncertainty Analysis in Planar Closed-Loop Structure with Joint Clearances" Metals 11, no. 11: 1872. https://doi.org/10.3390/met11111872




