Hasse-Schmidt Derivations and the Hopf Algebra of Non-Commutative Symmetric Functions
1. Introduction
 of the underlying Abelian group of A such that
of the underlying Abelian group of A such that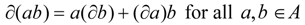
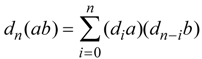
2. Hopf Algebras and Hopf Module Algebras
 ,
,  ,
,  ,
,  ,
,  such that (H,m,e) is an associative k-algebra with unit, (H,μ,ε) is a co-associative co-algebra with co-unit, μ and ε are algebra morphisms (or, equivalently, that m and e are co-algebra morphisms), and such that ι satisfies
such that (H,m,e) is an associative k-algebra with unit, (H,μ,ε) is a co-associative co-algebra with co-unit, μ and ε are algebra morphisms (or, equivalently, that m and e are co-algebra morphisms), and such that ι satisfies  ,
,  . The antipode ι will play no role in what follows. If there is no antipode (specified) one speaks of a bi-algebra. For a brief introduction to Hopf algebras (and co-algebras) with plenty of examples see Chapters 2 and 3 of [3].
. The antipode ι will play no role in what follows. If there is no antipode (specified) one speaks of a bi-algebra. For a brief introduction to Hopf algebras (and co-algebras) with plenty of examples see Chapters 2 and 3 of [3]. is called primitive if
is called primitive if  . These form a sub-k-module of H and form a Lie algebra under the commutator difference product
. These form a sub-k-module of H and form a Lie algebra under the commutator difference product  . I shall use Prim(H) to denote this k-Lie-algebra.
. I shall use Prim(H) to denote this k-Lie-algebra.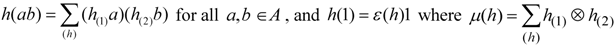
3. The Hopf Algebra NSymm of Non-Commutative Symmetric Functions
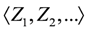 . The comultiplication and counit are given by
. The comultiplication and counit are given by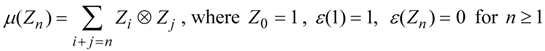
4. The Newton Primitives of NSymm
 by the recursion formulas
by the recursion formulas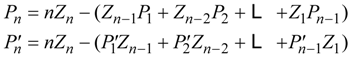
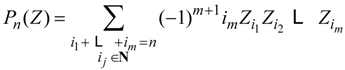
 . However, to do that one definitely needs to use rational numbers and not just integers [5]. For instance
. However, to do that one definitely needs to use rational numbers and not just integers [5]. For instance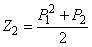
4.3. Proposition
 are primitive elements of the Hopf algebra NSymm.
are primitive elements of the Hopf algebra NSymm. an immediate corollary is the following main theorem from [2].
an immediate corollary is the following main theorem from [2].4.4. Theorem
 be a Hasse-Schmidt derivation on it. Then the δn defined recursively by
be a Hasse-Schmidt derivation on it. Then the δn defined recursively by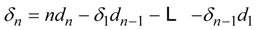
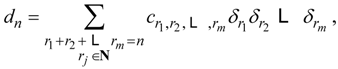
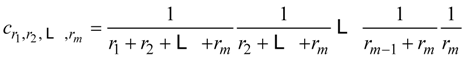
4.8. Comment
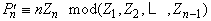
 are unique and so denominators are really needed.
are unique and so denominators are really needed.4.9. Comment and Example
 and Pn. One could hope that by using all of them, integral formulas for the Zn in terms of primitives would become possible. This is not the case. The full Lie algebra of primitives of NSymm was calculated in [6]. It readily follows from the description there that
and Pn. One could hope that by using all of them, integral formulas for the Zn in terms of primitives would become possible. This is not the case. The full Lie algebra of primitives of NSymm was calculated in [6]. It readily follows from the description there that  , the sub-algebra of NSymm generated by all primitive elements is strictly smaller than NSymm. In fact much smaller in a sense that is specified in locus citandi. Thus the theorem does not hold over the integers.
, the sub-algebra of NSymm generated by all primitive elements is strictly smaller than NSymm. In fact much smaller in a sense that is specified in locus citandi. Thus the theorem does not hold over the integers. . Now define an endomorphism dn of QSymm as the composed morphism
. Now define an endomorphism dn of QSymm as the composed morphism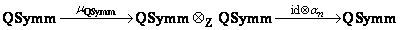
5. The Hopf Algebra LieHopf
 . However, this time the co-multiplication and co-unit are defined by
. However, this time the co-multiplication and co-unit are defined by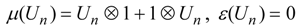
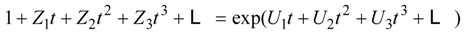

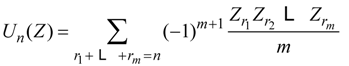
5.5. Theorem
 be a Hasse-Schmidt derivation on it. Then the
be a Hasse-Schmidt derivation on it. Then the  defined by
defined by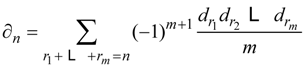
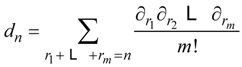
5.8. Comment
6. Conclusions
References and Notes
- Heerema, N. Higher derivations and automorphisms. Bull. American Math. Soc. 1970, 1212–1225. [Google Scholar] [CrossRef]
- Mirzavaziri, M. Characterization of higher derivations on algebras. Comm. Algebra 2010, 38, 981–987. [Google Scholar] [CrossRef]
- Hazewinkel, M.; Nadiya, G.; Vladimir, V.K. Algebras, Rings, and Modules:Lie Algebras and Hopf Algebras.; American Mathematicial Society: Providence, RI, USA, 2010. [Google Scholar]
- Gel’fand, I.M.; Daniel, K.; Alain, L.; Bernard, L.; Vladimir, S.R.; Jean-Yves, T. Noncommutative symmetric functions. Adv. Math. 1995, 112, 218–348. [Google Scholar]
- This is an instance where the noncommutative formulas are more elegant and also easier to prove than their commutative analogues. In the commutative case there are all kinds of multiplicities that mess things up.
- Hazewinkel, M. The primitives of the Hopf algebra of noncommutative symmetric functions. São Paulo J. Math. Sci. 2007, 1, 175–203. [Google Scholar]
- Hazewinkel, M. The Leibniz Hopf Algebra and Lyndon Words; CWI: Amsterdam, The Netherlands, 1996. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Hazewinkel, M. Hasse-Schmidt Derivations and the Hopf Algebra of Non-Commutative Symmetric Functions. Axioms 2012, 1, 149-154. https://doi.org/10.3390/axioms1020149
Hazewinkel M. Hasse-Schmidt Derivations and the Hopf Algebra of Non-Commutative Symmetric Functions. Axioms. 2012; 1(2):149-154. https://doi.org/10.3390/axioms1020149
Chicago/Turabian StyleHazewinkel, Michiel. 2012. "Hasse-Schmidt Derivations and the Hopf Algebra of Non-Commutative Symmetric Functions" Axioms 1, no. 2: 149-154. https://doi.org/10.3390/axioms1020149
APA StyleHazewinkel, M. (2012). Hasse-Schmidt Derivations and the Hopf Algebra of Non-Commutative Symmetric Functions. Axioms, 1(2), 149-154. https://doi.org/10.3390/axioms1020149



