Spacetime Metrics from Gauge Potentials
Abstract
: I present an approach to gravity in which the spacetime metric is constructed from a non-Abelian gauge potential with values in the Lie algebra of the group U(2) (or the Lie algebra of quaternions). If the curvature of this potential vanishes, the metric reduces to a canonical curved background form reminiscent of the Friedmann S3 cosmological metric.1. Introduction
The observational evidence in favor of Einstein's general theory of relativity has clarified that the spacetime manifold is not flat, and hence that it can be approximated by the flat Minkowski spacetime only over limited regions. Quantum Field Theory, and in particular the perturbative approach through the Feynman's integral, has shown the importance of expanding near a “classical” background configuration. Although we do not have at our disposal a quantum theory of gravity, it would be natural to take a background configuration which approximates as much as possible the homogeneous curved background that is expected to take place over cosmological scales accordingly to the cosmological principle. Therefore, it is somewhat surprising that most classical approaches to quantum gravity start from a perturbation of Minkowski's metric in the form gμv = ημv + hμv. This approach is ill defined in general unless the manifold is asymptotically flat. Indeed, the expansion depends on the chosen coordinate system, a fact which is at odds with the principle of general covariance.
Expanding over the flat metric is like Taylor expanding a function by taking the first linear approximation near a point. It is clear that the approximation cannot be good far from the point and that no firm global conclusion can be drawn from similar approaches. A good global expansion should be performed in a different way, taking into account the domain of definition of the function. So, a function defined over an interval would be better approximated with a Fourier series than with a Taylor expansion. Despite of these simple analogies, much research has been devoted to quantum gravity by means of expansions of the form g = η + h, possibly because of the lack of alternatives.
Actually, some years ago [1] I proposed a gauge approach to gravity that solves this problem in a quite simple way and which, I believe, deserves to be better known.
To start with let us observe that general relativity seems to privilege in its very formalism the flat background. Indeed, the Riemann curvature measures the extent by which the spacetime is far from flat, namely far from the background
2. Some Notations from Gauge Theory
Gauge theories were axiomatized in the fifties by Ehresmann [2] as connections over principal bundles. Since I need to fix the notation, here I shortly review that setting. A principal bundle is given by a differentiable manifold (the bundle) P, a differentiable manifold (the base) M, a projection
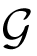 be the Lie algebra of G, and let τa be a base of generators
be the Lie algebra of G, and let τa be a base of generators
A connection over P is a 1-form ω : P →
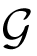
- (a)
ω(X*) = X X ∈
- (b)
The tangent space at p is split into the sum of two subspaces: the vertical space, that is the ker of π, and the horizontal space, that is the ker of ω
3. The Background Metric
We are used to define a manifold through charts ϕ : U → ℝ4, U ⊂ M, taking values on ℝ4. Let us instead take them with value in a four-dimensional canonical manifold with enough structure to admit some natural metric. We shall use a matrix Lie group G, but we do not really want to give any special role to the identity of G. We shall see later how to solve this problem. The metric g has to be constructed as a small departure from that naturally present in G and which plays the role of background metric.
We take as background metric the expression
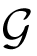 , which might depend on g ∈ G. The Maurer-Cartan form has the effect of mapping an element υ ∈ TgG to the Lie algebra element whose fundamental vector field at g is υ.
, which might depend on g ∈ G. The Maurer-Cartan form has the effect of mapping an element υ ∈ TgG to the Lie algebra element whose fundamental vector field at g is υ.Of course, we demand that gB be a Lorentzian metric in a four-dimensional Lie group, and furthermore we want it to represent an isotropic cosmological background, thus G has to contain the SO(3) subgroup. We are lead to the Abelian group of translations T4 or to the group U(2) (or equivalently the group of quaternions since it shares with U(2) the Lie algebra). In what follows we shall only consider the latter group, the case of the Abelian translation group being simpler.
Thus let us consider the group U(2). Every matrix of this group reads u = eiλr with 0 ≤ λ ≤ π where r ∈ SU(2) (while a quaternion reads eλr, λ ∈ ℝ)
More specifically, let σ0 = I, and let σi, i = 1, 2, 3, be the Pauli matrices. Let τμ = iσμ be a base for the Lie algebra of U(2). Let us parametrize ϕ ∈ U(2) through
These calculations, first presented in [1], show that the Friedmann metric appears rather naturally from the study of the U(2) group. Of course, since this argument depends only on the Lie algebra rather that the group structure, it can be repeated for the group of quaternions [3].
4. Perturbing the Background
In this section we shall suppose that Ig does not depend on g, namely that α and β are constants, this means that we ignore the time dependence of the cosmological background.
We mentioned that we wish to use charts ϕ : U → G, U ⊂ M, with value in a group G but that we do not want to assign to the identity of G any special role. To that end, let us assume for simplicity that M is simply connected, and let us introduce a trivial bundle P endowed with a flat connection ω̃. The connection being flat is integrable, thus given an horizontal section σ̃: M → P, and parametrizing every point of P through p(x, g) = σ̃(x)g, we obtain a splitting P ∼ M × G. In this way the identity of G does not play any special role since it refers to different points of P depending on the choice of section σ̃.
A second section σ: M → P is now related to the former by σ(x)ϕ−1(x) = σ̃(x), where ϕ: M → G is the chart we were looking for. In order to be interpreted as a chart, ϕ has to be injective. The idea is to define the metric
We observe that has 16 components, namely the same number of components as the metric. However, we have an additional degree of freedom given by ϕ(x). This function can be completely removed using the invertibility of this map, namely using the coordinates ϕμ on the Lie group to parametrize M. In this way the metric reads
One can further ask whether the Einstein equations can be rephrased as dynamical equations for the potential A. The answer is affirmative and passes through the vierbein reformulation of the Einstein-Hilbert Lagrangian.
We recall that a tetrad field (vierbein) , is a set of four vector fields ea such that . The inverse is defined through . The Einstein Lagrangian can be rewritten
In order to obtain a dynamics for A we select a base τa for the Lie algebra such that
In the Abelian case T4 (not in the U(2) case) the Lagrangian can also be expressed in terms of the curvature (7). Indeed, since the curvature becomes coincident with the tensors entering the above expression of the Lagrangian (however, observe that the potential still enters the metric and the vierbeins which are used to raise the indices of the curvature). The final expression is quadratic in the curvature F and is related to the teleparallel approach to general relativity [4–7]. Issues related to the renormalizability of the dynamics determined by (26) have yet to be fully studied.
The OT gauge approach has been used to infer the dynamics and is complementary to the internal coordinates approach mentioned above. Indeed, while the latter allows us to interpret the map ϕ : U → G, U ⊂ M, as a chart with values in G, the OT frame approach sends ϕ to the identity, so in the new gauge the non-injective map ϕ cannot be interpreted as a chart. Thus, after having developed the dynamics in the OT gauge we would have to make a last gauge transformation to reformulate it in internal coordinates.
Acknowledgments
This work has been partially supported by GNFM of INDAM.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Minguzzi, E. Gauge invariance in teleparallel gravity theories: A solution to the background structure problem. Phys. Rev. D 2002, 65, 084048. [Google Scholar] [CrossRef]
- Kobayashi, S.; Nomizu, K. Foundations of Differential Geometry. In Interscience Tracts in Pure and Applied Mathematics; Interscience Publishers: New York, NY, USA, 1963; Volume I. [Google Scholar]
- Trifonov, V. Natural Geometry of Nonzero Quaternions. Int. J. Theor. Phys. 2007, 46, 251–257. [Google Scholar]
- Cho, Y.M. Einstein Lagrangian as the translational Yang-Mills Lagrangian. Phys. Rev. D 1976, 14, 2521–2525. [Google Scholar]
- Hayashi, K.; Shirafuji, T. New general relativity. Phys. Rev. D 1979, 19, 3524–3553. [Google Scholar]
- Rodrigues, W.A., Jr.; de Souza, Q.A.G.; da Rocha, R. Conservation Laws on Riemann-Cartan, Lorentzian and Teleparallel Spacetimes. Bull. Soc. Sci. Lett. Lodz. Ser. Rech. Deform. 2007, 52. [Google Scholar]
- Aldrovandi, R.; Pereira, J.G. Teleparallel Gravity. In Fundamental Theories of Physics; Springer: Berlin, Germany, 2013; Volume 173. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Minguzzi, E. Spacetime Metrics from Gauge Potentials. Symmetry 2014, 6, 164-170. https://doi.org/10.3390/sym6020164
Minguzzi E. Spacetime Metrics from Gauge Potentials. Symmetry. 2014; 6(2):164-170. https://doi.org/10.3390/sym6020164
Chicago/Turabian StyleMinguzzi, Ettore. 2014. "Spacetime Metrics from Gauge Potentials" Symmetry 6, no. 2: 164-170. https://doi.org/10.3390/sym6020164



