Symmetry-Breaking in a Rate Model for a Biped Locomotion Central Pattern Generator
Abstract
:1. Introduction
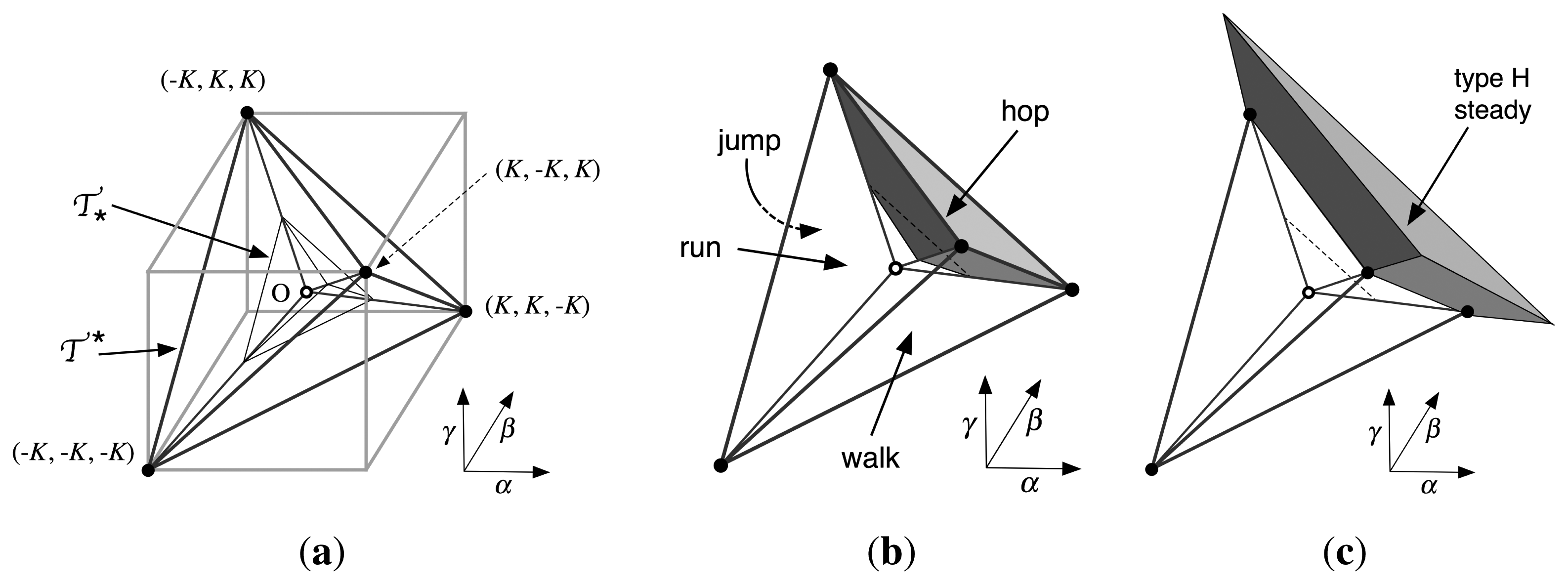
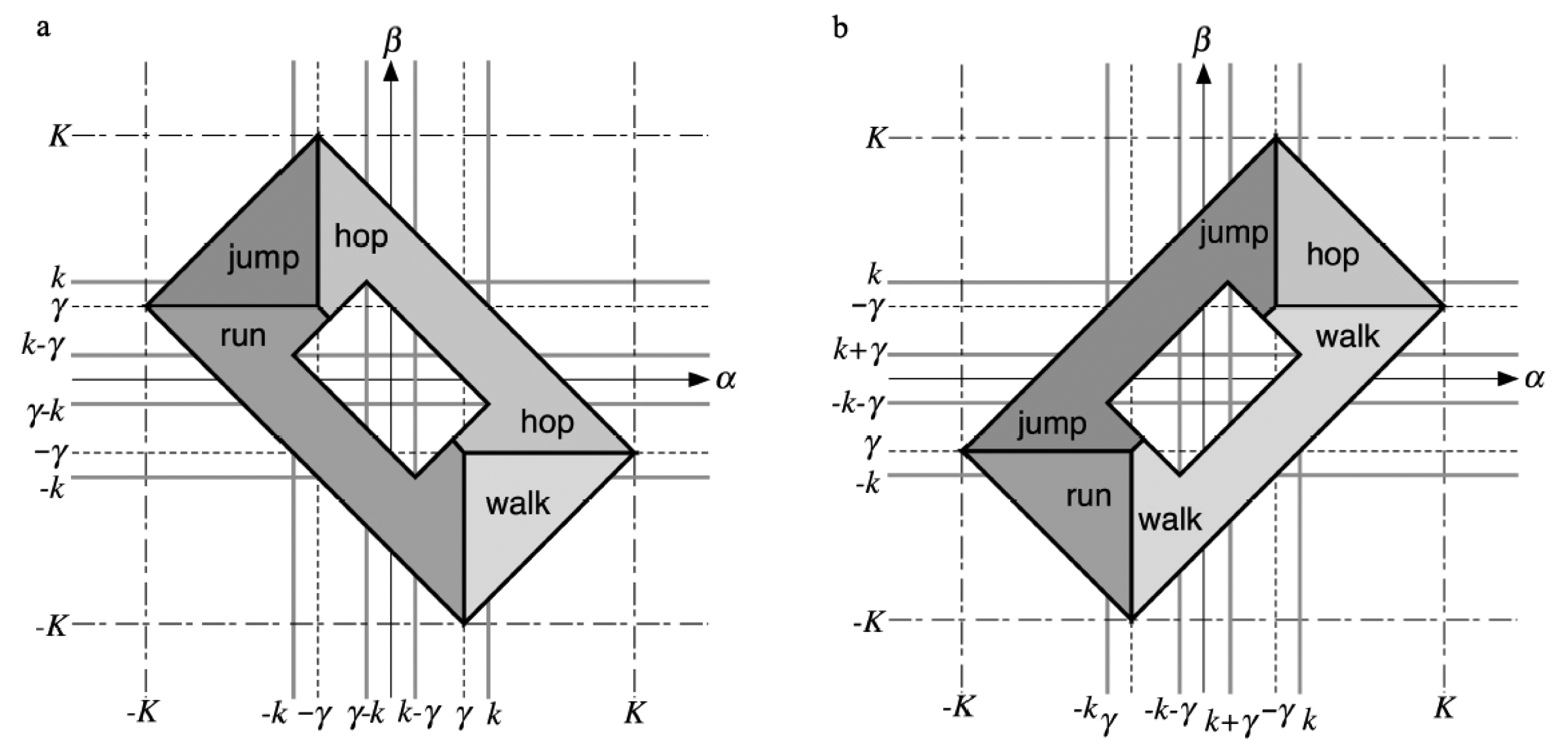
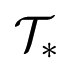 in a larger tetrahedron
in a larger tetrahedron
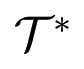 , whose vertices are indicated on the figure: here K is a constant, defined in Theorem (23). The inner tetrahedron
, whose vertices are indicated on the figure: here K is a constant, defined in Theorem (23). The inner tetrahedron
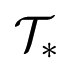 is similar, with K replaced by k, also defined in Theorem (23).
is similar, with K replaced by k, also defined in Theorem (23).1.1. Structure of the Paper
 that acts on the set of eigenvalues of the connection matrix in Section 11. Here we prove that
that acts on the set of eigenvalues of the connection matrix in Section 11. Here we prove that
 also acts on the set of regions defining the first local bifurcation. The group
also acts on the set of regions defining the first local bifurcation. The group
 is not a symmetry group or parameter symmetry group of the rate equations in the sense of equivariance [18]. We also describe some general representation-theoretic reasons that explain this structure. We then prove the main theorem in Section 12.
is not a symmetry group or parameter symmetry group of the rate equations in the sense of equivariance [18]. We also describe some general representation-theoretic reasons that explain this structure. We then prove the main theorem in Section 12.2. Gain Functions and Rate Models
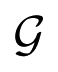 . This has a sigmoid shape, and ideally we take
. This has a sigmoid shape, and ideally we take
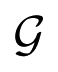 (x) = 0 for x < 0. In practice, it is common to assume slightly less:
(x) = 0 for x < 0. In practice, it is common to assume slightly less:
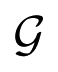 (x) ≪ 1 for x < 0. A node j is then considered to be quiescent if it is in equilibrium at a small value of
.
(x) ≪ 1 for x < 0. A node j is then considered to be quiescent if it is in equilibrium at a small value of
.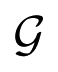 in Wilson [31] was a ratio of two quadratic terms. However, throughout this paper we follow later practice and assume a gain function of sigmoid form
in Wilson [31] was a ratio of two quadratic terms. However, throughout this paper we follow later practice and assume a gain function of sigmoid form
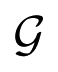 (x) is very small when x < 0. A standard choice in the literature is a = 0.8,b = 7.2, c = 0.9. For simplicity, we use a = 1, b = 8, c = 1 in simulations. In our analysis, a, b, c are arbitrary positive constants. We expect similar results to apply for any reasonable sigmoidal gain function, but proving this could be difficult, and some fine detail would be likely to change.
(x) is very small when x < 0. A standard choice in the literature is a = 0.8,b = 7.2, c = 0.9. For simplicity, we use a = 1, b = 8, c = 1 in simulations. In our analysis, a, b, c are arbitrary positive constants. We expect similar results to apply for any reasonable sigmoidal gain function, but proving this could be difficult, and some fine detail would be likely to change.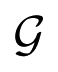 has an inverse
has an inverse
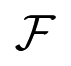 =
=
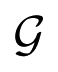 −1 given by
−1 given by
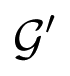 denote the derivative of
denote the derivative of
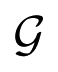 . There is an algebraic relation between
. There is an algebraic relation between
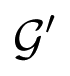 and
and
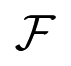 , which we exploit throughout this paper to obtain explicit formulas:
, which we exploit throughout this paper to obtain explicit formulas:
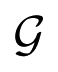 to a vector.
to a vector.3. The CPG Network
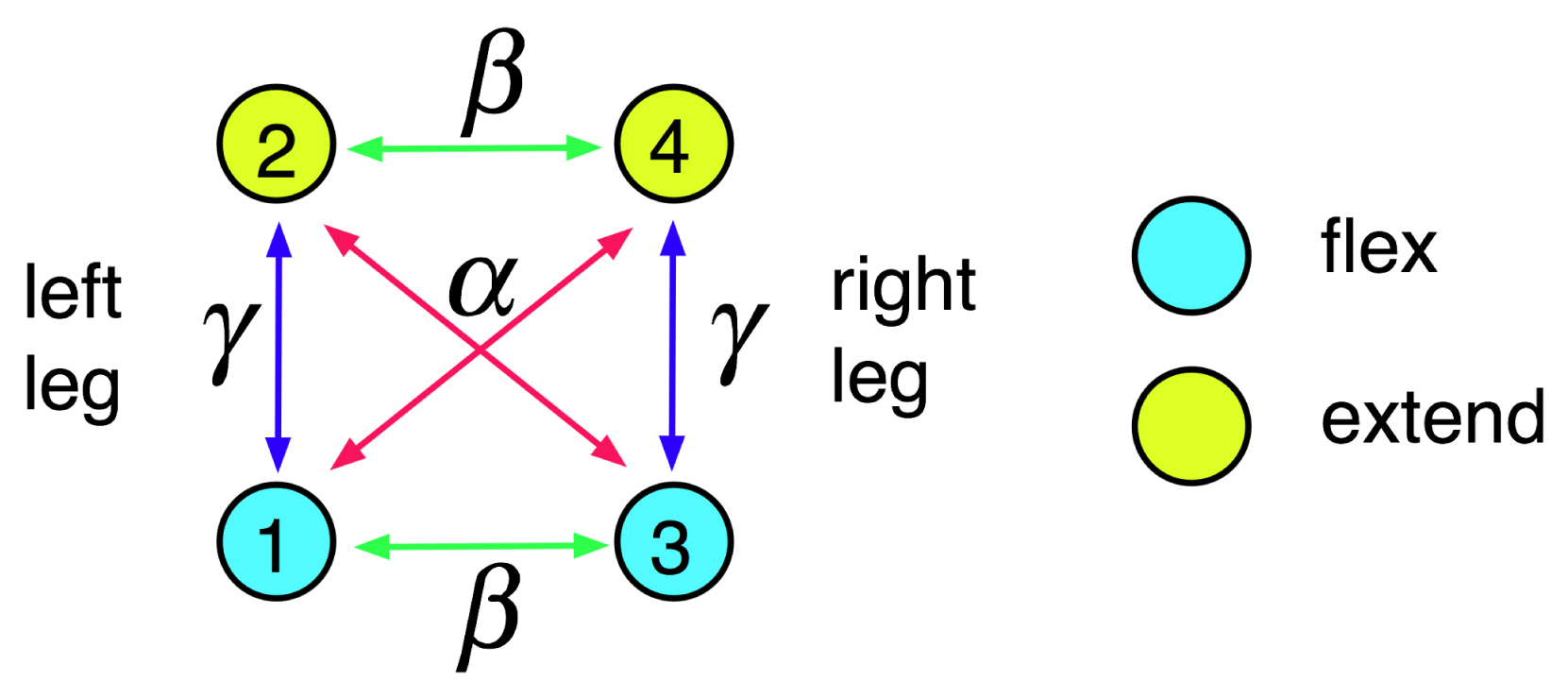
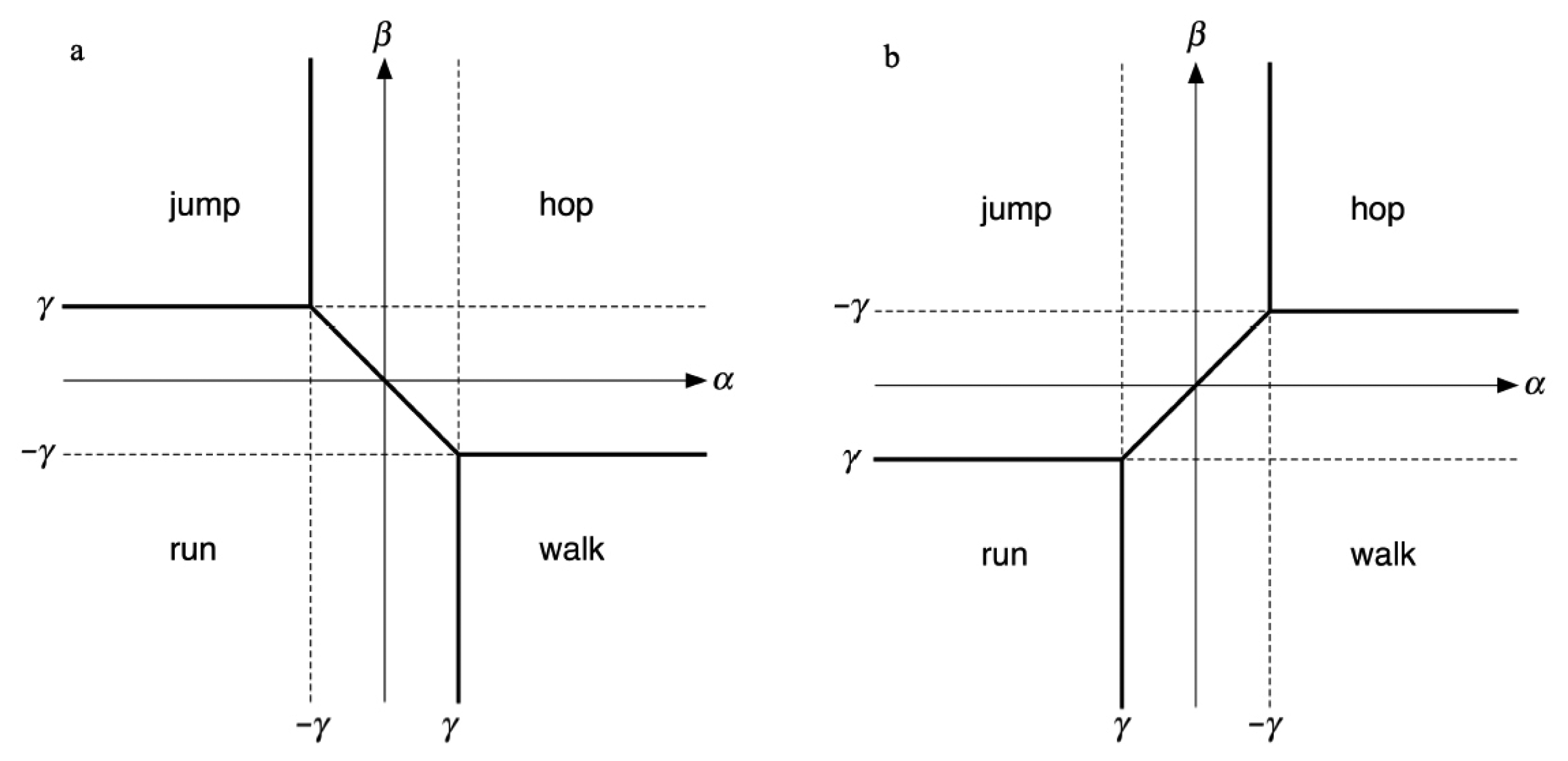
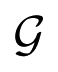 . This leads to the following proposition, which is valid for rate equations on any homogeneous network, that is, one on which every node has the same number of input arrows of each type (connection strength). For example, in Figure 1 every node has one input arrow of type α, one of type β, and one of type γ. For rate models, it is convenient to employ a slightly more general condition: a network is homogeneous if and only if each row of the connection matrix A has the same sum r. That is,
. This leads to the following proposition, which is valid for rate equations on any homogeneous network, that is, one on which every node has the same number of input arrows of each type (connection strength). For example, in Figure 1 every node has one input arrow of type α, one of type β, and one of type γ. For rate models, it is convenient to employ a slightly more general condition: a network is homogeneous if and only if each row of the connection matrix A has the same sum r. That is,
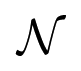 is homogeneous, with connection matrix A defining a rate model, so every row of A has the same sum r. Then the rate Equation (11) are invariant under the parameter symmetry η for which
is homogeneous, with connection matrix A defining a rate model, so every row of A has the same sum r. Then the rate Equation (11) are invariant under the parameter symmetry η for which| α = | strength of diagonal connection |
| γ = | strength of medial connection |
| β = | strength of lateral connection |
| ε = | fast/slow dynamic timescale |
| g = | strength of reduction of activity variable by fatigue variable |
| I = | input |
4. Synchronous Steady States
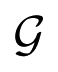 is monotonic strictly increasing and always positive. There is a unique inflection point at
and the slope at that point is
. The curve is asymptotic to 0 as x → −∞ and to a as x → +∞. See Figure 4 for the case a = 1, b = 8, c = 1.
is monotonic strictly increasing and always positive. There is a unique inflection point at
and the slope at that point is
. The curve is asymptotic to 0 as x → −∞ and to a as x → +∞. See Figure 4 for the case a = 1, b = 8, c = 1.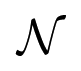 be a homogeneous network whose connection matrix A has all row-sums equal to r. Let
be a homogeneous network whose connection matrix A has all row-sums equal to r. Let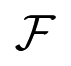 to deduce Equation (12).
to deduce Equation (12).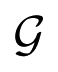 , hence of
, hence of
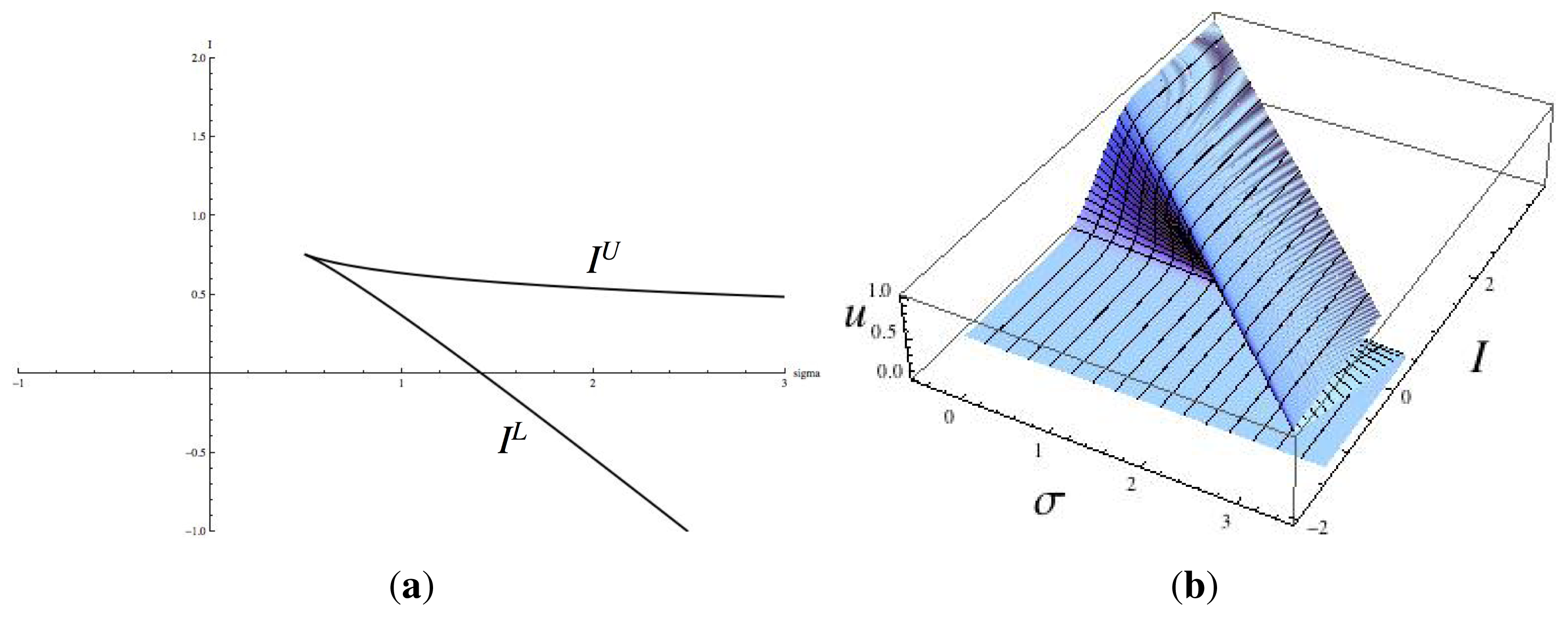
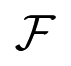 , implies that whenever σ ≤ c/2 there is a unique solution for all I. If σ > c/2 there exist IL, IU depending on σ for which there are three solutions when IL < I < IU , and two solutions (one of multiplicity 2) when I = IL, IU. See Figure 5 when a = 1, b = 8, c = 1.
, implies that whenever σ ≤ c/2 there is a unique solution for all I. If σ > c/2 there exist IL, IU depending on σ for which there are three solutions when IL < I < IU , and two solutions (one of multiplicity 2) when I = IL, IU. See Figure 5 when a = 1, b = 8, c = 1.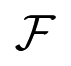 is
is
 . Define a projection
. Define a projection
 to the parameter space (σ, I), and its singularities determine the fold lines and cusp point. The bifurcation varieties for local bifurcation are the images under π ○ ξσ of the corresponding varieties in (σ, u)-space. Therefore, saddle-node (fold) bifurcations in the fully synchronous state u, which correspond to tangencies in Figure 5, are given by Equation (15), so that
to the parameter space (σ, I), and its singularities determine the fold lines and cusp point. The bifurcation varieties for local bifurcation are the images under π ○ ξσ of the corresponding varieties in (σ, u)-space. Therefore, saddle-node (fold) bifurcations in the fully synchronous state u, which correspond to tangencies in Figure 5, are given by Equation (15), so that
- If then ξσ : ℝ → (0, a; is a monotonic strictly increasing diffeomorphism.
- If then ξσ : ℝ → (0, a; is a monotonic strictly increasing homeomorphism.
- If and ξσ : (0,u−) → (−∞,IU) is a monotonic strictly increasing homeomorphism. It is a diffeomorphism when u < u−.
 . We therefore have:
. We therefore have:5. Review of Symmetric Steady-State and Hopf Bifurcation
5.1. Symmetric Steady-State Bifurcation
 1 is a compact Lie group. Finite-dimensional real linear representations of compact Lie groups occur in three classes, distinguished by the space of commuting linear maps. By Schur's Lemma this is a division algebra over ℝ, hence is isomorphic to one of ℝ, ℂ, and the quaternions (x0210D;. If this algebra is (x0211D; we call the representation absolutely irreducible. See Adams [42] 3.22.
1 is a compact Lie group. Finite-dimensional real linear representations of compact Lie groups occur in three classes, distinguished by the space of commuting linear maps. By Schur's Lemma this is a division algebra over ℝ, hence is isomorphic to one of ℝ, ℂ, and the quaternions (x0210D;. If this algebra is (x0211D; we call the representation absolutely irreducible. See Adams [42] 3.22.5.2. Symmetric Hopf Bifurcation
 2π,
be the loop spaces of continuous and once-differentiable 2π-periodic maps ℝ → ℝn. These are Banach spaces. Define the circle group
2π,
be the loop spaces of continuous and once-differentiable 2π-periodic maps ℝ → ℝn. These are Banach spaces. Define the circle group 1 acts on
1 acts on
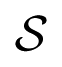 2π and
by
2π and
by
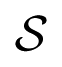 2π or
is fixed by (g, θ) if and only if
2π or
is fixed by (g, θ) if and only if
 1 for which Equation (20) is valid. A representation W of G is said to be G-simple if either
1 for which Equation (20) is valid. A representation W of G is said to be G-simple if either
- (1)
- W ≅ V ⊕ V where V is absolutely irreducible.
- (2)
- W is irreducible of type ℂ or ℍ.
 1-action. Define the restricted Jacobian
1-action. Define the restricted Jacobian 1 on Eiω by
1 on Eiω by
 1 acts on Eiω by
1 acts on Eiω by
 1 acting on Eiω for which
1 acting on Eiω for which
6. Data for Primary Gaits
 = ℝ/2πℤ so π is half the period.
= ℝ/2πℤ so π is half the period.7. Main Theorem
8. Local Bifurcation Analysis
8.1. Eigenvalues of the Jacobian
8.2. Conditions for Steady-State Bifurcation
8.3. Conditions for Hopf Bifurcation
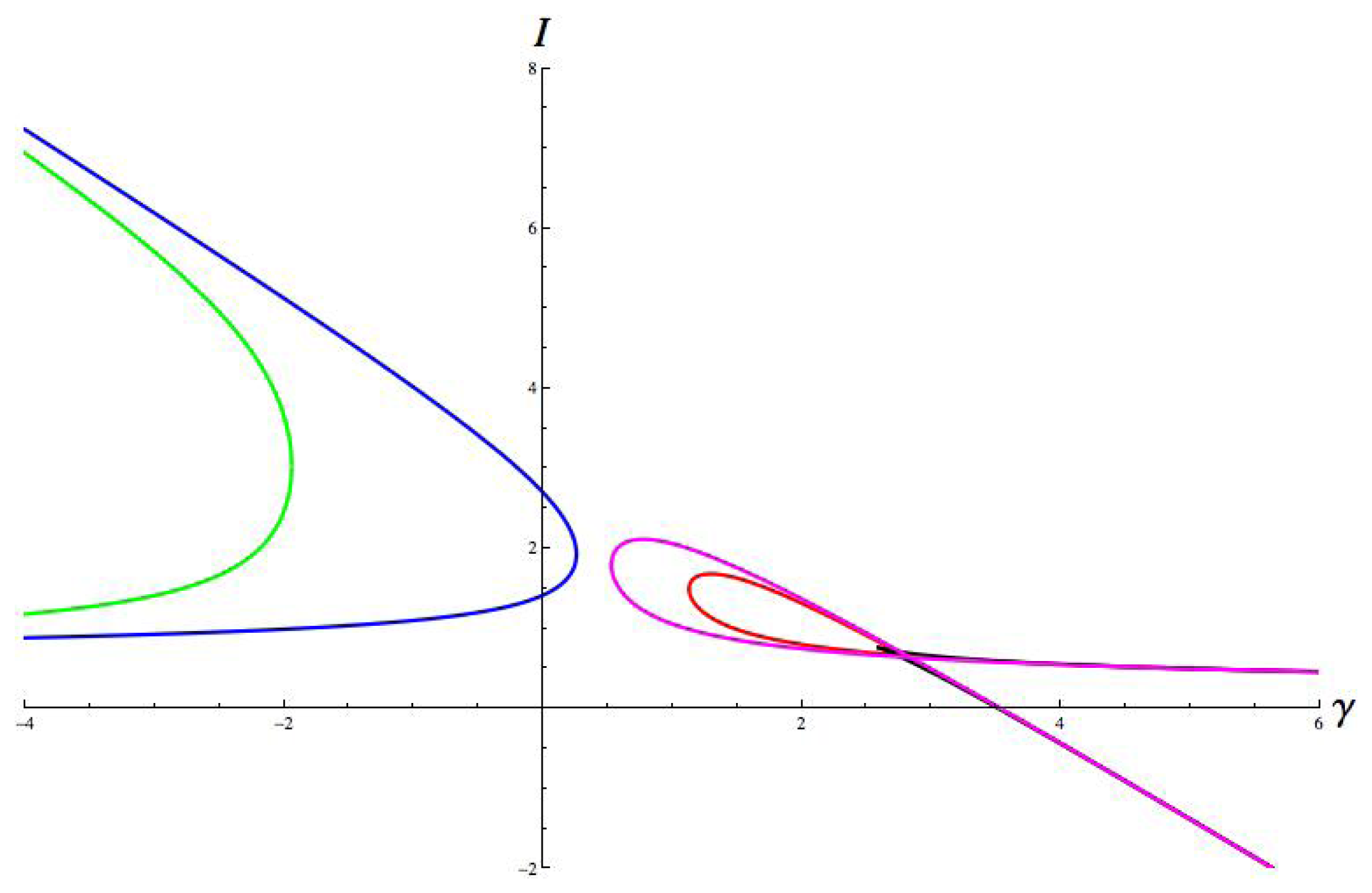
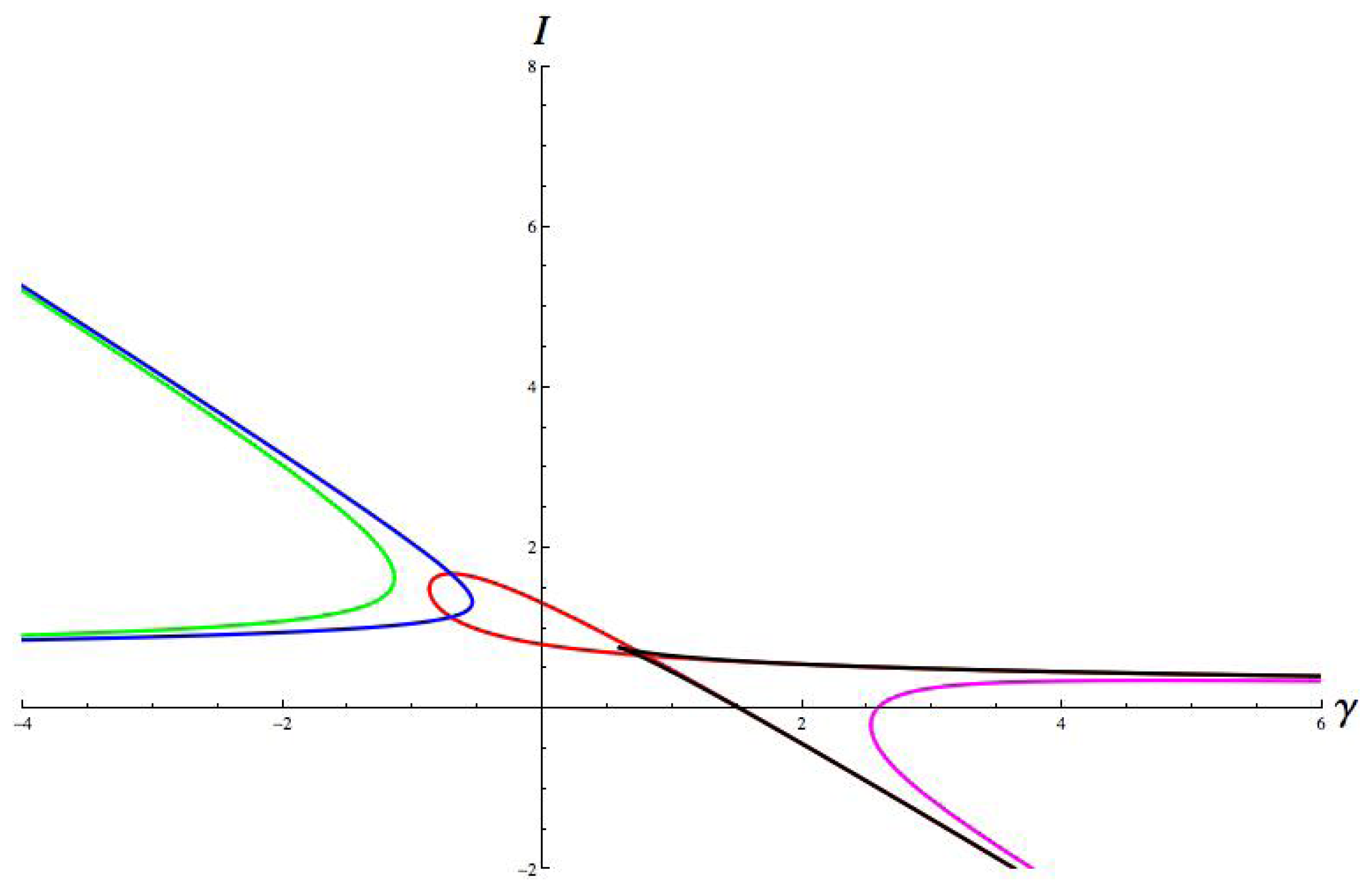
9. Plots of Hopf Bifurcation Curves
10. Dominant Eigenvalues
 with vertices at
with vertices at
 . In fact, since the vertices of c
. In fact, since the vertices of c  are (±c, ±c, ±c) with 1 or 3 minus signs, they contain the faces of c
are (±c, ±c, ±c) with 1 or 3 minus signs, they contain the faces of c  . Define the face FP of
. Define the face FP of
 corresponding to gait P as follows:
corresponding to gait P as follows:
- (1)
- FH is the face with vertices (−1, 1, 1), (1, −1, 1), (1, 1, −1)
- (2)
- FJ is the face with vertices (−1, 1, 1), (1, −1, 1), (−1, −1, −1)
- (3)
- FR is the face with vertices (−1, 1, 1), (1, 1, −1), (−1, −1, −1)
- (4)
- FW is the face with vertices (1, −1, 1), (1, 1, −1), (−1, −1, −1)
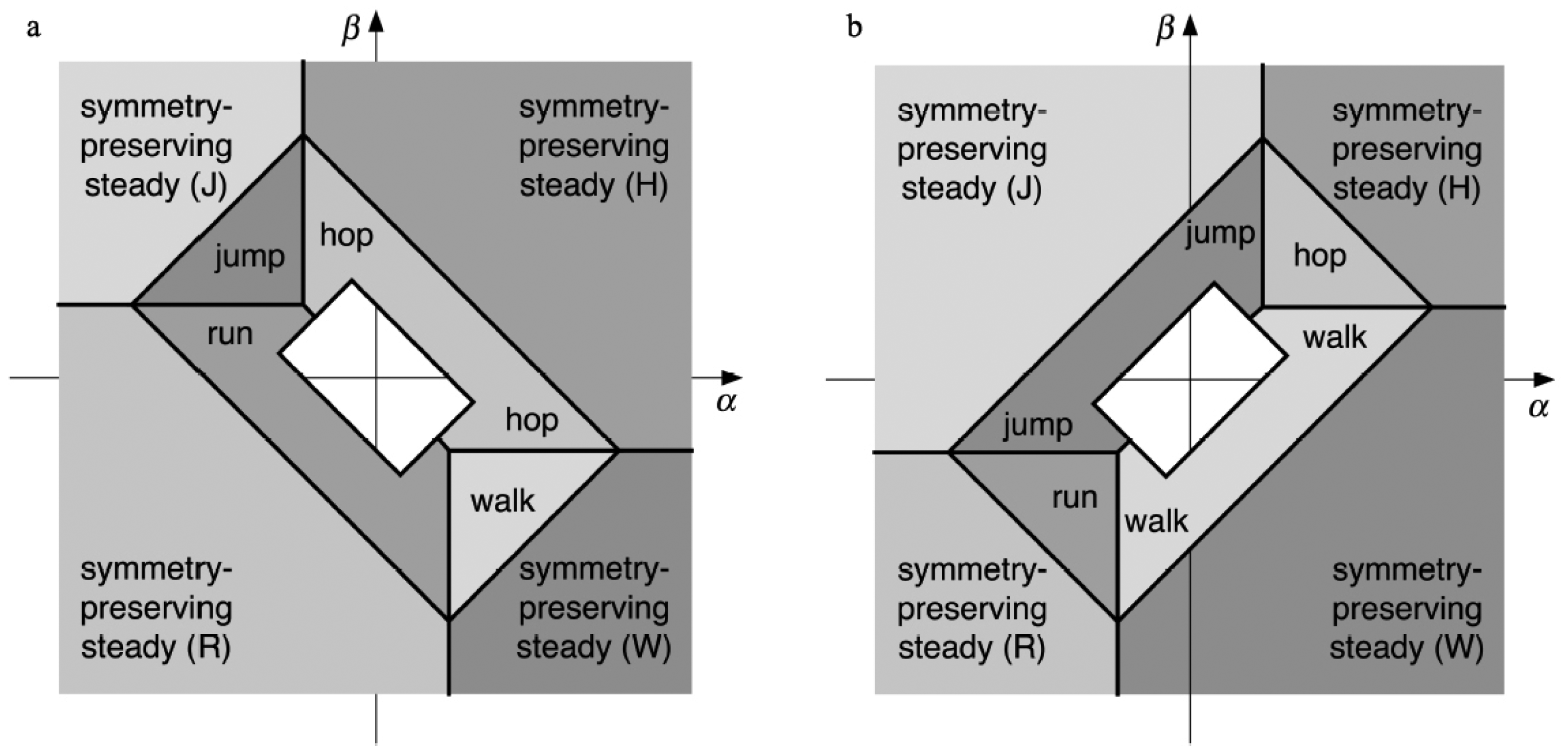
 . Figure 2b illustrates the three-dimensional geometry involved.
. Figure 2b illustrates the three-dimensional geometry involved.11. Tetrahedral Structure
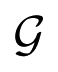 in Equation (5). Indeed, there is a general representation-theoretic reason for it, which we explain at the end of this section. The tetrahedral symmetry involved is richer than the symmetry group ℤ2 × ℤ2 of the CPG network, and also richer than the parameter symmetries
in Equation (5). Indeed, there is a general representation-theoretic reason for it, which we explain at the end of this section. The tetrahedral symmetry involved is richer than the symmetry group ℤ2 × ℤ2 of the CPG network, and also richer than the parameter symmetries
 3 acting on α, β, γ. It simplifies the proof of Theorem 3.
3 acting on α, β, γ. It simplifies the proof of Theorem 3.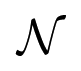 of Figure 1 can be represented as a tetrahedron, with the nodes corresponding to vertices and the arrows to edges. In fact, Figure 1 can be seen as the projection of a tetrahedron in which nodes 1 and 4 lie in a different horizontal plane from, nodes 2 and 3. Arrows of a given type (α, β, or γ) correspond to pairs of opposite edges—not having a common vertex.
of Figure 1 can be represented as a tetrahedron, with the nodes corresponding to vertices and the arrows to edges. In fact, Figure 1 can be seen as the projection of a tetrahedron in which nodes 1 and 4 lie in a different horizontal plane from, nodes 2 and 3. Arrows of a given type (α, β, or γ) correspond to pairs of opposite edges—not having a common vertex. 4 of the tetrahedron acts on the four vertices by permuting them. We will see that this action of the tetrahedral group does not fully explain the tetrahedral structure of the first bifurcations, although it goes part way. Instead, we require a subtler (though related) action. We first discuss the above action.
4 of the tetrahedron acts on the four vertices by permuting them. We will see that this action of the tetrahedral group does not fully explain the tetrahedral structure of the first bifurcations, although it goes part way. Instead, we require a subtler (though related) action. We first discuss the above action. 4 on nodes induces a permutation of the three pairs of opposite edges, that is, of the symbols (α, β, γ). This arises via the standard homomorphism
4 on nodes induces a permutation of the three pairs of opposite edges, that is, of the symbols (α, β, γ). This arises via the standard homomorphism
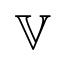 ≅ ℤ2 × ℤ2. See for example Rotman [43] page 42. Here
≅ ℤ2 × ℤ2. See for example Rotman [43] page 42. Here
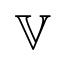 comprises the parameter symmetries that fix the parameters, that is, the symmetry group ℤ2 × ℤ2 of
comprises the parameter symmetries that fix the parameters, that is, the symmetry group ℤ2 × ℤ2 of
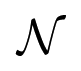 .
. 4, also with kernel
4, also with kernel
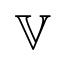 , and
, and
 4 acts as rigid motions of
4 acts as rigid motions of
 4 acts by parameter symmetries, the partition of ℝ3 into regions in Figures 15, 16 and 17 are preserved. This action preserves the face of the large tetrahedron that forms the base of the “hop” region, and permutes the other three regions.
4 acts by parameter symmetries, the partition of ℝ3 into regions in Figures 15, 16 and 17 are preserved. This action preserves the face of the large tetrahedron that forms the base of the “hop” region, and permutes the other three regions. 3 symmetry of Figure 15, but not the tetrahedral symmetry. To see how this arises, we consider a different group acting on the set of linear forms ±α ± β ± γ that include the four eigenvalues of A. This is the wreath product
3 symmetry of Figure 15, but not the tetrahedral symmetry. To see how this arises, we consider a different group acting on the set of linear forms ±α ± β ± γ that include the four eigenvalues of A. This is the wreath product
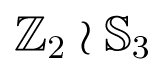 of order 48, Hall [44]. Here the base group ℤ2 × ℤ2 × ℤ2 changes the signs of α, β, γ, and
of order 48, Hall [44]. Here the base group ℤ2 × ℤ2 × ℤ2 changes the signs of α, β, γ, and
 3 permutes them. Geometrically,
3 permutes them. Geometrically,
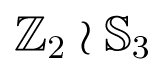 is the symmetry group of rigid motions of the cube with vertices (±1, ±1, ±1).
is the symmetry group of rigid motions of the cube with vertices (±1, ±1, ±1).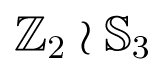 has a subgroup
has a subgroup
 of order 24 that changes signs in pairs. Geometrically,
of order 24 that changes signs in pairs. Geometrically,
 is the symmetry group of rigid motions of the tetrahedron
is the symmetry group of rigid motions of the tetrahedron
 with vertices (±1, ±1, ±1) in which the number of minus signs is 0 or 2.
with vertices (±1, ±1, ±1) in which the number of minus signs is 0 or 2. acts on the set of eigenvalues {μP : P = H, J, R, W}. It is easy to prove that
acts on the set of eigenvalues {μP : P = H, J, R, W}. It is easy to prove that
 ≅
≅
 4, and it permutes these eigenvalues faithfully.
4, and it permutes these eigenvalues faithfully.11.1. Representation-Theoretic Generalities
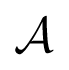 . That is, whenever A ∈
. That is, whenever A ∈
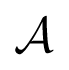 there exists à ∈
there exists à ∈
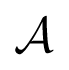 for which
for which
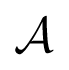 so there exists à satisfying Equation (46). Let υ be any eigenvector of à with eigenvalue μ̃. Then Bυ is an eigenvector of A with eigenvalue μ̃.
so there exists à satisfying Equation (46). Let υ be any eigenvector of à with eigenvalue μ̃. Then Bυ is an eigenvector of A with eigenvalue μ̃.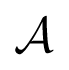 by conjugation. Proposition 6 implies that the group
by conjugation. Proposition 6 implies that the group
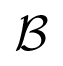 = 〈B〉 generated by all such B acts on the set of common eigenvectors of G, and also on the functions μ(A) expressing the eigenvalues of A.
= 〈B〉 generated by all such B acts on the set of common eigenvectors of G, and also on the functions μ(A) expressing the eigenvalues of A.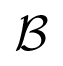 to consist of all 4 × 4 matrices that permute α, β, γ in the matrices A and multiply them by ±1. This is isomorphic to the wreath product
to consist of all 4 × 4 matrices that permute α, β, γ in the matrices A and multiply them by ±1. This is isomorphic to the wreath product
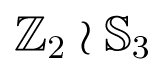 . However, minus the identity (−id) fixes all eigenvalues. Therefore, the effective action is by
. However, minus the identity (−id) fixes all eigenvalues. Therefore, the effective action is by
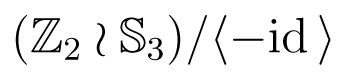
 4 that acts on the eigenvalues and creates the tetrahedral symmetry in the space of connection strengths α, β, γ.
4 that acts on the eigenvalues and creates the tetrahedral symmetry in the space of connection strengths α, β, γ. is not a symmetry group of the rate equations in the sense of equivariance. More generally, it is not induced by a parameter symmetry. This follows since the first bifurcation to a hop gait is a saddle-node, whereas the first bifurcation to a jump, run, or walk gait can be shown to be a pitchfork, as suggested by the normalizer symmetry NG(Σ)/Σ ≅ ℤ2. Thus
is not a symmetry group of the rate equations in the sense of equivariance. More generally, it is not induced by a parameter symmetry. This follows since the first bifurcation to a hop gait is a saddle-node, whereas the first bifurcation to a jump, run, or walk gait can be shown to be a pitchfork, as suggested by the normalizer symmetry NG(Σ)/Σ ≅ ℤ2. Thus
 consists of symmetries of the bifurcation varieties, but not of the dynamics (even allowing changes of parameters).
consists of symmetries of the bifurcation varieties, but not of the dynamics (even allowing changes of parameters).12. Proof of the Main Theorem
 of the eigenvalues of A simplifies this derivation and helps to explain the results, as we see below. First, we set up some notation.
of the eigenvalues of A simplifies this derivation and helps to explain the results, as we see below. First, we set up some notation. of Section 11.
of Section 11.- (1)
≅ ∅ ⇔ μP ≥ k
- (2)
≅ ∅ ⇔ μP ≥ m
- (3)
≅ ∅ ⇔ k < μP ≤ K
- (4)
- if and only if μP < K.if and only if μP > K.
- (1)
- , which is equivalent to μP ≥ k.
- (2)
- , which is equivalent to μP ≥ m.
- (3)
- (4)
 permutes the sets
permutes the sets
 ,
,
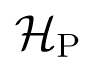 , and
, and
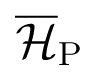 . The permutations act on the patterns {H, J, R, P} according to the
. The permutations act on the patterns {H, J, R, P} according to the
 4-action on the corresponding eigenvalues of A.
4-action on the corresponding eigenvalues of A. ,
, 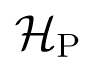 , and
, and
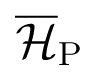 are defined by equations and inequalities (48)–(50) in u that depend only on μP, and do so in exactly the same manner for each gait type.
are defined by equations and inequalities (48)–(50) in u that depend only on μP, and do so in exactly the same manner for each gait type. . It therefore has tetrahedral symmetry.
. It therefore has tetrahedral symmetry.- (1)
- None if μP < k.
- (2)
- Hopf of type P if k < μP < K.
- (3)
- Steady-state of type P if μP > K.
 to deduce the other cases RP when P = J, R, W.
to deduce the other cases RP when P = J, R, W.12.1. Plot of Gait Regions
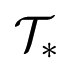 \
\
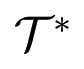 .
.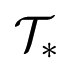 . We have
. We have
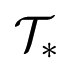 ⊊
⊊
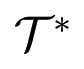 if and only if k < K, that is,
if and only if k < K, that is,
 , so the planes μP = q are parallel to the opposite faces. Regions in which μP < q are open half-spaces bounded by such planes. It is then easy to check that when q = K the planes are the faces of
, so the planes μP = q are parallel to the opposite faces. Regions in which μP < q are open half-spaces bounded by such planes. It is then easy to check that when q = K the planes are the faces of
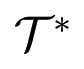 , extended to infinity, and when q = k they are the faces of
, extended to infinity, and when q = k they are the faces of
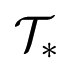 , extended to infinity For distinct patterns P and Q the planes μP = μq determine the transitions between first bifurcation to P and first bifurcation to Q, as in Section 13 below. The rest of the geometry then follows.
, extended to infinity For distinct patterns P and Q the planes μP = μq determine the transitions between first bifurcation to P and first bifurcation to Q, as in Section 13 below. The rest of the geometry then follows.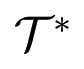 ,
,
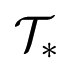 are three-dimensional sections δ = 0 of the corresponding four-dimensional decomposition.
are three-dimensional sections δ = 0 of the corresponding four-dimensional decomposition.13. Degeneracies
- (1)
- Transition from one primary Hopf mode to a different primary Hopf mode: change of gait.
- (2)
- Transition from one primary steady-state mode to a different primary steady-state mode: change of equilibrium type.
- (3)
- When μP = K there is a transition between a primary Hopf mode of symmetry-type P and a steady-state mode of the same symmetry-type. Also, when μP = k there is a transition between a primary Hopf mode of symmetry-type P and a fully synchronous steady-state mode. These transitions correspond to the onset or cessation of gait P.
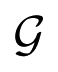 than the family used here. This stems from the linearity of the coupling in the argument of
than the family used here. This stems from the linearity of the coupling in the argument of
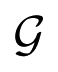 in Equation (5). This implies that if for given i, some linear combination of connection strengths αij is zero, and if moreover the corresponding cells j are in synchrony, then their combined input into cell i is zero. That is, cell i is decoupled from the cells j. We therefore have:
in Equation (5). This implies that if for given i, some linear combination of connection strengths αij is zero, and if moreover the corresponding cells j are in synchrony, then their combined input into cell i is zero. That is, cell i is decoupled from the cells j. We therefore have:
- (1)
- If α = − β and the gait is of types H or P, nodes 1, 2 decouple from 3, 4.
- (2)
- If α = −γ and the gait is of types H or J, nodes 1, 3 decouple from 2, 4.
- (3)
- If β = −γ and the gait is of types H or W, nodes 1, 4 decouple from 2, 3.
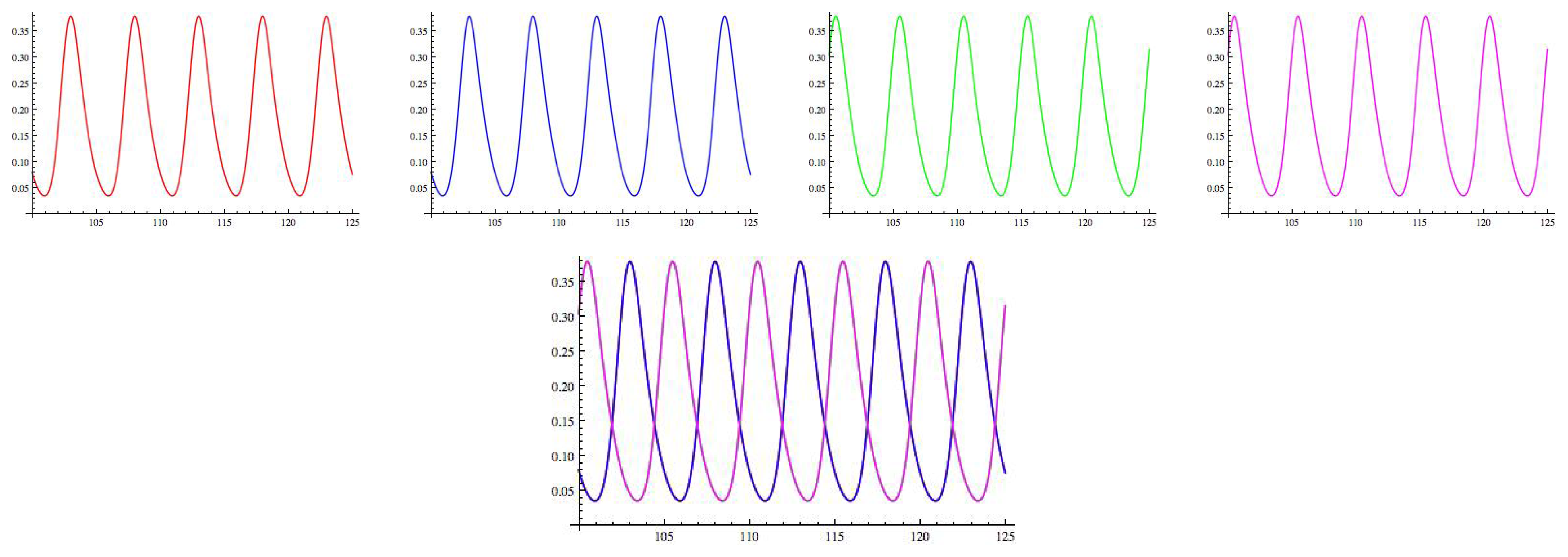
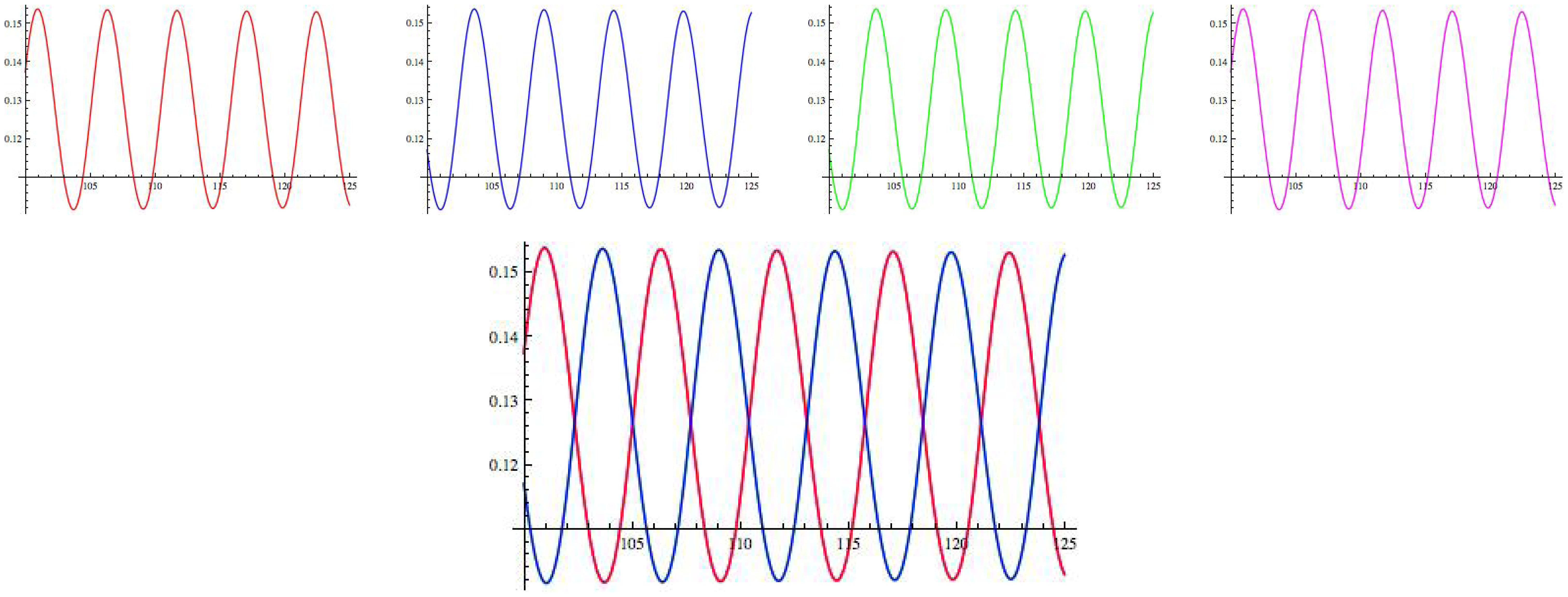
14. Simulations
Acknowledgments
Conflicts of Interest
References
- Gambaryan, P. How Mammals Run: Anatomical Adaptations; Wiley: New York, NY, USA, 1974. [Google Scholar]
- Muybridge, E. Animals in Motion; Chapman and Hall: London, UK, 1899; Reprinted Dover: New York, NY, USA, 1957.
- McGhee, R.B. Some finite state aspects of legged locomotion. Math. Biosci. 1968, 2, 67–84. [Google Scholar]
- Hildebrand, M. Vertebrate locomotion, an introduction: How does an animal's body move itself along? BioScience 1989, 39, 764–765. [Google Scholar]
- Kopell, N. Towards a Theory of Modelling Central Pattern Generators. In Neural Control of Rhythmic Movements in Vertebrates; Cohen, A.H., Rossignol, S., Grillner, S., Eds.; Wiley: New York, NY, USA, 1988. [Google Scholar]
- Kopell, N.; Ermentrout, G.B. Symmetry and phaselocking in chains of weakly coupled oscillators. Commun. Pure Appl. Math. 1986, 39, 623–660. [Google Scholar]
- Kopell, N.; Ermentrout, G.B. Coupled oscillators and the design of central pattern generators. Math. Biosci. 1988, 89, 14–23. [Google Scholar]
- Kopell, N.; Ermentrout, G.B. Phase transitions and other phenomena in chains of oscillators. SIAM J. Appl. Math. 1990, 50, 1014–1052. [Google Scholar]
- Collins, J.J.; Stewart, I. Symmetry-breaking bifurcation: A possible mechanism for 2:1 frequency-locking in animal locomotion. J. Math. Biol. 1992, 30, 827–838. [Google Scholar]
- Collins, J.J.; Stewart, I. Hexapodal gaits and coupled nonlinear oscillator models. Biol. Cybern. 1993, 68, 287–298. [Google Scholar]
- Collins, J.J.; Stewart, I. Coupled nonlinear oscillators and the symmetries of animal gaits. J. Nonlinear Sci. 1993, 3, 349–392. [Google Scholar]
- Collins, J.J.; Stewart, I. A group-theoretic approach to rings of coupled biological oscillators. Biol. Cybern. 1994, 71, 95–103. [Google Scholar]
- Hassard, B.D.; Kazarinoff, N.D.; Wan, Y.-H. Theory and Applications of Hopf Bifurcation; London Mathematical Society Lecture Note Series 41; Cambridge University Press: Cambridge, UK, 1981. [Google Scholar]
- Buono, P.-L. A Model of Central Pattern Generators for Quadruped Locomotion. Ph.D. Thesis, University of Houston, Houston, TX, USA, 1998. [Google Scholar]
- Buono, P.-L. Models of central pattern generators for quadruped locomotion: II. Secondary gaits. J. Math. Biol. 2001, 42, 327–346. [Google Scholar]
- Buono, P.-L.; Golubitsky, M. Models of central pattern generators for quadruped locomotion: I. Primary gaits. J. Math. Biol. 2001, 42, 291–326. [Google Scholar]
- Golubitsky, M.; Stewart, I. The Symmetry Perspective, Progress in Mathematics 200; Birkhäuser: Basel, Switzerland, 2002. [Google Scholar]
- Golubitsky, M.; Stewart, I.; Schaeffer, D.G. Singularities and Groups in Bifurcation Theory II; Applied Mathematics Series 69; Springer: New York, NY, USA, 1988. [Google Scholar]
- Golubitsky, M.; Stewart, I.; Buono, P.-L.; Collins, J.J. A modular network for legged locomotion. Physica D 1998, 115, 56–72. [Google Scholar]
- Golubitsky, M.; Stewart, I.; Collins, J.J.; Buono, P.-L. Symmetry in locomotor central pattern generators and animal gaits. Nature 1999, 401, 693–695. [Google Scholar]
- Pinto, C.A.; Golubitsky, M. Central pattern generators for bipedal locomotion. J. Math. Biol. 2006, 53, 474–489. [Google Scholar]
- Golubitsky, M.; Stewart, I. Nonlinear dynamics of networks: The groupoid formalism. Bull. Am. Math. Soc. 2006, 43, 305–364. [Google Scholar]
- Golubitsky, M.; Stewart, I.; Török, A. Patterns of synchrony in coupled cell networks with multiple arrows. SIAM J. Appl. Dyn. Syst. 2005, 4, 78–100. [Google Scholar]
- Stewart, I.; Golubitsky, M.; Pivato, M. Symmetry groupoids and patterns of synchrony in coupled cell networks. SIAM J. Appl. Dyn. Syst. 2003, 2, 609–646. [Google Scholar]
- Diekman, C.; Golubitsky, M.; Wang, Y. Derived patterns in binocular rivalry networks. J. Math. Neuro. 2013, 3. [Google Scholar] [CrossRef]
- Curtu, R. Mechanisms for oscillations in a biological competition model. Proc. Appl. Math. Mech. 2007, 7. [Google Scholar] [CrossRef]
- Curtu, R. Singular Hopf bifurcations and mixed-mode oscillations in a two-cell inhibitory neural network. Physica D 2010, 239, 504–514. [Google Scholar]
- Curtu, R.; Shpiro, A.; Rubin, N.; Rinzel, J. Mechanisms for frequency control in neuronal competition models. SIAM J. Appl. Dyn. Syst. 2008, 7, 609–649. [Google Scholar]
- Poston, T.; Stewart, I. Catastrophe Theory and Its Applications; Surveys and Reference Works in Mathematics 2; Pitman: London, UK, 1978. [Google Scholar]
- Zeeman, E.C. Catastrophe Theory: Selected Papers 1972–1977; Addison-Wesley: London, UK, 1977. [Google Scholar]
- Wilson, H.R. Computational evidence for a rivalry hierarchy in vision. Proc. Natl. Acad. Sci. USA 2003, 100, 14499–14503. [Google Scholar]
- Laing, C.R.; Chow, C.C. A spiking neuron model for binocular rivalry. J. Comput. Neurosci. 2002, 12, 39–53. [Google Scholar]
- Shpiro, A.; Curtu, R.; Rinzel, J.; Rubin, N. Dynamical characteristics common to neuronal competition models. J. Neurophysiol. 2007, 97, 462–473. [Google Scholar]
- Wilson, H.R. Requirements for Conscious Visual Processing. In Cortical Mechanisms of Vision; Jenkin, M., Harris, L., Eds.; Cambridge University Press: Cambridge, UK, 2009; pp. 399–417. [Google Scholar]
- Diekman, C.; Golubitsky, M. Algorithm for Constructing and Analyzing Wilson Networks for Binocular Rivalry Experiments; MBI: Columbus, OH, USA, 2014; in press. [Google Scholar]
- Diekman, C.; Golubitsky, M.; McMillen, T.; Wang, Y. Reduction and dynamics of a generalized rivalry network with two learned patterns. SIAM J. Appl. Dyn. Syst. 2012, 11, 1270–1309. [Google Scholar]
- Diekman, C.; Golubitsky, M.; Stewart, I. Modelling visual illusions using generalised Wilson networks; Mathematics Institute, University of Warwick: Coventry, UK, Unpublished work; 2013. [Google Scholar]
- Golubitsky, M.; Stewart, I. Hopf bifurcation in the presence of symmetry. Arch. Ration. Mech. Anal. 1985, 87, 107–165. [Google Scholar]
- Cicogna, G. Symmetry breakdown from bifurcations. Lett. Nuovo Cimento 1981, 31, 600–602. [Google Scholar]
- Vanderbauwhede, A. Local Bifurcation and Symmetry. Habilitation Thesis, Rijksuniversiteit Gent, Gent, Belgium, 1980. [Google Scholar]
- Vanderbauwhede, A. Local Bifurcation and Symmetry Research Notes in Mathematics Series 75; Pitman: London, UK, 1982. [Google Scholar]
- Adams, J.F. Lectures on Lie Groups; University of Chicago Press: Chigago, IL, USA, 1969. [Google Scholar]
- Rotman, J.J. An Introduction to the Theory of Groups; Allyn and Bacon: Boston, TX, USA, 1984. [Google Scholar]
- Hall, M., Jr. The Theory of Groups; Macmillan: New York, NY, USA, 1959. [Google Scholar]
- Loney, S.L. The Elements of Coordinate Geometry; Macmillan: London, UK, 1960. [Google Scholar]
- Guckenheimer, J.; Holmes, P. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields; Applied Mathematical Sciences; Vol. 42, Springer: New York, NY, USA, 1990. [Google Scholar]

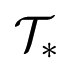 (x).
(x).
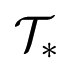 (x).
(x).
 (u)(curve) and I + σu (straight lines).
(u)(curve) and I + σu (straight lines).
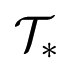 (u)(curve) and I + σu (straight lines).
(u)(curve) and I + σu (straight lines).



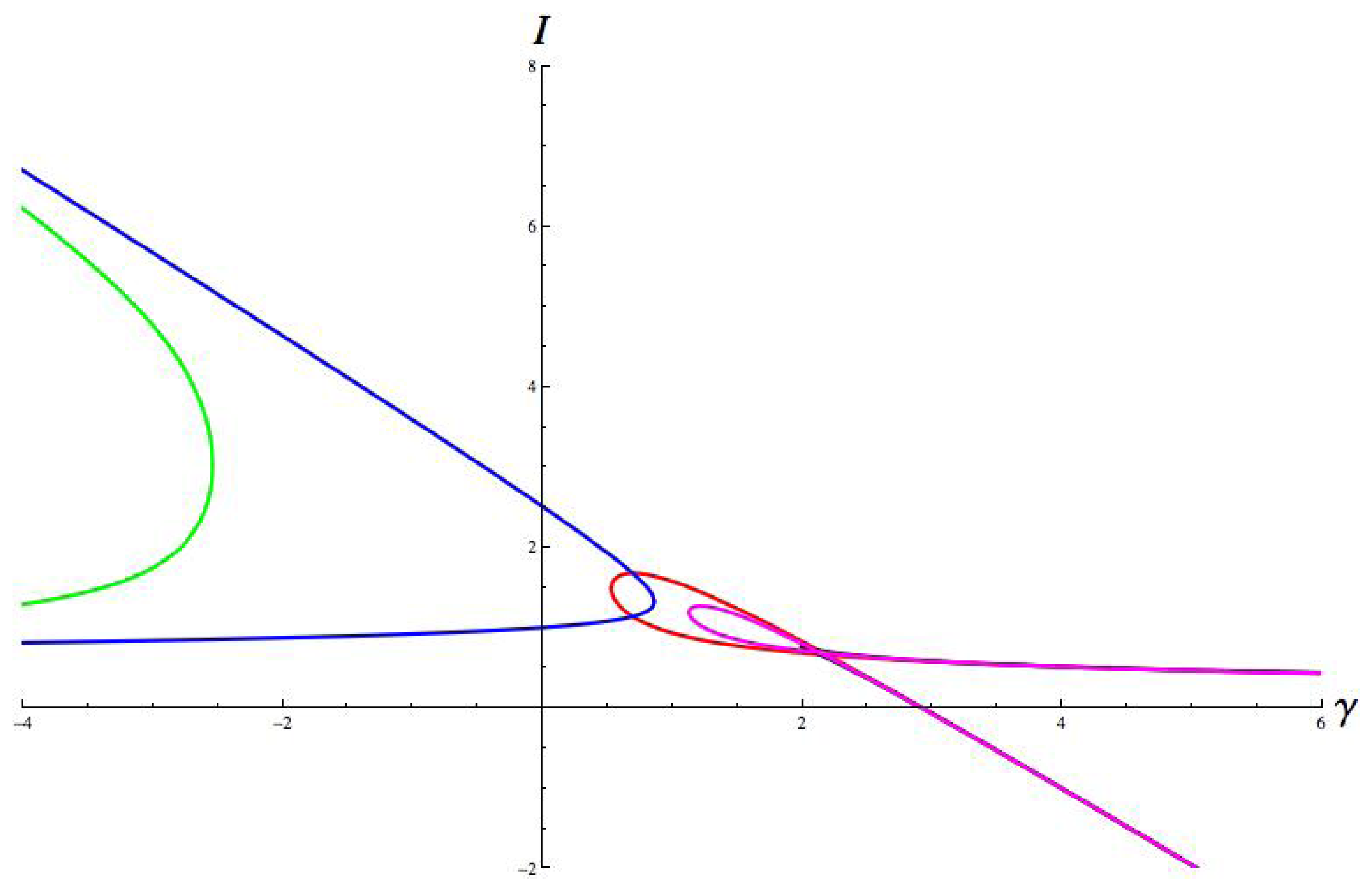
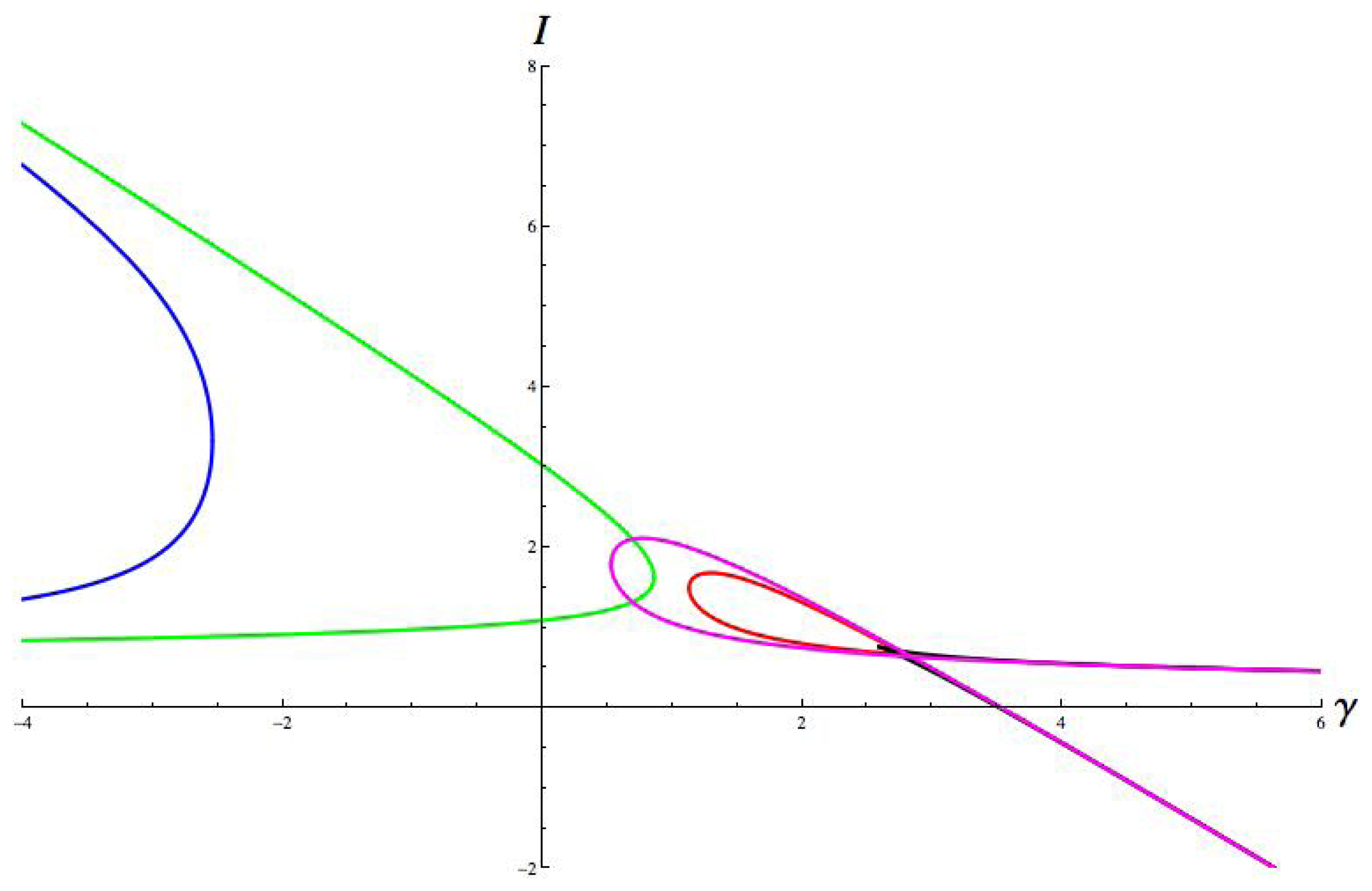
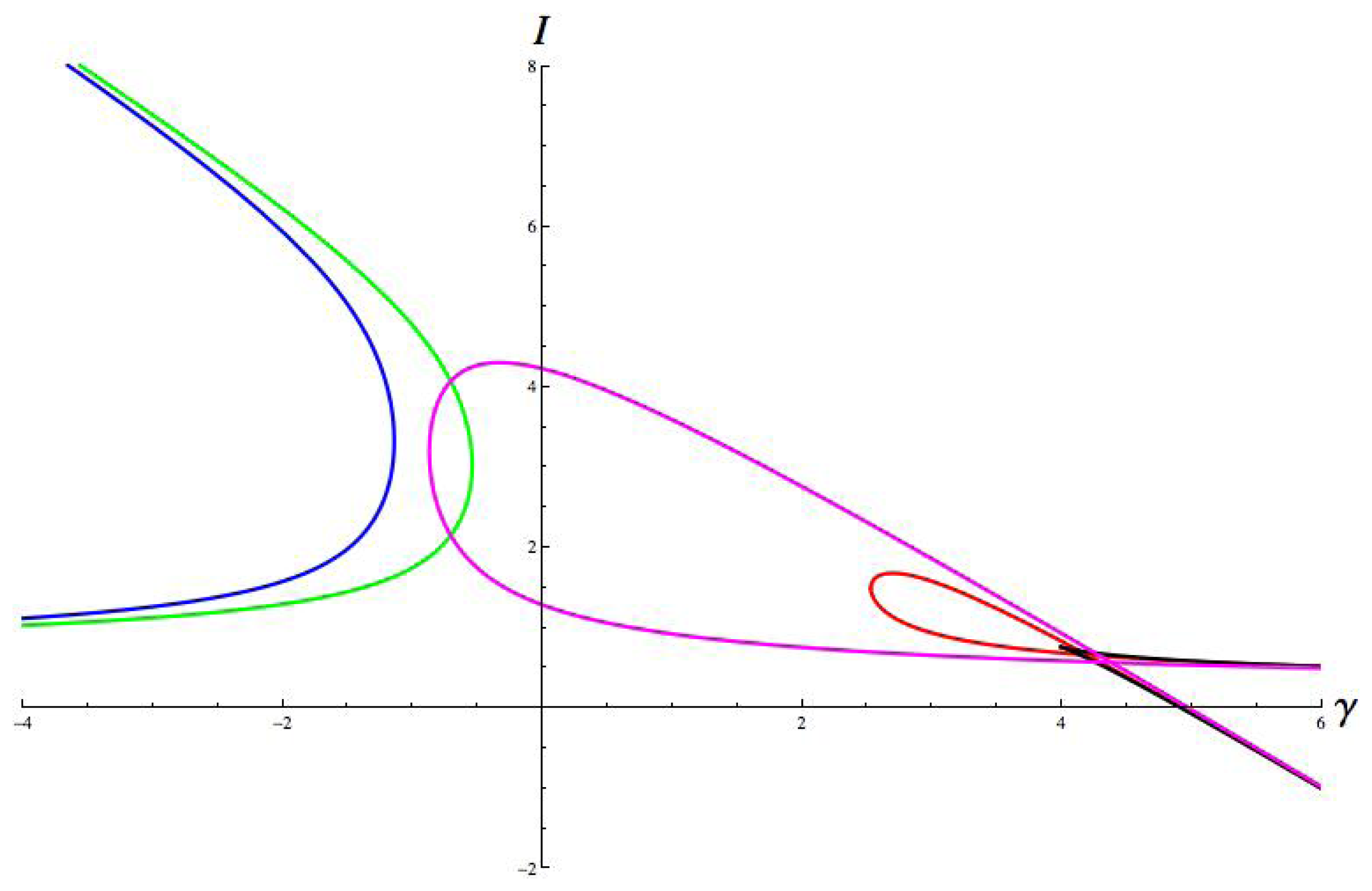



| Gait | Twist ϕ | Σ = ker ϕ | Fix(Σ) | Type |
|---|---|---|---|---|
| hop | ρ ↦ 0, τ ↦ 0 | ℤ2(ρ) x ℤ2〈τ〉 | {(x, x, x, x )} | H |
| jump | ρ ↦π, τ ↦ 0 | ℤ2〈ρ〉 | {(x, y, x, y)} | J |
| run | ρ ↦ 0, τ ↦ π | ℤ2(τ) | {(x, x, y, y)} | R |
| walk | ρ ↦ π, τ ↦ π | ℤ2〈ρτ〉 | {(x, y, y, x)} | W |
| Name | Parameters in A | Conditions involving k, K | |||
|---|---|---|---|---|---|
| None | μP < k for all patterns P | ||||
| all other types: | |||||
| Hop | α + γ>0 | α + β > 0 | γ + β > 0 | k<α+β +γ<K | |
| Jump | α + γ<0 | β>γ | β > α | k < −α + β − γ < K | |
| Run | α + β < 0 | γ > β | γ > α | k < −α − β + γ < K | |
| Walk | γ + β<0 | α > γ | α > β | k < α − β − γ < K | |
| Type H steady | α + γ>0 | α + β > 0 | γ + β > 0 | α +β +γ > K | |
| Type J steady | α + γ < 0 | β > γ | β > α | −α + β − γ > K | |
| Type R steady | α + β < 0 | γ > β | γ > α | −α − β + γ > K | |
| Type W steady | γ + β < 0 | α > γ | α > β | α − β − γ > K | |
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Stewart, I. Symmetry-Breaking in a Rate Model for a Biped Locomotion Central Pattern Generator. Symmetry 2014, 6, 23-66. https://doi.org/10.3390/sym6010023
Stewart I. Symmetry-Breaking in a Rate Model for a Biped Locomotion Central Pattern Generator. Symmetry. 2014; 6(1):23-66. https://doi.org/10.3390/sym6010023
Chicago/Turabian StyleStewart, Ian. 2014. "Symmetry-Breaking in a Rate Model for a Biped Locomotion Central Pattern Generator" Symmetry 6, no. 1: 23-66. https://doi.org/10.3390/sym6010023




