Towards Generalized Noise-Level Dependent Crystallographic Symmetry Classifications of More or Less Periodic Crystal Patterns

Abstract

Geometric Akaike Information Criteria (G-AICs) for generalized noise-level dependent crystallographic symmetry classifications of two-dimensional (2D) images that are more or less periodic in either two or one dimensions as well as Akaike weights for multi-model inferences and predictions are reviewed. Such novel classifications do not refer to a single crystallographic symmetry class exclusively in a qualitative and definitive way. Instead, they are quantitative, spread over a range of crystallographic symmetry classes, and provide opportunities for inferences from all classes (within the range) simultaneously. The novel classifications are based on information theory and depend only on information that has been extracted from the images themselves by means of maximal likelihood approaches so that these classifications are objective. This is in stark contrast to the common practice whereby arbitrarily set thresholds or null hypothesis tests are employed to force crystallographic symmetry classifications into apparently definitive/exclusive states, while the geometric feature extraction results on which they depend are never definitive in the presence of generalized noise, i.e. in all real-world applications. Thus, there is unnecessary subjectivity in the currently practiced ways of making crystallographic symmetry classifications, which can be overcome by the approach outlined in this review.

1. Introduction and Background

While there is a large variety of extraction algorithms for geometric features, such as point and translation symmetries from gray level patterns that are more or less periodic in two (2D) and one (1D) dimensions [1,2], related comments by Kenichi Kanatani [3] on symmetry as a continuous and hierarchic feature have been largely ignored for the last two decades by the computational symmetry and applied crystallography communities alike. The notable exceptions in this respect are the work by Yanxi Liu and coworkers [4,5,6] on 1D periodic time series in the form of subsequently recorded 2D images which were done more than a decade ago and much more recent work by the author of this review on objective 2D Bravais lattice type assignments to noisy images [7].

While the applied crystallography community typically speaks of ‘crystal patterns’ when it refers to atomically resolved images [8], more or less 2D and 1D periodic patterns where the individual pixels possess digitized intensity values (i.e. gray-levels rather than colors) are commonly referred to as ‘near regular textures’ within the computational symmetry community [1]. With the title of this review, it is, thus, implied that its main targets are fellow members of the applied crystallography community. This paper should, however, also be of interest to the computational symmetry community because the underlying mathematical and statistical frameworks are identical when images are considered as data planes from which geometric-structural information is to be extracted and classified, regardless of the instruments with which they were recorded.

For the computational symmetry community [1,2,4,5,6] and with regards to Kanatani’s associated developments in the robotics/computer vision fields [3,9,10,11,12], it is entirely natural to consider images as data planes. While this is largely because there are no microscopes and specifics of the underlying physics of the imaging process involved that may need modeling, modern microscopes are so good now that the data plane approach also works well in materials science and structural biology.

It should, therefore, not come as a surprise that this review follows the existing leads from the computational symmetry community but also goes beyond the current state of affairs in crystallographic symmetry classification schemes when multi-model inferences are discussed. The conclusion section of a recent review of the computational symmetry field states fittingly that “strategies … for handling real world complexity have to be developed to deal with … the issue of subgroup relations among symmetry groups, raised by Kanatani” [1]. The time seems indeed to be right for these kinds of developments and this paper reviews both the statistical foundation and the wider crystallographic implications of them. The latter is mainly done in appendices, which may be of limited interest to members of the computational symmetry community.

More or less 2D periodic Islamic building ornaments were assigned to plane symmetry groups in [2] on the basis of the careful elucidation of the approximate site symmetries of conspicuous parts of periodic motifs in direct space. These elucidations rely, however, critically on arbitrary thresholds and must, therefore, always be subjective. The final plane symmetry group assignment can in that kind of an approach never be objective.

Utilizing Kanatani’s approach [3,9,10,11,12], the authors of [2] could, in principle, transform their classifications into objective ones in spite of the multitude of irregularities/defects that their analyzed Islamic ornaments contain. When that was done, model selection uncertainties [13,14,15,16,17] would need to be addressed properly. A solution to the latter problem will be presented in this review in a qualitative way as well. Note that model selection uncertainties are not addressed in the work of Liu and coworkers [4,5,6] either.

The problems associated with the above-mentioned subjective [1,2] crystallographic symmetry classifications, Kanatani’s new statistical theory [3,9,10,11,12], and systematic ways of dealing with model selection uncertainties [13,14,15,16,17] became more relevant to the applied crystallography community with the recent emergence of both the crystalline ‘materials per design paradigm’ [18] and model-based approaches to the imaging of crystals and long-range ordered materials. Straton and co-workers [19,20] utilized, for example, the above-mentioned objective translation symmetry type classification scheme [7] for the detection and subsequent correction of double and multiple mini-tip artifacts in scanning tunneling microscope (STM) images of more or less 2D periodic arrays of molecules on a crystal surface by means of crystallographic image processing [21,22].

Independent of the type of microscope with which the data have been recorded, the purpose of crystallographic image processing is the extraction of geometric-structural information from noisy 2D periodic images. The translation and site/point symmetries in the hypothetical noise-free version of the image are taken advantage of as one averages over the asymmetric unit so that a better signal-to-noise ratio is obtained for the structure of interest. Note that the averaging over the asymmetric unit (rather than the translation periodic unit cell) ensures that better results are obtained than those achievable with traditional Fourier filtering [7]. This is because the multiplicity of the general position [23,24] boosts the number of entities over which one averages by a factor of up to 12.

The noisy 2D periodic image is considered to constitute a data plane and the models for the data at the foundation of crystallographic image processing are the 17 plane symmetry groups of 2D crystallography [23,24], which represent all possible combinations of translation and point/site symmetries in the Euclidean plane. Crystallographic image processing originated about 50 years ago within the structural biology community [25] and contributed under the name ‘crystallographic electron microscopy’ (monikers ‘Fourier or pseudo-kinematic electron microscopy’) to the award of the 1982 Nobel Prize in Chemistry to Sir Aaron Klug.

Another type of model-based imaging in atomic resolution microscopy [26,27,28,29,30] with a complementary foundation originated as a very promising approach to quantitative transmission electron microscopy (TEM) at the University of Antwerp (Belgium) at the beginning of the 21st century and led to the award of the 2017 Ernst Ruska Prize to Sandra Van Aert. The underlying procedures of that approach are analogous to single-crystal X-ray crystallography in so far as one distinguishes between the ‘solving’ of the structure and the ‘refinement’ of the resolved structure [26]. First, the structure is resolved by the imaging of individual projected atomic columns in a more or less 2D periodic array with a state-of-the-art TEM. This is followed by a maximal likelihood refinement of the position and chemical composition of the atomic columns in that array.

Since the number of atoms in projected columns can be determined with single-atom accuracy when an aberration corrected TEM is utilized for the model-based imaging [29,30], a tomographic enhancement, i.e. the combining of structural information that was obtained from several atomic resolution images in different projections, was not necessary for the determination of the 3D structure of nanocrystals for which the thickness did not vary widely from atomic column to atomic column. It is this author’s opinion that the aforementioned model-based atomic-resolution approach to quantitative TEM could benefit from both the complementary geometric Akaike Information Criterion (G-AIC) approach that is outlined below in general terms and crystallographic image processing.

A recent paper by Vasudevan and co-workers seems to be most suitable to illustrate the need for this review at the present time as it describes a geometric-structural feature extraction approach where a window is sliding over a noisy image of a transmitted crystal and the discrete Fourier transform (dFT) is calculated at consecutive window positions of that atomically-resolved image so that the locations of different crystal phases can be mapped in two dimensions [31]. The authors of that paper state that it would, in principle, be possible to derive the local crystallography, i.e. the Bravais lattice type and plane symmetry group, of different types of more or less 2D periodic entities on crystal surfaces or within crystalline matrices from the data that they recorded with their sliding dFT windows in a scanning transmission electron microscope (STEM), but also caution that this “would require substantial efforts at developing the appropriate image classification schemes” [31].

Crystallographic classification schemes for 2D periodic patterns have been in existence for over nine decades [32,33]; see [23] for an authoritative, brief and mathematically comprehensive modern description as well as [34] for a college-level textbook. The real problem that needs to be addressed in the above-mentioned context of the sliding dFT windows is, however, how to make crystallographic classifications objectively on the basis of results from some non-ideal algorithm and when only noisy data are available, as is the case in all real world applications.

The situation is analogous to what is encountered in the field of crystallographic 1D periodic classification schemes for gray-level patterns. The mathematical background of frieze symmetries and their projections from layer symmetries has been around for decades and is neatly summed up in an authoritative text [35], which follows the same outline as the comprehensive description of all plane symmetries of gray-level patterns [23,24] as projections from 3D space symmetries. The problem is again how to make classifications objectively on the basis of noisy experimental image data and without adding a subjective value judgment to arrive at one crystallographic symmetry class only.

More or less 1D periodic 2D images of crystalline materials, such as aberration-corrected STEM images of plane coincidence site lattice (CSL) grain boundaries in edge-on projections which are atomically resolved [36,37,38,39,40,41] are known to be underlain by both predictable [41] types of frieze symmetries and 3D atomic level bi-crystal structures [42,43,44,45,46]. There is, at present, however, no objective way to extract the parameters of grain boundary structures at the atomic level from such images. Subjectivity in the experimental determination of the very basic Σ value (CSL index) has, for example, been recently discussed in [47].

The core ideas of the crystallographic processing of noisy 2D images could be transferred to images that are periodic in 1D only as a first step towards the development of objective crystallographic symmetry classification schemes on the basis of Kanatani’s statistical theory [3,9,10,11,12] and systematic ways of dealing with model selection uncertainties [13,14,15,16,17]. This would be equivalent to the adaptation of the proposal of this review to 1D periodic cases. The atomistic model-based approach that was pioneered at the University of Antwerp [26,27,28,29,30] could also be brought to bear on the extraction of geometric-structural information from atomic resolution images of grain boundaries. Appendix A and [48,49] provide some more background on CSL (and approximate low-CSL index) grain boundaries in order to illustrate opportunities for 1D periodic symmetry classifications in that particular field.

As soon as suitable classification schemes have been demonstrated that work without any arbitrarily set thresholds, a robot could be programmed to classify input images automatically and sort them into crystallographic databases for more or less 2D or 1D periodic patterns objectively. It would then be up to the user of such databases to (subjectively) interpret the objectively-reported classification results. The author of this review presents here key aspects of his novel crystallographic symmetry classification scheme that is designed to work well in the presence of geometric-structural feature extraction uncertainties of the types that exist in more or less 2D and 1D periodic images.

Noise in the imaging process, as well as geometric-structural feature extraction uncertainties in the processing of an image with some real world (non-ideal) algorithm will necessarily break all pre-existing symmetries of a crystalline sample (or that a synthetic image may possess due to its design) so that there will only be non-genuine pseudo-symmetries left to be classified. The image is then, of necessity, only translation periodic to a larger or smaller extent so that none of the strict mathematically abstract restrictions of 2D [23,24] and 1D [35] crystallography are applicable anymore.

Further complications arise when there are genuine pseudo-symmetries [50] in the hypothetical noise-free version of a 2D or 1D periodic image. Geometric-structural feature extraction procedures can in the presence of noise not readily distinguish between non-genuine pseudo-symmetries that combine to form the underlying symmetry group structure of the hypothetical noise-free version of the image, on the one hand, and genuine pseudo-symmetries that exist in addition to this structure [50], on the other hand. Within this review, we will occasionally refer to non-genuine pseudo-symmetries as pseudo-symmetries of a different (or second) kind. Appendix B provides more information on different types of pseudo-symmetries.

Since instances of the latter kind of pseudo-symmetries may be mistaken for instances of the former kind, the wrong underlying symmetry group structure may be inferred so that subsequent crystallographic classifications would be in error. Vice versa, due to noise in the experiments, non-genuine pseudo-symmetries may be mistaken for genuine pseudo-symmetries so that crystallographic symmetry classifications result which underreport the factual existing symmetry when an extrapolation to a zero-noise level is made. Genuine pseudo-symmetries also play important roles in twinning and the formation of multiple domains in crystalline solids [51,52].

Mix-ups of genuine and non-genuine pseudo-symmetries that lead to symmetry classification problems in both inorganic crystal structures and molecule crystals (both small and large) in the presence of experimental noise are for the mainstream 3D crystallography case discussed in Appendix C and [53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82].

The three largest crystallographic databases for mainstream 3D crystallography results [83,84,85,86,87] are also briefly mentioned in Appendix C.1. Two of these databases are in open access [83,84,86,87]. Specifics of single-crystal X-ray protein crystallography are mentioned in [88] and [89]. A critical review of crystal structure determinations by means of single-crystal X-ray crystallography in general is provided in [90]. Standard statistical descriptions and the utility of contemporary null hypothesis tests in mainstream 3D single-crystal X-ray crystallography are discussed in Appendix D and [91,92,93,94,95,96,97,98,99,100].

On the basis of [101,102,103,104,105,106,107,108,109,110,111,112,113], Appendix C.3. presents this author’s assessment of the single-crystal X-ray crystallography structure study of a highly topical metal-organic framework (MOF) compound [101,102]. That compound is probably incorrectly classified in the major databases for that class of material [85,86,87] due to an unrecognized pseudo-symmetry arising from the co-existence of triple domains. The published crystal structure of that MOF [101] is most likely an over idealization and at the very least incomplete due to the deliberate removal of experimentally observed electron density during data processing [102]. The crystallographic analysis of a few low electron dose STEM images—see [109] or [110] for one of these images—of that structure (as mentioned briefly in Appendix C.3) proved to be crucial to this author’s arrival at this conclusion on that crystal structure’s validity [109].

In spite of all of the kinds of difficulties that are mentioned above, and because there is now an objective way for recognizing genuine pseudo-symmetries in the presence of noise as outlined below, it makes a great deal of sense to assign a set of approximate crystallographic symmetry classifications to a 2D image so that the models one is using for atomic or molecular resolution imaging are of comparatively small dimensionalities and allow for optimal geometric-structural information extraction processes in the presence of noise.

Any real world geometric feature extraction algorithm will with necessity introduce some small systematic error into geometric-structural feature extraction results so that none of the computer programs that implement such algorithms will ever deliver definitive results [9,10,114] (Kanatani’s dictum). Since there are no definitive feature extraction results, one should not attempt to classify these results into qualitatively exclusive (definitive) classes such as a single Bravais lattice type [7,23], Laue class [24], and plane symmetry group [23,24] in the 2D case but utilize Kanatani’s new statistics [9,10,11,12] instead.

This is because the traditional kinds of classifications imply that the extracted pseudo-symmetries adhere 100% (i.e. definitively) to the restrictions that are imposed by a mathematically-abstract crystallographic type, class, or group, which are all of a qualitatively strict nature per definition. Such an adherence can obviously not be genuine as there is noise in all image recording and processing steps in all real-world applications.

In spite of this, allegedly-definitive symmetry classifications are so far the common practice in both the computational symmetry and applied crystallography communities alike. They are, however, fundamentally unsound because all qualitative classifications will be in error insofar as they claim to be definitive; see Kanatani’s comments from 1997 in this context [3].

Fortunately, crystallographic symmetries are hierarchic and the majority of them are non-disjoint [7,23,24,35,114]. These features allow for a boot-strapping approach that does not require an initial estimate of the generalized noise level in a more or less 2D or 1D periodic image.

By means of pair-wise comparison of non-disjoint models with Kanatani’s G-AIC [9,10,11,12], one first obtains the model that minimizes the expected Kullback-Leibler information loss [13,14,15,16,17] within a set of models that represents a stretch of a symmetry hierarchy branch and later determines for this particular model the generalized noise level. When this has been achieved, one can calculate the relative likelihood that a model in a set of non-disjoint (or disjoint) models minimizes the expected Kullback-Leibler information loss and formulate so-called Akaike weights as conditional model probabilities that add up to 100% for the whole set [13,14,15,16,17].

Instead of a definitive classification that makes a 100% assignment to only one class, which cannot be guaranteed to be correct due to the unavoidable presence of experimental noise and feature extraction uncertainties that are due to the utilized algorithm as discussed above, one obtains by this route a fuzzy classification that is spread over several classes of non-disjoint models within one symmetry hierarchy branch. One may also end up with a fuzzy classification that is spread over several classes of both non-disjoint and disjoint models if there is a genuine pseudo-symmetry [50] in the data plane.

The derived percentages of the adherences to the individual classes of models within (and outside of) a symmetry hierarchy branch will be specific to the noise level of the image to be classified and also very slightly specific to the algorithm with which the classification has been made. The effects of experimental noise and the utilized real world algorithm are summarized in a generalized noise level term. Reduced generalized noise levels of future image data from the same crystalline sample that are recorded with more sophisticated instruments and processed with more ‘truthful’ feature extraction algorithms will have a tendency to change the individual percentages somewhat, but will also never allow for definitive classifications. Additionally a reduction in the experimental noise level per unit cell can be obtained by the processing of a significantly larger image area that contains many more repeats of the 2D or 1D periodic motif.

Major goals of this review are to bring Kanatani’s comments [3] and dictum [9,10,114], as well as his G-AIC approach [9,10,11,12] to the attention of both the applied crystallography and the computational symmetry communities. The utilization of the information theory concept of (i) Akaike weights [13,14,15,16,17] and (ii) their products [13] for complementing geometric-structural pieces of information (that were extracted from the results of the same imaging experiment or from the same synthetic data) for generalized noise-level dependent crystallographic classifications of more or less periodic crystal patterns constitute the novel ideas of this paper. This review will concentrate on crystal patterns in the form of 2D gray-level images that are more or less periodic in one and two dimensions.

Secondary goals of this review are popularizations of a Fourier space version of Liu’s G-AIC for the assignments of plane symmetry groups to more or less 2D periodic images [4,5] and the author’s versions of such criteria for Bravais lattice type [7] and Laue class assignments to such images. The combination of G-AICs for Bravais lattice types, Laue classes, and plane symmetry groups should be useful to deal with the consequences of genuine pseudo-symmetries [50] that the hypothetical noise-free version of an image may possesses, either per design or by the nature of the crystalline sample from which it was recorded.

The rest of the paper is organized as follows: We begin with explaining the nature of Kanatani’s comments on symmetry as a continuous and hierarchic feature in Section 2. This is followed by a discussion of Kanatani’s dictum in Section 3. Within that section, we will concern ourselves with genuine pseudo-symmetries [50]—see Figure 1—which exist per the design of both of the constituting images and quote the related lattice parameter extraction results (for these two images) by three different algorithms/computer programs from [114]. The purpose of that part of this review is to illustrate the non-definitiveness of geometric-structural feature extraction results that are obtained by any real-world algorithm from noise-free and noisy images alike.

Readers interested in the details of the three computer programs that implement these algorithms are referred to [114] for comprehensive information. Two of these programs [115,116] are used in the applied crystallography community and the third [117] one supports all aspects of crystallographic image processing and electron crystallography on the basis of high-resolution (phase-contrast) transmission electron microscope (HRTEM) images [118,119,120,121] that were recorded within the validity range of the weak phase object (WPO) approximation. While one of these programs [115], and most algorithms of the computational symmetry community [1] work in direct space, the other two programs [116,117] that were utilized in [114] work in Fourier/reciprocal space.

For easy references below, we will use the capital letters A, B, and C instead of either the actual names of these three computer programs or their entries in the final list of references at the end of this review.

Table 1. Letter key for references to the three algorithms/computer programs for which we will quote quantitative results [114] in this review.

Algorithm’s Number in the Final Reference Section	Algorithm’s Letter Reference in this Review
[115]	A
[116]	B
[117]	C

provides the conversion key.

The fourth section on G-AICs reviews first the general form of these criteria and then proceeds by giving specifics of Fourier space versions of such criteria for fuzzy, i.e. quantitative generalized noise-level dependent classifications of geometric-structural feature extraction results into plane symmetry groups, Laue classes, and Bravais lattice types. Liu and her co-workers’ frieze pattern assignments to time series recording of both a walking humanoid avatar and a walking human being [4,5,6] will be mentioned in this section briefly (and discussed further in Appendix E) as illustrations of the fact that one should not only report the most likely crystallographic symmetry classification for a real-world experiment, but also its relative likelihood, as well as the likelihoods of reasonable alternatives in order to make a fair assessment of the crystallographic model selection uncertainty [13,14,15,16,17].

In the fifth section, we will provide equations for the relative likelihoods of disjoint and non-disjoint crystallographic symmetry models within a set, their respective mutual evidence ratios, and their Akaike weights. There are also equations for the usage of Akaike weights for multi-model predictions that are based on the relative probabilities of crystallographic symmetry models within a set. Section 5.1 contains the equations for combined posterior model probabilities [13] that are based on complementing pieces of geometric-structural information in more or less 2D periodic (noisy) images. The corresponding combined Akaike weights should be helpful for distinguishing between genuine and non-genuine pseudo-symmetries [50] that the hypothetical noise-free version of an image processes.

The fourth and fifth sections constitute the core of this review and contain the equations/inequalities that refine its novel ideas. Finally, there is a brief summary and conclusions section.

As already mentioned above, there are five appendices that present: (i) the potential of the main proposal of this review with respect of the extraction of grain boundary structures from atomic resolution images that are more or less periodic in 1D; (ii) different types of pseudo-symmetries; (iii) pseudo-symmetry mediated misclassifications in both the scientific literature and the major databases of mainstream 3D crystallography as well as a brief discussion of the crystallographic R value; (iv) statistical descriptors and null hypothesis tests in mainstream 3D crystallography; and (v) crystallographic comments on the only so far existing experimental 1D periodic study that utilized a geometric Akaike Information Criterion.

2. Kanatani’s Comments on Symmetry as a Continuous and Hierarchic Feature

At the core of Kanatani’s comments is the observation that symmetries must, with geometric necessity, be part of disjoint and non-disjoint hierarchy branches. This applies obviously to both crystallographic and non-crystallographic symmetries alike, although no such distinctions were made in [3], as a few non-disjoint and disjoint point symmetries were discussed exclusively.

Since hierarchy branches do exist, crystallographic symmetry types, classes, and groups are quite often non-disjoint. For example, a hexagonal rhombus (with an angle of 120° between its two edges of equal length) is higher up in the symmetry hierarchy than a general rhombus (where this angle is neither 120° nor 90°). The general rhombus, on the other hand, is higher up in the hierarchy than a parallelogram, where the two edges have different lengths and the angle is not 90°.

The square and hexagonal rhombi are, however, disjoint as they are at the top of different hierarchy branches of the quadrilaterals that serve as crystallographic unit cells [7,114]. Analogously, the rectangle and the general rhombus are disjoint as they are part of different hierarchy branches.

Kanatani illustrates in [3] that a consequence of these kinds of hierarchies is that one can never assign extracted geometric-structural features in an objective way to a more constrained symmetry type on the basis of a distance measure alone.

3. Kanatani’s Dictum

A direct quote from [9,10] is in order here to start this section: “The reason why there exist so many feature extraction algorithms, none of them being definitive, is that they are aiming at an intrinsically impossible task.” While this statement might be somewhat shocking to researchers who never before thought about this topic deeply, it is certainly true. No real world feature extraction algorithm working on real world data will ever be able to deliver definitive results. This is because all algorithms (and the computer programs that implement them) are based on heuristics and use approximations, as well as internal thresholds, to achieve their goals. Additionally, all real world image data are of finite resolution and noisy.

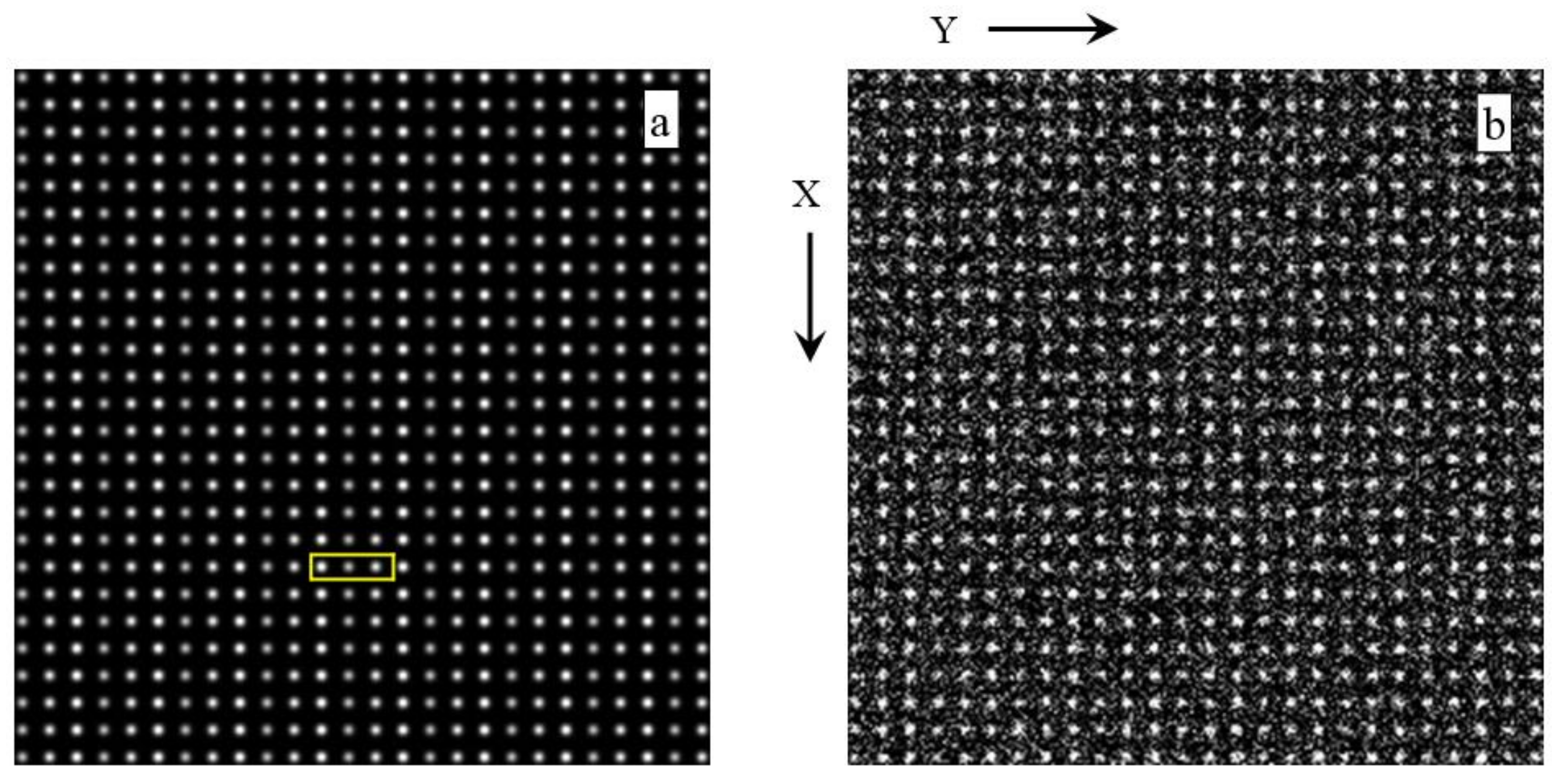
As mentioned above, a thorough illustration of Kanatani’s dictum within a crystallographic context is provided in [114]. We take from that paper the lattice parameter extraction results of the two images that are shown in Figure 1 but present them here in a form that is adjusted to the crystallographic setting that we use in this review.

The two images in Figure 1 are synthetic and freely downloadable (together with many more images of the same size and type) at the website that is listed as [122]. On the left hand side of this figure, there is the noise-free (original) image of the pair. The image on the right hand side of this figure has been obtained by adding independent Gaussian noise of mean zero and a standard deviation of 10% of the maximal image intensity to the individual pixels of the noise-free image to the left. The images in Figure 1 possess a rectangular (primitive) Bravais lattice and plane symmetry group pm in the crystallographic p1m1 setting [23,24] per design. One choice of a unit cell is outlined in Figure 1a by a rectangle in yellow ink. Other choices are possible because the origin is in this particular plane symmetry group not fixed at a specific point.

Per crystallographic convention [23,24], the x-axis ([10] vector) runs from the top-left corner of a unit cell to its bottom left corner (in the p1m1 setting). The y-axis ([01] vector) is perpendicular to the x-axis and runs from left to right. The unit cell edges x,0 = $\overrightarrow{a}$ and 0,y = $\overrightarrow{b}$ are in Figure 1 parallel to the image edges X,Y. The edge relationships between unit cells and images are usually arbitrary, i.e. not subject to any crystallographic restriction, so that Figure 1 shows a very special case of such a relationship.

Per crystallographic convention [23,24], the origin of each unit cell in plane symmetry group p1m1 (pm for short when the setting is not communicated), i.e. the position 0,0 from where all other positions are measured in fractions of the unit translation vectors, is located anywhere on a mirror line of position 0,y. 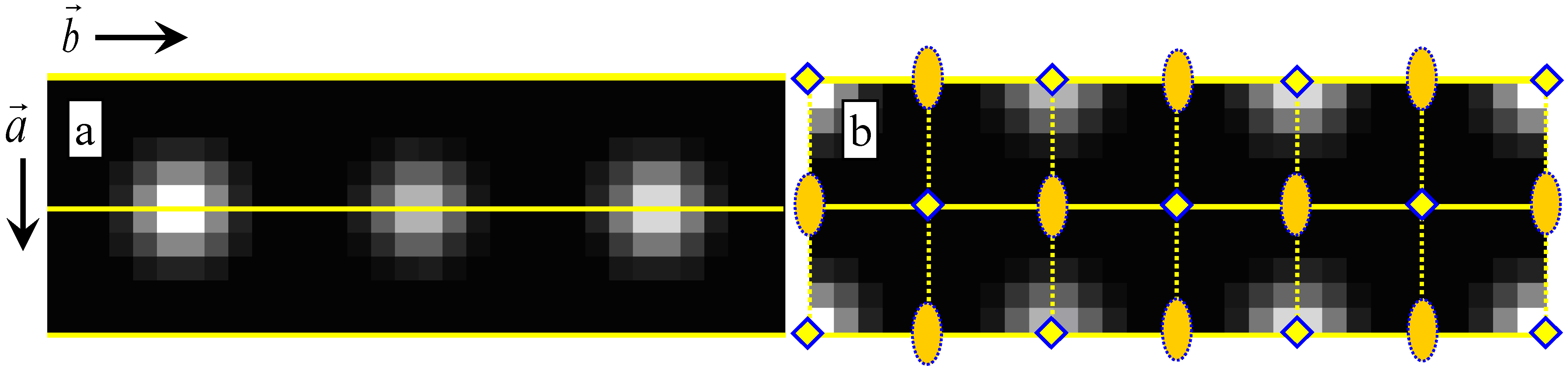Two possible choices of unit cells for Figure 1a that take the prevailing pseudo-symmetries of the Fedorov type [123] into account are given in Figure 2, where just one magnified single unit cell cutout is displayed both on the left- and right-hand sides of this figure. Pseudo-symmetries of the Fedorov type are compatible with a crystallographic lattice that is of the Bravais type. That lattice is not necessarily the prevailing (genuine) crystallographic lattice; see Appendix B for more information.

As Figure 2a shows, there is always a second mirror line at position ½,y in the unit cell in plane symmetry group p1m1. This mirror line and the 0,y (and 1,y) mirror line(s) are displayed by full yellow lines in both parts of Figure 2. The coordinate y varies from 0 to 1 in the 0,y and ½,y labels of sets of special points, which carry Wyckoff letters a and b, respectively [23,24]. The points y = 0 and y = 1 are symmetry equivalent by way of one unit translation along the y-axis. The genuine translation symmetry in all subfigures of Figure 1 and Figure 2 is that of the rectangular (primitive) Bravais lattice type per design.

As far as genuine point/site symmetries are concerned, the full (four letter) plane symmetry group symbol (p1m1) details that there are only one-fold rotation points in the plane of the image, mirror lines perpendicular to the [10] direction of the unit cell, and one-fold rotation points along its [01] direction; see Figure 1a and Figure 2a. Sets of mirror lines are in crystallography represented by their geometric normal, which are, in Figure 1a and Figure 2a oriented perpendicular to the vector [10] = $\overrightarrow{a}$ due to the p1m1 setting.

The ½,y mirror line (which carries Wyckoff letter b in p1m1 [23,24]) splits the three white blobs of the translation periodic motif (and their immediate black surroundings) in Figure 1a and Figure 2a into upper and lower halves. While this line is not drawn out in Figure 1a, it is given as a full yellow line in Figure 2a. The multiplicity of points that are located on that mirror line is one. All of these points are, therefore, at a special position in this plane symmetry group. The general position, on the other hand, possesses a multiplicity of two so that there is a symmetry equivalent $\overline{x},y$ position for each x,y position. Both of these positions carry Wyckoff letter c in plane symmetry group p1m1. The asymmetric unit is just one half of the unit cell as sectioned by the ½,y mirror line; see Figure 2a. The alternative asymmetric unit in Figure 2b is composed of one half each of the two less intense white blobs plus two quarters of the most intense white blob and their immediate black surroundings.

Genuine motif-based (four-fold rotation points plus vertical mirror lines) pseudo-symmetry is also present in both images of Figure 1 and Figure 2. This pseudo-symmetry is of the Fedorov type [123]—see Appendix B—and complicates the crystallographic analysis and symmetry classification. The complications are particularly severe in Figure 1b due to the added noise. Genuine translational pseudo-symmetry is caused by the similarity in intensity and size of the three white blobs that form (together with their immediate black surroundings) the content of the rectangular unit cell in Figure 2a.

While the 0,y and ½,y mirror lines in this figure are genuine and intersect the white blobs horizontally, there are also x,0, x,¹/₃, and x,²/₃ pseudo-mirror lines that intersect the while blobs vertically. In order to avoid overcrowding, these pseudo-mirrors are only given as dotted yellow lines in Figure 2b.

These three pseudo-mirror lines generate three more parallel pseudo-mirror lines at positions x,¹/₆, x,³/₆, and x,⁵/₆ , which intersect the black background areas between the white blobs in the middle vertically. The above-mentioned genuine mirror lines 0,y and ½,y (of Figure 1a and Figure 2a) combine with the perpendicular pseudo-mirror lines as drawn into Figure 2b. This generates pseudo-four-fold and pseudo-two-fold rotation points at the crossings of genuine mirror lines and pseudo-mirror lines so that Fedorov pseudosymmetry group p_b/34mm ⊃ p1m1 results on the basis of the rectangular Bravais lattice. The pseudo-four-fold rotation points contain in themselves pseudo-two-fold rotation points. There are alternatives to construct the Fedorov pseudosymmetry group that Figure 1a and Figure 2a,b possess, but they all lead to the same end result.

With respect to Figure 1a, the origins of the two unit cells in Figure 2 are shifted to the position of a four-fold pseudo-rotation point. There are two such points in pseudo-symmetry group p_b/34mm, which carry pseudo-Wyckoff letters a and b, and their locations with respect to the pseudo-square lattice are 0,0 and ½,½, respectively. As a result of the combination of the genuine symmetries and pseudo-symmetries in Figure 1a, the genuine rectangular lattice of Figure 1a and Figure 2a is “truncated” into a pseudo-square lattice as outlined in Figure 2b.

Due to its design history, the image in Figure 1b possesses also plane symmetry pm (in the p11m setting) but all genuine (point/site and translation) symmetries have been turned into non-genuine (second kind) pseudo-symmetries—see Appendix B—by the added noise. These pseudo-symmetries exist in addition to the above-mentioned genuine pseudo-symmetries. A complementary description of the two images in Figure 1 is provided in [114]. Note that a complementary setting has been used in that paper, but this is inconsequential to a crystallographic analysis. The results of any such analyses will be complementary, e.g., a unit cell angle in one setting would be the difference between 180° and that angle in another setting.

Note that Kanatani includes, per definition, all kinds of image feature extraction uncertainties into the generalized noise term in his G-AICs so that one cannot extract definitive results even from the image in Figure 1a, which is free of added Gaussian noise. In this review, noise is treated in the generalized sense that is in accord with Kanatani’s dictum [9,10].

As already mentioned above, the main thrust of [114] was to illustrate Kanatani’s dictum on multiple examples. Since three algorithms/computer programs were applied to a total of 12 images in [114], a measure of the reliability of subsequent geometric inferences on the basis of the outputs of the computer programs that implemented these algorithms was also obtained. Additionally, since the three algorithms were tested on both noise-free images (such as the one shown in Figure 1a) and noisy images that were derived from the noise-free images (such as the one in Figure 1b), the robustness of the algorithms/computer programs in the presence of Gaussian noise was also tested in [114].

The ratio of the lattice parameters (a/b) of the unit cells in the two images in Figure 1 and Figure 2 is one third and the unit cell angle γ is 90° per design. Values close to this ratio and angle should, therefore, be obtained as result of lattice parameter extractions with suitable computer programs even in the presence of noise.

Table 2. Extracted lattice parameters from the noise-free image in Figure 1a and derived unit cell areas utilizing the default settings of three computer programs. The qualitatively correct result is marked in bold font.

Algorithm’s Reference Letter	a/b	γ in °	Unit Cell Area in Square Pixels
A	0.333 ± 0.06	90.0 ± 0.4	300.0 ± 2.0
B	1.004 ± 0.01	90.0 ± 0.05	99.4 ± 1.0
C	0.998 ± 0.01	90.0 ± 0.05	99.8 ± 1.0

,

Table 3. Extracted lattice parameters from the noise-free image in Figure 1a and derived unit cell areas after a re-interpretation of the results from Algorithm B and as obtained in a non-default setting of Algorithm C. Both results are qualitatively correct and, therefore, marked in bold font.

Algorithm’s Reference Letter	a/b	γ in °	Unit Cell Area in Square Pixels
B	0.335 ± 0.01	90.0 ± 0.05	298.2 ± 3.0
C	0.333 ± 0.02	90.0 ± 0.05	300.0 ± 2.0

,

Table 4. Extracted lattice parameters from the noisy image in Figure 1b and derived unit cell areas utilizing the default settings of three different computer programs. There is no qualitatively correct result to be marked in bold font.

Algorithm’s Reference Letter	a/b	γ in °	Unit Cell Area in Square Pixels
A	1.414 ± 0.07	135.8 ± 0.6	98.6 ± 1.5
B	0.995 ± 0.01	90.2 ± 0.05	99.1 ± 1.0
C	1.000 ± 0.01	90.0 ± 0.05	100.0 ± 1.0

and

Table 5. Extracted lattice parameters from the noisy image in Figure 1b and derived unit cell areas after a re-interpretation of the results from Algorithm B and as obtained in a non-default setting of Algorithm C. Both results are qualitatively correct and, therefore, marked in bold font.

Algorithm’s Reference Letter	a/b	γ in °	Unit Cell Area in Square Pixels
B	0.332 ± 0.01	90.2 ± 0.05	297.3 ± 3.0
C	0.333 ± 0.02	90.0 ± 0.05	300.0 ± 2.0

list the results of the application of the three different computer programs [114] of Table 1 as adapted to the particular unit cell setting of this review (Figure 2). Results that were obtained in the default settings of the three computer programs that implement three different types of algorithms (A to C in Table 1) are listed for the image in Figure 1a in Table 2 and for the image in Figure 1b in Table 4. Table 3 list re-interpreted/re-calculated results from Algorithm B (on the basis of the displayed dFT amplitude map) and results that were obtained in a non-default setting of Algorithm C for the image in Figure 1a. Table 5 does the same kind of thing for the image in Figure 1b.

Somewhat surprisingly, Table 2 shows that only one of the three tested algorithms extracted qualitatively correct lattice parameters from the noise-free, but visibly pseudo-symmetric, image in Figure 1a. These lattice parameters are in good compliance with the rectangular Bravais lattice type that this image possesses per design. For easy reference, qualitatively-correct results are marked in bold font in all of the four image data tables in this review.

Only Algorithm A was, thus, capable of dealing with the translational pseudo-symmetry in Figure 1a effectively as its lattice parameter extraction results are given in bold font in Table 2. The other two algorithms extracted in their default settings a unit cell that is too small by a factor of three from this figure. This is also reflected by the ratio of the two basis vectors, which was incorrectly determined as nearly unity by Algorithms B and C in their respective default settings [114].

Extracted basis vectors that nearly possess the same magnitude, and are also perpendicular to each other within error bars, are, of course, what one would expect for a square Bravais lattice. In other words, to the Algorithms B and C in their default settings, the existing (genuine) translational pseudo-symmetry [50] in Figure 1a was apparently a crystallographic symmetry since ‘quantitatively wrong’ lattice parameter sets were extracted.

It was straightforward to re-interpret/re-calculate the lattice parameter extraction output for Figure 1a as obtained with Algorithm B on the basis of the dFT amplitude map that the program displayed [114]. This resulted in a bold font entry for qualitative correctness in Table 3 for Algorithm B. For Algorithm C, using a non-default setting in the processing of Figure 1a also resulted in a bold font entry in this table.

The added noise in Figure 1b ‘fooled’ all three computer programs (in their default settings) into extracting results that are obviously incorrect, see Table 4. This is a direct consequence of the noise-exacerbated pseudo-symmetries in the image shown in Figure 1b. The oblique unit cell that Algorithm A extracted from the image in Figure 1b—see Table 4—can be straightforwardly transformed into a pseudo-square unit cell with essentially the same parameters as those that were obtained with the other two algorithms.

Re-interpreting/re-calculating the lattice parameter extraction outputs for the image in Figure 1b as obtained with Algorithm B (on the basis of the dFT amplitude map of that image) and using a non-default setting of Algorithm C in the processing of this image led to qualitatively correct results and bold font entries for both algorithms in Table 5.

The stated error bars on the unit cell angles of 0.05° for the two algorithms/computer programs that extract lattice parameters in Fourier space, i.e. B and C, are based on the implied number of significant figures output by one of these programs [114], but seem to be too small to allow for agreement of the extraction results of the different algorithms in the case of lattice parameter extractions by the default program settings from the noisy image in Figure 1b.

The traditional way of assigning Bravais lattice types to the lattice parameters of the two images in Figure 1 that have been extracted by three different algorithms within the stated error bars as listed in Table 2, Table 3, Table 4 and Table 5 may, obviously, lead to misclassifications given the numerical variations in these tables. If one does not know the design parameters and history of the two images in Figure 1 in advance, one is hard pressed to figure out which of the results in these four tables are actually trustworthy, let alone to make definitive classifications into Bravais lattice types. One would certainly be ill advised to average the results from the three different algorithms in Table 2 and Table 4.

Guided by the ‘somewhat squarish’ visual appearance of what appears to be unit cells in the image of Figure 1b, most researchers would probably classify that image as belonging to the square Bravais lattice type. Two of the results listed in Table 4 would support this classification in the traditional way based on the numerical values of the extracted lattice parameters and their somewhat extended error bars. This would, however, be incorrect!

A fuzzy classification into Bravais lattice types on the basis of translation symmetry model probabilities (Akaike weights) would, on the other hand, be noise-level dependent and correct in a fundamental sense. Likewise fuzzy classifications into (i) Laue classes on the basis of point/site symmetry model probabilities and (ii) plane symmetry groups on the basis of plane symmetry model probabilities, both utilizing complementing types of Akaike weights, would also be correct in a fundamental sense and generalized-noise level dependent.

The crystallographic symmetry classifications of the image in Figure 1a would obviously be much less fuzzy than those of the image in Figure 1b, although still not completely definitive as a matter of principle when a real world algorithm is involved. It is expected that the crystallographic classifications of both images would peak for plane symmetry group pm, Laue class 2mm, and the rectangular (primitive) Bravais lattice type. This is because these crystallographic categories went into the design of both images.

In case of the image in Figure 1a, the peaking at these crystallographic categories will be much sharper than for the image in Figure 1b because only geometric-structural feature extraction uncertainties that are due to the particulars of the applied algorithms/computer programs will make the classifications of the former image fuzzy (as there is no added Gaussian noise present that disturbs the recognition of the design categories).

4. Geometric Akaike Information Criteria (G-AICs)

4.1. General Considerations

All G-AICs transfer the central idea of the very widely employed Akaike Information Criterion (AIC) [124,125] of traditional statistics, which is based on the asymptotic limit of an infinite number of observations, to Kanatani’s new type of statistics where a vanishing noise level serves as the asymptotic variable and where there is typically only one observation/image [9,10,11,12].

The following direct quote from Hirotugu Akaike’s original paper [124]: “AIC = (−2) log (maximum likelihood) + 2 (number of independently adjusted parameters within the model)” illustrates that the ‘accuracy’ of a model which constitutes the first term (and is obtained from a maximal likelihood estimation of the model’s parameters) is balanced by the ‘complexity’ of the model (by means of a penalty for having a certain number of free parameters available for the fitting of the model to the data), which constitutes the second term. The ‘log’ in this quote refers to a logarithm to the basis of Euler’s number, i.e. is typically referred to as ‘ln’ outside of the statistics community.

More precisely, the negative log-likelihood score of a model is a measure of the lack of its fit to the data. It forms the first term in an AIC. The second term of an AIC is simply a penalty for greater model complexity, i.e. represents a bias correction. When two frequency-based models for the same data are compared with respect to their predictive power, the model that possesses the smaller AIC value is considered to be the better one.

Traditional AICs, as stated above, and versions of them that account for unfavorable ratios between the number of observation and the number of model parameters are very widely used in countless branches of science and engineering [13,14,15,16,17]. Information criteria that are either derived from Akaike’s AIC or are based on traditional (frequentist) statistics alternatives to this criterion are also at the core of the quantitative model-based atomic resolution TEM approach [27] that was mentioned in the Introduction and Background section.

Akaike referred to his criterion simply as “an information criterion” [124]. The acronym MAICE, which stands for “minimum information theoretic criterion (AIC) estimate”, was also introduced by him. Akaike wrote in 1974 that “the need of the subjective judgment required in the hypothesis testing procedure … is completely eliminated” by the utilization of MAICEs because “the problem of statistical identification is explicitly formulated as a problem of estimation” [124].

As already mentioned above, geometric AICs contain two terms that are analogous to the two terms in the traditional (frequentist) AIC. The particulars of the form of the second term depend on the types of geometric models in a set, from which the one that minimizes the G-AIC value is to be selected as the best model for representing the image data information.

For the practical application of a G-AIC, noise in images must be (to a sufficient approximation) of the ‘white’ Gaussian type and systematic errors in the imaging and algorithmic processing procedures must be small in comparison to random errors. Since G-AICs are first-order approximations, the generalized noise level must be reasonably small. All these preconditions are fulfilled by image recordings with certain modern scientific instruments, where the extraction of model parameters from the recorded data planes proceeds, to a large extent, independently of the particulars and type of the instruments, e.g., STMs, STEMs, …, HRTEMs (in the WPO approximation) as mentioned in the Introduction and Background section, with which image data has been recorded [7,19,20,21,22,26,27,28,29,30,31,115,116,117,118,119,120,121].

With ‘independent to a large extent’, this author means that specifics of the point-spread function of a microscope should be included when better results are required. Approximate results are to be expected when these specifics are ignored. Similarly, the real structure of crystalline samples could either be included for better results or ignored for approximate results.

By virtue of the central limit theorem of frequentist statistics, the white/Gaussian noise requirement of G-AICs can often be considered as fulfilled when there are several different types of noise in a microscopic imaging process [26]. Different types of noise will originate from different sources, but none of these sources are allowed to be dominant for this theorem to be valid.

As a very notable difference to the AIC of traditional statistics, noise is not a model parameter in Kanatani’s G-AIC. Vanishing noise is instead the asymptotic limit in this new kind of statistics in a way similar to the number of observations going to infinity in frequentist statistics. The requirement of Gaussian noise results in maximal likelihood determination procedures of the model parameters that take on the form of least squares fits of the models to the data in G-AICs. Additionally, the number of data points and the dimension of the model enter the penalty term of the equation of the G-AIC, while their counterparts are absent in the equation for the traditional AIC.

When the experimental noise in a more or less 2D periodic image is of the Gaussian type, the standard deviations of the mean values of the intensity of corresponding pixels in repeating unit cells decrease with the square root of the number of repeats. This allows for more precise estimates of the mean values of the intensity of the group of individual pixels that collectively form the 2D periodic unit cell. Loosely speaking, this is analogous to a reduction of the noise level per unit cell. The disturbing effects of the 10% Gaussian noise in the image in Figure 1b are thereby reduced to less than 1% per unit cell.

4.2. G-AIC for Plane and Frieze Symmetry Groups

Liu and coworkers state in [4] (and in the appendix of the earlier version of their paper [5]) that the dimension of their data space is 1 and the dimension of their model space is 0, so that a co-dimension of 1 results. Simple algebra leads to the following ratio of the least-square residual, J, of a more symmetric model, S_more, to the least-squares residual of a less symmetric (more general) model (S_less) that is non-disjoint:

$$\frac{J[S_{more}]}{J[S_{less}]}<1+\frac{2(k_{more}-k_{less})}{k_{more}(k_{less}-1)}$$

(1)

The fulfillment of this inequality allows one to conclude that the (non-disjoint) more symmetric model is the one of the two models that minimizes the expected Kullback-Leibler information loss when one deals with the unit cell content. The variable k is thereby the so called multiplicity of the general position of a plane [23,24] or frieze [35] symmetry group. In the language of 1D and 2D crystallography, the non-disjoint relations of set theory are referred to as maximal non-isomorphic translationengleiche and klassengleiche type IIa subgroup-supergroup relationships, as exhaustively tabulated in [35] and [23,24].

Note that although the least squares residual of the more general (less symmetric) model will typically be smaller than its counterpart for the less general (more symmetric) model or, at most, equal to it, Inequality (1) still allows for the selection of the more symmetric model if its residual is not too large. This is because the model accuracy is balanced in the G-AIC by a penalty term that includes both the higher multiplicity of the general position of the more symmetric model and the lower multiplicity of the general position of the less symmetric model.

There was only one application of Inequality (1) to the identification of most likely frieze symmetry groups [4,5] so far in the scientific literature and none to the identification of most likely plane symmetry groups of which the author of this review is aware. This state of affairs might be due to the necessary computational effort for obtaining the residuals in direct space as the sums of all squared differences of pixel intensities between the raw image and its symmetrized versions [4,5]. Additionally, there is the non-trivial issue of aligning the raw image and its symmetrized versions in direct space; see Appendix E for possible consequences of misalignments and ignorance of the crystallographic origin conventions [23,24,35].

There is, however, a straightforward way to overcome both of these problems in Fourier space that goes by the name of crystallographic image processing [21,22,25]. Origin alignments are actually straightforward in reciprocal space and part of the crystallographic image processing procedures.

Since the intensity values of all pixels contribute to all Fourier coefficients (FCs), the sums of the squared differences of the complex FCs of the raw image and its symmetrized versions can be calculated in Fourier space and be substituted into Inequality (1) for the real space residuals. The complex FCs residuals enter Inequality (1) without modification of its right-hand side because one may substitute the multiplicity of the general position in direct space for the number of symmetry operators of a plane symmetry group. This number is the same in both direct [23,24] and reciprocal/Fourier space [126]. The Fourier space approach to the interpretation of Inequality (1) is enabled by the Fourier coefficient model residuals that approximate [127,128,129,130,131,132,133,134] the direct space least-squares model fitting residuals reasonably well.

While a more or less 2D periodic square image with an edge length of 512 pixels possesses 262,144 individual pixels, there may be less than a hundred FCs to represent all of the information that is contained in it in Fourier space. A large reduction in the computational effort will, therefore, result when one works in Fourier space for the determination of the ratios of the least-squares residuals in Inequality (1).

The precondition for going into Fourier space is from this author’s experience that there are at least some 50—or better yet more than 100—unit cell repeats in the image in order to keep series truncation artifacts and edge effects small. Inequality (1) implies the presence of an integral number of unit cells in the more or less 2D periodic image. Artifacts due to incomplete unit cells and the multiplicities of special positions [23,24,35] should become negligible when the pixels within a unit cell are numerous and there are many repeats of the more or less translation periodic motif in the image.

While large numbers of repeating noisy unit cells are often not present in images that are usually studied by the computational symmetry community [1,2,4,5,6], they are commonplace in images that are processed by the applied crystallography community.

4.3. G-AIC for 2D Laue Classes

The Laue class of a more or less 2D periodic image is visibly displayed in the amplitude map of its dFT. As a matter of fact, the FC amplitudes are laid out in such a map as discrete values at the positions of the nodes of the reciprocal lattice of the image.

One can, therefore, use Inequality (1) as well when one bases the residuals on the sums of the squared differences between the dFT amplitudes of the raw image and the dFT amplitudes of its symmetrized versions. Crystallographic image processing [21,22] provides, again, the means to obtain the residuals in a computationally efficient manner. The same kinds of considerations of the number of pixels in the image and the number of repeating noisy unit cells in direct space apply as in the previous section.

There are six Laue classes in 2D in both direct and reciprocal/Fourier space. In the latter space, the Laue symmetry classes are defined with respect to the central 0,0 FC amplitude peak in a dFT.

When the Laue class is, for example, assigned to the image in Figure 1a by means of a G-AIC, one will for sure obtain the highest model probability for class 2mm. This is because the plane symmetry of that noise-free image is per design pm, which is ‘mathematically linked’ to Laue class 2mm. The visible four-fold rotation points plus mirror lines (motif-based) pseudo-symmetry in this figure will then be revealed as such.

Plane symmetry pm is of the non-centrosymmetric type [23,24], which means the phase angles of the FCs of the image intensity are not all restricted to be either 0° or 180°. This fact should come in handy when one is trying to deal with the noise-exacerbated pseudo-symmetries in the image in Figure 1b. The associated Akaike weight products of joint fuzzy assignments to Bravais lattice types, Laue classes, and plane symmetry groups (on the basis of the applicable G-AICs) should be able to reveal the pseudo-symmetries also for this image.

One should, therefore, at least for manifestly pseudo-symmetric images, strive for combinations of G-AICs and Akaike weight products in order to make the best use of the available types of complementing geometric-structural information in more or less 2D periodic images.

4.4. G-AIC for 2D Bravais Lattice Types

The author of this review derived the G-AIC for Bravais lattice type assignments to lattice parameters that were extracted from more or less 2D periodic images [7]. For identifying the (non-disjoint) higher symmetric translation symmetry model that minimizes the expected Kullback-Leibler information loss, the following inequality:

$$\frac{J[S_{more}]}{J[S_{less}]}<\frac{2L_{more}-L_{less}}{L_{less}}$$

(2)

suffices, where L is the number of constraints on a quadrilateral that serves as the shape of a crystallographic unit cell. The fulfillment of this inequality means that the more symmetric translation symmetry model is, on information theory grounds, to be preferred over the less-symmetric translation symmetry model.

Table 6. Number of constraints that enter Inequality (2) in a G-AIC for the fuzzy classification into Bravais lattice types.

Parallelogram	Rectangle	General Rhombus	Square	Hexagonal Rhombus
2	3	3	4	4

lists these numbers for easy reference.

4.5. When is a Noise Level Estimate Mandatory?

There is obviously no need to make an estimate of the generalized noise level of a more or less 2D periodic image in order to use Inequalities (1) and (2). This is due to our dealing with non-disjoint models in these cases, i.e. with models within a crystallographic symmetry hierarchy branch. One can, for the comparison of a pair of such models, as implicitly stated in Inequalities (1) and (2), eliminate the need to know the noise level by algebraic means.

As already mentioned above, comparing disjoint models does, on the other hand, require an estimate of the generalized noise level (Equation (3) below) on the basis of the best model in the set. Such estimates are of particular importance when there are both genuine and non-genuine pseudo-symmetries [50] in a noisy 2D periodic image that is to be classified.

5. Utilizing Geometric Akaike Information Criteria

5.1. Highlights of the Underlying Information Theory

When one has identified the model that minimizes the expected Kullback-Leibler information loss, i.e. the so-called ‘Kullback-Leibler best’ [13,14,15,16,17] model, by a boot-strapping approach within a symmetry branch, one can obtain a good estimate for the noise level on the basis of this model by the following equation:

$${\widehat{\sigma }}^2\approx \frac{J[S_{best}]}{r_{best}N-n_{best}}$$

(3)

where r is the co-dimension, N is the number of data points, n is the degree of freedom (in the mathematical sense, i.e. the number of independent pieces of information that enter into this equation), and the subscript _best represents the best model in the set [10,11,12]. The hat over the sigma means that it is an estimator.

For this particular model, one can be confident to have extracted the maximum of geometric-structural information from the image by the least-squares fitting of the model parameters to the image data while also separating out the ‘non-information’ that is summed up in the generalized noise estimate of Equation (3).

The estimate of the noise level in the image according to Equation (3) becomes part of the full (first-order) equation for the G-AIC of all i models S_i within a set:

$$AI{C}_i[S_i]=J_i[S_i]+2(d_{i}N+n_i){\widehat{\sigma }}^2$$

(4)

where d is the dimension of the model.

All G-AIC values are relative and on the scale of information. Only the relative differences of the AIC_i values of the i models in either a disjoint or a non-disjoint set matter for crystallographic symmetry classifications.

These differences are standardized on the basis of the Kullback-Leibler best model in the set, i.e. the one for which we obtained the minimum G-AIC value from Equation (4). The (standardized or rescaled) model-specific G-AIC differences are obtained by:

$${\Delta }_i=AI{C}_i-AI{C}_{best}$$

(5)

for all i models in a set of models. This kind of difference is obviously zero for the best model in the set, which possesses the smallest G-AIC value and is designated by the subscript _best.

The relative likelihoods of all i models in the set are obtained by Akaike’s transformation [13,14,15,16,17,125]:

$${\ell }_i\propto \exp (-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\Delta }_i)$$

(6)

where ∝ represents ‘proportional to’ and the pre-factor of ½ on the standardized G-AIC differences is due to the original definition of the traditional AIC [124,125]. The best model in the set obtains a relative likelihood of unity and all other models come in at a fraction of unity.

The evidence ratio of one model with respect to another one within the model set is obtained by:

$$E_{i,j}=\raisebox{1ex}{${\ell }_i$}\!\left/ \!\raisebox{-1ex}{${\ell }_j$}\right.=\exp (-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\{{\Delta }_i-{\Delta }_j\})$$

(7)

Evidence ratios have a “raffle ticket interpretation” in quantifying the strength of evidence in favor of one model with respect to another in the same set [13]. When, for example, the evidence ratio of model X with respect to model Y is 20, there is at the very least moderate if not strong evidence in support of model X. The difference of the two related relative G-AIC differences in the inner parentheses in Equation (7) is then approximately 6.

This is analogous to model X possessing 20 raffle tickets while model Y possesses only a single ticket. Clearly model X is then more likely to win a raffle and the evidence in support of it is stronger than for model Y, which is, however, not to be discarded as it is not entirely without merit [13] given the generalized noise level.

Note in passing that twenty-to-one odds are incidentally also the basis of many traditional ad hoc ‘tail probability threshold ≤ 0.05’ null hypothesis (‘p-value significance’, ‘α-level’) testing schemes [13]. Note also in passing that Walter Clark Hamilton pioneered the application of such a hypothesis testing scheme for nested crystal structure models in mainstream 3D crystallography on the basis of the ratio of generalized crystallographic ‘R factors’ in 1965 [98]. The information theory-based approach utilized above is, however, much more powerful [13,14,15,16,17] than that kind of null hypothesis testing and does not ‘clip off’ models with moderate and small likelihoods as they could turn out to be correct when data with significantly reduced noise levels becomes available in the future. In Kenneth P. Burnham’s and David R. Anderson’s own words: “information-theoretic criteria … are not a ‘test’ in any sense, and there are no associated concepts such as test power or p-values or α-levels” [15]. Standard statistical descriptors and the utility of contemporary null hypothesis tests in mainstream 3D crystallography are further discussed in Appendix D.

Individual model probabilities that add up to 100% for the whole set of R models are commonly referred to as either Akaike weights [13,14,15,16,17] or “Bayesian posterior model probabilities” [13]. These probabilities are obtained by the normalization of the relative model likelihoods:

$$w_i=\frac{\exp (-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\Delta }_i)}{{\displaystyle \sum _{r=1}^R\exp (-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\Delta }_r)}}\cdot 100\%$$

(8)

where a given w_i is the probability that model i is the Kullback-Leibler best model. Akaike weights for a subset of models are additive and can be summed into confidence sets [13]. Obviously, the sum of all Akaike weights in the full set is 100%. While summing into confidence sets is somewhat subjective, there is certainly no arbitrariness in the usage of the equations and inequalities of this review. Note that the alternative name of Akaike weights, i.e. Bayesian posterior model probabilities, does not imply that the information theory approach is to be considered a “Bayesian approach” to statistics. As it can also not be classified as frequentist, it represents something new because it combines the positive features of both approaches while being essentially free of their negative features.

Akaike weights are also useful for the averaging of model parameters and predictions that are based on a multitude of ‘low-Δ_i models’ within a set [13,14,15,16,17]. Model parameters are in the context of this review the values of the unit cell parameters in direct and reciprocal space, the discrete Fourier coefficient amplitude and phase angles of the image intensity that form (in reciprocal space) the ‘Fourier equivalent’ [126] of the asymmetric unit of a plane symmetry group, and the gray level values of the group of individual pixels that collectively form the asymmetric unit in direct space.

Higher symmetric translation symmetry, Laue symmetry, and plane symmetry models possess obviously fewer parameters than their lower-symmetric counterparts. Just as unit cell parameters are restricted by translation symmetries in all Bravais lattice types higher than oblique, the values of the gray levels of the individual pixels that form a unit cell in direct space are restricted by site symmetries higher than the identity rotation in all plane symmetry groups higher than p1 and pg.

Typical predictions of higher symmetric plane symmetry models in direct space are the values of all pixels in the unit cell rather than just of those pixels that form collectively the asymmetric unit. Model predictions in Fourier space refer to the whole discrete and complex reciprocal data plane rather than just the Fourier space equivalent of the asymmetric unit [126].

Model averaged parameters or predictions are simply the weighted averages over parameters or predictions within a model set:

$${\widehat{\theta }}_{average}={\displaystyle \sum _{i=1}^R{w}_i\cdot {\widehat{\theta }}_i}$$

(9)

where the ‘hat’ over the symbol for the parameter or prediction refers to an estimate [13]. An estimator of the variance of a parameter or prediction estimate that incorporates a variance component for model selection uncertainty is given by:

$$\mathrm{v}\widehat{\mathrm{a}}\mathrm{r}({\widehat{\theta }}_{average})={\displaystyle \sum _{i=1}^R{w}_i\cdot \left\{\mathrm{v}\widehat{\mathrm{a}}\mathrm{r}({\widehat{\theta }}_i|g_i)+{({\widehat{\theta }}_i-{\widehat{\theta }}_{average})}^2\right\}}$$

(10)

where g_i is the ith model and the extended notation ${\widehat{\theta }}_i|g_i$ clarifies that the parameter or prediction estimator is in each of the R cases specific to a model in the set.

The variance estimate assesses the precision of the parameter or prediction estimate over the considered set of models and allows for the generation of confidence intervals that incorporate a measure for the model selection uncertainty. The standard error of a parameter or prediction is in multi-model averaging given by:

$$se({\widehat{\theta }}_{average})=\sqrt{\mathrm{var}({\widehat{\theta }}_{average})}$$

(11)

Thus, a 95% confidence interval [13] (or reasonable error bar widths on the model averaged parameters or predictions in other words) can be approximated by:

$${\theta }_{average}\pm 1.96\cdot se$$

(12)

Equation (8) may also be utilized to combine for a more or less 2D periodic image the probability of its fuzzy classification into a Bravais lattice type with the probability of its fuzzy classification into a Laue class. The combined fuzzy classification of such an image into a Bravais lattice type and a plane symmetry group is also possible on the basis of Equation (8). This particular combination of fuzzy classifications is probably effective for dealing with genuine pseudo-symmetries in the presence of noise and will be further discussed below in Section 5.2.

When a set of discrete prior probabilities on models, p_q, exists (in a Bayesian sense [13]) that is best at representing complementary (other) aspects of the finite information in the image data, one is justified to obtain ‘updated’ Bayesian posterior model probabilities by an extension of Equation (8) to:

$$w_{i,q}{}^{updated}=w_i\cdot w_q=\frac{\exp (-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\Delta }_i)\cdot p_q}{{\displaystyle \sum _{r=1}^R\exp (-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\Delta }_r)\cdot {\displaystyle \sum _{h=1}^H{p}_h}}}\cdot 100\%$$

(13)

where:

$$\begin{array}{l}\frac{p_q}{{\displaystyle \sum _{h=1}^H{p}_h}}=w_q\\ \frac{p_q}{{\displaystyle \sum _{h=1}^H{p}_h}}=\frac{\exp (-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\Delta }_q{}^{other\_aspects})}{{\displaystyle \sum _{h=1}^H\exp (-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\Delta }_h{}^{other\_aspects})}}\cdot 100\%\end{array}$$

(14)

Fuzzy plane symmetry group and Laue class assignments complement fuzzy Bravais lattice type assignments in 2D because all three of them are based on different (but complementary) pieces of geometric-structural information in the same complex dFT data plane. Equation (13) may, therefore, be expanded by a third factor as defined by Equation (14). A combined Akaike weight with factors for Bravais lattice types, Laue classes, and plane symmetry groups would constitute some kind of a comprehensive probabilistic crystallographic symmetry classification of a more or less 2D periodic image at a given signal to noise ratio.

While the translation symmetry of a Bravais lattice type is contained in a plane symmetry group, a Laue symmetry is just a point symmetry that includes the symmetry of the Fourier transform itself.

5.2. Updated Bayesian Posterior Model Probabilities and Confidence Sets for Crystallographic Symmetry Classifications

5.2.1. Illustration of the Updated Bayesian Posterior Model Probabilities Idea

It is expected that the Bayesian posterior model probability update approach of Equations (13) and (14) will be helpful for the recognition of genuine pseudo-symmetries in noisy 2D periodic images that exist either per design of the image or by the nature of the crystalline sample that has been imaged. This expectation is founded on the fact that Equation (13) represents a product of normalized probabilities.

If we take, for example, the two images in Figure 1, it was demonstrated in Section 3 that the parameters of a rectangular Bravais lattice can be readily extracted in reciprocal space even in the presence of the given amount of Gaussian noise (in the image in Figure 1b) and a genuine translational pseudo-symmetry when one takes the amplitude map of the dFT into account; see Table 5.

Both of these images will, therefore, obtain large Akaike weights for the rectangular Bravais lattice type by the application of Equation (8). The Akaike weights for the square lattice type with the same unit cell area, on the other hand, will on the basis of Equation (8) be very small for both images given the extracted (qualitatively correct) lattice parameters in Table 5. This should settle the question of the prevailing translation symmetry in the presence of a genuine translational pseudo-symmetry for these two images.

As for the 2D periodic motif of the image in Figure 1b, its somewhat ‘squarish’ appearance suggests that the individual Akaike weights (as obtained by the application of Equation (8) to the fuzzy classification of plane symmetry groups) for groups p4 and p4mm are comparably high, while being somewhat modest for the plane symmetry group pm. We know, however, from the design history of this image that (i) plane symmetry group pm and (ii) the rectangular Bravais lattice type combine to the correct crystallographic symmetry classifications for this image.

When we calculate the product of both types of Akaike weights for this particular image with Equations (13) and (14), there should be a good chance that we obtain the correct plane symmetry classification even in the presence of noise and strong genuine pseudo-symmetries. This should be the outcome of the significant down weighting of the Akaike weights of plane symmetry groups p4 and p4mm by the very small Akaike weight for a square Bravais lattice given the (qualitatively correct) extracted lattice parameters of the rectangular Bravais lattice type and the (qualitatively correct) unit cell areas of Table 5 for the image in Figure 1b.

5.2.2. Illustration of the Idea of Rescaled Confidence Sets over Stretches of Crystallographic Symmetry Hierarchy Branches

There are three different types of crystallographic symmetries in noisy 2D periodic images. Each of these symmetry types is hierarchic and there are several distinct hierarchy branches [7,23,24]. Accordingly, there are several different ways of summing individual Akaike weights or their products up into different kinds of confidence sets. When products of Akaike weights of different types of crystallographic symmetries are involved as in updated Bayesian posterior model probabilities, rescaling all model probabilities so that they add up to 100% in the end is a good idea.

Figure 3 illustrates the idea of rescaled confidence sets of updated Bayesian posterior model probabilities for the combination of Bravais lattice types and plane symmetry groups. Three images with plane symmetry group pm, a combination of a translational pseudo-symmetry with a motif-based (four-fold rotation points plus mirror lines) pseudo-symmetry, and varying amounts of noise are chosen for this illustration. The actual translation periodic motifs and the metric relations of the unit cells are supposed to be different in all of these images, but are utterly unimportant for the following considerations because we are only concerned with the combined crystallographic symmetry classifications of these three images. This makes all other details of the images irrelevant with respect to what we want to demonstrate in this section.

We discuss the sketch in the middle of Figure 3 first. Plane symmetry group pm possesses, for the underlying image, the largest, i.e. 40%, combined (and rescaled) Akaike weight for the Bravais lattice type and plane symmetry group in this figure. The fact that there are significant updated (and rescaled) Bayesian model probabilities in the symmetry hierarchy branches p1–p2–p2mm–p4mm and p1–p2–p4–p4mm is due to both noise and the prevailing combination of translational and motif-based pseudo-symmetries. Note that neither of these two symmetry hierarchy branches contains the correct plane symmetry group pm.

The 40% combined probability that plane symmetry group pm is underlying the image for which the joint fuzzy crystallographic symmetry classification is sketched (in rescaled form) in the middle in Figure 3 results from a high Akaike weight for the rectangular Bravais lattice type and a somewhat moderate Akaike weight for plane symmetry group pm. The significantly lower updated (and rescaled) Bayesian posterior model probabilities for plane symmetry groups p4 and p4mm in this figure results from the product of their low Akaike weight for the square Bravais lattice type with the individual Akaike weights for these two plane symmetry groups. These kinds of anticipated results for highly pseudo-symmetric and noisy images are (at least) the ‘promise’ of the mathematical form of Equations (13) and (14). To which extent this is indeed so in practical cases of interest needs, of course, to be demonstrated experimentally for more or less 2D periodic images with various genuine pseudo-symmetries and noise levels.

The calculation of confidence sets for stretches of each of the hierarchy branches and each of the symmetry types should be helpful for the recognition of genuine pseudo-symmetries in noisy images. One may, for example, compare the confidence set p1–pm–p2mm, which represents in the sketch in the middle of Figure 3, a 75% total probability that the correct symmetry classification is within this particular stretch of a plane symmetry hierarchy branch, with the confidence set p1–p2–p4. The latter confidence set sums to only 35% total (rescaled) probability and represents some kind of a measure for the likelihood of the presence of two-fold and four-fold rotation points in the imaginary noise-free version of the underlying image. The confidence set p1–p2–p2mm, which represents some kind of a measure for the likelihood of the presence of two-fold rotation points and a perpendicular set of mirror lines in that particular image, sums up to a total of 45% joint (and rescaled) probability.

As for the first sketch (at the left) in Figure 3, the p1–pm–p2mm confidence set commands a total probability of 90% with a by far largest contribution from the plane symmetry group pm model itself. In order to obtain such a result, the corresponding image must feature a low amount of pseudo-symmetry and noise.

The third sketch (at the right) in Figure 3, on the other hand, shows a total probability of only 55% for this particular confidence set, which is not much larger than for the other two confidence sets that are mentioned above. The underlying features of the corresponding image for such a result to emerge are both a very strong pseudo-symmetry and a large amount of noise.

In spite of the amounts of noise and strengths of pseudo-symmetries, the general feature of all three sketches in Figure 3 is that the confidence set p1–pm–p2mm commands the largest total probability (even if this is only so by a slim margin in the case of the sketch to the right). This is due to two reasons: (i) that pm is indeed the correct plane symmetry and (ii) that plane symmetries p1 and p2mm are in maximal translationengleiche sub-group and super-group relationships with respect to plane symmetry pm.

While the three examples of Figure 3 illustrate the potential utility of confidence sets of summed-up and rescaled joint Akaike weights, it needs again to be demonstrated experimentally for more or less 2D periodic images with various genuine pseudo-symmetries and noise levels to what extent this approach is, indeed, helpful in practical cases of interest.

5.3. Multi-Model Averaging for Better Predictions and Safer Conclusions

The common symmetry classification practice in crystallographic image processing [21,22] and electron crystallography [25,118,119,120,121] is currently characterized by attempts to infer the plane symmetry of a more or less 2D periodic image on the basis of the three traditional symmetry deviation quantifiers of electron crystallography, which are succinctly described in [7]. That approach does, however, rely on judiciously set thresholds [121] as already stated in the Introduction and Background section of this review and is, therefore, not objective.

As a result of the prevailing subjective practice, one ends up with one model description of the image only, which allows for only one set of lattice parameters and defines all pixel intensities within the asymmetric unit. That particular unit is the part of the translation periodic motif from which all other pixel intensities within a unit cell are created by the application of the 2D space group symmetries of the model. The individual pixel intensities within the asymmetric unit are in effect the average over the whole image of all symmetry-related pixel intensities according to the chosen crystallographic model description (i.e. plane symmetry group). One cannot, however, be sure that one has selected the best possible model given the amount of generalized noise in the data as there was subjectivity in the model’s selection when one chooses it in accord with the common practice.

The raffle ticket discussion of Section 5.1, where a set of model probabilities adds up to 100%, allows one to take a broader view and feel comfortable with the spreading of a crystallographic symmetry classification over a range of models that form a set. This is because each of the models in the set possesses an objectively-quantified amount of merit for representing the geometric-structural information in the noisy data optimally, while the model with the highest probability (Δ_i = 0) is the one that does this job best in the sense that it minimizes the expected Kullback-Leibler information loss. Since one ends up with several model descriptions in the information theory inspired approach of this review while following objective criteria, one also has several sets of unit cell parameters and pixel intensities for the asymmetric units, which one may call, collectively, individual model parameters.

It is a good idea to average over all of the related parameters (and predictions) from all of the models in a set on the basis of their respective Akaike weights, w_i, as defined in Equation (8). The main advantage of multi-model averaging is summed up by Akaike himself in his statement: “If the choice of one single model is not the sole purpose of the analysis of the data the average of the models with respect to the approximate posterior probability C exp {(½) AIC(k)} will provide a better estimate of the true distribution of Y.” [125], where C represents a constant, AIC(k) represents the Δ_i values of a set of models, and Y stands for a set of observations.

In cases of geometric AICs and more or less 2D periodic images, the observations are the unit cell parameters and the gray levels of the individual pixels. There is typically, as already mentioned above, only one image (or at most a few images) with a given generalized noise level to be classified.

Multi-model averaging safeguards against the obtaining of results that may actually refer to symmetries that would not survive extrapolations to vanishing feature extraction uncertainties (or a generalized noise level of zero, in other words). Such slightly broken symmetries may already be present in a sample when it is, for example, a mixed crystal where various transition metal atoms substitute for each other at sites of otherwise moderately high symmetry as it happens in many lower symmetric minerals. It may be difficult (or with currently available technologies quite impossible) to distinguish between such substituted transition metal atoms in imaging experiments reliably so that the above-mentioned multi-model averaging safeguard could be important in order to avoid conclusions that are wrong. Multi-model averaging will typically result in few to zero symmetries but provides the statistically best value of a parameter in the presence of generalized noise.

To illustrate averaging over model predictions and estimated model parameter values in the context of this review briefly, let us assume that the Akaike weights for oblique, rectangular (primitive), rectangular-centered, and square Bravais lattice types are 10%, 50%, 25%, and 15% for a noisy 2D image with many repeats of a more or less translation periodic motif. The averaged unit cell angle is then, for example, obtained by multiplying the individual ‘angle parameter estimates’ of the four models by weights 0.1, 0.5, 0.25, and 0.15, respectively, and the subsequent summing of the four products.

The last of these products is simply 90° times 0.15 for the square Bravais lattice type. Note that the angle between the two unit vectors of equal length of the primitive subunit of the corresponding (two times larger) rectangular-centered unit cell [7,114] needs to be used in the averaging procedure in the penultimate one of the four products. This angle will be somewhat close to 90° for our example as the corresponding Akaike weight for that particular translation symmetry model is 25%.

While the unit cell angle of the oblique Bravais lattice is also somewhat close to 90°, it is precisely 90° for the rectangular (primitive) Bravais lattice type. The averaged angle will consequently be rather close to 90° since the exact 90° value has a combined probability of 65% for this particular example. Note that while the rectangular (primitive) Bravais lattice type is, for our example, the translation symmetry model that minimizes the expected Kullback-Leibler information loss (since it possesses with 50% the largest Akaike weight), the averaged unit cell angle is not restricted to be exactly 90°.

5.4. Acknowledging Model Selection Uncertainties in Qualitative Ways

Akaike weights [13,14,15,16,17], i.e. Equations (8), (13), and (14), are also useful for qualitative acknowledgments of model selection uncertainties. Obviously, if the best model has only a probability of 30% and the second best comes in at 28%, the selection of the first model is quite uncertain given the fact that geometric AICs are first-order approximations for small Gaussian noise levels. One should, therefore, not rule out the second best model and, at least, communicate that model’s probability (and, even better, all of the probabilities of the models in the set) for inclusion into databases.

When better experimental data (with improved signal to noise ratio) and more accurate processing algorithms become available later on in the future, these two models may either change their respective likelihood rankings or the better model may command a higher percentage of the probability of being the Kullback-Leibler best model. For the time being, one is, however, stuck with two models that possess a relative likelihood ratio of nearly unity so that the evidence for the Δ_i = 0 model is not much stronger than that for the Δ_i > 0.

To illustrate this with the, so far, only available examples from the literature, we turn to [4,5]. Liu and coworkers give in the earlier version [5] of their 2004 paper [4] details of frieze group classifications for both a walking humanoid avatar and a walking human being. With an inconsistency that is probably due to ignoring the applicable crystallographic origin conventions [35] and further discussed in Appendix E, the walking avatar features most likely frieze symmetry 2mg with a comparatively small model selection uncertainty.

The time series data for the walking human being is much noisier so that the least-squares residuals for the disjoint frieze symmetries 2mg and 2mm [135] are nearly equal to each other, signifying a large model selection uncertainty. The reason for this could well be the simultaneous existence of genuine pseudo-symmetries in the form a glide-line and a horizontal mirror-line in the recorded time series data; see Appendix E for further discussions.

Returning to the two images of Figure 1, the model selection uncertainty for the noise-free image to the left (Figure 1a) is clearly going to be much smaller than for the image where Gaussian noise has been added (Figure 1b). Note, finally, that the question of model appropriateness is irrelevant in the context of this review because the mathematical frameworks of 2D and 1D crystallography [23,24,35] are without any doubt appropriate for crystallographic symmetry classification of more or less periodic crystal patterns.

6. Summary and Conclusions

Geometric Akaike Information Criteria and associated Akaike weights for generalized noise-level-dependent crystallographic symmetry classification of 2D images that are more or less periodic in 2D (or 1D) and considered to constitute 2D data planes have been reviewed. These kinds of classifications are always fuzzy and, in a sense, preliminary, since images with reduced generalized noise levels may become available in the future. In other words, these kinds of classifications are never definitive and static in all real-world applications, in compliance with Kanatani’s dictum.

While this review concentrates on more or less periodic crystal patterns in two dimensions (and mentioned such patterns in one dimension only briefly on a few occasions), it goes without explicitly saying that the outlined approach is, in principle, also applicable to crystal patterns of dimensions three to six.

It was demonstrated by an example that pseudo-symmetries present challenges to extraction algorithms for geometric-structural features from more or less 2D periodic images, as well as to their subsequent crystallographic symmetry classifications. Pseudo-symmetries in 3D and the problems they cause in mainstream single-crystal X-ray crystallography are discussed in Appendix C. It is noted in that appendix that there are, so far, no statistical descriptors in mainstream 3D crystallography beyond the Hamilton test, which is a form of null hypothesis testing, that are related to Kanatani’s comments. Similarly, there is, so far, no systematic procedure to deal with genuine pseudo-symmetries in 3D on the basis of noisy diffraction data.

The point is also made repeatedly in Appendix C that crystallographically misclassified 3D crystal structures could essentially no longer be found within crystallographic databases as soon as the objective information theory-based approach of this review was implemented and symmetry classifications were allowed to spread over several classes as a function of the generalized noise level of the experimental data. Such a spreading would allow for an objective reporting of the results of crystal structure determinations, but is not necessary for very highly-symmetric and very well-characterized atomic arrangements, where there is no lingering doubt about the validity of the reported ideal structure. For lower-symmetric and poorly-characterized atomic arrangements (as in many biopolymers), on the other hand, the spreading over several crystallographic symmetry classes would be helpful to the users of the databases as uncertainties about the structures’ validity are faithfully/objectively reported. When better crystal structure determinations become available in the future (at lower generalized noise levels), the spreading would allow for a simple updating of the database entry rather than a re-classification.

Crystallographic model selection uncertainties were illustrated in a qualitative manner on the basis of results from the single relevant experimental study (in 1D) in the literature that the author of this review is aware of after quite substantial background searches. Multi-model inferences and averaging were also discussed.

The combining of Akaike weights for Bravais lattice types, Laue classes, and plane symmetry groups should enable successful crystallographic symmetry classifications even in the presence of manifest pseudo-symmetries that exist per design of an image or that pre-exist within a crystalline sample that has been imaged.

Despite the lack of a guarantee that Kanatani’s geometric AIC approach will work well for fuzzy, but quantitative, crystallographic symmetry classifications, the members of the applied crystallography and computational symmetry communities are hereby invited to test them out on the basis of the above-listed equations and inequalities. Demonstrated success in that endeavor could lead, over time, to a widespread adaptation of the information theoretic approach (as briefly outlined in this review for the 2D case) to mainstream 3D periodic crystallography and its higher-dimensional extensions.

Appendix A is directed at the applied crystallography/materials science community and briefly assesses the potential of the main proposal of this review in connection with the extraction of grain boundary structures from atomic resolution images that are more or less periodic in 1D. Appendix B distinguishes between pseudo-symmetries of different types. Experimental noise turns genuine symmetries in data that were collected from a crystal structure into pseudo-symmetries that can be very hard to distinguish from genuine pseudo-symmetries.

Appendix D is concerned with standard statistical descriptions and the utility of contemporary null hypothesis tests in mainstream X-ray crystallography. By quoting from a very recent paper that the great Indian-American statistician Calyampudi Radhakrishna Rao authored (with Miodrag M. Lovric as co-author), it is shown that there is no point in disputing the validity of Kanatani’s dictum by means of null hypothesis testing in all real-world applications.

Appendix E provides comments of a crystallographic nature on the only relevant experimental study in 1D from the literature that has employed a geometric AIC. These comments are peripheral to the main topic of this review, but still worthwhile making for the benefit of the computational symmetry community.