Impact of Geophysical and Datum Corrections on Absolute Sea-Level Trends from Tide Gauges around Taiwan, 1993–2015
Abstract
:1. Introduction
2. Data Sets
2.1. Tide Gauge Records
2.2. Satellite Altimetric Data
2.3. Climate Indices
3. Tide Gauge Processing
3.1. Ocean Tides
3.2. Atmospheric Pressure Loading
3.3. Datum Shifts in the Tide Gauge Records
3.4. Vertical Land Motion Derived from Altimetry and Tide Gauge Data
4. Results and Discussion
4.1. Impacts of Geophysical and Datum Shift Corrections on Sea-Level Trends
4.2. Mean Sea-Level Around Taiwan: Trend and Interannual Variability
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cazenave, A.; Le Cozannet, G. Sea-level rise and its coastal impacts. Earth’s Future 2014, 2, 15–34. [Google Scholar] [CrossRef]
- Douglas, B.C. Sea-level change in the era of the recording tide gauge. In Sea Level Rise—History and Consequences; Douglas, B.C., Kearney, M.S., Leatherman, S.P., Eds.; Academic Press: San Diego, CA, USA, 2001; Volume 75, pp. 37–64. [Google Scholar]
- Woodworth, P.L.; Teferle, F.N.; Bingley, R.M.; Shennan, I.; Williams, S.D.P. Trends in UK mean sea level revisited. Geophys. J. Int. 2009, 176, 19–30. [Google Scholar] [CrossRef]
- Willis, J.; Chambers, D.P.; Kuo, C.Y.; Shum, C.K. Global Sea Level Rise: Recent Progress and Challenges for the Decade to Come. Oceanography 2010, 23, 26–35. [Google Scholar] [CrossRef]
- Church, J.A.; White, N.J. Sea-level rise from the late 19th to the Early 21st Century. Surv. Geophys. 2011, 32, 585–602. [Google Scholar] [CrossRef]
- White, N.J.; Haigh, I.D.; Church, J.A.; Koen, T.; Watson, C.S.; Pritchard, T.R.; Watson, P.J.; Burgette, R.J.; McInnes, K.L.; You, Z.J.; et al. Australian sea levels: Trends, regional variability and influencing factors. Earth Sci. Rev. 2014, 136, 155–174. [Google Scholar] [CrossRef]
- Huang, C.J.; Hsu, T.W.; Wu, L.C. Technology Development on Sea Level Change Estimation by In-Situ and Satellite Data (2/2); Water Resources Agency, R.O.C.: Taichung, Taiwan, 2010; pp. 1–302. (In Chinese) [Google Scholar]
- Tseng, Y.H.; Breaker, C.L.; Chang, T.Y. Sea-level variations in the regional seas around Taiwan. J. Oceanogr. 2010, 66, 27–39. [Google Scholar] [CrossRef]
- Liu, W.C.; Liu, H.M. Assessing the impacts of sea level rise on salinity intrusion and transport time scales in a tidal estuary, Taiwan. Water 2014, 6, 324–344. [Google Scholar] [CrossRef]
- Feng, X.; Tsimplis, M.N. Sea level extremes at the coasts of China. J. Geophys. Res. Oceans 2014, 119, 1593–1608. [Google Scholar] [CrossRef]
- Feng, X.; Tsimplis, M.N.; Woodworth, P.L. Nodal variations and long-term changes in the main tides on the coasts of China. J. Geophys. Res. Oceans 2015, 120, 1215–1232. [Google Scholar] [CrossRef]
- Chen, K.H.; Yang, M.; Huang, Y.T.; Ching, K.E.; Rau, R.J. Vertical displacement rate field of Taiwan from geodetic levelling data 2000–2008. Surv. Rev. 2011, 43, 296–302. [Google Scholar] [CrossRef]
- Ching, K.E.; Hsieh, M.L.; Johnson, K.M.; Chen, K.H.; Rau, R.J.; Ying, M. Modern vertical deformation rates and mountain building in Taiwan from precise leveling and continuous GPS observations, 2000–2008. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Willis, J.K.; Chambers, D.P.; Nerem, R.S. Assessing the globally averaged sea level budget on seasonal to interannual timescales. J. Geophys. Res. Oceans 2008, 113. [Google Scholar] [CrossRef]
- Cazenave, A.; Dominh, K.; Guinehut, S.; Berthier, E.; Llovel, W.; Ramillien, G.; Ablain, M.; Larnicol, G. Sea level budget over 2003–2008: A reevaluation from GRACE space gravimetry, satellite altimetry and Argo. Glob. Planet. Chang. 2009, 65, 83–88. [Google Scholar] [CrossRef]
- Leuliette, E.W.; Miller, L. Closing the sea level rise budget with altimetry, Argo, and GRACE. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Henry, O.; Prandi, P.; Llovel, W.; Cazenave, A.; Jevrejeva, S.; Stammer, D.; Meyssignac, B.; Koldunov, N. Tide gauge-based sea level variations since 1950 along the Norwegian and Russian coasts of the Arctic Ocean: Contribution of the steric and mass components. J. Geophys. Res. Oceans 2012, 117. [Google Scholar] [CrossRef]
- Volkov, D.L.; Pujol, M.I. Quality assessment of a satellite altimetry data product in the Nordic, Barents, and Kara seas. J. Geophys. Res. Oceans 2012, 117. [Google Scholar] [CrossRef]
- Kuo, C.Y.; Shum, C.K.; Braun, A.; Cheng, K.C.; Yi, Y. Vertical Motion determined using Satellite Altimetry and tide Gauges. Terr. Atmos. Ocean. Sci. 2008, 19, 21–35. [Google Scholar] [CrossRef]
- Ray, R.D.; Beckley, B.D.; Lemoine, F.G. Vertical crustal motion derived from satellite altimetry and tide gauges, and comparisons with DORIS measurements. Adv. Space Res. 2010, 45, 1510–1522. [Google Scholar] [CrossRef]
- Walker, G.T. Correlation in seasonal variations of weather, VIII: A preliminary study of world weather. Mem. Indian Meteorol. Dep. 1923, 24, 75–131. [Google Scholar]
- Montgomery, R.B. Report on the work of G.T. Walker. Mon. Weather Rev. 1940, 68, 1–26. [Google Scholar]
- Mantua, N.J.; Hare, S.R.; Zhang, Y.; Wallace, J.M.; Francis, R.C. A Pacific interdecadal climate oscillation with impacts on salmon production. Bull. Am. Meteorol. Soc. 1997, 78, 1069–1079. [Google Scholar] [CrossRef]
- Zhang, Y.; Wallace, J.M.; Battisti, D.S. ENSO-like interdecadal variability: 1900–93. J. Clim. 1997, 10, 1004–1020. [Google Scholar] [CrossRef]
- Parker, B. Tides. In Encyclopedia of Coastal Science; Schwartz, M.L., Ed.; Springer: Dordrecht, The Netherlands, 2005; pp. 987–996. [Google Scholar]
- Chang, E.T.Y.; Chao, B.F.; Chiang, C.C.; Hwang, C. Vertical crustal motion of active plate convergence in Taiwan derived from tide gauge, altimetry, and GPS data. Tectonophysics 2012, 578, 98–106. [Google Scholar] [CrossRef]
- Wunsch, C.; Stammer, D. Atmospheric loading and the oceanic “inverted barometer” effect. Rev. Geophys. 1997, 35, 79–107. [Google Scholar] [CrossRef]
- Wunsch, C. Bermuda sea-level in relation to tides, weather and baroclinic fluctuations. Geophys. Space Phys. 1972, 10, 1–49. [Google Scholar] [CrossRef]
- Dalrymple, R.A.; Breaker, L.C.; Brooks, B.A.; Cayan, D.R.; Griggs, G.B.; Han, W.; Horton, B.P.; Hulbe, C.L.; McWilliams, J.C.; Mote, P.W.; et al. Sea-Level Rise for the Coasts of California, Oregon, and Washington: Past, Present, and Future; The National Academies Press: Washington, DC, USA, 2012; pp. 1–217. [Google Scholar]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Ponte, R.M. Low-frequency sea level variability and the inverted barometer effect. J. Atmos. Ocean. Technol. 2006, 23, 619–629. [Google Scholar] [CrossRef]
- Patullo, J.; Munk, W.; Revelle, R.; Strong, E. The seasonal oscillation in sea level. J. Mar. Res. 1955, 14, 88–155. [Google Scholar]
- Church, J.A.; White, N.J.; Coleman, R.; Lambeck, K.; Mitrovica, J.X. Estimates of regional distribution of sea-level rise over the 1950-2000 period. J. Clim. 2004, 17, 2609–2625. [Google Scholar] [CrossRef]
- Mallat, S.G. Multiresolution approximations and wavelet orthonormal bases of L2(R). Trans. Am. Math. Soc. 1989, 315, 69–89. [Google Scholar] [CrossRef]
- Chicken, E.; Loper, D.E.; Werner, C.L. Estimating tidal effects in spring discharge: A multiscale method using correlated phenomena. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Kuo, C.Y.; Shum, C.K.; Braun, A.; Mitrovica, J.X. Vertical crustal motion determined by satellite altimetry and tide gauge data in Fennoscandia. Geophys. Res. Lett. 2004, 31, 4–7. [Google Scholar] [CrossRef]
- Wöppelmann, G.; Marcos, M. Coastal sea-level rise in southern Europe and the nonclimate contribution of vertical land motion. J. Geophys. Res. 2012, 117. [Google Scholar] [CrossRef]
- Yildiz, H.; Andersen, O.B.; Simav, M.; Aktug, B.; Ozdemir, S. Estimates of vertical land motion along the southwestern coasts of Turkey from coastal altimetry and tide gauge data. Adv. Space Res. 2013, 51, 1572–1580. [Google Scholar] [CrossRef]
- Wang, H.S.; Wu, P.; Jia, L.L.; Hu, B.; Jiang, L.M. The role of glacial isostatic adjustment in the present-day crustal motion and sea levels of East Asia. Earth Planets Space 2011, 63, 915–928. [Google Scholar] [CrossRef]
- Woodworth, P.L. Some important issues to do with long-term sea level change. Philos. Trans. R. Soc. A 2006, 364, 787–803. [Google Scholar] [CrossRef] [PubMed]
- Yen, J.Y.; Lu, C.H.; Chang, C.P.; Hooper, A.J.; Chang, Y.H.; Liang, W.T.; Chang, T.Y.; Lin, M.S.; Chen, K.S. Investigating active deformation in the northern Longitudinal Valley and City of Hualien in eastern Taiwan using persistent scatterer and small-baseline SAR interferometry. Terr. Atmos. Ocean. Sci. 2011, 22, 291–304. [Google Scholar] [CrossRef]
- Kuo, C.Y.; Cheng, Y.J.; Lan, W.H.; Kao, H.C. Monitoring Vertical Land Motions in Southwestern Taiwan with Retracked Topex/Poseidon and Jason-2 Satellite Altimetry. Remote Sens. 2015, 7, 3808–3825. [Google Scholar] [CrossRef]
- Zhang, X.; Church, J.A. Sea-level trends, interannual and decadal variability in the Pacific Ocean. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Cheng, Y.C.; Ezer, T.; Hamlington, B.D. Sea Level Acceleration in the China Seas. Water 2016, 8. [Google Scholar] [CrossRef]
- Kohl, A.; Stammer, D.; Cornuelle, B. Interannual to decadal changes in the ECCO global synthesis. J. Phys. Oceanogr. 2007, 37, 313–337. [Google Scholar] [CrossRef]
- Merrifield, M.A.; Thompson, P.R.; Lander, M. Multidecadal sea level anomalies and trends in the western tropical Pacific. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Peng, D.; Palanisamy, H.; Cazenave, A.; Meyssignac, B. Interannual Sea Level Variations in the South China Sea Over 1950–2009. Mar. Geod. 2013, 36, 164–182. [Google Scholar] [CrossRef]
- Strassburg, M.W.; Hamlington, B.D.; Leben, R.R.; Manurung, P.; Lumban Gaol, J.; Nababan, B.; Vignudelli, S.; Kim, K.Y. Sea level trends in Southeast Asian seas. Clim. Past 2015, 11, 743–750. [Google Scholar] [CrossRef]
- Cherniawsky, J.Y.; Foreman, M.G.G.; Kang, S.K.; Scharroo, R.; Eert, A.J. 18.6-year lunar nodal tides from altimeter data. Cont. Shelf. Res. 2010, 30, 575–587. [Google Scholar] [CrossRef]
- Woodworth, P.L. A Note on the Nodal Tide in Sea Level Records. J. Coast. Res. 2012, 28, 316–323. [Google Scholar] [CrossRef]
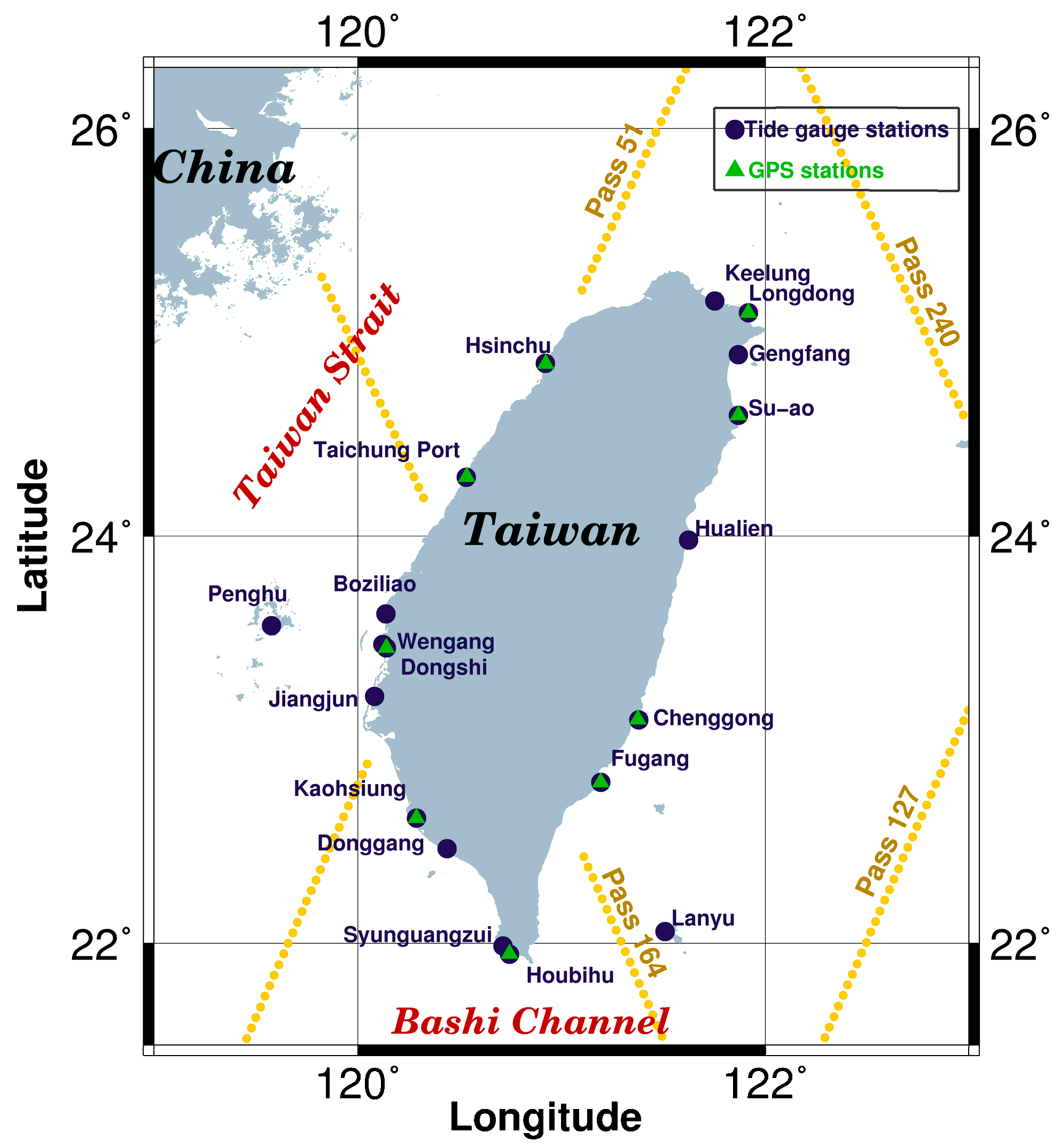

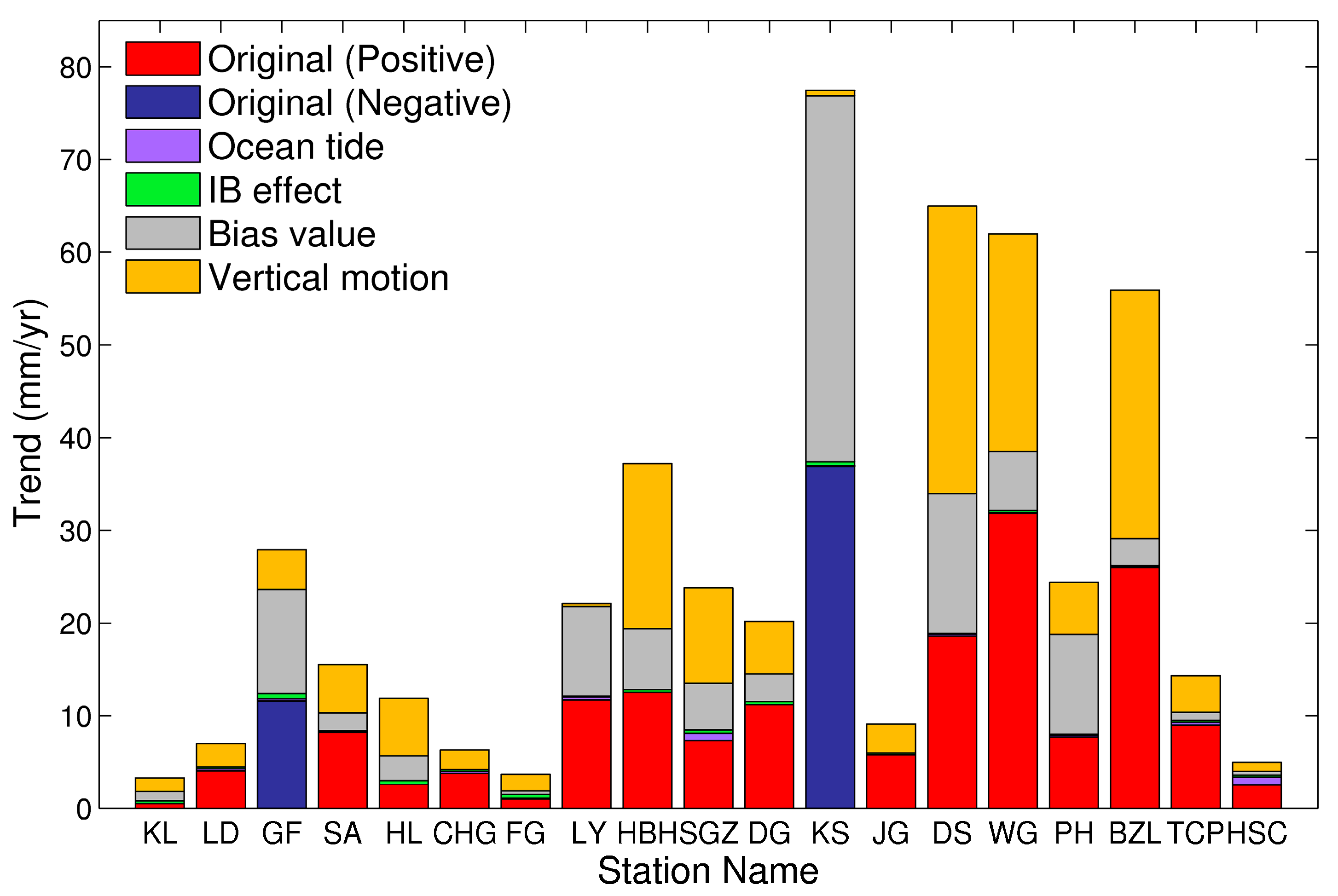

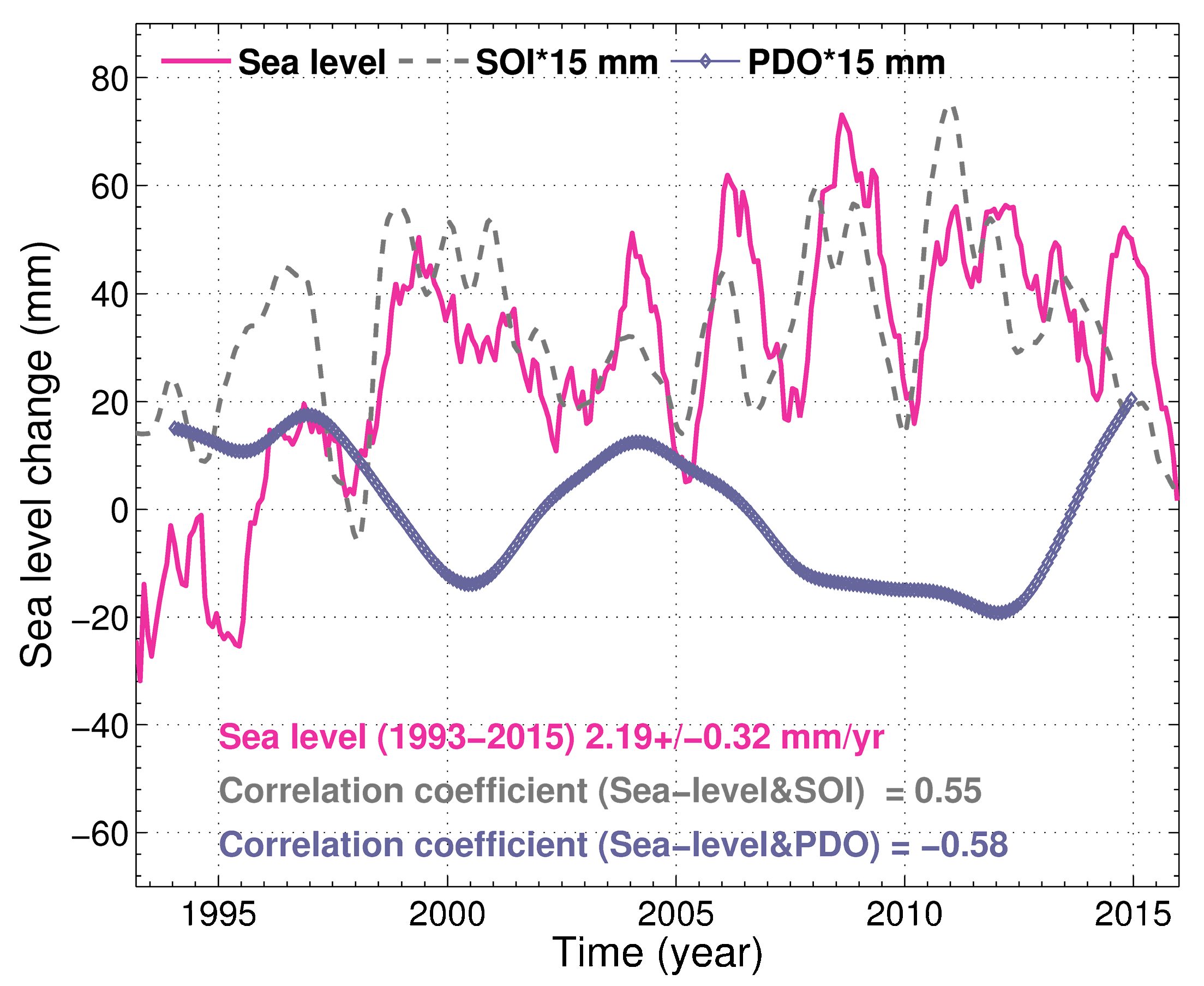
| Station Name | Data Period | Coordinates | Absolute Sea-Level Trend (mm/yr) | Vertical Land Motion Rates (mm/yr) | GPS Period | Dist. (km) | C.C. | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Lat. (° N) | Lon. (° E) | Tide gauge (TG) | Altimetry 1993–2015 | ALT–TG | GPS | |||||
| Keelung (KL) | 1993–2015 | 25.155 | 121.752 | 2.7 ± 0.3 (±0.6) | 2.3 ± 0.3 | 1.5 ± 0.5 | N/A | N/A | N/A | 0.73 |
| Longdong (LD) | 2001–2015 | 25.098 | 121.918 | 1.6 ± 0.6 (±1.1) | 2.4 ± 0.3 | −2.5 ± 0.9 | −3.5 ± 0.1 | 2003–2012 | 0.01 | 0.73 |
| Gengfang (GF) | 1993–2008 | 24.892 | 121.869 | 3.5 ± 0.6 (±0.9) | 2.4 ± 0.3 | 4.2 ± 0.7 | N/A | N/A | N/A | 0.62 |
| Su-ao (SA) | 1997–2015 | 24.593 | 121.867 | 1.1 ± 0.4 (±0.6) | 2.3 ± 0.3 | −5.2 ± 0.5 | −4.6 ± 0.1 | 2002–2012 | 0.02 | 0.68 |
| Hualien (HL) | 1997–2015 | 23.981 | 121.624 | −0.5 ± 0.5 (±1.1) | 1.9 ± 0.5 | −6.2 ± 1.0 | N/A | N/A | N/A | 0.25 |
| Chenggong (CHG) | 1993–2015 | 23.097 | 121.380 | 1.3 ± 0.4 (±1.0) | 2.0 ± 0.6 | −2.1 ± 0.9 | 1.5 ± 0.1 | 2002–2012 | 0.60 | 0.20 |
| Fugang (FG) | 1993–2015 | 22.791 | 121.192 | 2.9 ± 0.4 (±0.6) | 2.2 ± 0.5 | 1.8 ± 0.5 | −1.2 ± 0.1 | 2003–2012 | 0.00 | 0.57 |
| Lanyu (LY) | 2001–2015 | 22.058 | 121.507 | 1.9 ± 1.1 (±1.3) | 3.0 ± 0.5 | −0.4 ± 0.7 | N/A | N/A | N/A | 0.85 |
| Houbihu (HBH) | 1998–2015 | 21.946 | 120.745 | 1.6 ± 0.8 (±1.5) | 2.5 ± 0.5 | −17.8 ± 1.3 | −23.4 ± 0.3 | 2009–2012 | 0.32 | 0.23 |
| Syunguangzui (SGZ) | 1993–2015 | 21.986 | 120.712 | 2.4 ± 0.4 (±0.7) | 2.5 ± 0.5 | −10.3 ± 0.6 | N/A | N/A | N/A | 0.49 |
| Donggang (DG) | 1998–2015 | 22.465 | 120.438 | 2.8 ± 0.7 (±1.0) | 2.2 ± 0.4 | −5.7 ± 0.7 | N/A | N/A | N/A | 0.73 |
| Kaohsiung (KS) | 1993–2014 | 22.614 | 120.288 | 2.7 ± 0.4 (±0.6) | 2.2 ± 0.4 | 0.6 ± 0.4 | −0.9 ± 0.1 | 2004–2012 | 0.01 | 0.82 |
| Jiangjun (JG) | 1993–2015 | 23.213 | 120.083 | 2.5 ± 0.5 (±0.7) | 2.2 ± 0.4 | −3.1 ± 0.5 | N/A | N/A | N/A | 0.69 |
| Dongshi (DS) | 1993–2015 | 23.450 | 120.139 | 2.4 ± 0.5 (±0.9) | 2.3 ± 0.5 | −31.0 ± 0.7 | −32.4 ± 0.1 | 2004–2012 | 0.27 | 0.43 |
| Wengang (WG) | 1993–2015 | 23.467 | 120.123 | 1.8 ± 0.6 (±1.1) | 2.4 ± 0.5 | −23.5 ± 0.9 | N/A | N/A | N/A | 0.43 |
| Penghu (PH) | 1993–2015 | 23.560 | 119.577 | 2.2 ± 0.4 (±0.6) | 2.4 ± 0.4 | 5.6 ± 0.4 | N/A | N/A | N/A | 0.70 |
| Boziliao (BZL) | 1995–2015 | 23.619 | 120.138 | 2.1 ± 0.6 (±1.1) | 2.5 ± 0.5 | −26.8 ± 0.9 | N/A | N/A | N/A | 0.37 |
| Taichung Port (TCP) | 1993–2015 | 24.288 | 120.533 | 3.7 ± 0.5 (±1.2) | 3.2 ± 0.8 | −3.9 ± 1.1 | −3.3 ± 0.1 | 2004–2012 | 0.39 | 0.44 |
| Hsinchu (HSC) | 1993–2015 | 24.849 | 120.921 | 2.8 ± 0.4 (±1.2) | 2.9 ± 0.8 | 1.0 ± 1.1 | −3.3 ± 0.1 | 2004–2012 | 0.42 | 0.23 |
| Mean | 1993–2015 | 2.2 | 2.2 ± 0.3 | −6.5 | −7.9 | 2002–2012 | 0.23 | 0.54 | ||
| Station Name | Trend (mm/yr) | ||||
|---|---|---|---|---|---|
| Original | With Ocean Tides Correction | With Ocean Tides and IB Corrections | With Ocean Tides, IB, and Datum Corrections | With Ocean Tides, IB, Datum, and Vertical Land Motion Corrections ** | |
| Keelung (KL) | 0.5 ±0.5 | 0.5 ± 0.5 | 0.2 ± 0.5 | 1.2 ± 0.3 | 2.7 ± 0.3 (±0.6) |
| Longdong (LD) | 4.1 ± 0.7 | 4.3 ± 0.7 | 4.1 ± 0.6 | 4.1 ± 0.6 * | 1.6 ± 0.6 (±1.1) |
| Gengfang (GF) | −11.6 ± 1.0 | −11.4 ± 0.9 | −12.0 ± 0.9 | −0.8 ± 0.6 | 3.5 ± 0.6 (±0.9) |
| Su-ao (SA) | 8.2 ± 0.7 | 8.3 ± 0.6 | 8.2 ± 0.6 | 6.3 ± 0.4 | 1.1 ± 0.4 (±0.6) |
| Hualien (HL) | 2.6 ± 0.7 | 2.6 ± 0.7 | 3.0 ± 0.7 | 5.7 ± 0.5 | −0.5 ± 0.5 (±1.1) |
| Chenggong (CHG) | 3.8 ± 0.5 | 3.6 ± 0.5 | 3.4 ± 0.4 | 3.4 ± 0.4 * | 1.3 ± 0.4 (±1.0) |
| Fugang (FG) | 1.0 ± 0.5 | 1.1 ± 0.5 | 0.7 ± 0.5 | 1.1 ± 0.4 | 2.9 ± 0.4 (±0.6) |
| Lanyu (LY) | 11.7 ± 1.3 | 12.0 ± 1.3 | 11.9 ± 1.2 | 2.2 ± 1.1 | 1.9 ± 1.1 (±1.3) |
| Houbihu (HBH) | 12.5 ± 1.3 | 12.5 ± 1.2 | 12.8 ± 1.2 | 19.4 ± 0.8 | 1.6 ± 0.8 (±1.5) |
| Syunguangzui (SGZ) | 7.3 ± 0.6 | 8.1 ± 0.6 | 7.7 ± 0.6 | 12.7 ± 0.4 | 2.4 ± 0.4 (±0.7) |
| Donggang (DG) | 11.2 ± 0.8 | 11.2 ± 0.8 | 11.5 ± 0.7 | 8.5 ± 0.7 | 2.8 ± 0.7 (±1.0) |
| Kaohsiung (KS) | −36.9 ± 1.7 | −37.0 ± 1.7 | −37.4 ± 1.6 | 2.1 ± 0.4 | 2.7 ± 0.4 (±0.6) |
| Jiangjun (JG) | 5.8 ± 0.5 | 5.8 ± 0.5 | 5.6 ± 0.5 | 5.6 ± 0.5 * | 2.5 ± 0.5 (±0.7) |
| Dongshi (DS) | 18.6 ± 0.9 | 18.4 ± 0.9 | 18.3 ± 0.9 | 33.4 ± 0.5 | 2.4 ± 0.5 (±0.9) |
| Wengang (WG) | 31.8 ± 1.1 | 31.9 ± 1.1 | 31.7 ± 1.1 | 25.3 ± 0.6 | 1.8 ± 0.6 (±1.1) |
| Penghu (PH) | 7.7 ± 0.6 | 7.5 ± 0.6 | 7.4 ± 0.6 | −3.4 ± 0.4 | 2.2 ± 0.4 (±0.6) |
| Boziliao (BZL) | 26.0 ± 1.1 | 26.1 ± 1.0 | 26.0 ± 1.0 | 28.9 ± 0.6 | 2.1 ± 0.6 (±1.1) |
| Taichung Port (TCP) | 9.0 ± 0.7 | 8.7 ± 0.6 | 8.5 ± 0.6 | 7.6 ± 0.5 | 3.7 ± 0.5 (±1.2) |
| Hsinchu (HSC) | 2.5 ± 0.7 | 1.6 ± 0.6 | 1.4 ± 0.6 | 1.8 ± 0.4 | 2.8 ± 0.4 (±1.2) |
| Mean | 6.1 | 6.1 | 5.9 | 8.7 | 2.2 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lan, W.-H.; Kuo, C.-Y.; Kao, H.-C.; Lin, L.-C.; Shum, C.K.; Tseng, K.-H.; Chang, J.-C. Impact of Geophysical and Datum Corrections on Absolute Sea-Level Trends from Tide Gauges around Taiwan, 1993–2015. Water 2017, 9, 480. https://doi.org/10.3390/w9070480
Lan W-H, Kuo C-Y, Kao H-C, Lin L-C, Shum CK, Tseng K-H, Chang J-C. Impact of Geophysical and Datum Corrections on Absolute Sea-Level Trends from Tide Gauges around Taiwan, 1993–2015. Water. 2017; 9(7):480. https://doi.org/10.3390/w9070480
Chicago/Turabian StyleLan, Wen-Hau, Chung-Yen Kuo, Huan-Chin Kao, Li-Ching Lin, C. K. Shum, Kuo-Hsin Tseng, and Jung-Chieh Chang. 2017. "Impact of Geophysical and Datum Corrections on Absolute Sea-Level Trends from Tide Gauges around Taiwan, 1993–2015" Water 9, no. 7: 480. https://doi.org/10.3390/w9070480
APA StyleLan, W.-H., Kuo, C.-Y., Kao, H.-C., Lin, L.-C., Shum, C. K., Tseng, K.-H., & Chang, J.-C. (2017). Impact of Geophysical and Datum Corrections on Absolute Sea-Level Trends from Tide Gauges around Taiwan, 1993–2015. Water, 9(7), 480. https://doi.org/10.3390/w9070480







