Assessing the Impact of Climate Change and Extreme Value Uncertainty to Extreme Flows across Great Britain
Abstract
:1. Introduction
1.1. Flood Risk in the UK and Climate Change
1.2. Uncertainties Related to Climate Change
1.3. Extreme Values Assessment and Automating Approaches
1.4. Aims
2. Materials and Methods
2.1. The Future Flow Database
2.2. Block Maxima and Peak over Threshold Methods
- (i)
- G(z) belongs to the GEV family distribution:with μ the location parameter, σ > 0 the scale parameter, and ξ (≠0) the shape parameter.
- (ii)
- For large enough u, the distribution function of y = X − u conditional on X > u, is approximately the GP distribution:
2.3. Automated Computing
- Identify a series of n suitable thresholds, u1 < u2 < … < un, equally spaced, between the median and the 98% quantile of the data series. For j = 1, …, n, fit a GP model and estimate the likelihood estimator of the scale (σuj) and shape (ξuj) parameters for the declustered data above the threshold uj.
- Test the sequence (τ(uj) − τ(uj−1))j=2, …, n for j = 1 against the Pearson’s Chi-square Test, with the test variable τ(uj) = σuj − ξuj × uj. For any u < uj−1 < uj, the difference τ(uj) − τ(uj − 1) is approximately normally distributed with mean 0. If the null hypothesis of normality is rejected then u1 is not a suitable threshold.
- Repeat Step 2 for j = 2, …, n if u1 is not suitable, until finding and extracting the first threshold uj for which the difference sequence fulfils the normality condition.
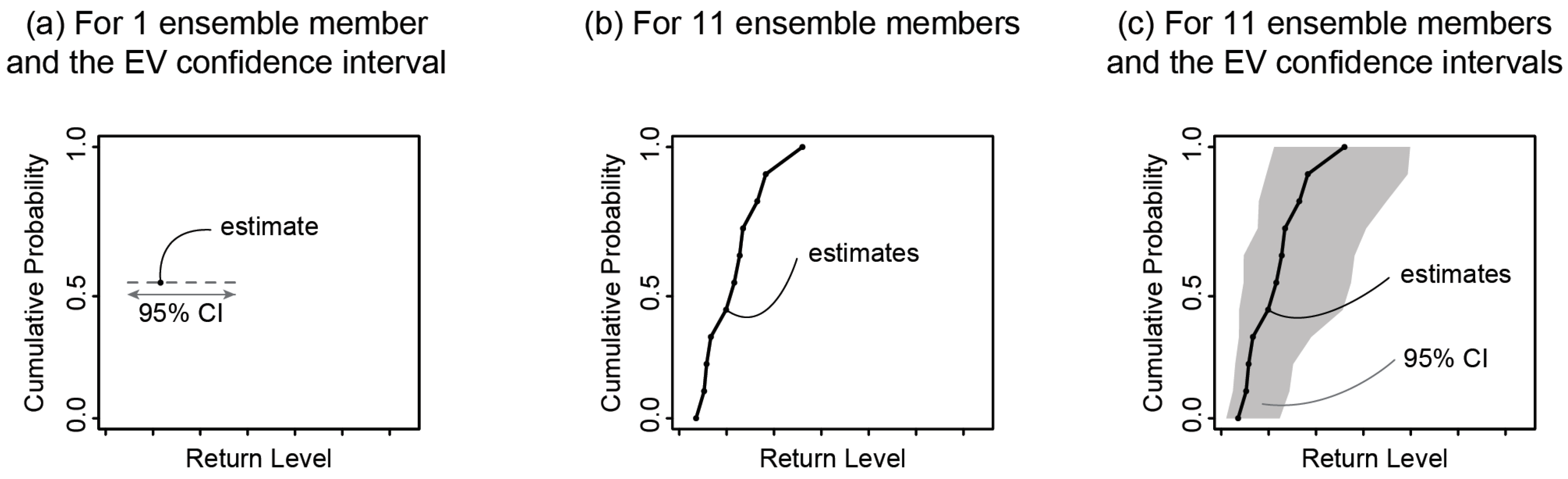
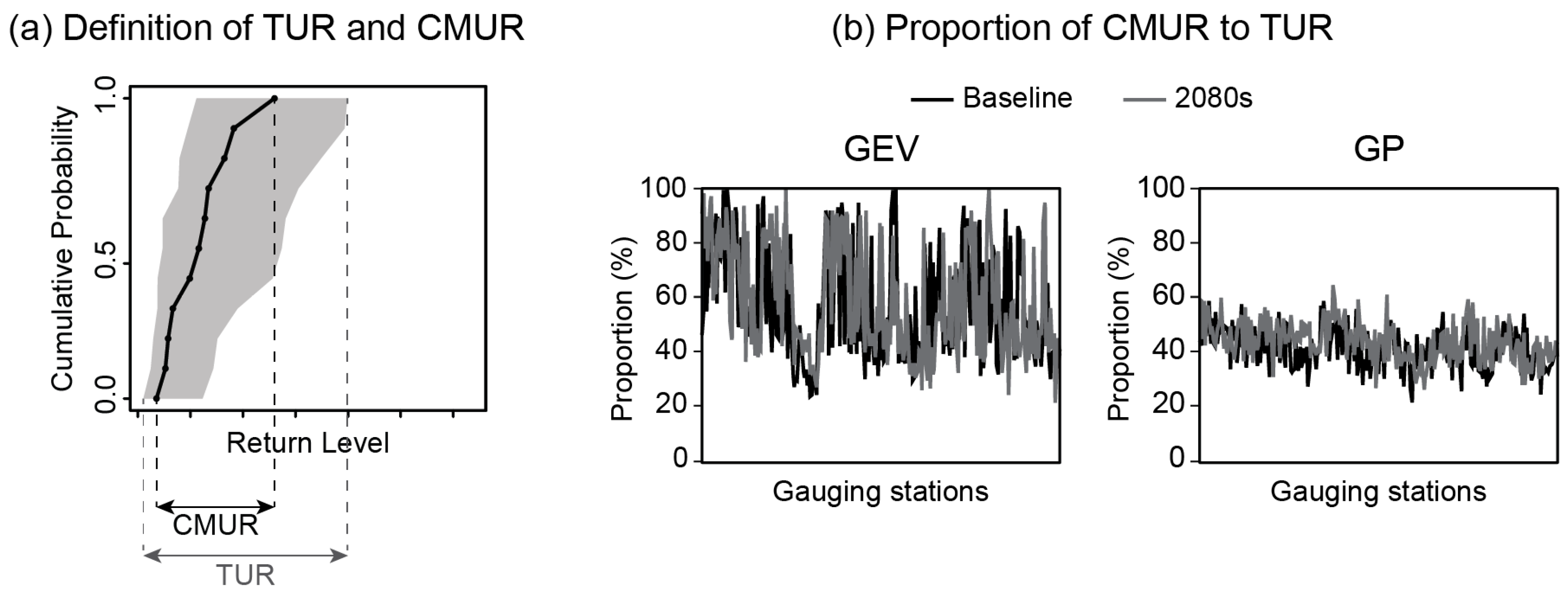
2.4. Assessment of Uncertainties Associated with the Return Level Estimate
3. Results
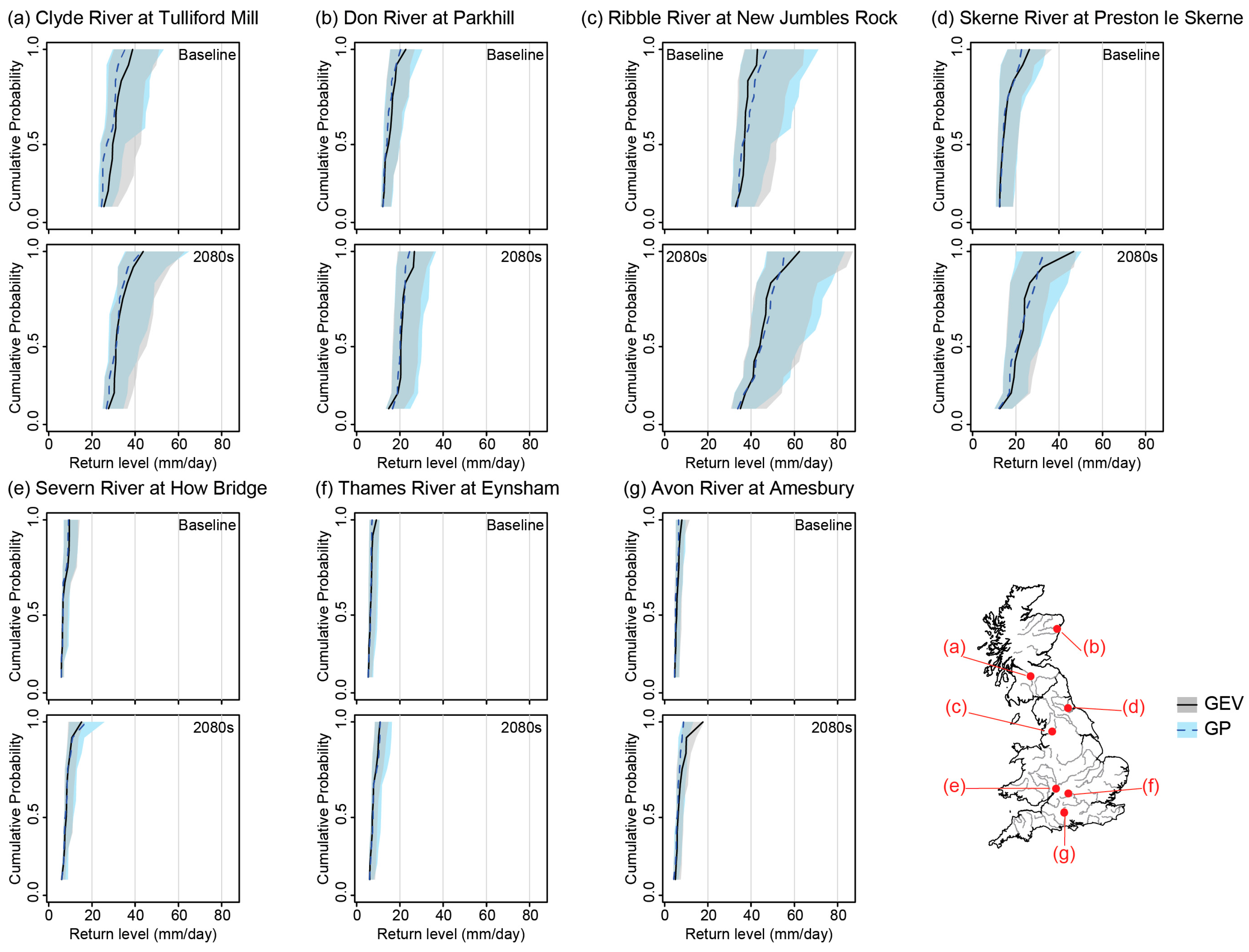
3.1. Uncertainties on the Baseline
3.2. Change in Flood Peak by the 2080s
3.3. Combined Uncertainties
4. Discussion
4.1. Main Results
4.1.1. National Picture
4.1.2. Cascading Uncertainties
4.1.3. GEV vs. GP and Automated Procedure
4.2. Limits
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Jonkman, S.; Vrijling, J. Loss of life due to floods. J. Flood Risk Manag. 2008, 1, 43–56. [Google Scholar] [CrossRef]
- Guha-Sapir, D.; Below, R.; Hoyois, P. Natural Disasters Reported. EM-DAT: International Disaster Database; Université Catholique de Louvain: Brussels, Belgium, 2015. [Google Scholar]
- Kantamaneni, K.; Phillips, M. Transformation of climate: Will floods and coastal erosion crumble the UK economy? Int. J. Clim. Chang. Impacts Responses 2016, 8, 45–59. [Google Scholar]
- Alfieri, L.; Feyen, L.; di Baldassarre, G. Increasing flood risk under climate change: A pan-European assessment of the benefits of four adaptation strategies. Clim. Chang. 2016, 136, 507–521. [Google Scholar] [CrossRef]
- Wagenaar, D.J.; de Bruijn, K.M.; Bouwer, L.M.; de Moel, H. Uncertainty in flood damage estimates and its potential effect on investment decisions. Nat. Hazards Earth Syst. Sci. 2016, 16, 1–14. [Google Scholar] [CrossRef]
- UK Parliament. Current Parliamentary Material Available on Flooding. Available online: http://www.parliament.uk/topics/Flooding.htm (accessed on 16 August 2013).
- Stewart, L.; Vesuviano, G.; Morris, D.; Prosdocimi, I. The new FEH rainfall depth-duration-frequency model: Results, comparisons and implications. In Proceedings of the 12th British Hydrological Society National Symposium, Birmingham, UK, 2–4 September 2014; Available online: http://nora.nerc.ac.uk/510563/ (accessed on 23 March 2016).
- Wilby, R.L.; Beven, K.J.; Reynard, N.S. Climate change and fluvial flood risk in the UK: More of the same? Hydrol. Process. 2008, 22, 2511–2523. [Google Scholar] [CrossRef]
- Faulkner, D. Rainfall Frequency Estimation. In Flood Estimation Handbook; Institute of Hydrology: Wallingford, UK, 1999; Volume 2, 110p. [Google Scholar]
- Arnell, N.W.; Gosling, S.N. The impacts of climate change on river flood risk at the global scale. Clim. Chang. 2016, 134, 387–401. [Google Scholar] [CrossRef]
- Di Baldassarre, G.; Schumann, G.; Bates, P.; Freer, J.; Beven, K. Flood-plain mapping: A critical discussion of deterministic and probabilistic approaches. Hydrol. Sci. J. 2010, 55, 364–376. [Google Scholar] [CrossRef]
- Beevers, L.; Douven, W.; Lazuardi, H.; Verheij, H. Cumulative impacts of road developments in floodplains. Transp. Res. D 2012, 17, 398–404. [Google Scholar] [CrossRef]
- Balica, S.; Beevers, L.; Popescu, I.; Wright, N. Parametric and physically based modelling techniques for flod risk and vulnerability assessment: A comparison. Environ. Model. Softw. 2013, 41, 81–92. [Google Scholar] [CrossRef]
- Beven, K.; Hall, J. (Eds.) Applied Uncertainty Analysis for Flood Risk Management; Imperial College Press: London, UK, 2014.
- Von Christierson, B.; Wade, S.; Counsell, C.; Arnell, N.; Charlton, M.; Prudhomme, C.; Hannaford, J.; Lawson, R.; Tattersall, C.; Fenn, C.; et al. Climate Change Approaches in Water Resources Planning—Overview of New Methods; Report SC090017/R3; Environment Agency: London, UK, 2013.
- Prudhomme, C.; Jakoba, D.; Svensson, C. Uncertainty and climate change impact on the flood regime of small UK catchments. J. Hydrol. 2003, 277, 1–23. [Google Scholar] [CrossRef]
- Wilby, R.L. Evaluating climate model outputs for hydrological applications. Hydrol. Sci. J. 2010, 55, 1090–1093. [Google Scholar] [CrossRef]
- Augustin, N.; Beevers, L.; Sloan, W. Predicting river flows for future climates using an autoregressive multinomial logit model. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Murphy, J.M.; Sexton, D.M.H.; Jenkins, G.J.; Boorman, P.M.; Booth, B.B.B.; Brown, C.C.; Clark, R.T.; Collins, M.; Harris, G.R.; Kendon, E.J.; et al. UK Climate Projections Science Report: Climate Change Projections; Met Office Hadley Centre: Exeter, UK, 2009. [Google Scholar]
- Prudhomme, C.; Haxton, T.; Crooks, S.; Jackson, C.; Barkwith, A.; Williamson, J.; Kelvin, J.; Mackay, J.; Wang, L.; Young, A.; et al. Future Flows Hydrology: An ensemble of daily river flow and monthly groundwater levels for use for climate change impact assessment across Great Britain. Earth Syst. Sci. Data 2013, 5, 101–107. [Google Scholar] [CrossRef]
- Coles, S. An Introduction to Statistical Modelling of Extreme Values; Springer: London, UK, 2001. [Google Scholar]
- Centre for Ecology & Hydrology. Flood Estimation Handbook; Centre for Ecology & Hydrology: Wallingford, UK, 1999; Volumes 1–5. [Google Scholar]
- Bocchiola, D.; De Michele, C.; Rosso, R. Review of recent advances in index flood estimation. Hydrol. Earth Syst. Sci. 2003, 7, 283–296. [Google Scholar] [CrossRef]
- Svensson, C.; Jones, D. Review of rainfall frequency estimation methods. J. Flood Risk Manag. 2010, 3, 296–313. [Google Scholar] [CrossRef]
- Prosdocimi, I.; Kjeldsen, T.; Miller, J. Detection and attribution of urbanization effect on flood extremes using nonstationary flood-frequency models. Water Resour. Res. 2015, 51, 4244–4262. [Google Scholar] [CrossRef] [PubMed]
- Esteves, L.S. Consequences to flood management of using different probability distributions to estimate extreme rainfall. J. Environ. Manag. 2013, 115, 98–105. [Google Scholar] [CrossRef] [PubMed]
- Madsen, H.; Rasmussen, P.; Rosbjerg, D. Comparison of annual maximum series and partial duration series methods for modeling extreme hydrologic events, 1, At-site modeling. Water Resour. Res. 1997, 33, 747–757. [Google Scholar] [CrossRef]
- Ferreira, A.; de Haan, L. On the block maxima method in extreme value theory: PWM estimator. Ann. Stat. 2015, 43, 276–298. [Google Scholar] [CrossRef]
- Bayliss, A.C.; Jones, R.C. Peaks-over-Threshold Flood Database: Summary Statistics and Seasonality; IH Report No. 121; Institute of Hydrology: Wallingford, UK, 1993; 68p. [Google Scholar]
- Thompson, P.; Cai, Y.; Reeve, D.; Stander, J. Automated threshold selection methods for extreme wave analysis. Coast. Eng. 2009, 56, 1013–1021. [Google Scholar] [CrossRef]
- Fukutome, S.; Liniger, M.A.; Süveges, M. Automatic threshold and run parameter selection: A climatology for extreme hourly precipitation in Switzerland. Theor. Appl. Climatol. 2013, 120, 403–416. [Google Scholar] [CrossRef]
- Süveges, M.; Davison, A.C. Model misspecification in peaks over threshold analysis. Ann. Appl. Stat. 2010, 4, 203–221. [Google Scholar] [CrossRef]
- Prudhomme, C.; Dadson, S.; Morris, D.; Williamson, J.; Goodsell, G.; Crooks, S.; Boelee, L.; Davies, H.; Buys, G.; Lafon, T.; et al. Future Flows Climate: An ensemble of 1-km climate change projections for hydrological application in Great Britain. Earth Syst. Sci. Data 2012, 4, 143–148. [Google Scholar] [CrossRef]
- Murphy, J.M.; Booth, B.B.B.; Collins, M.; Harris, G.R.; Sexton, D.M.H.; Webb, M.J. A methodology for probabilistic predictions of regional climate change from perturbed physics ensembles. Philos. Trans. R Soc. A 2007, 365, 1993–2028. [Google Scholar] [CrossRef] [PubMed]
- Brown, I.; Poggio, L.; Gimona, A.; Castellazzi, M. Climate change, drought risk and land capability for agriculture: Implications for land use in Scotland. Reg. Environ. Chang. 2011, 11, 503–518. [Google Scholar] [CrossRef]
- Gilleland, E.; Katz, R.W. New software to analyze how extremes change over time. Eos 2011, 92, 13–14. [Google Scholar] [CrossRef]
- Prescott, P.; Walden, A.T. Maximum likelihood estimation of the parameters of the generalized extreme-value distribution. Biometrika 1980, 67, 723–724. [Google Scholar] [CrossRef]
- Katz, R.W.; Parlange, M.; Naveau, P. Statistics of extremes in hydrology. Adv. Water Resour. 2002, 25, 1287–1304. [Google Scholar] [CrossRef]
- Scarrott, C.; MacDonald, A. A review of extreme value threshold estimation and uncertainty quantification. REVSTAT Stat. J. 2012, 10, 33–60. [Google Scholar]
- Griffiths, J.; Young, A.R.; Keller, V. Continuous Estimation of River Flows (CERF)—Technical Report: Task 1.3: Model Scheme for Representing Rainfall Interception and Soil Moisture; CEH: Wallingford, UK, 2006; 45p. [Google Scholar]
- Moore, R.J. The PDM rainfall-runoff model. Hydrol. Earth Syst. Sci. 2007, 11, 483–499. [Google Scholar] [CrossRef]
- Crooks, S.M.; Naden, P.S. CLASSIC: A semi-distributed rainfall-runoff modelling system. Hydrol. Earth Syst. Sci. 2007, 11, 516–531. [Google Scholar] [CrossRef]
- Wilby, R.L.; Dessai, S. Robust adaptation to climate change. Weather 2010, 65, 180–185. [Google Scholar] [CrossRef]
- Ludwig, F.; van Slobbe, E.; Cofino, W. Climate change adaptation and Integrated Water Resource Management in the water sector. J. Hydrol. 2014, 518, 235–242. [Google Scholar] [CrossRef]
- Di Baldassarre, G.; Castellarin, A.; Montanari, A.; Brath, A. Probability-weighted hazard maps for comparing different flood risk management strategies: A case study. Nat. Hazards 2009, 50, 479–496. [Google Scholar] [CrossRef]


| River | CCMU (mm) Baseline | CCMU (mm) 2080s | TCCU (mm) Baseline | TCCU (mm) 2080s |
|---|---|---|---|---|
| Clyde | 13.66 | 16.37 | 30.16 | 40.13 |
| Don | 10.81 | 12.08 | 19.62 | 23.39 |
| Ribble | 14.39 | 28.19 | 39.82 | 56.13 |
| Skerne | 14.07 | 35.41 | 25.97 | 42.70 |
| Severn | 3.84 | 10.08 | 8.63 | 18.11 |
| Thames | 4.11 | 4.96 | 5.54 | 10.22 |
| Avon | 3.39 | 13.64 | 7.41 | 14.15 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Collet, L.; Beevers, L.; Prudhomme, C. Assessing the Impact of Climate Change and Extreme Value Uncertainty to Extreme Flows across Great Britain. Water 2017, 9, 103. https://doi.org/10.3390/w9020103
Collet L, Beevers L, Prudhomme C. Assessing the Impact of Climate Change and Extreme Value Uncertainty to Extreme Flows across Great Britain. Water. 2017; 9(2):103. https://doi.org/10.3390/w9020103
Chicago/Turabian StyleCollet, Lila, Lindsay Beevers, and Christel Prudhomme. 2017. "Assessing the Impact of Climate Change and Extreme Value Uncertainty to Extreme Flows across Great Britain" Water 9, no. 2: 103. https://doi.org/10.3390/w9020103
APA StyleCollet, L., Beevers, L., & Prudhomme, C. (2017). Assessing the Impact of Climate Change and Extreme Value Uncertainty to Extreme Flows across Great Britain. Water, 9(2), 103. https://doi.org/10.3390/w9020103





