Runoff Simulation by SWAT Model Using High-Resolution Gridded Precipitation in the Upper Heihe River Basin, Northeastern Tibetan Plateau
Abstract
:1. Introduction
2. Study Area and Data Availability
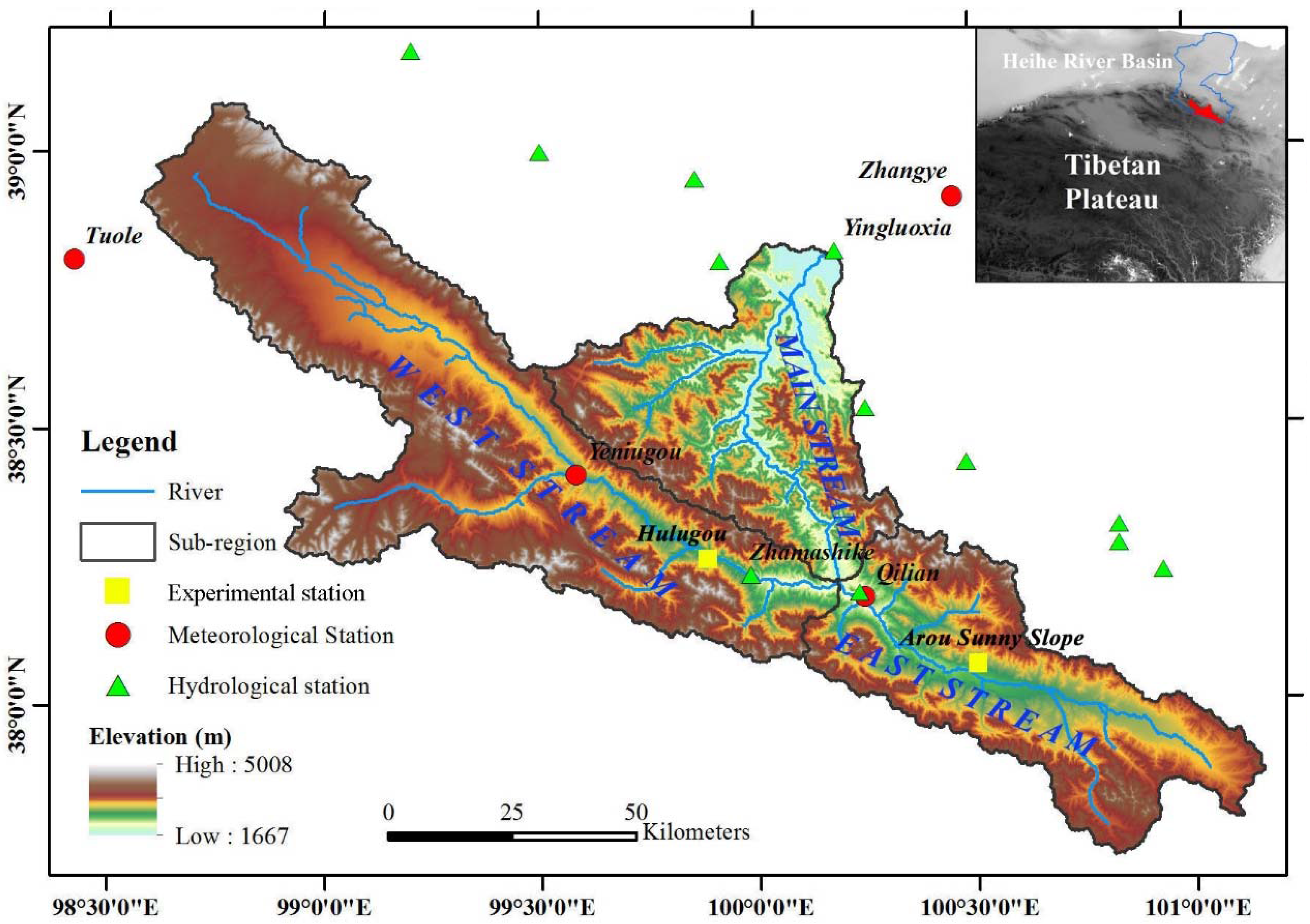
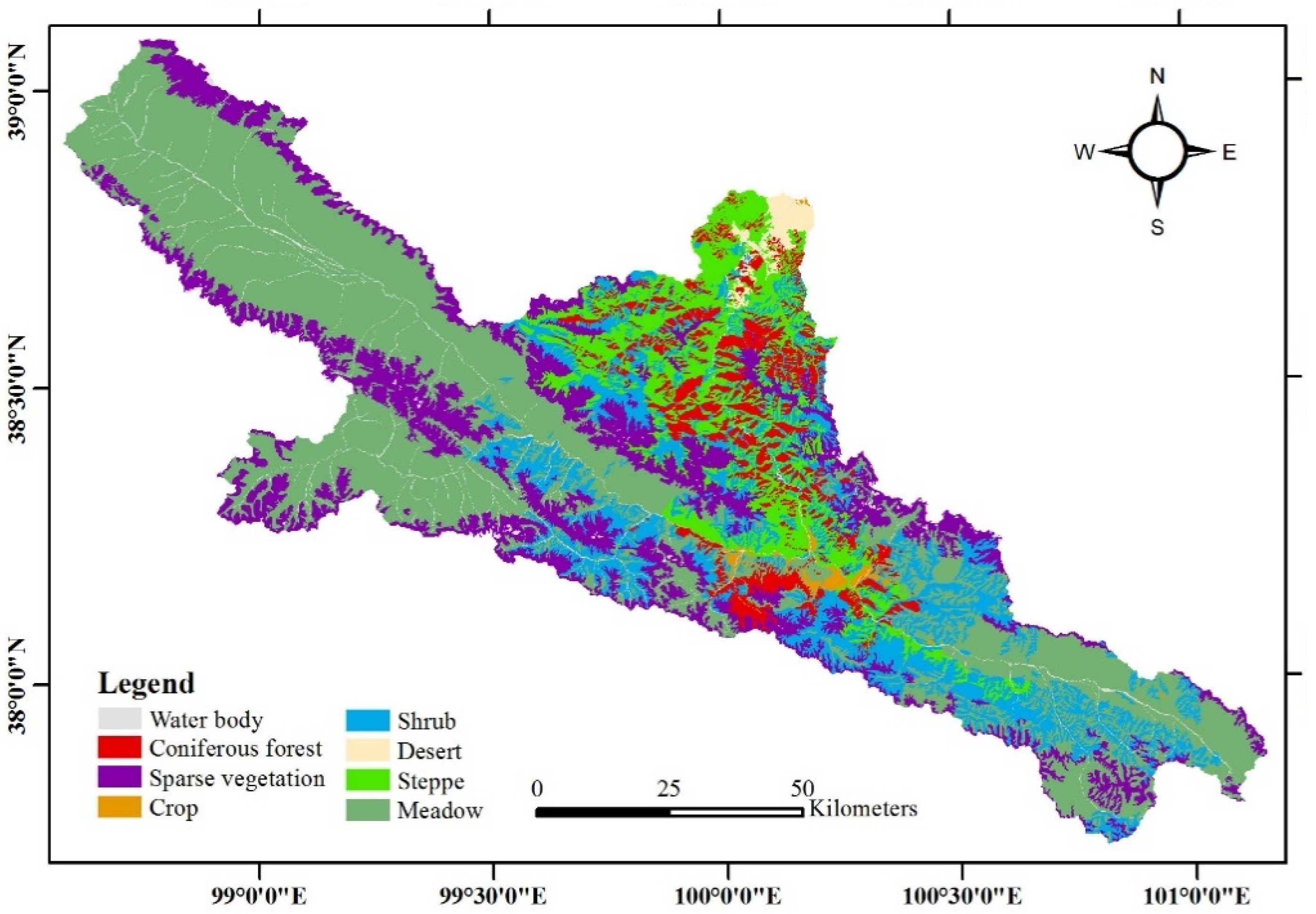
2.1. Study Area
2.2. Data Availability
3. Methods
3.1. SWAT Model
3.2. Gridded Precipitation
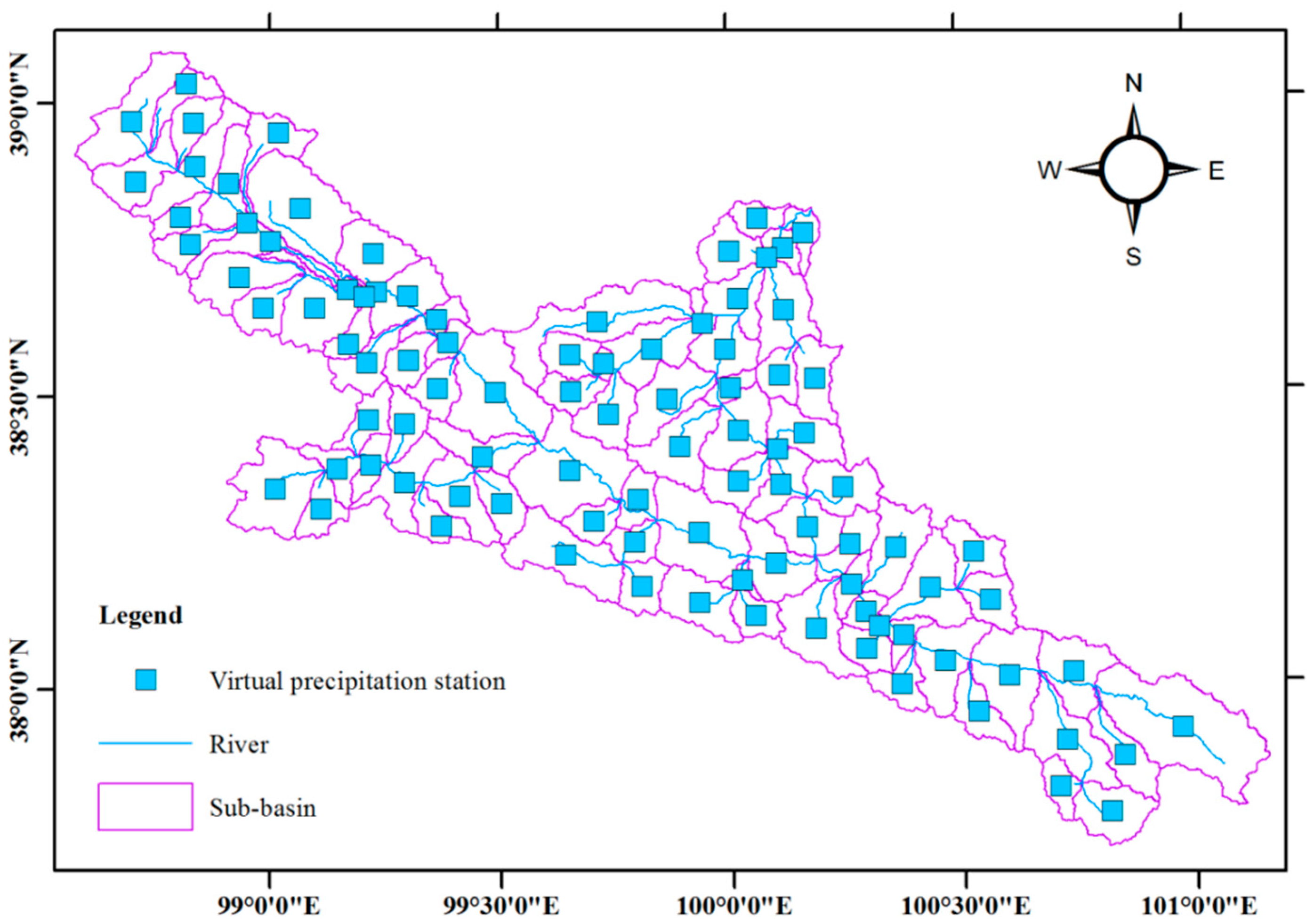
3.3. Virtual Precipitation Station
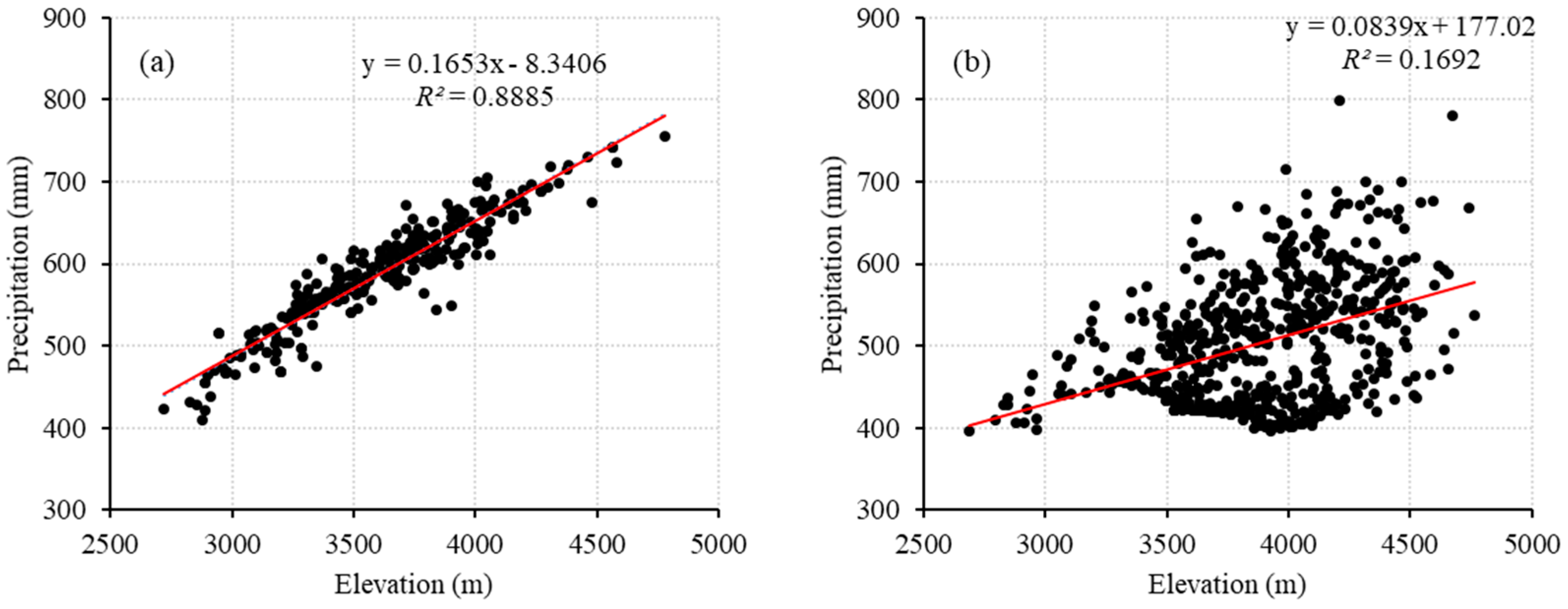
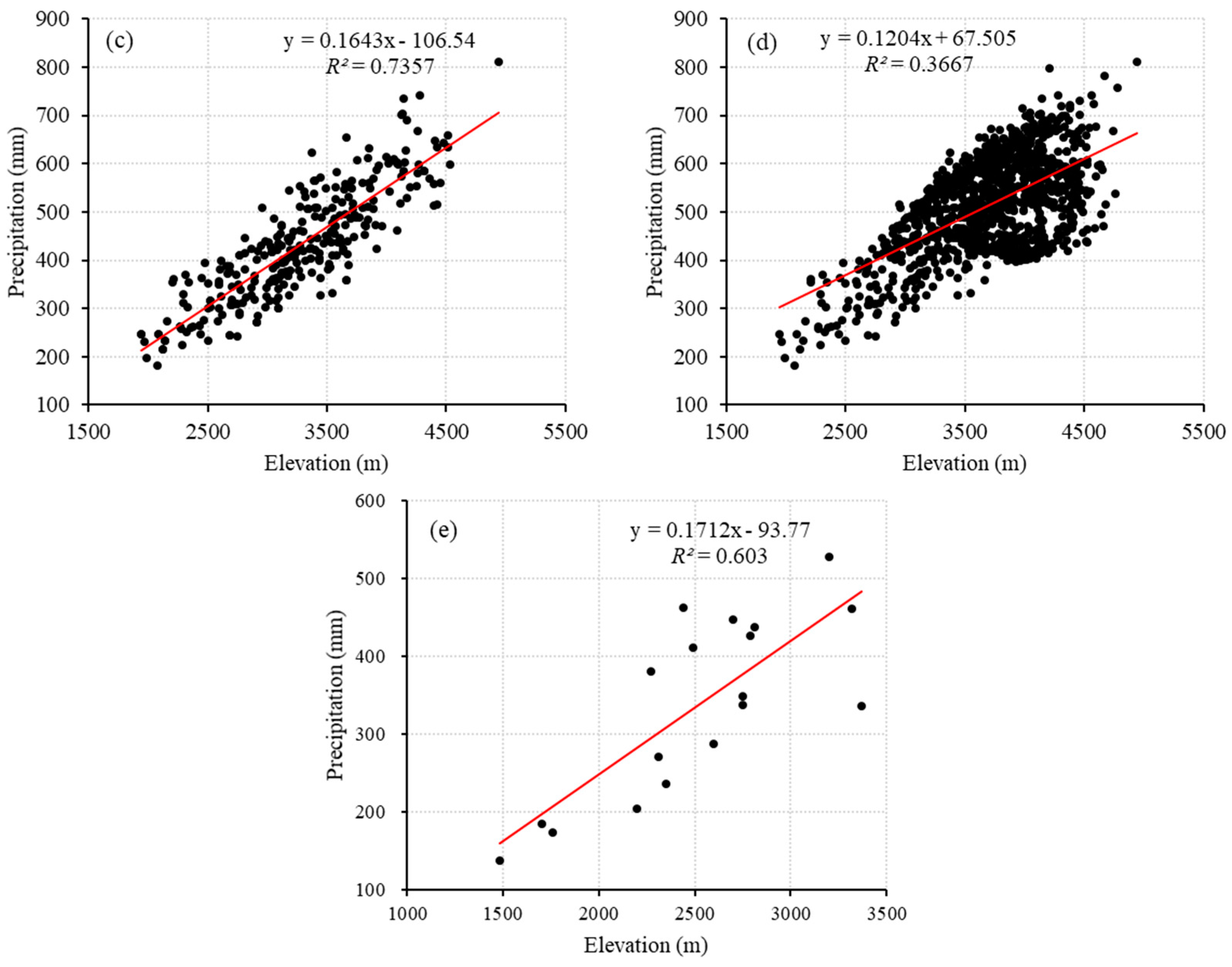
3.4. Precipitation Lapse Rate
4. Results
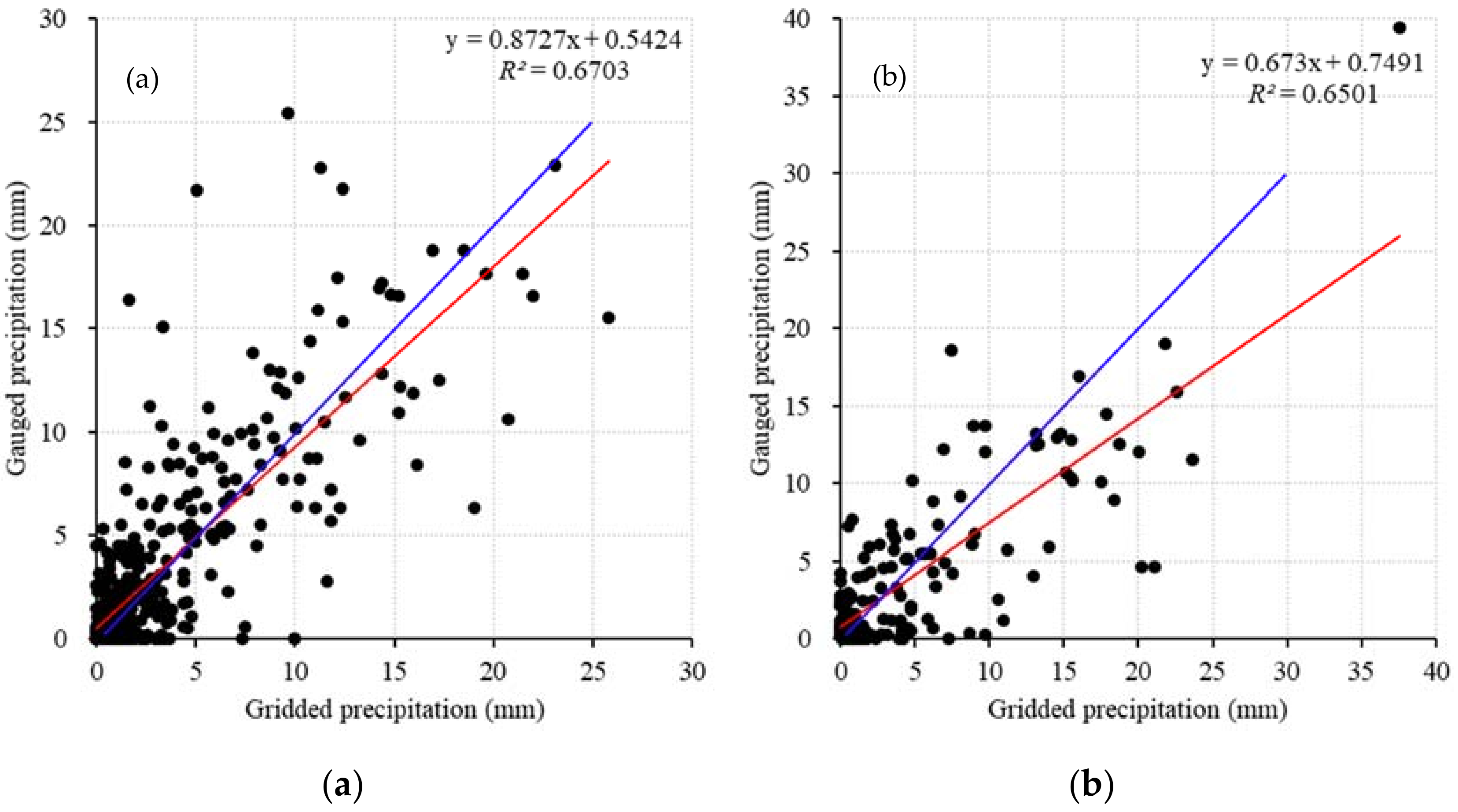
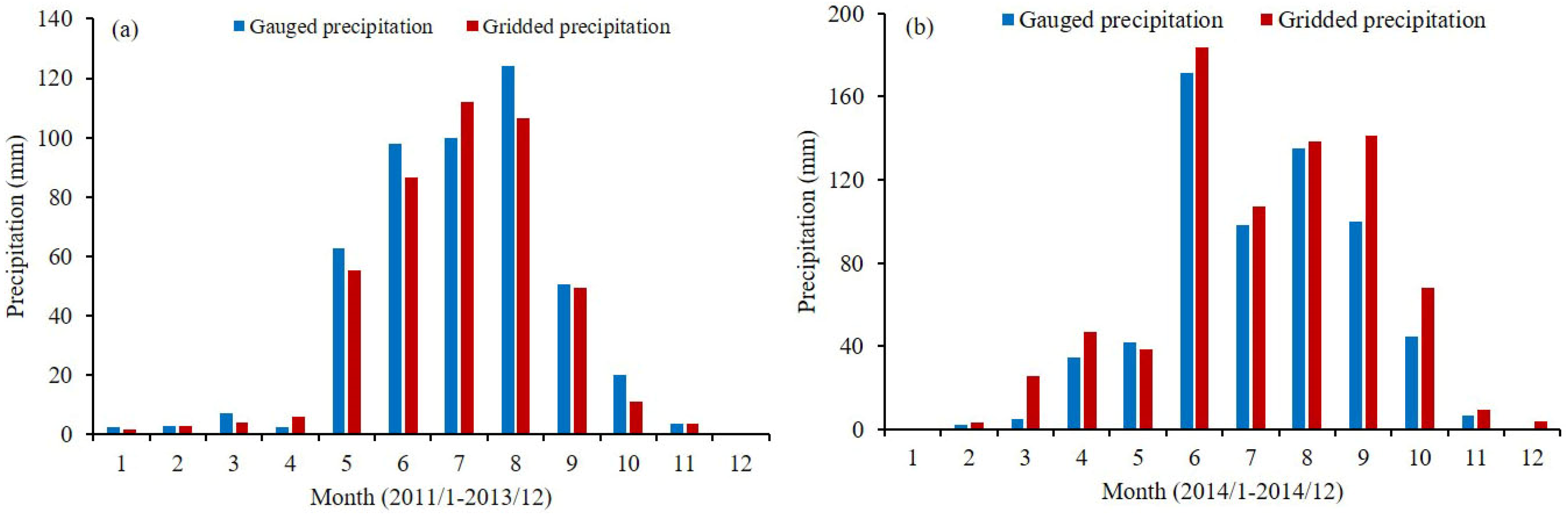
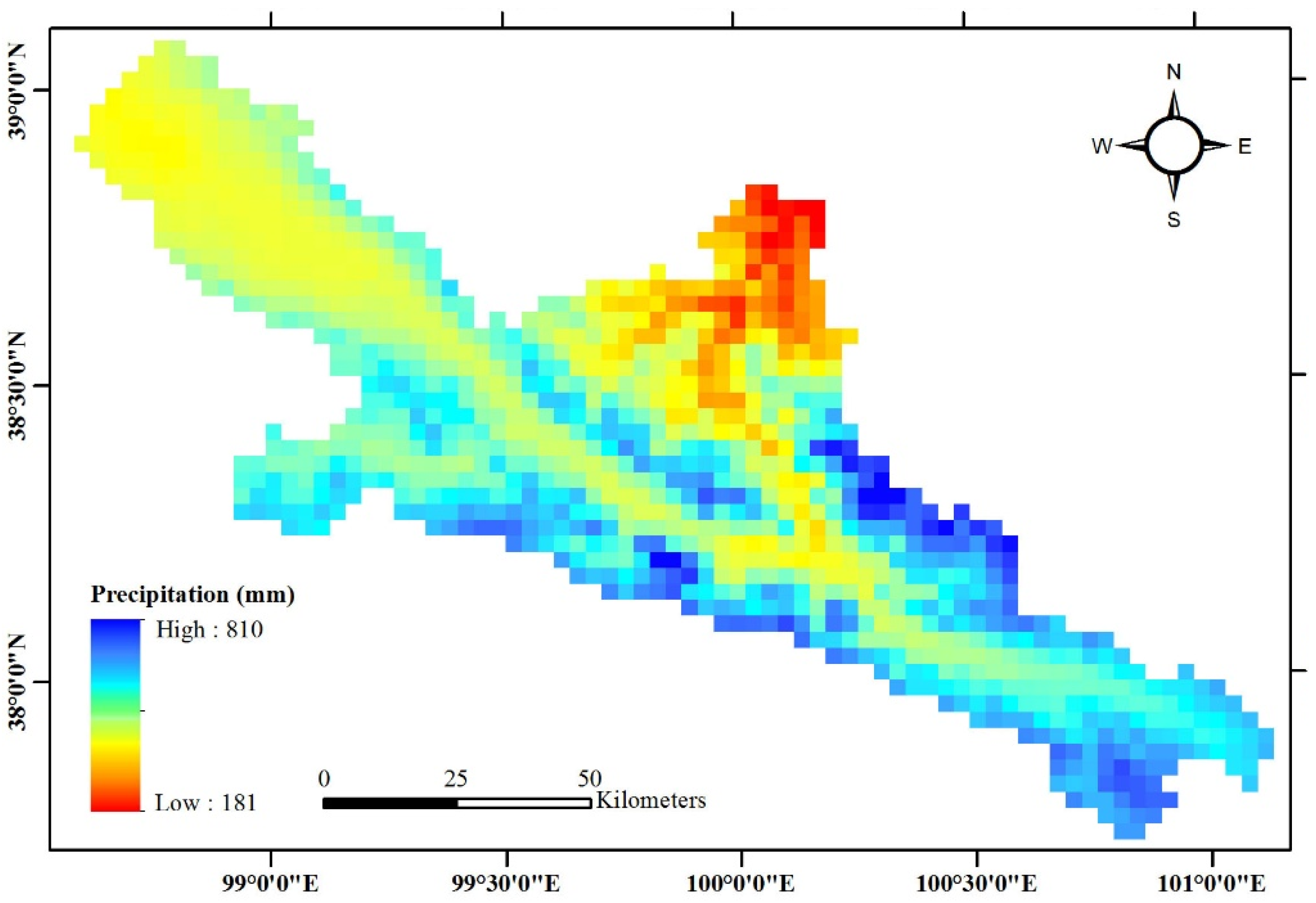
4.1. Assessing Gridded Precipitation
4.1.1. Assessing Gridded Precipitation
4.1.2. Spatial Description Capability
4.2. Distribution of Virtual Stations
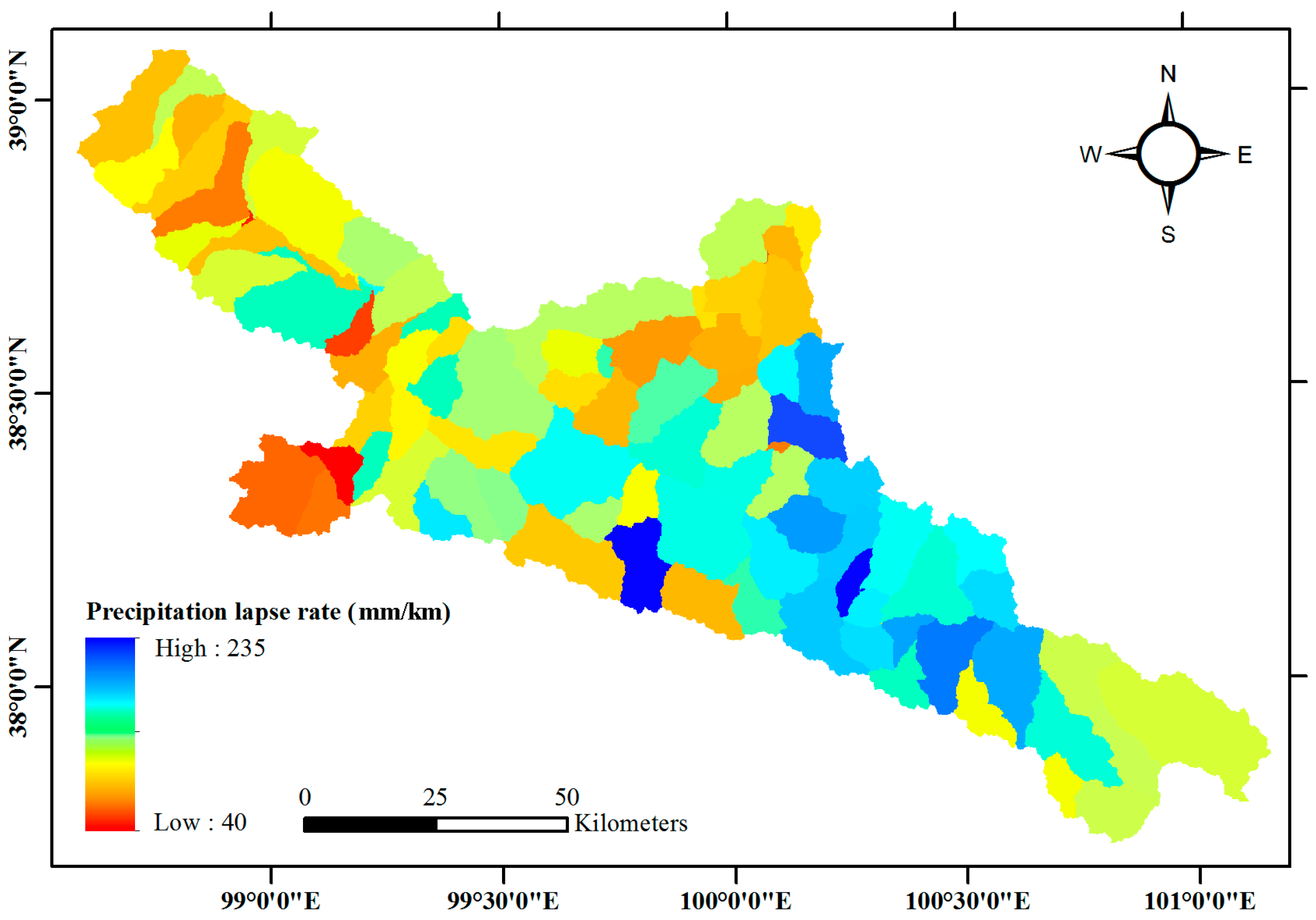
4.3. Distribution of Precipitation Lapse Rate
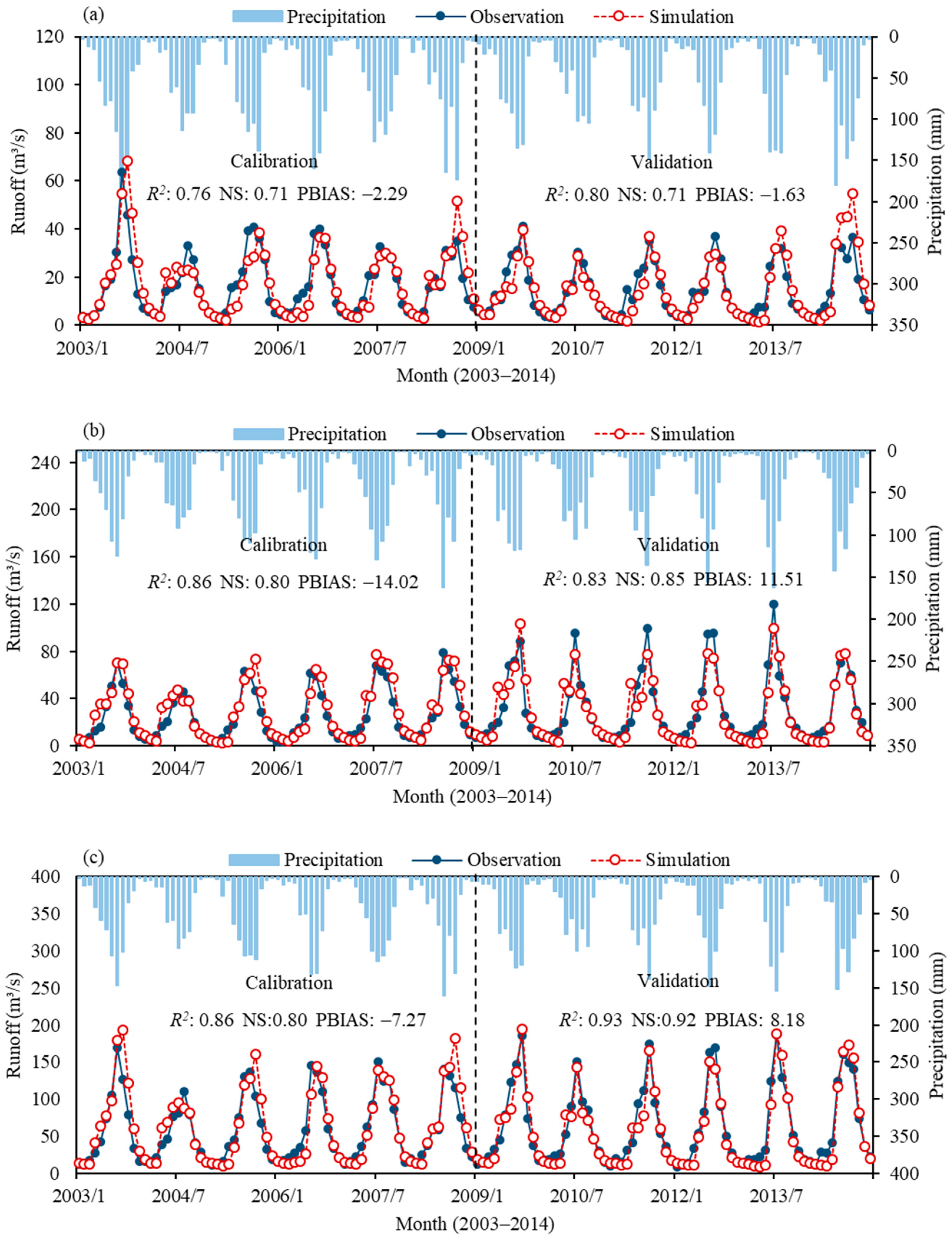
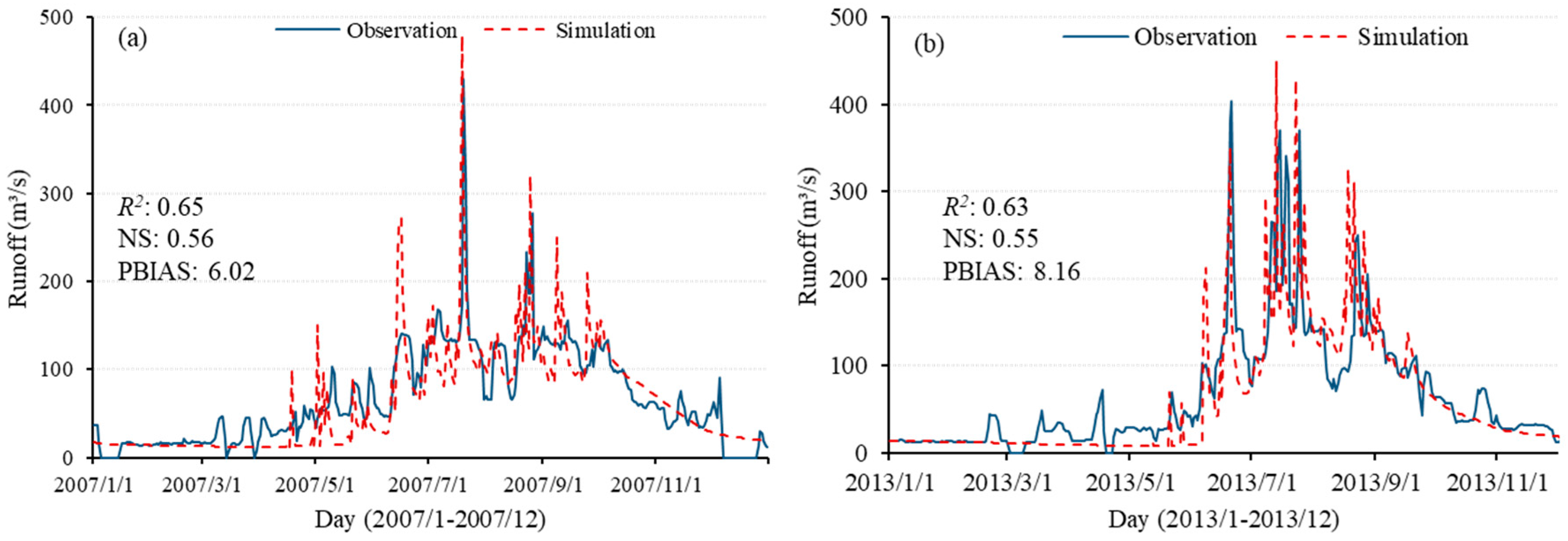
4.4. Model Calibration and Performance
4.5. Water Balance Component Characteristics
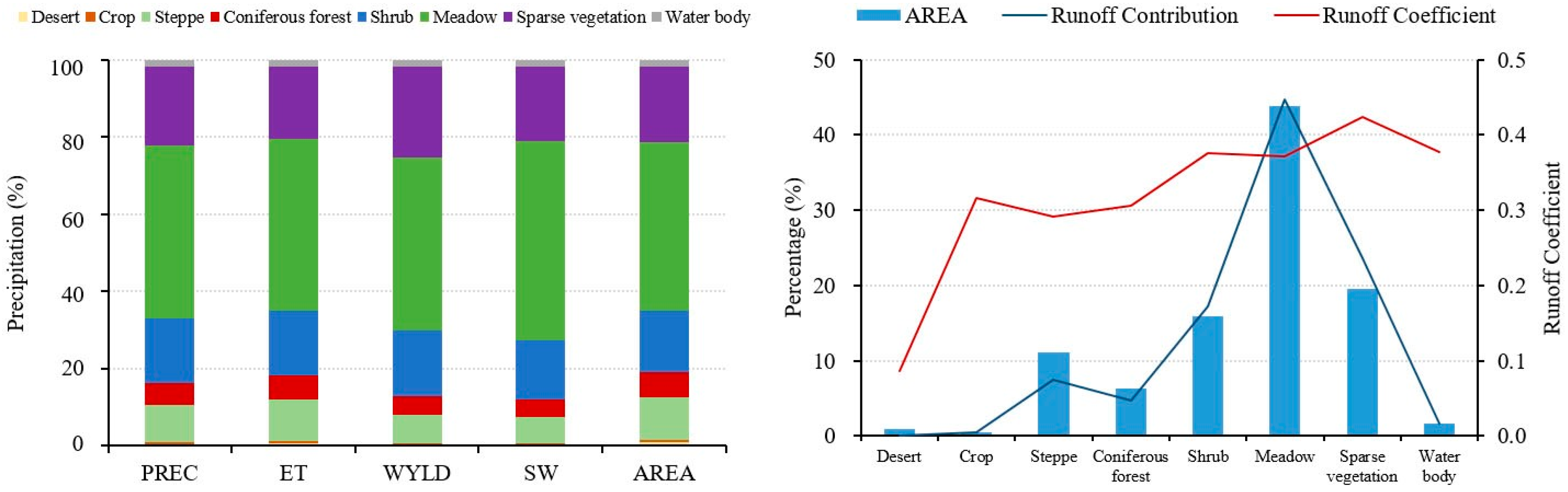
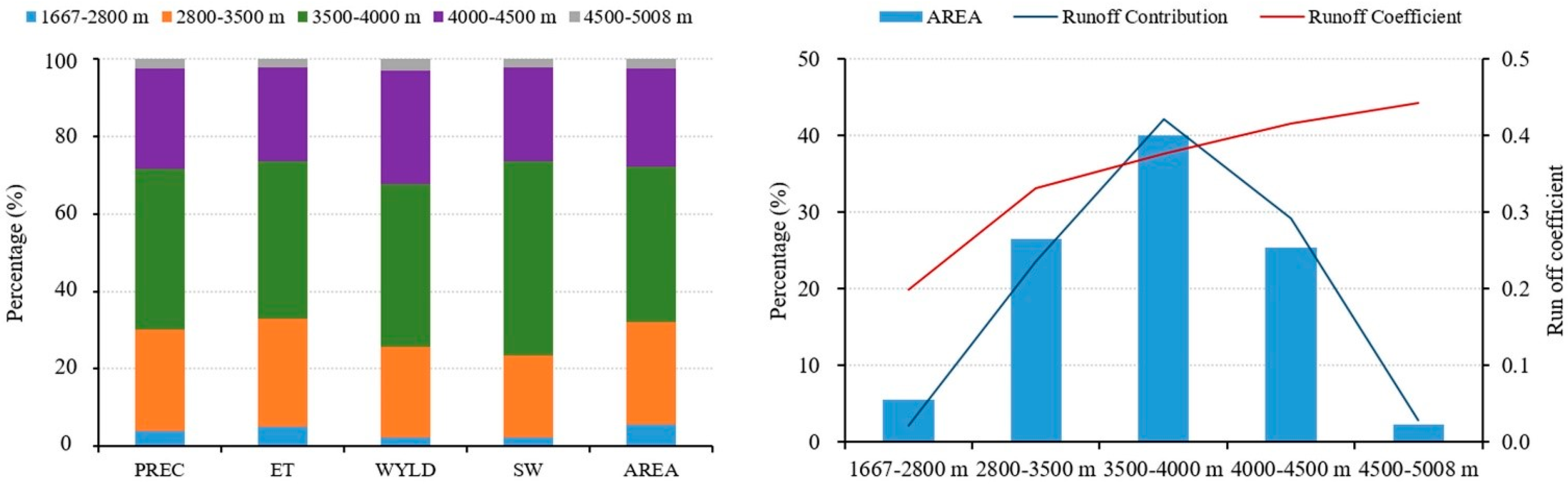
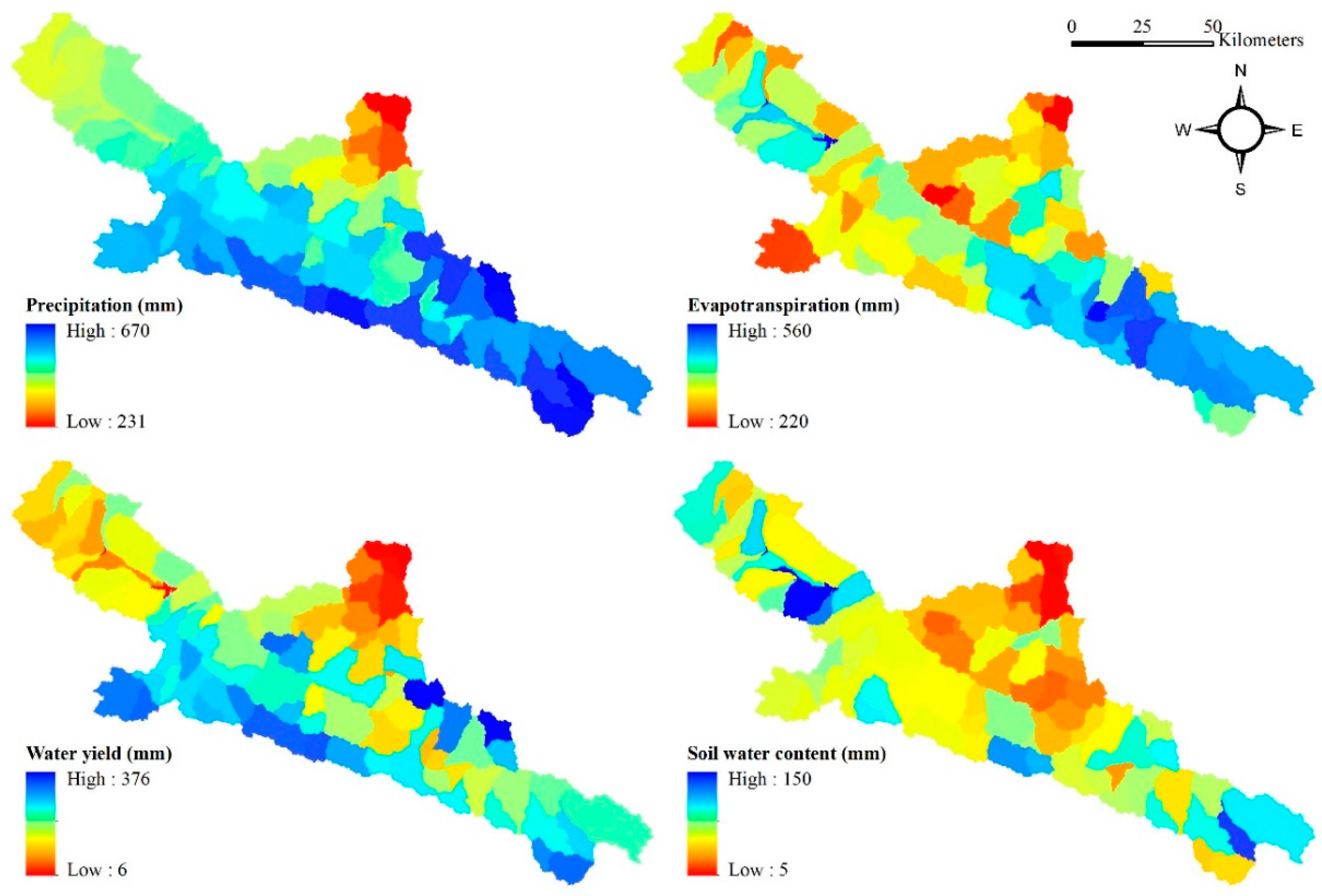
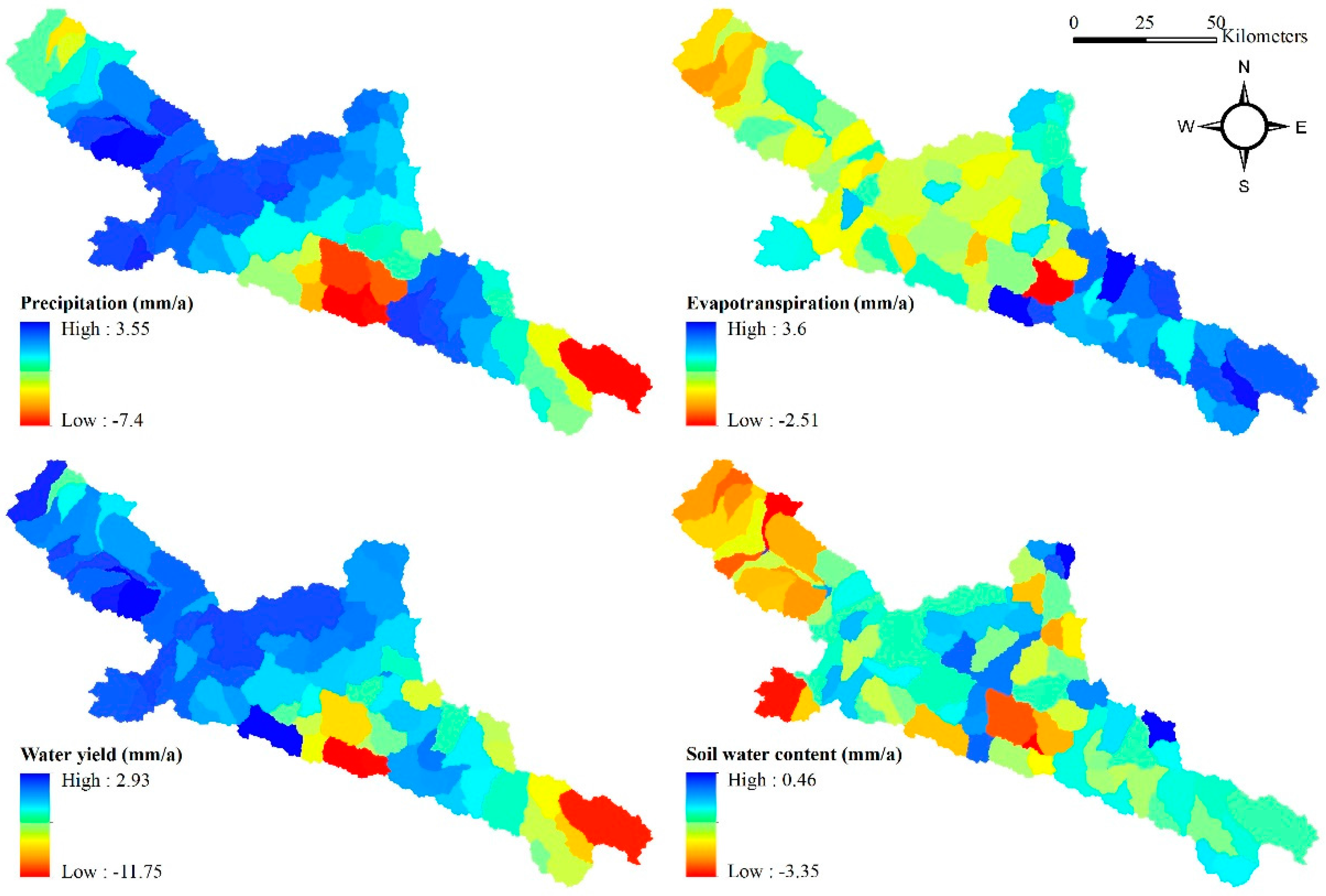
4.5.1. Spatial Variability of Water Balance Components at the Landscape Scale
4.5.2. Spatial Variability of Water Balance Components at the Elevation Band Scale
4.5.3. Spatial Variability of Water Balance Components at the Sub-Basin Scale
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Deng, X.Z.; Shi, Q.L.; Zhang, Q.; Shi, C.C.; Yin, F. Impacts of land use and land cover changes on surface energy and water balance in the Heihe River Basin of China, 2000–2010. Phys. Chem. Earth Parts A/B/C 2015, 79–82, 2–10. [Google Scholar] [CrossRef]
- Yang, D.W.; Gao, B.; Jiao, Y.; Lei, H.M.; Zhang, Y.L.; Yang, H.B.; Cong, Z.T. A distributed scheme developed for eco–hydrological modeling in the upper Heihe River. Sci. China Earth Sci. 2015, 58, 36–45. [Google Scholar] [CrossRef]
- Deng, X.Z.; Singh, R.B.; Liu, J.G.; Güneralp, B. Water use efficiency and integrated water resource management for river basin. Phys. Chem. Earth 2015, 89, 1–2. [Google Scholar] [CrossRef]
- Gao, B.; Qin, Y.; Wang, Y.H.; Yang, D.W.; Zheng, Y.R. Modeling ecohydrological processes and spatial patterns in the upper Heihe Basin in China. Forests 2016, 7, 10. [Google Scholar] [CrossRef]
- Morrissey, M.L.; Shafer, M.A.; Postawko, S.E.; Gibson, B. The Pacific rain gauge rainfall database. Water Resour. Res. 1995, 31, 2111–2113. [Google Scholar] [CrossRef]
- Yu, M.Y.; Chen, X.; Li, L.H.; Bao, A.M.; Paix, M.J. Streamflow simulation by SWAT using different precipitation sources in large arid basins with scarce raingauges. Water Resour. Manag. 2011, 25, 2669–2681. [Google Scholar] [CrossRef]
- Lu, Z.X.; Zou, S.B.; Xiao, H.L.; Zheng, C.M.; Yin, Z.L.; Wang, W.H. Comprehensive hydrologic calibration of SWAT and water balance analysis in mountainous watersheds in northwest China. Phys. Chem. Earth 2015, 79, 76–85. [Google Scholar] [CrossRef]
- Becker, A.; Finger, P.; Meyer-Christoffer, A.; Rudolf, B.; Schamm, K.; Schneider, U.; Ziese, M. A description of the global land–surface precipitation data products of the Global Precipitation Climatology Centre with sample applications including centennial (trend) analysis from 1901–present. Earth Syst. Sci. Data 2013, 5, 71–99. [Google Scholar] [CrossRef]
- Li, T.; Zheng, X.G.; Dai, Y.J.; Yang, C.; Chen, Z.Q.; Zhang, S.P.; Wu, G.C.; Wang, Z.L.; Huang, C.C.; Shen, Y.; et al. Mapping near–surface air temperature, pressure, relative humidity and wind speed over mainland China with high spatiotemporal resolution. Adv. Atmos. Sci. 2014, 31, 1127–1135. [Google Scholar] [CrossRef]
- Huang, C.C.; Zheng, X.G.; Tait, A.; Dai, Y.J.; Yang, C.; Chen, Z.Q.; Li, T.; Wang, Z.L. On using smoothing spline and residual correction to fuse rain gauge observations and remote sensing data. J. Hydrol. 2014, 508, 410–417. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, G.Q.; Wang, L.J.; Yu, J.S.; Xu, Z.X. Evaluation of gridded precipitation data for driving SWAT model in area upstream of Three Gorges Reservoir. PLoS ONE 2014, 9, e112725. [Google Scholar] [CrossRef] [PubMed]
- Fuka, D.R.; Walter, M.T.; MacAlister, C.; Degaetano, A.T.; Steenhuis, T.S.; Easton, Z.M. Using the Climate Forecast System Reanalysis as weather input data for watershed models. Hydrol. Process. 2013, 28, 5613–5623. [Google Scholar] [CrossRef]
- Shen, Y.; Xiong, A.Y. Validation and comparison of a new gauge–based precipitation analysis over mainland China. Int. J. Climatol. 2015, 36, 252–265. [Google Scholar] [CrossRef]
- Xiong, Z.; Yan, X.D. Building a high–resolution regional climate model for the Heihe River Basin and simulating precipitation over this region. Chin. Sci. Bull. 2013, 58, 4670–4678. [Google Scholar] [CrossRef]
- Wang, Y.H.; Yang, H.B.; Yang, D.W.; Qin, Y.; Gao, B.; Cong, Z.T. Spatial interpolation of daily precipitation in a high mountainous watershed based on gauge observations and a regional climate model simulation. J. Hydrometeorol. 2017, 18, 845–862. [Google Scholar] [CrossRef]
- Qin, Y.; Lei, H.M.; Yang, D.W.; Gao, B.; Wang, Y.H.; Cong, Z.T.; Fan, W.J. Long–term change in the depth of seasonally frozen ground and its ecohydrological impacts in the Qilian Mountains, northeastern Tibetan Plateau. J. Hydrol. 2016, 542, 204–221. [Google Scholar] [CrossRef]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.D.; Van Griensven, A.; Van Liew, M.W.; et al. SWAT: Model use, calibration, and validation. Trans. ASABE 2015, 55, 1491–1508. [Google Scholar] [CrossRef]
- Tobin, K.J.; Bennett, M.E. Using SWAT to model streamflow in two river basins with ground and satellite precipitation data. J. Am. Water Resour. Assoc. 2009, 45, 253–271. [Google Scholar] [CrossRef]
- Evans, J.P. Improving the characteristics of stream flow modeled by regional climate models. J. Hydrol. 2003, 284, 211–227. [Google Scholar] [CrossRef]
- Lakhtakia, M.N.; Yarnal, B.; Johnson, D.L.; White, R.A.; Miller, D.A.; Yu, Z. A simulation of river-basin response to mesoscale meteorological forcing: The Subsequenhanna River Basin Experiment (SRBEX). JAWRA 1998, 43, 921–937. [Google Scholar] [CrossRef]
- Zou, S.B.; Ruan, H.W.; Lu, Z.X.; Yang, D.W.; Xiong, Z.; Yin, Z.L. Runoff simulation in the upper Reaches of Heihe River Basin Based on the RIEMS–SWAT model. Water 2016, 8, 455. [Google Scholar] [CrossRef]
- Sood, A.; Muthuwatta, L.; McCartney, M. A SWAT evaluation of the effect of climate change on the hydrology of the Volta River basin. Water Int. 2013, 38, 297–311. [Google Scholar] [CrossRef]
- Masih, I.; Maskey, S.; Uhlenbrook, S.; Smakhtin, V. Assessing the impact of areal precipitation input on streamflow simulations using the SWAT model. J. Am. Water Resour. Assoc. 2011, 47, 179–195. [Google Scholar] [CrossRef]
- Li, Z.L.; Xu, Z.X.; Shao, Q.X.; Yang, J. Parameter estimation and uncertainty analysis of SWAT model in upper reaches of the Heihe river basin. Hydrol. Process. 2009, 23, 2744–2753. [Google Scholar] [CrossRef]
- Li, Z.L.; Shao, Q.X.; Xu, Z.X.; Cai, X.T. Analysis of parameter uncertainty in semi–distributed hydrological models using bootstrap method: A case study of SWAT model applied to Yingluoxia watershed in northwest China. J. Hydrol. 2010, 385, 76–83. [Google Scholar] [CrossRef]
- Li, Z.L.; Xu, Z.X.; Li, Z.J. Performance of WASMOD and SWAT on hydrological simulation in Yingluoxia watershed in northwest of China. Hydrol. Process. 2011, 25, 2001–2008. [Google Scholar] [CrossRef]
- Zang, C.F.; Liu, J.G. Trend analysis for the flows of green and blue water in the Heihe River basin, northwestern China. J. Hydrol. 2013, 502, 27–36. [Google Scholar] [CrossRef]
- Yin, Z.L.; Xiao, H.L.; Zou, S.B.; Zhu, R.; Lan, Y.C.; Shen, Y.P. Simulation of hydrological process of mountainous watersheds in inland river basin: Taking the Heihe Mainstream River as an example. J. Arid Land 2014, 6, 16–26. [Google Scholar] [CrossRef]
- Yin, Z.L.; Feng, Q.; Zou, S.B.; Yang, L.S. Assessing variation in water balance components in mountainous inland river basin experiencing climate change. Water 2016, 8, 472. [Google Scholar] [CrossRef]
- Thompson, S.E.; Harman, C.J.; Troch, P.A.; Brooks, P.D.; Sivapalan, M. Spatial scale dependence of ecohydrologically mediated water balance partitioning: A systhesis framework for catchment Ecohydrology. Water Resour. Res. 2011, 47, 143–158. [Google Scholar] [CrossRef]
- Gregory, J.M.; David, M.W. Temporal and spatial variability of the global water balance. Clim. Chang. 2013, 120, 375–387. [Google Scholar]
- Herrmann, F.; Keller, L.; Kunkel, R.; Vereechen, H.; Wendland, F. Determination of spatially differentiated water balance components including groundwater recharge on the Federal State level—A case study using them GROWA model in North Rhine–Westphalia (Germany). J. Hydrol. Reg. Stud. 2015, 4, 294–312. [Google Scholar] [CrossRef] [Green Version]
- Jian, S.Q.; Zhao, C.Y.; Fang, S.M.; Yu, K. Effects of different vegetation restoration on soil water storage and water balance in the Chinese Loess Plateau. Agric. For. Meteorol. 2015, 206, 85–96. [Google Scholar] [CrossRef]
- Liu, Y.Q.; Xu, Z.M.; Nan, Z.T. Study on ecological compensation in upper stream of Heihe river basin based on SWAT model and minimum–data approach. Trans. Chin. Soc. Agric. Eng. 2012, 28, 124–130. [Google Scholar]
- Lu, Z.X.; Zou, S.B.; Xiao, H.L.; Yin, Z.L.; Ruan, H.W.; Gao, H.S. How to determine drainage area threshold in alpine regions of upper reaches of Heihe River. J. Glaciol. Geicryol. 2015, 37, 493–499. [Google Scholar]
- Wu, F.; Zhan, J.Y.; Wang, Z.; Zhang, Q. Streamflow variation due to glacier melting and climate change in upstream Heihe River Basin, Northwest China. Phys. Chem. Earth Parts A/B/C 2015, 79, 11–19. [Google Scholar] [CrossRef]
- Kang, E.S.; Cheng, G.D.; Lan, Y.C.; Jin, H.J. A model for simulating the response of runoff from the mountainous watersheds of inland river basins in the arid area of northwest China to climatic changes. Sci. China Ser. D Earth Sci. 1999, 42, 53–63. [Google Scholar] [CrossRef]
- Zhang, A.J.; Liu, W.B.; Yin, Z.L.; Fu, G.B.; Zheng, C.M. How will climate change affect the water availability in the Heihe River Basin, northwest China? J. Hydrometeorol. 2016, 17, 1517–1542. [Google Scholar] [CrossRef]
- Jarvis, A.; Reuter, H.I.; Nelson, A. Hole-Filled SRTM for the Globe Version 4; CGIAR–CSI SRTM 90 m Database. Available online: http://srtm.csi.cgiar.org (accessed on 5 July 2012).
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation Version 2009; USDA–ARS Grassland, Soil and Water Research Laboratory: Temple, TX, USA, 2011.
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation: Version 2005; USDA–ARS Grassland, Soil and Water Research Laboratory: Temple, TX, USA, 2005.
- Gandin, L.S. Objective Analysis of Meteorological Fields; Israel Program for Scientific Translations: Jerusalem, Israel, 1965; Volume 242. [Google Scholar]
- Paxian, A.; Hertig, E.; Seubert, G.; Vogt, G.; Jacobeit, J.; Paeth, H. Present-day and future mediterranean precipitation extremes assessed by different statistical approaches. Clim. Dyn. 2015, 44, 845–860. [Google Scholar] [CrossRef]
- Price, K.; Purucker, S.T.; Kraemer, S.R.; Babendreier, J.E.; Knightes, C.D. Comparison of radar and gauge precipitation data in watershed models across varying spatial and temporal scales. Hydrol. Process. 2013, 28, 3505–3520. [Google Scholar] [CrossRef]
- Tuo, Y.; Duan, Z.; Disse, M.; Chiogna, G. Evaluation of precipitation input for SWAT modeling in alpine catchment: A case study in the Adige river basin (Italy). Sci. Total Environ. 2016, 573, 66–82. [Google Scholar] [CrossRef] [PubMed]
- Zhang, A.J.; Zheng, C.M.; Wang, S.; Yao, Y.Y. Analysis of streamflow variations in the Heihe River Basin, northwest China: Trends, abrupt changes, driving factors and ecological influences. J. Hydrol. Reg. Stud. 2015, 3, 106–124. [Google Scholar] [CrossRef]
- Liu, J.F.; Chen, R.S.; Qin, W.W.; Yang, Y. Study on the vertical distribution of precipitation in mountainous regions using TRMM data. Adv. Water Sci. 2011, 22, 447–454. [Google Scholar]
- Chen, R.S.; Song, Y.X.; Kang, E.S.; Han, C.T.; Liu, J.F.; Yang, Y.; Qing, W.W.; Liu, Z.W. A Cryosphere–Hydrology Observation System in a small alpine watershed in the Qilian Mountains of China and is meteorological gradient. Arct. Antarct. Alp. Res. 2014, 46, 505–523. [Google Scholar] [CrossRef]
- Chang, X.X.; Zhao, A.F.; Wang, J.Y.; Chang, Z.Q.; Jin, B.W. Precipitation Characteristic and Interception of Forest in Qilian Mountain. Plateau Meteorol. 2002, 21, 274–280. [Google Scholar]
- Ding, Y.J.; Ye, B.S.; Zhou, W.J. Temporal and spatial precipitation distribution in the Heihe Catchment, Northwest China, during the past 40 a. J. Glaciol. Geocryol. 1999, 21, 42–48. [Google Scholar]
- Legates, D.R.; McCabe, J. Evaluating the use of “Goodness-of-Fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Status of automatic calibration for hydrologic models: Comparison with multilevel expert calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar] [CrossRef]
- Singh, J.; Knapp, H.V.; Arnold, J.G.; Demissie, M. Hydrologic modeling of the Iroquois River watershed using HSPF and SWAT. J. Am. Water Resour. Assoc. 2005, 41, 343–360. [Google Scholar] [CrossRef]
- Wang, N.L.; He, J.Q.; Jiang, X.; Song, G.J.; Pu, J.C.; Wu, X.B.; Chen, L. Study on the zone of maximum precipitation in the north slopes of the central Qilian mountains. J. Glaciol. Geocryol. 2009, 31, 396–403. [Google Scholar]
- Li, X.; Cheng, G.D.; Liu, S.M.; Xiao, Q.; Ma, M.G.; Jin, R.; Che, T.; Liu, Q.H.; Wang, W.Z.; Qi, Y.; et al. Heihe watershed allied telemetry experimental research (HiWATER): Scientific objectives and experimental design. Bull. Am. Meteorol. Soc. 2013, 94, 1145–1160. [Google Scholar] [CrossRef]
- Wang, J.; Li, S. Effect of climatic change on snowmelt runoffs in mountainous regions of inland rivers in Northwestern China. Sci. China Ser. D Earth Sci. 2016, 49, 881–888. [Google Scholar] [CrossRef]
- Zhao, D.Z.; Zhang, W.C. Rainfall–runoff simulation using the VIC–3L model over the Heihe River mountainous basin, China. In Proceedings of the 2005 IEEE International Geoscience and Remote Sensing Symposium, Seoul, Korea, 29 July 2005; Volume 6, pp. 4391–4394. [Google Scholar]
- Jia, Y.; Ding, X.; Qin, C.; Wang, H. Distributed modeling of landsurface water and energy budgets in the inland Heihe river basin of China. Hydrol. Earth Syst. Sci. 2009, 13, 1849–1866. [Google Scholar] [CrossRef]
- Li, Z.; Liu, W.Z.; Zhang, X.C.; Zheng, F.L. Impacts of land use change and climate variability on hydrology in an agricultural catchment on the Loess Plateau of China. J. Hydrol. 2009, 377, 35–42. [Google Scholar] [CrossRef]
- Xu, B.R.; Lu, Z.X.; Liu, S.Y.; Li, J.; Xie, J.L.; Long, A.H.; Yin, Z.L.; Zou, S.B. Glacier changes and their impacts on the discharge in the past half–century in Tekes watershed, Central Asia. Phys. Chem. Earth 2015, 89, 96–103. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models: Part 1. A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, B.; Zhao, C.Y. Annual base flow change and its causes in the upper reaches of Heihe River. Geogr. Res. 2011, 30, 1411–1430. [Google Scholar]
- Wu, B.F.; Yan, N.N.; Xiong, J.; Bastiaanssen, W.; Zhu, W.; Stein, A. Validation of ETWatch using field measurements at diverse landscapes: A case study in Hai Basin of China. J. Hydrol. 2012, 436, 67–80. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- He, Z.B.; Zhao, W.Z.; Liu, H.; Tang, Z.X. Effect of forest on annual water yield in the mountains of an arid inland river basin: A case study in the Pailugou catchment on northwestern China’s Qilian Mountains. Hydrol. Process. 2012, 26, 613–621. [Google Scholar] [CrossRef]
- Daly, C.; Neilson, P.R.; Phillips, D.L. A statistical–topographic model for mapping climatological precipitation over mountainous terrain. J. Appl. Meteorol. 1994, 33, 140–158. [Google Scholar] [CrossRef]
- Wei, J.F.; Liu, S.Y.; Guo, W.Q.; Yao, X.J.; Xu, J.L.; Bao, W.J.; Jiang, Z.L. Surface–area changes of glaciers in the Tibetan Plateau interior area since the 1970s using recent Landsat images and historical maps. Annu. Glaciol. 2014, 55, 213–222. [Google Scholar]
- Jamilatou, C.B.; Seifeddine, J.; Sihem, B.; Pibgnina, B.; Abel, A.; Michael, R. Multi-Site Validation of the SWAT Model on the Bani Catchment: Model Performance and Predictive Uncertainty. Water 2016, 8, 178. [Google Scholar] [CrossRef]
| Station | Yearly Scale | Daily Scale | Monthly Scale | |||||
|---|---|---|---|---|---|---|---|---|
| Gauge Data (mm) | Gridded Data (mm) | R2 | RMSE (mm) | PBIAS (%) | R2 | RMSE (mm) | PBIAS (%) | |
| Hulugou | 474.3 | 439.6 | 0.67 | 1.78 | 7.31 | 0.95 | 10.78 | 7.31 |
| Arou sunny slope | 639.4 | 766.4 | 0.65 | 2.57 | −19.87 | 0.96 | 16.12 | −19.87 |
| Parameter | Description | Range | Value | Sensitivity |
|---|---|---|---|---|
| Ch_K2 | Effective hydraulic conductivity in main channel alluvium (mm/h) | 0–500 | 8–15 | 1 |
| Cn2 | Initial SCS runoff curve number for moisture condition II | 35–98 | 43–95 | 2 |
| Plaps | Precipitation lapse rate (mm/km) | −1000–1000 | 40–235 | 3 |
| Esco | Soil evaporation compensation factor | 0–1 | 0.83–0.90 | 4 |
| Alpha_Bf | Base flow alpha factor (days) | 0–1 | 0.06–0.072 | 5 |
| Smfmn | Melt factor on 21 December (mm H2O/°C day) | 0–20 | 1 | 6 |
| Sol_Awc | Available water capacity of the soil layer (mm H2O/mm soil) | 0–1 | 0.1–0.22 | 7 |
| Tlaps | Temperature lapse rate (°C/km) | −10–10 | −5 | 8 |
| Gw_Delay | Groundwater delay time (days) | 0–500 | 31 | 9 |
| Smfmx | Melt factor on 21 June (mm H2O/°C day) | 0–20 | 2.5 | 10 |
| Region | Area (km2) | PREC (mm) | ET (mm) | WYLD (mm) | SW (mm) | Runoff Coefficient | Runoff Contribution (%) |
|---|---|---|---|---|---|---|---|
| East Tributary | 2504 | 609.8 | 364.4 | 229.9 | 63.5 | 0.37 | 29 |
| West Tributary | 5032 | 522.8 | 310.3 | 199.5 | 58.5 | 0.38 | 52 |
| Main Stream | 2482 | 446.2 | 287.4 | 148.3 | 27.7 | 0.33 | 19 |
| Entire Basin | 10018 | 525.5 | 318.1 | 194.4 | 52.1 | 0.37 | 100 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruan, H.; Zou, S.; Yang, D.; Wang, Y.; Yin, Z.; Lu, Z.; Li, F.; Xu, B. Runoff Simulation by SWAT Model Using High-Resolution Gridded Precipitation in the Upper Heihe River Basin, Northeastern Tibetan Plateau. Water 2017, 9, 866. https://doi.org/10.3390/w9110866
Ruan H, Zou S, Yang D, Wang Y, Yin Z, Lu Z, Li F, Xu B. Runoff Simulation by SWAT Model Using High-Resolution Gridded Precipitation in the Upper Heihe River Basin, Northeastern Tibetan Plateau. Water. 2017; 9(11):866. https://doi.org/10.3390/w9110866
Chicago/Turabian StyleRuan, Hongwei, Songbing Zou, Dawen Yang, Yuhan Wang, Zhenliang Yin, Zhixiang Lu, Fang Li, and Baorong Xu. 2017. "Runoff Simulation by SWAT Model Using High-Resolution Gridded Precipitation in the Upper Heihe River Basin, Northeastern Tibetan Plateau" Water 9, no. 11: 866. https://doi.org/10.3390/w9110866





