The Probability Density Evolution Method for Flood Frequency Analysis: A Case Study of the Nen River in China
Abstract
:1. Introduction
2. Probability Density Evolution Method
3. The Flood Frequency Analysis Method Based on PDEM
3.1. The Joint PDF Model for Peak Discharge
3.2. Model Solution and Frequency Values Calculation of Peak Discharge
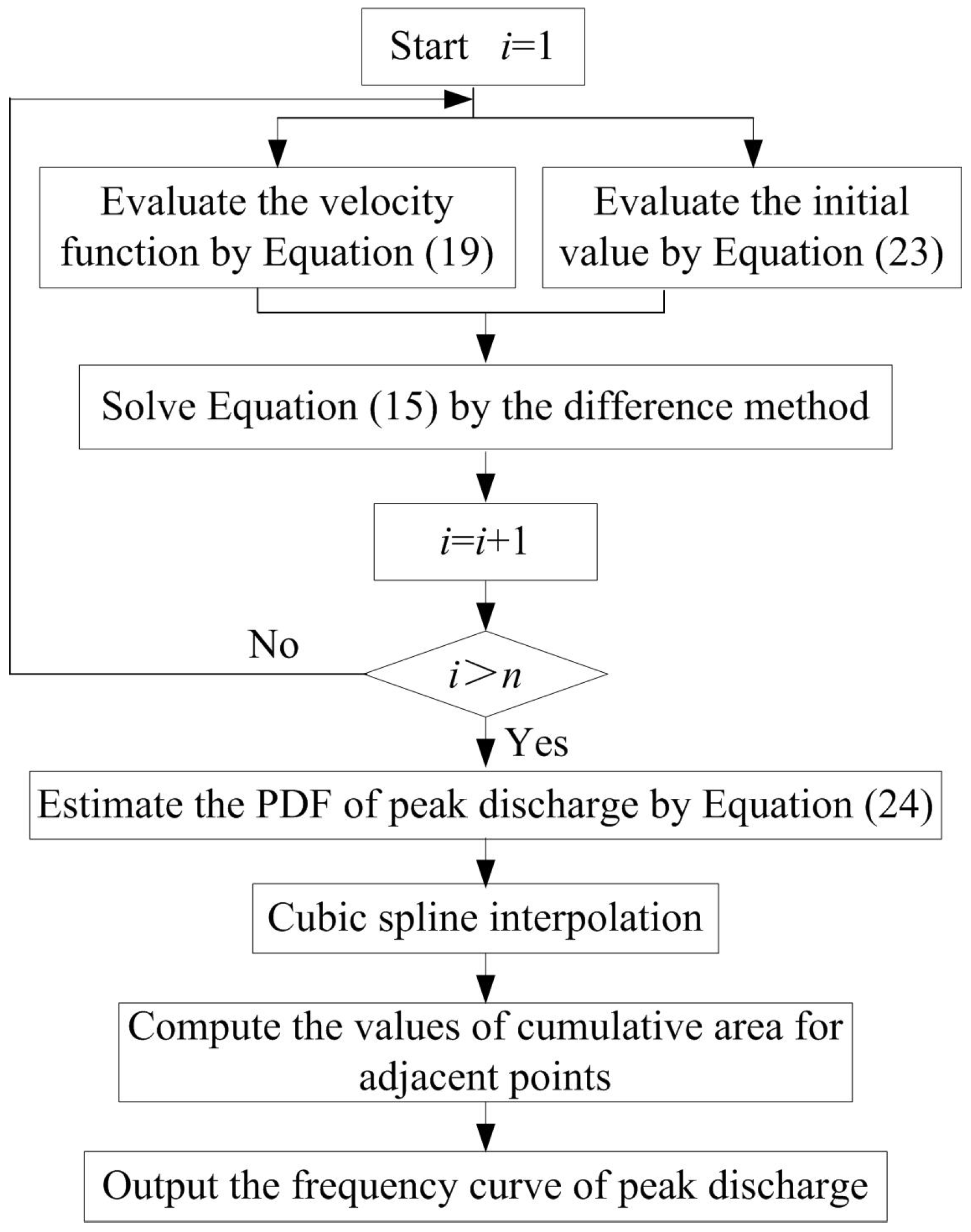
3.3. The Robustness Study for PDEM
- Give the parent parameters of statistical distribution and assume their distribution types, then extract m group of sample series with the length of n from every parent distribution.
- Calculate the design value of design frequency with PDEM.
- Analyze various types of error of design value and study their robustness.
- (1)
- The parent distribution: Pearson Type III, Log Normal.
- (2)
- Estimation method: the probability density evolution method (PDEM).
- (3)
- Sample size: n = 30, n = 50.
- (4)
- Design frequency: p1 = 0.02, p2 = 0.01.
- (5)
- Parent parameters: As seen in Table 1.
- (6)
- Sampling times: m = 50.
- (7)
- Evaluation criteria: Relative mean square (RMS) error and relative error of the mean design value (as shown in Equations (25) and (26)).
| No. | Mean (EX) | Coefficient of Variation (Cv) | Coefficient of Skewness (Cs) |
|---|---|---|---|
| 1 | 1000 | 1.0 | 2.5 |
| 2 | 1000 | 1 | 3 |
| 3 | 1000 | 2 | 4 |
| 4 | 1000 | 2.5 | 5 |
| No. | p | n | Parent Parameters | True Value | Mean Value of Design Value | δ | ω |
|---|---|---|---|---|---|---|---|
| 1 | 0.02 | 30 | 3913.10 | 4022.49 | 26.45 | 2.80 | |
| 2 | 0.01 | Cv = 1 | 4899.40 | 4713.69 | 27.9 | 3.79 | |
| 3 | 0.02 | 50 | Cs = 2.5 | 3913.10 | 4161.22 | 24.19 | 6.34 |
| 4 | 0.01 | 4899.40 | 4442.61 | 28.92 | 9.32 | ||
| 5 | 0.02 | 30 | 3913.10 | 3685.51 | 34.58 | 5.82 | |
| 6 | 0.01 | Cv = 1 | 4899.40 | 4416.54 | 34.5 | 9.86 | |
| 7 | 0.02 | 50 | Cs = 3 | 3913.10 | 4262.01 | 27.46 | 8.92 |
| 8 | 0.01 | 4899.40 | 5169.09 | 29.37 | 5.50 | ||
| 9 | 0.02 | 30 | 6063.75 | 6468.00 | 29.21 | 6.67 | |
| 10 | 0.01 | Cv =2 | 8540.85 | 8944.98 | 36.21 | 4.73 | |
| 11 | 0.02 | 50 | Cs = 4 | 6063.75 | 6797.37 | 30.62 | 12.10 |
| 12 | 0.01 | 8540.85 | 7806.87 | 34.83 | 8.59 | ||
| 13 | 0.02 | 30 | 6698.42 | 7196.04 | 31.69 | 7.43 | |
| 14 | 0.01 | Cv = 2.5 | 9795.19 | 8829.59 | 36.55 | 9.86 | |
| 15 | 0.02 | 50 | Cs = 5 | 6698.42 | 7307.51 | 19.11 | 9.09 |
| 16 | 0.01 | 9795.19 | 10,340.84 | 29.9 | 5.57 |
| No. | p | n | Parent Parameters | True Value | Mean Value of Design Value | δ | ω |
|---|---|---|---|---|---|---|---|
| 17 | 0.02 | 30 | 4040 | 3926.20 | 17.74 | 2.82 | |
| 18 | 0.01 | Cv = 1 | 4850 | 4468.80 | 27.9 | 7.86 | |
| 19 | 0.02 | 50 | Cs = 2.5 | 4040 | 4076.80 | 17.71 | 0.91 |
| 20 | 0.01 | 4850 | 4645.50 | 25.58 | 4.22 | ||
| 21 | 0.02 | 30 | 4150 | 3967.60 | 29.5 | 4.40 | |
| 22 | 0.01 | Cv = 1 | 5050 | 4714.50 | 29.83 | 6.64 | |
| 23 | 0.02 | 50 | Cs = 3 | 4150 | 4372.20 | 21.08 | 5.35 |
| 24 | 0.01 | 5050 | 5118.10 | 24.99 | 1.35 | ||
| 25 | 0.02 | 30 | 7300 | 7045.80 | 16.75 | 3.48 | |
| 26 | 0.01 | Cv = 2 | 9100 | 8454.10 | 28.66 | 7.10 | |
| 27 | 0.02 | 50 | Cs = 4 | 7300 | 6910 | 24.95 | 5.34 |
| 28 | 0.01 | 9100 | 9001 | 33.44 | 1.09 | ||
| 29 | 0.02 | 30 | 8875 | 8135 | 23.3 | 8.34 | |
| 30 | 0.01 | Cv = 2.5 | 11,125 | 9593 | 24.43 | 13.77 | |
| 31 | 0.02 | 50 | Cs = 5 | 8875 | 8506 | 28.62 | 4.16 |
| 32 | 0.01 | 11,125 | 10,104 | 30.72 | 9.18 |
4. Case sStudy
4.1. Study Area
| Year | AMPD (m3/s) | Year | AMPD (m3/s) | Year | AMPD (m3/s) | Year | AMPD (m3/s) | Year | AMPD (m3/s) |
|---|---|---|---|---|---|---|---|---|---|
| 1951 | 3760 | 1962 | 4090 | 1973 | 2410 | 1984 | 4250 | 1995 | 1610 |
| 1952 | 2100 | 1963 | 3470 | 1974 | 825 | 1985 | 2500 | 1996 | 3970 |
| 1953 | 4750 | 1964 | 1510 | 1975 | 1270 | 1986 | 3690 | 1997 | 2100 |
| 1954 | 1480 | 1965 | 2980 | 1976 | 1370 | 1987 | 1980 | 1998 | 16100 |
| 1955 | 3200 | 1966 | 2330 | 1977 | 1770 | 1988 | 5640 | 1999 | 1890 |
| 1956 | 6370 | 1967 | 1410 | 1978 | 899 | 1989 | 5280 | 2000 | 1380 |
| 1957 | 7790 | 1968 | 740 | 1979 | 588 | 1990 | 3950 | 2001 | 1160 |
| 1958 | 4570 | 1969 | 8810 | 1980 | 3110 | 1991 | 6370 | 2002 | 541 |
| 1959 | 2920 | 1970 | 1990 | 1981 | 2950 | 1992 | 2010 | 2003 | 4590 |
| 1960 | 5760 | 1971 | 1400 | 1982 | 1060 | 1993 | 5780 | 2004 | 2280 |
| 1961 | 3130 | 1972 | 1920 | 1983 | 3860 | 1994 | 1710 | - | - |
4.2. Data Analysis Method and Parameters Selection
- (1)
- The comparison between frequency histogram and the PDF of peak discharge calculated by PDEM as well as parametric method.
- (2)
- The comparison between empirical frequency and the frequency values of peak discharge calculated by PDEM as well as parametric method.
4.3. Results and Discussion
| Distribution | Log Pearson Type III | Log Normal | Gamma | Weibull (3P) | Pearson Type III | Gumbell |
|---|---|---|---|---|---|---|
| Parameters | α = 59226 | σ = 0.699 μ = 7.842 | α =1.5753 β =2061.6 | α = 1.114 | α = 3.822 | σ = 2017.500 μ = 2083.100 |
| β = 0.003 | β = 2825.100 | β = 11163 | ||||
| γ = −163.820 | γ = 532.690 | γ = −670.590 |
| Distribution | Kolmogorov Smirnov | Anderson Darling | Chi-Squared | |||
|---|---|---|---|---|---|---|
| Statistic | Rank | Statistic | Rank | Statistic | Rank | |
| Log Pearson Type III | 0.059 | 1 | 0.151 | 1 | 2.011 | 3 |
| Log Normal | 0.060 | 2 | 0.153 | 2 | 1.999 | 2 |
| Gamma | 0.071 | 4 | 0.247 | 4 | 1.624 | 1 |
| Weibull (3P) | 0.079 | 5 | 0.310 | 5 | 2.957 | 5 |
| Pearson Type III | 0.067 | 3 | 0.185 | 3 | 2.039 | 4 |
| Gumbell | 0.082 | 6 | 0.379 | 6 | 3.313 | 6 |

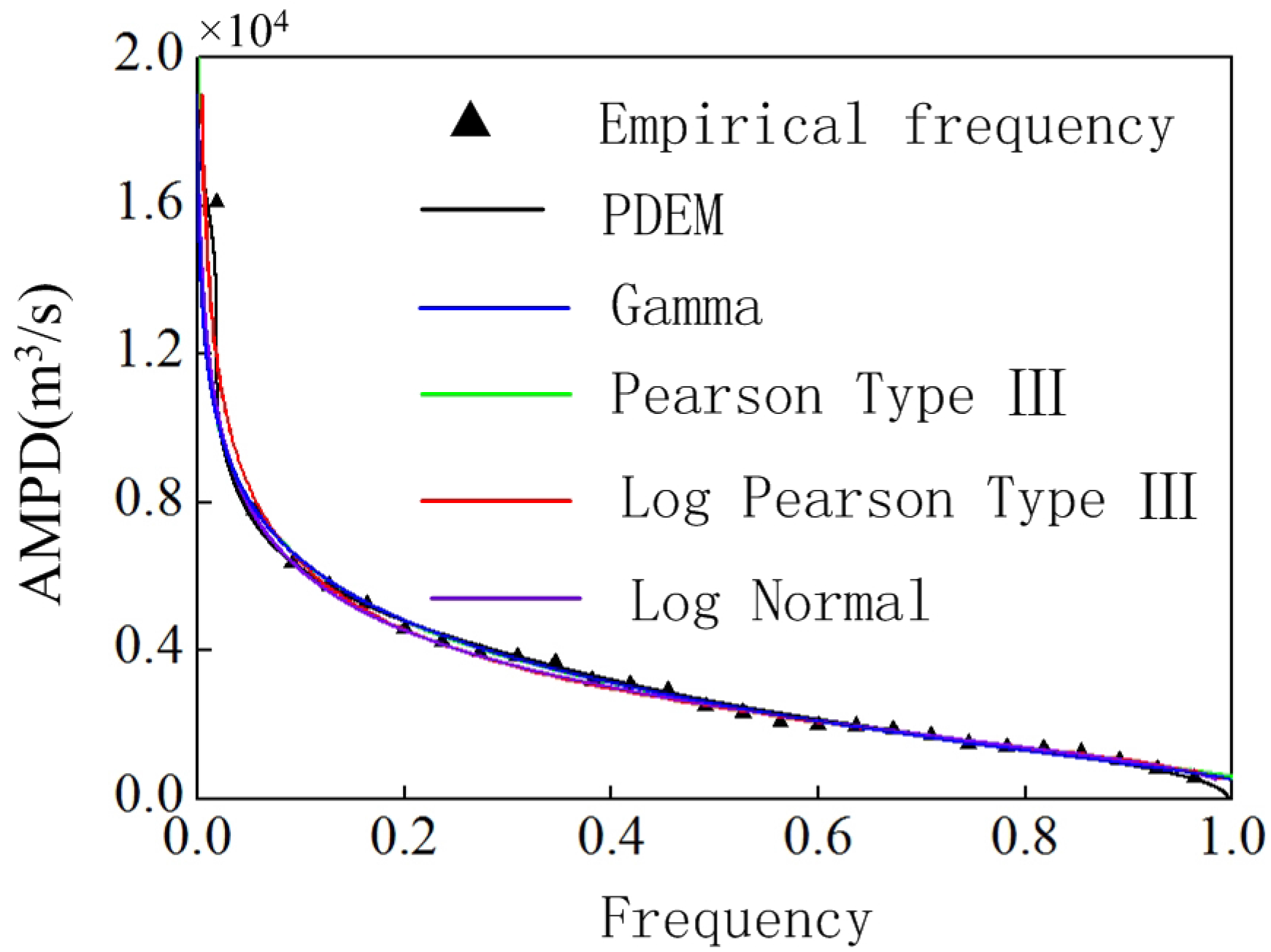
| Methods | Parametric Method | PDEM | |||
|---|---|---|---|---|---|
| Pearson Type III | Log Pearson Type III | Log Normal | Gamma | ||
| RMS error | 0.033 | 0.023 | 0.022 | 0.021 | 0.019 |
| Method | Number (Ratio) of the Relative Error | Maximum Relative Error | ||||
|---|---|---|---|---|---|---|
| <1% | <3% | <5% | <10% | |||
| Parametric method | Pearson Type III | 5 (9.259%) | 13 (24.074%) | 26 (48.148%) | 43 (79.630%) | 89.000% |
| Gamma(3P) | 7 (12.963%) | 26 (48.148%) | 38 (70.370%) | 49 (90.741%) | 94.179% | |
| Log Normal | 8 (14.815%) | 25 (46.296%) | 36 (66.667%) | 45 (83.333%) | 88.126% | |
| Log Pearson Type III | 7 (12.963%) | 25 (46.296%) | 33 (61.111%) | 41 (75.926%) | 61.500% | |
| PDEM | 13 (24.074%) | 28 (51.852%) | 40 (74.074%) | 50 (92.593%) | 47.602% | |
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cong, S.Z.; Hu, S.Y. Some problems on flood-frequency analysis. Chin. J. Appl. Probab. Stat. 1989, 5, 358–368. (In Chinese) [Google Scholar]
- Chow, V.T. Handbook of Applied Hydrology; McGrawHill: New York, NY, USA, 1964. [Google Scholar]
- Kuczera, G. Comprehensive at-site flood frequency analysis using Monte Carlo Bayesian inference. Water Resour. Res. 1999, 35, 1551–1557. [Google Scholar] [CrossRef]
- Kite, G.W. Frequency and Risk Analyses in Hydrology; Water Resources Publications: Fort Collins, CO, USA, 1977. [Google Scholar]
- Gupta, V.L. Selection of frequency distribution models. Water Resour. Res. 1970, 6, 1193–1198. [Google Scholar] [CrossRef]
- Turkman, K.F. The choice of extremal models by Akaike’s information criterion. J. Hydrol. 1985, 82, 307–315. [Google Scholar] [CrossRef]
- Ahmad, M.I.; Sinclair, C.D.; Werritty, A. Log-logistic flood frequency analysis. J. Hydrol. 1988, 98, 205–224. [Google Scholar] [CrossRef]
- Rahman, A.S.; Rahman, A.; Zaman, M.A.; Haddad, K.; Ahsan, A.; Imteaz, M. A study on selection of probability distributions for at-site flood frequency analysis in Australia. Nat. Hazards 2013, 69, 1803–1813. [Google Scholar] [CrossRef]
- Filliben, J.J. The probability plot correlation coefficient test for normality. Technometrics 1975, 17, 111–117. [Google Scholar] [CrossRef]
- Vogel, R.M. The probability plot correlation coefficient test for the normal, lognormal, and Gumbel distributional hypotheses. Water Resour. Res. 1986, 22, 587–590. [Google Scholar] [CrossRef]
- Vogel, R.W.; Mcmartin, D.E. Probability plot goodness-of-fit and skewness estimation procedures for the Pearson Type 3 distribution. Water Resour. Res. 1991, 27, 3149–3158. [Google Scholar] [CrossRef]
- Heo, J.H.; Kho, Y.W.; Shin, H.; Kim, S.; Kim, T. Regression equations of probability plot correlation coefficient test statistics from several probability distributions. J. Hydrol. 2008, 355, 1–15. [Google Scholar] [CrossRef]
- Kite, G.W. Flood and Risk Analyses in Hydrology; Water Resources Publications: Littleton, MA, USA, 1988. [Google Scholar]
- Wang, Q.J. Direct sample estimators of L moments. Water Resour. Res. 1996, 32, 3617–3619. [Google Scholar] [CrossRef]
- Gubareva, T.S.; Gartsman, B.I. Estimating distribution parameters of extreme hydrometeorological characteristics by L-moments method. Water Resour. 2010, 37, 437–445. [Google Scholar] [CrossRef]
- Zafirakou-Koulouris, A.; Vogel, R.M.; Craig, S.M.; Habermeier, J. L-moment diagrams for censored observations. Water Resour. Res. 1998, 34, 1241–1249. [Google Scholar] [CrossRef]
- Hosking, J.R.M. L-moments: Analysis and estimation of distributions using linear combinations of order statistics. J. R. Statist. Soc. B 1990, 52, 105–124. [Google Scholar]
- Bhattarai, K.P. Use of L-Moments in Flood Frequency Analysis. Master Thesis, National University of Ireland, Galway, Ireland, 1997. [Google Scholar]
- Greenwood, J.A.; Landwehr, J.M.; Matalas, N.C.; Wallis, J.R. Probability weighted moments: Definition and relation to parameters of several distributions expressable in inverse form. Water Resour. Res. 1979, 15, 1049–1054. [Google Scholar] [CrossRef]
- Landwehr, J.M.; Matalas, N.C.; Wallis, J.R. Probability weighted moments compared with some traditional techniques in estimating Gumbel parameters and quantiles. Water Resour. Res. 1979, 15, 1055–1064. [Google Scholar] [CrossRef]
- Hosking, J.R.M.; Wallis, J.R.; Wood, E.F. Estimation of the generalized extreme-value distribution by the method of probability-weighted moments. Technometrics 1985, 27, 251–261. [Google Scholar] [CrossRef]
- Hosking, J.R.M.; Wallis, J.R. Parameter and quantile estimation for the generalized Pareto distribution. Technometrics 1987, 29, 339–349. [Google Scholar] [CrossRef]
- Seckin, N.; Yurtal, R.; Haktanir, T.; Dogan, A. Comparison of probability weighted moments and maximum likelihood methods used in flood frequency analysis for Ceyhan River Basin. Arab. J. Sci. Eng. 2010, 35, 49–69. [Google Scholar]
- Raynal-Villasenor, J.A. Probability weighted moments estimators for the GEV distribution for the minima. Int. J. Res. Rev. Appl. Sci. 2013, 15, 33–40. [Google Scholar]
- Wang, Q.J. Estimation of the GEV distribution from censored samples by method of partial probability weighted moments. J. Hydrol. 1990, 120, 103–114. [Google Scholar] [CrossRef]
- Wang, Q.J. Unbiased estimation of probability weighted moments and partial probability weighted moments from systematic and historical flood information and their application to estimating the GEV distribution. J. Hydrol. 1990, 120, 115–124. [Google Scholar] [CrossRef]
- Wang, Q.J. Using partial PWM to fit the extreme value distributions to censored samples. Water Resour. Res. 1996, 32, 1767–1771. [Google Scholar] [CrossRef]
- Diebolt, J.; Guillou, A.; Naveau, P.; Ribereau, P. Improving probability-weighted moment methods for the generalized extreme value distribution. REVSTAT-Stat. J. 2008, 6, 33–50. [Google Scholar]
- Prescott, P.; Walden, A.T. Maximum likeiihood estimation of the parameters of the three-parameter generalized extreme-value distribution from censored samples. J. Stat. Comput. Simul. 1983, 16, 241–250. [Google Scholar] [CrossRef]
- Jam, D.; Singh, V.P. Estimating parameters of EV1 distribution for flood frequency analysis. J. Am. Water Resour. Assoc. 1987, 23, 59–71. [Google Scholar] [CrossRef]
- Cohn, T.A.; Stedinger, J.R. Use of historical information in a maximum-likelihood framework. J. Hydrol. 1987, 96, 215–223. [Google Scholar] [CrossRef]
- El Adlouni, S.; Ouarda, T.B.M.J.; Zhang, X.; Roy, R.; Bobée, B. Generalized maximum likelihood estimators for the nonstationary generalized extreme value model. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Chen, Y.; Hou, Y.; Pieter, V.G.; Sha, Z. Study of parameter estimation methods for Pearson-III distribution in flood frequency analysis. In The Extremes of the Extremes: Extraordinary Floods; International Association of Hydrological Sciences (IAHS): Wallingford, UK, 2002; pp. 263–270. [Google Scholar]
- Cong, S.Z.; Tan, W.Y.; Huang, S.X.; Xu, Y.B.; Zhang, W.R.; Chen, Y.Z. Statistical testing research on the methods of parameter estimation in hydrological computation. J. Hydraul. Eng. 1980, 3, 1–15. (In Chinese) [Google Scholar]
- Song, S.B.; Kang, Y. Design flood frequency curve optimization fitting method based on 3 intelligent optimization algorithms. J. Northwest A F Univ. (Nat. Sci. Ed.) 2008, 36, 205–209. (In Chinese) [Google Scholar]
- Dong, C.; Song, S.B. Application of swarm intelligence optimization algorithm in optimization fitting of hydrologic frequency curve. J. China Hydrol. 2011, 31, 20–26. (In Chinese) [Google Scholar]
- Tung, Y.K.; Mays, L.W. Reducing hydrologic parameter uncertainty. J. Water Resour. Plan. Manag. Div. 1981, 107, 245–262. [Google Scholar]
- Adamowski, K. Nonparametric kernel estimation of flood frequencies. Water Resour. Res. 1985, 21, 1585–1590. [Google Scholar] [CrossRef]
- Wu, K.; Woo, M.K. Estimating annual flood probabilities using Fourier series method. J. Am. Water Resour. Assoc. 1989, 25, 743–750. [Google Scholar] [CrossRef]
- Bardsley, W.E. Using historical data in nonparametric flood estimation. J. Hydrol. 1989, 108, 249–255. [Google Scholar] [CrossRef]
- Guo, S.L. Nonparametric variable kernel estimation with historical floods and paleoflood information. Water Resour. Res. 1991, 27, 91–98. [Google Scholar] [CrossRef]
- Adamowski, K.; Feluch, W. Nonparametric flood-frequency analysis with historical information. J. Hydraul. Eng. 1990, 116, 1035–1047. [Google Scholar] [CrossRef]
- Lall, U.; Moon, Y.I.; Bosworth, K. Kernel flood frequency estimators: Bandwidth selection and kernel choice. Water Resour. Res. 1993, 29, 1003–1015. [Google Scholar] [CrossRef]
- Karmakar, S.; Simonovic, S.P. Bivariate flood frequency analysis: Part 1. Determination of marginals by parametric and nonparametric techniques. J. Flood Risk Manag. 2008, 1, 190–200. [Google Scholar] [CrossRef]
- Dong, J.; Xie, Y.B.; Zhai, J.B. Application of nonparametric statistic approach to flood frequency analysis and prospect of its development trend. J. Hohai Univ. (Nat. Sci.) 2004, 32, 23–26. (In Chinese) [Google Scholar]
- Li, J.; Chen, J. Advances in the research on probability density evolution equations of stochastic dynamical systems. Adv. Mech. 2010, 40, 170–188. [Google Scholar]
- Li, J.; Chen, J. The principle of preservation of probability and the generalized density evolution equation. Struct. Saf. 2008, 30, 65–77. [Google Scholar] [CrossRef]
- Li, J.; Chen, J. The probability density evolution method for analysis of dynamic nonlinear response of stochastic structures. Acta Mech. Sin. Chin. Ed. 2003, 35, 722–728. (In Chinese) [Google Scholar]
- Chen, J.; Li, J. The probability density evolution method for dynamic reliability assessment of nonlinear stochastic structures. Acta Mech. Sin. Chin. Ed. 2004, 36, 196–201. (In Chinese) [Google Scholar]
- Chen, J.; Li, J. Extreme value distribution and reliability of nonlinear stochastic structures. Earthq. Eng. Eng. Vib. 2005, 4, 275–286. [Google Scholar] [CrossRef]
- Gentle, J.E. Elements of Computational Statistics; Springer-Verlag New York, Inc.: New York, NY, USA, 2002. [Google Scholar]
- Wu, Y.B.; Jin, G.F. Probability distribution of mechanical property of fiber reinforced polymer. J. Cent. South Univ. (Sci. Technol.) 2011, 42, 3851–3857. (In Chinese) [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Zhou, J.; Zhang, L. The Probability Density Evolution Method for Flood Frequency Analysis: A Case Study of the Nen River in China. Water 2015, 7, 5134-5151. https://doi.org/10.3390/w7095134
Wang X, Zhou J, Zhang L. The Probability Density Evolution Method for Flood Frequency Analysis: A Case Study of the Nen River in China. Water. 2015; 7(9):5134-5151. https://doi.org/10.3390/w7095134
Chicago/Turabian StyleWang, Xueni, Jing Zhou, and Leike Zhang. 2015. "The Probability Density Evolution Method for Flood Frequency Analysis: A Case Study of the Nen River in China" Water 7, no. 9: 5134-5151. https://doi.org/10.3390/w7095134
APA StyleWang, X., Zhou, J., & Zhang, L. (2015). The Probability Density Evolution Method for Flood Frequency Analysis: A Case Study of the Nen River in China. Water, 7(9), 5134-5151. https://doi.org/10.3390/w7095134





