Modeling of Breaching Due to Overtopping Flow and Waves Based on Coupled Flow and Sediment Transport
Abstract
:1. Introduction
2. Governing Equations of Flow and Sediment Transport in Breaching Process
3. Numerical Methods
3.1. Model Discretization
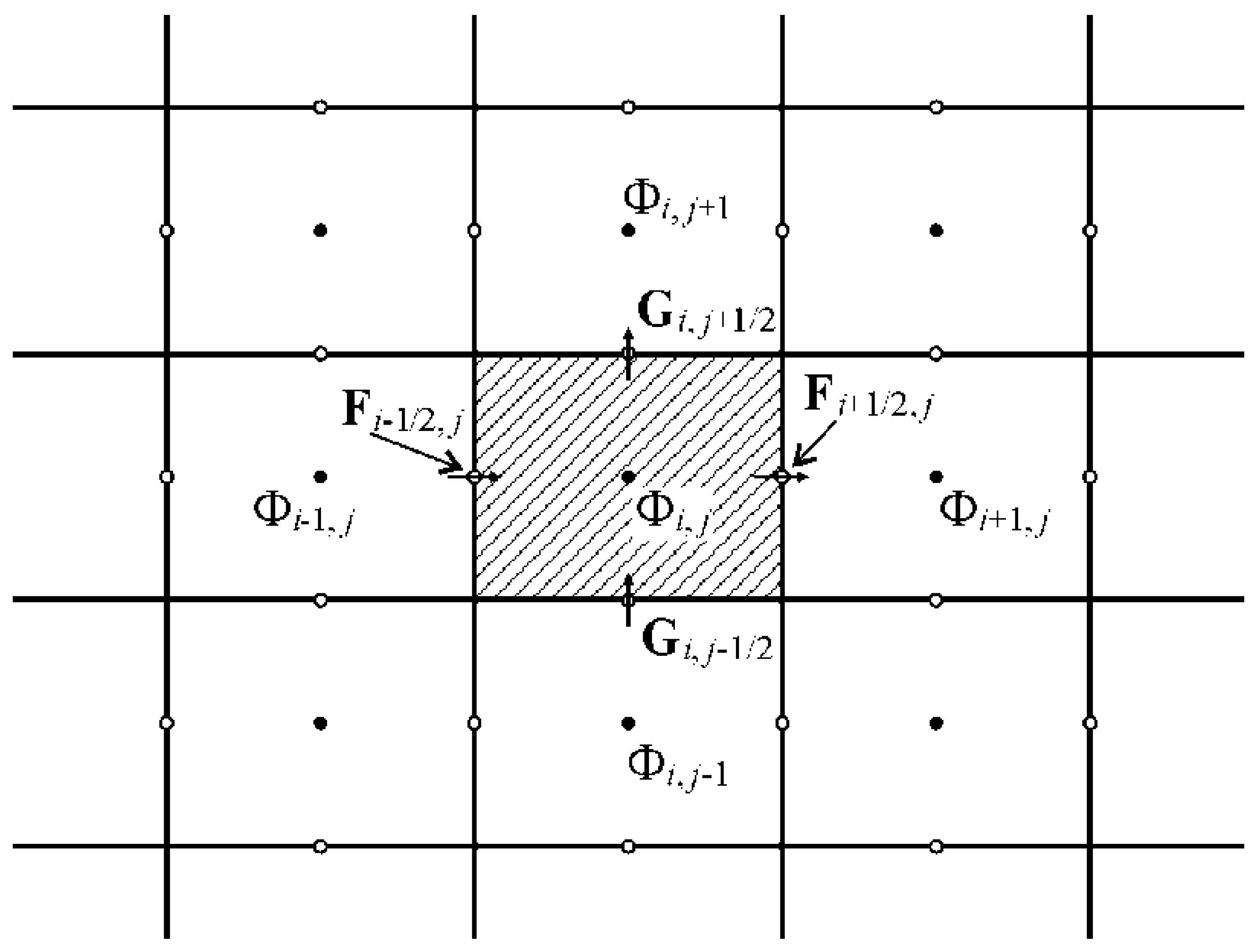
3.2. Nonnegative Reconstruction of Riemann State
3.3. Central Upwind Scheme
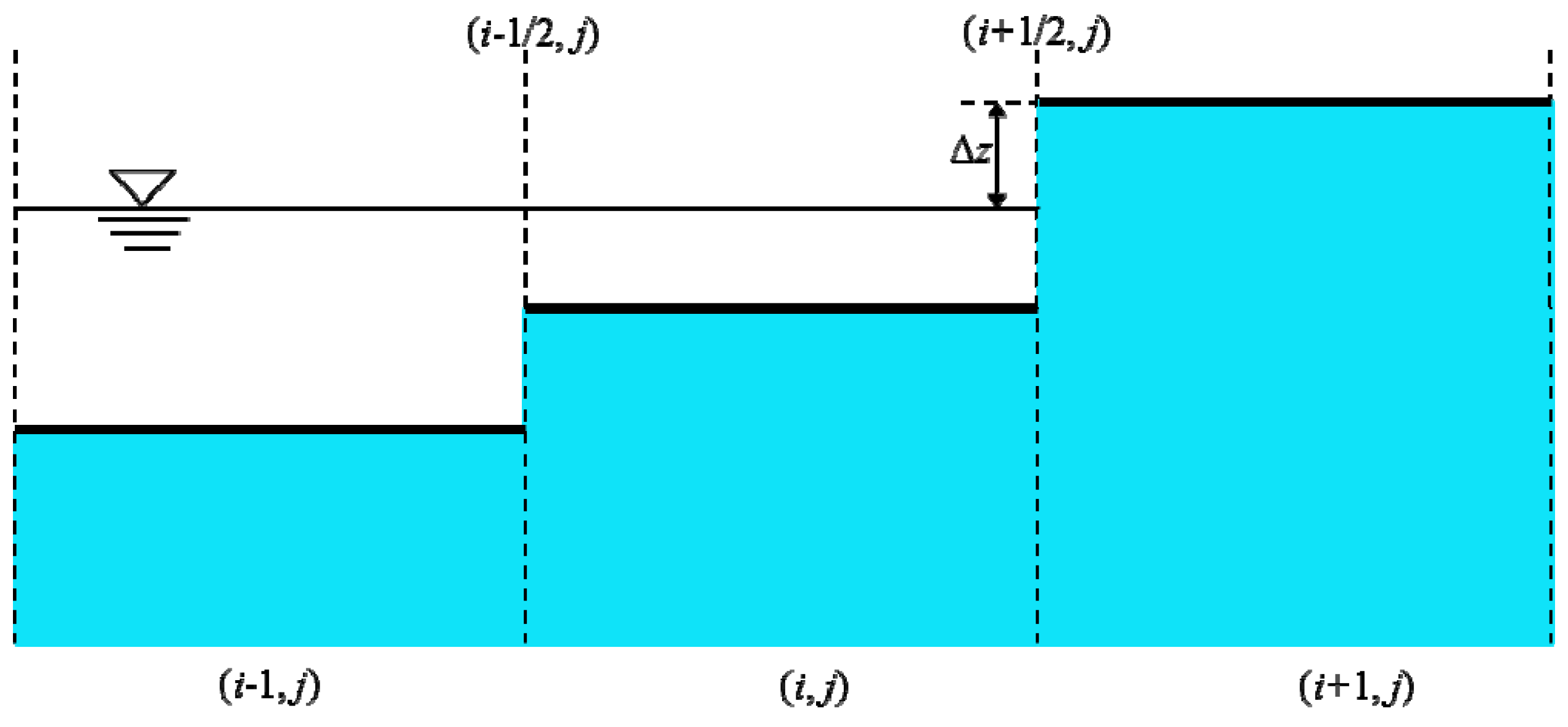
3.4. Treatments of the Source Terms
3.5. Calculation of Sediment Transport
3.6. Stability Criterion and Boundary Conditions
4. Model Verification
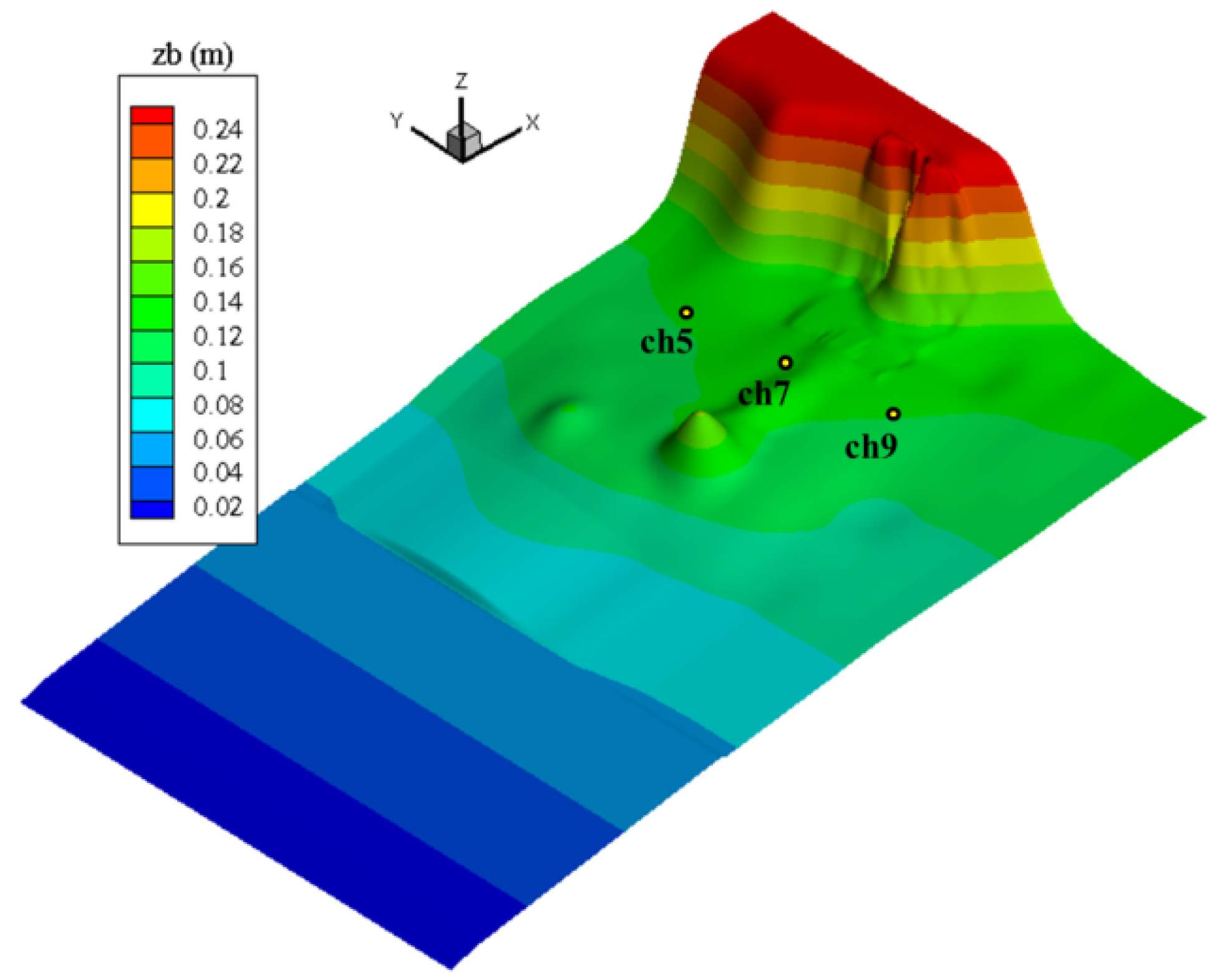
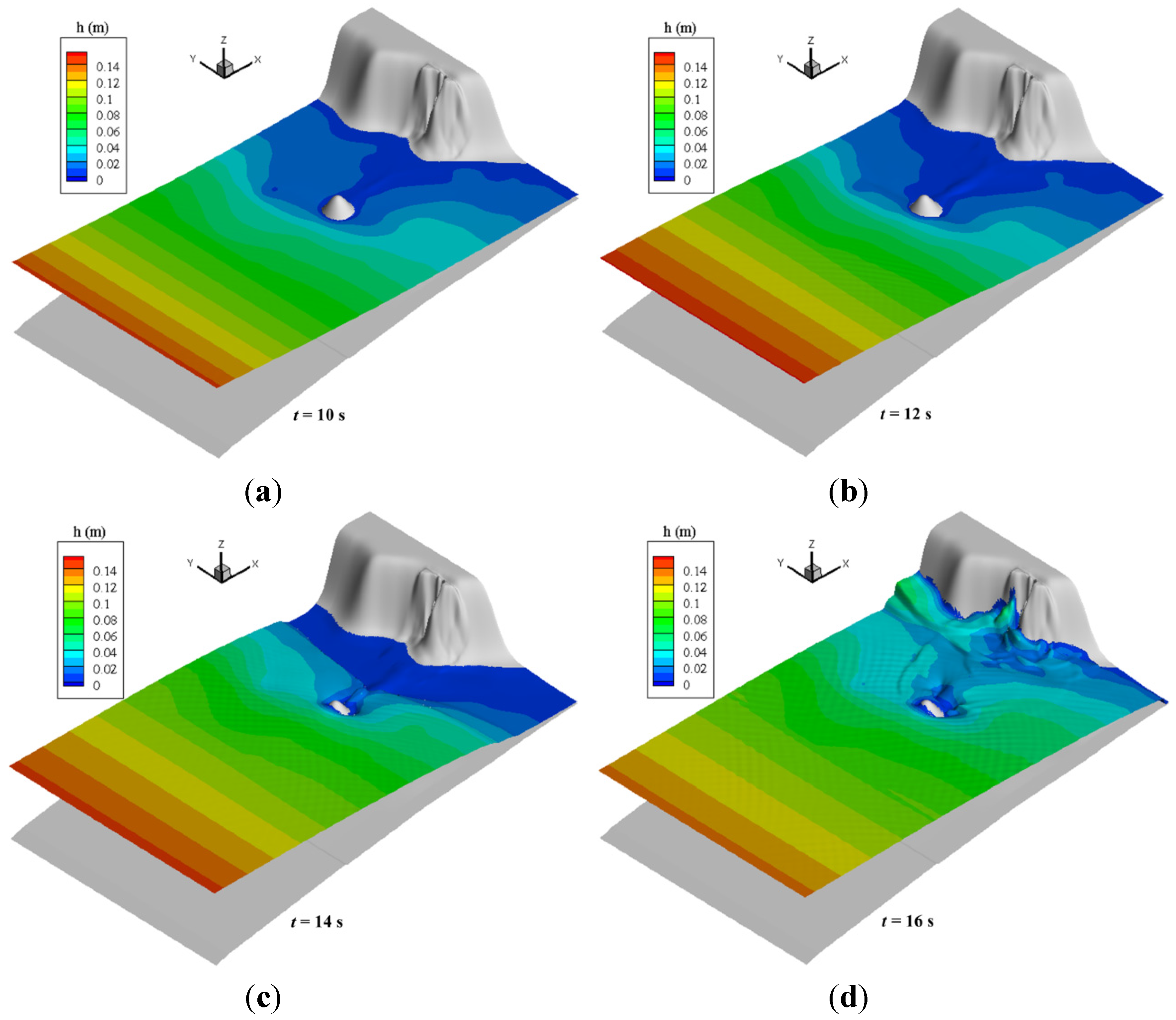
4.1. Case 1: Tsunami Run-Up onto a Complex Three-Dimensional (3D) Beach
4.2. Case 2: One-Dimensional Dam Break Flow over Moveable Bed
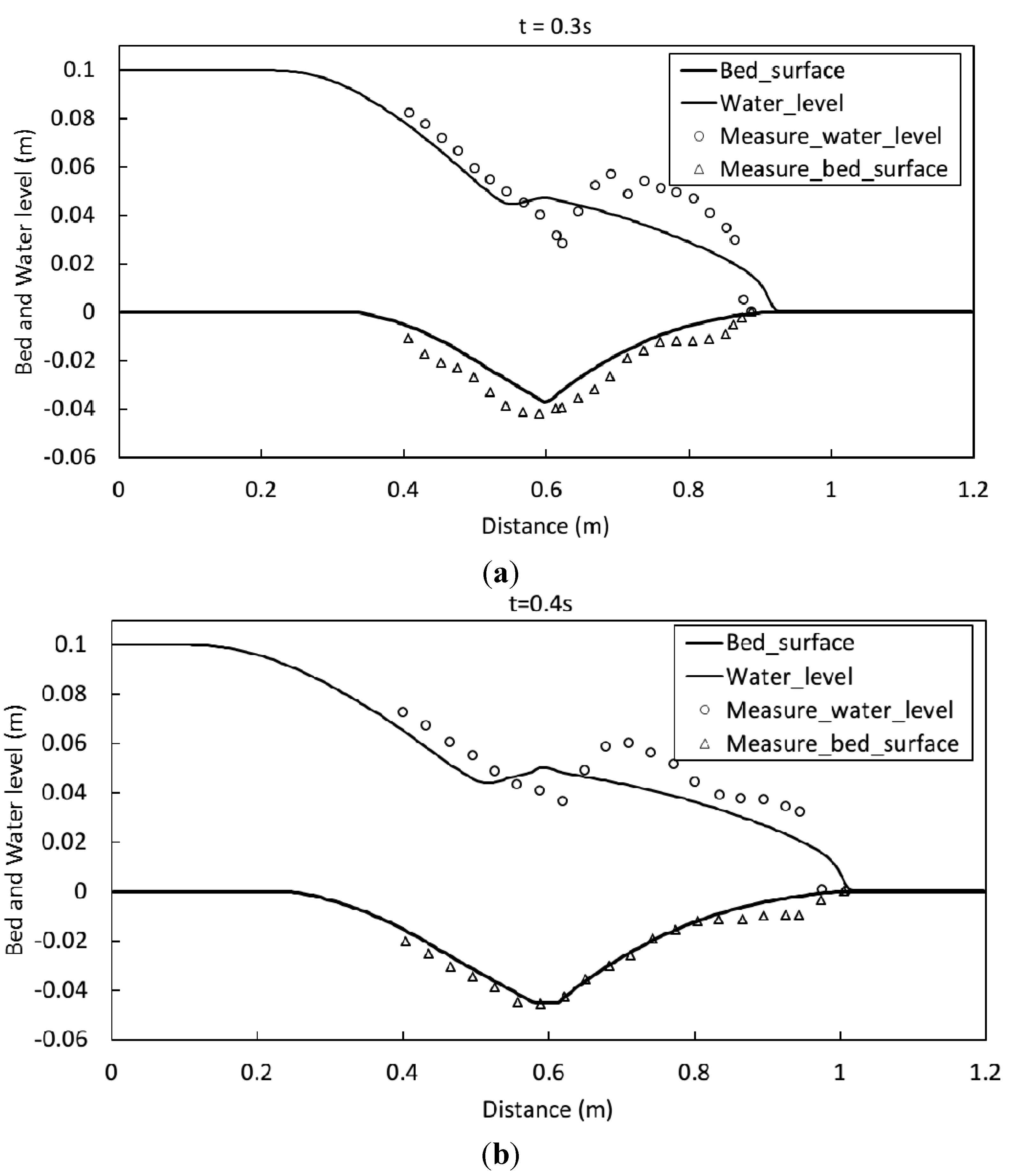

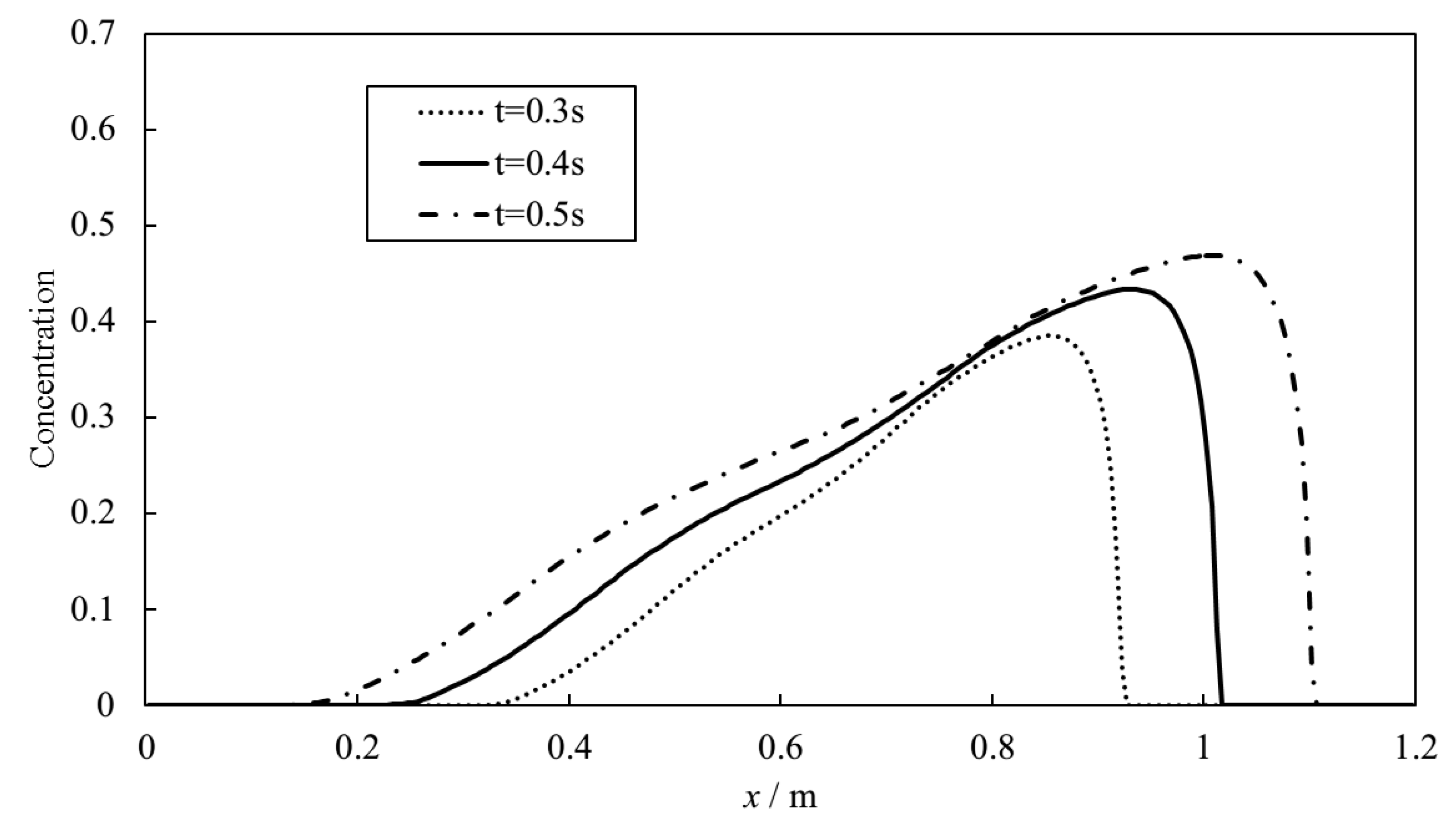
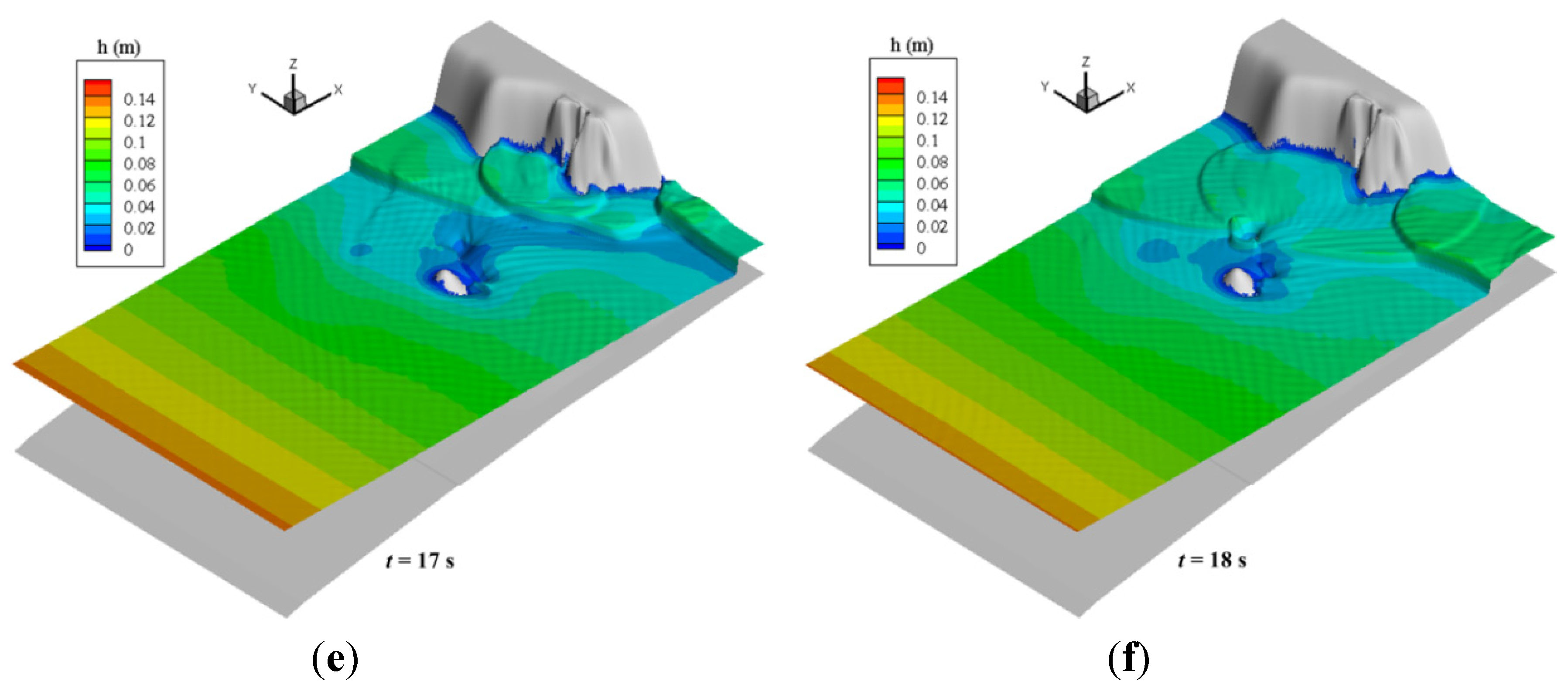
5. Numerical Investigation of 2D Dam Breaching Processes with Overtopping Flow and Waves
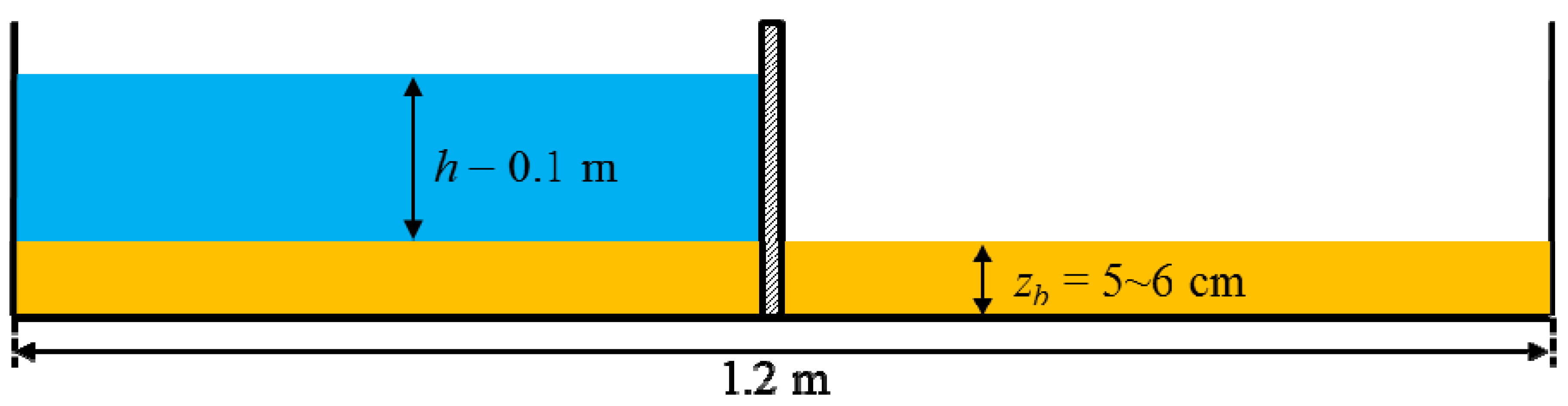
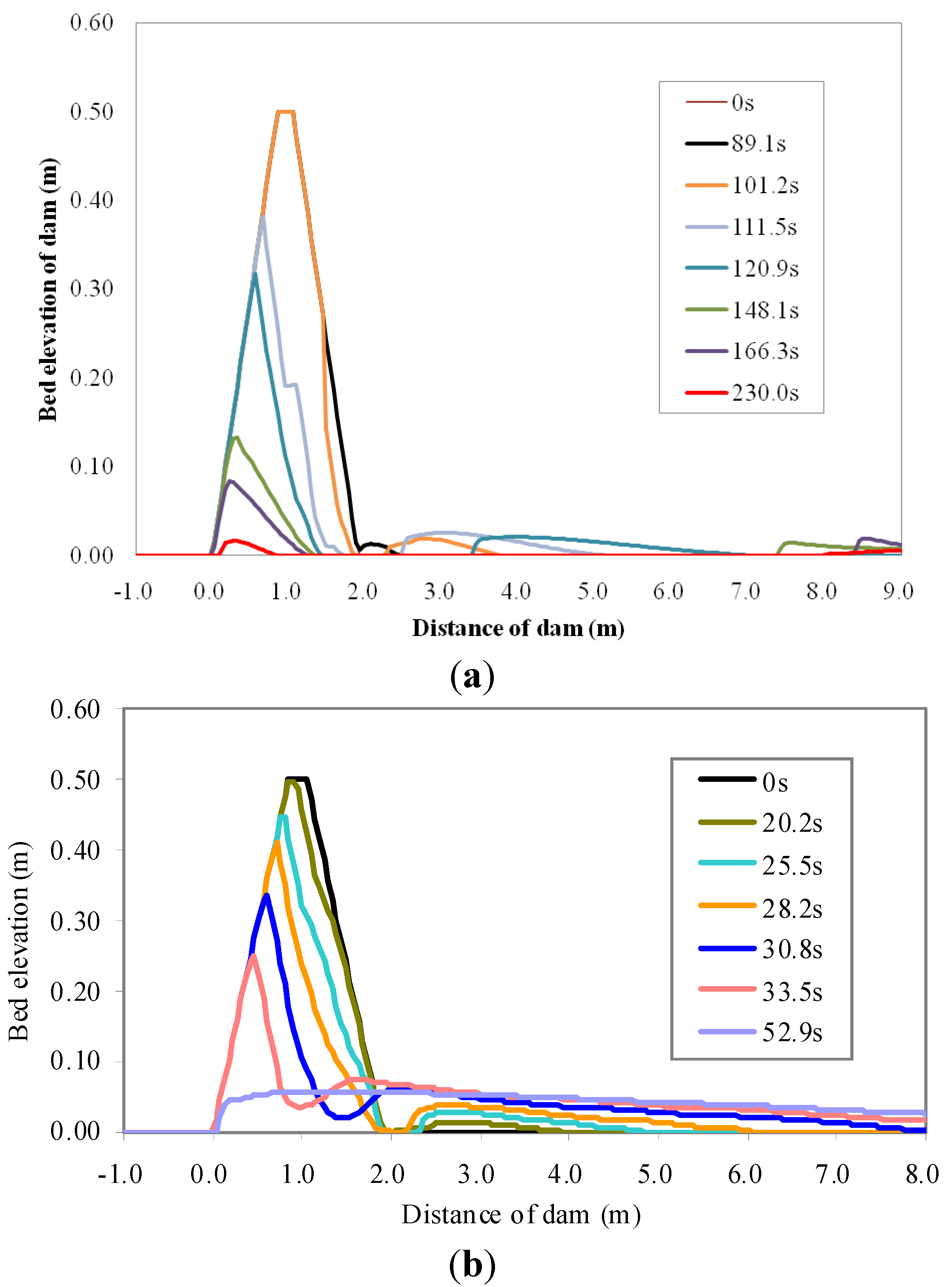
5.1. Breaching Processes Due to Overtopping Flow
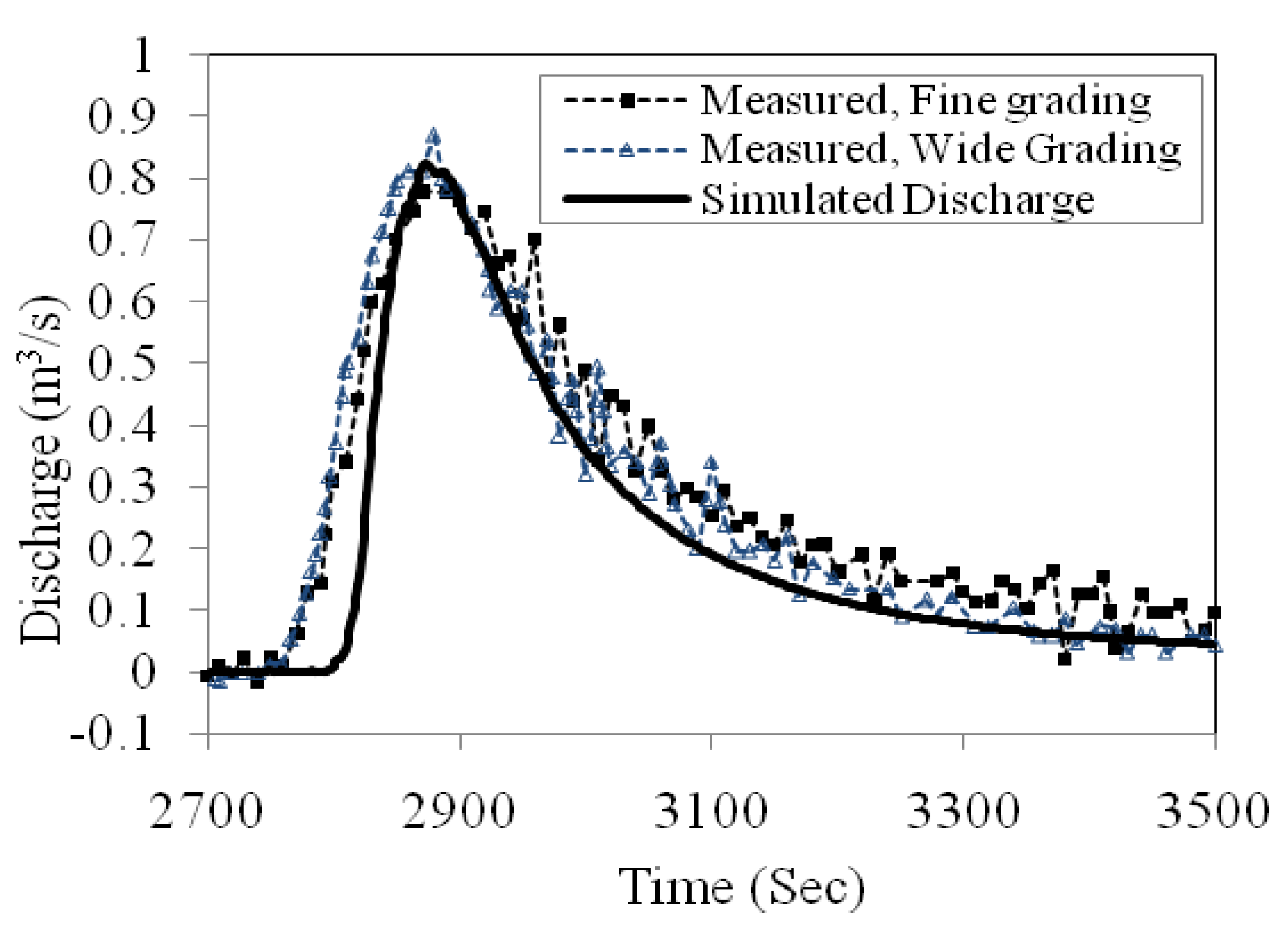
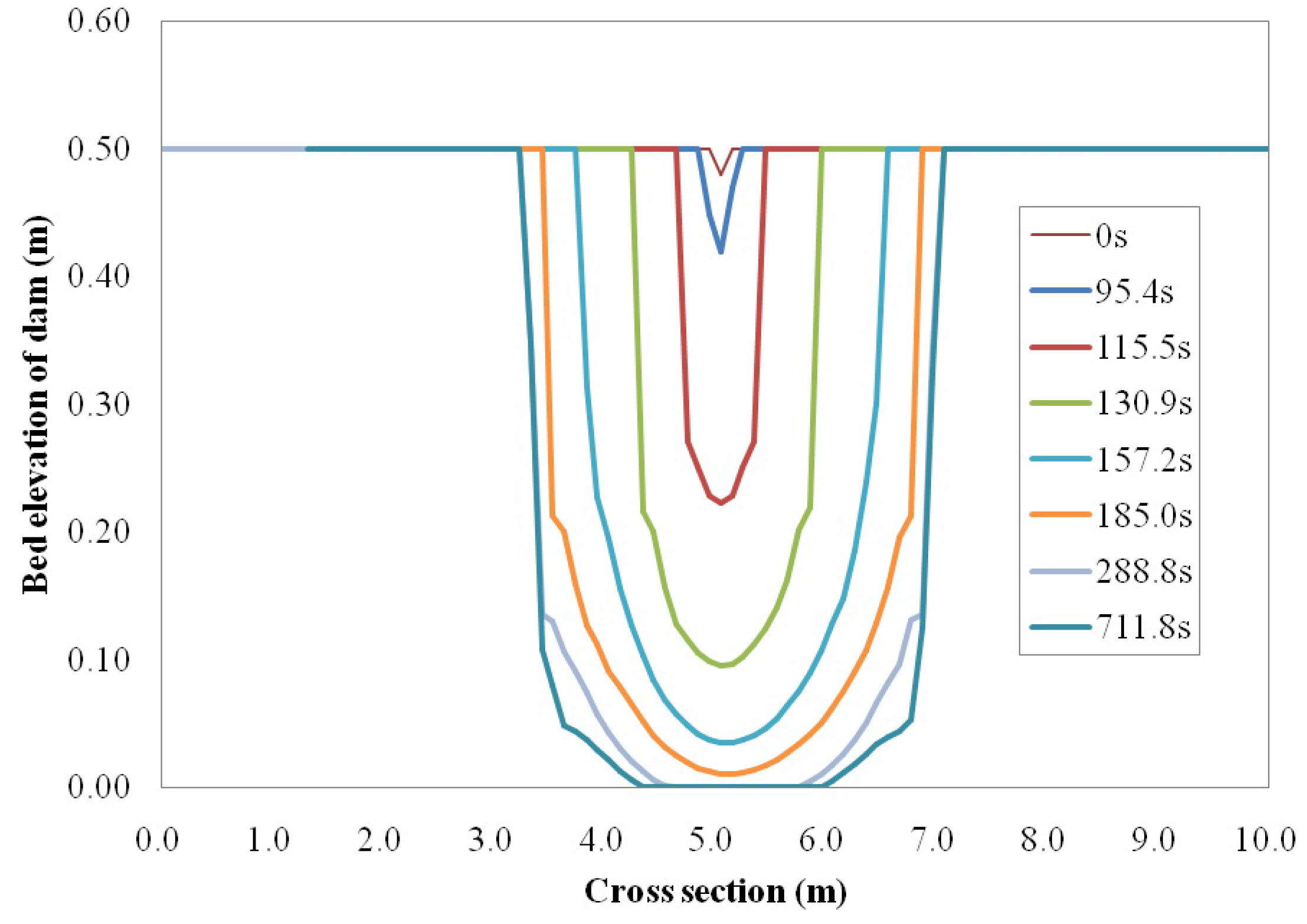
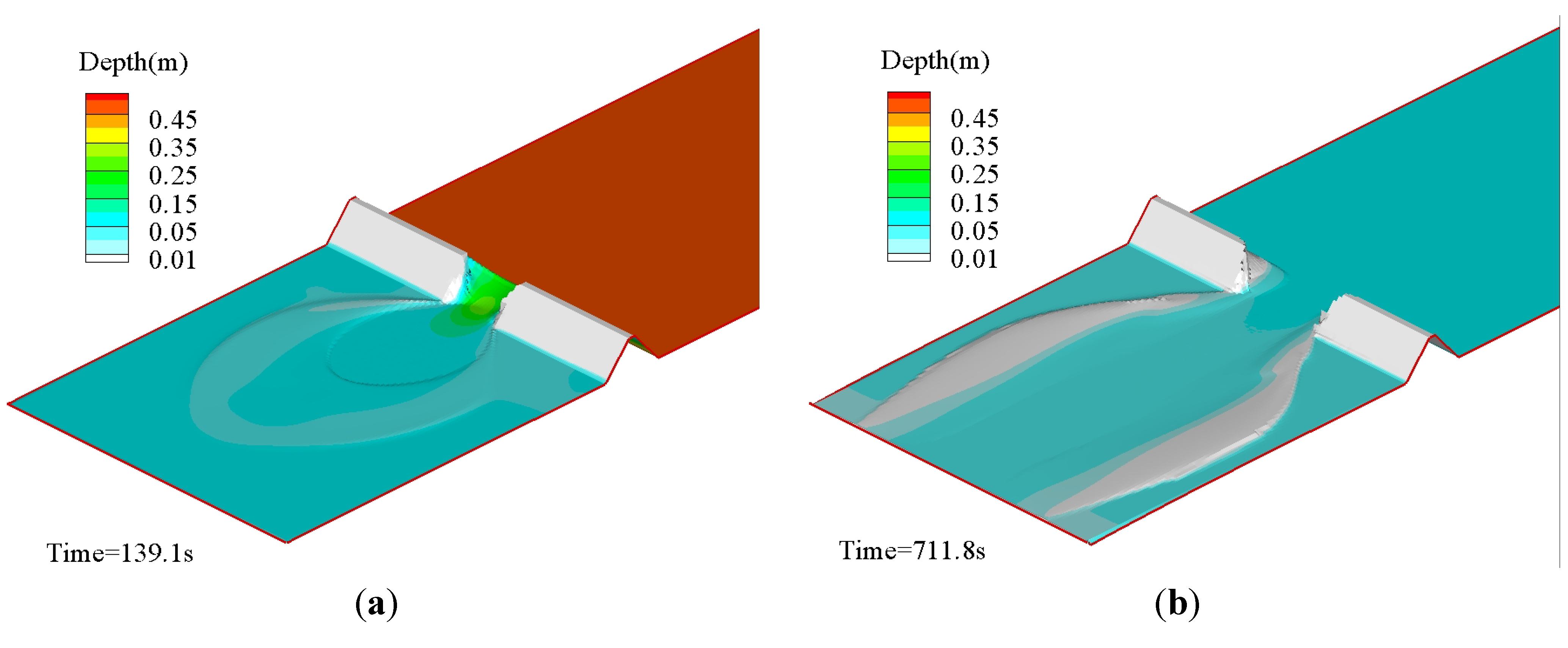
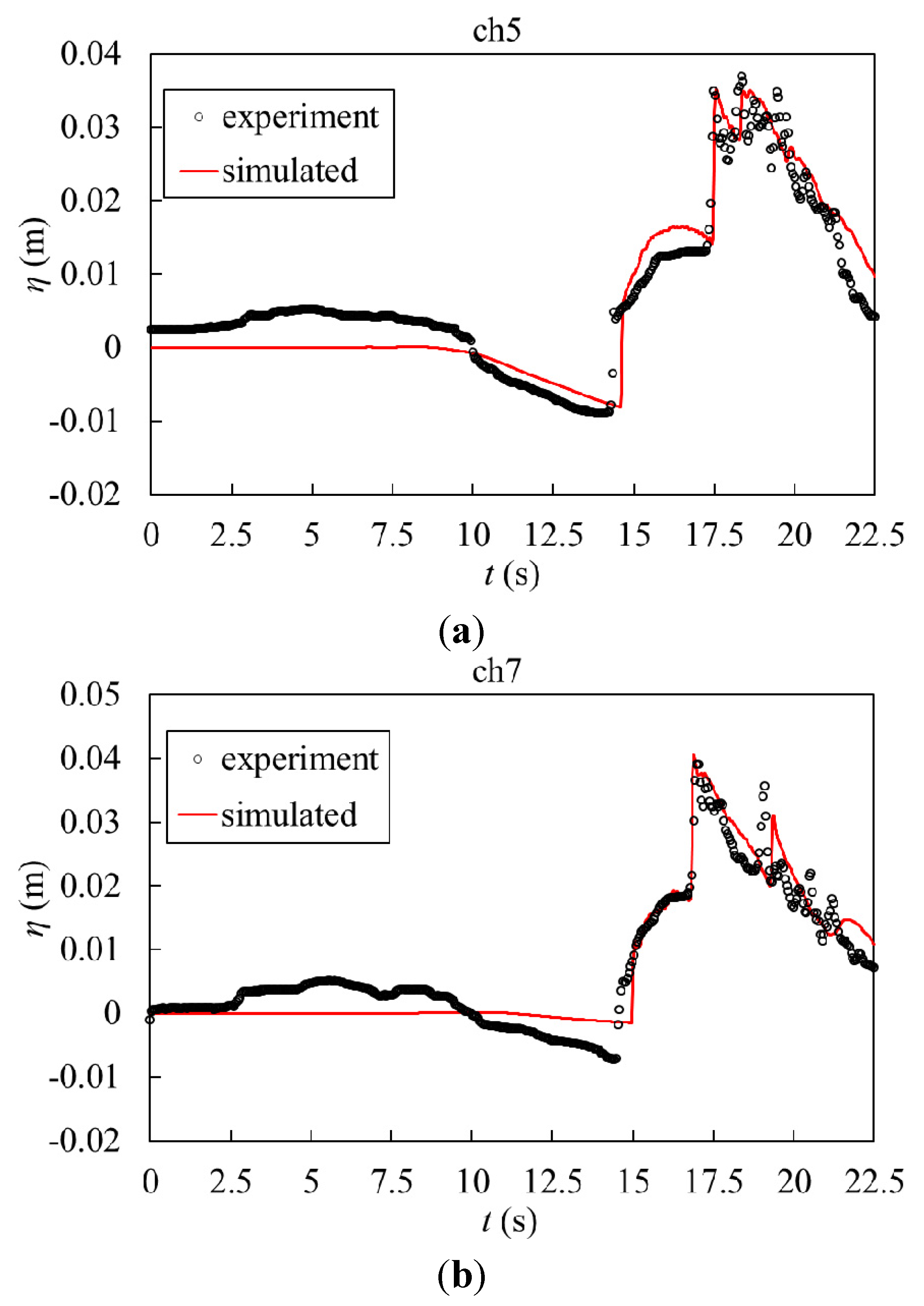
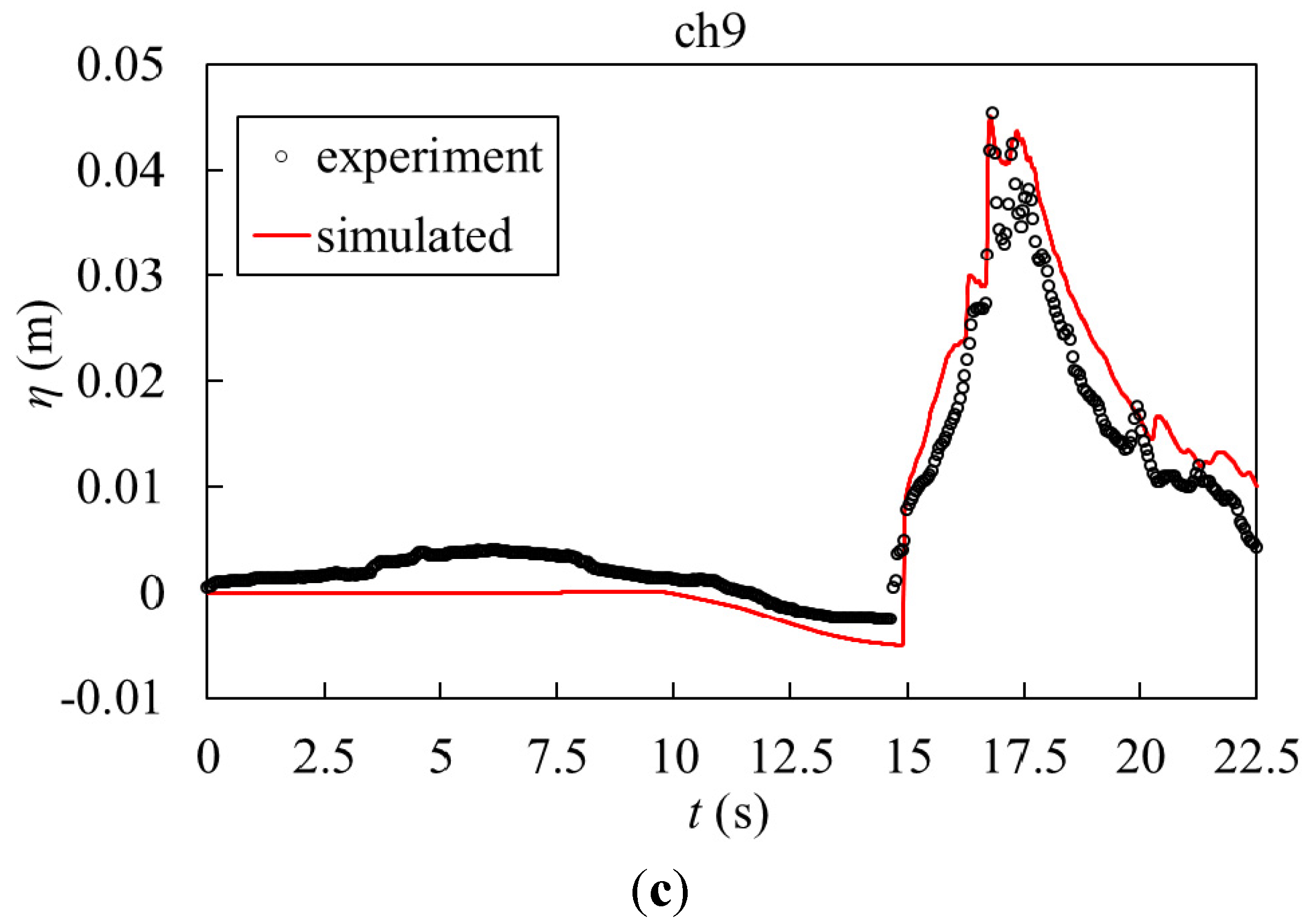
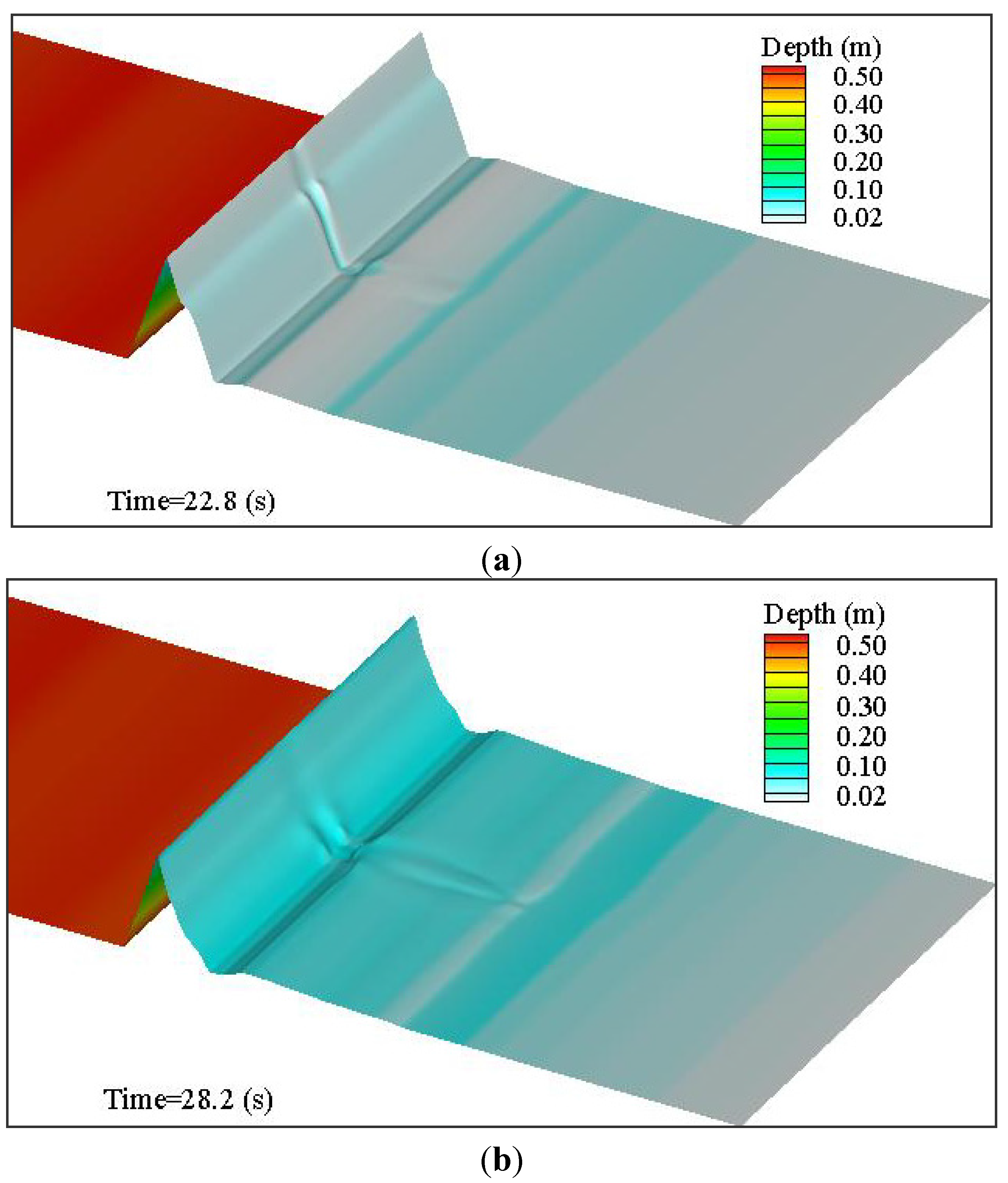
5.2. Breaching Processes Due to Wave Overtopping
5.3. Discussion of Results
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Donnelly, C.; Kraus, N.; Larson, M. State of knowledge on measurement and modeling of coastal overwash. J. Coast. Res. 2006, 22, 965–991. [Google Scholar] [CrossRef]
- Kobayashi, N.; Buck, M.; Payo, A.; Johnson, B.D. Berm and dune erosion during a storm. J. Waterw. Port Coast. Ocean Eng. 2009, 135, 1–10. [Google Scholar] [CrossRef]
- Figlus, J.; Kobayashi, N.; Gralher, C.; Iranzo, V. Wave overtopping and overwash of dunes. J. Waterw. Port Coast. Ocean Eng. 2010, 137, 26–33. [Google Scholar] [CrossRef]
- Wu, W.M.; Altinakar, M.S.; Al-Riffai, M.; Bergman, N.; Bradford, S.F.; Cao, Z.X.; Chen, Q.J.; Constantinescu, S.G.; Duan, J.G.; Gee, D.M.; et al. Earthen embankment breaching. J. Hydraul. Eng. 2011, 137, 1549–1564. [Google Scholar]
- Harten, A.; Lax, P.D.; Leer, B.V. On upstream differencing and godunov-type schemes for hyperbolic conservation laws. SIAM Rev. 1983, 25, 35–61. [Google Scholar] [CrossRef]
- Toro, E.F. Shock-Capturing Methods for Free-Surface Shallow Flows; John Wiley: Chichester, Britain, 2001. [Google Scholar]
- Wu, W.; Marsooli, R.; He, Z. Depth-averaged two-dimensional model of unsteady flow and sediment transport due to noncohesive embankment break/breaching. J. Hydraul. Eng. 2011, 138, 503–516. [Google Scholar] [CrossRef]
- Li, S.; Duffy, C.J. Fully coupled approach to modeling shallow water flow, sediment transport, and bed evolution in rivers. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Xia, J.; Lin, B.; Falconer, R.A.; Wang, G. Modelling dam-break flows over mobile beds using a 2d coupled approach. Adv. Water Resour. 2010, 33, 171–183. [Google Scholar] [CrossRef]
- Wu, W.; Wang, S.S. One-dimensional explicit finite-volume model for sediment transport. J. Hydraul. Eng. 2008, 46, 87–98. [Google Scholar] [CrossRef]
- Cao, Z.; Pender, G.; Wallis, S.; Carling, P. Computational dam-break hydraulics over erodible sediment bed. J. Hydraul. Eng. 2004, 130, 689–703. [Google Scholar] [CrossRef]
- Capart, H.; Young, D.L. Formation of a jump by the dam-break wave over a granular bed. J. Fluid Mech. 1998, 372, 165–187. [Google Scholar] [CrossRef]
- Odd, N.; Roberts, W.; Maddocks, J. Simulation of lagoon breakout. In Proceedings of the 26th Congress-International Association for Hydraulic Research, London, UK, 11–15 September 1995; pp. 92–97.
- Kurganov, A.; Levy, D. Central-upwind schemes for the saint-venant system. ESAIM: Math. Modell. Numer. Anal. 2002, 36, 397–425. [Google Scholar] [CrossRef]
- Wu, W. Computational River Dynamics; Taylor & Francis: London, UK, 2008. [Google Scholar]
- Pähtz, T.; Parteli, E.J.; Kok, J.F.; Herrmann, H.J. Analytical model for flux saturation in sediment transport. Phys. Rev. E 2014, 89, 052213. [Google Scholar] [CrossRef]
- Pähtz, T.; Kok, J.F.; Parteli, E.J.; Herrmann, H.J. Flux saturation length of sediment transport. Phys. Rev. Lett. 2013, 111, 218002. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.; Wang, S.S.Y.; Jia, Y. Nonuniform sediment transport in alluvial rivers. J. Hydraul. Res. 2000, 38, 427–434. [Google Scholar] [CrossRef]
- Wu, W.; Wang, S.S. A depth-averaged two-dimensional numerical model of flow and sediment transport in open channels with vegetation. Riparian Veg. Fluv. Geomorphol. 2004, 2004, 253–265. [Google Scholar]
- Richardson, J.T. Sedimentation and fluidisation: Part i. Trans. Inst. Chem. Eng. 1954, 32, 35–53. [Google Scholar] [CrossRef]
- Liang, Q. Flood simulation using a well-balanced shallow flow model. J. Hydraul. Eng. 2010, 136, 669–675. [Google Scholar] [CrossRef]
- Kurganov, A.; Petrova, G. A second-order well-balanced positivity preserving central-upwind scheme for the saint-venant system. Commun. Math. Sci. 2007, 5, 133–160. [Google Scholar] [CrossRef]
- Audusse, E.; Bouchut, F.; Bristeau, M.-O.; Klein, R.; Perthame, B. A fast and stable well-balanced scheme with hydrostatic reconstruction for shallow water flows. SIAM J. Sci. Comput. 2004, 25, 2050–2065. [Google Scholar] [CrossRef]
- Liang, Q.; Marche, F. Numerical resolution of well-balanced shallow water equations with complex source terms. Adv. Water Resour. 2009, 32, 873–884. [Google Scholar] [CrossRef]
- Begnudelli, L.; Sanders, B.F. Unstructured grid finite-volume algorithm for shallow-water flow and scalar transport with wetting and drying. J. Hydraul. Eng. 2006, 132, 371–384. [Google Scholar] [CrossRef]
- Wu, G.F.; He, Z.G.; Liu, G.H. Development of a cell-centered godunov-type finite volume model for shallow water flow based on unstructured mesh. Math. Problems Eng. 2014, 2014. [Google Scholar] [CrossRef]
- Yoon, T.H.; Kang, S.-K. Finite volume model for two-dimensional shallow water flows on unstructured grids. J. Hydraul. Eng. 2004, 130, 678–688. [Google Scholar] [CrossRef]
- Hu, K.; Mingham, C.G.; Causon, D.M. Numerical simulation of wave overtopping of coastal structures using the non-linear shallow water equations. Coast. Eng. 2000, 41, 433–465. [Google Scholar] [CrossRef]
- Song, L.; Zhou, J.; Guo, J.; Zou, Q.; Liu, Y. A robust well-balanced finite volume model for shallow water flows with wetting and drying over irregular terrain. Adv. Water Resour. 2011, 34, 915–932. [Google Scholar] [CrossRef]
- Nikolos, I.K.; Delis, A.I. An unstructured node-centered finite volume scheme for shallow water flows with wet/dry fronts over complex topography. Comput. Methods Appl. Mech. Eng. 2009, 198, 3723–3750. [Google Scholar] [CrossRef]
- Conclusions and Recommendations from the Impact Project WP2: Breach Formation. Available online: http://www.impact-project.net/cd4/cd/Presentations/THUR/17-1_WP2_10Summary_v2_0.pdf (accessed on 28 July 2015).
- Kuiry, S.N.; Ding, Y.; Wang, S.S. Modelling coastal barrier breaching flows with well-balanced shock-capturing technique. Comput. Fluids 2010, 39, 2051–2068. [Google Scholar] [CrossRef]
- Reed, C.W.; Militello, A. Wave-adjusted boundary condition for longshore current in finite-volume circulation models. Ocean Eng. 2005, 32, 2121–2134. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Z.; Hu, P.; Zhao, L.; Wu, G.; Pähtz, T. Modeling of Breaching Due to Overtopping Flow and Waves Based on Coupled Flow and Sediment Transport. Water 2015, 7, 4283-4304. https://doi.org/10.3390/w7084283
He Z, Hu P, Zhao L, Wu G, Pähtz T. Modeling of Breaching Due to Overtopping Flow and Waves Based on Coupled Flow and Sediment Transport. Water. 2015; 7(8):4283-4304. https://doi.org/10.3390/w7084283
Chicago/Turabian StyleHe, Zhiguo, Peng Hu, Liang Zhao, Gangfeng Wu, and Thomas Pähtz. 2015. "Modeling of Breaching Due to Overtopping Flow and Waves Based on Coupled Flow and Sediment Transport" Water 7, no. 8: 4283-4304. https://doi.org/10.3390/w7084283




