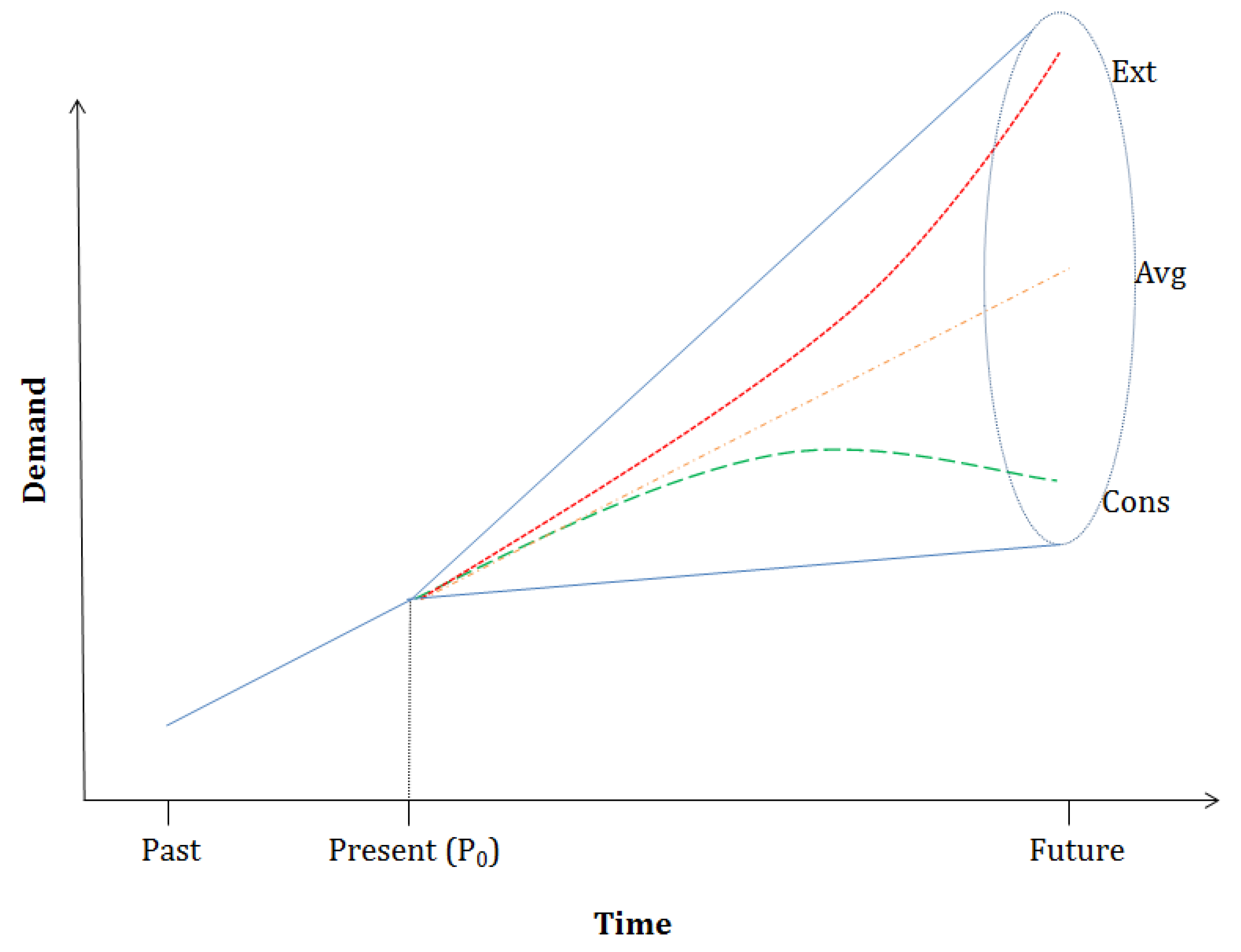
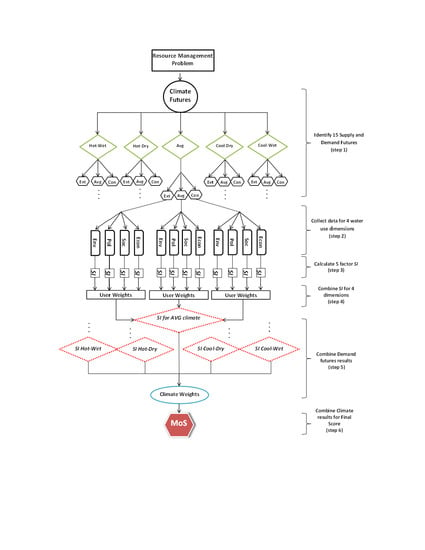
1. Introduction
In the 20th century, the world population has tripled, but water use has increased six-fold, indicating augmented stresses on limited resources [
1]. In light of this, politicians and decision-makers seek solutions to meet demand [
2]. One approach is a shift to include both supply and demand management through Integrated Water Resources Management (IWRM) (e.g., [
3,
4,
5,
6,
7,
8,
9]). Of growing importance in IWRM, one such method has been to improve resource efficiency through watershed-scale application of water reuse and recycling (WRR) technologies [
10,
11,
12].
Equitable water use as proposed by IWRM faces challenges due to continuous structural transformations in society and the environment [
13], yielding problems of high complexity and uncertainty [
14,
15,
16]. Climate change will lead to uncertain future water supplies [
17], while population growth, technological innovation, composition of future economies, and dynamic stakeholder goals add further demand-side uncertainties [
18]. As such, methodological tools are required that enable the assessment of sustainability under an uncertain future.
It is well known, however, that defining sustainability in a rigorous and meaningful manner is challenging at best [
19,
20]. The first widely accepted articulation of the term sustainable development, published in the Brundtland report, calls for a “development that meets the needs of the present without compromising the ability of future generations to meet their own needs” [
21]. Since its publication, close to 300 other attempts at a definition of “sustainability” have been published (e.g., [
19,
22,
23,
24]), none of which is universally accepted, but there is increasing consensus that discussions thereof should include uncertainty [
25]. Under uncertainty, we must seek solutions that may not be the most optimal under present conditions, but are the most robust (
i.e., less likely to fail and more immune to the effects of failure due to factors of uncertainty) [
26,
27]. We argue that any robust measure of water resources sustainability must consider three major sources of uncertainty under a decision support analysis as represented by the following questions [
20,
22]: (1) for whom is the resource being sustained; (2) at what time will sustainability be determined; (3) under what future conditions will the resources remain sustainable. From hereafter the sources of uncertainty associated with these questions will be respectively referred as to
Whomever,
Whenever, and
No Matter What.
In line with this, for over three decades there have been attempts to create water risk indices, easy for lay-users to understand but capable of merging the intricacies of resource scarcity into a single unified number, a “synthesis of numerous factors into one given factor” [
28]. Decision support tools in water resource management often aim to do this (e.g., [
29,
30,
31,
32,
33,
34,
35]). For example, to quantify risk in a reservoir to optimize water management under uncertainty and scarcity, Hashimoto
et al. proposed a landmark methodology, called RRV, that quantifies risk in terms of the frequency (Reliability, R), duration (Resilience, R), and magnitude (Vulnerability, V) of system failure [
29]. RRV has been applied in numerous hydrologic settings to quantify water quantity and quality risk under varying scenarios (
i.e., [
13,
36,
37]). Loucks [
31] and Sandoval-Solis
et al. [
35] unified the RRV factors, proposing multi-criteria analysis methodologies that consider not only the needs of various stakeholders but also incorporate multiple risk measures.
These methodologies, however, are similar to traditional analyses techniques in that, while addressing the first two sources of resource uncertainty (Whomever and Whenever) through dynamic multi-criteria analysis, their simplification of variable trajectories overlooks the resources’ supply and demand futures (No Matter What). By assuming unchanging climate parameters and resource use, these previous studies are susceptible to adopting solutions that, while optimal for present conditions, are incapable of responding to variations in these. Overlooking uncertainty in future conditions risks the possibility of espousing solutions unsustainable in the very future for which they are proposed.
The objective of this study is to propose a methodology that encompasses multiple sources of uncertainty in decision-making, including climate change, population growth, and demand trajectories defined by future socio-economic scenarios. While traditional engineering solutions operating under deterministic parameters often invoke “optimization” as the problem-solving goal, in stochastic or uncertain situations “robustness” must serve as the objective so as to maintain performance of the system when subjected to unpredictable perturbations [
38]. By evaluating the performance of a dynamic and multivariate risk index in response to the range of potential supply and demand futures, this methodology seeks robust sustainable options under future uncertainties [
39]. In our approach, we incorporate climate change projections, based on downscaled Global Climate Projections (GCP) following Special Report on Emission scenarios (SRES) and Representative Concentration Pathway (RCP) scenarios, as well as growth projections provided by experts in each water sector, considering conservative, average, and extreme demand scenarios. These are integrated into a Water Evaluation And Planning (WEAP)-MODFLOW coupled hydrology model that simulates the surface-subsurface system. To assess future outcomes we propose a new dynamic multidimensional evaluation methodology for sustainable water management plan ranking and selection.
This new methodology for robust sustainability analysis is presented in
Section 2 of this paper, and in
Section 3 is applied to the Copiapó River basin in Chile, one of the most arid regions in the world in which strong economic and population growth is taking place due to agricultural and mining industries. A recent study of this site [
40] explored several water management strategies, calling for a reduction in demand of 20%–30%, a range achievable in practice through effective WRR [
41]. This study, while providing useful planning information, adopted the oversimplifying assumptions common to current water management analyses of constant supply and demand futures, single variable analysis, and static rather than dynamic evaluation of sustainability (e.g., [
42,
43,
44]). Results from the application of our new dynamic, multivariate, robust sustainability measure are compared in
Section 4 with those using a static, single-variable, deterministic future (
i.e., [
40]) to demonstrate the importance of considering these often overlooked factors in resource decision-making. Finally,
Section 5 presents the main conclusions of this work.
4. Results and Discussion
In order to demonstrate the importance of utilizing a dynamic, multivariate, robust analysis methodology in resource decision support, results from our WEAP-MODFLOW simulations were compared with those from Suarez
et al. [
40] who employed the static, single-variable analytics common to traditional water management. This previous research selected five general management schemes (
Table 7) as an experimental manipulation of time, space, and quantity variables. While our work supports this attempt to address these variables, Suarez
et al. [
40] neglected the uncertain factors previously mentioned (
i.e., global change, time-independent risk measures) which are necessary for robust resource planning. Utilizing the before-mentioned methodology for future planning (climate and demand) in our WEAP-MODFLOW simulation, as well as the MoS risk analysis methodology outlined in
Section 2, we evaluated the same management scenarios as Suarez
et al. [
40] and found a nearly identical ranking of plans despite our methodological refinements (
Table 7).
Table 7.
Original plan results comparison between Suarez
et al. [
40] and MoS.
Table 7.
Original plan results comparison between Suarez et al. [40] and MoS.
| Water Management Plan | Suarez et al., Rank | MoS Rank |
|---|
| 7 | 7 |
- 2.
Uniform reduction of water demand.
| 20% | 4 | 4 |
| 30% | 2 | 2 |
| 50% | 1 | 1 |
- 3.
Segmented reduction of water demand.
| 3 | 3 |
- 4.
Water resource management with uniform reduction of water demand and translocation of water between aquifer zones.
| 6 | 5 |
- 5.
Water resource management with segmented reduction of water demand and translocation of water between aquifer zones.
| 5 | 6 |
This parallel between the Suarez
et al. [
40] and MoS results is to be expected. These original management plans have widely varying values of demand reduction (0%–50%), thus making total water use the dominant variable. A simple analysis shows that the plan that consumes the least amount of water would be the highest rated in terms of sustainability. Indeed, the correlation between the percentage of overall demand reduction and the MoS scores is extremely high (
R2 = 0.94), thus indicating a direct linear dependence of MoS upon the amount of water consumed by each plan. Therefore, to eliminate the dominating effects of demand reduction upon the MoS score in order to objectively compare the management schemes without conflicting variables, we propose four new management plan options that offer the same overall demand reduction (20%, a level achievable through water reuse technologies) while maintaining the original proportionality between water users and administrative sectors of demand reduction presented in Suarez
et al. [
40] defined by local stakeholders. For example, plan 5.1 (
Table 8) originally called for the mining and agriculture users to reduce water demand by 20% in sectors 1 and 2, 35% in sector 3, and 50% in sectors 4 and 5. To achieve an overall demand reduction of 20%, these sectorial values were reduced proportionally by the same 4:7:10 ratio, so that in the new plan 5.1, reduction levels are 14.4% in sectors 1 and 2, 25.2% in sector 3, and 36% in sectors 4 and 5. For plan 4.1, which originally required a reduction in demand of 35% in agriculture and mining, demand reduction for these users was merely lowered to 21% so that the total reduction over all water users would be 20%. Demand transfers are not reduced as they do not affect the total demand reduction. No changes were required for plans 2.1 or 3.1 as they originally resulted in the desired 20% total demand reduction. Having eliminated demand reduction as the dominating variable in sustainability analysis, we are now able to determine the most sustainable distribution of resources between stakeholders and geographical sectors.
Following the MoS flow chart in
Figure 3 to evaluate the functioning of the tested management plans outlined above, the constructed WEAP model was run 75 times considering three demand scenarios, five climate futures, and five management schemes. Utilizing the five-factor sustainability index outlined above (Equation (9)) to consider performance in the four different variable dimensions (environmental, economic, political, social), we obtained numerous results for each plan tested. These individual results were recorded in tables similar to that below (
Table 9 shows results for water use plan 2.1). To obtain a unique final value for management plan comparison and ranking, the four variable dimensions and the three demand scenarios are each given equal weight, as suggested by Loucks [
31]. These weights, however, are flexible and should be adjusted according to the opinions and values of the user of the MoS algorithm. Decision-makers predicting a certain demand future over another or placing more importance in one water use sector than another might weight these as they see fit. Climate, however, should remain weighted as expressed above, as these weights are derived as a general consensus of many climate models. Considering all five-factor Sustainability Index values (Equation 9) for the 60 permutations of climate (
Table 6), demand (
Table 5), and dimension (
Table 2), and the weightings described, the final MoS is listed in the bottom right corner of the table as a single and simple number ranging from 0 to 1 (higher values represent more desirable sustainability situations). MoS scores and relative rankings for all five management schemes are presented in
Table 10.
Table 8.
Management schemes, original and adjusted for equal demand reduction (“sec” refers to administrative sectors, see
Figure 4).
Table 8.
Management schemes, original and adjusted for equal demand reduction (“sec” refers to administrative sectors, see Figure 4).
| Mgmt. Plan | 1.1 | 2.1 | 3.1 | 4.1 | 5.1 |
|---|
| Old plan (Suarez et al., 2014 [40]) | No reduction | All uses: 20% demand reduction | All uses: 20% demand reduction in sec 1 and 2, 35% in sec 3, 50% in sec 4 | Mining/Agriculture: 30% reduction
Potable: 50% demand transfer from 4a to 5a | Mining/Agriculture: 20% in sec 1 and 2, 35% in sec 3, 50% in sec 4 and 5
Potable: 50% demand transfer from 4a to 5a |
| Total demand Reduction | - | 20% | 20% | 28% | 27% |
| New Plan | No reduction | All uses: 20% demand reduction | All uses: 20% demand reduction in sec 1 and 2, 35% in sec 3, 50% in sec 4 | Mining/Agriculture: 21% reduction
Potable: 50% demand transfer from 4a to 5a | Mining/Agriculture: 14.4% in sec 1 and 2, 25.2% in sec 3, 36% in sec 4 and 5
Potable: 50% demand transfer from 4a to 5a |
| Total demand reduction | - | 20% | 20% | 20% | 20% |
Table 9.
Example table for the computation of MoS completed for each management option under Extreme (Ext), Average (Avg), and Conservative (Con) demand futures (using management scheme 2.1 as example).
Table 9.
Example table for the computation of MoS completed for each management option under Extreme (Ext), Average (Avg), and Conservative (Con) demand futures (using management scheme 2.1 as example).
| Water Use (2.1) | Environmental | Economic | Political | Social |
|---|
| Demand Model | Ext | Avg | Con | Ext | Avg | Con | Ext | Avg | Con | Ext | Avg | Con |
| Climate Scenario | Dry Hot | 0.198 | 0.218 | 0.226 | 0.077 | 0.344 | 0.449 | 0.207 | 0.492 | 0.732 | 0.638 | 1.000 | 1.000 |
| Dry Cool | 0.213 | 0.231 | 0.239 | 0.080 | 0.346 | 0.455 | 0.209 | 0.506 | 0.900 | 0.630 | 1.000 | 1.000 |
| Wet Hot | 0.204 | 0.224 | 0.231 | 0.078 | 0.345 | 0.450 | 0.199 | 0.493 | 0.772 | 0.615 | 1.000 | 1.000 |
| Wet Cool | 0.198 | 0.230 | 0.238 | 0.077 | 0.345 | 0.453 | 0.207 | 0.518 | 0.839 | 0.630 | 1.000 | 1.000 |
| Average | 0.208 | 0.227 | 0.234 | 0.079 | 0.345 | 0.452 | 0.202 | 0.498 | 0.780 | 0.630 | 1.000 | 1.000 |
| Weighted Total | 0.207 | 0.228 | 0.235 | 0.079 | 0.345 | 0.453 | 0.205 | 0.502 | 0.819 | 0.629 | 1.000 | 1.000 |
| MoS | 0.475 |
Table 10.
MoS Scores and rankings of adjusted management plans.
Table 10.
MoS Scores and rankings of adjusted management plans.
| New Mgmt Plan | 1.1 | 2.1 | 3.1 | 4.1 | 5.1 |
|---|
| MoS score | 0.324 | 0.475 | 0.547 | 0.361 | 0.348 |
| Ranking | 5 | 2 | 1 | 3 | 4 |
While the purpose of the MoS was to create an index able to combine the range of supply and demand futures and their impact upon numerous variables affecting different water use dimensions into a single, easily understandable number, the analysis of the individual sustainability scores such as those in
Table 9 also presents results of interest. Maintaining constant one of the two variables of future scenario uncertainty (demand and climate), the variability in sustainability introduced by the other factor may be measured for each of the four water use dimensions. Comparing the change in sustainability caused by differences in demand scenario with that produced by modification of the climate future, we observe that for all four water dimensions, demand is the more influential variable (Effect on
SI of demand variance/Effect of climate variance by dimension: env., 1.89; econ., 89.5; pol., 6.9; soc., 31.4;
Table 11). While much attention has been placed upon the effects of climate change on water resource availability, in arid regions where water is naturally scarce, the efficient use of this resource might perhaps be a much more important determinant of future sustainability, as indicated by these numbers.
Table 11.
Effect on SI caused by future variables (second variable held constant) and relative impact.
Table 11.
Effect on SI caused by future variables (second variable held constant) and relative impact.
| Water Use Dimension | Environmental | Economic | Political | Social |
|---|
| Demand | 0.0272 | 0.3003 | 0.5228 | 0.3965 |
| Climate | 0.0144 | 0.0034 | 0.0758 | 0.0126 |
| Demand/Climate | 1.89 | 89.49 | 6.90 | 31.38 |
Higher-rated plans in the MoS index, however, are not necessarily the most practical solutions. Management plan implementation cost is an essential variable in decision-making and cannot be overlooked. A plan requiring 50% reduction in water demand, for example, would logically conserve more water, but without considering the costs of enacting such a measure we are unable to compare trade-offs. For the calculation of plan implementation costs, we assume that, without improvements in technological efficiency or philanthropy on the part of economic sectors, the reduction in fresh water demand must be replaced by other means. Following the suggestion of Suarez and current practices of the Candelaria Mine in Copiapó and other mines in arid Northern Chile, we propose SWRO (sea water reverse osmosis) as the source for replacement resources.
Currently, the cost of desalinating and transporting 0.5 m
3/s to the Candelaria Mine, the principal mine in the river basin located at 675 m, is approximately $3 USD/m
3. On the other hand, a lower cost of $1.78/m
3 is estimated for production and transport of potable water to the city of Copiapó using SWRO [
84]. Being that no study has yet to calculate the economic feasibility of utilizing desalinated water for agricultural purposes in Copiapó, we chose to utilize an average of the values for desalination already observed in Copiapó ($2.39/m
3). While this value is approximately four times more expensive than the highly efficient Ashkalon desalination plant in Israel ($0.57/m
3), it falls within international norms [
85,
86]. Based on projected demands for each stakeholder under the three different future demand scenarios and the associated demand reduction percentages proposed by each management plan, we calculated a first-order approximation of plan implementation costs under the above-stated desalination costs (
Table 12, column 2).
Table 12.
Cost and performance evaluations of new management plans. Costs are calculated using the average cost of all demand and climate scenarios.
Table 12.
Cost and performance evaluations of new management plans. Costs are calculated using the average cost of all demand and climate scenarios.
| Plan | Implementation Cost (Million $$) | Deficit Reduction Cost (Million $$) | Total Cost (Million $$) | MoS |
|---|
| 1.1 | 0 | 15,953 | 15,953 | 0.324 |
| 2.1 | 6901 | 7718 | 14,619 | 0.475 |
| 3.1 | 6865 | 7115 | 13,980 | 0.547 |
| 4.1(new) | 6671 | 14,935 | 21,606 | 0.361 |
| 5.1(new) | 6632 | 7705 | 14,337 | 0.348 |
The highest-performing management plan utilizing the traditional single-variable static approach seen in Suarez
et al. (50% reduction in all demands) would also be the most expensive option to implement, costing an estimated $9.3 billion USD more than the next most expensive option [
40]. Suarez
et al. [
40] agree upon the infeasibility of this option due to difficulty of implementation and instead propose plan 2.2 (30% reduction in all demands), which still happens to be the second most expensive option, costing an estimated $2.8 billion USD more than the next most expensive option. These additional costs over a more traditional method that employs static future demand scenarios result from the fact that even in the best case scenario, conservative demand projections are greater than current consumption.
Implementation, however, is not the only cost inherent in a management plan, but as Suarez
et al. [
40] correctly argue, each plan will result in a different future water deficit based upon the ability to meet demand after implementation. While Suarez’s cost calculations were a necessary first attempt to convert hydrological performance into an economic value, certain assumptions led to a large underestimation of deficit cost. The potential effects associated with assuming static futures in climate and markets have been addressed in this work, but the assumption that
ex post facto deficit recovery involves the same cost as preventative resource production must also be addressed. While the nearly deterministic nature of their demands allows the mining and potable water sectors to prepare for deficits, the fact that additional water demand and deficits are calculated after the fact for agricultural purposes dependent upon stochastic rainfall limits the plausibility of desalination for deficit reduction (at the rate of $1.35–$2.01/m
3 as employed by Suarez). Rather, the most likely costs to be incurred by farmers will come in the form of reduced crop yield. Taking the crop irrigation demand requirements for Copiapó [
59] of 17,735 m
3/ha/year, the average yield for table grape production in climatic zones similar to Copiapó [
87] of 19,952 metric tons/ hectare, and the average table grape prices over the last five years for produce originating in Copiapó of $1.1/kg as reported by the Chilean Office of Agrarian Studies and Politics ODEPA [
88], we find that average economic product lost by deficit is $14.85/m
3. Clearly, when compared with the marginal cost of SWRO (~$2.39/m
3), economic loss due to water deficit is much greater and should be avoided. Were it not possible to reutilize the desalination plants mentioned for management plan implementation, increasing their capacity so as to meet deficit needs, this new factor, combined with the dominance of deficits by the agricultural sector, would greatly raise the costs of deficit reduction and increase the importance of implementing preventative sustainability plans.
Independent of this decision to calculate crop losses or agricultural drought prevention, the accepted static futures methodology for resource analysis (e.g., [
40]) underestimates deficit by a factor of more than 10 times by overlooking the projections of mainly increased demand and, to a minor extent, decreased supply. It should also be noted that although Suarez
et al. [
40] estimated that a 50% demand reduction would lead to aquifer recharge and thus an environmentally sustainable position, by excluding the potential effects of climate change and demand growth, they likely overstate their case. According to calculations in this study that consider these factors, even a 50% reduction in future demand, at a cost of at least $16.1 billion USD for implementation, would not be sufficient to reach absolute sustainability in Copiapó, and would still require additional expenditure for deficit reduction through SWRO. As might be seen in
Table 12 below, at that cost it would be more economic to follow nearly any other management scheme, thus the consideration of future demand growth is integral to the decision-making process.
Combing the costs of implementation of the new management plans (equal percentage of demand reduction,
Table 8) with the costs of deficits caused by the failure of these plans to meet demand requirements, we arrive at a first order estimation for the total cost of adopting the management plans for water resource sustainability. As might be seen in
Table 12 below, plan 3.1 (previously ranked only third by Suarez
et al. [
40]) now not only stands as the best-performing option according to our MoS, but also is estimated to be the least expensive.
Merely by showing that results are different does not necessarily prove that the MoS methodology is any more appropriate than the traditional method which does not account for climate change, demand change, or multi-sectorial multivariable analysis. Being that these techniques are intended to aid in resource planning for uncertain futures, their sensitivity to variations in future variables is of prime concern. A more robust analysis methodology would be one that either eliminates variable uncertainty or includes the range of uncertainty into calculations. Maintaining constant the climate scenario (dry-cool, dry-hot, wet-cool, wet-hot, average), we calculate the range of total water deficit during the 30-year period over all three demand scenarios (conservative, average, extreme) (
Table 13). By eliminating the effects of the climate variable, we observe that the range of uncertainty introduced by the demand variable is much greater (between 3200 and 5600 Mm
3 depending on the management scheme) than the range between all management schemes using the traditional methodology (500 Mm
3) observed in Suarez
et al. [
40]. The uncertainty caused by climate also results in a much greater range under the extreme demand scenario (1200–2000 Mm
3) and also under conservative and average demand if we exclude the base scheme in which no water conservation measures are taken. In fact, by overlooking climate and demand changes altogether, the traditional method underestimates water deficits even in the best-case scenario (conservative demand and cool-wet climate future) in all but the base scenario by an average of 250%. These ranges of uncertainty introduced by variables that are overlooked by the traditional analysis technique observed in Suarez
et al. [
40], being greater than the range of deficit values between the potential management schemes being analyzed (experimental variable), demonstrate the need for a robust analytical methodology. Reliant upon uncontrolled stochastic variables rather than upon robust analysis makes the conclusions of the traditional method highly fragile for decision-making under an uncertain future. The MoS methodology, however, includes these uncertainties in its calculations by estimating the range of effects caused by potential futures rather than gambling on a single demand and climate scenario. Thus, the high range of potential water deficits resultant from uncertain futures, rather than introducing a conflicting variable, is incorporated into the MoS evaluation of management schemes.
Table 13.
Range of deficits introduced by uncertain variables in million m3, considering either a single demand scenario over all climates or a single climate scenario over all demands. To the right are projected deficits using the traditional and MoS techniques.
Table 13.
Range of deficits introduced by uncertain variables in million m3, considering either a single demand scenario over all climates or a single climate scenario over all demands. To the right are projected deficits using the traditional and MoS techniques.
| Mgmt Scheme | Single Demand Scenario (All Climates Considered) | Single Climate Scenario (All Demands Considered) | All Variables Considered |
|---|
| Cons. | Avg. | Ext. | Avg. | Dry-Cool | Dry-Hot | Wet-Cool | Wet-Hot | Suarez et al. | MoS |
|---|
| 1.1 | 139 | 267 | 1972 | 5397 | 5275 | 5588 | 5300 | 5501 | 528 | 2311 |
| 2.1 | 52 | 120 | 1408 | 3982 | 3887 | 4128 | 3913 | 4052 | 32 | 1534 |
| 3.1 | 27 | 91 | 1364 | 3936 | 3814 | 4122 | 3841 | 4038 | 18 | 1438 |
| 4.1 | 52 | 789 | 1409 | 3982 | 3887 | 4122 | 3914 | 8686 | 54 | 1795 |
| 5.1 | 62 | 128 | 1428 | 3999 | 3925 | 4118 | 3946 | 4051 | 45 | 1571 |
While the entirety of the difference in the MoS score does not lie in a single category but rather is distributed throughout the different sustainability indicators and water use dimensions, a gain in 0.072 MoS as that observed between plans 3.1 and 2.1 is equivalent to 25.8 more months where water is provided to all water utility clients during the 30-year period, or it is equivalent to the average aquifer depth being 5.59 m closer to the surface. This 25.8-month difference in reliability multiplied by 239 clients without water on average per failure and 16.2 m3/client average monthly usage reported by Aguas Chañar, who charges approximately $1.31/m3, gives a total of $130,868 USD gained by choosing the better-performing option. The 5.59 m difference in average aquifer depth translates into a difference of $15.1 million USD extra expenditure in pumping costs during the 30-year period when choosing plan 2.1 over 3.1. According to these numbers it may be observed that the MoS does not have a strict monetary interpretation as the same reduction of 0.072 in the index score would correlate to incurred costs that vary over two orders of magnitude. This difference is to be expected, however, as potable water usage is nearly two orders of magnitude lower than total aquifer pumping. These translations of the MoS into monetary values are merely examples to aid in user understanding of the index. Nevertheless, decision-makers should be presented with both plans and costs to aid in decision-making.
5. Conclusions
Addressing issues of oversimplification of futures observed in current sustainability analysis methods, this research proposes a robust, dynamic, and multivariate approach for decision support in water resources. While the simulation of results in multiple climate and demand scenarios increases calculation cost, by evaluating the range of watershed performance in response to these uncertain parameters avoids potentially costly underestimations produced by simpler techniques. To demonstrate its application, this new methodology (the Measure of Sustainability or “MoS”) was applied to the Copiapó, Chile, watershed, an example of an arid watershed under extreme natural and anthropogenic water stress. Results of the MoS were compared to those previously calculated by a more traditional approach in which climate and water demands are considered to be stationary.
The MoS results, coupled with first order estimated costs, provide decision-makers with a simplified manner of selecting resource management possibilities whose economic feasibility might further be analyzed by financial experts. In the analysis of Copiapó we observed that the sustainability of the original plans evaluated by a more traditional approach [
40] is highly dependent upon the water reduction and thus the inherent implementation cost proposed by each. Even in the best possible scenario of a conservative demand future, the traditional method of static demand underestimates the cost to implement any management scheme while overlooking the effects of climate change also misjudges the magnitude of future water deficits. Specifically in the agricultural sector, the marginal cost of crop loss due to water deficit is much greater than the marginal cost of SWRO and thus should be avoided where possible through preparation rather than remediation. This leads us to suggest further investigation into the economic feasibility of SWRO solutions for agricultural deficit mitigation.
Independently analyzing the uncertain future variables of climate and demand, we observe that the uncertainty introduced by each of these is larger than the range of the experimental variable deficit of each management scheme in the traditional methodology. In addition, we observe that in arid regions, such as Copiapó, Chile, where water resources are naturally scarce, demand variability might introduce more risk to sustainability than potential changes in climate, leading us to suggest increased efforts in hydrologic efficiency. Combining these two variables, however, to compare four management schemes with equal water reduction but different distribution structures, we were able to find that reducing all demands by a strict 20% (plan 2.1) and reducing all demands by geographic sector (plan 3.1) are the best performing management schemes, with 3.1 scoring slightly higher in the MoS index (0.072) but also costing slightly less (approximately $639 million USD). Not only for lower economic cost but also for improved performance in the Measure of Sustainability (MoS) index, we propose the adoption of plan 3.1 over Suarez et al.’s selection of 2.1 for water management in the Copiapó basin.
Mounting concerns about the impacts of human activities, potential climatic shifts, expanding populations and water demands as well as new knowledge are part of the pressing need to develop alternative management schemes in an integrated manner, particularly in environments with scarce natural resources. In this background, it is important to emphasize the transition in theory and practice from Environmental Impact Assessment to Risk Assessment, and then to Sustainability Analysis and Vulnerability Assessment. Thus, given the uncertainty of future events and the dependence upon climate and market trajectories, we reiterate that the plans selected by this methodology are not necessarily the most optimal solutions to problems in water resource sustainability. By considering the performance of each plan under the expected range of likely futures, however, the MoS methodology proposes solutions that are robust to variations in future parameter values and are thus the best management options in a stochastic natural world. While important, sustainability and cost are not the only factors that influence environmental decision-making. Social acceptance, political feasibility, and technological capabilities also influence the opinions of stakeholders and thus add a component of uncertainty in values not directly addressed by the MoS methodology. Further research in decision support should address issues of political and social will for integrated conservation measures. In particular, due to its dominance of demand, inelasticity of infrastructure, and disjointed individualist organization, the agricultural sector’s motivation to participate in water demand management should be of pressing interest for future study. As observed by considering the range of future water supply and demand trajectories, the MoS demonstrates that sustainability management is even more vital than previously thought.