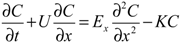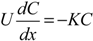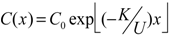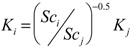1. Introduction
Aquatic life requires adequate levels of dissolved oxygen (DO) for survival. Therefore, DO content is a standard monitoring tool to determine the health of fresh water systems. A major consumer of DO in aquatic systems is the microbial degradation of organic matter. A stream’s ability to make up this oxygen deficit and return to its solubility equilibrium with the atmosphere is vital. This is accomplished primarily through gas exchange at the air-water interface, where oxygen is either lost or reabsorbed into the stream, due to the concentration gradient between the atmosphere and water. If levels of demand exceed reaeration into the system, a body of water will struggle to support life and may reach hypoxic conditions; in extreme cases, the surface water will become anoxic.
Reaeration coefficients vary widely due to their dependence on turbulence at the air water interface, which is poorly understood and hard to measure. Previous work has related reaeration coefficients to stream characteristics, such as mean depth, current velocity, stream channel slope and discharge (e.g., [
1,
2,
3,
4,
5]). A number of equations have been postulated, with no one equation appropriate for every channel. The empirical equations also disagree significantly within the same channel. For instance, the equations respond differently to increasing flow: velocity-depth equations predict decreasing reaeration rates, while energy-dissipation models (utilizing channel slope and velocity) predict increasing rates (e.g., [
3]). When applied to wastewater management, an underestimation in the reaeration coefficient would result in overly restrictive regulations. With overestimation, a stream or creek will be less resilient to wastewater discharge than predicted, risking hypoxia and collapse of the aquatic ecosystem.
In addition to DO studies, high quality reaeration coefficients are needed for understanding most biogeochemical cycles within streams and other surface water bodies. Many of the gases involved in these cycles, such as CO
2, N
2O and CH
4, are greenhouse gases. They are also needed for interpreting
222Rn distributions that are commonly used to investigate groundwater-surface water interactions (e.g., [
6,
7,
8]). For instance, the results of the tracer experiment described here provided an estimate of the loss rate of
222Rn from Martis Creek, which allowed for the quantification of the groundwater influx when combined with
222Rn measurements in the stream and an estimate of the
222Rn concentration in shallow groundwater [
8].
Gas tracers can be used to accurately estimate a stream’s reaeration coefficient through point-source injection as either a continuous release (as is the case here) or a single pulse that includes a conservative ion, dye or a second gas tracer [
9,
10,
11,
12]. Tracer concentrations are measured at specific intervals downstream from injection after the experimental reach has been flushed. Tracer loss from the water to the atmosphere can be used as a proxy for gas exchange across the interface, ultimately allowing for a calculation of reaeration rates.
Two trace gases, sulfur hexafluoride (SF
6) and the noble gas, xenon (Xe), were selected for the tracer experiments conducted in two headwater creeks in the Sierra Nevada of California. SF
6 was selected, because it has been used in numerous earlier experiments [
9,
10,
11,
13]. As discussed below, it is a very strong greenhouse gas and is currently regulated in California, so during the second experiment, a second gas tracer was tested to determine if it could be used as an alternative tracer for these experiments. The additional objectives of this study are to compare the reaeration rates between the two creeks and with empirical relationships, as others have done [
1,
2,
3,
4,
5].
1.1. Study Area
The first experiment used only SF
6 and was conducted in Sagehen Creek, a headwater catchment to the Truckee River about 35 km northwest of Lake Tahoe. The second included both SF
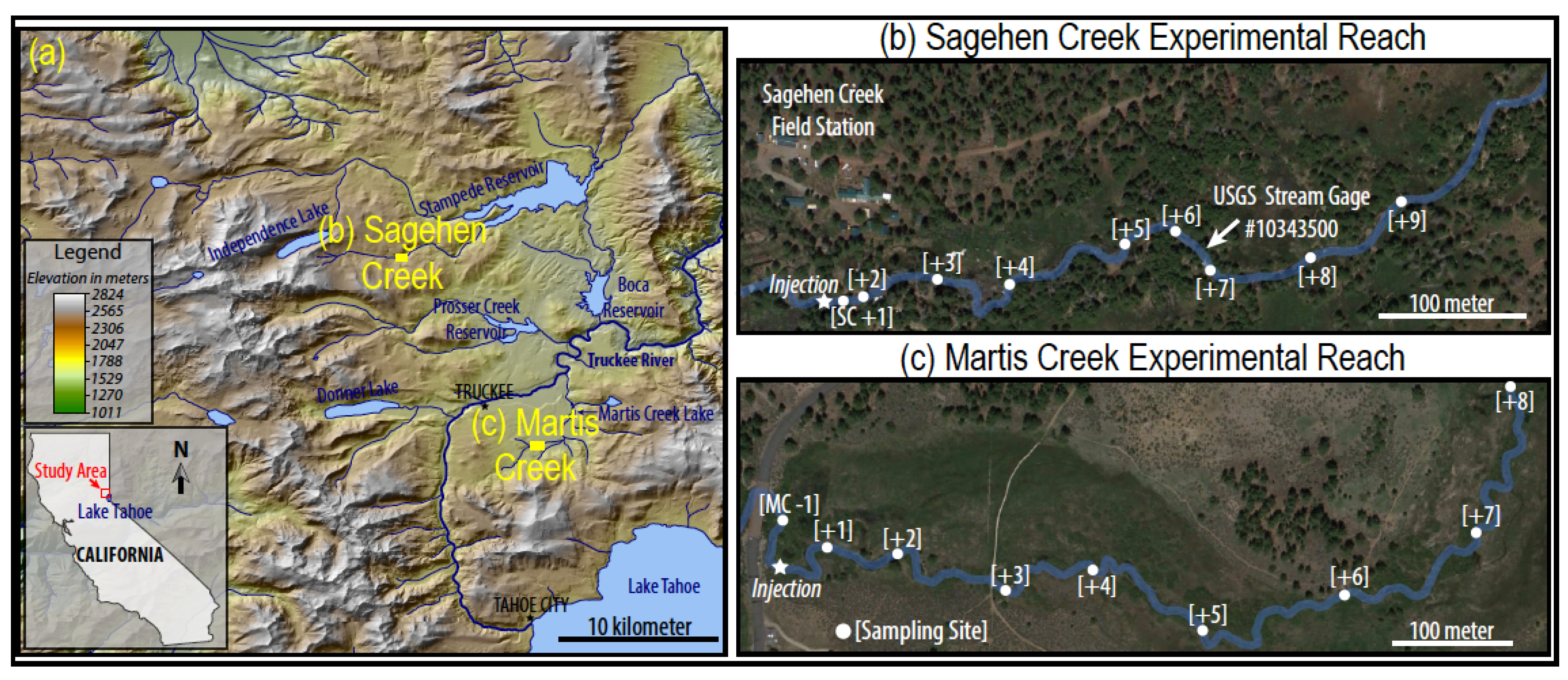
6 and Xe and was conducted in another tributary to the Truckee River, Martis Creek, about 15 km southeast of Sagehen near the town of Truckee, CA, USA (
Figure 1a). The Sagehen experiment occurred along an approximately 500-m reach of the creek in 2009, adjacent to the Sagehen Creek Field Station (SCFS). The Martis experiment occurred along an approximately 1000-m reach in 2012 (prior to the implementation of the SF
6 regulations that began 1 January 2013). SCFS is part of the University of California (UC) Natural Reserve system and is managed by UC Berkeley.
Figure 1.
(
a) The study area is located northwest of Lake Tahoe within the Sierra Nevada. Main base map from the United States Geologic Survey (USGS) 10-m National Elevation Dataset [
14]. Experimental stream reaches of (
b) Sagehen and (
c) Martis Creeks.
Figure 1.
(
a) The study area is located northwest of Lake Tahoe within the Sierra Nevada. Main base map from the United States Geologic Survey (USGS) 10-m National Elevation Dataset [
14]. Experimental stream reaches of (
b) Sagehen and (
c) Martis Creeks.
Both creeks are on the eastern side of the Sierra Nevada at elevations above 1800 m and flow through glacial till deposits (derived from andesite and granodiorite basement rocks) to the Truckee River. They are shallow (mean reach depths of ca. 10 cm), meandering streams with riffle and pool morphology and receive discharge perennially from shallow aquifers. At the time of the tracer experiments, the mean water temperatures were 8.3 °C (Sagehen) and 15.8 °C (Martis), though diurnal temperature fluctuations were observed. Both watersheds receive more than 80 cm of precipitation per year, most of which falls as snow between October and April. Peak and minimum discharge typically occur, respectively, during the month of May and September (as baseflow).
2. Materials and Methods
2.1. One-Dimensional Advection-Dispersion Equation
To obtain the reaeration coefficients for the gas tracers (SF
6 and Xe), dissolved gas transport was approximated using a one-dimensional (1D) advection-dispersion equation assuming first order decay of a continuously released solute in a river; gas exchange is assumed to be a first order chemical reaction. The 1D transport equation for a pollutant or tracer in a stream is written as (e.g., [
11,
15,
16]):
Where
C is the concentration of the dissolved gas in excess of its solubility equilibrium value (
i.e.,
C = Cob − Ceq, where
Cob and
Ceq are, respectively, the observed gas concentration and the solubility equilibrium value);
t is time;
U is the mean stream velocity;
x is the distance downstream;
Ex is the longitudinal dispersion coefficient; and
K is the reaeration coefficient.
The concentration gradient (∂
C/∂
x) is small, because the tracer is being continuously released, and thus, the flux due to dispersion is negligible when compared to the flux due to advection (e.g., [
15,
16]). Once the stream reach has been flushed with tracer, the stream is assumed to be at a steady state (
i.e.,
∂C/∂t = 0), and samples can be collected. With these conditions, the advection-dispersion equation can be simplified to:
Solving this differential equation gives the relationship between concentration and sampling distance,
x, from injection:
where
C0 is the initial concentration of gas tracer at the injection point (
x = 0).
Injecting the SF6 and Xe into the stream introduces a problem when calculating the appropriate initial concentration (C0), because the injection rate is not known perfectly, especially when injecting by bubbling, as was done during the 2009 Sagehen Creek experiment. C0 is obtained from the downstream data. Fortunately, C0 is not needed to determine the reaeration coefficient.
To be useful for other applications and comparisons to earlier works, the reaeration coefficient for the gas tracers must be converted to analogous values for other gases, such as DO, CO
2, Rn and N
2O. This is done using Schmidt numbers (
Sci, dimensionless ratios of the kinematic viscosity of water and the diffusion coefficient of the gas in question). The reaeration rate of SF
6 (
KSF6) or Xe (
KXe) is related to other gases (
Ki) by [
1,
9,
17]:
where the
Sci for each gas is defined at a given temperature usually using temperature relations developed by Wanninkhof
et al. [
18] and Raymond
et al. [
1] and
j refers to the gas tracer.
The method used to estimate the reaeration coefficient here is significantly different from most methods reported in the literature, but similar to that used by Cook
et al. [
6]. This work uses a continuous gas tracer source of SF
6 and allows the concentration distribution to come to equilibrium. A more common approach is to use instantaneous point sources of a gas tracer paired with either a solute tracer or a second gas (e.g., [
9,
10,
11,
12]). The main advantages of using a continuous source are that the solution to the differential equation (1) is much simpler than the solution for a point source, only one gas tracer is needed and fewer samples need to be analyzed. Having a concentration in terms of distance downstream makes it easy to calculate the reaeration coefficient graphically. The slope of the line created when the log of the concentration is plotted
versus distance is equal to –
K/U, and the y-intercept is
C0. Most works present reaeration values normalized to a Schmidt number of 600, which is similar to CO
2 at 20 °C in seawater or oxygen at 17.5 °C (
KDO or
K2) in freshwater; we will also use this convention.
2.2. Tracer Injection
SF
6 and Xe were utilized as the deliberate gas tracer in these experiments for a number of reasons. SF
6 is: (1) non-reactive; (2) non-toxic [
19]; (3) man-made, so the background concentrations are negligible, especially away from urban areas; (4) detectable at very low levels using gas chromatography, so little gas needs to be released; and (5) relatively inexpensive. However, SF
6 emissions are being regulated in California, because it is a strong greenhouse gas (~24,000 times stronger than CO
2 on a per molecule basis over a 100-y period [
20]). Therefore, a second gas, Xe, was released during the Martis Creek experiment to evaluate its potential as a deliberate tracer for gas exchange. Xe, being a noble gas, is also non-reactive and non-toxic. The natural atmospheric concentration is low (87 ppt by volume) and well established. Xe can be measured at atmospheric abundance levels using membrane inlet mass spectrometry [
21], so little gas needs to be released. While the cost per liter is similar for the two gases, Xe is not a greenhouse gas and, therefore, not regulated.
Different methods were used to inject the gas tracers during the two experiments. During the September 2009, Sagehen experiment, an injection system (
Figure 2) was built and placed next to the stream. Approximately a 1:10 SF
6:N
2 mixture was created (so that the concentration would be within the calibration range of the analytical method) and released semi-continuously using a switcher valve set to switch every 30 s and bubble into the stream through a diffusion stone placed at the bottom of a small pool near mid-channel (see [
13] for the details of the injection device). Injection began the evening before the collection of the first samples and continued until after the collection of the final set. The injection rate of the SF
6 mixture was 0.34 mL/min for the first three sets and then increased to 0.68 mL/min for the final set.
Based on 100% dissolution of the bubbles and the injection rate, the initial concentrations of SF6 should have been 4.3 × 106 pmol/L for the Sagehen Creek experiment. Because the gas was being bubbled into the stream, most of it was lost to the atmosphere and only a small amount (less than 0.01%) of it actually dissolved into the stream. In the Martis Creek Experiment, tracer introduction via gas permeable silicon tubing achieved a gas introduction efficiency of 100%.
Figure 2.
The diagram of the sulfur hexafluoride (SF6) injectors used during the Sagehen Creek (top) and Martis Creek (bottom) experiments.
Figure 2.
The diagram of the sulfur hexafluoride (SF6) injectors used during the Sagehen Creek (top) and Martis Creek (bottom) experiments.
The Martis Creek injection began at 14:15 on 14 August 2012. Injection occurred through 1/8” inner diameter gas permeable silicon tubing fully submerged in the stream (
Figure 2) following methods similar to those of Cook
et al. [
6] and Clark [
22]. The tubing was coiled and weighted down with carabiners across the creek. The end of the tubing was knotted tightly, so that no large gas bubbles could escape (and none were observed). Copper tubing was attached to the submerged silicon tubing and fastened to the gas tracer tank on the creek bank. Separate setups of silicone tubing were used for the SF
6 and Xe tracers with 6 m of tubing submerged for SF
6 and 11 m for Xe. The Xe pressure in the silicone tubing was set to about 2 psi using a pressure regulator. A pressure gauge in line with the copper tubing recorded a constant pressure of 15 psi over the course of the 3-day injection in the N
2-SF
6 line. Once again, a 1:10 diluted SF
6 mixture was used during this experiment.
2.3. Creek Sampling
For both SF
6 experiments, eight or nine sampling locations were selected every 15–100 m downstream of the injection apparatus (
Figure 1). At each location, five samples were collected in pre-weighed 10 mL Vacutainers™ evenly distributed across the channel 5–10 cm below the air-water interface. The samples were collected by submerging the Vacutainers™, piercing the septa with a needle, until 2–5 mL of stream water were collected. During the Sagehen experiment, samples were collected during the morning, afternoon and evening of 11 September 2009. A fourth set was collected the following morning on 12 September 2009, after the injection rate was changed.
The Xe samples were collected at the same locations as the SF6 samples during the Martis Creek experiment. Duplicate samples were collected from the center of the stream by submersing an empty 40-mL glass vial upside down and filling it at 5–10 cm below the surface. The vial was capped under water. At two downstream locations (Martis Creek (MC) + 1 and MC + 8), additional cross-section samples were collected (in duplicate) at the left and right bank and in between the banks and the center.
During the Martis Creek experiment, sampling began about 1 h after the injection started. It was interrupted by a 2-h rain event that dropped considerable water onto the field site. While this precipitation event may have changed the creek flow, stream gauging shows that the discharge was the same on Days 2 and 3, so if any changes occurred, they were short lived. The first full set was collected 18 h after injection, with six complete sets collected over the next three days. Four sets were collected on 15 August 2012 (morning, afternoon with duplicates and evening), and one set each was collected during the mornings of 16 August 2012, and 17 August 2012. Xe samples were collected on the morning of 17 August 2012. Background sampling occurred at one location upstream of the injector in Martis Creek. This paper will discuss only the 17 August 2012, data, when both gases were analyzed.
2.4. Creek Measurements
To quantify channel geometry in Sagehen Creek, stream transect data were collected at 27 locations along the creek starting approximately 41 m upstream of the injection point and continuing approximately 550 m downstream. At each transect, the stream width and the depth every 20 cm (from the north bank to the south bank) were measured. In addition, the grain size of the streambed was descriptively characterized at each depth determination (for details, see [
23]). A United States Geological Survey (USGS) river gauging station located about 370 m downstream from the injection point provided continuous 15-min discharge data, which showed little variation and averaged 43 L/s during the experiment. The gauge also represents the place where the mean channel geometry changes. In the upper reach, the average measured depth, cross-sectional area and flow velocity were, respectively, 0.11 m, 0.41 m
2 and 0.11 m/s, while below the gauge, they were, respectively, 0.15 m, 0.49 m
2 and 0.09 m/s.
The flow velocity in Martis Creek was determined by gauging with an FP111 Global Water™ flow probe at four stations (MC − 1, MC + 2, MC + 5, and MC + 8). Cross-sectional data were also measured at these stations. The average depth, cross-sectional area, flow velocity and discharge were, respectively, 0.11 m, 0.20 m2, 0.29 m/s and 57 L/s. Flow velocity varied from a low average of 0.14 m/s at MC + 2 to a high average of 0.65 m/s at MC + 5; the average velocity at a given cross-sectional location did not vary significantly over the course of the experiment.
The channel gradient in Sagehen Creek was measured using a combination of GPS coordinates and a 1-m digital elevation model (DEM) provided by the Sagehen Creek Field Station that was created from aerial LiDAR flown in September 2005. The gradient was then calculated by dividing the measured center channel length by the difference in elevation based on the DEM and was found to be 0.0143; there was little change in slope between the upper and lower reaches. The channel slope for Martis Creek was determined in a similar fashion, but using Google Earth rather than ArcGIS and LiDAR elevations. It was determined to be 0.0145, very similar to Sagehen Creek, and it also did not vary substantially along the creek.
At Martis Creek, two deep pools along the experimental reach were sampled at three depths (top, middle and bottom) to assess vertical mixing. Little stratification was suspected, due to the stream’s generally shallow depth. One pool was ~3 m downstream of MC + 4 with a maximum depth of 0.56 m; the other was ~1 m upstream of MC + 7 with a maximum depth of 0.66 m. Temperature and oxygen measurements were also made using a YSI™ 556 multi-meter (Yellow Springs, OH, USA) and averaged 16.3 °C and 15.4 °C for the two pools. This temperature difference was likely due to the typical diurnal fluctuation found in most shallow creeks rather than an indication of the groundwater discharge of cooler water.
2.5. Laboratory Analysis
SF
6 samples were processed using the modified headspace method of Clark
et al. [
24], which employs Vacutainers™. In order to minimize contamination, the containers were kept separate from the injection equipment, during the transport to, from and while at the field sites. The laboratory procedure was as follows: (1) each sample was weighed in order to calculate the volume of water collected; (2) the headspace of each vial was filled with ultra-high purity N
2 to atmospheric pressure in the lab (about 1 atm); (3) vials were agitated by gently shaking in order to allow the gasses in the headspace to become well-mixed; and (4) gases in the headspace were then fed into a gas chromatograph system via displacement with water. SF
6 standards of known concentrations (1.95 parts per billion by volume (ppbv) and 10.0 ppbv) purchased from and certified by Scott-Marrin, Inc. Riverside, CA, USA) were run every ~10 samples to ensure accurate instrument calibration. Ultra-high purity nitrogen was used to flush the system of residual SF
6 between runs. The analytical uncertainty of the Vacutainer™ method is typically better than ±5%.
Xe samples were analyzed three days after collection on 20 August 2012, using a noble gas membrane inlet mass spectrometer (NG-MIMS) [
21]. The NG-MIMS system consists of a membrane inlet, a dry ice water trap, a liquid nitrogen carbon-dioxide trap, two getters, a gate valve, a turbomolecular pump and a quadrupole mass spectrometer equipped with an electron multiplier. Vials were opened, and the sample was withdrawn from the bottom of the vial through the membrane inlet for 5 min at 0.5 mL/min. The last two minutes of measurements were averaged to reduce measurement noise. Dissolved Xe concentrations are determined from measurements made every 10 seconds at mass over charge ratios of 124 and 132, by comparing against air equilibrated water (AEW) standards, with a laboratory determined uncertainty of ±8%. The linearity of the NG-MIMS was demonstrated across a wide range of noble gas concentrations [
21].
3. Results and Discussion
As expected, average SF
6 and Xe concentrations at each sampling site decreased downstream (
Table 1,
Figure 3 and
Figure 4). The standard deviation is used as a measure of horizontal mixing. When the deviation of bank-to-bank concentrations at each sampling location stabilizes, the tracer is assumed to be well-mixed across the creek. For all sets collected during the Sagehen Creek experiment, the standard deviation of the first sample location (SC + 1) ranges from 20% to 28% of the cross-sectional mean, while, with a few exceptions, the standard deviation for the rest of the samples is generally less than 5% of the mean, equivalent to analytical uncertainty. The first sample location is close to the injector (15 m downstream), and SF
6 had yet to become well mixed across the stream. By the second sampling location (44 m downstream), it had. The first samples were collected further downstream during the Martis Creek Experiment (69 m
vs. 15 m) and showed a lower standard deviation (<15%) across the creek. The standard deviation of Xe concentrations in the first (MC + 1) and last (MC + 8) cross-sections was 14% and 10%, respectively. The duplicate reproducibility was 9% for the Xe samples.
In Sagehen Creek, at the location immediately upstream (SC + 6) and downstream (SC + 7) of the USGS stream gauge (about 370 m downstream injector), the drop in concentrations of SF
6 is quite large over a very short distance. This drop indicates a higher reaeration rate, due to the waterfall created by the gauge, as is commonly observed at spillways [
25].
Furthermore, in the large pool immediately upstream of the gauge, the concentration suddenly increased for samples from Sets 1–3. After further inspection, the increases in concentration were coincident with a method change that required the use of different standards. It is important to note that after the offset in standards was found, the fourth set was analyzed using the same method (high standard) from the top to the bottom of the reach. In this paper, only the fourth set is discussed.
Table 1.
Average tracer concentrations and standard deviations (SD) at each cross-section during the 12 September 2009, Sagehen Creek (SC) and 17 August 2012, Martis Creek (MC) experiments.
Table 1.
Average tracer concentrations and standard deviations (SD) at each cross-section during the 12 September 2009, Sagehen Creek (SC) and 17 August 2012, Martis Creek (MC) experiments.
| Station | Distance (m) | [SF6] (pmol/L) | SD (%) | Station | Distance (m) | [SF6] (pmol/L) | SD (%) | [Xe]
(nmol/L) | SD (%) |
|---|
| SC + 1 | 16 | 118 | 27 | MC − 1 | | 0 | 0.0 | 0.46 | - |
| SC + 2 | 44 | 74.9 | 7.8 | MC + 1 | 69 | 315 | 20 | 43.5 | 14 |
| SC + 3 | 114 | 55.9 | 2.8 | MC + 2 | 139 | 325 | 2 | 40.2 | - |
| SC + 4 | 180 | 42.0 | 4.3 | MC + 3 | 257 | 270 | 3 | 34.1 | - |
| SC + 5 | 294 | 27.1 | 2.8 | MC + 4 | 352 | 244 | 2 | 29.9 | - |
| SC + 6 | 364 | 23.9 | 5.5 | MC + 5 | 481 | 203 | 2 | 24.4 | - |
| SC + 7 | 372 | 20.5 | 4.9 | MC + 6 | 641 | 169 | 2 | 19.9 | - |
| SC + 8 | 445 | 13.5 | 5.6 | MC + 7 | 798 | 125 | 3 | 13.5 | - |
| SC + 9 | 507 | 10.5 | 2.4 | MC + 8 | 964 | 111 | 3 | 10.8 | 10 |
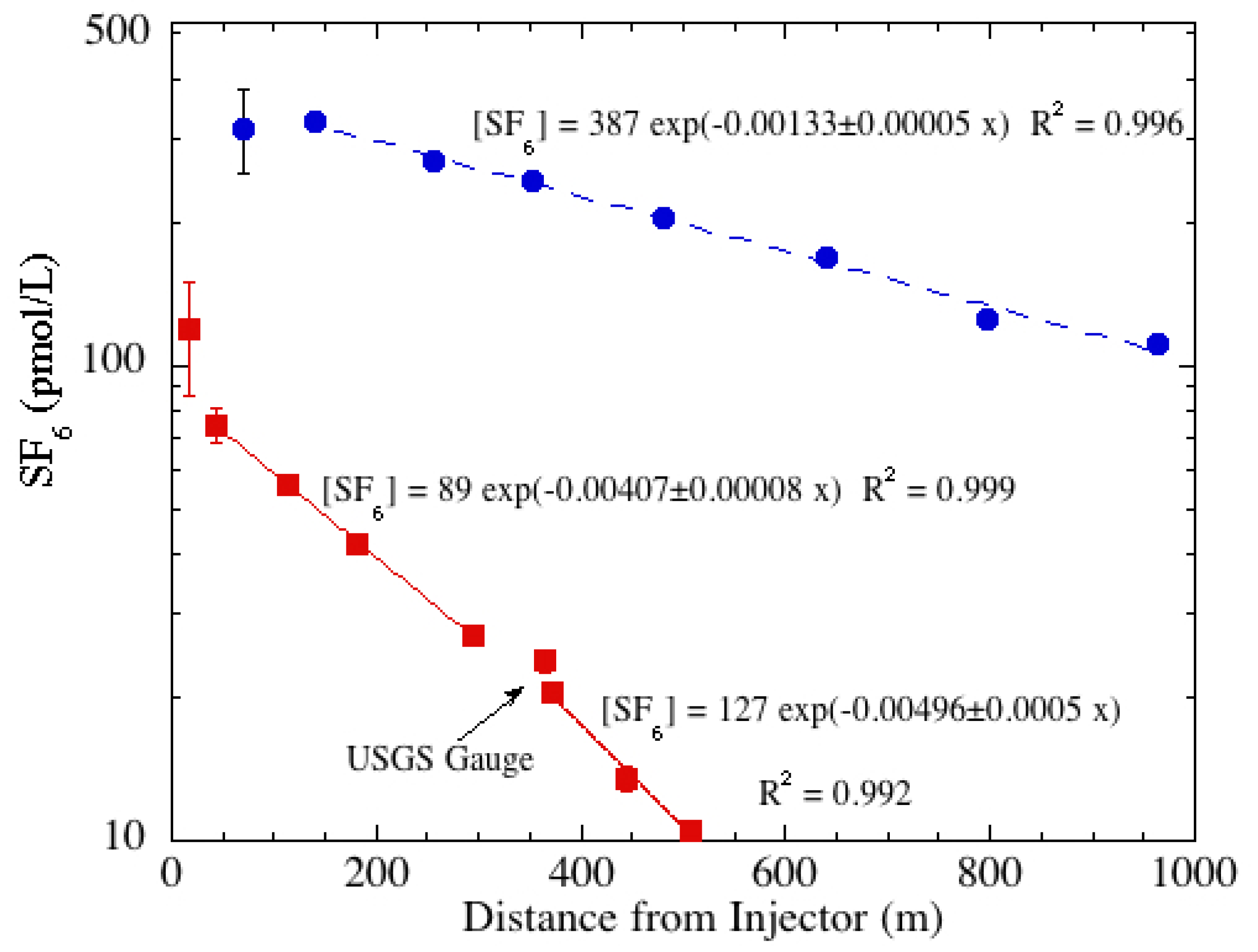
The semi-log plot of the concentration for Sagehen Creek shows that the slope (−
K/U) for the lower reach is generally steeper than that of the upper reach (
Figure 3). In fact, it is about 22% larger. Detailed analysis of the channel geometry, as noted above, revealed that the mean depth of the lower portion (0.15 m) was about 35% larger than the upper section (0.11 m).
Figure 3.
Semi-log plot of SF6 concentrations with least squares fit trend lines showing the different slopes (−K/U) for the upper and lower reaches in Sagehen Creek (red squares from 12 September 2009) and for Martis Creek (blue circles from 17 August 2012). In the equations, “x” is the distance downstream.
Figure 3.
Semi-log plot of SF6 concentrations with least squares fit trend lines showing the different slopes (−K/U) for the upper and lower reaches in Sagehen Creek (red squares from 12 September 2009) and for Martis Creek (blue circles from 17 August 2012). In the equations, “x” is the distance downstream.
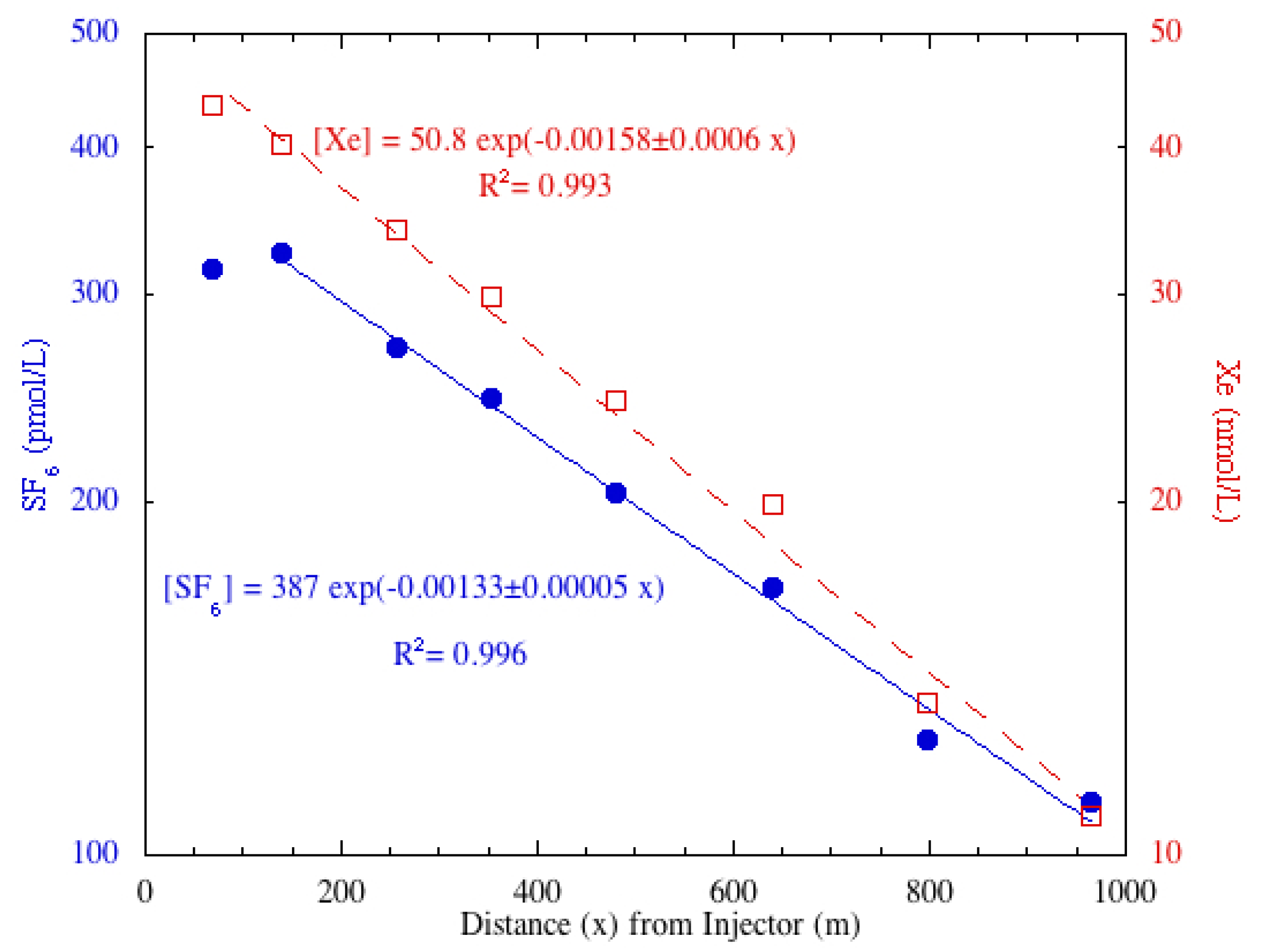
In Martis Creek, relatively more tracer degassing occurred per meter between stations MC + 6 and MC + 7 than elsewhere along the creek. A few locations of riffles with white water that accelerate gas transfer across the air-water interface were noted between these stations. A comparison of SF
6 and Xe tracers show more similarities than differences (
Figure 4). Both gases show reaeration, with SF
6 degassing at a faster rate. This is most apparent when examining the reaeration coefficient normalized for DO (
Table 2).
Reaeration rates are calculated from the semi-log plot of gas concentration
versus sampling distance (
Figure 3 and
Figure 4). The slope of the exponential best-fit equals −
K/U, where
K is the reaeration rate and
U is mean velocity.
Table 2 presents mean stream characteristics and reaeration rates by sampling date and location.
Figure 4.
Semi-log plot of SF6 (filled blue circles) and Xe (open red squares) concentrations with trend lines for the Martis Creek 17 August 2012, sampling event. The station closest to the injector was not used for the least squares fit and that only center samples were used for calculating the Xe distribution. In the equations, “x” is the distance downstream.
Figure 4.
Semi-log plot of SF6 (filled blue circles) and Xe (open red squares) concentrations with trend lines for the Martis Creek 17 August 2012, sampling event. The station closest to the injector was not used for the least squares fit and that only center samples were used for calculating the Xe distribution. In the equations, “x” is the distance downstream.
Table 2.
Reaeration (K) values for the gas tracers (KSF6 or Xe ) and normalized to dissolved oxygen (DO) (KDO) using temperature-dependent Schmidt numbers of 1875 and 1192 for SF6 (Sagehen and Martis Creek), 1230 for Xe (Martis Creek) and 600 for DO (Sagehen and Martis Creek) and Equation (4).
Table 2.
Reaeration (K) values for the gas tracers (KSF6 or Xe ) and normalized to dissolved oxygen (DO) (KDO) using temperature-dependent Schmidt numbers of 1875 and 1192 for SF6 (Sagehen and Martis Creek), 1230 for Xe (Martis Creek) and 600 for DO (Sagehen and Martis Creek) and Equation (4).
| Location | Sampling Date | Tracer | Discharge (L/s) | Velocity U (m/s) | Depth (m) | −K/U (m−1) | KSF6 or Xe (day−1) | KDO (day−1) |
|---|
| Sagehen-Upper | 12 September 2009 | SF6 | 43 | 0.11 | 0.11 | 0.00407 | 34 | 61 |
| Sagehen-Lower | 12 September 2009 | SF6 | 43 | 0.09 | 0.15 | 0.00496 | 37 | 66 |
| Martis Creek | 17 August 2012 | SF6 | 57 | 0.29 | 0.11 | 0.00133 | 33 | 47 |
| Martis Creek | 17 August 2012 | Xe | 57 | 0.29 | 0.11 | 0.00156 | 40 | 57 |
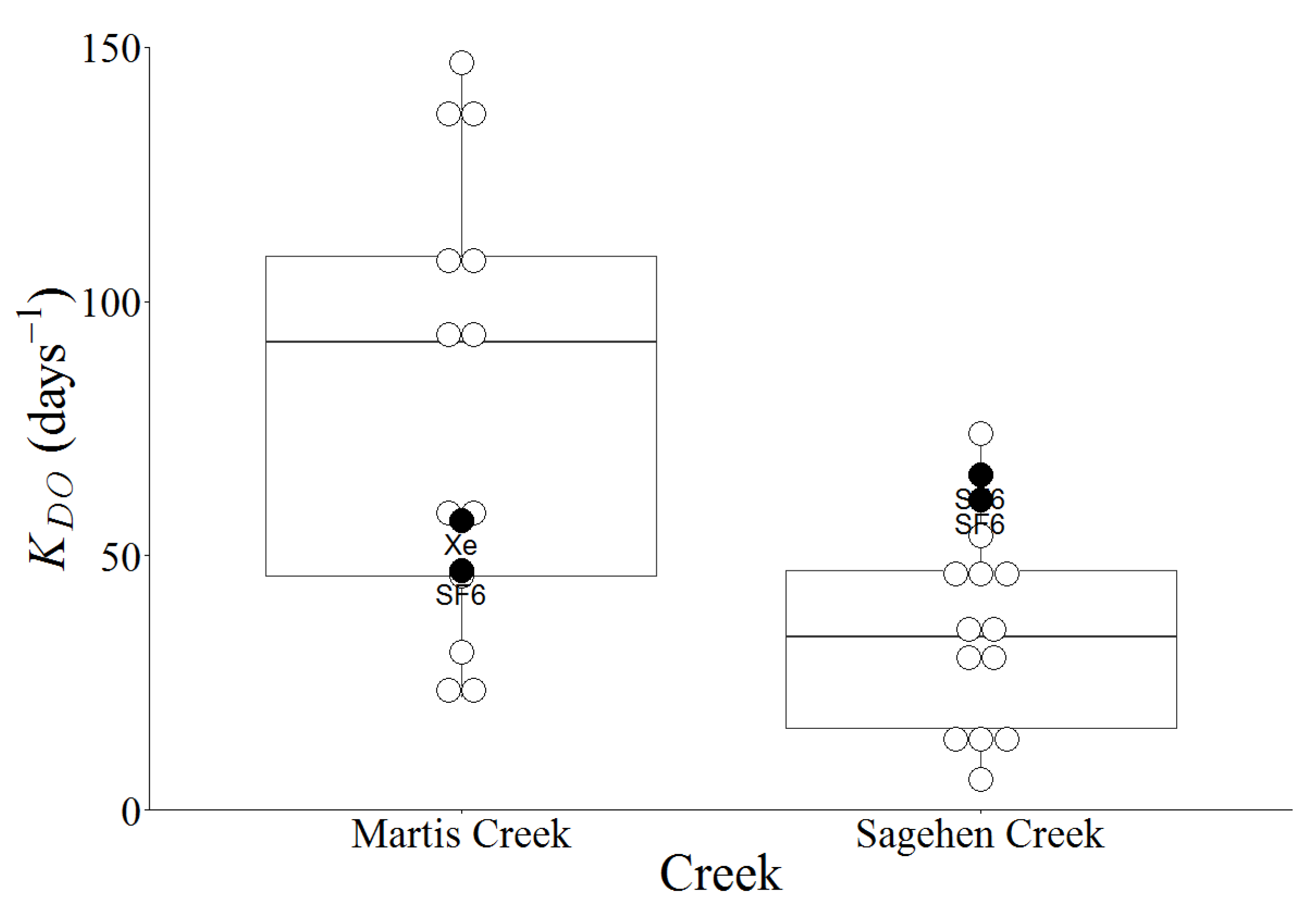
For comparison,
KDO values for Sagehen and Martis Creeks were calculated using empirical relationships for the experimental reaches (
Table 3,
Figure 5). Predictive equations show a very wide range of values for
KDO (6 to142 day
−1) with a mean of 43 ± 34 day
−1 for Sagehen Creek and (22 to 544 day
−1) with a mean of 117 ± 131 day
−1 for Martis Creek. In both creeks, the Thyssen-Jeppesen [
26] relationship appears to be an outlier. Removing that relationship from the data set reduces the range and mean to 6–74 day
−1 (35 ± 20 day
−1) and 22–147 day
−1 (84 ± 48 day
−1), respectively, for Sagehen and Martis Creeks.
Table 3.
Predictive equations for reaeration (
KDO) compiled by Raymond
et al. [
1] and Cox [
4]. See these publications for the citations to the original papers. Please note: Raymond
et al. [
1] models calculate gas transfer velocities (m day
−1) rather than reaeration coefficients, so the equations listed have been converted, and only the equations that matched their metadata set with a
R2 > 0.7 are presented.
Table 3.
Predictive equations for reaeration (KDO) compiled by Raymond et al. [1] and Cox [4]. See these publications for the citations to the original papers. Please note: Raymond et al. [1] models calculate gas transfer velocities (m day−1) rather than reaeration coefficients, so the equations listed have been converted, and only the equations that matched their metadata set with a R2 > 0.7 are presented.
| Reference | Predictive Equation | Sagehen Creek KDO (day−1) | Martis Creek KDO (day−1) |
|---|
| [27] | KDO = 3.93U0.5 H−1.5 | 28 | 58 |
| [28] | KDO = 5.026UH−1.67 | 16 | 59 |
| [29] | KDO = 5.35UV0.67 H−1.85 | 54 | 139 |
| [30] | KDO = 5.5773U0.607 H−1.689 | 47 | 109 |
| [31] | KDO = 3170 S | 45 | 46 |
| [32] | KDO = 22,700 SU | 32 | 95 |
| [33] | KDO = 8784S0.93U0.734H−0.42 | 74 | 147 |
| [34] | KDO = 596(SU) 0.528Q−0.136 | 12 | 22 |
| [35] | KDO = 23.04(1 + 0.17 F 2)(US0.375)H−1(1.0212)(T−20) | 16 | 27 |
| [36] | KDO = 23,000(1 + 0.17 F)2.66S1.13H−0.6 | 142 | 544 |
| [1] #1 | KDO = 5037 (SU)0.89D−0.46 | 34 | 107 |
| [1] #2 | KDO = 5937 (1−2.54 F)(SU)0.89D−0.42 | 37 | 92 |
| [1] #7 | KDO = 4725(SU)0.86Q−0.14 D−0.34 | 48 | 135 |
| | Mean and Standard Deviation * | 43 ± 34 | 117 ± 131 |
| SF6 tracer | | 61, 66 † | 47 |
| Xe tracer | | | 57 |
Despite the fact that most predictive equations produced wildly differing reaeration rates, underestimation is better than overestimation when considering wastewater discharge to streams. Over predictions could lead to assumptions of a higher level of resiliency and less stringent and potentially dangerous management strategies. Under-predictions, on the other hand, would lead to overly precautious management, which, while inaccurate, would not threaten stream health.
Figure 5.
A comparison of the field
KDO (filled circles) listed in
Table 2 with the model predicted
KDO (open circles) listed in
Table 3, with the exception that the Thyssen-Jeppesen [
36] model values are not shown or used in the calculation of median or quartile values.
Figure 5.
A comparison of the field
KDO (filled circles) listed in
Table 2 with the model predicted
KDO (open circles) listed in
Table 3, with the exception that the Thyssen-Jeppesen [
36] model values are not shown or used in the calculation of median or quartile values.
4. Implications and Conclusions
Sagehen and Martis Creeks are very similar in terms of their morphology (both have pool and riffle characteristics and similar channel slopes) and hydrology (with much of the late summer flow derived from groundwater discharge and a similar mean depth at the time of the experiments). As shown in
Table 2, the discharge and current velocity in Martis Creek were higher (respectively, 57
vs. 43 L/s and 0.3
vs. 0.1 m/s). The SF
6 tracer experiments revealed that the reaeration coefficients corrected to a Schmidt number of 600 (
KDO) differed substantially, with Sagehen Creek (>60 day
−1) being larger than Martis (<50 day
−1). Interestingly, the results of the Xe tracer experiment (57 day
−1) agree better with the SF
6 result from Sagehen Creek (61–66 day
−1) than from Martis Creek (47 day
−1). This difference between the SF
6 and Xe results could be due to the bubble-enhanced gas transfer [
26] that generally removes lower solubility gases faster (SF
6 is less soluble than Xe).
Most empirical formulas of reaeration rates, expressed as KDO, rely on an assessment of the current velocity. The actual reaeration rate over a stretch of river or stream is directly observed as a change in tracer concentration. Established empirical formulas of KDO using stream characteristics did a poor job of predicting KDO for the two creeks. Although some agree with the field experiments in either Sagehen or Martis Creek, no one relationship worked well for both of them.
Dissolved oxygen is one of the most important indicators of a stream’s biologic potential and health. The United States Environmental Protection Agency’s criteria for dissolved oxygen are designed to protect freshwater aquatic life under “worst case conditions”; the suggested DO limit expressed as a seven-day mean minimum for cold water is 4.0 mg/L [
37]. In this study, DO concentrations in Martis Creek ranged between 5 mg/L and 9 mg/L throughout the summer. Considering that minimum criteria estimations are conservative, DO content in this stream reach is sometimes close to threatening levels. This exemplifies the need for accurate measurements of reaeration to ensure a healthy aquatic environment. Future expansion of development in the Tahoe and Truckee areas could also increase biological oxygen demand on the creek and lead to noncompliance.
With mounting concerns and subsequent regulations of greenhouse gasses, the future of SF
6 as a hydrologic tracer is in doubt. Noble gasses, such as helium and Xe, are on their way to replacing SF
6, and we demonstrate that Xe is a viable replacement option for reaeration studies, as shown by others [
12]. Future SF
6 use may depend on more efficient injection methods. Traditional bubbling results in an immediate loss of most of the gas to the atmosphere, requiring more SF
6 for water tagging. The semi-permeable silicon tubing, used in the Martis Creek study, is very promising in this regard and results in very high injection efficiency.