1. Introduction
Water is an indispensable input for industrial production and human existence. Currently, people are increasingly concerned about their health, and their interest in the safety of drinking water has increased. Some people prefer purchasing bottled water and using water-treatment equipment to drinking tap water. These actions can be interpreted as preventive behavior against the decline in tap water quality. Since such behavior entails defensive expenses and deteriorates the level of welfare by diminishing real income, the government attempts to provide a policy to improve the quality of tap water.
Policymakers in Pusan, the second largest city in Korea, are currently addressing the likely effectiveness of improving tap water quality. They plan to implement a new project of improving tap water quality. This can be carried out by several instruments such as advanced water treatment facilities, new pipes and monitoring systems. After the policy is implemented, people do not have to use water-treatment equipment at home and they can drink clean and safe water directly from the tap. If adopted, costs of the improvement will be incurred now, with the expectation that inhabitants in Pusan will reap the ensuing benefits. Employing economic efficiency as the sole criterion, the policy to improve tap water quality should be evaluated in a conventional cost-benefit analysis context. In other words, policy implications of whether to improve tap water quality could, in principle, be deduced from an examination of costs and benefits associated with such actions. Moreover, an important first step in fostering a productive debate over whether to improve tap water quality is a better understanding of its benefits and costs.
Such situations require researchers to provide policy-makers with accessible and responsible information on the economic benefit of improving tap water quality. In order to make an informed public decision, some information on the economic benefits would be useful. This study attempts to addresses a component of the benefits that such an analysis would consider: the benefits of tap water quality improvement. To this end, we here report the findings of the application of a contingent valuation (CV) to quantify the economic benefit of tap water quality improvement to households.
The principle that is the cornerstone in measuring the benefits from a proposed policy is the concept of consumer’s willingness to pay (WTP) for the policy [
1,
2]. This concept represents how much people would be willing to pay for tap water quality improvements and can be interpreted as the value they attach to tap water quality.
To derive the value of improved tap water quality and ascertain the benefits from such improvement, we will adopt a survey approach—the CV method. The CV method can be used to estimate economic values for all kinds of ecosystem and environmental services. It can derive and estimate both use and non-use values. The existence of non-use value is very important for the environmental goods such as water and air. Estimating observed costs does not reflect this aspect. Moreover, the most widely used technique in measuring the economic benefits of tap water quality improvement in the literature is CV method. Thus, we have chosen CV method and estimated the economic benefits by applying the method.
CV method involves constructing a hypothetical market or referendum scenario and uses questionnaires in a survey to elicit respondents’ preferences for the policy on tap water quality improvements by determining their WTP [
3]. Respondents utilize the established hypothetical market to state their WTP or vote for or against the new policy at a particular price. For example, Brox
et al. [
4] estimated the WTP for residential water quality improvements in the Grand River watershed in the province of Ontario, Canada. Koss and Khawaja [
5] and Barton [
6] employed an identical CV method to derive WTP. In addition, Atkins
et al. [
7] applied CV and decision tree analysis to investigate public preferences for water quality improvements. From these studies, the validity of using CV method has been reinforced.
Even though there are many studies on improvements in water quality—for example, Atkins
et al. [
7], Barton [
6], Brox
et al. [
4], Gupta and Mythili [
8], and Hayes
et al. [
9]—few studies analyze consumers’ preferences for tap water quality in Korea. The level of WTP can be differentiated among regions. Case studies for many regions are needed and the results of the studies need to be compared. In this study, we focus on measuring the economic benefits of tap water quality improvement in Pusan, Korea.
One of the most evident advantages of such improvement is that people can drink clean and safe water directly from the tap without using water-treatment equipment. In particular, this study employs a one-and-one-half bound (OOHB) dichotomous choice (DC) CV model for measuring statistical efficiency. Furthermore, in CV, respondents who say “no” to the given bids can be divided into two groups: those who really have a zero WTP and those who have a positive WTP that is less than the second lowest bid. To address this aspect, this study attempts to apply the spike model suggested by Kriström [
10]. The spike means the proportion of the respondents that state zero WTP.
The remainder of this paper is organized in the following manner: In
Section 2, we explain the method employed in this study and the methodological issues. In
Section 3, we discuss the WTP model. In
Section 4, we present an explanation and discussion of the results. In
Section 5, we provide some concluding remarks.
2. Methodology
2.1. Measurement Method: CV
As mentioned above, we measure the economic benefits of improvements in tap water quality by employing the CV method. CV is a survey-based value elicitation approach and queries consumers in systematic ways to estimate their WTP for a proposed policy or environmental management program. Moreover, CV is enormously flexible in that it can be used to estimate the economic value of various goods and services [
11]. By applying the CV method, it is possible to recover nonusage or existence values that cannot be assessed through market mechanisms. The fact that the CV method is based on asking people questions, as opposed to observing their actual behavior, is the source of both its greatest strengths and its greatest weaknesses.
Although there can be some controversies, a blue-ribbon National Oceanic and Atmospheric Administration (NOAA) Panel concluded that the CV method can produce estimates that are sufficiently reliable to be the starting point for administrative and judicial determinations and presented several recommendations [
12]. The validity and accuracy of a CV study is enhanced if people are familiar with the good to be valued, if professional interviewers are used, and if other conventions suggested by the NOAA Panel are followed. Our study meets all these conditions, which are discussed below in detail.
2.2. Sampling and Survey Methods
A professional polling firm conducted the survey to gather households’ WTP for tap water quality improvement and its characteristics by drawing a random sample of the population. The sampling method of this survey followed the convention of a household survey. The survey, administered to heads of households or housewives whose ages ranged from 20 to 65 years in Pusan in 2010, yielded 400 usable interviews. The unit of the CV survey is household rather than individual. The head of household or housewife can respond responsibly to any valuation questions representing his/her household. This is because he/she is in charge of a family and pay utility bills. A stratified random sampling strategy was adopted for creating representative samples of the designated area. Moreover, we chose to use face-to-face interviews with well-trained interviewers for the CV survey rather than telephonic interviews or e-mail, because such interviews provide the greatest scope for detailed questions and answers [
13,
14]. The well-trained interviewers are actually enumerators. They are people who are adequately trained by professional polling firms regarding guidelines of surveys and are able to elicit responses from respondents. They are the best people to engage respondents and promptly obtain desired information.
2.3. Survey Development
Before beginning the survey design, we reviewed the available technical information on the tap water quality. The survey instrument (questionnaire) was set up with the assistance of experts at the polling firm. Questionnaires should be pre-tested before a survey is conducted. This pre-testing was done using a small focus group (30 persons) assembled to discuss their understanding of and reaction to the questions prior to the main survey. As a result, the questionnaire and visual aids made it easier to understand the general information about the improvement, and were simplified because participants’ perceptions of tap water quality were high. The final version reflected this focus group’s input as well as advice from experts at the survey firm employed to organize the fieldwork. The survey instrument listed a brief explanation of the purpose and contents of the interviews, and clarified the context of the policy decision by providing general background information on the tap water quality improvement program in Pusan.
2.4. Survey Structure
In designing a CV survey, a scenario should offer respondents information about the characteristics of a specific good and the context that will meet the requirements of understandability, plausibility, and meaningfulness so that it can enhance the credibility of the survey and make it more likely to produce reliable results. The questionnaire format consists of (i) introductory questions like respondents’ perception after general background information on tap water quality; (ii) a monthly WTP question for improvement in tap water quality; and (iii) questions seeking household information.
Before the key WTP questions were asked, the questionnaire was used to attempt to construct the general situation of the contingent market. It did so by providing general background information on the tap water quality. Respondents were then asked whether they were satisfied with current tap water quality. They also were asked how important improving tap water quality was to them as compared with other environmental problems such as air pollution, natural resources damage or waste problems (i.e., potential substitute public goods). Additionally, respondents’ subjective judgments about tap water functions were checked. Respondents were specifically presented with substitutes for the goods to be valued in this study, which may result in an overestimation of the true WTP. In other words, other public investment projects proposed were considered as possible substitutes.
We also presented a detailed description of what is known about the likely effects of the hypothetical policy change and, importantly, what is likely to happen if nothing is done. Among other things, this description could spell out the beneficial effects expected to result from improving tap water quality and where and when those benefits will occur. Moreover, this study strove to present the sample households with the best information possible about where the positive effects of tap water quality improvement would be felt by providing several well-illustrated visual cards. It explained, for example, how a tax on various products would be transferred into increased prices for clothes, electricity, and other products not initially subject to the tax, but making use of the taxed products as inputs. Finally, household information included monthly recreational and environmental expenditure, income, age, education, gender, membership of environmental organizations, occupation, and so on.
2.5. Elicitation Method
The elicitation format employed in this study is a DC question, which is in accordance with Arrow
et al. [
12]. Generally, the DC question format is divided into the single-bounded DC (SBDC) question and the double-bounded DC (DBDC) question formats. The SBDC asks the respondent only one DC question, and DBDC presents each respondent with a sequence of two bids and asks the question twice. The DC question means a question that the respondents can identify their WTP by “yes” or “no” answer. Although each format has both merits and demerits, the SBDC has low statistical efficiency, and the DBDC may manifest a correlation between the responses to the two bids. McFadden [
15], Bateman
et al. [
16], and Cooper
et al. [
17] have explicitly dealt with this issue.
To solve this problem, we adopted the OOHBDC question format, which is presented by Cooper
et al. [
17]. In the OOHBDC format, the interviewer randomly chooses between lower and upper bids as an initial value at which to elicit the respondent’s WTP. The lower and upper bids are determined by the result of a pre-test for a focus group. The sets of bids used in this study were (1000; 3000), (2000; 4000), (3000; 5000), (4000; 6000), (5000; 7000), (6000; 8000), (7000; 9000), (8000; 10,000), (9000; 11,000) and (10,000; 12,000)—the first element of each set is the lower bid and the second corresponds to the upper bid.
2.6. Payment Vehicle
The payment vehicle used for this study was water bills, with which most respondents are likely to be familiar. Several previous studies such as Saz-Salazar
et al. [
18] and Ramajo-Hernández and Saz-Salazar [
19] also used water bills as a payment vehicle. The WTP question format asked each household to pay a particular amount of money each month. In this case, the individual had to decide merely whether he or she believed that the value of the program was at least worth this price. The WTP question was:
“Most people usually purchase bottled water or use water-treatment equipment for drinking water. Few people drink tap water; however, they feel unpleasant about the quality of tap water. The government plans to promote a new project to improve tap water quality. People can drink clean and safe water directly from the tap without using water-treatment equipment when the project is implemented. The improvement goal for the proposed policy to be evaluated is to have no future water quality incidents issued in Pusan, using a variety of policy instruments. The main instruments include: introducing advanced tertiary treatment facilities, changing old water-pipe, and installing automatic water quality measurement devices. Would your household be willing to pay a higher amount in the monthly water bill for tap water quality improvement, provided that the success of the improvement is guaranteed? If the majority of the people are not willing to pay the cost of the improvement, tap water quality will not be improved. However, if the majority of the people agree to pay the cost, tap water quality would be improved.”
With regard to the definition of costs that the households themselves were likely to bear, we used a provision point mechanism. Respondents were told that:
“The amount you indicate will tell us what it is really worth to your household to have the improvement implemented. If the improvement actually costs less than people are willing to pay, you would only have to pay what it would cost. If the improvement turns out to cost more than what people are willing to pay, it would not be implemented.”
The information given to respondents on all aspects of the hypothetical market and on the good being valued constituted the model framework.
4. Estimation Results
4.1. WTP Responses
Based on the interviewers’ comments, the WTP elicitation procedures were well within the respondents’ abilities.
Table 1 presents the distribution of responses to the valuation question and indicates the total number of respondents who stated that they would be willing to pay for the tap water quality improvement at each bid level, ranging from KRW 1,000 to KRW 12,000 per month. The number of respondents who did not want to pay any amount of money was 287 (71.8% of the sample). This fact justifies the application of the spike model. A considerable portion of zero responses could be handled as protest bids rather than true zero bids. However, we treat all zero responses as true zero bids so as to conservatively estimate the economic benefits of tap water quality improvement since the improvement requires additional financial burden on Pusan residents.
Table 1.
Distribution of responses by the bid amount.
Table 1.
Distribution of responses by the bid amount.
| Bid amount (KRW) | From the lower bid to the upper bid | From the upper bid to the lower bid |
|---|
| yes–yes | yes–no | no–yes | no–no | yes | no–yes | no–no–yes | no–no–no |
|---|
| 1,000/3,000 | 4 | 2 | 0 | 14 | 1 | 7 | 0 | 12 |
| 2,000/4,000 | 5 | 2 | 2 | 11 | 0 | 2 | 1 | 17 |
| 3,000/5,000 | 2 | 4 | 1 | 13 | 1 | 0 | 2 | 17 |
| 4,000/6,000 | 5 | 0 | 2 | 13 | 0 | 0 | 4 | 16 |
| 5,000/7,000 | 5 | 2 | 0 | 13 | 1 | 3 | 4 | 12 |
| 6,000/8,000 | 0 | 2 | 1 | 17 | 1 | 1 | 1 | 17 |
| 7,000/9,000 | 3 | 2 | 4 | 11 | 1 | 0 | 2 | 17 |
| 8,000/10,000 | 4 | 2 | 1 | 13 | 2 | 0 | 3 | 15 |
| 9,000/11,000 | 4 | 1 | 3 | 12 | 0 | 0 | 3 | 17 |
| 10,000/12,000 | 3 | 0 | 4 | 13 | 0 | 0 | 3 | 17 |
4.2. Estimation Results of the Models
The conventional model in Equation (2) and the spike model in Equation (6) were estimated by the maximum likelihood estimation method. The conventional model assumes that the additional follow-up question has not been used.
Table 2 describes the estimation results. All the parameters in the spike model are statistically significant at the 1% level, while the constant term in the conventional model is not. The coefficient for the bid amount is negative. This means that a higher bid makes a “yes” response less likely. Welfare measures are also provided in
Table 2. To estimate the mean WTP, we used Equation (4) in the conventional model and Equation (9) in the spike model. Several interesting findings emerge from these results.
The conventional model gives an estimated mean of KRW −2,182 and an estimated standard error of 1134. The
t-value is calculated to be −1.92. Accordingly; hypothesis that the mean WTP is statistically different from zero can be rejected at the 5% level and it is concluded that mean WTP is not different from zero. However, the mean WTP in the spike model, computed as KRW 2,124, is highly significant, as evidenced by the standard error of 286 and the
t-value of 7.43. Moreover, the Monte Carlo simulation technique of Krinsky and Robb [
27] was used with 5000 replications to get the 95% confidence intervals for the point estimates of mean WTP. The confidence interval of the mean in the spike model is quite tight, while that in the conventional model is not. Consequently, it can be concluded that the information at zero drastically decreases the standard error of the mean and makes the confidence interval fairly tight in this application. These results strongly support the application of the spike model when estimating WTP. Thus, we hereinafter deal with spike model only.
Table 2.
Estimation results of the conventional and spike models.
Table 2.
Estimation results of the conventional and spike models.
| Variables | Conventional model e | Spike model e |
|---|
| Constant | −0.480 (−2.46) | −0.933 (−8.41) # |
| Bid amount a | −0.220 (−7.02) # | −0.156 (−8.87) # |
| Spike | | 0.718 (31.90) # |
| Number of observations | 400 | 400 |
| Log-likelihood | −238.28 | −363.190 |
| Wald statistic: b | 174.04 # | 1017.87 # |
| (p-value) | (0.000) | (0.000) |
| Mean WTP | KRW −2,182 (USD −2.1) | KRW 2,124 (USD 2.2) |
| t-value c | −1.92 | 7.43 # |
| 95% confidence interval d | −5062 to −373 | 1719 to 2689 |
| 99% confidence interval d | −4490 to −560 | 1652 to 2807 |
4.3. Estimation Results of the Spike Model with Covariates
One can examine how characteristics of the respondents or their households affect the likelihood that they will approve of the tap water quality improvement policy. It is also common to test for internal consistency (theoretical validity) in CV studies by estimating the model with covariates. If we would estimate the model with covariates, in former equations,
a is simply replaced with
![Water 05 01638 i008]()
where
xi is a vector of covariates and
β is a vector of corresponding parameters to be estimated.
Definitions and sample statistics of variables used in this study are presented in
Table 3. We will use five variables as covariates. The variables of ODOR, GENDER, AGE, EDUCATION, and INCOME are defined as dummy for the respondent’s experiencing chlorine odor while using tap water (1 = Yes; 0 = No), gender of the respondent (1 = Male; 0 = Female), dummy for the respondent’s age being larger than forty five (1 = Yes; 0 = No), dummy for educational level of the respondent in years being larger than twelve (1 = Yes; 0 = No), and monthly household total income after tax deduction (Unit: million Korean won).
Table 4 shows the estimation results of the spike model that includes covariates, or variables other than the bid amount, that one might expect to affect the likelihood of voting “yes”. We included ODOR, GENDER, AGE, EDUCATION, and INCOME covariates. All the coefficient estimates for the variables are statistically significant at the 5% level. Moreover, using the Wald statistic, the estimated equation is statistically significantly different from zero at the 1% level. As in the model without covariates, the coefficient for the bid amount is negative and significantly different from zero. On the whole, respondents accepted the contingent market and were willing to contribute a significant amount, on average, per household. This willingness varies according to some individual characteristics.
Table 3.
Definitions and sample statistics of the variables.
Table 3.
Definitions and sample statistics of the variables.
| Variables | Definitions | Mean | Standard deviation |
|---|
| ODOR | Dummy for the respondent’s experiencing chlorine odor while using tap water (1 = Yes; 0 = No) | 0.263 | 0.441 |
| GENDER | Gender of the respondent (1 = Male; 0 = Female) | 0.500 | 0.501 |
| AGE | Dummy for the respondent’s age being larger than forty five (1 = Yes; 0 = No) | 0.363 | 0.481 |
| EDUCATION | Dummy for educational level of the respondent in years being larger than twelve (1 = Yes; 0 = No) | 0.520 | 0.500 |
| INCOME | Monthly household total income after tax deduction (Unit: million Korean won a) | 2.980 | 1.158 |
Table 4.
Estimation results of the spike model with covariates.
Table 4.
Estimation results of the spike model with covariates.
| Variables a | Estimates | t-value d |
|---|
| Constant | −1.247 | −3.71 # |
| ODOR | −0.646 | −2.33 * |
| GENDER | 0.603 | 2.55 * |
| AGE | −0.563 | −2.20 * |
| EDUCATION | −0.926 | −3.53 # |
| INCOME | 0.271 | 2.89 # |
| Bid amount b | −0.165 | −8.95 # |
| Number of observations | 400 | |
| Log-likelihood | –350.56 | |
| Wald statistic c | 182.67 # | |
| (p-value) | (0.000) | |
Respondents who report experience of chlorine odor while using tap water are less likely to pay for tap water quality improvements than others, other things equal. This suggests an important point. It can be interpreted that the chlorine odor is one of the fatal elements and people who experienced the chlorine odor regard tap water quality improvements with skepticism. They may prefer other preventive behaviors such purchasing bottled water and using water-treatment equipment to drinking tap water. Male respondents are more willing to pay than female respondents. As respondents are more aged, so their likelihood is lower. More highly educated respondents are less willing to pay than less well-educated respondents. We can conclude that the respondent’s education level makes a negative effect on the likelihood of voting “yes” to a given bid. Judging from the interviewers’ comments, a number of well-educated persons thought that they have already paid more taxes than the money needed in tap water quality improvement and denied saying “yes” to a given bid. Finally, the household income is strongly positively related to the likelihood.
4.4. Expanding Sample Estimates of the WTP to the Population Value
The individual estimates of the mean WTP for the improvement in tap water quality can be used to estimate the aggregate benefits in the designated area. Arrow
et al. [
12] has identified this property as one of the significant issues in using CV results. When expanding the sample to the population, one critical concern is the external generalization of the sample values to the population. This is dependent on the representativeness of the sample frame and the survey response rate. As described earlier, the sample frame was a random sample of the households selected by a professional polling firm. The sample response rate from face-to-face interviews was almost 100%. Thus, our data appear to provide precise figures for the social value of improvement in tap water quality. We expand the sample WTP estimate for the model without covariates to the population value here. According to the Korea Statistical Service [
28], there were 1,223,884 households in Pusan in 2010. Multiplying this by the mean WTP and annualizing it yields a total of approximately KRW 31.2 billion (USD 32.1 million), as shown in
Table 5.
Table 5.
Annual willingness to pay (WTP) of tap water quality improvement in Pusan, Korea.
Table 5.
Annual willingness to pay (WTP) of tap water quality improvement in Pusan, Korea.
| Monthly household mean WTP | Annual benefits to Pusan residents |
|---|
| Value | 95% confidence interval |
|---|
| KRW 2,214 | KRW 31.2 billion
(USD 32.1 million) | KRW 25.25 to 39.49 billion a
(USD 25.97 to 40.62 million) |
4.5. Discussions of the Results
Three interesting observations emerge from the results of our study. The first observation is concerned with the elicitation method. The OOHBDC question format, used to reduce the potential for response bias in multiple-bound formats such as SBDC and DBDC while maintaining much of the efficiency, was successful in eliciting WTP values for the improvement in water quality. To the best of the authors’ knowledge, this study is the first one to apply OOHBDC CV model to tap water management-related issues.
Second, we combined the OOHBDC question format with the spike model to deal with zero WTP data. Applying the OOHBDC spike model to our study was a successful strategy. This is because the conventional OOHBDC model produces statistically insignificant mean WTP estimate and even negative value, but the OOHBDC spike model gives us statistically significant mean WTP estimate and fitted our data well. Thus, the message of our paper is all the more useful since it vividly portrays the usefulness of the OOHBDC spike model suggested by us here.
Finally, the results are useful starting points in understanding the possible indication of the WTP of tap water quality improvement. This study illustrates that there is a statistically significant nonmarket WTP for improvement in tap water quality. The analysis provides a preliminary indication of the benefits of such improvement, which can be used in conventional cost–benefit analysis. The results can offer a useful framework for organizing information on the consequences of actions for addressing the issue of improvement in tap water quality. This valuation information should be considered by the Pusan local government in its decision regarding whether to undertake an improvement in tap water quality and how much money it should invest in the process.
Three extensions of the framework employed in our study could be fruitful. First, we did not implement a cost-benefit analysis on the tap water quality improvement project in Pusan because of a number of complications involved in the cost data on the improvement. However, as the second stage of the study, it would be useful to conduct the analysis in order to obtain at least a preliminary evaluation of the proposed project for the local governmental policy options. Second, we analyzed the OOHBDC spike model in a parametric setting assuming logistic distribution as in Equation (3). However, the application of the model without assuming any functional form of the distribution as a non-parametric approach gives us more robust values that can be used in policy analysis [
29]. Third, we can discuss how variations in the type of water quality improvements affect the results of the economic studies and check the sensitivity to changes in the content of the question posed to the respondents.
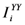 ,
,  ,
,  ,
, 
 , and
, and  , respectively, such that:
, respectively, such that:
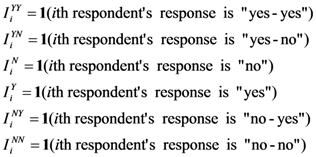
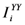 = 1(ith respondent’s response is “yes–yes”) means that if the response of ith respondent is “yes” for the first question and “yes” for the second question, the value of
= 1(ith respondent’s response is “yes–yes”) means that if the response of ith respondent is “yes” for the first question and “yes” for the second question, the value of 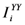 is one and zero otherwise.
is one and zero otherwise.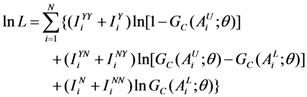
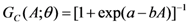
 . For people who gave a “no” or “no-no” response, an additional follow-up question was asked: “Are you willing to pay anything at all?” Those providing a “no” answer to this question represent a valid representation of their zero WTP. Thus, “no” answers to the question after deleting protest zeros are taken as zero WTP responses.
. For people who gave a “no” or “no-no” response, an additional follow-up question was asked: “Are you willing to pay anything at all?” Those providing a “no” answer to this question represent a valid representation of their zero WTP. Thus, “no” answers to the question after deleting protest zeros are taken as zero WTP responses.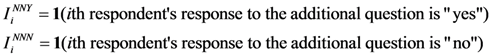
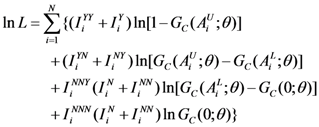
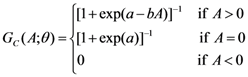
 where xi is a vector of covariates and β is a vector of corresponding parameters to be estimated.
where xi is a vector of covariates and β is a vector of corresponding parameters to be estimated.





