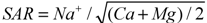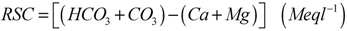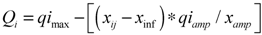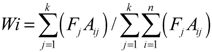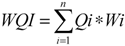2.1. Study Area
Darb El-Arbaein, a historic desert track running between Sudan and Egypt and passing El-Kharga Oasis to Assuit, is geographically located between 30°21′56.7″–31°27′4.1″ E and 24°40′28.5″–23°40′31.6″ N, in Southwestern Desert, Egypt. Arid climatic conditions are dominant and rainfall is rare. The area is considered one of the horizontal extensions for settlement developments in the Western Desert, which aims at establishing a link between the South Valley Project and Al-Kharga Oasis. The current project aims at reclamation 4654 ha and digging 85 wells of 150–500 m depth.
The project “Development of Trans-Sahara camel route between the Sudan and Egypt (Darb El-Arbaein)” is intended to: (a) reduce camel mortality due to inadequacy of water and services on a 1500 km long route to markets; (b) promote regional camel trade and improve the economies of the region; and (c) motivate desert nomads to become more interested in camel breeding and marketing [
21]. Groundwater is the only available source of water in the area. The assessment of agricultural potentiality in the Darb El-Arbaein area requires water resource evaluation. The general geology and geomorphology of the area studied are outlined in the geology of Egypt [
22] which is a desertic plateau with vast flat expansions of rocky deep closed in depressions (
Figure 1). The greatest altitude is attained in the extreme southwestern corner where the general plateau character is disturbed by the great mountain Gebel Uweinat. The study area (
Figure 1), which consists of four villages 1–4, encompasses around 5723.18 ha. The area of villages 1,2 is equal to 1933.45 ha, however; villages 3,4 have an area equal to 3789.73 ha.
2.2. Overall the Proposed Methodology
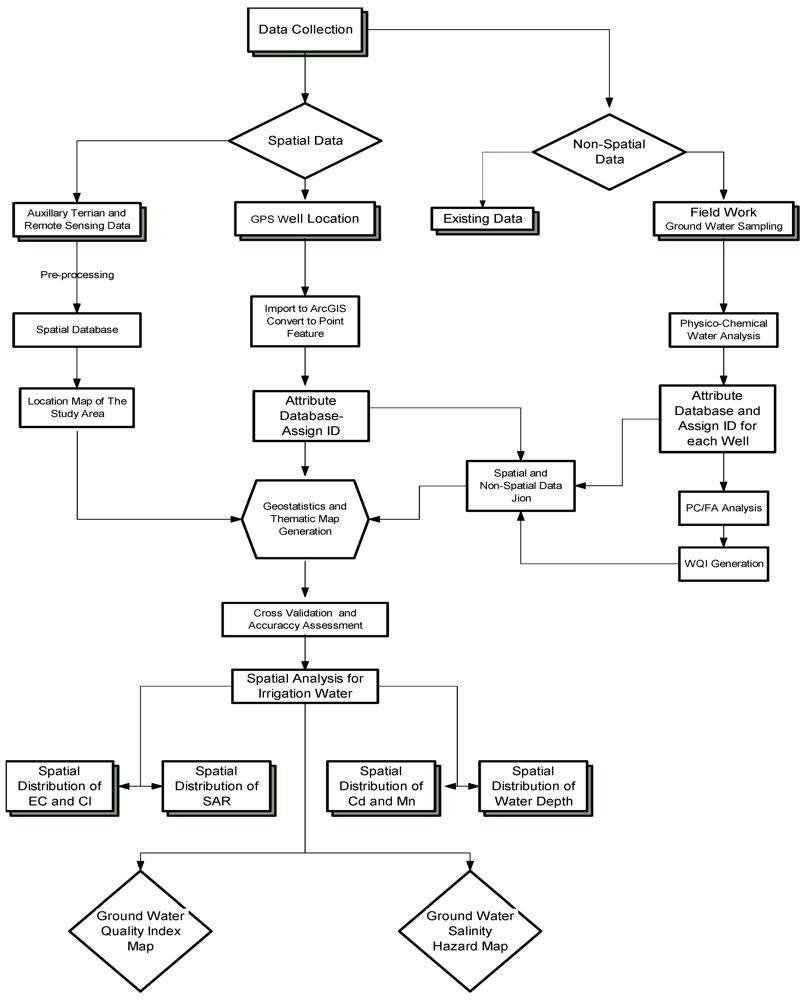
The methodology adopted for groundwater quality mapping using water quality data in the GIS environment is shown in
Figure 2. The study was carried out with the help of four major components: input from remote sensing data, topographic sheets, groundwater quality data and data collected during field visits. In order to evaluate the quality of groundwater for irrigation in the Darb El-Arbaein area, 36 surveyed wells (13 in villages 1,2 and 23 in villages 3,4) with GPS (Garmin eTrex Venture HC) data were used to produce the evaluation map. The water samples were collected after 30 min of pumping to avoid stagnant and contaminated water. White plastic containers of 1 L capacity were rinsed out three to four times with sampling water. Then the containers were filled up to the brim and immediately sealed to avoid exposure to air [
23]. The containers were labeled for identification and brought to the laboratory. The groundwater samples were analyzed for (pH, EC, Na
+, Ca
++, Mg
++, B, Cl
− and HCO
3-) irrigation purposes. Sodium Adsorption Ratio (SAR), Soluble Sodium Percentage (SSP) and Residual Sodium Carbonate (RSC) were calculated on some standard equations basis. These equations are as follows:
The concentrations of the heavy metals (Co, Fe, Pb, Ni, Cd, Zn and Cu) were determined using atomic absorption spectrophotometer. Area elevation and depth to water were also measured. Water quality maps were generated for different water properties and surfaces were interpolated using Kriging interpolation technique. A salinity hazard map was prepared and delineated into three classes: unsuitable, moderate, and suitable. Thus the final groundwater quality map for irrigation purposes was prepared by overlying the above-mentioned grid data. Finally the study area was delineated.
Figure 1.
Location map of the study area in relation to Egypt.
Figure 1.
Location map of the study area in relation to Egypt.
Figure 2.
Flow chart showing the methodology adopted for groundwater quality mapping.
Figure 2.
Flow chart showing the methodology adopted for groundwater quality mapping.
2.3. Proposed Water Quality Evaluation Model
The water quality evaluation model proposed in this study was developed in three steps. In the first step, principle component and factor model were developed. Parameters that contribute to most variability in irrigation water quality were identified using Principal Components and Factor Analysis (PC/FA) as described in SPSS (v.13). Factor analysis provides a useful tool to draw information from multivariate data by exploring the covariance structure among observable variables in terms of a smaller number of unobservable variables. In exploratory factor analysis, the model is usually estimated by the maximum likelihood method with the use of efficient algorithms and then a rotation technique, such as the Varimax method, is utilized to find a meaningful relationship between the observable variables and the common factors. A rotation method gets factors that are as different from each other as possible and helps you interpret the factors by putting each variable primarily on one of the factors. In other words, rotation of factors helps to define which underlying factor a set of items is most strongly associated with.
Indexes based on statistical techniques favor the recognition of the most characteristic indicators of the water under study. Factorial analysis allows the reduction of a great number of data obtained upon monitoring and permits an interpretation of the various constituents separately [
24], making it possible to find a better selection of the relevant parameters for water quality classification [
25,
26]. The correlation matrix was calculated based on the normalized data of the 13 parameters, evaluated for the sampling sites throughout the Darb El-Arbaein. A preliminary analysis of the representative parameters of water quality was performed upon correlation matrix. According to [
27] only values above 0.5 should be considered; this rationale was used in this study. In order to identify the most significant interrelation of water quality parameters in the Darb El-Arbaein area with each resulting factor of PC, a matrix rotation procedure was adopted using the Varimax method. This method minimizes the contribution of parameters with a lower significance to the factor such that the parameters will present loads close to one or zero, eliminating the intermediate values, which makes interpretation more difficult.
In a second step, a water quality index WQI model was proposed. A definition of quality measurement values (Qi) and aggregation weights (Wi) was established. Values of (Qi) were estimated based on each parameter value shown in
Table 1.
Table 1.
Parameters of limiting values for quality measurement (Qi) calculation.
Table 1.
Parameters of limiting values for quality measurement (Qi) calculation.
| Qi | EC (μScm−1) | SAR | Na | Cl | HCO3 |
|---|
| Meql−1 |
|---|
| 85–100 | 200 ≤ EC < 750 | SAR < 3 | 2 ≤ Na < 3 | Cl < 4 | 1 ≤ HCO3 < 1.5 |
| 60–85 | 750 ≤ EC < 1,500 | 3≤ SAR < 6 | 3 ≤ Na < 6 | 4 ≤ Cl < 7 | 1.5 ≤ HCO3 < 4.5 |
| 35–60 | 1,500 ≤ EC < 3,000 | 6≤ SAR < 12 | 6 ≤ Na < 9 | 7 ≤ Cl < 10 | 4.5 ≤ HCO3 < 8.5 |
| 0–35 | EC < 200 or | SAR ≥ 12 | Na 2 < 2 or | Cl ≥ 10 | HCO3 < 1 or |
| EC ≥ 3,000 | Na ≥ 9 | HCO3 ≥ 8.5 |
Water quality parameters were represented by a non-dimensional number: the higher the value, the better the water quality. Values of Qi were calculated using the following equation, based on the tolerance limits shown in
Table 1 and water quality results determined in the laboratory:
where qimax is the maximum value of Qi for the class; xij is the observed value for the parameter; xinf is the value corresponding to the lower limit of the class to which the parameter belongs; qiamp is the class amplitude; xamp is the class amplitude to which the parameter belongs.
In order to evaluate xamp of the last class of each parameter, the upper limit was considered to be the highest value determined in the physical-chemical and chemical analysis of the water samples, then Wi values were normalized such that their sum equaled one.
where Wi is the weight of the parameter for the WQI; F = component 1 autovalue; Aij is the explainability of parameter i by factor j; i is the number of physical- chemical and chemical parameters selected by the model, ranging from 1 to n; j is the number of factors selected in the model, varying from 1 to k.
The water quality index was calculated by summation of Qi, and Wi values as:
where WQI is a dimensionless parameter ranging from 0 to 100; Qi is the quality of the ith parameter, a number from 0 to 100, a function of its concentration or measurement; Wi is the normalized weight of the ith parameter, a function of its importance in explaining the global variability in water quality.
Division in classes based on the proposed water quality index, which was based on existent water quality indexes, and classes were defined considering the risk of salinity problems, soil water infiltration reduction, as well as toxicity to plants as observed in the classifications presented by [
29]. Restrictions to water use classes were characterized as shown in
Table 2.
Table 2.
Water quality index characteristics.
Table 2.
Water quality index characteristics.
| WQI | Water use restrictions |
|---|
| 85 ≤ 100 | No restriction (Excellent) |
| 70 ≤ 85 | Low restriction (Good) |
| 55 ≤ 70 | Moderate restriction (Poor) |
| 40 ≤ 55 | High restrictions (Very poor) |
| 0 ≤ 40 | Severe restrictions (Unsuitable for irrigation) |
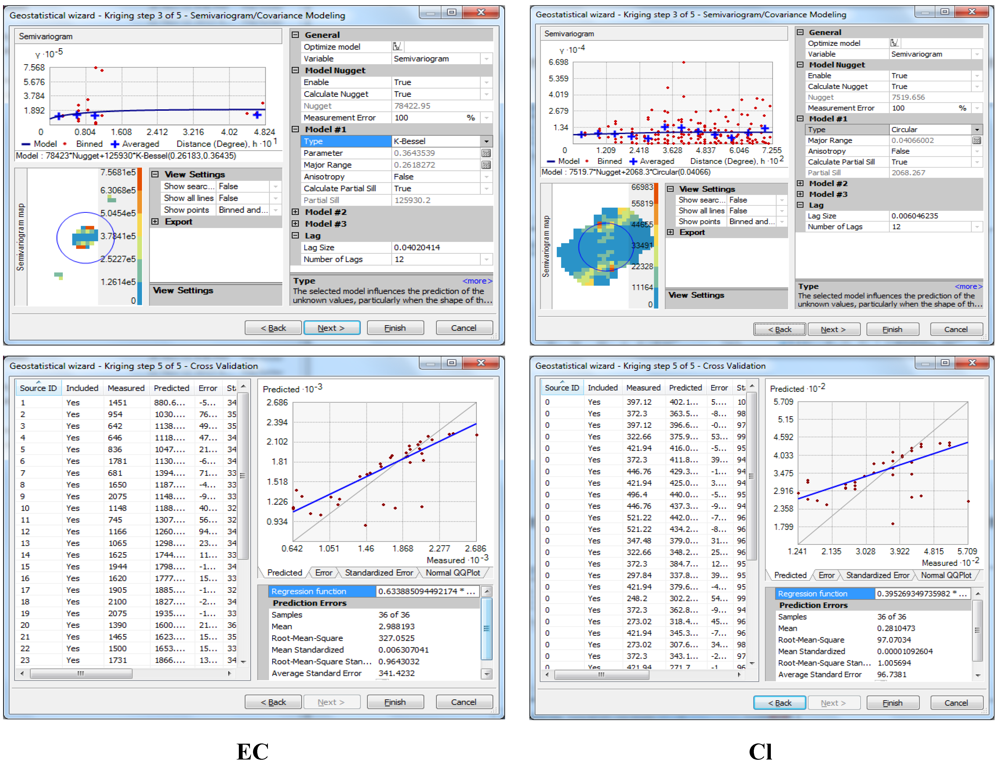
In a third step, the water quality data (attribute) was linked to the sampling location (spatial) in ArcGIS and maps showing spatial distribution were prepared to identify the variation in concentrations of the groundwater parameters at various locations of the study area. Different water quality maps were produced using point data like pH, EC, SAR, Cl, and B by ArcMap GIS software. Geostatistical analyses were performed using the Geostatistical analyst extension available in ESRI ArcMap (v. 10) [
30]. Kriging differs from other methods (such as IDW), in which the weight function is no longer arbitrary, being calculated from the parameters of the fitted semivariogram model under the conditions of unbiasedness and minimized estimation variance for the interpolation. Thus, Kriging is regarded as best linear unbiased estimation (BLUE). A more detailed explanation of the method is given by [
31,
32,
33,
34,
35]. Of the different Kriging techniques, the ordinary Kriging (OK) method was used in the present study because of its simplicity and prediction accuracy in comparison to other Kriging methods [
31].
Geostatistical analysis was the first to fully explore the data in which the histogram, normality, trend of data, semivariogram cloud and cross covariance cloud of the raw data were observed [
36]. Kriging methods work best if the data is approximately normally distributed [
37]. Transformations were used to make the data normally distributed and satisfy the assumption of equal variability for the data. In ArcGIS Geostatistial Analyst, the histogram and normal QQPlots were used to see what transformations were needed to make the data more normally distributed. For each water quality parameter, an analysis trend was made. Directional influences (anisotropy) are critical to the accurate estimation of water quality surface. The directional search tool was used to remove the directional influences from the groundwater quality data. In this study, the semivariogram models were tested for each parameter data set. Prediction performances were assessed by cross validation. Cross validation allows determination of which model provides the best predictions. For a model that provides accurate predictions, the standardized mean error should be close to 0, the root-mean-square error and average standard error should be as small as possible (useful when comparing models), and the root-mean square standardized error should be close to 1 [
37]. Finally, to produce a simple (salinity and WQI) hazard map, simple classes were used. The suitability map obtained from the computed index value was evaluated according to three categories: unsuitable (0–40), moderate (40–70), and suitable (70–100). Also the salinity hazard map was assessed based on three categories: unsuitable (˃1500 μScm
−1), moderate (1500–750 μScm
−1), and suitable (˂750 μScm
−1). The area with WQI value of less than 40 was considered to be poor quality irrigation water not suitable for irrigating agricultural fields. Such water could impair soil quality and result in yield loss. As a rule of thumb, water extraction from such areas should be avoided.