Minimizing Errors in the Prediction of Water Levels Using Kriging Technique in Residuals of the Groundwater Model
Abstract
:1. Introduction
2. Methodology
2.1. Study Area
2.2. Data
2.3. Modeling
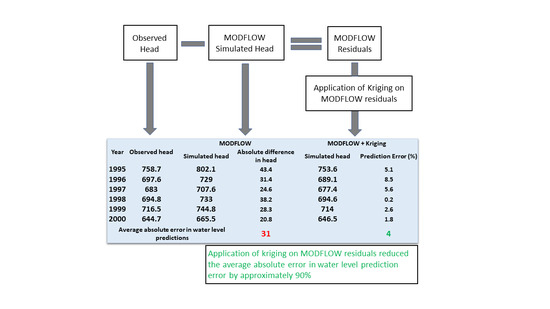
- Mapping MODFLOW simulated groundwater heads (model imported from TWDB) into their corresponding coordinates and overlap with observation data to find the MODFLOW estimated values in the observation point.
- Subtracting the observed groundwater head with MODFLOW simulated head and consider as the model residuals.
- Dividing the residuals into two separate datasets, 90 percent of data for fitting kriging methods (calibrating residuals) and 10 percent for validating part (validating residuals), in a random selection.
- Pre-evaluating the calibrating residuals and fit kriging method to generate the estimated residual map for the study domain.
- Comparing the validating residuals with an estimated one to evaluate the accuracy of the kriging method.
2.3.1. Data Preparation
2.3.2. Kriging Method
3. Results and Discussion
3.1. Data Investigation
3.2. Model Simulation
3.3. Model Validation
3.4. Comparison to Other Studies
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Adhikari, K.; Fedler, C.B. Water sustainability using pond-in-pond wastewater treatment system: Case studies. J. Water Process Eng. 2020, 36, 101281. [Google Scholar] [CrossRef]
- Adhikari, K.; Fedler, C.B. Pond-In-Pond: An alternative system for wastewater treatment for reuse. J. Environ. Chem. Eng. 2020, 8, 103523. [Google Scholar] [CrossRef]
- Mehan, G.T., III; Scientific American. The EPA Says We Need to Reuse Wastewater. 2019. Available online: https://blogs.scientificamerican.com/observations/the-epa-says-we-need-to-reuse-wastewater/ (accessed on 11 December 2019).
- FAO. AQUASTAT Main Database, Food and Agriculture Organization of the United Nations (FAO). 2018. Available online: http://www.fao.org/nr/water/aquastat/didyouknow/index.stm (accessed on 26 January 2022).
- FAO. AQUASTAT Main Database, Food and Agriculture Organization of the United Nations (FAO). 2016. Available online: http://www.fao.org/nr/water/aquastat/data/query/index.html?lang=en (accessed on 26 January 2022).
- NGWA. The Groundwater Association. 2020. Available online: https://www.ngwa.org/what-is-groundwater/About-groundwater/information-on-earths-water (accessed on 26 January 2022).
- Fendekova, M.; Demeterova, B.; Slivova, V.; Macura, V.; Fendek, M.; Machlica, A.; Gregor, M.; Jalcovikova, M. Surface and groundwater drought evaluation with respect to aquatic habitat quality applied in Torysa river catchment, Slovakia. Ecohydrol. Hydrobiol. 2011, 11, 49–61. [Google Scholar] [CrossRef]
- Lange, B.; Holman, I.; Bloomfield, J.P. A framework for a joint hydro-meteorological-social analysis of drought. Sci. Total Environ. 2017, 578, 297–306. [Google Scholar] [CrossRef] [Green Version]
- Chakraborty, S.; Maity, P.K.; Das, S. Investigation, simulation, identification and prediction of groundwater levels in coastal areas of Purba Midnapur, India, using MODFLOW. Environ. Dev. Sustain. 2020, 22, 3805–3837. [Google Scholar] [CrossRef]
- Hutchison, W.R.; Jones, I.; Anaya, R. Update of the Groundwater Availability Model for the Edwards-Trinity (Plateau) and Pecos Valley Aquifers of Texas; Unpublished Report; Texas Water Development Board: Austin, TX, USA, 2011. [Google Scholar]
- Xue, S.; Yu Liu, S.L.; Li, W.; Wu, Y.; Pei, Y. Numerical simulation for groundwater distribution after mining in Zhuanlongwan mining area based on visual MODFLOW. Environ. Earth Sci. 2018, 77, 400. [Google Scholar] [CrossRef]
- Tapoglou, E.; Karatzas, G.P.; Trichakis, I.C.; Varouchakis, E.A. A spatio-temporal hybrid neural network-Kriging model for groundwater level simulation. J. Hydrol. 2014, 519, 3193–3203. [Google Scholar] [CrossRef]
- Theodossiou, N.; Latinopoulos, P. Evaluation and optimisation of groundwater observation networks using the Kriging methodology. Environ. Model. Softw. 2006, 21, 991–1000. [Google Scholar] [CrossRef]
- Marchant, B.P.; Bloomfield, J.P. Spatio-temporal modelling of the status of groundwater droughts. J. Hydrol. 2018, 564, 397–413. [Google Scholar] [CrossRef]
- Oikonomou, P.D.; Alzraiee, A.H.; Karavitis, C.A.; Waskom, R.M. A novel framework for filling data gaps in groundwater level observations. Adv. Water Resour. 2018, 119, 111–124. [Google Scholar] [CrossRef]
- Varouchakis, Ε.; Hristopulos, D. Comparison of stochastic and deterministic methods for mapping groundwater level spatial variability in sparsely monitored basins. Environ. Monit. Assess. 2013, 185, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Ruybal, C.J.; Hogue, T.S.; McCray, J.E. Evaluation of groundwater levels in the Arapahoe aquifer using spatiotemporal regression kriging. Water Resour. Res. 2019, 55, 2820–2837. [Google Scholar] [CrossRef]
- Ziolkowska, J.R.; Reyes, R. Groundwater level changes due to extreme weather—An evaluation tool for sustainable water management. Water 2017, 9, 117. [Google Scholar] [CrossRef] [Green Version]
- Kuria, D.N.; Gachari, M.K.; Macharia, M.W.; Mungai, E. Mapping groundwater potential in Kitui District, Kenya using geospatial technologies. Int. J. Water Resour. Environ. Eng. 2011, 4, 15–22. [Google Scholar]
- Minor, T.B.; Russell, C.E.; Mizell, S.A. Development of a GIS-based model for extrapolating mesoscale groundwater recharge estimates using integrated geospatial data sets. Hydrogeol. J. 2007, 15, 183–195. [Google Scholar] [CrossRef]
- Aboufirassi, M.; Mariño, M.A. Kriging of water levels in the Souss aquifer, Morocco. J. Int. Assoc. Math. Geol. 1983, 15, 537–551. [Google Scholar] [CrossRef]
- Pucci, A.A., Jr.; Murashige, J.A.E. Applications of universal kriging to an aquifer study in New Jersey. Groundwater 1987, 25, 672–678. [Google Scholar] [CrossRef]
- Hoeksema, R.J.; Clapp, R.B.; Thomas, A.L.; Hunley, A.E.; Farrow, N.D.; Dearstone, K.C. Cokriging model for estimation of water table elevation. Water Resour. Res. 1989, 25, 429–438. [Google Scholar] [CrossRef]
- Desbarats, A.J.; Logan, C.E.; Hinton, M.J.; Sharpe, D.R. On the kriging of water table elevations using collateral information from a digital elevation model. J. Hydrol. 2002, 255, 25–38. [Google Scholar] [CrossRef]
- Olea, R.; Davis, J. Optimaizing the High Plains Aquifer Water-Level Observation Network; Kansas Geological Surveying: Lawrence, KS, USA, 1999. [Google Scholar]
- Ahmadi, S.H.; Sedghamiz, A. Geostatistical analysis of spatial and temporal variations of groundwater level. Environ. Monit. Assess. 2007, 129, 277–294. [Google Scholar] [CrossRef]
- Ahmadi, S.H.; Sedghamiz, A. Application and evaluation of kriging and cokriging methods on groundwater depth mapping. Environ. Monit. Assess. 2008, 138, 357–368. [Google Scholar] [CrossRef] [PubMed]
- Rivest, M.; Marcotte, D.; Pasquier, P. Hydraulic head field estimation using kriging with an external drift: A way to consider conceptual model information. J. Hydrol. 2008, 361, 349–361. [Google Scholar] [CrossRef]
- Anaya, R.; Jones, I. Groundwater Availability Model for the Edwards-Trinity (Plateau) and Pecos Valley Aquifers of Texas; Texas Water Development Board: Austin, TX, USA, 2009. [Google Scholar]
- Texas Water Development Board, Groundwater Models. Available online: https://www.twdb.texas.gov/groundwater/models/alt/eddt_p_2011/alt1_eddt_p.asp (accessed on 11 May 2020).
- Noack, M.M.; Yager, K.G.; Fukuto, M.; Doerk, G.S.; Li, R.; Sethian, J.A. A kriging-based approach to autonomous experimentation with applications to X-ray scattering. Sci. Rep. 2019, 9, 11809. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pinto, J.A.; Kumar, P.; Alonso, M.F.; Andreao, W.L.; Pedruzzi, R.; Espinosa, S.I.; Albuquerque, T.T. Kriging method application and traffic behavior profiles from local radar network database: A proposal to support traffic solutions and air pollution control strategies. Sustain. Cities Soc. 2020, 56, 102062. [Google Scholar] [CrossRef]
- Gotway, C.A.; Ferguson, R.B.; Hergert, G.W.; Peterson, T.A. Comparison of kriging and inverse-distance methods for mapping soil parameters. Soil Sci. Soc. Am. J. 1996, 60, 1237–1247. [Google Scholar] [CrossRef]
- Venäläinen, A.; Heikinheimo, M. Meteorological data for agricultural applications. Phys. Chem. Earth Parts A/B/C 2002, 27, 1045–1050. [Google Scholar] [CrossRef]
- Laslett, G.M. Kriging and splines: An empirical comparison of their predictive performance in some applications. J. Am. Stat. Assoc. 1994, 89, 391–400. [Google Scholar] [CrossRef]
- Wackernagel, H. Multivariate Geostatistics: An Introduction with Applications; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- esri. How Kriging Works. 2021. Available online: https://pro.arcgis.com/en/pro-app/latest/tool-reference/3d-analyst/how-kriging-works.htm (accessed on 26 January 2022).
- ArcGIS Desktop. 2021. Available online: https://desktop.arcgis.com/en/arcmap/latest/extensions/geostatistical-analyst/what-is-arcgis-geostatistical-analyst-.htm (accessed on 26 January 2022).
- Sharp, M.J., Jr.; Green, R.T.; Schindel, G.M. The Edwards Aquifer: The Past, Present, and Future of a Vital Water Resource; Geological Society of America: Boulder, CO, USA, 2019; Volume 215. [Google Scholar]
- Liu, A.; Troshanov, N.; Winterle, J.; Zhang, A.; Eason, S. Updates to the MODFLOW Groundwater Model of the San Antonio Segment of the Edwards Aquifer; Edwards Aquifer Authority: San Antonio, TX, USA, 2017. [Google Scholar]








| Year | Observations 1 | MODFLOW (m) | MODFLOW + Kriging (m) | |||||
|---|---|---|---|---|---|---|---|---|
| Mean a 2 | Observed Residuals 3 | Standard Error | Mean b 4 | Predicted Residuals 5 | Error 6 | Standard Error | ||
| 1995 | 727.5 | 764.7 | −37.2 | 3.1 | 728.7 | −36 | 1.2 | 0.7 |
| 1996 | 665.5 | 706 | −40.5 | 3.3 | 667.1 | −38.9 | 1.6 | 0.4 |
| 1997 | 692.4 | 725.5 | −33.1 | 2.9 | 693.5 | −32 | 1.1 | 0.4 |
| 1998 | 682.4 | 716.6 | −34.2 | 2.9 | 682.8 | −33.8 | 0.4 | 0.5 |
| 1999 | 708.3 | 747.1 | −38.8 | 2.9 | 708.6 | −38.5 | 0.3 | 0.3 |
| 2000 | 686 | 724.7 | −38.7 | 3.2 | 685.3 | −39.4 | −0.7 | 1.1 |
| Year | Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. | |
|---|---|---|---|---|---|---|---|
| 1995 | Observed Residuals | −141.6 | −53.1 | −32.2 | −37.2 | −20.8 | 55.2 |
| Predicted Residuals | −147.1 | −52.1 | −31.9 | −36 | −22.5 | 52.3 | |
| Error | −97.3 | −6.7 | −0.1 | 1.2 | 5.2 | 84.5 | |
| Standard Error | 0.4 | 0.7 | 0.8 | 0.7 | 0.8 | 0.8 | |
| 1996 | Observed Residuals | −137.1 | −60.8 | −40.9 | −40.5 | −16.1 | 30.4 |
| Predicted Residuals | −132.7 | −56.8 | −43.3 | −38.9 | −14.3 | 33.6 | |
| Error | −49.6 | −6.4 | 0.8 | 1.6 | 11.6 | 72.8 | |
| Standard Error | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 | |
| 1997 | Observed Residuals | −135.4 | −51.7 | −32.6 | −33.1 | −11.3 | 62.5 |
| Predicted Residuals | −148.1 | −47 | −31.7 | −32 | −9.1 | 45.7 | |
| Error | −59 | −6.4 | 0.5 | 1 | 7.7 | 78 | |
| Standard Error | 0.2 | 0.4 | 0.4 | 0.4 | 0.4 | 0.5 | |
| 1998 | Observed Residuals | −131 | −54.3 | −32.3 | −34.2 | −16.9 | 64 |
| Predicted Residuals | −145.8 | −53.2 | −33.4 | −33.8 | −19.3 | 43.8 | |
| Error | −50 | −8.7 | 0.4 | 0.4 | 7.1 | 61.3 | |
| Standard Error | 0.4 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | |
| 1999 | Observed Residuals | −144.6 | −54 | −31.7 | −38.8 | −18.4 | 52.5 |
| Predicted Residuals | −150 | −53.1 | −31.1 | −38.5 | −20.9 | 52.2 | |
| Error | −55.2 | −8.2 | 0.4 | 0.3 | 7.7 | 75.9 | |
| Standard Error | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | |
| 2000 | Observed Residuals | −141.1 | −59.3 | −35.7 | −38.7 | −15.8 | 48 |
| Predicted Residuals | −139.3 | −56.4 | −39.5 | −39.4 | −19.1 | 36.1 | |
| Error | −79.7 | −8.7 | 0 | −0.7 | 8.3 | 66.2 | |
| Standard Error | 0.4 | 1.2 | 1.2 | 1.1 | 1.2 | 1.3 |
| Year | Observations | MODFLOW (m) | MODFLOW + Kriging (m) | |||||
|---|---|---|---|---|---|---|---|---|
| Mean | Observed Residuals | Standard Error | Mean | Predicted Residuals | Error | Standard Error | ||
| 1995 | 758.7 | 802.1 | −43.5 | 8.7 | 753.6 | −48.5 | −5.1 | 3 |
| 1996 | 697.6 | 729 | −31.4 | 14.7 | 689.1 | −39.9 | −8.5 | 5.3 |
| 1997 | 683 | 707.6 | −24.6 | 5.9 | 677.4 | −30.1 | −5.5 | 3.9 |
| 1998 | 694.8 | 733 | −38.1 | 10.7 | 694.6 | −38.3 | −0.2 | 8.1 |
| 1999 | 716.5 | 744.8 | −28.3 | 8.4 | 714 | −30.8 | −2.5 | 3.8 |
| 2000 | 644.7 | 665.5 | −20.8 | 10 | 646.5 | −19 | 1.8 | 4.6 |
| Year | Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. | |
|---|---|---|---|---|---|---|---|
| 1995 | Observed Residuals | −131.8 | −50 | −33.9 | −43.5 | −24 | −15 |
| Predicted Residuals | −132.5 | −55 | −31.8 | −48.5 | −24.8 | −18.9 | |
| Error | −7.1 | −1.3 | 0.8 | 5.1 | 8.9 | 29.3 | |
| Standard Error | - | - | - | 3 | - | - | |
| 1996 | Observed Residuals | −138.1 | −55.2 | −30.1 | −31.4 | −1.8 | 61 |
| Predicted Residuals | −143.1 | −46.5 | −37.2 | −40 | −5.3 | 40.3 | |
| Error | −20.5 | −5.2 | 5 | 8.5 | 20.3 | 52.1 | |
| Standard Error | - | - | - | 5.3 | - | - | |
| 1997 | Observed Residuals | −82.3 | −36.6 | −28.1 | −24.6 | −6.9 | 16.2 |
| Predicted Residuals | −80.9 | −44.9 | −31.1 | −30.2 | −7.3 | 16.7 | |
| Error | −18.5 | −3.1 | 0 | 5.5 | 20.6 | 38.7 | |
| Standard Error | - | - | - | 3.9 | - | - | |
| 1998 | Observed Residuals | −134.5 | −56.6 | −33.7 | −38.1 | −25.2 | 62 |
| Predicted Residuals | −76.3 | −51.7 | −45 | −38.3 | −22.5 | −10.1 | |
| Error | −87.3 | −6 | 0.8 | 0.2 | 10.4 | 72.9 | |
| Standard Error | - | - | - | 8.1 | - | - | |
| 1999 | Observed Residuals | −68.1 | −54.8 | −33.6 | −28.3 | −19.3 | 65.5 |
| Predicted Residuals | −71 | −52.1 | −39.1 | −30.8 | −22.8 | 32 | |
| Error | −38.6 | −2.7 | 0.3 | 2.5 | 9.7 | 35.8 | |
| Standard Error | - | - | - | 3.8 | - | - | |
| 2000 | Observed Residuals | −120.5 | −46.4 | −16.2 | −20.8 | −3.2 | 65.6 |
| Predicted Residuals | −71.7 | −45.9 | −20.4 | −19.1 | 4.2 | 41 | |
| Error | −48.9 | −4 | 0.5 | −1.7 | 10.2 | 24.7 | |
| Standard Error | - | - | - | 4.6 | - | - |
| Observation Well | Observed Head (m) | MODFLOW (m) | MODFLOW + Kriging (m) | ||
|---|---|---|---|---|---|
| Simulated Head | Residuals | Predicted Head | Residuals | ||
| 1 | 769 | 786.9 | −17.9 | 764.4 | 4.6 |
| 2 | 745.7 | 760.1 | −14.4 | 741.8 | 3.8 |
| 3 | 748.3 | 868.8 | −120.5 | 797.2 | −48.9 |
| 4 | 1059.2 | 993.6 | 65.6 | 1034.6 | 24.7 |
| 5 | 662.2 | 713.2 | −50.9 | 652.3 | 10 |
| 6 | 548.9 | 595.9 | −47 | 552.5 | −3.6 |
| 7 | 586.6 | 608.2 | −21.6 | 574.7 | 12 |
| 8 | 648.8 | 695 | −46.2 | 647.2 | 1.6 |
| 9 | 585 | 617.7 | −32.6 | 570.1 | 14.9 |
| 10 | 616.1 | 663.8 | −47.7 | 618.4 | −2.3 |
| 11 | 613.4 | 619.5 | −6.2 | 602.2 | 11.1 |
| 12 | 618.5 | 623.3 | −4.8 | 629.4 | −10.9 |
| 13 | 623.6 | 620.6 | 3 | 624.1 | −0.5 |
| 14 | 588.9 | 568.3 | 20.5 | 594 | −5.1 |
| 15 | 555.1 | 568.4 | −13.3 | 593 | −37.8 |
| 16 | 346.3 | 344.7 | 1.6 | 347.4 | −1.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asadi, A.; Adhikari, K. Minimizing Errors in the Prediction of Water Levels Using Kriging Technique in Residuals of the Groundwater Model. Water 2022, 14, 426. https://doi.org/10.3390/w14030426
Asadi A, Adhikari K. Minimizing Errors in the Prediction of Water Levels Using Kriging Technique in Residuals of the Groundwater Model. Water. 2022; 14(3):426. https://doi.org/10.3390/w14030426
Chicago/Turabian StyleAsadi, Alireza, and Kushal Adhikari. 2022. "Minimizing Errors in the Prediction of Water Levels Using Kriging Technique in Residuals of the Groundwater Model" Water 14, no. 3: 426. https://doi.org/10.3390/w14030426