Seasonal Variations of the Depletion Factor during Recession Periods in the Senegal, Gambia and Niger Watersheds
Abstract
:1. Introduction
1.1. Background, Context
- Relationship between Q(T) and Q(T + dT): correlation method. With dT = 1 day, [29] uses this mean relationship as an empirical recession curve, and [30] represents the upper envelope curve by a line passing through the origin, whose slope corresponds to the depletion factor K of the Maillet equation (1). With dT = 5 days, [31] represents the mean relationship by a line passing through the origin, whose slope corresponds to K5.
- Relationships between T and Log(Q) established for different recession sequences. Reference [32] uses these relationships and interprets their slope in each point as −α (Maillet’s formula). He derives an empirical model giving α as a function of Q and T. Ref. [33] set the Maillet formula by representing the relationships obtained for the different sequences by linear relationships, whose common slope corresponds to −α.
- Relationship between Log(Q) and Log(−dQ/dT). Refs. [34,35] represent the low envelope curve of this relationship by sections of linear functions, whose slope and ordinate at the origin correspond respectively to (n + 1)/n and Log(nσ0Q0−1/n), where n and σ0 are the parameters of the Coutagne equation (3). The 3/2 slope obtained for low flows gives n = 2, according to the Tison equation (2). Reference [36] obtains an average relationship with a slope close to 1, according to the Maillet equation (1).
- Relationship between Q and −dQ/dT. For different periods varying in distance from the beginning of recession, [37] represent the upper and lower envelopes of this relationship by lines passing through the origin, whose slope corresponds to the α parameter of the Maillet equation (1). These authors find that α is not very variable for low envelopes associated with baseflow from groundwater, while it decreases over time for high envelopes.
1.2. Objectives of the Project
- The knowledge of groundwater, since K describes the recharge of the river flow by the groundwater in the absence of rainfall. A high K coefficient, close to 1, corresponds to a slow decrease in the discharge, thanks to important contributions from the water tables. Conversely, a low K coefficient corresponds to a rapid decrease in the flow of rivers, with little discharge supply from groundwater. K thus characterizes the capacity of groundwater to supply rivers. This capacity depends both on geological and pedological characteristics (transmissivity, storage, permeability) and on the abundance of previous rainfall inputs to the basin.
- The forecasting of discharge during recession periods, which can extend more than 6 months in the region. Flow forecasts can, therefore, be made over very long horizons of several months, which can be of great interest to managers of hydraulic structures such as dams.
2. Materials and Methods
2.1. Methods
2.1.1. Observed Values of the Daily Depletion Factor K
- C1: times T − 2 to T + 2 fall within the usual recession period, which starts and ends on invariable dates T1 and T2, expressed in days/months;
- C2: between times T − 2 and T + 2, the discharge is known at a daily time step with no missing data and decreases in the broad sense, meaning that Q(T + k) ≤ Q(T + k − 1) for all integer numbers k between −1 and 2;
- C3: the discharge Q(T + 2) is greater than a minimum threshold Qthr arbitrarily set at 0.1 m3·s−1.
2.1.2. Analyses Performed
- The Maillet’s conceptual model (model 0). This model was chosen because it is the most often used model of recession.
- An empirical model representing K as a function of time (model 1).
- An empirical model representing K as a function of discharge (model 2).
- The generalized Coutagne conceptual model. This model was chosen because it is the only usual conceptual model capable of representing the non-monotonic evolution of K observed in the Senegal River basin during the recession period (see above). The generalized Coutagne model is used to represent K as a function of time (model 3) or as a function of discharge (model 4).
- model 0: average Km of the observed values of K(T), constant value compatible with the Maillet formula;
- model 1: empirical polynomial function f of the delay D(T) elapsed between the initial time T0 (invariable, expressed in day/month) and T, defined with parameters A1 to A6 by:
- model 2: empirical function g of the discharge Q(T), polynomial of the decimal logarithm of Q defined with parameters B1 to B6 by:
- model 3: function fb of the delay D(T), verifying with the parameters Q0, W, σ0 and n the relationship (15) imposed by the generalized Coutagne formula:
- model 4: function gb of the discharge Q(T), verifying with the parameters Q0, W, σ0 and n the relationship (16) imposed by the generalized Coutagne formula:
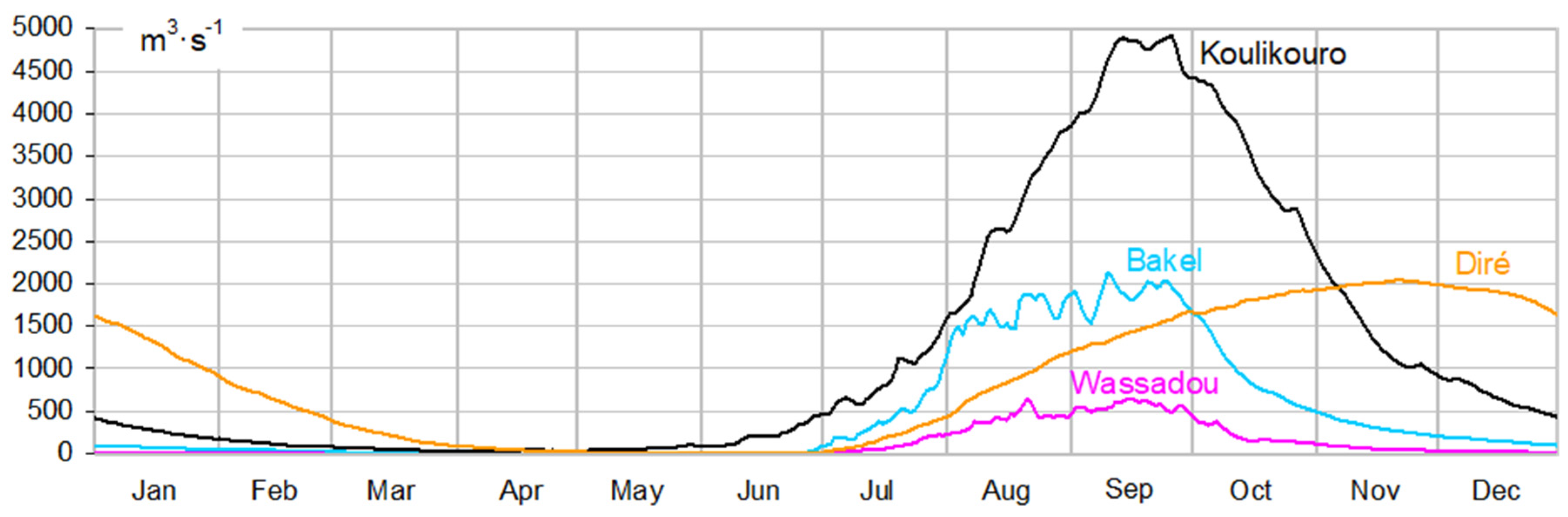
2.2. Data
- T1 = 15 October and T2 = 30 June for Akka on Niger (rank 50), due to the slower spread of flows as they pass the DIN;
- T1 = 15 November and T2 = 31 July for for Diré, Koryoumé, Tossaye and Ansongo on Niger (ranks 51 to 54), for the same reasons as Akka;
- T1 = 15 September and T2 = 30 April for Moussala and Siramakana in the Senegal watershed (ranks 12 and 17), Diaguery and Niokolokoba in the Gambia watershed (ranks 29 and 30) and Manankoro in the Niger watershed (rank 42), where the discharge ceases each year before the end of April.
3. Results
3.1. Calibration of Models Representing K
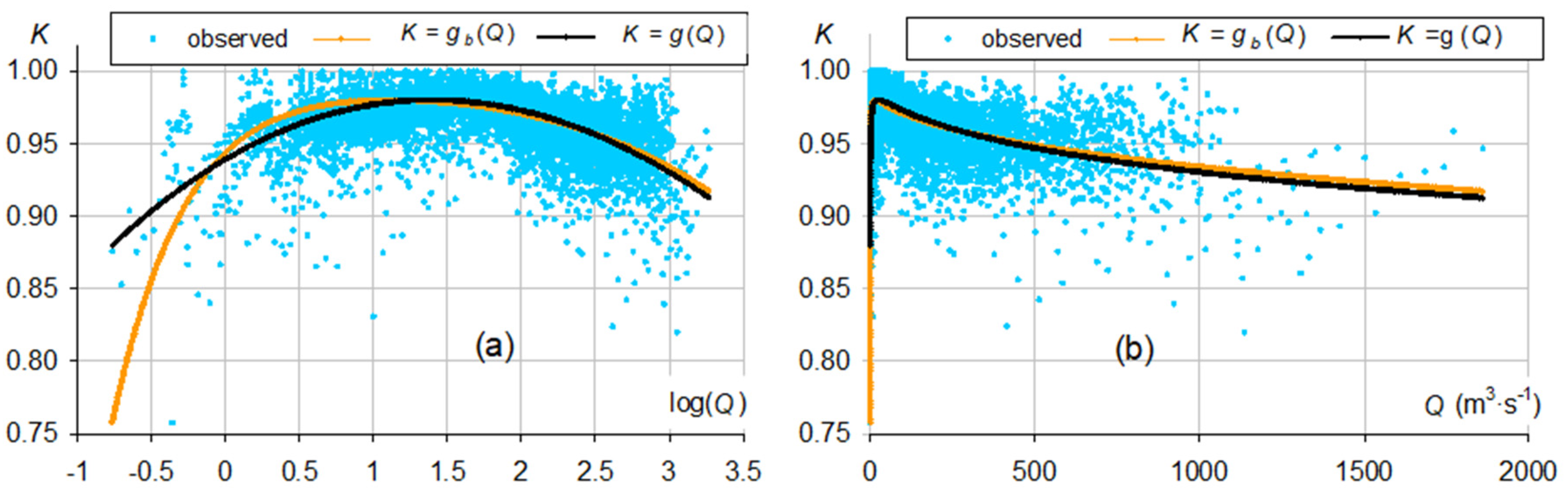
3.1.1. Results for Daka Saidou Station
3.1.2. Results for All Stations
3.1.3. Results for Model 1, Describing K as an Empirical Function of D
3.1.4. Results for Model 2, Describing K as an Empirical Function of Q
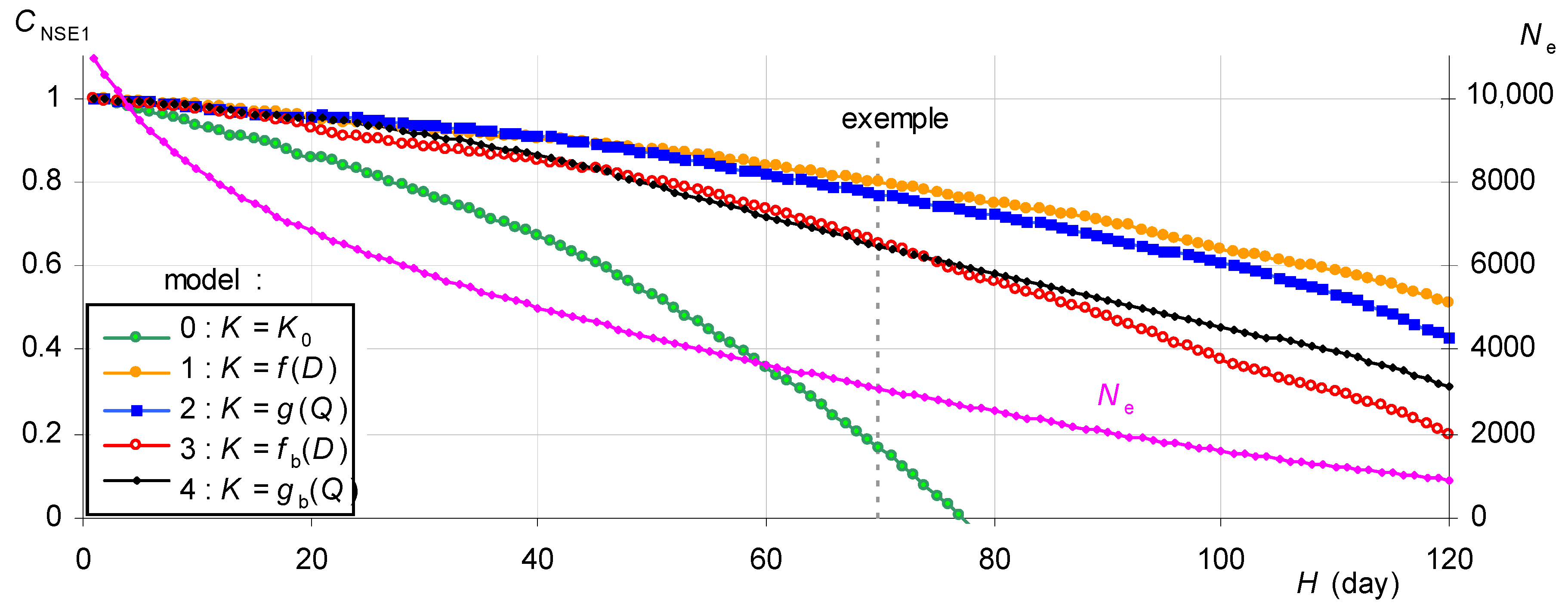
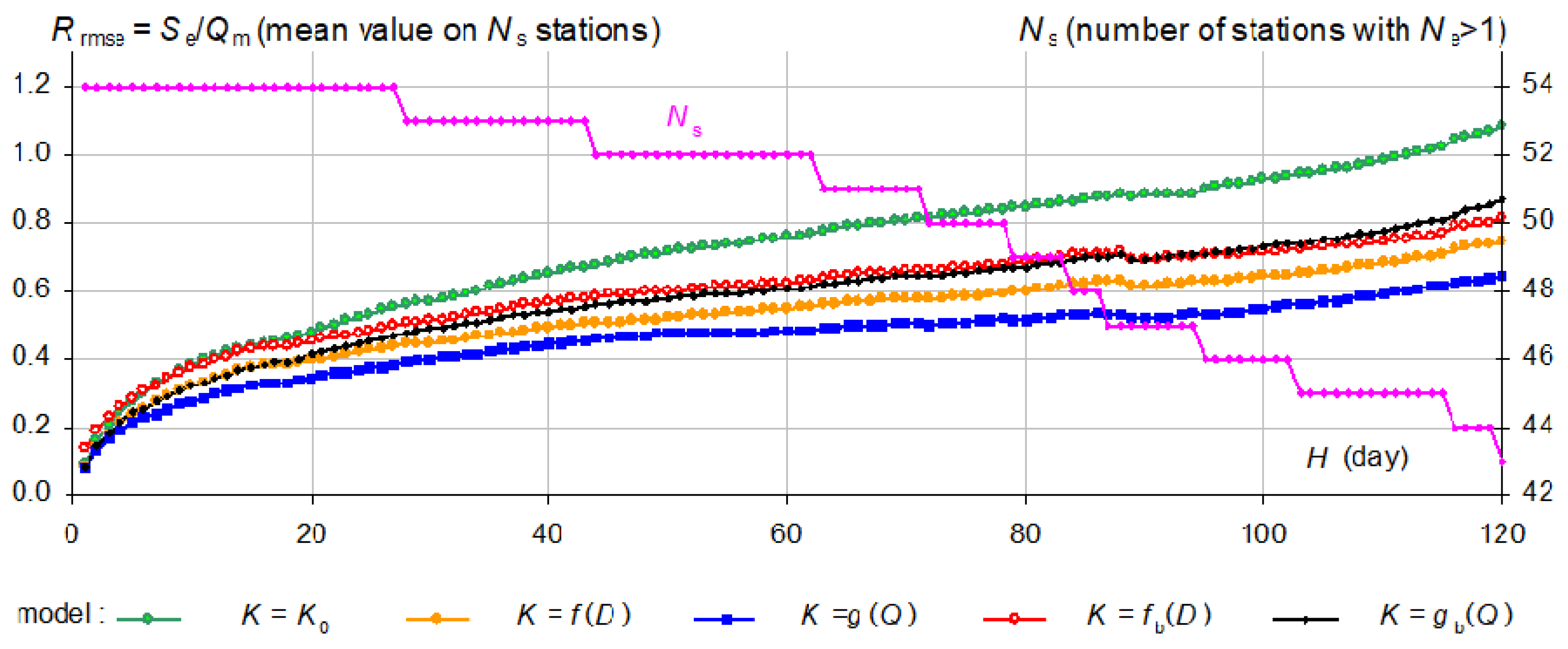
3.2. Performance of the Recession Models in Forecasting Discharge
3.2.1. Calculation Details
3.2.2. Results for All Forecasting Horizons
3.2.3. Results for Each Forecasting Horizon
3.3. Interannual Evolution of the Recession Regime
3.3.1. Results for Daka Saidou Station
3.3.2. Results for All Stations
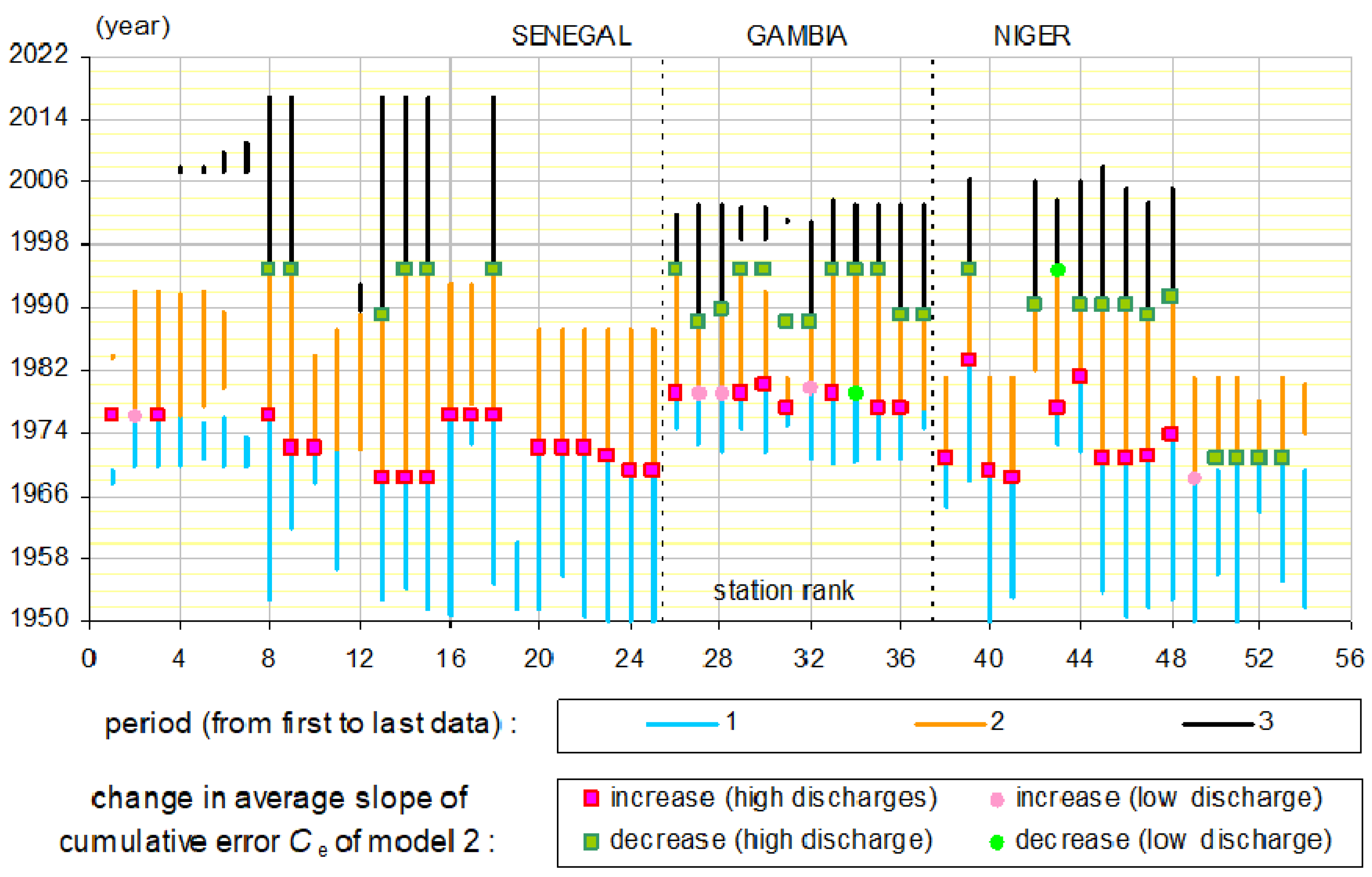
- for 44 stations, a transition between period 1 and 2 can be detected by Ce(Rc) overall change in slope under high flows (38 stations) or low flows (6 stations). Except for the station of rank 1, for which data are lacking, this transition can be dated between March 1968 and March 1983, depending on the station. For 39 of these 44 stations, the transition from period 1 to period 2 corresponds to an increase in errors in the average model and therefore a decrease in K observed for the same Q, like for Daka Saidou;
- for 26 stations, a transition between period 2 and 3 can be detected by a change in Ce(Rc) slope under high flows (25 stations) or under low flows (1 station). Except for stations 29 to 31, for which data are lacking, this transition can be dated between March 1988 and December 1994, depending on the station. For these 26 stations, the transition from period 2 to period 3 corresponds to a decrease in the errors of the average model and therefore to an increase in K observed for the same Q, like for Daka Saidou;
- the following results are observed for the average Km of the observed values of K (Table S1): Km decreases by an average of 1.2% between periods 1 and 2 and increases by an average of 0.8% between periods 2 and 3. This evolution of Km is observed at all stations with rare exceptions. With α = −Log(K) according to equation (1), these average changes in K over all the stations correspond to an average increase of 0.0120 d−1 between periods 1 and 2 and a decrease of 0.0080 d−1 between periods 2 and 3 for the parameter α generally used with the Maillet formula. This evolution of α between periods 1 and 2 is consistent with the results presented by [44,45] for several basins of West and Central Africa, [46] for the Niger River and [47] for the Bani.
4. Discussion
- In the Senegal and Gambia basins, K is generally quite low at the beginning of the recession (between 0.80 and 0.95 under the highest discharges Q). It then increases over time (K(Q) decreasing) to reach a fairly high value (between 0.96 and 0.98), for a specific flow rate Qs between 0.3 and 2 l·s−1·km−2 depending on the sub-basin concerned, before decreasing (K(Q) strongly increasing) until the end of the recession. The downstream stations are characterized by a decrease of K at the beginning of the recession (K(Q) increasing), from very high values, close to 1 under the highest flows;
- In the Niger basin, K is generally very high at the beginning of the recession (higher than 0.975 under the highest flows). It then decreases (K(Q) slightly increases) to a value greater than 0.95, reached for a specific discharge Qs between 7 and 17 l·s−1·km−2 upstream of the Inner Delta or for a discharge Q of about 133 m3·s−1 for stations downstream. Then, K evolves relatively little according to the flow and in a variable way according to the station, until the end of the recession.
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Ai (d−i) | with i integer between 0 and 6: model 1 parameters (K = f(D)), polynomial coefficients of D |
| Bi (-) | with i integer between 0 and 6: model 2 parameters (K = g(Q)), polynomial coefficients of log(Q) |
| Ce (-) | chronological accumulation of model 2 errors in relation to observed values of K |
| CNSE0 (-) | Nash and Sutcliffe model efficiency coefficient, equal to 1-((standard error)/(standard deviation))2, for the modeling of K |
| CNSE1 (-) | Nash and Sutcliffe model efficiency coefficient, for the forecast of Q at a given horizon H |
| CNSE2 (-) | Nash and Sutcliff model efficiency coefficient, for the forecast of Q at all horizons H |
| D (d) | period elapsed since the previous 15 September |
| Dmax (d) | upper limit of the calibration range of the function f(D) |
| Dmin (d) | lower limit of the calibration range of the function f(D) |
| f (-) | relationship giving K as a function of D (model 1, empirical) |
| fb (-) | relationship giving K as a function of D (model 3, based on the generalized Coutagne formula) |
| g (-) | relationship giving K as a function of Q (model 2, empirical) |
| gb (-) | relationship giving K as a function of Q (model 4, based on the generalized Coutagne formula) |
| H (d) | horizon of discharge forecast |
| i (-) | rank of a recession sequence |
| j (-) | rank of a recession sequence |
| K (-) | daily discharge depletion factor, between 0 (end of flow) and 1 (flow constancy) |
| K0 (-) | optimal constant value of K, maximizing the CNSE2 of the Nt forecast discharges with the recession model 0 at all H horizons between 1 and 120 days |
| Km (-) | average of the N observed values of K |
| Log (-) | neperian logarithm |
| log (-) | decimal logarithm |
| m (-) | positive exponent of volume V, used in the Coutagne theory |
| n (-) | positive exponent of time in the Coutagne formula |
| N (-) | number of observed values of K |
| Ne (-) | number of discharge values forecast by recession model, for a given forecast horizon H |
| Ns (-) | number of stations for which Ne is greater than 1 |
| Nt (-) | number of discharge values forecast per recession model, for all forecast horizons H between 1 and 120 days |
| p (-) | positive exponent of time used in the Horton formula |
| P (-) | percentage of stations, between 0 (no stations) and 100 (all stations) |
| Q (m3·s−1) | discharge |
| QA (m3·s−1) | discharge at time TA |
| QB (m3·s−1) | discharge at time TB |
| Qlim (m3·s−1) | upper limit of the application range of function g(Q) |
| Qm (m3·s−1) | average of observed discharges |
| Qmax (m3·s−1) | upper limit of the calibration range of function g(Q) |
| Qmin (m3·s−1) | lower limit of the calibration range of function g(Q) |
| Q0 (m3·s−1) | discharge at the beginning of a recession sequence |
| Qs (l·s−1·km−2) | specific discharge (discharge per unit of drained area) |
| Qsm (l·s−1·km−2) | mean interannual specific discharge |
| Qthr (m3·s−1) | minimum discharge required to account for the observed values of K |
| r (-) | exponent of time used in the Otnes model |
| Ra | rank of a recession model for a given station, between 1 for the best (maximum CNSE) and 5 for the worst (minimum CNSE) |
| Rc | chronological rank of K modeled |
| Rrmse | relative standard error of the discharges forecast per recession model, for a given time horizon |
| S (-) | homothety slope between hydrographs of distinct recession sequences |
| Se (m3·s−1) | standard error of the discharge forecasts calculated by a recession model, for a given horizon H |
| T (d) | time |
| TA (d) | initial time |
| TB (d) | initial time |
| Tb (d) | date of the oldest K observed during an uninterrupted sequence of recession |
| Tr (d) | time translation duration |
| T0 (d) | initial time, used in the Maillet and Tison formulas |
| T1 (d) | usual start date of the recession period, expressed in “dd/mm” format |
| T2 (d) | usual end date of the recession period, expressed in “dd/mm” format |
| V (m3) | remaining water volume in a reservoir used in the Coutagne theory |
| W (m3·s−1) | constant used in the generalized Maillet and generalized Coutagne formulas. If positive, it is the theoretical value of the discharge reached after an infinite time during a recession phase |
| Z (m3(1−m)·s−1) | proportionality constant between Q and Vm in the Coutagne theory |
| α (d−1) | positive recession coefficient, used in the Maillet formula (exponential form) |
| β (d−p) | positive recession coefficient, used in the Horton formula |
| λ (m3·s−1·dr) | parameter used in the Otnes model |
| μ (m3·s−1) | parameter used in the Otnes model |
| σ0 (d−1) | positive recession coefficient, used in the Tison and Coutagne formulas |
References
- Roche, M. Hydrologie de Surface; Gauthier-Villars/ORSTOM: Paris, France, 1963; p. 430. [Google Scholar]
- Hall, F.R. Base Flow Recessions—A review. Water Resour. Res. 1968, 4, 973–983. [Google Scholar] [CrossRef]
- Tallaksen, L.M. A Review of Baseflow Recession Analysis. J. Hydrol. 1995, 165, 349–370. [Google Scholar] [CrossRef]
- Boussinesq, J. Recherches théoriques sur l’écoulement des nappes d’eau infiltrées dans le sol et sur le débit des sources. J. Math. Pure Appl. 1904, 10, 5–78. [Google Scholar]
- Lang, C. Etiages et Tarissements: Vers Quelles Modélisations ? L’approche Conceptuelle et L’analyse Statistique en Réponse à la Diversité Spatiale des Ecoulements en Etiage des Cours d’eau de l’Est Français; Thèse de l’université Paul Verlaine de Metz: Metz, France, 2007; Available online: https://tel.archives-ouvertes.fr/tel-00534656/document (accessed on 3 January 2014).
- Barnes, B.S. The structure of discharge-recession curves. Trans. Am. Geophys Union 1939, 20, 721–725. [Google Scholar] [CrossRef]
- Maillet, E. Essai d’hydraulique Souterraine et Fluviale; Herman, A., Ed.; Libraire Sci. Hall: Paris, France, 1905. [Google Scholar]
- Tison, G. Courbe de Tarissement, Coefficient D’écoulement et Perméabilité du Bassin; Mém. A.I.H.S.: Helsinki, Finland, 1960; pp. 229–243. [Google Scholar]
- Coutagne, A. Meteorologie et Hydrologie. Etude Générale des Variations de Débit en Fonction des Facteurs qui les Conditionnent. 2me Partie. Les Variations de Débit en Période non Influencée par les Précipitations. Le Débit D’infiltration (Corrélations Fluviales Internes); La Houille Blanche: Grenoble, France, 1948; pp. 416–436. Available online: https://www.shf-lhb.org/articles/lhb/pdf/1948/07/lhb1948053.pdf (accessed on 24 June 2019).
- Carlier, M. Hydraulique Générale et Appliquee; Eyrolles: Paris, France, 1972; p. 565. [Google Scholar]
- Thomson, S.H. Hydrologic conditions in the chalk at Compton, West-Sussex. Trans. Inst. Water Eng. 1921, 26, 228–261. [Google Scholar]
- Wicht, C.L. Determination of the effects of watershed-management on mountain streams. Trans. Am. Geophys. Union 1943, 24, 594–606. [Google Scholar] [CrossRef]
- Toebes, C.; Strang, D.D. On recession curves, 1-Recession equations. J. Hydrol. NZ 1964, 3, 2–15. [Google Scholar]
- Radczuk, L.; Szarska, O. Use of the flow recession curve for the estimation of conditions of river supply by underground water. IAHS Publ. 1989, 187, 67–74. [Google Scholar]
- Clausen, B. Modelling streamflow recession in two Danish streams. Nord. Hydrol. 1992, 23, 73–88. [Google Scholar] [CrossRef]
- Padilla, A.; Pulido-Bosh, A.; Mangin, A. Relative importance of baseflow and quickflow from hydrographs of karst spring. Ground Water 1994, 32, 267–277. [Google Scholar] [CrossRef]
- Otnes, J. Uregulerte elvers vassføring i tørrværsperioder. Nor. Geogr. Tidsskr. 1953, 14, 210–218. [Google Scholar] [CrossRef]
- Otnes, J. Tørrværskurven. In Hydrologi i Praksis; Otnes, J., Ræstad, E., Eds.; Ingeniørforlaget: Oslo, Norway, 1978; pp. 227–233. [Google Scholar]
- Gjørsvik, O.G. Grosetbekken. En Vurdering av Vannbalansen; NVE Rep. 2, Part I, 1970; Norwegian Water and Energy Admin: Oslo, Norway, 1970. [Google Scholar]
- Andersen, T. En Undersøkelse av Grunnvannsmagasinet i et Representativt Høyfjellsområde. Master’s Thesis, University of Oslo, Oslo, Norway, 1972. [Google Scholar]
- Tjomsland, T.; Ruud, E.; Nordseth, K. The physiographic influence on recession runoff in small Norwegian rivers. Nord. Hydrol. 1978, 9, 17–30. [Google Scholar] [CrossRef]
- Horton, R.E. The role of infiltration in the hydrologic cycle. Trans. Am. Geophys. Union 1933, 14, 446–460. [Google Scholar] [CrossRef]
- Werner, P.W.; Sundquist, K.J. On the groundwater recession curve for large watersheds. IAHS Publ. 1951, 33, 202–212. [Google Scholar]
- Pereira, L.S.; Keller, H.M. Recession characteristics of small mountain basins, derivation of master recession curves and optimization of recession parameters. IAHS Publ. 1982, 138, 243–255. [Google Scholar]
- Nutbrown, D.A. Normal mode analysis of the linear equation of groundwater flow. Water Resour. Res. 1975, 11, 979–987. [Google Scholar] [CrossRef]
- Petras, I. An approach to the mathematical expression of recession curves. Water S. Afr. 1986, 12, 145–150. [Google Scholar]
- Ishihara, T.; Takagi, F. A study of the variation of low flow. Disaster Prev. Res. Inst. Kyoto Univ. Bull. 1965, 15, 75–98. [Google Scholar]
- Dewandel, B.; Lachassagne, P.; Bakalowicz, M.; Weng, P.; Al-Malki, A. Evaluation of aquifer thickness by analysing recession hydrographs. Application to the Oman ophiolite hard-rock aquifer. J. Hydrol. 2003, 274, 248–269. [Google Scholar] [CrossRef]
- Langbein, W.B. Some channel-storage studies and their application to the determination of infiltration. Trans. Am. Geophys. Union 1938, 19, 435–445. [Google Scholar] [CrossRef]
- Knisel, W.G. Baseflow recession analysis for comparison of drainage basin and geology. J. Geophys. Res. 1963, 68, 3649–3653. [Google Scholar] [CrossRef]
- Lebaut, S. L’apport de L’analyse et de la Modélisation Hydrologiques de Bassins Versants Dans la Connaissance du Fonctionnement d’un Aquifère: Les Grès d’Ardenne-Luxembourg; Thèse de l’université de Metz: Metz, France, 2000; Available online: http://docnum.univ-lorraine.fr/public/UPV-M/Theses/2000/Lebaut_Sebastien.LMZ0010.pdf (accessed on 2 October 2019).
- Federer, C.A. Forest transpiration greatly speeds streamflow recession. Water Resour. Res. 1973, 9, 1599–1604. [Google Scholar] [CrossRef]
- Bako, M.D.; Hunt, D.N. Derivation of baseflow recession constant using computer and numerical analysis. Hydrol. Sci. J. 1988, 33, 357–367. [Google Scholar] [CrossRef]
- Brutsaert, W.; Nieber, J.L. Regionalized drought flow hydrographs from a mature glaciated plateau. Water Resour. Res. 1977, 13, 637–643. [Google Scholar] [CrossRef]
- Troch, P.A.; De Troch, P.; Brutsaert, W. Effective water table depth to describe initial conditions prior to storm rainfall in humid regions. Water Resour. Res. 1993, 29, 427–434. [Google Scholar] [CrossRef]
- Vogel, R.M.; Kroll, C.N. Regional geohydrologic-geomorphic relationships for the estimation of low flow statistics. Water Resour. Res. 1992, 28, 2451–2458. [Google Scholar] [CrossRef]
- Zecharias, Y.B.; Brutsaert, W. Recession characteristics of groundwater outflow and base flow from mountainous watersheds. Water Resour. Res. 1988, 24, 1651–1658. [Google Scholar] [CrossRef]
- Lang, C.; Gilles, E. Une méthode d’analyse du tarissement des cours d’eau pour la prévision des débits d’étiage. Norois 2006, 201, 31–43. [Google Scholar] [CrossRef] [Green Version]
- Bader, J.C.; Cauchy, S.; Duffar, L.; Saura, P. Monographie Hydrologique du Fleuve Sénégal: De L’origine des Mesures Jusqu’en 2011; Bader, J.C., Ed.; IRD: Marseille, France, 2015; pp. 79–920. ISBN 978-2-7099-1885-5. [Google Scholar]
- Rochette, C.; Camus, H.; Danuc, R.; Pereira-Barreto, S. Le Bassin du Fleuve Senegal. Monographies Hydrologiques, 1; ORSTOM: Paris, France, 1974; p. 440. ISBN 2-7099-0344-X. [Google Scholar]
- Brunet-Moret, Y.; Chaperon, P.; Lamagat, J.P.; Molinier, M. Monographie Hydrologique du Fleuve Niger; Monographies hydrologiques, 8; ORSTOM: Paris, France, 1986; pp. 402–510. [Google Scholar]
- Lamagat, J.P.; Albergel, J.; Bouchez, J.M.; Descroix, L. Monographie Hydrologique du Fleuve Gambie; ORSTOM, OMVG: Dakar, Sénégal, 1990; p. 247. [Google Scholar]
- Vauchel, P.; Guiguen, N.; Gomis, D.; Konaté, L. Appui Institutionnel Aux Brigades Régionales du Ministère de L’hydraulique: Rapports D’avancement de Septembre 1998 à Septembre 2000; IRD, SGPRE: Dakar, Sénégal, 2000; p. 88. [Google Scholar]
- Olivry, J.C. Etudes Régionales Sur Les Basses Eaux, Les Effets Durables du Déficit des Précipitations Sur Les Etiages et Les Tarissements en Afrique de L’ouest et du Centre; XIIèmes journées hydrologiques de l’ORSTOM: Montpellier, France, 1996. [Google Scholar]
- Bricquet, J.P.; Bamba, F.; Mahé, G.; Toure, M.; Olivry, J.C. Evolution récente des ressources en eau de l’Afrique atlantique. Revue des Sciences de l’eau 1997, 3, 321–337. [Google Scholar] [CrossRef] [Green Version]
- Bricquet, J.P.; Mahé, G.; Bamba, F.; Olivry, J.C. Changements climatiques récents et modification du régime hydrologique du fleuve Niger à Koulikouro (Mali). L’hydrologie Tropicale: Géoscience et Outil Pour le Développement. 1995, Volume 238. Available online: https://books.google.fr/books?hl=fr&lr=&id=azUCAebIN-YC&oi=fnd&pg=PA157&dq=46.%09Bricquet,+J.P.%3B+Mah%C3%A9,+G.%3B+Bamba,+F.%3B+Olivry,+J.C.+Changements+climatiques+r%C3%A9cents+et+modification+du+r%C3%A9gime+hydrologique+du+fleuve+Niger+%C3%A0+Koulikouro+(Mali)&ots=MXLgArm6vz&sig=QUNj1kfsu8aHq4b-ivKMTMR0eII#v=onepage&q&f=false (accessed on 8 June 2020).
- Mahé, G.; Olivry, J.C.; Dessouassi, R.; Orange, D.; Bamba, F.; Servat, E. Relations eaux de surface–eaux souterraines d’une rivière tropicale au Mali. C.R. Acad. Sci. 2000, 330, 689–692. [Google Scholar] [CrossRef]
- L’Hôte, Y.; Mahé, G. Afrique de L’ouest et Centrale: Précicpitations Moyennes Annuelles (Période 1951–1989); ORSTOM: Paris, France, 1996; Available online: https://horizon.documentation.ird.fr/exl-doc/pleins_textes/divers16-08/010058020.pdf (accessed on 24 August 2020).
- Descroix, L.; Diongue, N.A.; Panthou, G.; Bodian, A.; Sane, Y.; Dacosta, H.; Malam, A.M.; Vandervaere, J.-P.; Quantin, G. Evolution récente de la pluviométrie en Afrique de l’ouest à travers deux régions: La Sénégambie et le bassin du Niger moyen. Climatologie 2015, 12, 25–43. [Google Scholar] [CrossRef] [Green Version]











| Sub-Basin | River | Station | Rank | Long. (° W) | Lat. (° N) | Area (km2) | Qsm l·s−1·km−1 |
|---|---|---|---|---|---|---|---|
| High Bafing | Bafing | Pont km17 | 1 | 12°09′ | 10°29′ | 18 | 17.45 |
| High Bafing | Samenta | Doureko | 2 | 11°42′ | 11°18′ | 225 | 17.38 |
| High Bafing | Kioma | Teliko | 3 | 11°53′ | 11°22′ | 360 | 17.34 |
| High Bafing | Kioma | Salouma | 4 | 11°42′ | 11°17′ | 775 | 15.96 |
| High Bafing | Téné | Bebele | 5 | 11°49′ | 11°01′ | 3470 | 17.59 |
| High Bafing | Bafing | Balabori | 6 | 11°22′ | 11°18′ | 11,600 | 13.29 |
| Bafing | Bafing | Boureya | 7 | 10°44′ | 11°45′ | 14,800 | 12.77 |
| Bafing | Bafing | Daka Saidou | 8 | 10°37′ | 11°57′ | 15,700 | 12.50 |
| Bafing | Bafing | Makana | 9 | 10°17′ | 12°33′ | 22,000 | 10.44 |
| Bafing | Bafing | Soukoutali | 10 | 10°25′ | 13°12′ | 27,800 | 9.11 |
| Bafing | Bafing | Dibia | 11 | 10°48′ | 13°14′ | 33,500 | 7.74 |
| Faleme | Faleme | Moussala | 12 | 11°18′ | 12°31′ | 3103 | 10.04 |
| Faleme | Faleme | Fadougou | 13 | 11°23′ | 12°31 | 9300 | 5.75 |
| Faleme | Faleme | Gourbassy | 14 | 11°38′ | 13°24′ | 17,100 | 5.01 |
| Faleme | Faleme | Kidira | 15 | 12°13′ | 14°27′ | 28,900 | 3.61 |
| Bakoye | Bakoye | Toukoto | 16 | 09°53′ | 13°27′ | 16,500 | 2.94 |
| Bakoye | Baoule | Siramakana | 17 | 09°53′ | 13°35′ | 59,500 | 0.56 |
| Bakoye | Bakoye | Oualia | 18 | 10°23′ | 13°36′ | 84,700 | 1.05 |
| Bakoye | Bakoye | Kalé | 19 | 10°39′ | 13°43′ | 85,600 | 1.05 |
| Senegal | Senegal | Galougo | 20 | 11°03′ | 13°51′ | 128,400 | 2.79 |
| Senegal | Senegal | Gouina | 21 | 11°06′ | 14°00′ | 128,600 | 2.83 |
| Senegal | Senegal | Kayes | 22 | 11°27′ | 14°27′ | 157,400 | 2.32 |
| Senegal | Senegal | Bakel | 23 | 12°27′ | 14°54′ | 218,000 | 2.36 |
| Senegal | Senegal | Matam | 24 | 13°15′ | 15°39′ | 230,000 | 1.99 |
| Senegal | Senegal | Kaédi | 25 | 13°30′ | 16°08′ | 253,000 | 1.53 |
| Sub-Basin | River | Station | Rank | Long. (° W) | Lat. (° N) | Area (km2) | Qsm l·s−1km−1 |
|---|---|---|---|---|---|---|---|
| tributaries | Sili | pont routier | 26 | 12°16′ | 13°32′ | 90 | 9.12 |
| tributaries | Diarha | pont routier | 27 | 12°37′ | 12°36′ | 760 | 10.00 |
| tributaries | Tiokoye | pont routier | 28 | 12°32′ | 12°34′ | 950 | 9.41 |
| tributaries | Diaguery | pont routier | 29 | 12°05′ | 12°38′ | 1010 | 7.52 |
| tributaries | Niokolokoba | pont routier | 30 | 12°44′ | 13°04′ | 3000 | 2.65 |
| tributaries | Koulountou | Gué (parc) | 31 | 13°29′ | 12°47 | 5350 | 4.88 |
| tributaries | Koulountou | Missira Gounasse | 32 | 13°37′ | 13°12′ | 6200 | 5.13 |
| Gambia | Gambia | Kedougou | 33 | 12°11′ | 12°33′ | 7550 | 10.69 |
| Gambia | Gambia | Mako | 34 | 12°21′ | 12°52′ | 10,450 | 8.86 |
| Gambia | Gambia | Simenti | 35 | 13°18′ | 13°02′ | 20,500 | 6.42 |
| Gambia | Gambia | Wassadou amont | 36 | 13°22′ | 13°21′ | 21,200 | 6.20 |
| Gambia | Gambia | Wassadou aval | 37 | 13°23′ | 13°21′ | 33,500 | 3.96 |
| Sub-Basin | River | Station | Rank | Long. (° W) | Lat. (° N) | Area (km2) | Qsm l·s−1km−1 |
|---|---|---|---|---|---|---|---|
| High Niger | Sankarani | Selingue | 38 | 08°13′ | 11°38′ | 34,200 | 9.51 |
| High Niger | Niger | Banankoro | 39 | 08°40′ | 11°41′ | 70,740 | 12.72 |
| High Niger | Niger | Koulikouro | 40 | 07°33′ | 12°51′ | 120,000 | 10.60 |
| High Niger | Niger | Ke Macina | 41 | 05°21′ | 13°58′ | 141,000 | 8.41 |
| Bani | Degou | Manankoro | 42 | 07°27′ | 10°27′ | 1550 | 5.52 |
| Bani | Banifing | Kolondieba | 43 | 06°51′ | 11°03′ | 3050 | 3.36 |
| Bani | Baoulé | Madina Diassa | 44 | 07°40′ | 10°47′ | 7880 | 6.60 |
| Bani | Baoulé | Dioila | 45 | 06°48′ | 12°31 | 32,500 | 3.25 |
| Bani | Bani | Douna | 46 | 05°54′ | 13°12′ | 101,600 | 2.73 |
| Bani | Bani | Beneny Kegny | 47 | 04°54′ | 13°23′ | 116,000 | 2.47 |
| Bani | Bani | Sofara | 48 | 04°05′ | 14°05′ | 125,400 | 1.96 |
| Niger | Niger | Mopti | 49 | 04°12′ | 14°30′ | 281,600 | 3.00 |
| Niger | Niger | Akka | 50 | 04°14′ | 15°24′ | - | - |
| Niger | Niger | Diré | 51 | 03°23′ | 16°16′ | - | - |
| Niger | Niger | Koryoumé | 52 | 03°01′ | 16°40′ | - | - |
| Niger | Niger | Tossaye | 53 | 00°35′ | 16°57′ | - | - |
| Niger | Niger | Ansongo | 54 | −00°30′ | 15°40′ | - | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bader, J.-C.; Dacosta, H.; Pouget, J.-C. Seasonal Variations of the Depletion Factor during Recession Periods in the Senegal, Gambia and Niger Watersheds. Water 2020, 12, 2520. https://doi.org/10.3390/w12092520
Bader J-C, Dacosta H, Pouget J-C. Seasonal Variations of the Depletion Factor during Recession Periods in the Senegal, Gambia and Niger Watersheds. Water. 2020; 12(9):2520. https://doi.org/10.3390/w12092520
Chicago/Turabian StyleBader, Jean-Claude, Honoré Dacosta, and Jean-Christophe Pouget. 2020. "Seasonal Variations of the Depletion Factor during Recession Periods in the Senegal, Gambia and Niger Watersheds" Water 12, no. 9: 2520. https://doi.org/10.3390/w12092520




