Sensitivity of Potential Groundwater Recharge to Projected Climate Change Scenarios: A Site-Specific Study in the Nebraska Sand Hills, USA
Abstract
:Highlights
- (1)
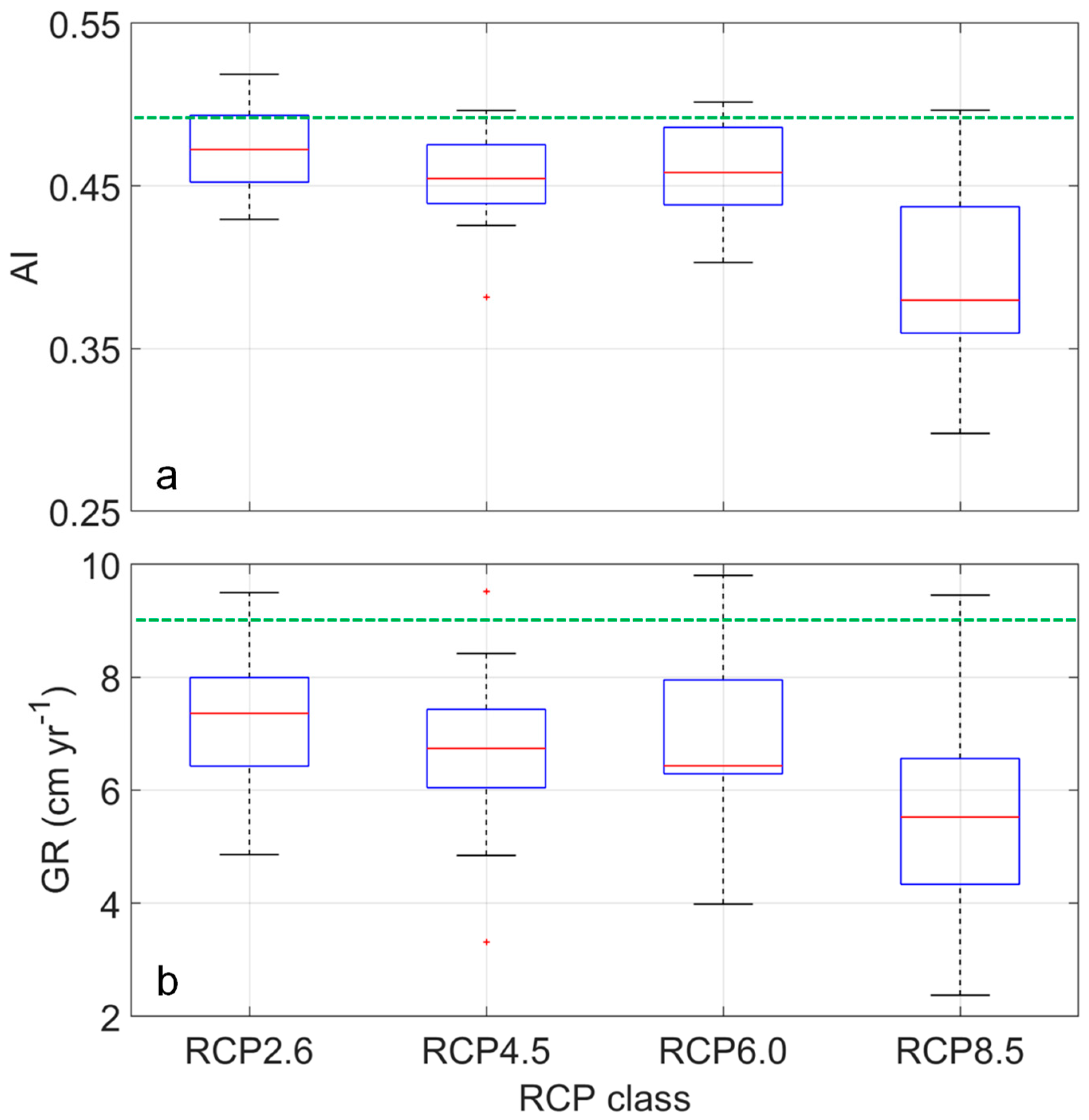
- Multi-decadal averages of groundwater recharge rates will likely decrease in all emission scenarios despite the region maintaining its historic climate classification as semi-arid.
- (2)
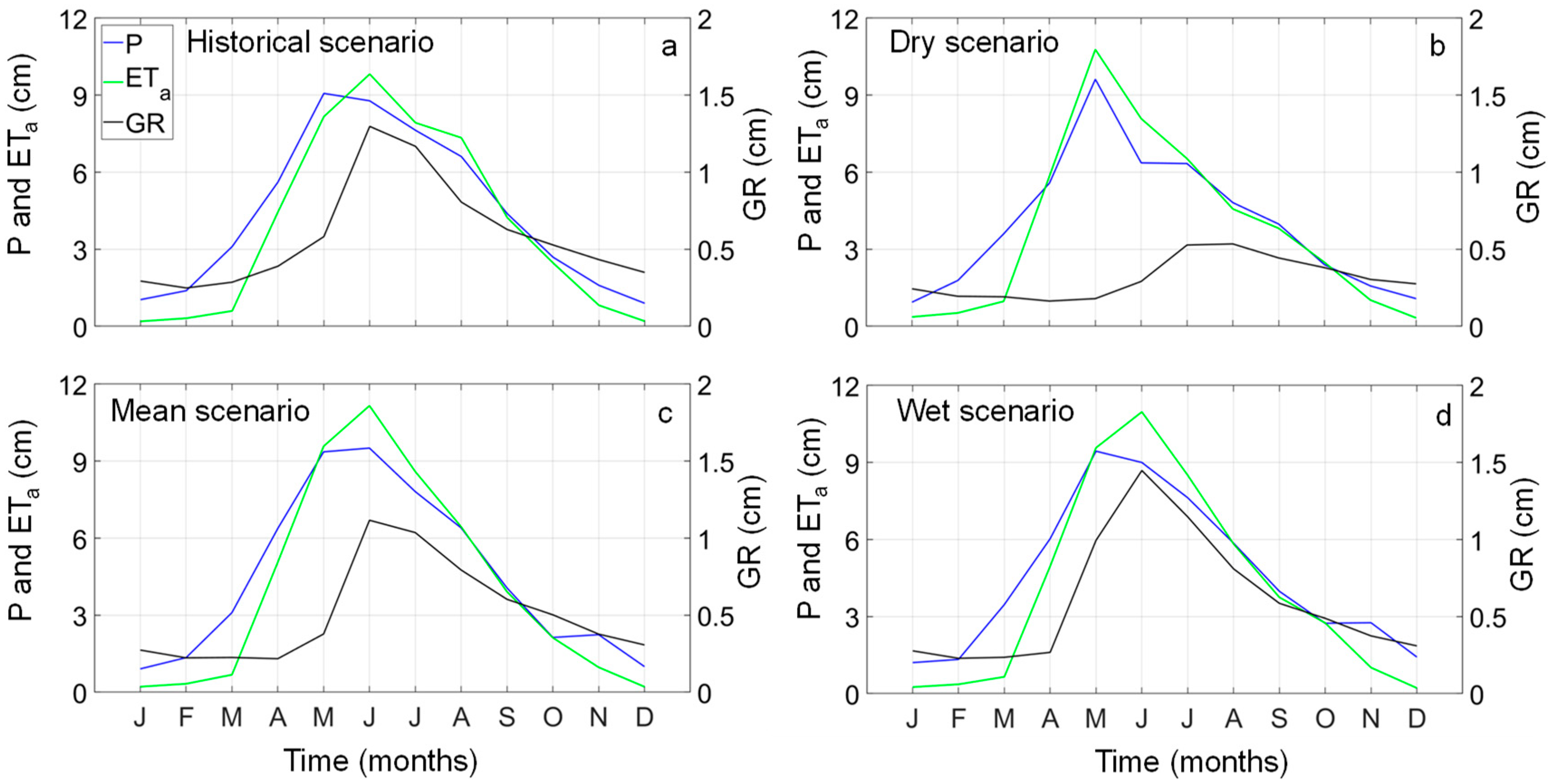
- In the dry climate scenario analysis, summer is the most sensitive season with a projected reduction in precipitation by 25% and in groundwater recharge rates by 60%.
- (3)
- The dry climate scenario indicates a notable increase in root water stress and a greater likelihood of desiccation of grass and desertification.
1. Introduction
2. Study Area and Modeling Approach
- (a)
- one numerical simulation under historic climate conditions (1950–2000);
- (b)
- sixty-five numerical simulations under future climate projections (2000–2100).
3. Results and Discussion
3.1. Multi-Decadal-Average Results of Historical and Projected ETa and GR
3.2. Annual-Average Results of Historical and Projected AI, ETa, and GR
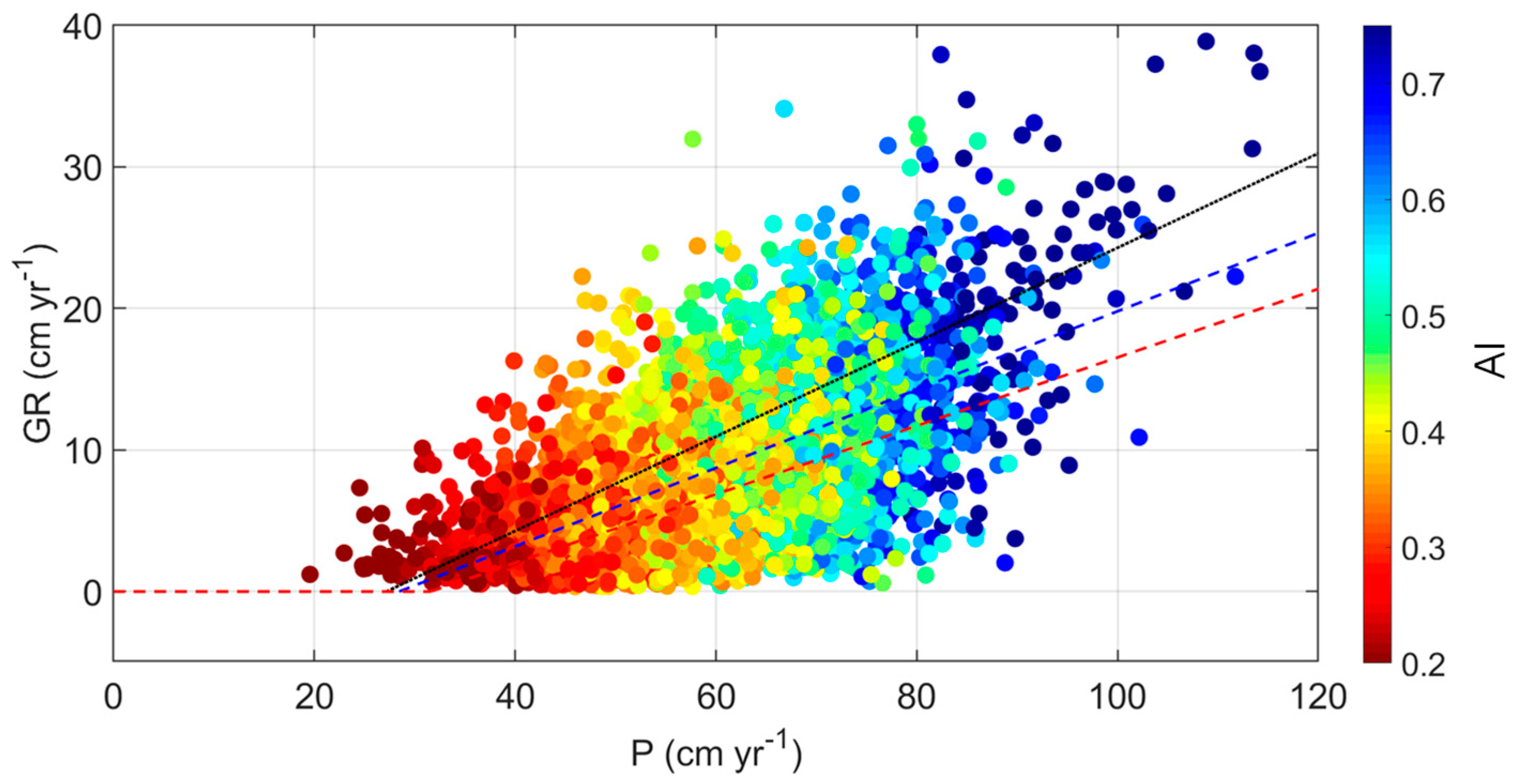
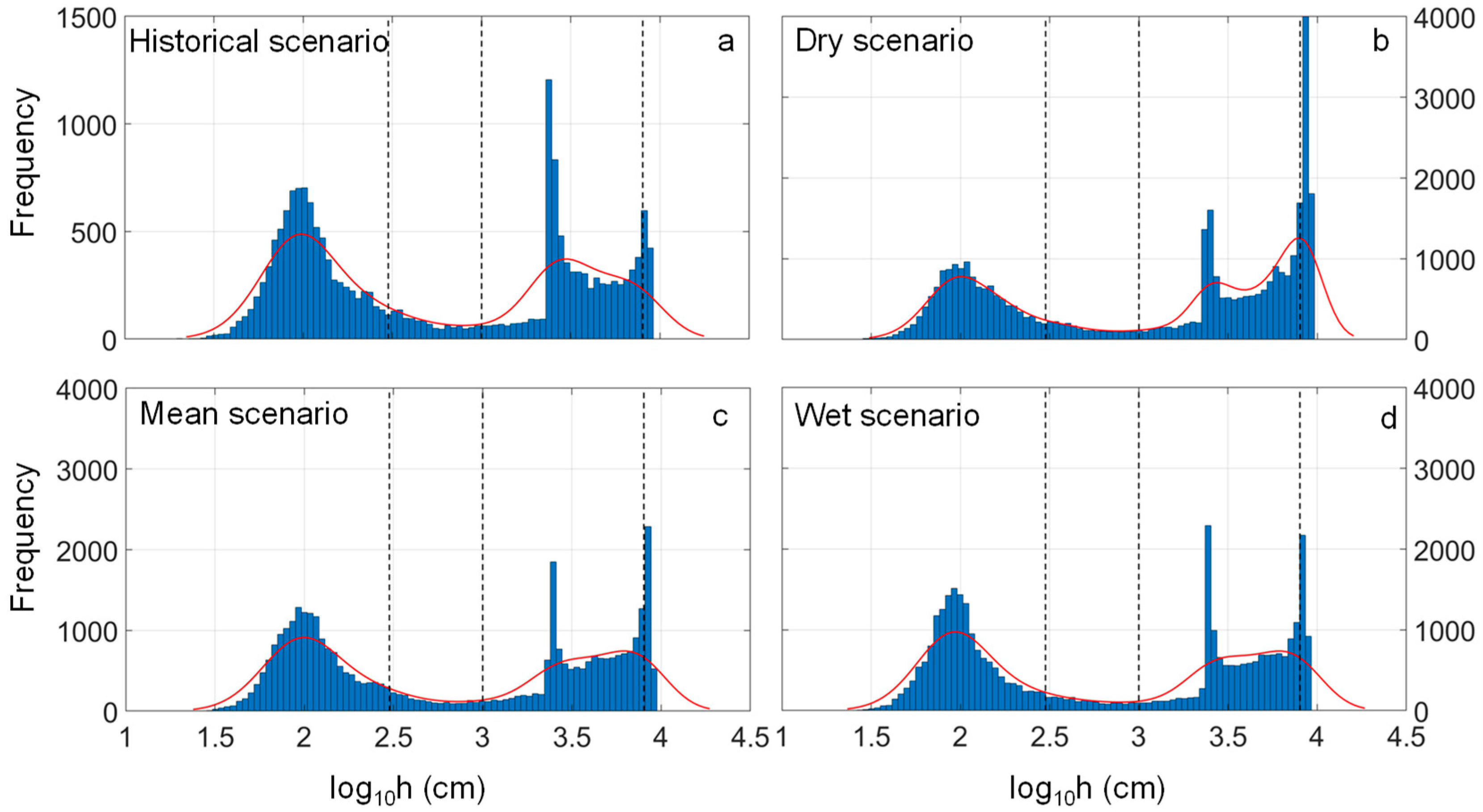
3.3. Selection of Three Representative Climate Projections for Assessing the Relation between Precipitation and Groundwater Recharge Rates at Sub-Annual Time Scale
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Data Sets | Model | P | ET0 | AI | ETp | ETa | GR |
|---|---|---|---|---|---|---|---|
| cm yr−1 | cm yr−1 | - | cm yr−1 | cm yr−1 | cm yr−1 | ||
| Historic data 1950–2000 | NA | 55.7 | 114.1 | 0.49 | 78.5 | 45.8 | 9.02 |
| RCP 2.6 2000–2100 | BCC_CSM | 56.9 | 124.0 | 0.46 | 85.3 | 49.2 | 8.0 |
| CANESM | 58.0 | 127.9 | 0.45 | 87.6 | 48.5 | 6.9 | |
| CCSM | 59.8 | 123.1 | 0.49 | 84.5 | 49.2 | 8.2 | |
| CESM_BGC | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | |
| CNRM_CM | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | |
| CSIRO | 56.6 | 125.3 | 0.45 | 86.6 | 46.0 | 7.2 | |
| GFDL_CM | 66.3 | 127.4 | 0.52 | 87.8 | 55.4 | 7.5 | |
| GFDL_G1 | 55.7 | 122.2 | 0.46 | 84.3 | 47.8 | 5.8 | |
| GFDL_M1 | 59.4 | 119.6 | 0.50 | 82.0 | 48.0 | 6.7 | |
| INMCM | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | |
| IPSL_CM | 57.9 | 123.3 | 0.47 | 86.4 | 49.1 | 5.9 | |
| IPSL_MR | 56.2 | 124.6 | 0.45 | 85.3 | 46.9 | 7.0 | |
| MIROC_ESM | 59.3 | 129.0 | 0.46 | 87.3 | 46.8 | 9.5 | |
| MIRCO_ESM | 60.6 | 128.4 | 0.47 | 88.9 | 49.5 | 7.4 | |
| MICROC | 53.9 | 125.6 | 0.43 | 85.5 | 47.3 | 4.9 | |
| MPI_LR | 56.4 | 120.7 | 0.47 | 83.0 | 48.6 | 6.3 | |
| MPI_MR | 61.9 | 120.4 | 0.51 | 82.8 | 50.6 | 9.2 | |
| MRI_GCM | 58.6 | 117.1 | 0.50 | 80.6 | 50.2 | 5.9 | |
| NORESM | 62.7 | 122.2 | 0.51 | 84.2 | 51.6 | 8.0 | |
| RCP 4.5 2000–2100 | BCC_CSM | 56.2 | 126.6 | 0.44 | 87.7 | 47.2 | 7.4 |
| CANESM | 58.3 | 129.8 | 0.45 | 89.3 | 48.4 | 7.2 | |
| CCSM | 57.5 | 126.8 | 0.45 | 88.2 | 46.9 | 6.2 | |
| CESM_BGC | 59.6 | 125.1 | 0.48 | 85.9 | 48.1 | 7.7 | |
| CNRM_CM | 58.2 | 124.3 | 0.47 | 85.5 | 47.4 | 8.5 | |
| CSIRO | 55.7 | 128.6 | 0.43 | 88.0 | 46.5 | 6.3 | |
| GFDL_CM | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | |
| GFDL_G1 | 59.5 | 123.7 | 0.48 | 85.3 | 49.8 | 6.0 | |
| GFDL_M1 | 60.7 | 120.9 | 0.50 | 82.7 | 50.7 | 6.0 | |
| INMCM | 54.5 | 121.7 | 0.45 | 83.8 | 44.8 | 7.5 | |
| IPSL_CM | 53.7 | 127.6 | 0.42 | 89.4 | 47.3 | 4.8 | |
| IPSL_MR | 54.1 | 128.3 | 0.42 | 87.7 | 45.7 | 6.8 | |
| MIROC_ESM | 60.3 | 131.6 | 0.46 | 89.7 | 49.0 | 9.5 | |
| MIRCO_ESM | 60.8 | 133.0 | 0.46 | 90.2 | 49.5 | 7.4 | |
| MICROC | 49.4 | 132.8 | 0.37 | 89.7 | 44.1 | 3.3 | |
| MPI_LR | 56.5 | 124.2 | 0.45 | 85.6 | 47.5 | 6.7 | |
| MPI_MR | 58.9 | 124.8 | 0.47 | 85.8 | 48.9 | 8.4 | |
| MRI_GCM | 58.7 | 119.8 | 0.49 | 82.4 | 49.8 | 5.6 | |
| NORESM | 59.1 | 127.1 | 0.46 | 87.5 | 50.8 | 8.4 | |
| RCP 6.0 2000–2100 | BCC_CSM | 61.7 | 126.1 | 0.49 | 87.0 | 49.1 | 9.8 |
| CANESM | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | |
| CCSM | 56.2 | 126.6 | 0.44 | 87.2 | 47.5 | 6.3 | |
| CESM_BGC | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | |
| CNRM_CM | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | |
| CSIRO | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | |
| GFDL_CM | 65.3 | 128.5 | 0.51 | 88.6 | 55.2 | 8.2 | |
| GFDL_G1 | 59.0 | 124.2 | 0.47 | 85.2 | 50.9 | 6.4 | |
| GFDL_M1 | 59.3 | 121.9 | 0.49 | 83.7 | 49.3 | 7.2 | |
| INMCM | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | |
| IPSL_CM | 55.7 | 126.5 | 0.44 | 88.2 | 46.6 | 6.3 | |
| IPSL_MR | 52.5 | 129.1 | 0.41 | 88.2 | 43.6 | 6.4 | |
| MIROC_ESM | 60.1 | 130.8 | 0.46 | 88.8 | 48.6 | 7.7 | |
| MIRCO_ESM | 59.6 | 131.6 | 0.45 | 89.3 | 48.5 | 8.9 | |
| MICROC | 52.4 | 128.4 | 0.41 | 88.1 | 45.9 | 4.0 | |
| MPI_LR | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | |
| MPI_MR | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | |
| MRI_GCM | 58.2 | 118.5 | 0.49 | 81.8 | 50.6 | 5.8 | |
| NORESM | 57.4 | 126.1 | 0.46 | 86.5 | 48.4 | 6.4 | |
| RCP 8.5 2000–2100 | BCC_CSM | 60.8 | 163.2 | 0.37 | 89.7 | 48.5 | 9.5 |
| CANESM | 62.4 | 133.5 | 0.47 | 112.6 | 52.6 | 6.8 | |
| CCSM | 61.0 | 165.1 | 0.37 | 110.1 | 51.5 | 5.5 | |
| CESM_BGC | 60.7 | 128.0 | 0.47 | 107.6 | 52.1 | 5.6 | |
| CNRM_CM | 56.7 | 128.7 | 0.44 | 108.4 | 49.2 | 5.2 | |
| CSIRO | 54.0 | 131.8 | 0.41 | 111.7 | 48.0 | 3.9 | |
| GFDL_CM | 67.8 | 131.4 | 0.52 | 110.8 | 58.4 | 6.6 | |
| GFDL_G1 | 59.0 | 161.8 | 0.36 | 109.2 | 52.2 | 4.8 | |
| GFDL_M1 | 60.2 | 158.1 | 0.38 | 107.1 | 51.8 | 6.4 | |
| INMCM | 53.2 | 125.6 | 0.42 | 108.3 | 46.5 | 5.1 | |
| IPSL_CM | 54.7 | 164.9 | 0.33 | 113.3 | 47.8 | 4.0 | |
| IPSL_MR | 49.8 | 166.9 | 0.30 | 112.7 | 44.3 | 3.4 | |
| MIROC_ESM | 60.3 | 170.5 | 0.35 | 112.8 | 50.6 | 7.8 | |
| MIRCO_ESM | 61.5 | 170.4 | 0.36 | 113.5 | 52.4 | 6.1 | |
| MICROC | 51.8 | 167.8 | 0.31 | 111.7 | 47.3 | 2.4 | |
| MPI_LR | 54.8 | 130.9 | 0.42 | 110.4 | 48.6 | 4.2 | |
| MPI_MR | 61.2 | 127.7 | 0.48 | 108.1 | 50.8 | 6.6 | |
| MRI_GCM | 61.0 | 153.7 | 0.40 | 104.0 | 52.9 | 5.6 | |
| NORESM | 57.7 | 165.9 | 0.35 | 111.5 | 50.2 | 5.3 |
References
- Eckhardt, K.; Ulbrich, U. Potential impacts of climate change on groundwater recharge and streamflow in a central European low mountain range. J. Hydrol. 2003, 284, 244–252. [Google Scholar] [CrossRef]
- Ng, G.-H.C.; McLaughlin, D.; Entekhabi, D.; Scanlon, B.R. Probabilistic analysis of the effects of climate change on groundwater recharge. Water Resour. Res. 2010, 46, 1–18. [Google Scholar] [CrossRef]
- Kim, J.H.; Jackson, R.B. A Global Analysis of Groundwater Recharge for Vegetation, Climate, and Soils. Vadose Zone J. 2012, 11. [Google Scholar] [CrossRef] [Green Version]
- Nasta, P.; Gates, J.B.; Wada, Y. Impact of climate indicators on continental-scale potential groundwater recharge in Africa. Hydrol. Process. 2016, 30, 3420–3433. [Google Scholar] [CrossRef] [PubMed]
- Terrell, B.L.; Johnson, P.N.; Segarra, E. Ogallala aquifer depletion: Economic impact on the Texas high plains. Water Policy 2002, 4, 33–46. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Keese, K.E.; Flint, A.L.; Flint, L.E.; Gaye, C.B.; Edmunds, W.M.; Simmers, I. Global synthesis of groundwater recharge in semiarid and arid regions. Hydrol. Process. 2006, 20, 3335–3370. [Google Scholar] [CrossRef]
- Cheng, L.; Hoerling, M.; Aghakouchak, A.; Livneh, B.; Quan, X.W.; Eischeid, J. How has human-induced climate change affected California drought risk? J. Clim. 2016, 29, 111–120. [Google Scholar] [CrossRef]
- Carson, M.; Köhl, A.; Stammer, D.; Slangen, A.A.B.; Katsman, C.A.; van de Wal, R.S.W.; Church, J.; White, N. Coastal sea level changes, observed and projected during the 20th and 21st century. Clim. Chang. 2016, 134, 269–281. [Google Scholar] [CrossRef]
- Turco, M.; Llasat, M.C.; von Hardenberg, J.; Provenzale, A. Climate change impacts on wildfires in a Mediterranean environment. Clim. Chang. 2014, 125, 369–380. [Google Scholar] [CrossRef]
- Mori, N.; Yasuda, T.; Mase, H.; Tom, T.; Oku, Y. Projection of Extreme Wave Climate Change under Global Warming. Hydrol. Res. Lett. 2010, 4, 15–19. [Google Scholar] [CrossRef]
- Arnell, N.W.; Gosling, S.N. The impacts of climate change on river flood risk at the global scale. Clim. Chang. 2016, 134, 387–401. [Google Scholar] [CrossRef]
- Bellard, C.; Bertelsmeier, C.; Leadley, P.; Thuiller, W.; Courchamp, F. Impacts of climate change on the future of biodiversity. Ecol. Lett. 2012, 15, 365–377. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gunkel, A.; Shadeed, S.; Hartmann, A.; Wagener, T.; Lange, J. Model signatures and aridity indices enhance the accuracy of water balance estimations in a data-scarce Eastern Mediterranean catchment. J. Hydrol. Reg. Stud. 2015, 4, 487–501. [Google Scholar] [CrossRef] [Green Version]
- Milly, P.C.D.; Dunne, K.A. Potential evapotranspiration and continental drying. Nat. Clim. Chang. 2016, 6, 946. [Google Scholar] [CrossRef]
- Trenberth, K.E. Changes in precipitation with climate change. Clim. Res. 2011, 47, 123–138. [Google Scholar] [CrossRef] [Green Version]
- Graham, L.P.; Andreáasson, J.; Carlsson, B. Assessing climate change impacts on hydrology from an ensemble of regional climate models, model scales and linking methods—A case study on the Lule River basin. Clim. Chang. 2007, 81, 293–307. [Google Scholar] [CrossRef]
- Kling, H.; Fuchs, M.; Paulin, M. Runoff conditions in the upper Danube basin under an ensemble of climate change scenarios. J. Hydrol. 2012, 424–425, 264–277. [Google Scholar] [CrossRef]
- Huang, J.; Zhang, Z.; Feng, Y.; Hong, H. Hydrologic response to climate change and human activities in a subtropical coastal watershed of southeast China. Reg. Environ. Chang. 2013, 13, 1195–1210. [Google Scholar] [CrossRef]
- López-Moreno, J.I.; Zabalza, J.; Vicente-Serrano, S.M.; Revuelto, J.; Gilaberte, M.; Azorin-Molina, C.; Morán-Tejeda, E.; García-Ruiz, J.M.; Tague, C. Impact of climate and land use change on water availability and reservoir management: Scenarios in the Upper Arago’n River, Spanish Pyrenees. Sci. Total Environ. 2014, 493, 1222–1231. [Google Scholar] [CrossRef]
- Le Roux, P.C.; Aalto, J.; Luoto, M. Soil moisture’s underestimated role in climate change impact modelling in low-energy systems. Glob. Chang. Biol. 2013, 19, 2965–2975. [Google Scholar] [CrossRef]
- Goderniaux, P.; Brouyère, S.; Fowler, H.J.; Blenkinsop, S.; Therrien, R.; Orban, P.; Dassargues, A. Large scale surface-subsurface hydrological model to assess climate change impacts on groundwater reserves. J. Hydrol. 2009, 373, 122–138. [Google Scholar] [CrossRef]
- Herrmann, F.; Baghdadi, N.; Blaschek, M.; Deidda, R.; Duttmann, R.; La Jeunesse, I.; Sellami, H.; Vereecken, H.; Wendland, F. Simulation of future groundwater recharge using a climate model ensemble and SAR-image based soil parameter distributions—A case study in an intensively-used Mediterranean catchment. Sci. Total Environ. 2016, 543, 889–905. [Google Scholar] [CrossRef]
- Meixner, T.; Manning, A.H.; Stonestrom, D.A.; Allen, D.M.; Ajami, H.; Blasch, K.W.; Brookfield, A.E.; Castro, C.L.; Clark, J.F.; Gochis, D.J.; et al. Implications of projected climate change for groundwater recharge in the western United States. J. Hydrol. 2016, 534, 124–138. [Google Scholar] [CrossRef] [Green Version]
- Taylor, R.G.; Scanlon, B.; Döll, P.; Rodell, M.; Van Beek, R.; Wada, Y.; Longuevergne, L.; Leblanc, M.; Famiglietti, J.S.; Edmunds, M.; et al. Ground water and climate change. Nat. Clim. Chang. 2013, 3, 322. [Google Scholar] [CrossRef]
- Kitabata, H.; Nishizawa, K.; Yoshida, Y.; Maruyama, K. Permafrost Thawing in Circum-Arctic and Highlands under Climatic Change Scenario Projected by Community Climate System Model (CCSM3). SOLA 2006, 2, 53–56. [Google Scholar] [CrossRef] [Green Version]
- Nyenje, P.M.; Batelaan, O. Estimating the effects of climate change on groundwater recharge and baseflow in the upper Ssezibwa catchment, Uganda. Hydrol. Sci. J. 2009, 54, 713–726. [Google Scholar] [CrossRef] [Green Version]
- Crosbie, R.S.; McCallum, J.L.; Walker, G.R.; Chiew, F.H.S. Modelling climate-change impacts on groundwater recharge in the Murray-Darling Basin, Australia. Hydrogeol. J. 2010, 18, 1639–1656. [Google Scholar] [CrossRef]
- Goodarzi, M.; Abedi-Koupai, J.; Heidarpour, M.; Safavi, H.R. Evaluation of the Effects of Climate Change on Groundwater Recharge Using a Hybrid Method. Water Resour. Manag. 2016, 30, 133–148. [Google Scholar] [CrossRef]
- Bouraoui, F.; Vachaud, G.; Li, L.Z.X.; Le Treut, H.; Chen, T. Evaluation of the impact of climate changes on water storage and groundwater recharge at the watershed scale. Clim. Dyn. 1999, 15, 153–161. [Google Scholar] [CrossRef]
- Green, T.R.; Taniguchi, M.; Kooi, H.; Gurdak, J.J.; Allen, D.M.; Hiscock, K.M.; Treidel, H.; Aureli, A. Beneath the surface of global change: Impacts of climate change on groundwater. J. Hydrol. 2011, 405, 532–560. [Google Scholar] [CrossRef]
- Rossman, N.R.; Zlotnik, V.A.; Rowe, C.M.; Szilagyi, J. Vadose zone lag time and potential 21st century climate change effects on spatially distributed groundwater recharge in the semi-arid Nebraska Sand Hills. J. Hydrol. 2014, 519, 656–669. [Google Scholar] [CrossRef] [Green Version]
- Adane, Z.; Nasta, P.; Gates, J.B. Links between soil hydrophobicity and groundwater recharge under plantations in a sandy grassland setting, Nebraska Sand Hills, USA. For. Sci. 2017, 63, 388–401. [Google Scholar] [CrossRef]
- Adane, Z.A.; Nasta, P.; Zlotnik, V.; Wedin, D. Impact of grassland conversion to forest on groundwater recharge in the Nebraska Sand Hills. J. Hydrol. Reg. Stud. 2018, 15, 171–183. [Google Scholar] [CrossRef]
- Rossman, N.R.; Zlotnik, V.A.; Rowe, C.M. Using cumulative potential recharge for selection of GCM projections to force regional groundwater models: A Nebraska Sand Hills example. J. Hydrol. 2018, 561, 1105–1114. [Google Scholar] [CrossRef]
- Miao, X.; Mason, J.A.; Johnson, W.C.; Wang, H. High-resolution proxy record of Holocene climate from a loess section in Southwestern Nebraska, USA. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2007, 245, 368–381. [Google Scholar] [CrossRef]
- Wang, T.; Wedin, D.; Zlotnik, V.A. Field evidence of a negative correlation between saturated hydraulic conductivity and soil carbon in a sandy soil. Water Resour. Res. 2009. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Faunt, C.C.; Longuevergne, L.; Reedy, R.C.; Alley, W.M.; McGuire, V.L.; McMahon, P.B. Groundwater depletion and sustainability of irrigation in the US High Plains and Central Valley. Proc. Natl. Acad. Sci. USA 2012, 109, 9320–9325. [Google Scholar] [CrossRef] [Green Version]
- Allen, R.G. FAO Irrigation and Drainage Paper Crop by. Irrig. Drain. 1998, 300, 300. [Google Scholar]
- Adane, Z.A.; Gates, J.B. Determining the impacts of experimental forest plantation on groundwater recharge in the Nebraska Sand Hills (USA) using chloride and sulfate. Hydrogeol. J. 2015, 23, 81–94. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Allen, R.G. History and Evaluation of Hargreaves Evapotranspiration Equation. J. Irrig. Drain. Eng. 2003, 129, 53–63. [Google Scholar] [CrossRef]
- Pelosi, A.; Medina, H.; Villani, P.; D’Urso, G.; Chirico, G.B. Probabilistic forecasting of reference evapotranspiration with a limited area ensemble prediction system. Agric. Water Manag. 2016, 178, 106–118. [Google Scholar] [CrossRef]
- Droogers, P.; Allen, R.G. Estimating reference evapotranspiration under inaccurate data conditions. Irrig. Drain. Syst. 2002, 16, 33–45. [Google Scholar] [CrossRef]
- Archibald, J.A.; Walter, M.T. Do energy-based PET models require more input data than temperature-based models?—An evaluation at four humid fluxnet sites. J. Am. Water Resour. Assoc. 2014, 50, 497–508. [Google Scholar] [CrossRef]
- Huo, Z.; Dai, X.; Feng, S.; Kang, S.; Huang, G. Effect of climate change on reference evapotranspiration and aridity index in arid region of China. J. Hydrol. 2013, 492, 24–34. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, D.; Luo, Y.; Liu, C. Spatial and temporal changes in aridity index in northwest China: 1960 to 2010. Theor. Appl. Climatol. 2013, 112, 307–316. [Google Scholar] [CrossRef]
- Nastos, P.T.; Politi, N.; Kapsomenakis, J. Spatial and temporal variability of the Aridity Index in Greece. Atmos. Res. 2013, 119, 140–152. [Google Scholar] [CrossRef]
- Zhang, K.X.; Pan, S.M.; Zhang, W.; Xu, Y.H.; Cao, L.G.; Hao, Y.P.; Wang, Y. Influence of climate change on reference evapotranspiration and aridity index and their temporal-spatial variations in the Yellow River Basin, China, from 1961 to 2012. Quat. Int. 2015, 380, 75–82. [Google Scholar] [CrossRef]
- Arora, V.K. The use of the aridity index to assess climate change effect on annual runoff. J. Hydrol. 2002, 265, 164–177. [Google Scholar] [CrossRef]
- Nkomozepi, T.; Chung, S.O. The effects of climate change on the water resources of the Geumho River Basin, Republic of Korea. J. Hydro-Environ. Res. 2014, 8, 358–366. [Google Scholar] [CrossRef]
- Gudmundsson, L.; Greve, P.; Seneviratne, S.I. The sensitivity of water availability to changes in the aridity index and other factors—A probabilistic analysis in the Budyko space. Geophys. Res. Lett. 2016, 43, 6985–6994. [Google Scholar] [CrossRef]
- Šimůnek, J.; van Genuchten, M.T.; Šejna, M. Recent developments and applications of the HYDRUS computer software packages. Vadose Zone J. 2016, 15, 25. [Google Scholar] [CrossRef]
- Nasta, P.; Gates, J.B. Plot-scale modeling of soil water dynamics and impacts of drought conditions beneath rainfed maize in Eastern Nebraska. Agric. Water Manag. 2013, 128, 120–130. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils1. Soil Sci. Soc. Am. J. 1980, 44, 892. [Google Scholar] [CrossRef]
- Spinoni, J.; Vogt, J.; Naumann, G.; Carrao, H.; Barbosa, P. Towards identifying areas at climatological risk of desertification using the Köppen-Geiger classification and FAO aridity index. Int. J. Climatol. 2015, 35, 2210–2222. [Google Scholar] [CrossRef]
- Billesbach, D.P.; Arkebauer, T.J. First long-term, direct measurements of evapotranspiration and surface water balance in the Nebraska SandHills. Agric. For. Meteorol. 2012, 156, 104–110. [Google Scholar] [CrossRef] [Green Version]
- Crosbie, R.S.; Scanlon, B.R.; Mpelasoka, F.S.; Reedy, R.C.; Gates, J.B.; Zhang, L. Potential climate change effects on groundwater recharge in the High Plains Aquifer, USA. Water Resour. Res. 2013, 49, 3936–3951. [Google Scholar] [CrossRef] [Green Version]
- Szilagyi, J.; Zlotnik, V.A.; Gates, J.B.; Jozsa, J. Mapping mean annual groundwater recharge in the Nebraska Sand Hills, USA. Hydrogeol. J. 2011, 19, 1503–1513. [Google Scholar] [CrossRef]
- Lauffenburger, Z.H.; Gurdak, J.J.; Hobza, C.; Woodward, D.; Wolf, C. Irrigated agriculture and future climate change effects on groundwater recharge, northern High Plains aquifer, USA. Agric. Water Manag. 2018, 204, 69–80. [Google Scholar] [CrossRef]
- Greve, P.; Seneviratne, S.I. Assessment of future changes in water availability and aridity. Geophys. Res. Lett. 2015, 42, 5493–5499. [Google Scholar] [CrossRef] [Green Version]
- Thomas, B.F.; Behrangi, A.; Famiglietti, J.S. Precipitation intensity effects on groundwater recharge in the southwestern United States. Water 2016, 8, 90. [Google Scholar] [CrossRef]
- Tabari, H.; Aghajanloo, M.B. Temporal pattern of aridity index in Iran with considering precipitation and evapotranspiration trends. Int. J. Climatol. 2013, 33, 396–409. [Google Scholar] [CrossRef]
- Oglesby, R.; Bathke, D.; Wilhite, D.; Rowe, C. Understanding and assessing projected future climate change for Nebraska and the great plains. Gt. Plains Res. 2015, 25, 97–107. [Google Scholar] [CrossRef]
- Dawes, W.; Zhang, L.; Dyce, P. WAVES V3.5 user manual. Available online: https://research.csiro.au/software/wp-content/uploads/sites/6/2016/07/preface.pdf (accessed on 4 September 2018).
- Liang, X.; Lettenmaier, D.P.; Wood, E.F.; Burges, S.J. A simple hydrologically based model of land surface water and energy fluxes for general circulation models. J. Geophys. Res. 2004, 99, 14415–14428. [Google Scholar] [CrossRef]
- Nasta, P.; Adane, Z.; Lock, N.; Houston, A.; Gates, J.B. Links between episodic groundwater recharge rates and rainfall events classified according to stratiform-convective storm scoring: A plot-scale study in eastern Nebraska. Agric. For. Meteorol. 2018, 259, 154–161. [Google Scholar] [CrossRef]



| Acronym | Institution | |
|---|---|---|
| 1 | BCC_CSM | Beijing Climate Center (China) |
| 2 | CANESM | Canadian Centre for Climate Modelling and Analysis (Canada) |
| 3 | CCSM | University Corporation for Atmospheric Research (UCAR) (USA) |
| 4 | CESM_BGC | NCAR Earth System Laboratory (USA) |
| 5 | CNRM_CM | National Centre for Meteorological Research |
| 6 | CSIRO | Commonwealth Scientific and Industrial Research Organization (Australia) |
| 7 | GFDL_CM | Geophysical Fluid Dynamics Laboratory (USA) |
| 8 | GFDL_G1 | Geophysical Fluid Dynamics Laboratory (USA) |
| 9 | GFDL_M1 | Geophysical Fluid Dynamics Laboratory (USA) |
| 10 | INMCM | Institute of Numerical Mathematics (Russia) |
| 11 | IPSL_CM | Institute Pierre-Simon Laplace (France) |
| 12 | IPSL_MR | Institute Pierre-Simon Laplace (France) |
| 13 | MIROC_ESM | Japan Agency for Marine-Earth Science and Technology (Japan) |
| 14 | MIRCO_ESM | Japan Agency for Marine-Earth Science and Technology (Japan) |
| 15 | MICROC | Japan Agency for Marine-Earth Science and Technology (Japan) |
| 16 | MPI_LR | Max Planck Institute (Germany) |
| 17 | MPI_MR | Max Planck Institute (Germany) |
| 18 | MRI_GCM | Meteorological Research Institute (Japan) |
| 19 | NORESM | Norwegian Climate Center (Norway) |
| Value | Class | Probability | Median GR |
|---|---|---|---|
| % | cm yr−1 | ||
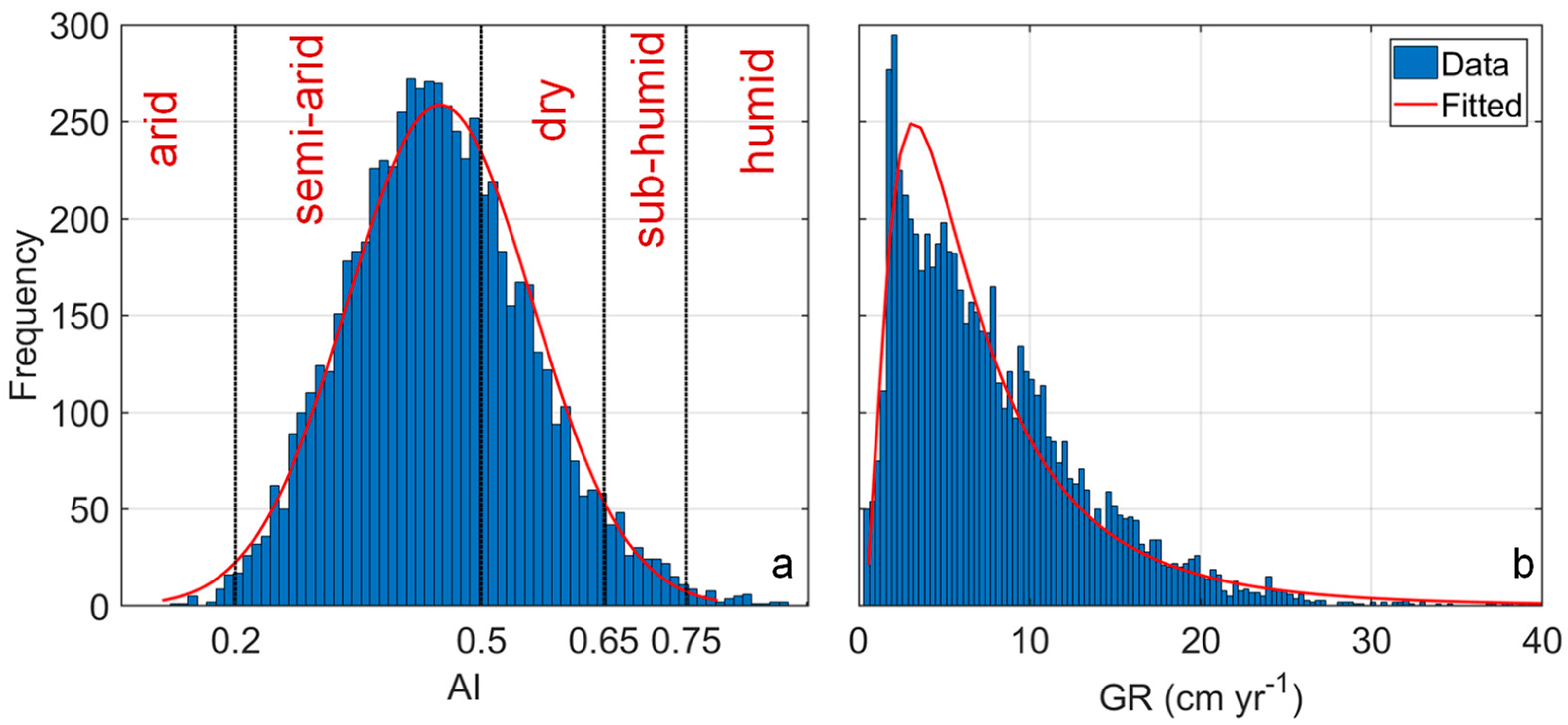
| AI ≤ 0.2 | Arid | 0.56 | 1.87 |
| 0.2 < AI ≤ 0.5 | Semi-arid | 68.58 | 5.19 |
| 0.5 < AI ≤ 0.65 | Dry | 26.24 | 9.64 |
| 0.65 < AI ≤ 0.75 | Sub-humid | 3.76 | 14.19 |
| A > 0.75 | Humid | 0.86 | 21.93 |
| Scenario | Regression Line | R2 |
|---|---|---|
| Historic | GR = 0.335P − 9.06 | 0.407 |
| RCP2.6 | GR = 0.2767P − 7.87 | 0.351 |
| RCP4.5 | GR = 0.2829P − 8.37 | 0.371 |
| RCP6.0 | GR = 0.2794P − 8.33 | 0.351 |
| RCP8.5 | GR = 0.2419P − 7.64 | 0.349 |
| Scenario | No Stress | Stress | Wilting Point |
|---|---|---|---|
| % | % | % | |
| Historic | 48.8 | 46.9 | 4.3 |
| Dry | 35.1 | 46.4 | 18.5 |
| Mean | 46.1 | 45.4 | 8.5 |
| Wet | 46.9 | 44.8 | 8.3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adane, Z.; Zlotnik, V.A.; Rossman, N.R.; Wang, T.; Nasta, P. Sensitivity of Potential Groundwater Recharge to Projected Climate Change Scenarios: A Site-Specific Study in the Nebraska Sand Hills, USA. Water 2019, 11, 950. https://doi.org/10.3390/w11050950
Adane Z, Zlotnik VA, Rossman NR, Wang T, Nasta P. Sensitivity of Potential Groundwater Recharge to Projected Climate Change Scenarios: A Site-Specific Study in the Nebraska Sand Hills, USA. Water. 2019; 11(5):950. https://doi.org/10.3390/w11050950
Chicago/Turabian StyleAdane, Zablon, Vitaly A. Zlotnik, Nathan R. Rossman, Tiejun Wang, and Paolo Nasta. 2019. "Sensitivity of Potential Groundwater Recharge to Projected Climate Change Scenarios: A Site-Specific Study in the Nebraska Sand Hills, USA" Water 11, no. 5: 950. https://doi.org/10.3390/w11050950
APA StyleAdane, Z., Zlotnik, V. A., Rossman, N. R., Wang, T., & Nasta, P. (2019). Sensitivity of Potential Groundwater Recharge to Projected Climate Change Scenarios: A Site-Specific Study in the Nebraska Sand Hills, USA. Water, 11(5), 950. https://doi.org/10.3390/w11050950





