Application of SWAT Model with CMADS Data to Estimate Hydrological Elements and Parameter Uncertainty Based on SUFI-2 Algorithm in the Lijiang River Basin, China
Abstract
:1. Introduction
2. Materials and Methods
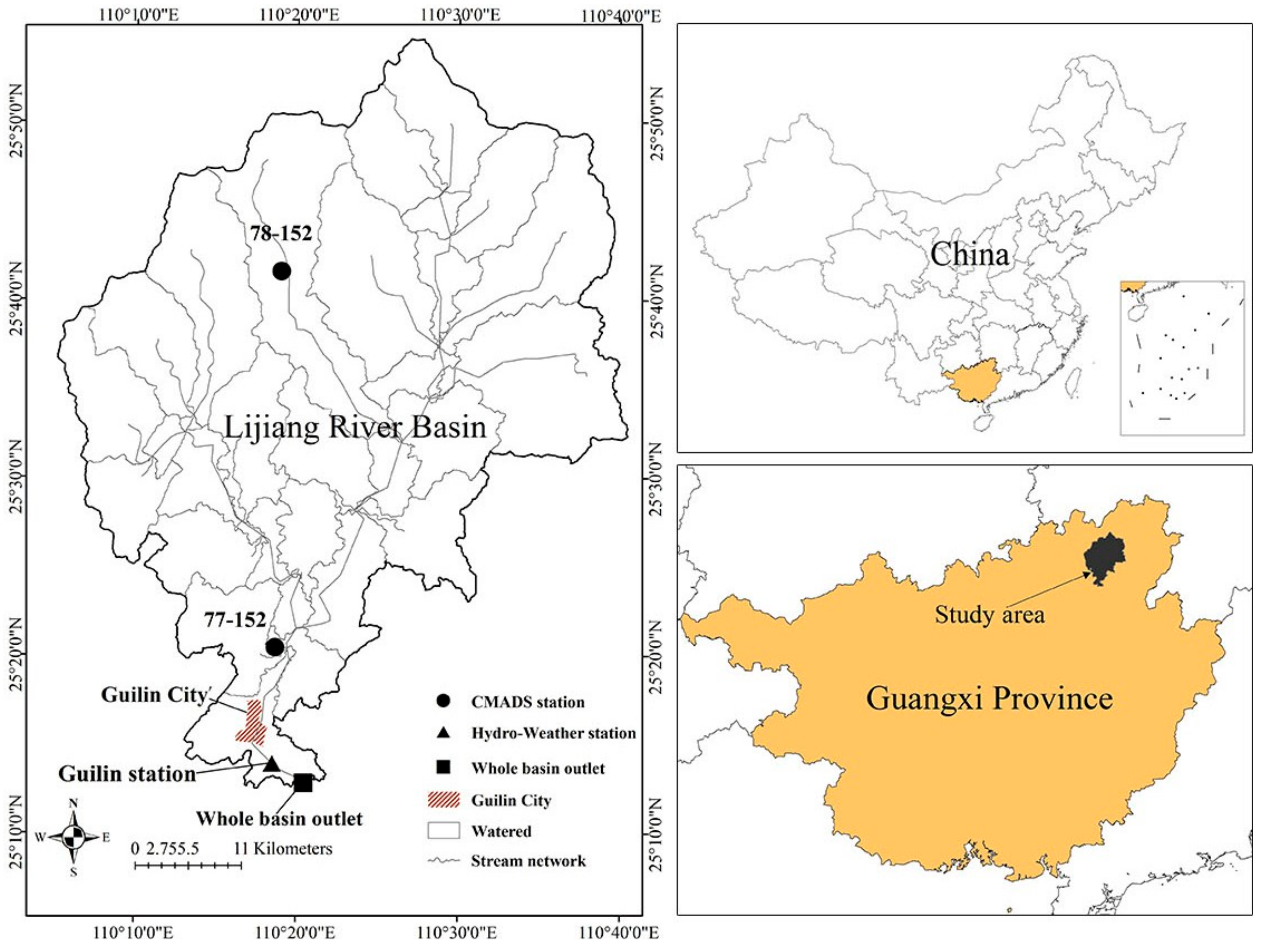
2.1. Study Area
2.2. SWAT Model Input
- (i)
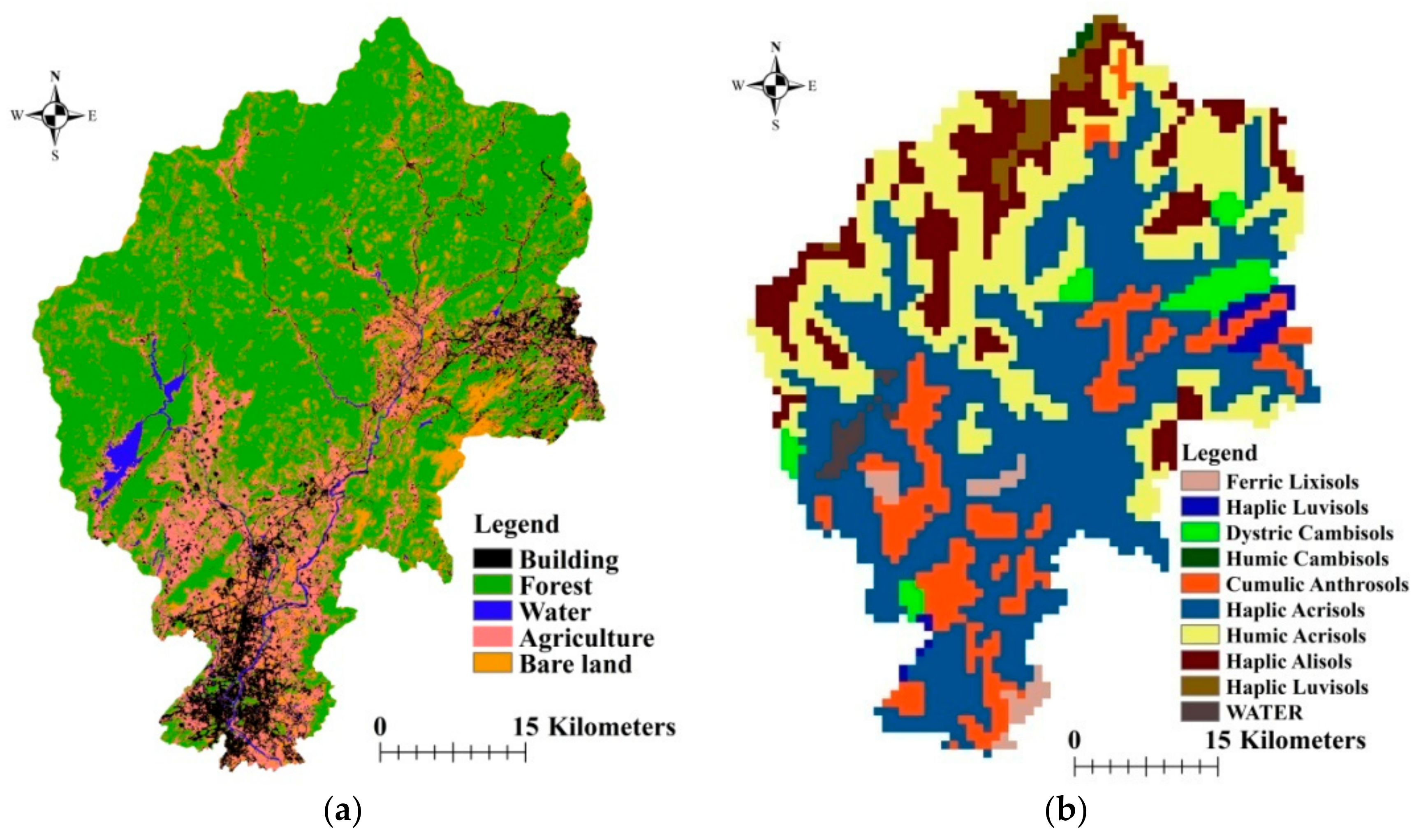
- The digital elevation model used is the first version of the Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) Global Digital Elevation Model (GDEM) (grid cell: 30 m × 30 m). The outliers have been processed, and the original Digital Elevation Model (DEM) has been spliced, cropped, and projected using ArcMAP (ESRI, Redlands, CA, America) software. Sub-watershed divisions, river formation, and slope reclassification were all generated from the pre-treated DEM.
- (ii)
- The soil data were taken from the 1:1 million soil dataset created by the Second National Land Survey Nanjing Soil Institute and were supplied by the Cold and Arid Regions Sciences Data Center at Lanzhou.
- (iii)
- The land use data were derived from Landsat-8 remote sensing data (multi-spectral band resolution of 30 m) after supervised classification and post-processing steps. The remote sensing data were provided by the Geospatial Data Cloud site, the Computer Network Information Center, the Chinese Academy of Sciences.
- (iv)
- The meteorological data are taken from the CMADS version 1.1 (http://www.cmads.org). This dataset includes precipitation, temperature, relative humidity, solar radiation, wind speed, location, and the elevation of each site. The data of temperature, relative humidity and wind speed were generated using the information from 2421 national automatic stations and 39,439 regional automatic stations. Precipitation was achieved through the integration of multiple satellite data and precipitation from ground automatic stations. The production of radiation data was based on the Discrete Ordinates Radiative Transfer (DISORT) radiative transfer model and the acquisition of products from the FY2E satellite primary product for inversion of solar shortwave radiation. Two CMADS weather stations are used in the study area.
- (v)
- The hydrological data were provided by the Guangxi Water Conservancy, and comprise measured daily and monthly data from 2008 to 2016 at the Guilin Hydrological Station.
3. Results and Analysis
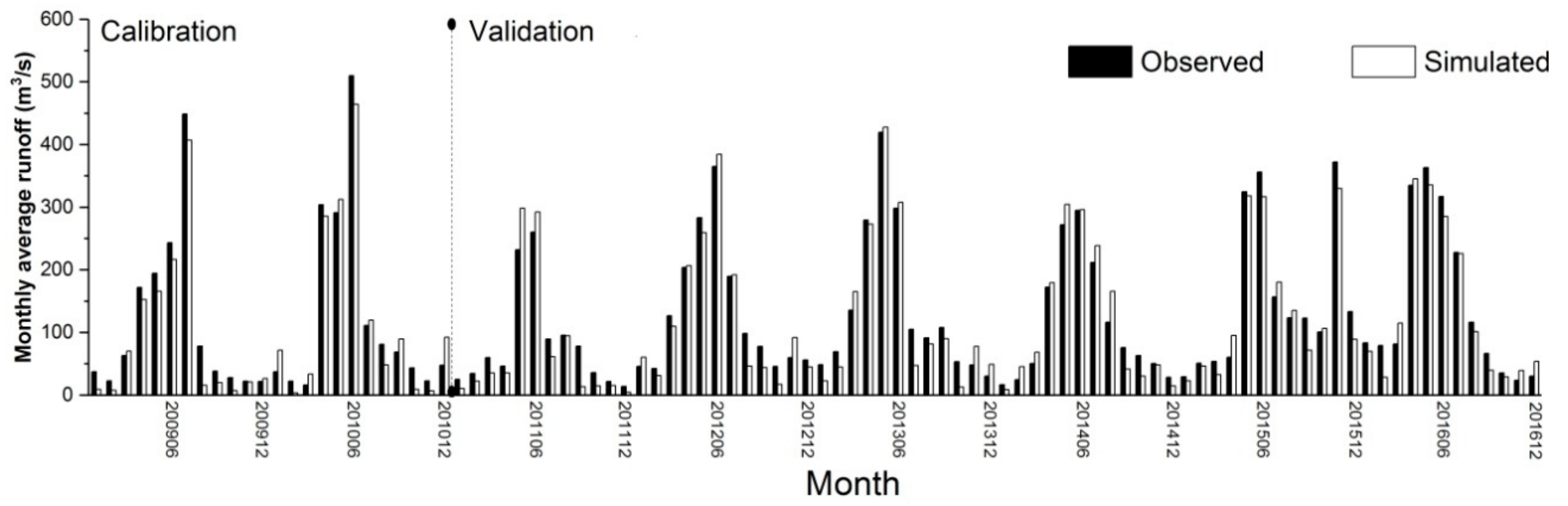
3.1. Model Calibration and Validation
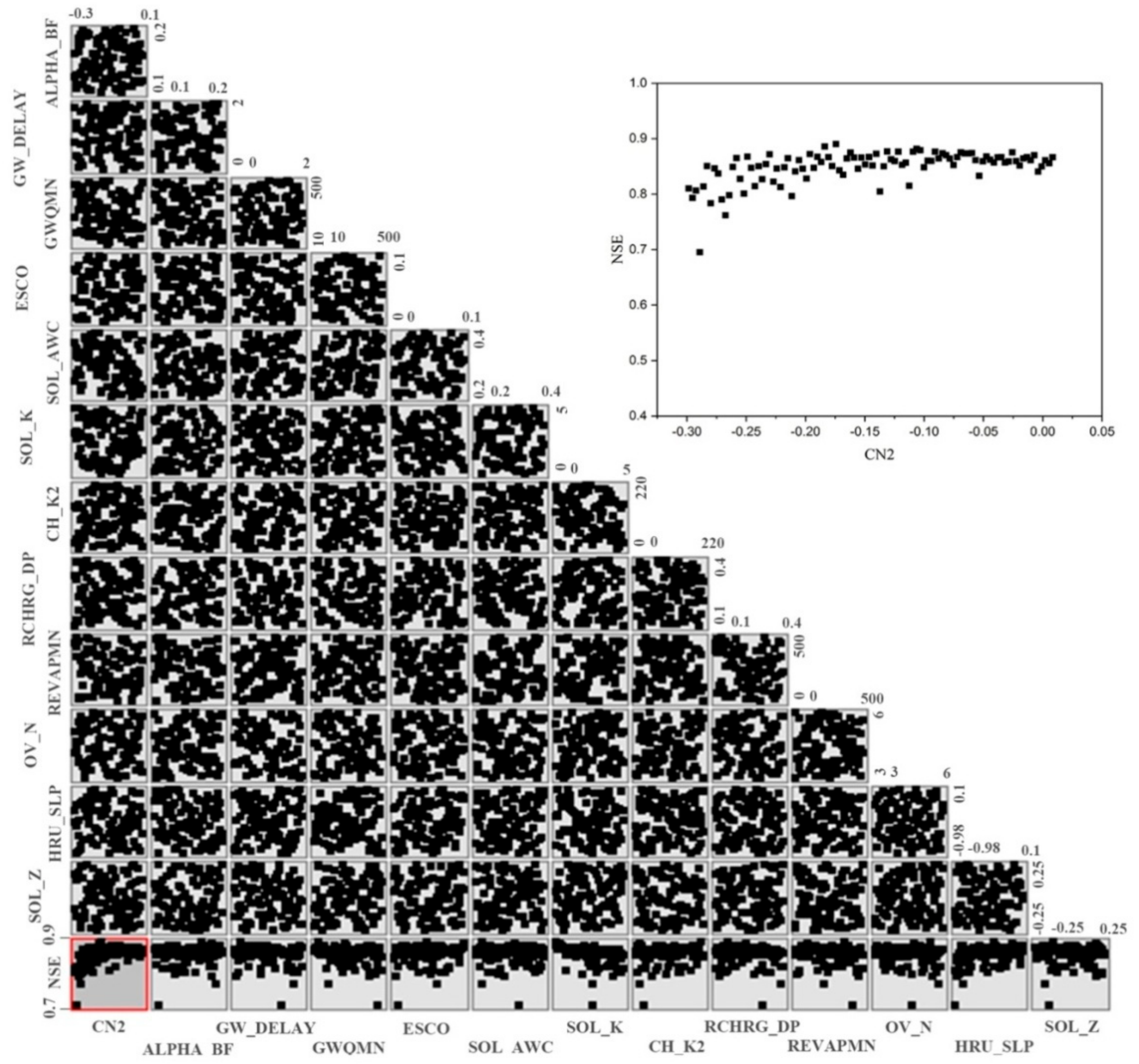
3.2. Uncertainty Analysis
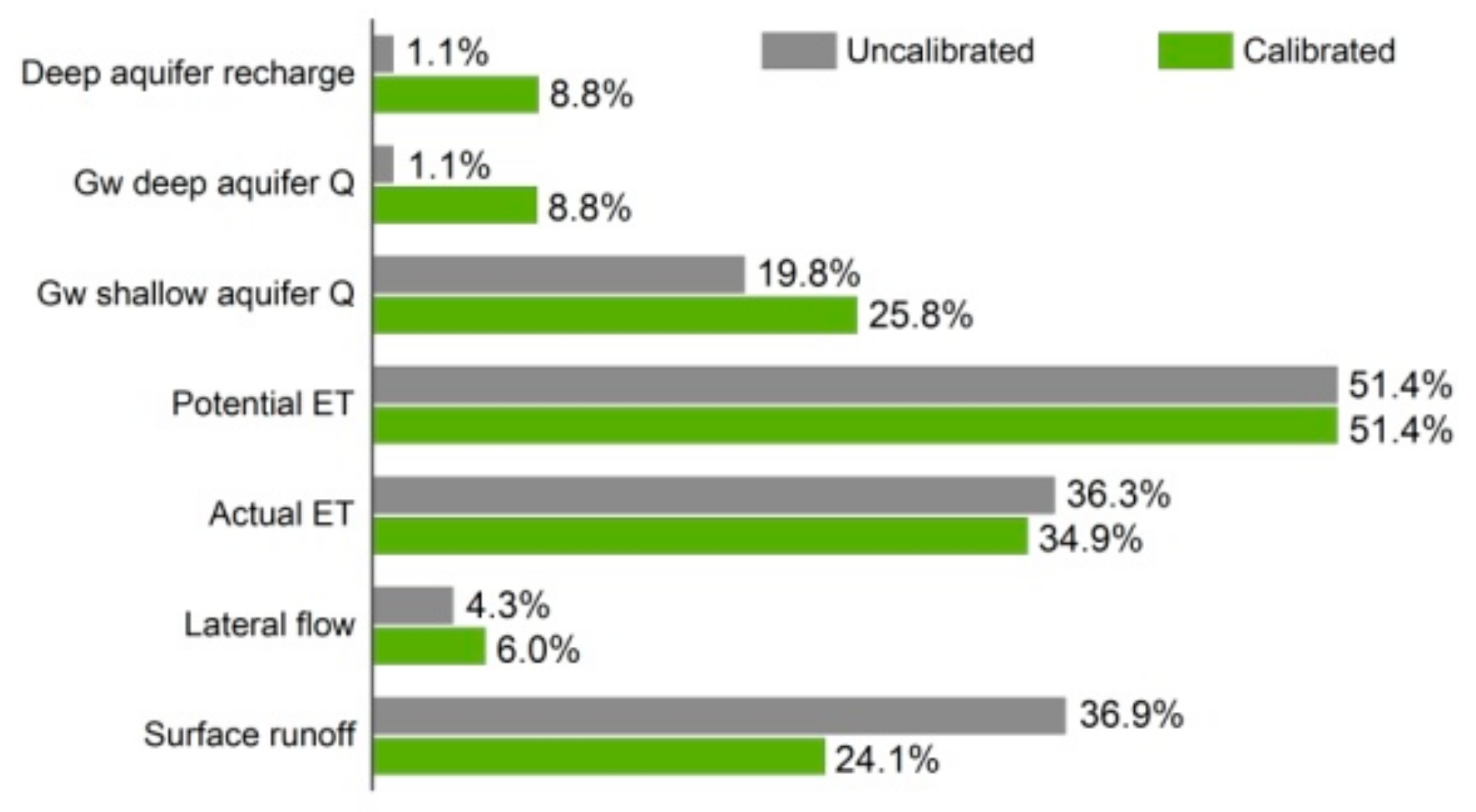
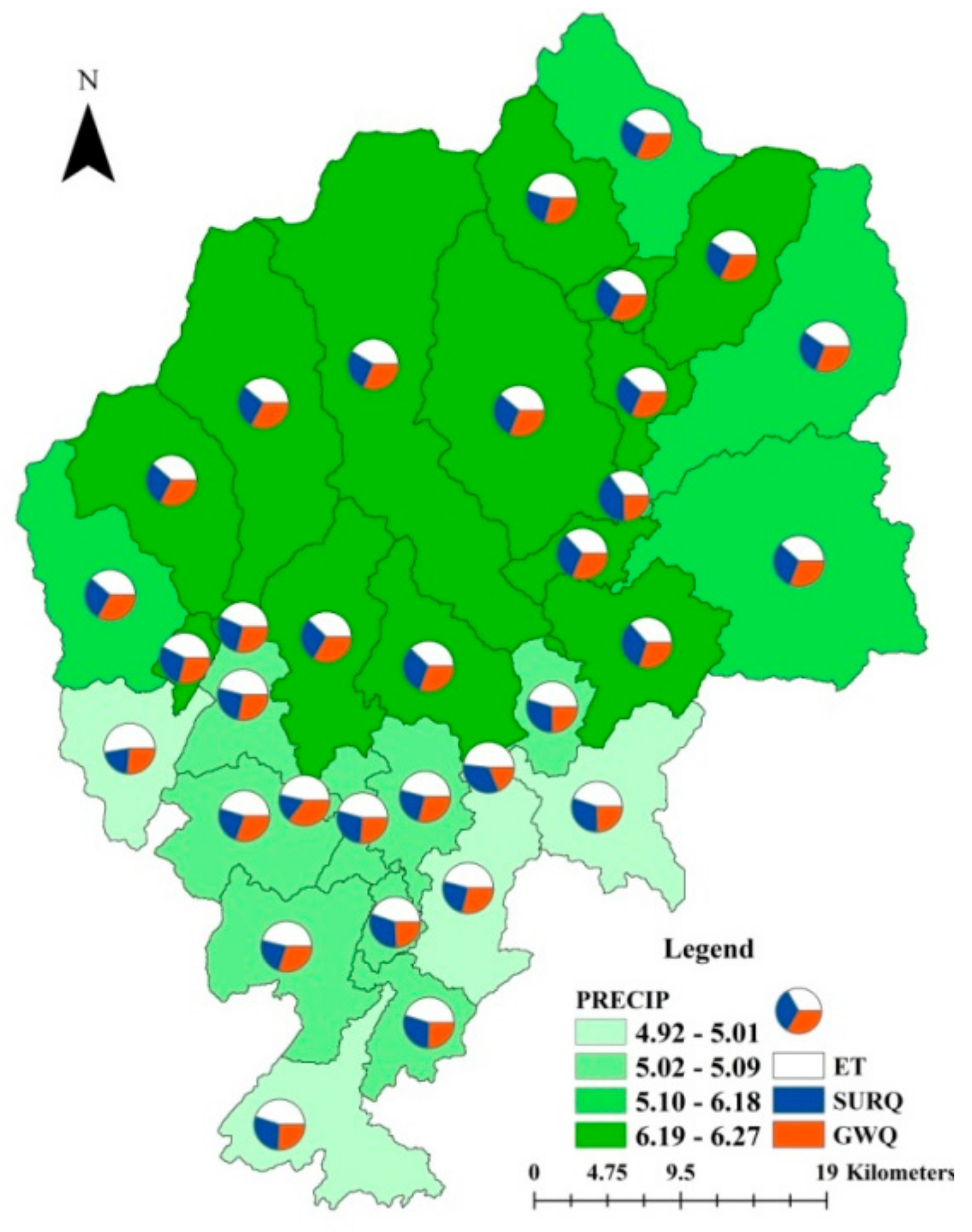
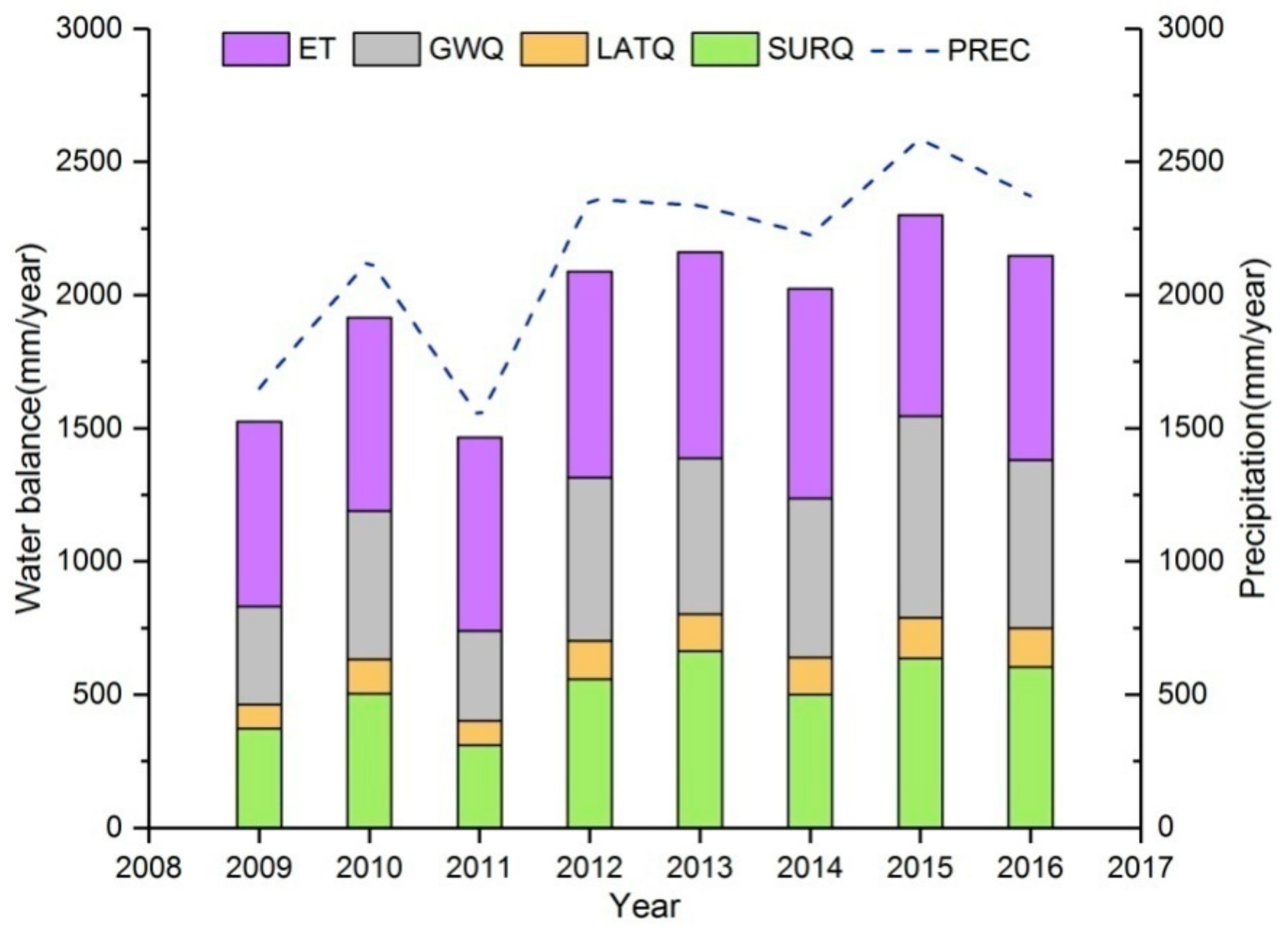
3.3. Water Balance Components
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Meng, X.; Wang, H.; Wu, Y.; Long, A.; Wang, J.; Shi, C.; Ji, X. Investigating spatiotemporal changes of the land-surface processes in Xinjiang using high-resolution CLM3.5 and CLDAS: Soil temperature. Sci. Rep. 2017, 7, 13286. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Meng, X.; Sun, Z.; Zhao, H.; Ji, X.; Wang, H.; Xue, L.; Wu, H.; Zhu, Y. Spring flood forecasting based on the WRF-TSRM mode. Teh. Vjesn. 2018, 25, 141–151. [Google Scholar] [CrossRef]
- Allen, M.R.; Ingram, W.J. Constraints on future changes in climate and the hydrologic cycle. Nature 2002, 419, 224–232. [Google Scholar] [CrossRef] [PubMed]
- Sandra, G.; Sathian, K.K. Assessment of water balance of a watershed using swat model for water resources management. Int. J. Eng. Sci. Res. Technol. 2016, 5, 177–184. [Google Scholar] [CrossRef]
- Arnold, J.G.; Allen, P.M. Estimating hydrologic budgets for three Illinois watersheds. J. Hydrol. 1996, 176, 57–77. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Q.; Guo, B.; Gong, H. The comparative study of multi-site uncertainty evaluation method based on SWAT model. Hydrol. Process. 2015, 29, 2994–3009. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment. Part I: Model development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Sophocleous, M.A.; Koelliker, J.K.; Govindaraju, R.S. Integrated numerical modeling for basin-wide water management: The case of the Rattlesnake Creek basin in south-central Kansans. J. Hydrol. 1999, 214, 179–196. [Google Scholar] [CrossRef]
- Eckhardt, K.; Haverkamp, S.; Fohrer, N.; Frede, H.G. SWAT-G, a version of SWAT99.2 modified for application to low mountain range catchments. Phys. Chem. Earth 2002, 27, 641–644. [Google Scholar] [CrossRef]
- Eckhardt, K.; Nicola, F.; Frede, H.G. Automatic model calibration. Hydrol. Process. 2005, 19, 651–658. [Google Scholar] [CrossRef]
- Easton, Z.M.; Fuka, D.R.; Walter, M.T.; Cowan, D.M.; Schneiderman, E.M.; Steenhuis, T.S. Re-conceptualizing the Soil and Water Assessment Tool (SWAT) model to predict runoff from variable source areas. J. Hydrol. 2008, 348, 279–291. [Google Scholar] [CrossRef]
- Meng, X.; Long, A.; Wu, Y.; Yin, G.; Wang, H.; Ji, X. Simulation and spatiotemporal pattern of air temperature and precipitation in Eastern Central Asia using RegCM. Sci. Rep. 2018, 8, 3639. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Meng, X.; Yu, D.; Liu, Z. Energy balance-based SWAT model to simulate the mountain snowmelt and runoff—Taking the application in Juntanghu watershed (China) as an example. J. Mt. Sci. 2015, 12, 368–381. [Google Scholar] [CrossRef]
- Meng, X.; Wang, H. Significance of the China Meteorological Assimilation Driving Datasets for the SWAT Model (CMADS) of East Asia. Water 2017, 9, 765–769. [Google Scholar] [CrossRef]
- Liu, J.; Shangguan, D.; Liu, S.; Ding, Y. Evaluation and hydrological simulation of CMADS and CFSR reanalysis datasets in the Qinghai-Tibet Plateau. Water 2018, 10, 513. [Google Scholar] [CrossRef]
- Liu, J.; Liu, S.; Shangguan, D.; Xu, J. Applicability evaluation of precipitation datasets from CMADS, ITPCAS and TRMM 3B42 in Yurungkax River Basin. J. North China Univ. Water Res. Electr. Power 2017, 38, 28–37. (In Chinese) [Google Scholar] [CrossRef]
- Meng, X.; Wang, H.; Lei, X.; Cai, S.; Wu, H.; Ji, X.; Wang, J. Hydrological modeling in the Manas River Basin using soil and water assessment tool driven by CMADS. Teh. Vjesn. 2017, 24, 525–534. [Google Scholar] [CrossRef]
- Meng, X.; Wang, H.; Cai, S.; Zhang, X.; Leng, G.; Lei, X.; Shi, C.; Liu, S.; Shang, Y. The China Meteorological Assimilation Driving Datasets for the SWAT Model (CMADS) application in China: A case study in Heihe River Basin. Available online: https://www.preprints.org/manuscript/201612.0091/v2 (accessed on 18 December 2016).
- Zhao, F.; Wu, Y.; Qiu, L.; Sun, Y.; Sun, L.; Li, Q.; Niu, J.; Wang, G. Parameter uncertainty analysis of the SWAT model in a mountain-loess transitional watershed on the Chinese Loess Plateau. Water 2018, 10, 690. [Google Scholar] [CrossRef]
- Leta, O.T.; EI-Kadi, A.I.; Dulai, H. Implications of climate change on water budgets and reservoir water harvesting of Nuuanu Area Watersheds, Oahu, Hawaii. J. Water Resour. Plan. Manag. 2017, 143. [Google Scholar] [CrossRef]
- Cuceloglu, G.; Abbaspour, K.C.; Ozturk, I. Assessing the water-resources potential of Istanbul by using a Soil and Water Assessment Tool (SWAT) hydrological model. Water 2017, 9, 814–833. [Google Scholar] [CrossRef]
- Zhou, G.-Y.; Wei, X.-H.; Wu, Y.-P.; Liu, S.-G.; Huang, Y.-H.; Yan, J.-H.; Zhang, D.-Q.; Zhang, Q.-M.; Liu, J.-X.; Meng, Z. Quantifying the hydrological responses to climate change using an intact forested small watershed in southern China. Glob. Chang. Biol. 2011, 17, 3736–3746. [Google Scholar] [CrossRef]
- Wu, Y.-P.; Liu, S.-G.; Yan, W.-D.; Xia, J.-Z.; Xiang, W.-H.; Wang, K.-L.; Luo, Q.; Fu, W.; Yuan, W.-P. Climate change and consequences on the water cycle in the humid Xiangjiang River Basin, China. Stoch. Environ. Res. Risk Assess. 2016, 30, 225–235. [Google Scholar] [CrossRef]
- Dhami, B.; Himanshu, S.K.; Pandey, A.; Gautam, A.K. Evaluation of the SWAT model for water balance study of a mountainous snowfed river basin of Nepal. Environ. Earth Sci. 2018, 77, 1–20. [Google Scholar] [CrossRef]
- Troin, M.; Caya, D. Evaluating the SWAT’s snow hydrology over a Northern Quebec watershed. Hydrol. Process. 2014, 28, 1858–1873. [Google Scholar] [CrossRef]
- Zhang, Y.-Q.; Luo, Y.; Sun, L.; Liu, S.-Y.; Chen, X.; Wang, X.-L. Using glacier area ratio to quantify effects of melt water on runoff. J. Hydrol. 2016, 538, 269–277. [Google Scholar] [CrossRef] [Green Version]
- Golmohammadi, G.; Rudra, R.; Prasher, S. Impact of tile drainage on water budget and spatial distribution ofsediment generating areas in an agricultural watershed. Agric. Water Manag. 2017, 184, 124–134. [Google Scholar] [CrossRef]
- Ale, S.; Bowling, L.C.; Brouder, S.M.; Frankenberger, J.R.; Youssef, M.A. Simulated effect of drainage water management operational strategy onhydrology and crop yield for Drummer soil in the Midwestern United States. Agric. Water Manag. 2009, 96, 653–665. [Google Scholar] [CrossRef]
- Singh, R.; Helmers, M.J.; Crumpton, W.G.; Lemke, D.W. Predicting effects of drainage water management in Iowa’s subsurface drained landscapes. Agric. Water Manag. 2007, 92, 162–170. [Google Scholar] [CrossRef]
- Vu, T.T.; Li, L.; Jun, K.S. Evaluation of multi-satellite precipitation products for streamflow simulations: A case study for the Han River Basin in the Korean Peninsula, East Asia. Water 2018, 10, 642. [Google Scholar] [CrossRef]
- Gao, M.-H.; Wu, Z.-Q.; Huang, L.-L.; Ding, Y.; Zhu, Z.-J. Length–weight relationships of 13 fish species from the Lijiang River, China. Tech. Contrib. 2018, 34, 180–182. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Y.; Qin, Q.-M.; Yan, Y.-G. Investigating the impact of human activity on land use/cover change in China’s Lijiang River Basin from the perspective of flow and type of population. Sustainability 2017, 9, 383. [Google Scholar] [CrossRef]
- Liu, G.; Jin, Q.-W.; Li, J.-Y.; Li, L.; He, C.-X.; Huang, Y.-Q.; Yao, Y.-F. Policy factors impact analysis based on remote sensing data and the CLUE-S model in the Lijiang River Basin, China. CATENA 2017, 158, 286–297. [Google Scholar] [CrossRef]
- Schuol, J.; Abbaspour, K.C. Using monthly weather statistics to generate daily data in a SWAT model application to West Africa. Ecol. Model. 2007, 201, 301–311. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Genuchten, M.T.; Schulin, R.; Schlappi, E. A sequential uncertainty domain inverse procedure for estimating subsurface flow and transport parameters. Water Resour. Res. 1997, 33, 1879–1892. [Google Scholar] [CrossRef] [Green Version]
- Abbaspour, K.C.; Johnson, C.A.; Van Genuchten, M.T. Estimating uncertain flow and transport parameters using a sequential uncertainty fitting procedure. Vadose Zone J. 2004, 3, 1340–1352. [Google Scholar] [CrossRef]
- Moriasi, D.; Arnold, J.G.; Vanliew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Bekele, E.G.; Nicklow, J.W. Multi-objective automatic calibration of SWAT using NSGA-II. J. Hydrol. 2007, 341, 165–176. [Google Scholar] [CrossRef]




| Data Type | Source | Spatial Resolution |
|---|---|---|
| DEM | ASTER GDEM https://earthexplorer.usgs.gov/ | 30 m |
| Land use | Landsat-8 https://earthexplorer.usgs.gov/ | 30 m |
| Soil | HWSD http://westdc.westgis.ac.cn/data/ | 30 m |
| Weather | CMADS version 1.1 http://www.cmads.org/ | 28 km |
| Parameter Name | Description | Min | Max | Value Adopted | Calibration | ||
|---|---|---|---|---|---|---|---|
| t-Stat | p-Value | Rank | |||||
| R__OV_N | Manning’s “n” value for overland flow | 10.00 | 20.00 | 17.25 | −2.68 | 0.02 | 1 |
| V__ALPHA_BF | Baseflow alpha factor (days) | 0.00 | 0.50 | 0.41 | 2.48 | 0.03 | 2 |
| R__CN2 | SCS runoff curve number for moisture condition II | 0.00 | 0.60 | 0.41 | 1.57 | 0.14 | 3 |
| V__CH_K2 | Effective hydraulic conductivity in main channel alluvium | 100.00 | 150.00 | 131.25 | −1.25 | 0.24 | 4 |
| V__GWQMN | Treshold depth of water in the shallow aquifer required for return flow to occur (mm) | 0.00 | 3.00 | 2.63 | −0.45 | 0.66 | 5 |
| R__ESCO | Soil evaporation compensation factor | 0.00 | 0.80 | 0.30 | 0.41 | 0.69 | 6 |
| R__SOL_AWC(1) | Available water capacity of the soil layer | 0.00 | 0.60 | 0.11 | −0.31 | 0.76 | 7 |
| V__GW_DELAY | Groundwater delay (days) | 0.00 | 170.00 | 46.75 | 0.04 | 0.97 | 8 |
| Parameter Name | Description | Min | Max | Value Adopted | Calibration | ||
|---|---|---|---|---|---|---|---|
| t-Stat | p-Value | Rank | |||||
| R__CN2 | SCS runoff curve number for moisture condition II | −0.30 | 0.01 | −0.17 | 8.77 | 0.00 | 1 |
| R__HRU_SLP | Average slope steepness | −0.98 | 0.10 | −0.35 | 6.08 | 0.00 | 2 |
| R__SOL_K(1) | Saturated hydraulic conductivity | 0.00 | 5.00 | 0.03 | −4.99 | 0.00 | 3 |
| V__RCHRG_DP | Deep aquifer percolation fraction | 0.10 | 0.40 | 0.15 | −3.65 | 0.00 | 4 |
| V__GW_DELAY | Groundwater delay (days) | 0.00 | 2.00 | 0.17 | −3.14 | 0.00 | 5 |
| V__OV_N | Manning’s “n” value for overland flow | 3.00 | 6.00 | 5.47 | −2.55 | 0.01 | 6 |
| V__ALPHA_BF | Baseflow alpha factor (days) | 0.10 | 0.20 | 0.16 | 2.50 | 0.01 | 7 |
| V__GWQMN | Treshold depth of water in the shallow aquifer required for return flow to occur (mm) | 10.00 | 500.00 | 46.75 | −2.40 | 0.02 | 8 |
| R__SOL_Z(1) | Depth from soil surface to bottom of layer | −0.25 | 0.25 | −0.11 | 1.52 | 0.13 | 9 |
| V__CH_K2 | Effective hydraulic conductivity in main channel alluvium | 0.00 | 220.00 | 212.30 | 1.14 | 0.25 | 10 |
| V__REVAPMN | Threshold depth of water in the shallow aquifer for “revap” to occur (mm) | 0.00 | 500.00 | 367.5 | −0.65 | 0.51 | 11 |
| R__SOL_AWC(1) | Available water capacity of the soil layer | 0.20 | 0.40 | 0.21 | 0.58 | 0.55 | 12 |
| R__ESCO | Soil evaporation compensation factor | 0.00 | 0.10 | 0.04 | 0.46 | 0.64 | 13 |
| Object | Calibration (2009–2010) | Validation (2011–2016) |
|---|---|---|
| P-factor (Monthly) | 0.79 | 0.63 |
| R-factor (Monthly) | 0.33 | 0.37 |
| R2 (Monthly) | 0.96 | 0.96 |
| NSE (Monthly) | 0.96 | 0.95 |
| PBIAS (Monthly) | 7.70 | 7.80 |
| RSR (Monthly) | 0.20 | 0.22 |
| P-factor (Daily) | 0.70 | 0.77 |
| R-factor (Daily) | 0.30 | 0.43 |
| R2 (Daily) | 0.92 | 0.89 |
| NSE (Daily) | 0.89 | 0.88 |
| PBIAS (Daily) | 20.70 | 14.40 |
| RSR (Daily) | 0.33 | 0.35 |
| Hydrological Elements | Calibration |
|---|---|
| Precipitation | 2150.20 mm |
| Surface runoff | 518.36 mm |
| Lateral flow | 129.21 mm |
| Shallow groundwater contribute to streamflow | 555.34 mm |
| Deep groundwater contribute to streamflow | 188.62 mm |
| Total aquifer recharge | 746.08 mm |
| Deep groundwater recharge | 189.88 mm |
| Water yield | 1391.51 mm |
| Evapotranspiration | 750.6 mm |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Y.; Zhang, J.; Yang, M.; Lei, X.; Guo, B.; Yang, L.; Zeng, Z.; Qu, J. Application of SWAT Model with CMADS Data to Estimate Hydrological Elements and Parameter Uncertainty Based on SUFI-2 Algorithm in the Lijiang River Basin, China. Water 2018, 10, 742. https://doi.org/10.3390/w10060742
Cao Y, Zhang J, Yang M, Lei X, Guo B, Yang L, Zeng Z, Qu J. Application of SWAT Model with CMADS Data to Estimate Hydrological Elements and Parameter Uncertainty Based on SUFI-2 Algorithm in the Lijiang River Basin, China. Water. 2018; 10(6):742. https://doi.org/10.3390/w10060742
Chicago/Turabian StyleCao, Yang, Jing Zhang, Mingxiang Yang, Xiaohui Lei, Binbin Guo, Liu Yang, Zhiqiang Zeng, and Jiashen Qu. 2018. "Application of SWAT Model with CMADS Data to Estimate Hydrological Elements and Parameter Uncertainty Based on SUFI-2 Algorithm in the Lijiang River Basin, China" Water 10, no. 6: 742. https://doi.org/10.3390/w10060742






