Parameter Uncertainty Analysis of the SWAT Model in a Mountain-Loess Transitional Watershed on the Chinese Loess Plateau
Abstract
:1. Introduction
2. Materials and Methods
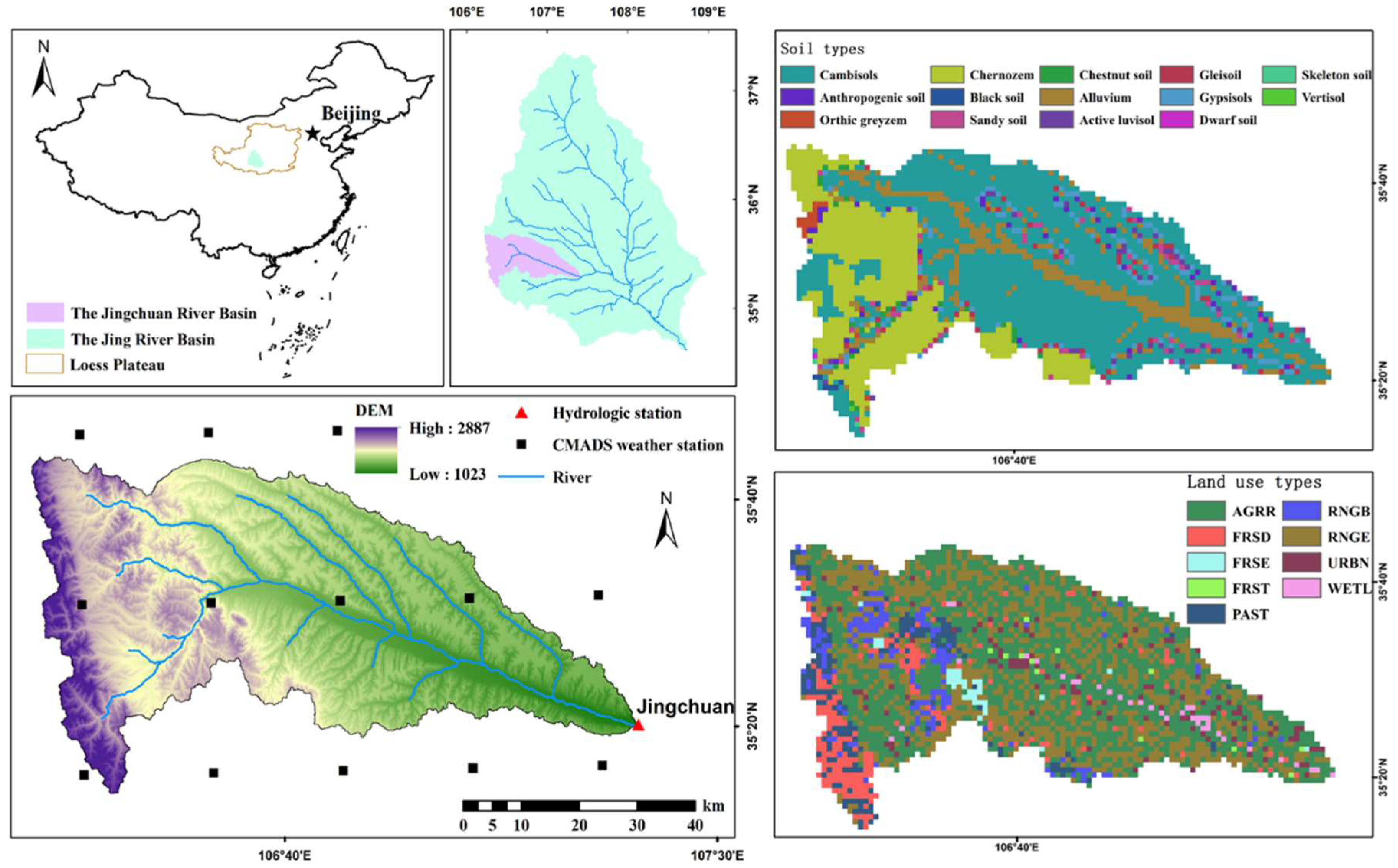
2.1. Study Area
2.2. Model Description
2.3. Model Input and Setup
2.4. Methodology
2.4.1. ParaSol
2.4.2. SUFI2
2.4.3. GLUE
3. Results
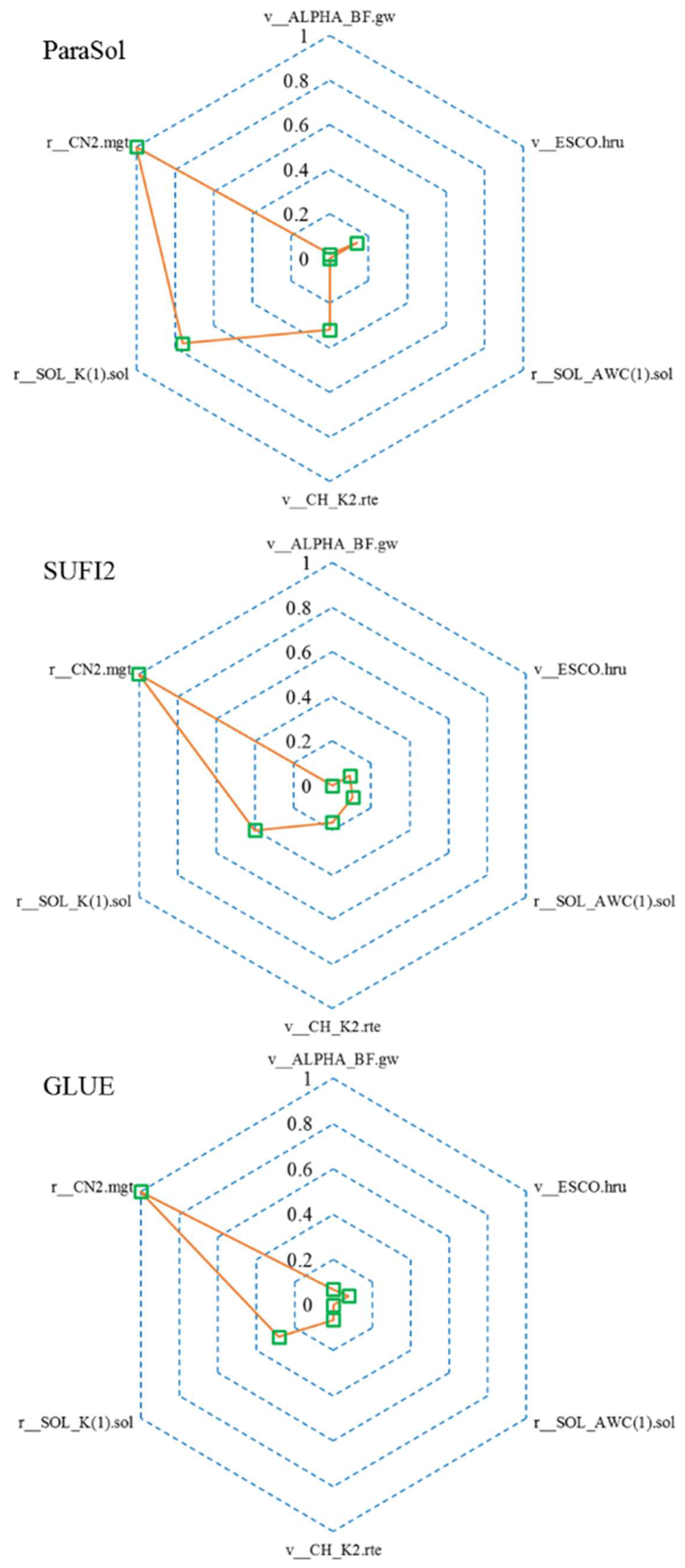
3.1. Global Sensitivity
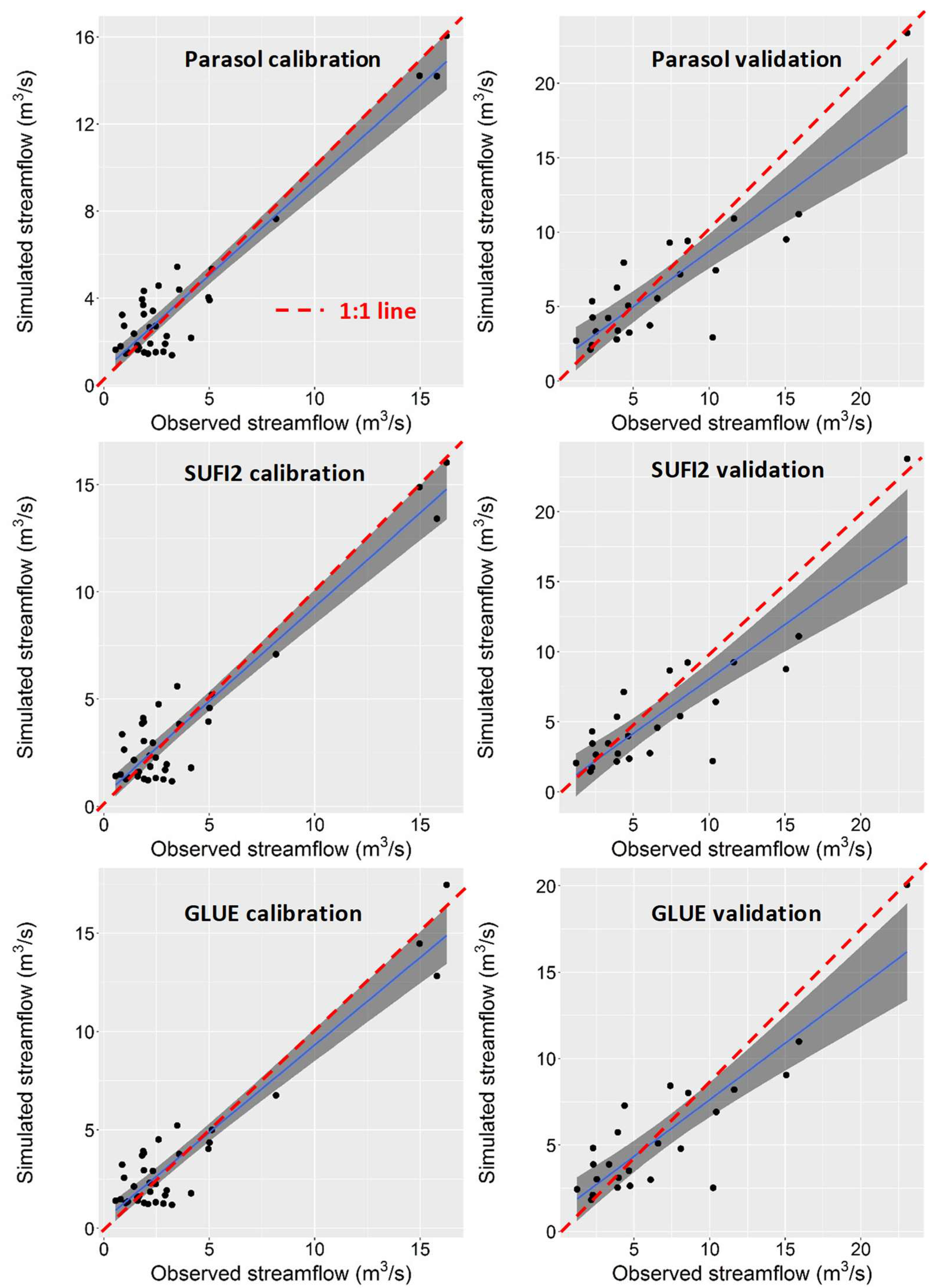
3.2. Model Calibration and Validation Results
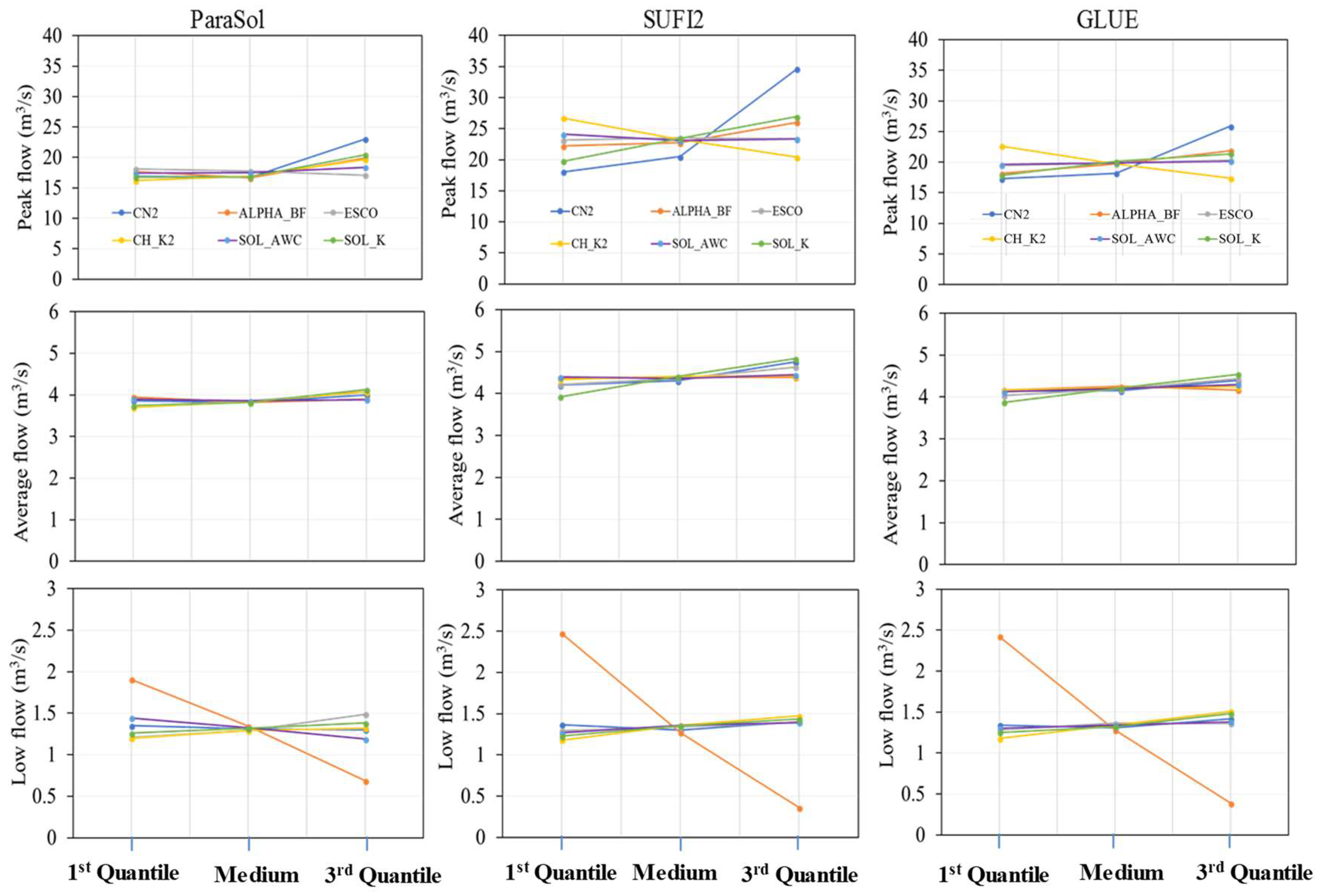
3.3. Uncertainty Analysis
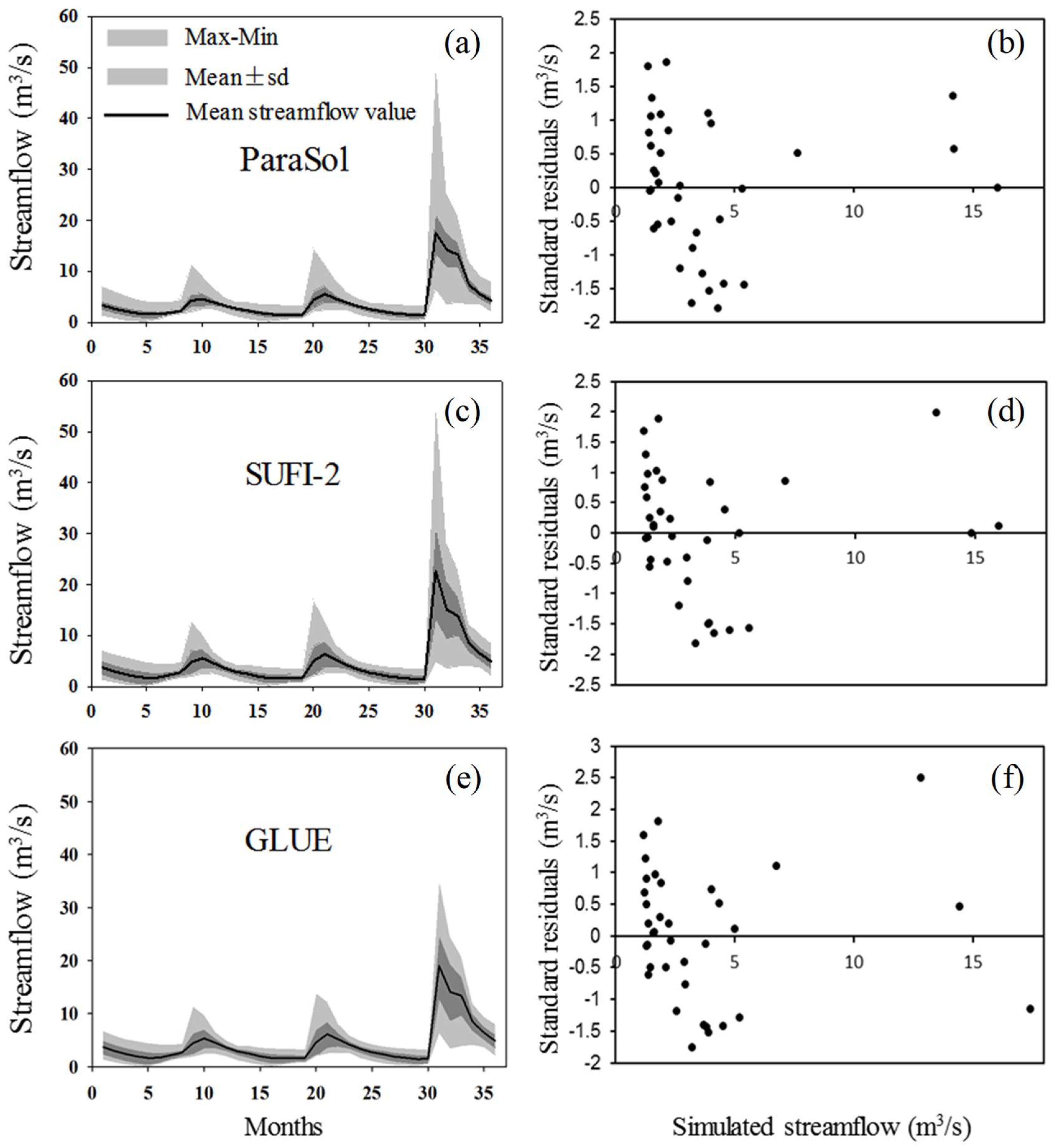
3.3.1. Parasol
3.3.2. SUFI2
3.3.3. GLUE
4. Discussion
4.1. Model Parameterization and Performance
4.2. Parameter Sensitivity and Uncertainty
4.3. Model Prediction Uncertainty
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Uniyal, B.; Jha, M.K.; Verma, A.K. Parameter identification and uncertainty analysis for simulating streamflow in a river basin of eastern India. Hydrol. Process. 2015, 29, 3744–3766. [Google Scholar] [CrossRef]
- Gyamfi, C.; Ndambuki, J.; Salim, R. Hydrological responses to land use/cover changes in the Olifants Basin, South Africa. Water 2016, 8, 588. [Google Scholar] [CrossRef]
- Viviroli, D.; Zappa, M.; Gurtz, J.; Weingartner, R. An introduction to the hydrological modelling system prevah and its pre- and post-processing-tools. Environ. Model. Softw. 2009, 24, 1209–1222. [Google Scholar] [CrossRef]
- Wu, K.; Xu, Y.J. Evaluation of the applicability of the SWAT model for coastal watersheds in southeastern Louisiana. J. Am. Water Resour. Assoc. 2006, 42, 1247–1260. [Google Scholar] [CrossRef]
- Zhu, X.; Zhang, C.; Qi, W.; Cai, W.; Zhao, X.; Wang, X. Multiple climate change scenarios and runoff response in Biliu River. Water 2018, 10, 126. [Google Scholar] [CrossRef]
- Beven, K.; Freer, J. Equifinality, data assimilation, and uncertainty estimation in mechanistic modelling of complex environmental systems using the glue methodology. J. Hydrol. 2001, 249, 11–29. [Google Scholar] [CrossRef]
- Zheng, Y.; Han, F. Markov Chain Monte Carlo (MCMC) uncertainty analysis for watershed water quality modeling and management. Stoch. Environ. Res. Risk Assess. 2015, 30, 293–308. [Google Scholar] [CrossRef]
- Li, Z.; Xu, Z.; Shao, Q.; Yang, J. Parameter estimation and uncertainty analysis of SWAT model in upper reaches of the Heihe River Basin. Hydrol. Process. 2009, 23, 2744–2753. [Google Scholar] [CrossRef]
- Song, X.; Zhang, J.; Zhan, C.; Xuan, Y.; Ye, M.; Xu, C. Global sensitivity analysis in hydrological modeling: Review of concepts, methods, theoretical framework, and applications. J. Hydrol. 2015, 523, 739–757. [Google Scholar] [CrossRef]
- Li, Z.; Shao, Q.; Xu, Z.; Cai, X. Analysis of parameter uncertainty in semi-distributed hydrological models using bootstrap method: A case study of SWAT model applied to Yingluoxia watershed in Northwest China. J. Hydrol. 2010, 385, 76–83. [Google Scholar] [CrossRef]
- Yen, H.; Wang, X.; Fontane, D.G.; Harmel, R.D.; Arabi, M. A framework for propagation of uncertainty contributed by parameterization, input data, model structure, and calibration/validation data in watershed modeling. Environ. Model. Softw. 2014, 54, 211–221. [Google Scholar] [CrossRef]
- Xue, C.; Chen, B.; Asce, M.; Wu, H. Parameter uncertainty analysis of surface flow and sediment yield in the Huolin Basin, China. J. Hydrol. Eng. 2014, 19, 1224–1236. [Google Scholar] [CrossRef]
- Refsgaard, J.C.; van der Sluijs, J.P.; Brown, J.; van der Keur, P. A framework for dealing with uncertainty due to model structure error. Adv. Water Res. 2006, 29, 1586–1597. [Google Scholar] [CrossRef]
- Wu, H.; Chen, B. Evaluating uncertainty estimates in distributed hydrological modeling for the Wenjing River watershed in China by GLUE, SUFI-2, and ParaSol methods. Ecol. Eng. 2015, 76, 110–121. [Google Scholar] [CrossRef]
- Nandakumar, N.; Mein, R.G. Uncertainty in rainfall-runoff model simulations and the implications for predicting the hydrologic effects of land-use change. J. Hydrol. 1997, 193, 211–232. [Google Scholar] [CrossRef]
- Zhou, J.; Liu, Y.; Guo, H.; He, D. Combining the SWAT model with sequential uncertainty fitting algorithm for streamflow prediction and uncertainty analysis for the lake Dianchi Basin, China. Hydrol. Process. 2014, 28, 521–533. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Q.; Guo, B.; Gong, H. The comparative study of multi-site uncertainty evaluation method based on SWAT model. Hydrol. Process. 2015, 29, 2994–3009. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Yang, J.; Maximov, I.; Siber, R.; Bogner, K.; Mieleitner, J.; Zobrist, J.; Srinivasan, R. Modelling hydrology and water quality in the pre-alpine/alpine Thur watershed using SWAT. J. Hydrol. 2007, 333, 413–430. [Google Scholar] [CrossRef]
- Vilaysane, B.; Takara, K.; Luo, P.; Akkharath, I.; Duan, W. Hydrological stream flow modelling for calibration and uncertainty analysis using SWAT model in the Xedone River Basin, Lao PDR. Procedia Environ. Sci. 2015, 28, 380–390. [Google Scholar] [CrossRef]
- Zhang, X.; Srinivasan, R.; Bosch, D. Calibration and uncertainty analysis of the swat model using Genetic Algorithms and Bayesian Model Averaging. J. Hydrol. 2009, 374, 307–317. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, S. Automating calibration, sensitivity and uncertainty analysis of complex models using the R package Flexible Modeling Environment (FME): SWAT as an example. Environ. Model. Softw. 2012, 31, 99–109. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, S.; Yan, W. A universal model-R coupler to facilitate the use of r functions for model calibration and analysis. Environ. Model. Softw. 2014, 62, 65–69. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Rouholahnejad, E.; Vaghef, S.; Srinivasan, R.; Yang, H.; Kløve, B. A continental-scale hydrology and water quality model for Europe: Calibration and uncertainty of a high-resolution large-scale SWAT model. J. Hydrol. 2015, 524, 733–752. [Google Scholar] [CrossRef]
- van Griensven, A.; Meixner, T. Methods to quantify and identify the sources of uncertainty for river basin water quality models. Water Sci. Technol. 2006, 53, 51–59. [Google Scholar] [CrossRef] [PubMed]
- Abbaspour, K.C. SWAT Calibration and Uncertainty Programs: A User Mannual; Swiss Federal Institute of Aquatic Science and Technology (Eawag): Dübendorf, Switzerland, 2011. [Google Scholar]
- Beven, K.; Binley, A. The future of distributed models-model calibration and uncertainty prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Yang, J.; Reichert, P.; Abbaspour, K.C.; Xia, J.; Yang, H. Comparing uncertainty analysis techniques for a SWAT application to the Chaohe Basin in China. J. Hydrol. 2008, 358, 1–23. [Google Scholar] [CrossRef]
- Khalid, K.; Ali, M.F.; Rahman, N.F.A.; Mispan, M.R.; Haron, S.H.; Othman, Z.; Bachok, M.F. Sensitivity analysis in watershed model using SUFI-2 algorithm. Procedia Eng. 2016, 162, 441–447. [Google Scholar] [CrossRef]
- Kouchi, D.H.; Esmaili, K.; Faridhosseini, A.; Sanaeinejad, S.H.; Khalili, D.; Abbaspour, K.C. Sensitivity of calibrated parameters and water resource estimates on different objective functions and optimization algorithms. Water 2017, 9, 384. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasn, R.; Muttiah, R.S.; Willians, J.R. Large area hydrologic modeling and assessment—Part I: Model development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Zhang, L.; Podlasly, C.; Feger, K.-H.; Wang, Y.; Schwärzel, K. Different land management measures and climate change impacts on the runoff—A simple empirical method derived in a mesoscale catchment on the loess plateau. J. Arid Environ. 2015, 120, 42–50. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Willianms, J.R. Soil and Water Assessment Tool Theoretical Documentation Version 2009; Texas Water Resources Institute: Ollege Station, TX, USA, 2011. [Google Scholar]
- Panagopoulos, Y.; Gassman, P.W.; Arritt, R.W.; Herzmann, D.E.; Campbell, T.D.; Valcu, A.; Jha, M.K.; Kling, C.L.; Srinivasan, R.; White, M.; et al. Impacts of climate change on hydrology, water quality and crop productivity in the Ohio-Tennessee River Basin. Int. J. Agric. Biol. Eng. 2015, 8, 36–53. [Google Scholar]
- Arnold, J.G.; Muttiah, R.S.; Srinivasan, R.; Allen, P.M. Regional estimation of base flow and groundwater recharge in the upper Mississippi River Basin. J. Hydrol. 2000, 227, 21–40. [Google Scholar] [CrossRef]
- Meng, X.; Wang, H. Significance of the china meteorological assimilation driving datasets for the SWAT model (CMADS) of East Asia. Water 2017, 9, 765. [Google Scholar] [CrossRef]
- Duan, Q.; Sorooshian, S.; Gupta, V. Effective and efficient global optimation for conceptual rainfall-runoff models. Water Resour. Manag. 1992, 28, 1015–1031. [Google Scholar] [CrossRef]
- Ashraf Vaghefi, S.; Abbaspour, K.; Faramarzi, M.; Srinivasan, R.; Arnold, J. Modeling crop water productivity using a coupled SWAT–MODSIM model. Water 2017, 9, 157. [Google Scholar] [CrossRef]
- Li, Z.; Liu, W.-Z.; Zhang, X.-C.; Zheng, F.-L. Impacts of land use change and climate variability on hydrology in an agricultural catchment on the Loess Plateau of China. J. Hydrol. 2009, 377, 35–42. [Google Scholar] [CrossRef]
- Wang, H.; Sun, F.; Xia, J.; Liu, W. Impact of lucc on streamflow based on the SWAT model over the Wei River Basin on the Loess Plateau in China. Hydrol. Earth Syst. Sci. 2017, 21, 1929–1945. [Google Scholar] [CrossRef]
- Zuo, D.; Xu, Z.; Peng, D.; Song, J.; Cheng, L.; Wei, S.; Abbaspour, K.C.; Yang, H. Simulating spatiotemporal variability of blue and green water resources availability with uncertainty analysis. Hydrol. Process. 2015, 29, 1942–1955. [Google Scholar] [CrossRef]
- Zhao, F.; Wu, Y.; Qiu, L.; Bellie, S.; Zhang, F.; Sun, Y.; Sun, L.; Li, Q.; Alexey, V. Spatiotemporal features of the hydro-biogeochemical cycles in a typical loess gully watershed. Ecol. Indic. 2018, 91, 542–554. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Datta, A.R.; Bolisetti, T. Second-order autoregressive model-based likelihood function for calibration and uncertainty analysis of SWAT model. J. Hydrol. Eng. 2015, 20, 04014045. [Google Scholar] [CrossRef]
- Neupane, R.P.; Kumar, S. Estimating the effects of potential climate and land use changes on hydrologic processes of a large agriculture dominated watershed. J. Hydrol. 2015, 529, 418–429. [Google Scholar] [CrossRef]
- Van Griensven, A.; Meixner, T.; Grunwald, S.; Bishop, T.; Di luzio, M.; Srinivasan, R. A global sensitivity analysis tool for the paramters of multi-variable catchment models. J. Hydrol. 2006, 324, 10–23. [Google Scholar] [CrossRef]
- Abbaspour, K.; Vaghefi, S.; Srinivasan, R. A guideline for successful calibration and uncertainty analysis for soil and water assessment: A review of papers from the 2016 International SWAT Conference. Water 2017, 10, 6. [Google Scholar] [CrossRef]
- Liu, Y.R.; Li, Y.P.; Huang, G.H.; Zhang, J.L.; Fan, Y.R. A bayesian-based multilevel factorial analysis method for analyzing parameter uncertainty of hydrological model. J. Hydrol. 2017, 553, 750–762. [Google Scholar] [CrossRef]

| Parameter | Description | Range | Calibrated Value | ||
|---|---|---|---|---|---|
| ParaSol | SUFI2 | GLUE | |||
| r_CN2 | SCS curve number for soil condition II | −50% to +10% | −46% | −38% | −29% |
| v_ALPHA_BF | Baseflow alpha factor (day) | 0.01–0.1 | 0.04 | 0.05 | 0.04 |
| v_ESCO | Soil evaporation percolation fraction | 0.1–1.0 | 0.93 | 0.5 | 0.16 |
| v_CH_K2 | Effective hydraulic conductivity in main channel alluvium | 8.0–18.0 | 8.0 | 8.4 | 8.06 |
| r_SOL_AWC | Available water capacity of soil layer | −20% to +10% | −17% | 9% | 6% |
| r_SOL_K | Saturated hydraulic conductivity (mm/h) | −10% to +40% | −10% | −4% | −4% |
| Method | Period | RMSE (m3/s) | NSE | R2 | RSR | PB (%) |
|---|---|---|---|---|---|---|
| ParaSol | Calibration | 1.2 | 0.90 | 0.91 | 0.31 | 6.6 |
| Validation | 2.6 | 0.74 | 0.75 | 0.50 | −6.8 | |
| SUFI2 | Calibration | 1.3 | 0.89 | 0.89 | 0.33 | 2.3 |
| Validation | 2.9 | 0.69 | 0.75 | 0.54 | −18.2 | |
| GLUE | Calibration | 1.3 | 0.89 | 0.89 | 0.33 | 0.9 |
| Validation | 2.9 | 0.68 | 0.76 | 0.55 | −18.8 |
| Parameter | Initial Range | 95CI (Confidence Interval) | ||
|---|---|---|---|---|
| ParaSol | SUFI2 | GLUE | ||
| r_CN2 | −50% to +10% | (−48.0, 0.2) | (−48.5, 8.5) | (−48.5, 8.5) |
| v_ALPHA_BF | 0.01–0.1 | (0.01, 0.09) | (0.01, 0.1) | (0.01, 0.1) |
| v_ESCO | 0.1–1.0 | (0.14, 0.98) | (0.13, 0.98) | (0.12, 0.98) |
| v_CH_K2 | 8.0–18.0 | (8.5, 16.7) | (8.3, 17.7) | (8.3, 17.7) |
| r_SOL_AWC | −20% to +10% | (−18.2, 8.5) | (−19.2, 9.2) | (−19.2, 9.2) |
| r_SOL_K | −10% to +40% | (−8.9, 29.5) | (−8.7, 38.7) | (−8.7, 38.7) |
| Method | Parameter | r_CN2 | v_ALPHA_BF | v_ESCO | v_CH_K2 | r_SOL_AWC | r_SOL_K |
|---|---|---|---|---|---|---|---|
| ParaSol | r_CN2 | 1 | 0.11 | −0.24 | 0.48 | 0.11 | 0.37 |
| v_ALPHA_BF | 1 | −0.27 | 0.27 | 0.25 | 0.21 | ||
| v_ESCO | 1 | −0.24 | −0.40 | −0.25 | |||
| v_CH_K2 | 1 | 0.20 | 0.57 | ||||
| r_SOL_AWC | 1 | 0.15 | |||||
| r_SOL_K | 1 | ||||||
| SUFI2 | r_CN2 | 1 | −0.01 | 0.02 | −0.02 | −0.02 | −0.02 |
| v_ALPHA_BF | 1 | 0.01 | 0.02 | −0.03 | −0.02 | ||
| v_ESCO | 1 | 0.03 | −0.00 | −0.00 | |||
| v_CH_K2 | 1 | −0.02 | −0.02 | ||||
| r_SOL_AWC | 1 | 0.03 | |||||
| r_SOL_K | 1 | ||||||
| GLUE | r_CN2 | 1 | −0.02 | −0.03 | −0.02 | 0.01 | −0.02 |
| v_ALPHA_BF | 1 | 0.01 | 0.02 | −0.02 | −0.01 | ||
| v_ESCO | 1 | 0.01 | −0.01 | −0.00 | |||
| v_CH_K2 | 1 | 0.03 | 0.01 | ||||
| r_SOL_AWC | 1 | −0.00 | |||||
| r_SOL_K | 1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, F.; Wu, Y.; Qiu, L.; Sun, Y.; Sun, L.; Li, Q.; Niu, J.; Wang, G. Parameter Uncertainty Analysis of the SWAT Model in a Mountain-Loess Transitional Watershed on the Chinese Loess Plateau. Water 2018, 10, 690. https://doi.org/10.3390/w10060690
Zhao F, Wu Y, Qiu L, Sun Y, Sun L, Li Q, Niu J, Wang G. Parameter Uncertainty Analysis of the SWAT Model in a Mountain-Loess Transitional Watershed on the Chinese Loess Plateau. Water. 2018; 10(6):690. https://doi.org/10.3390/w10060690
Chicago/Turabian StyleZhao, Fubo, Yiping Wu, Linjing Qiu, Yuzhu Sun, Liqun Sun, Qinglan Li, Jun Niu, and Guoqing Wang. 2018. "Parameter Uncertainty Analysis of the SWAT Model in a Mountain-Loess Transitional Watershed on the Chinese Loess Plateau" Water 10, no. 6: 690. https://doi.org/10.3390/w10060690







