A Non-Equilibrium Sediment Transport Model for Dam Break Flow over Moveable Bed Based on Non-Uniform Rectangular Mesh
Abstract
:1. Introduction
2. Governing Equations
2.1. Hydrodynamic Equations
2.2. Morphodynamic Equations
2.3. Empirical Relations
2.3.1. Non-Equilibrium Adaptation Length
2.3.2. Sediment Transport Rate
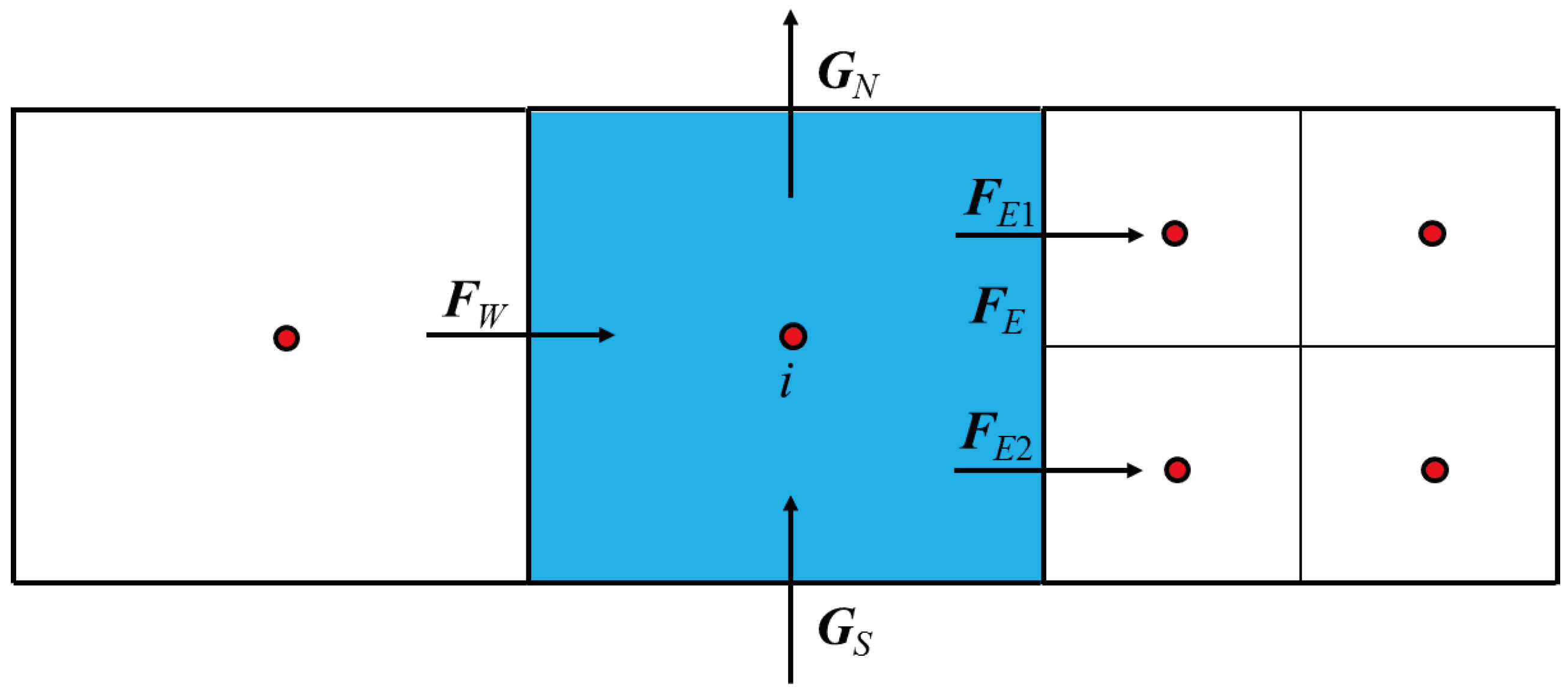
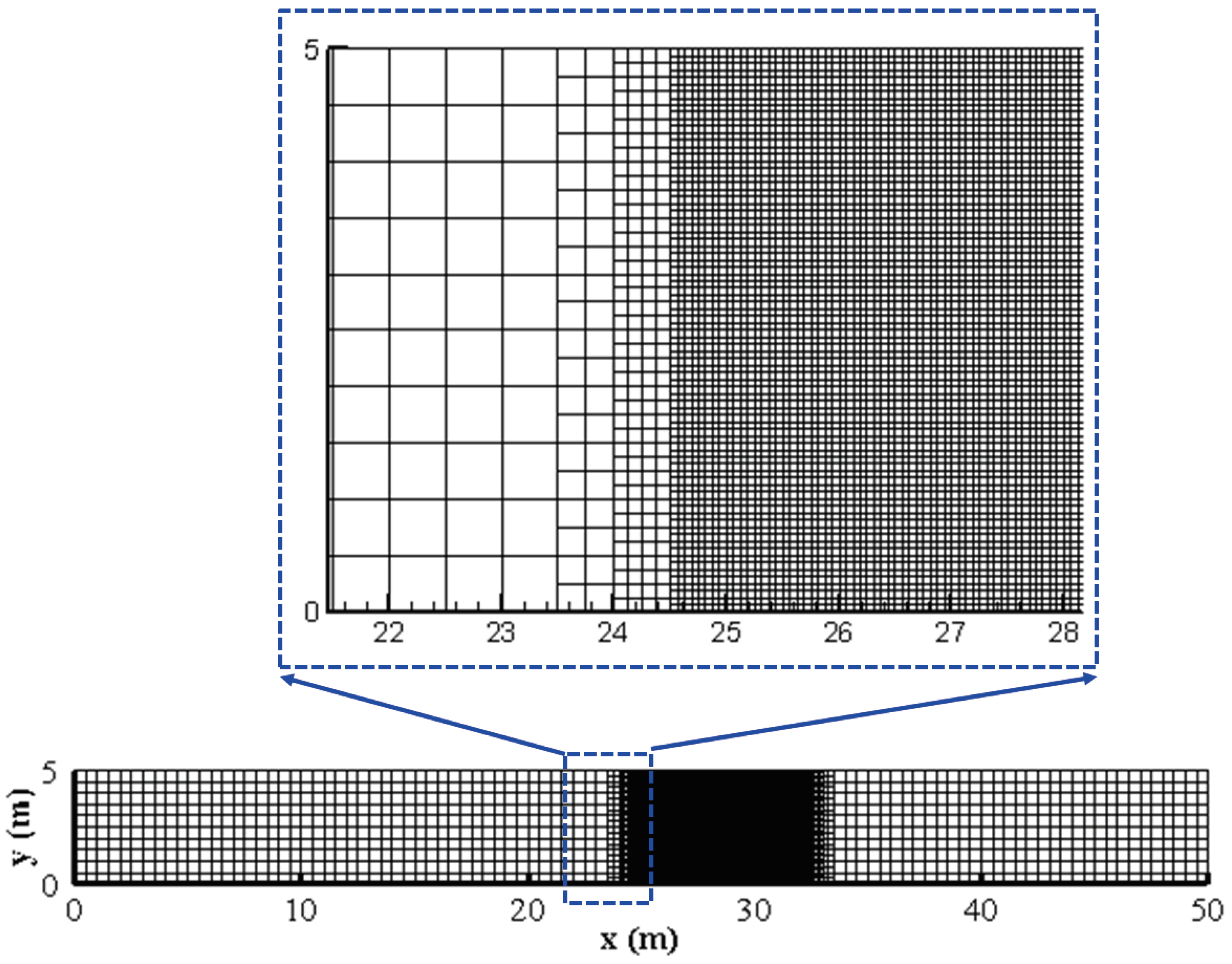
2.4. Non-Uniform Rectangular Mesh
3. Numerical Method
3.1. Finite Volume Discretization
3.2. Nonnegative Water Depth Reconstruction
3.3. Numerical Fluxes Calculation
3.4. Treatment of Bed Slope and Friction Source Terms
3.5. Bed Deformation Calculation
3.6. Model Stability
4. Model Validation
4.1. Partial Dam Break Experiment
4.2. Simulation of Dam Break Flow over Triangular Obstacle
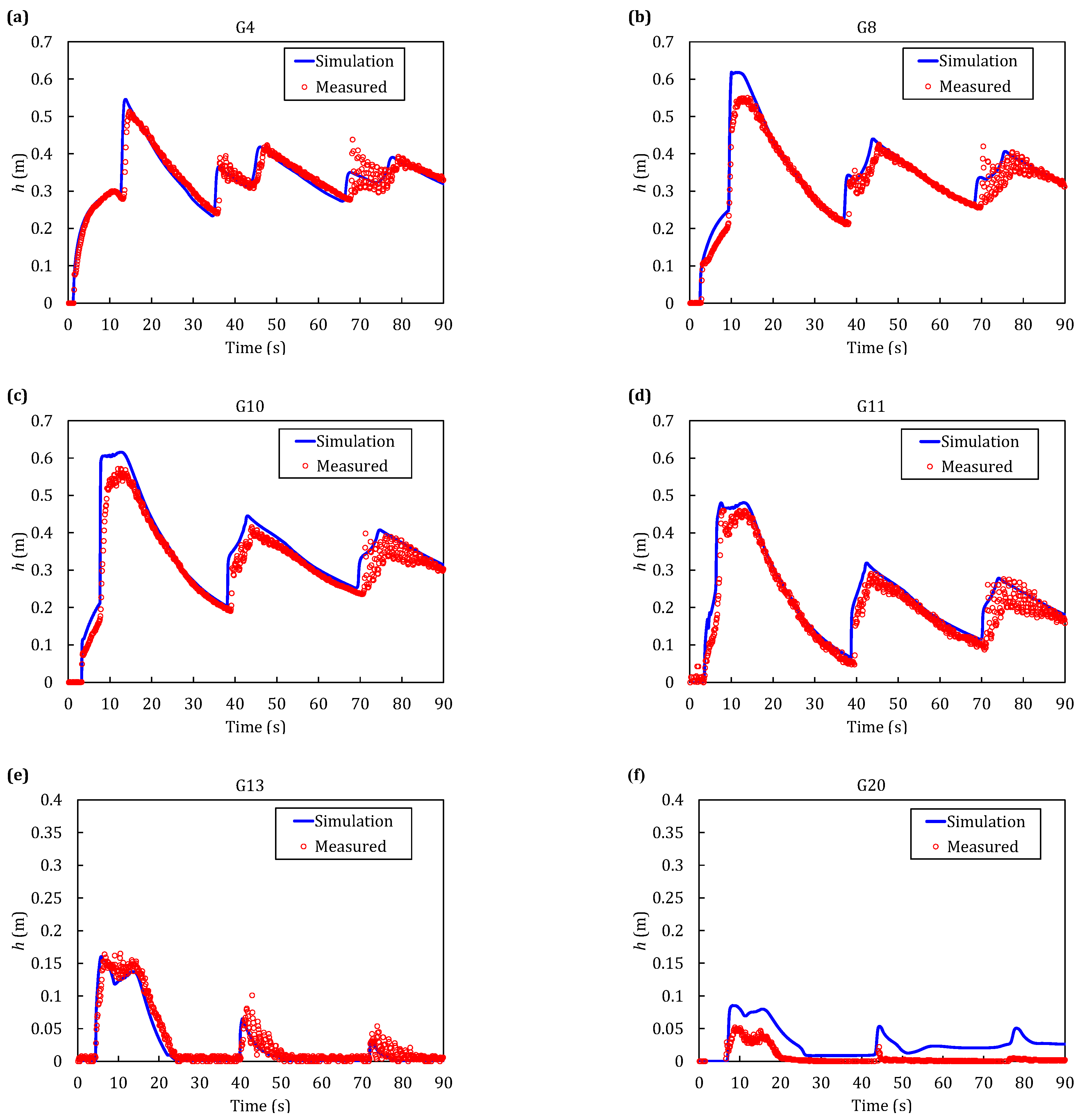
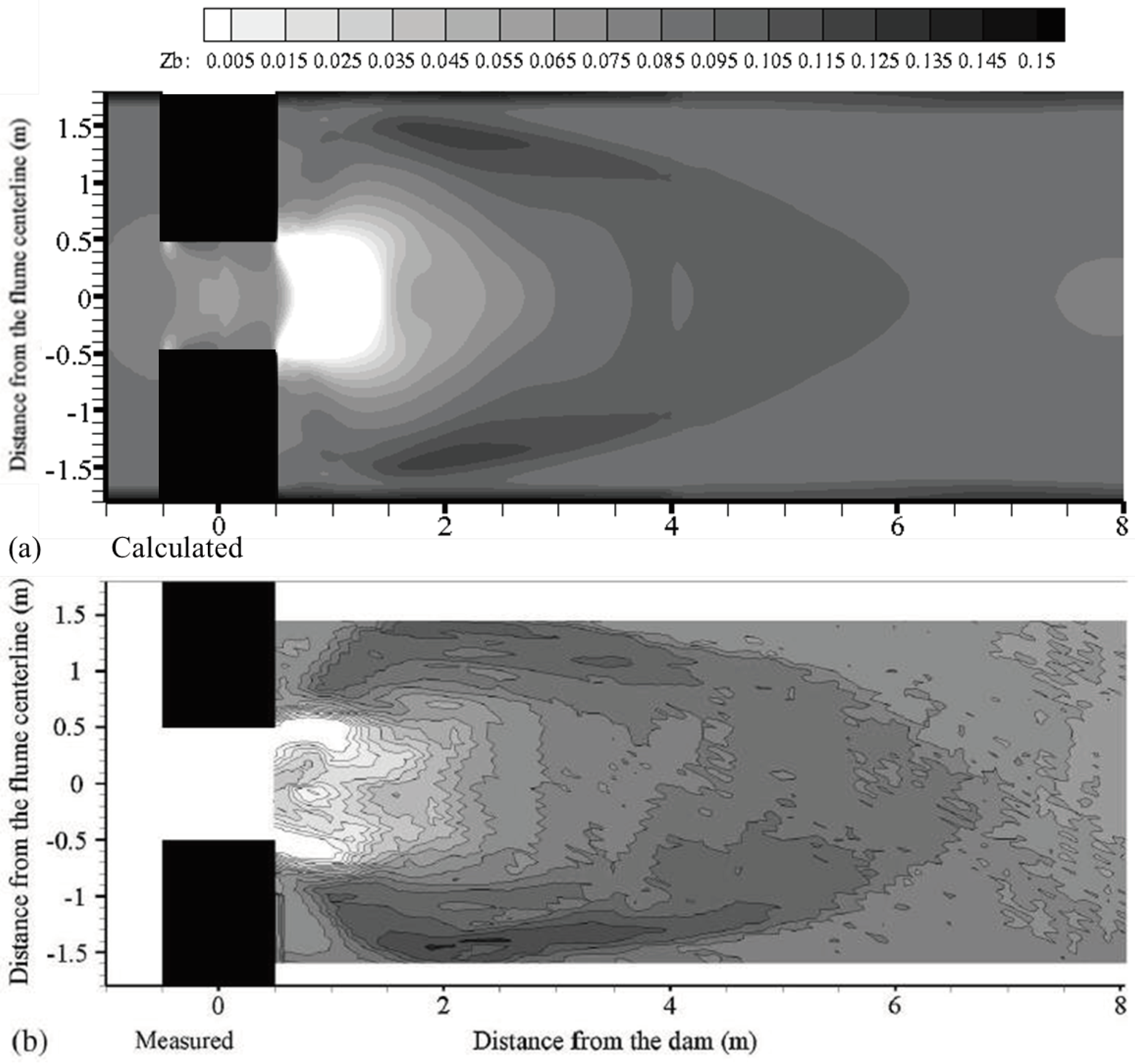
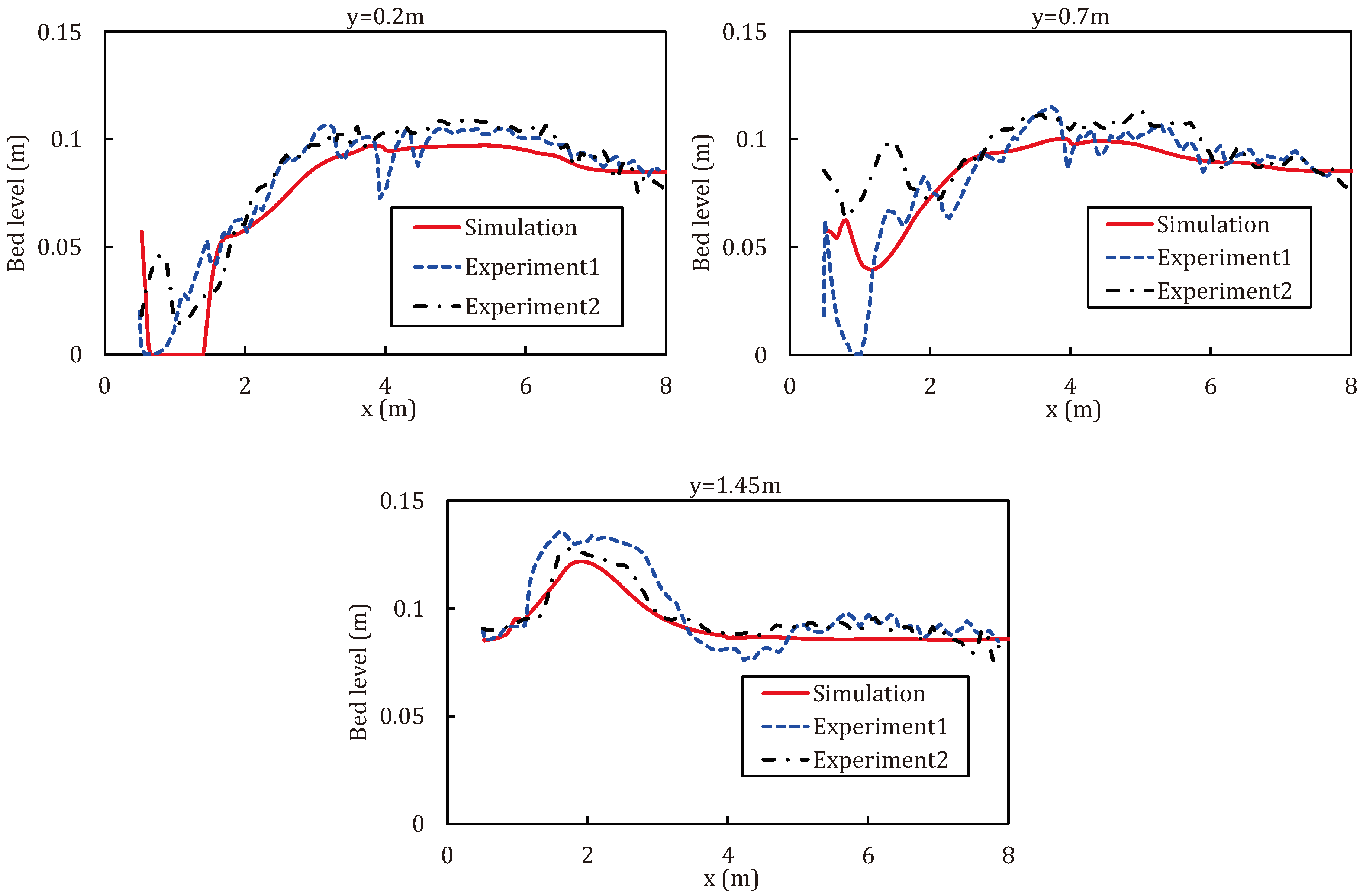
4.3. Dam-Break Flow in an Erodible Channel with a Sudden Enlargement
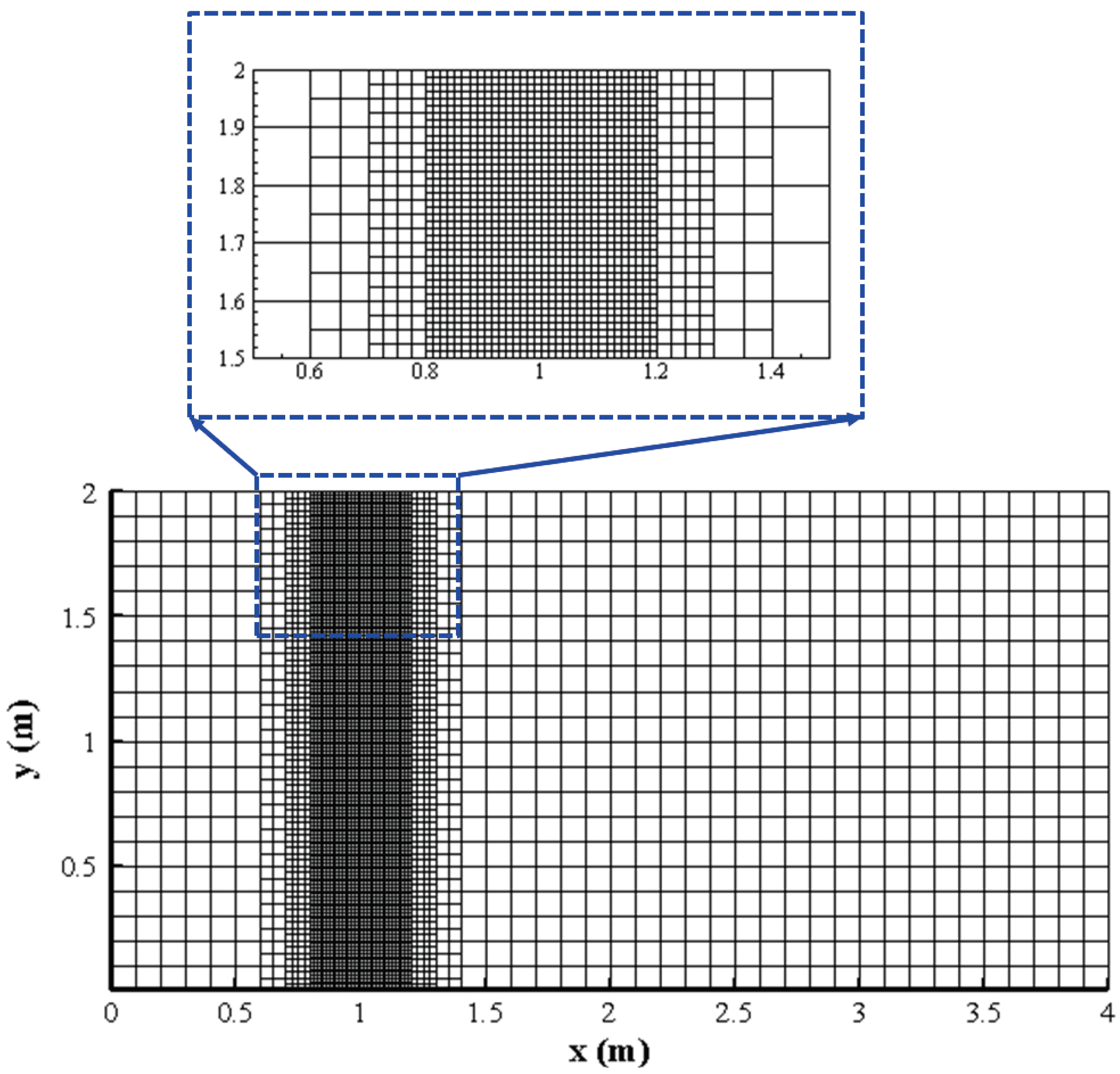
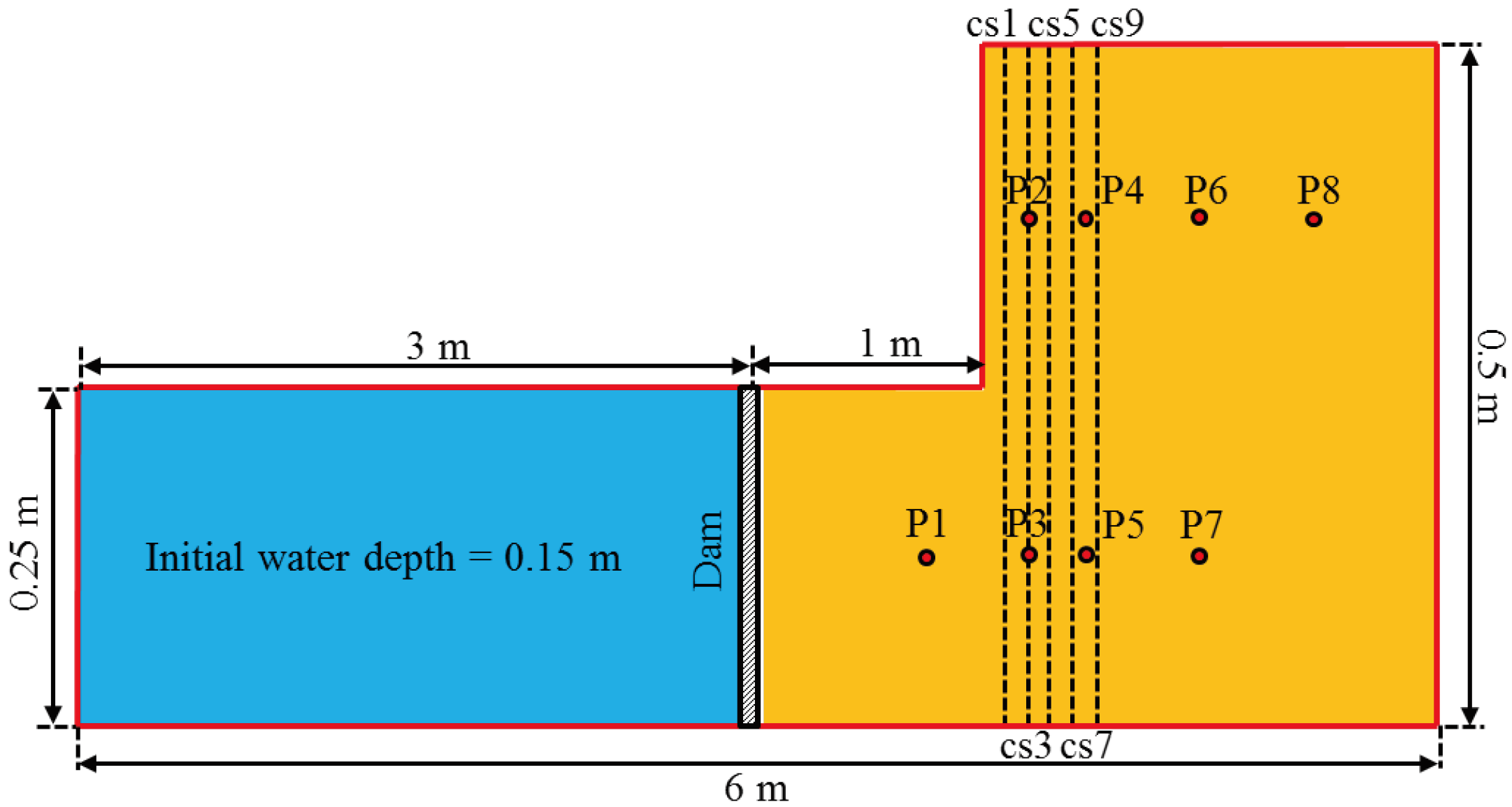
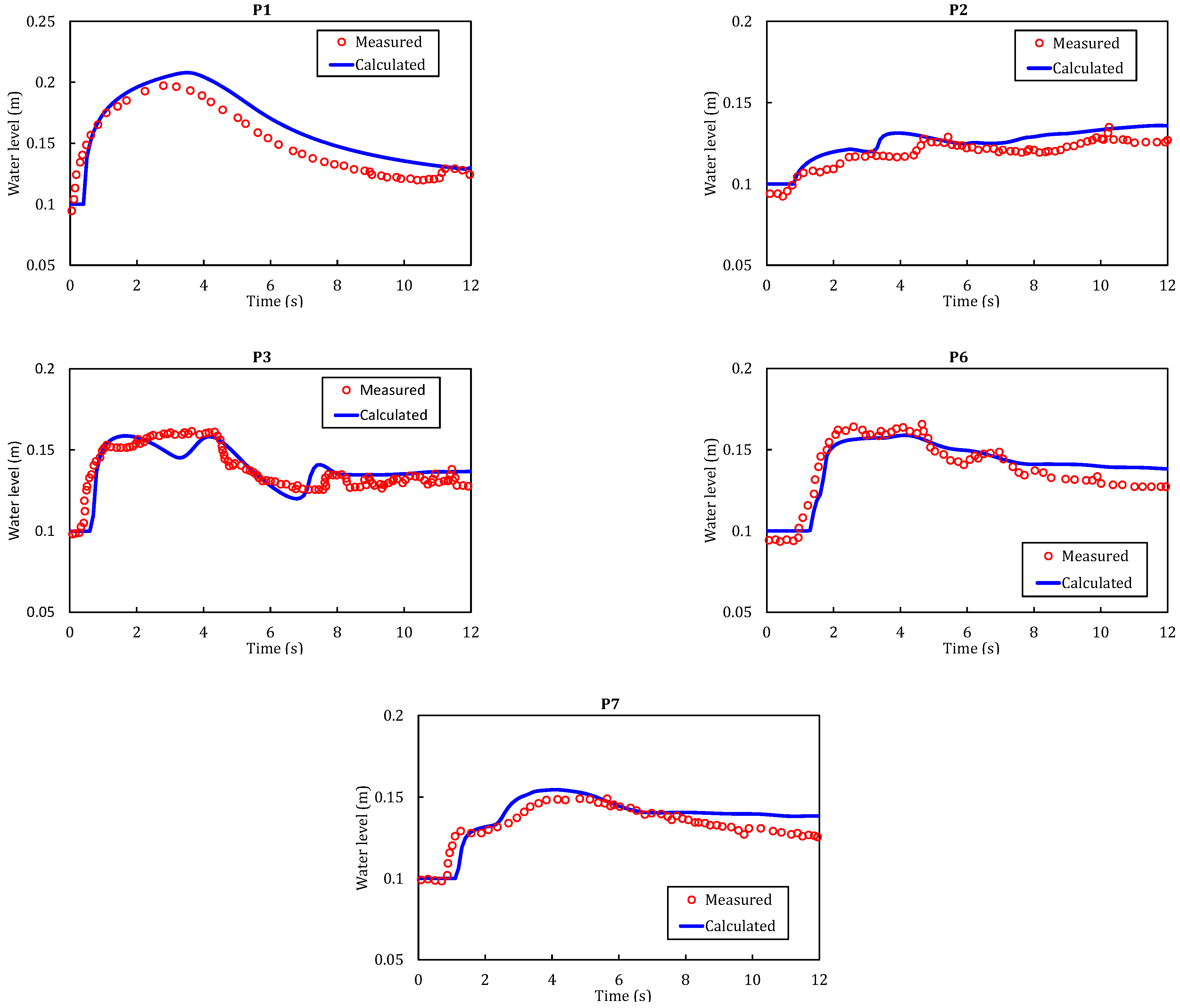
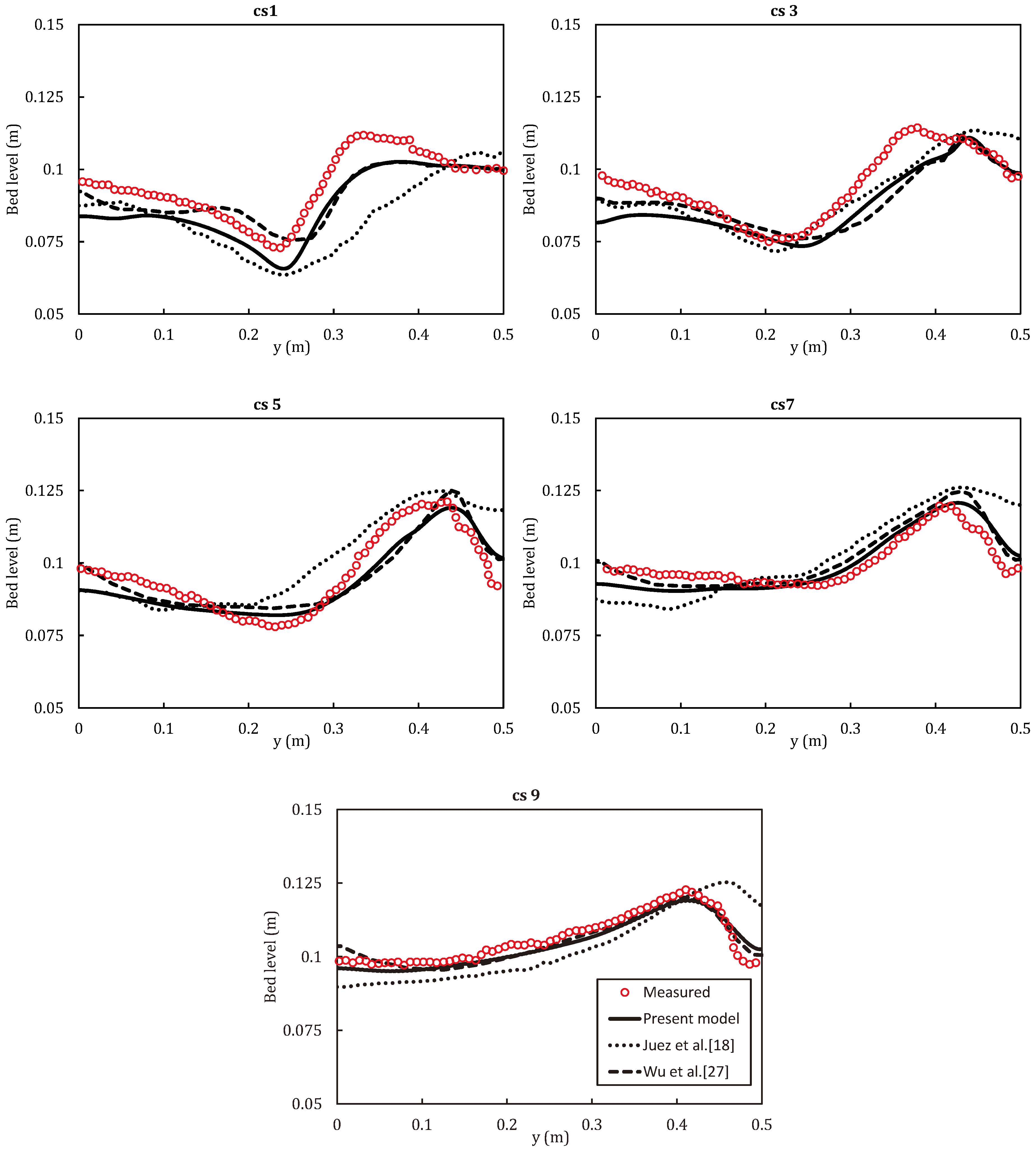
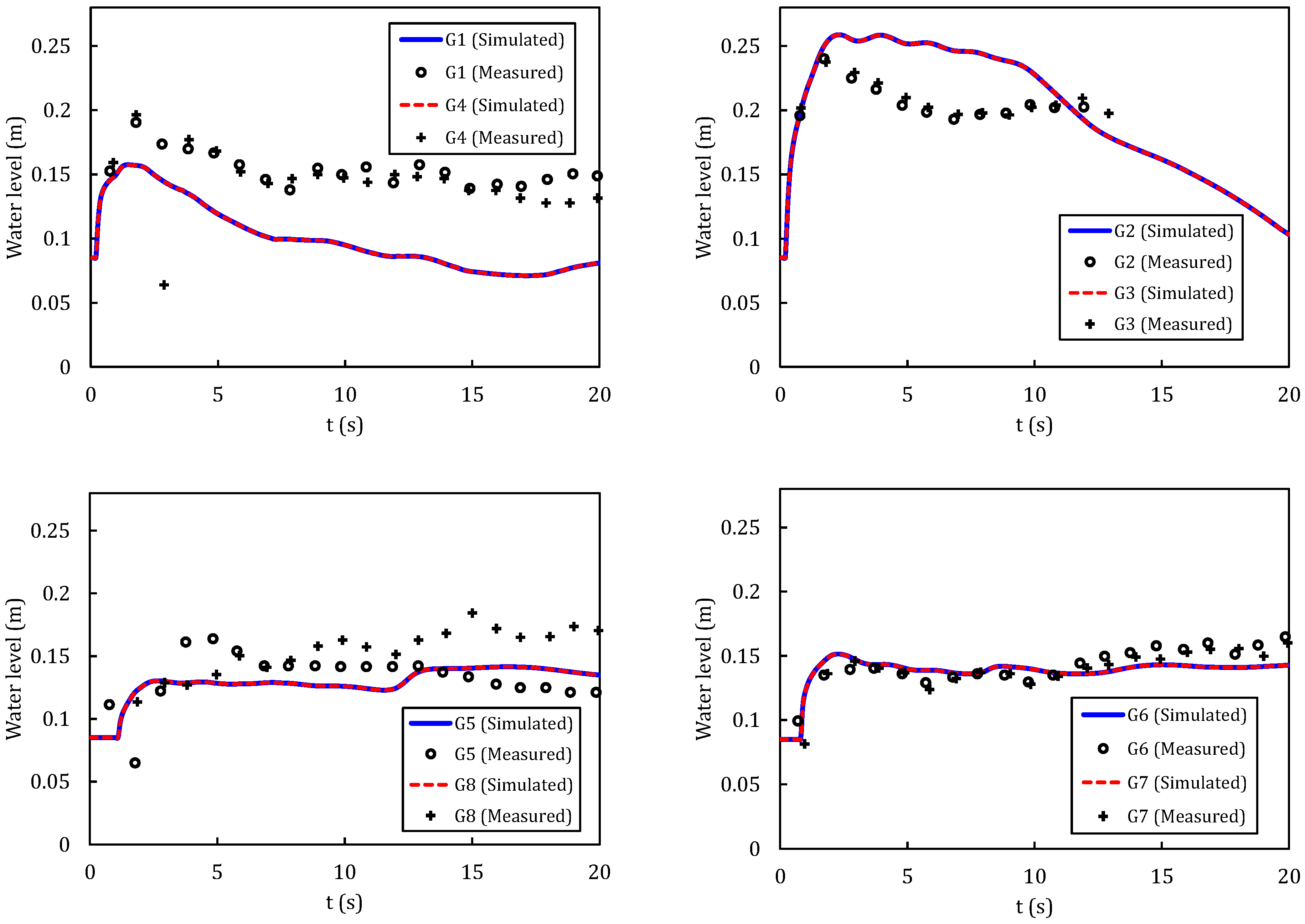
4.4. Partial Dam-Break Flow over Mobile Bed
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Wu, W. Computational River Dynamics; Taylor & Francis: London, UK, 2008; Volume 78. [Google Scholar]
- Fraccarollo, L.; Toro, E.F. Experimental and numerical assessment of the shallow water model for two-dimensional dam-break type problems. J. Hydraul. Res. 1995, 33, 843–864. [Google Scholar] [CrossRef]
- Zhou, J.G.; Causon, D.M.; Mingham, C.G.; Ingram, D.M. The surface gradient method for the treatment of source terms in the shallow-water equations. J. Comput. Phys. 2001, 168, 1–25. [Google Scholar] [CrossRef]
- Liang, Q. Flood simulation using a well-balanced shallow flow model. J. Hydraul. Eng. 2010, 136, 669–675. [Google Scholar] [CrossRef]
- Song, L.; Zhou, J.; Li, Q.; Yang, X.; Zhang, Y. An unstructured finite volume model for dam-break floods with wet/dry fronts over complex topography. Int. J. Numer. Methods Fluids 2011, 67, 960–980. [Google Scholar] [CrossRef]
- Wu, G.; He, Z.; Liu, G. Development of a cell-centered Godunov-type finite volume model for shallow water flow based on unstructured mesh. Math. Probl. Eng. 2014, 2014, 257915. [Google Scholar] [CrossRef]
- Fraccarollo, L.; Capart, H. Riemann wave description of erosional dam-break flows. J. Fluid Mech. 2002, 461, 183–228. [Google Scholar] [CrossRef]
- Spinewine, B.; Zech, Y. Small-scale laboratory dam-break waves on movable beds. J. Hydraul. Res. 2007, 45, 73–86. [Google Scholar] [CrossRef]
- Cao, Z.; Pender, G.; Wallis, S.; Carling, P. Computational dam-break hydraulics over erodible sediment bed. J. Hydraul. Eng. 2004, 130, 689–703. [Google Scholar] [CrossRef]
- Wu, W.; Wang, S.S. One-dimensional modeling of dam-break flow over movable beds. J. Hydraul. Eng. 2007, 133, 48–58. [Google Scholar] [CrossRef]
- Abderrezzak, K.E.K.; Paquier, A.; Gay, B. One-dimensional numerical modelling of dam-break waves over movable beds: Application to experimental and field cases. Environ. Fluid Mech. 2008, 8, 169–198. [Google Scholar] [CrossRef]
- Xia, J.; Lin, B.; Falconer, R.A.; Wang, G. Modelling dam-break flows over mobile beds using a 2D coupled approach. Adv. Water Resour. 2010, 33, 171–183. [Google Scholar] [CrossRef]
- Benkhaldoun, F.; Sari, S.; Seaid, M. A flux-limiter method for dam-break flows over erodible sediment beds. Appl. Math. Model. 2012, 36, 4847–4861. [Google Scholar] [CrossRef]
- Li, S.; Duffy, C.J. Fully coupled approach to modeling shallow water flow, sediment transport, and bed evolution in rivers. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Liu, X.; Sedano, J.A.I.; Mohammadian, A. A robust coupled 2-D model for rapidly varying flows over erodible bed using central-upwind method with wetting and drying. Can. J. Civ. Eng. 2015, 42, 530–543. [Google Scholar] [CrossRef]
- Soares-Frazão, S.; Canelas, R.; Cao, Z.; Cea, L.; Chaudhry, H.M.; Die Moran, A.; El Kadi, K.; Ferreira, R.; Cadórniga, I.F.; Gonzalez-Ramirez, N.; et al. Dam-break flows over mobile beds: Experiments and benchmark tests for numerical models. J. Hydraul. Res. 2012, 50, 364–375. [Google Scholar] [CrossRef]
- Juez, C.; Murillo, J.; García-Navarro, P. Numerical assessment of bed-load discharge formulations for transient flow in 1D and 2D situations. J. Hydroinform. 2013, 15, 1234–1257. [Google Scholar] [CrossRef]
- Juez, C.; Murillo, J.; García-Navarro, P. A 2D weakly-coupled and efficient numerical model for transient shallow flow and movable bed. Adv. Water Resour. 2014, 71, 93–109. [Google Scholar] [CrossRef]
- Juez, C.; Ferrer-Boix, C.; Murillo, J.; Hassan, M.; García-Navarro, P. A model based on Hirano-Exner equations for two-dimensional transient flows over heterogeneous erodible beds. Adv. Water Resour. 2016, 87, 1–18. [Google Scholar] [CrossRef]
- Juez, C.; Soares-Frazao, S.; Murillo, J.; García-Navarro, P. Experimental and numerical simulation of bed load transport over steep slopes. J. Hydraul. Res. 2017, 55, 455–469. [Google Scholar] [CrossRef]
- He, Z.; Wu, T.; Weng, H.; Hu, P.; Wu, G. Numerical simulation of dam-break flow and bed change considering the vegetation effects. Int. J. Sediment Res. 2017, 32, 105–120. [Google Scholar] [CrossRef]
- Di Cristo, C.; Evangelista, S.; Greco, M.; Iervolino, M.; Leopardi, A.; Vacca, A. Dam-break waves over an erodible embankment: Experiments and simulations. J. Hydraul. Res. 2018, 56, 196–210. [Google Scholar] [CrossRef]
- Sánchez, A.; Wu, W. A non-equilibrium sediment transport model for coastal inlets and navigation channels. J. Coast. Res. 2011, 59, 39–48. [Google Scholar] [CrossRef]
- Cao, Z.; Day, R.; Egashira, S. Coupled and decoupled numerical modeling of flow and morphological evolution in alluvial rivers. J. Hydraul. Eng. 2002, 128, 306–321. [Google Scholar] [CrossRef]
- Greenberg, J.M.; LeRoux, A.Y. A well-balanced scheme for the numerical processing of source terms in hyperbolic equations. SIAM J. Numer. Anal. 1996, 33, 1–16. [Google Scholar] [CrossRef]
- Bermudez, A.; Vázquez, M.E. Upwind methods for hyperbolic conservation laws with source terms. Comput. Fluids 1994, 23, 1049–1071. [Google Scholar] [CrossRef]
- Wu, W.; Marsooli, R.; He, Z. Depth-averaged two-dimensional model of unsteady flow and sediment transport due to noncohesive embankment break/breaching. J. Hydraul. Eng. 2011, 138, 503–516. [Google Scholar] [CrossRef]
- Kurganov, A.; Noelle, S.; Petrova, G. Semidiscrete central-upwind schemes for hyperbolic conservation laws and Hamilton–Jacobi equations. SIAM J. Sci. Comput. 2001, 23, 707–740. [Google Scholar] [CrossRef]
- He, Z.; Hu, P.; Zhao, L.; Wu, G.; Pähtz, T. Modeling of breaching due to overtopping flow and waves based on coupled flow and sediment transport. Water 2015, 7, 4283–4304. [Google Scholar] [CrossRef]
- Singh, J.; Altinakar, M.S.; Ding, Y. Two-dimensional numerical modeling of dam-break flows over natural terrain using a central explicit scheme. Adv. Water Resour. 2011, 34, 1366–1375. [Google Scholar] [CrossRef]
- Kurganov, A.; Petrova, G. A second-order well-balanced positivity preserving central-upwind scheme for the Saint-Venant system. Commun. Math. Sci. 2007, 5, 133–160. [Google Scholar] [CrossRef]
- Evangelista, S.; Altinakar, M.S.; Di Cristo, C.; Leopardi, A. Simulation of dam-break waves on movable beds using a multi-stage centered scheme. Int. J. Sediment Res. 2013, 28, 269–284. [Google Scholar] [CrossRef]
- Liang, Q. A structured but non-uniform Cartesian grid-based model for the shallow water equations. Int. J. Numer. Methods Fluids 2011, 66, 537–554. [Google Scholar] [CrossRef]
- Benkhaldoun, F.; Sahmim, S.; Seaid, M. A two-dimensional finite volume morphodynamic model on unstructured triangular grids. Int. J. Numer. Methods Fluids 2010, 63, 1296–1327. [Google Scholar] [CrossRef]
- Huang, W.; Cao, Z.; Pender, G.; Liu, Q.; Carling, P. Coupled flood and sediment transport modelling with adaptive mesh refinement. Sci. China Technol. Sci. 2015, 58, 1425–1438. [Google Scholar] [CrossRef]
- Zhang, M.; Wu, W. A two dimensional hydrodynamic and sediment transport model for dam break based on finite volume method with quadtree grid. Appl. Ocean Res. 2011, 33, 297–308. [Google Scholar] [CrossRef]
- Wu, W.; Sánchez, A.; Zhang, M. An implicit 2-D shallow water flow model on unstructured quadtree rectangular mesh. J. Coas. Res. 2011, 15–26. [Google Scholar] [CrossRef]
- Armanini, A.; Di Silvio, G. A one-dimensional model for the transport of a sediment mixture in non-equilibrium conditions. J. Hydraul. Res. 1988, 26, 275–292. [Google Scholar] [CrossRef]
- Greimann, B.; Lai, Y.; Huang, J. Two-dimensional total sediment load model equations. J. Hydraul. Eng. 2008, 134, 1142–1146. [Google Scholar] [CrossRef]
- Wu, W. Depth-averaged two-dimensional numerical modeling of unsteady flow and nonuniform sediment transport in open channels. J. Hydraul. Eng. 2004, 130, 1013–1024. [Google Scholar] [CrossRef]
- Zhang, R.; Xie, J. Sedimentation Research in China: Systematic Selections; China Water and Power Press: Beijing, China, 1993. [Google Scholar]
- Wu, W.; Wang, S.S.; Jia, Y. Nonuniform sediment transport in alluvial rivers. J. Hydraul. Res. 2000, 38, 427–434. [Google Scholar] [CrossRef]
- Audusse, E.; Bouchut, F.; Bristeau, M.O.; Klein, R.; Perthame, B.T. A fast and stable well-balanced scheme with hydrostatic reconstruction for shallow water flows. SIAM J. Sci. Comput. 2004, 25, 2050–2065. [Google Scholar] [CrossRef]
- Morris, M. CADAM: Concerted Action on Dam-Break Modeling—Final Report; Report SR 571; HR Wallingford: Wallingford, UK, 2000. [Google Scholar]
- Liang, Q.; Marche, F. Numerical resolution of well-balanced shallow water equations with complex source terms. Adv. Water Resour. 2009, 32, 873–884. [Google Scholar] [CrossRef]
- Brufau, P.; Garcia-Navarro, P. Two-dimensional dam break flow simulation. Int. J. Numer. Methods Fluids 2000, 33, 35–57. [Google Scholar] [CrossRef]
- Liang, D.; Falconer, R.A.; Lin, B. Comparison between TVD-MacCormack and ADI-type solvers of the shallow water equations. Adv. Water Resour. 2006, 29, 1833–1845. [Google Scholar] [CrossRef]
- Goutiere, L.; Soares-Frazão, S.; Zech, Y. Dam-break flow on mobile bed in abruptly widening channel: Experimental data. J. Hydraul. Res. 2011, 49, 367–371. [Google Scholar] [CrossRef]
- Palumbo, A.; Soares-Frazao, S.; Goutiere, L.; Pianese, D.; Zech, Y. Dam-break flow on mobile bed in a channel with a sudden enlargement. River Flow 2008, 1, 645–654. [Google Scholar]
- Canelas, R.; Murillo, J.; Ferreira, R.M. Two-dimensional depth-averaged modelling of dam-break flows over mobile beds. J. Hydraul. Res. 2013, 51, 392–407. [Google Scholar] [CrossRef]

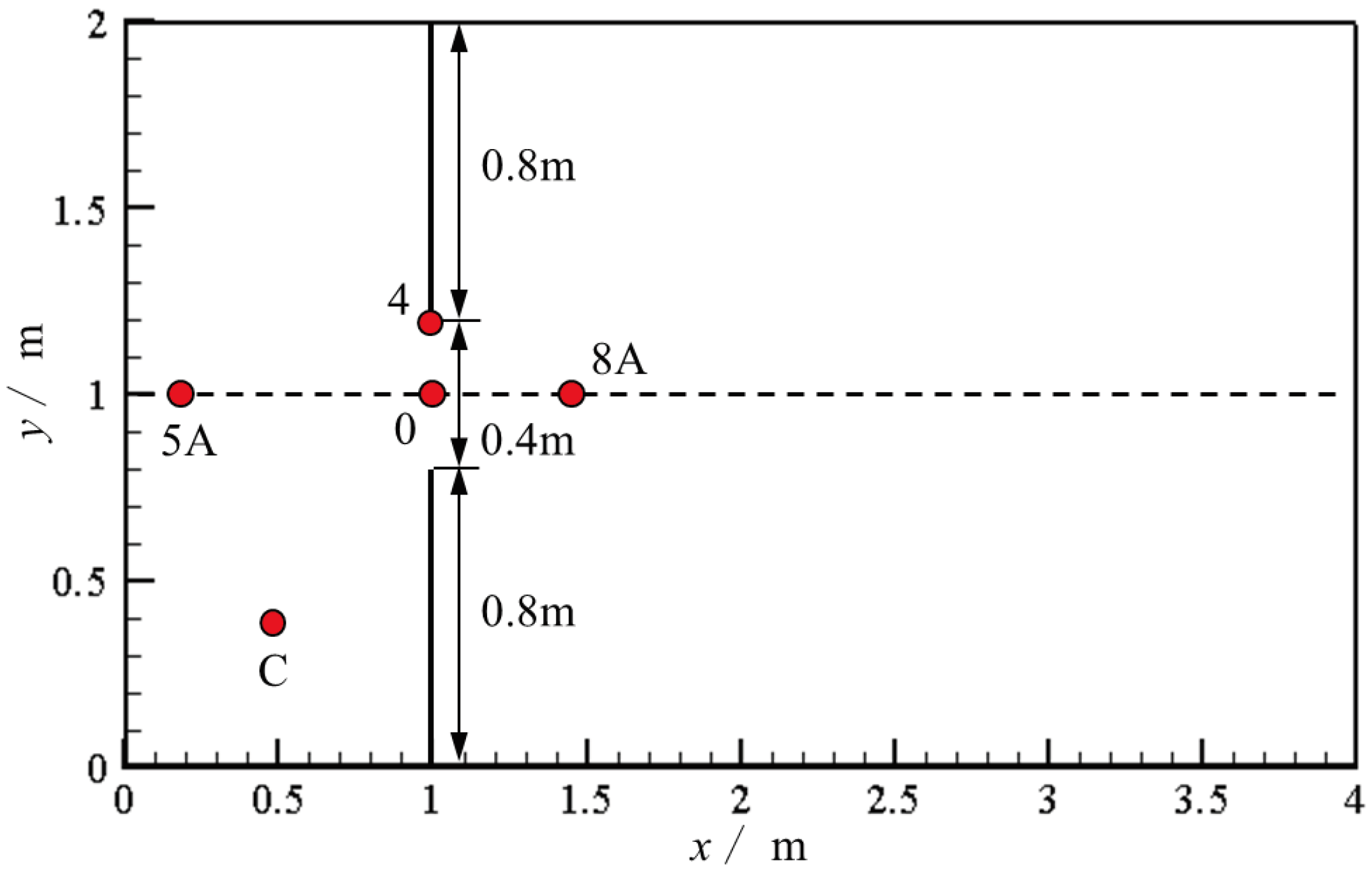
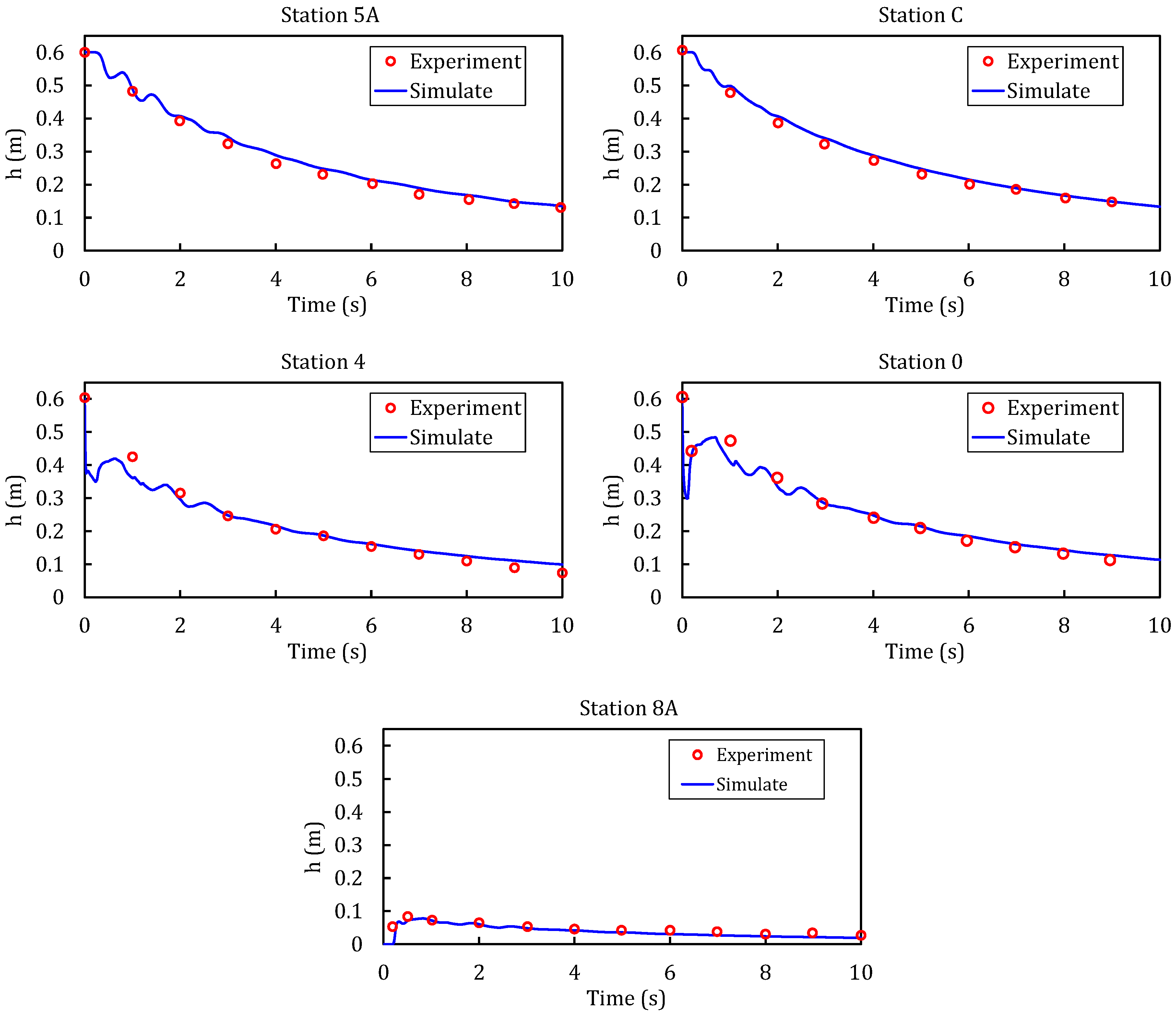




| Stations | 5A | C | 4 | 0 | 8A |
|---|---|---|---|---|---|
| x/m | 0.18 | 0.48 | 1.00 | 1.00 | 1.72 |
| y/m | 1.00 | 0.40 | 1.16 | 1.00 | 1.00 |
| Gauges | P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 |
|---|---|---|---|---|---|---|---|---|
| x/m | 0.75 | 1.20 | 1.20 | 1.45 | 1.45 | 1.95 | 1.95 | 2.45 |
| y/m | 0.00 | 0.25 | 0.00 | 0.25 | 0.00 | 0.25 | 0.00 | 0.25 |
| Gauges | G1 | G2 | G3 | G4 | G5 | G6 | G7 | G8 |
|---|---|---|---|---|---|---|---|---|
| x/m | 0.64 | 0.64 | 0.64 | 0.64 | 1.94 | 1.94 | 1.94 | 1.94 |
| y/m | −0.50 | −0.165 | 0.165 | 0.50 | −0.99 | −0.33 | 0.33 | 0.99 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, G.; Yang, Z.; Zhang, K.; Dong, P.; Lin, Y.-T. A Non-Equilibrium Sediment Transport Model for Dam Break Flow over Moveable Bed Based on Non-Uniform Rectangular Mesh. Water 2018, 10, 616. https://doi.org/10.3390/w10050616
Wu G, Yang Z, Zhang K, Dong P, Lin Y-T. A Non-Equilibrium Sediment Transport Model for Dam Break Flow over Moveable Bed Based on Non-Uniform Rectangular Mesh. Water. 2018; 10(5):616. https://doi.org/10.3390/w10050616
Chicago/Turabian StyleWu, Gangfeng, Zhehao Yang, Kefeng Zhang, Ping Dong, and Ying-Tien Lin. 2018. "A Non-Equilibrium Sediment Transport Model for Dam Break Flow over Moveable Bed Based on Non-Uniform Rectangular Mesh" Water 10, no. 5: 616. https://doi.org/10.3390/w10050616
APA StyleWu, G., Yang, Z., Zhang, K., Dong, P., & Lin, Y.-T. (2018). A Non-Equilibrium Sediment Transport Model for Dam Break Flow over Moveable Bed Based on Non-Uniform Rectangular Mesh. Water, 10(5), 616. https://doi.org/10.3390/w10050616





