Post-Monsoon Season Precipitation Reduction over South Asia: Impacts of Anthropogenic Aerosols and Irrigation
Abstract
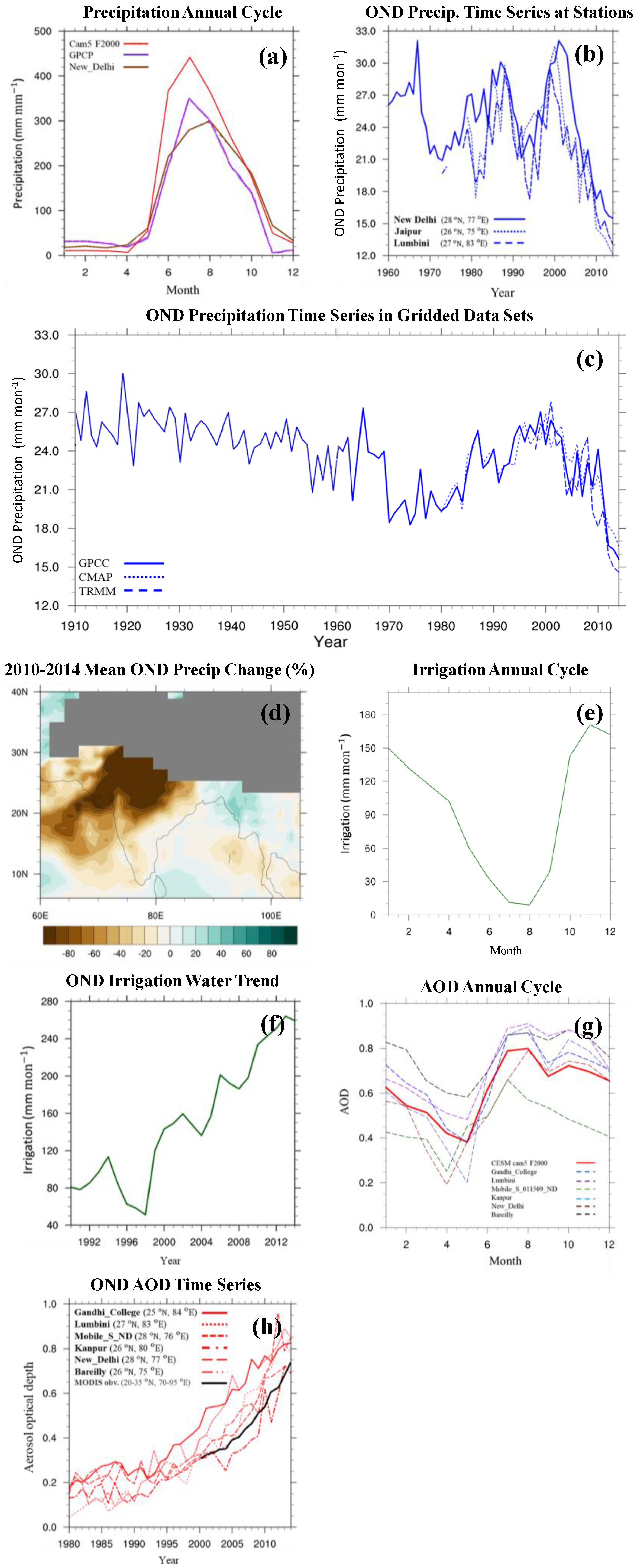
:1. Introduction
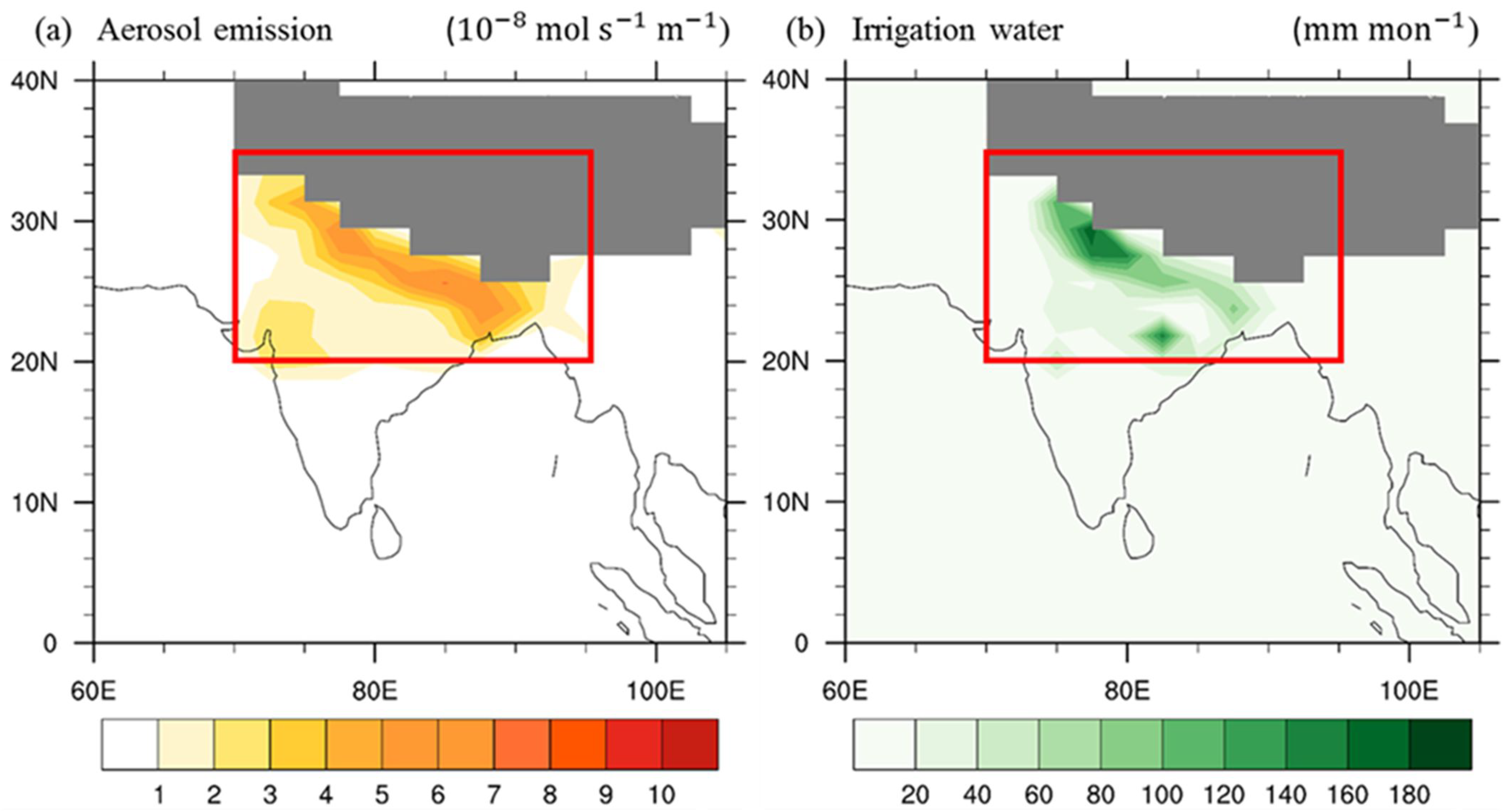
2. Model Description and Experimental Design
3. Post-Monsoon Season Climate Responses
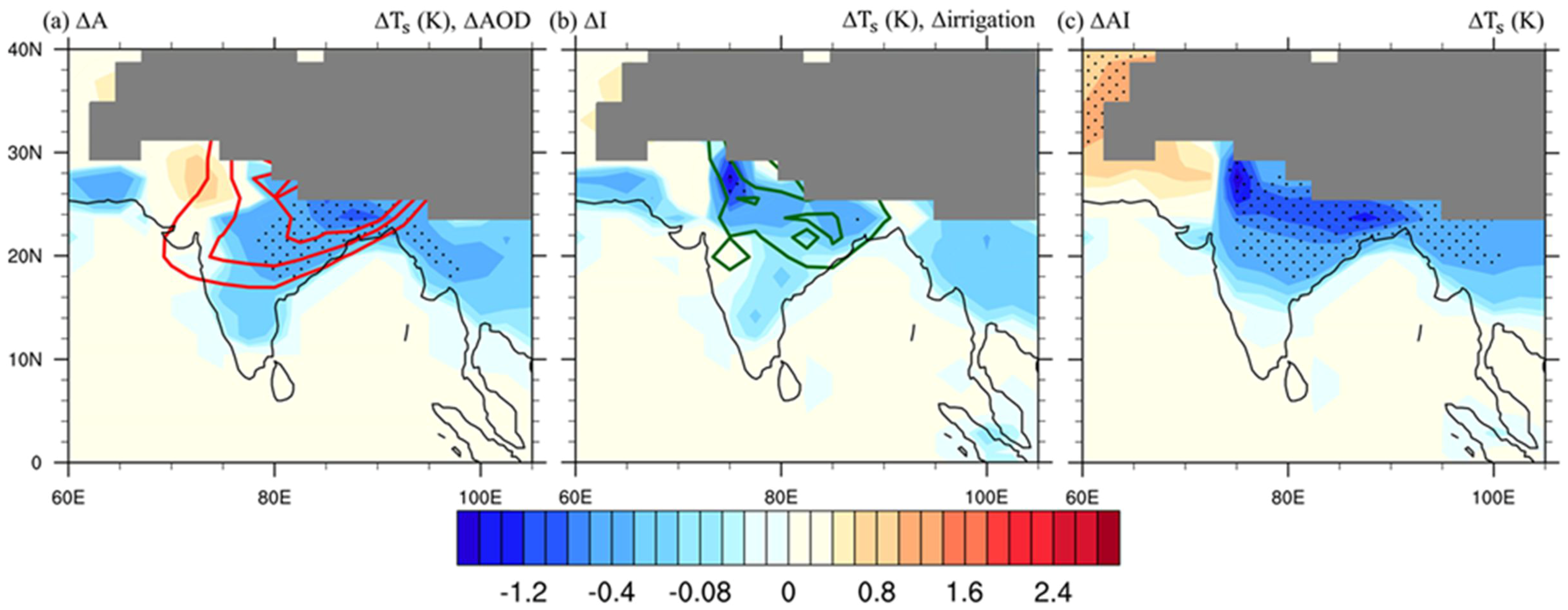
3.1. Surface Temperature Responses
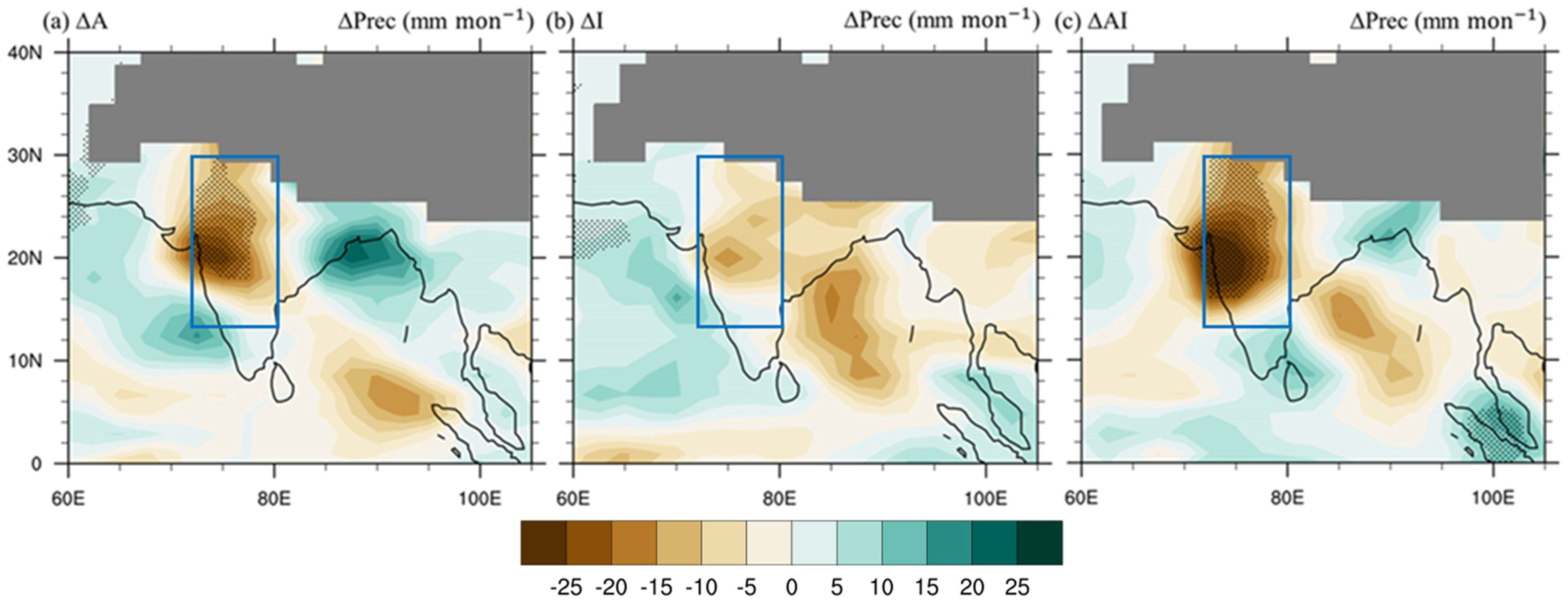
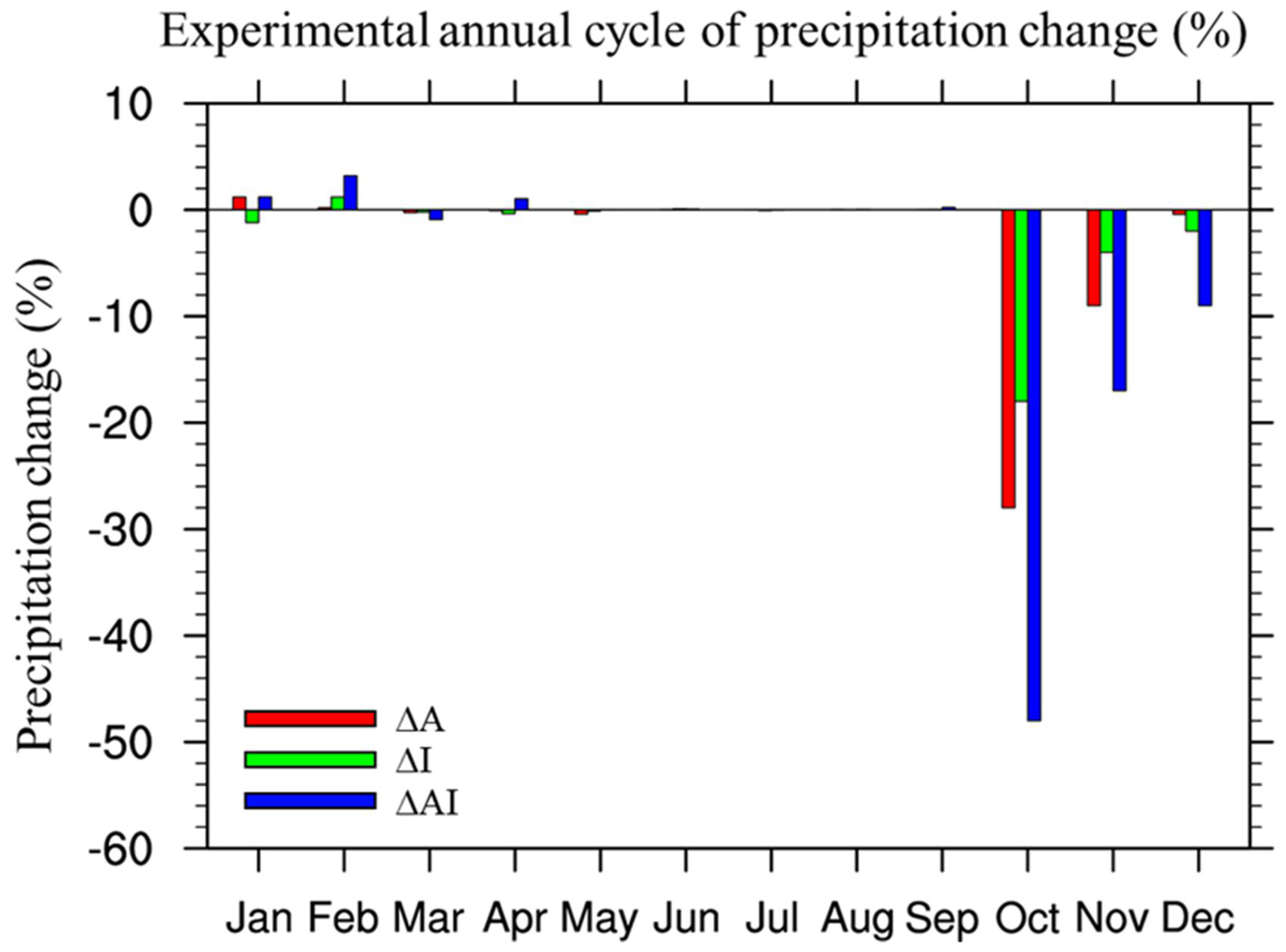
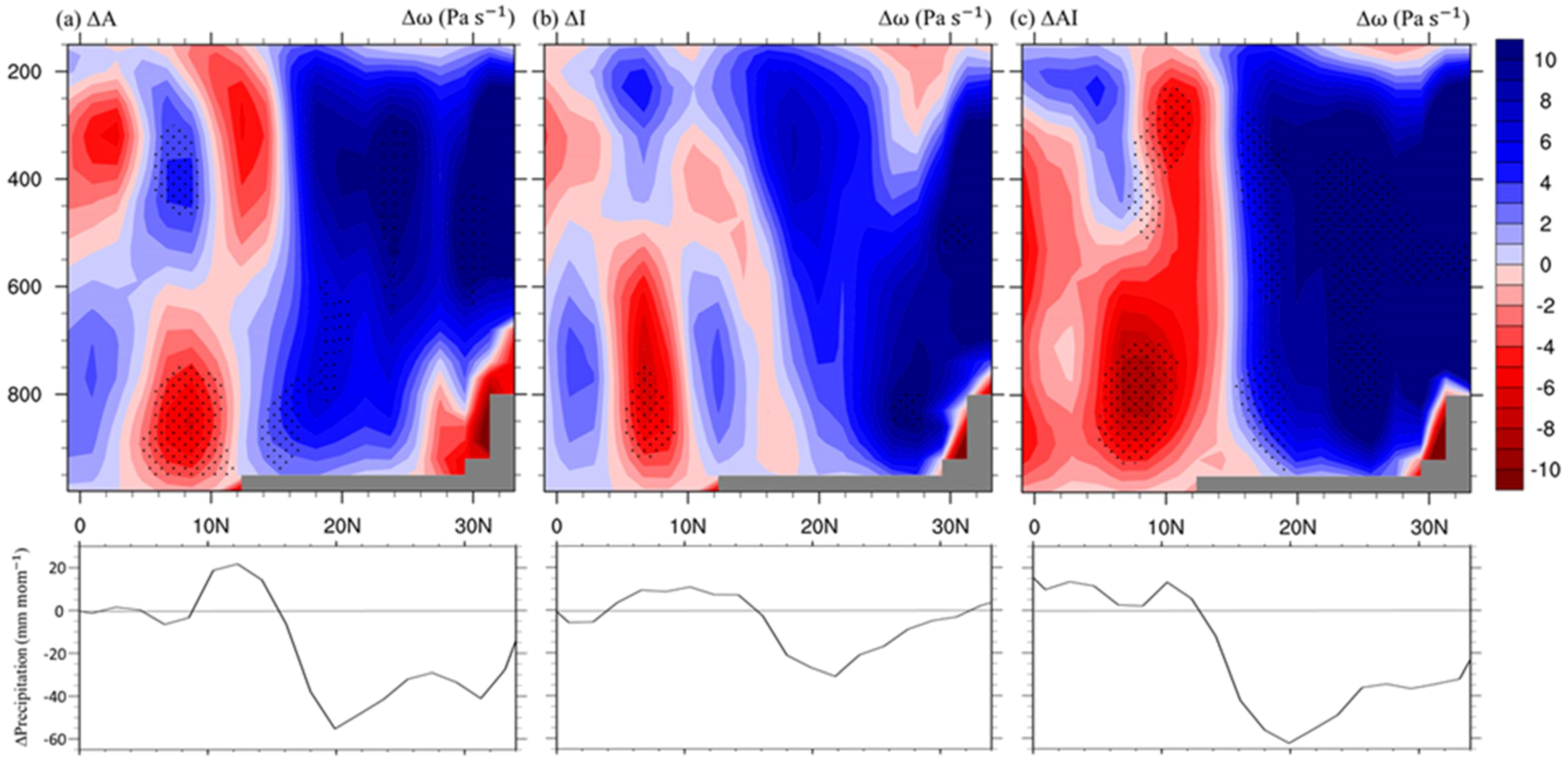
3.2. Precipitation Change and Moisture Budget
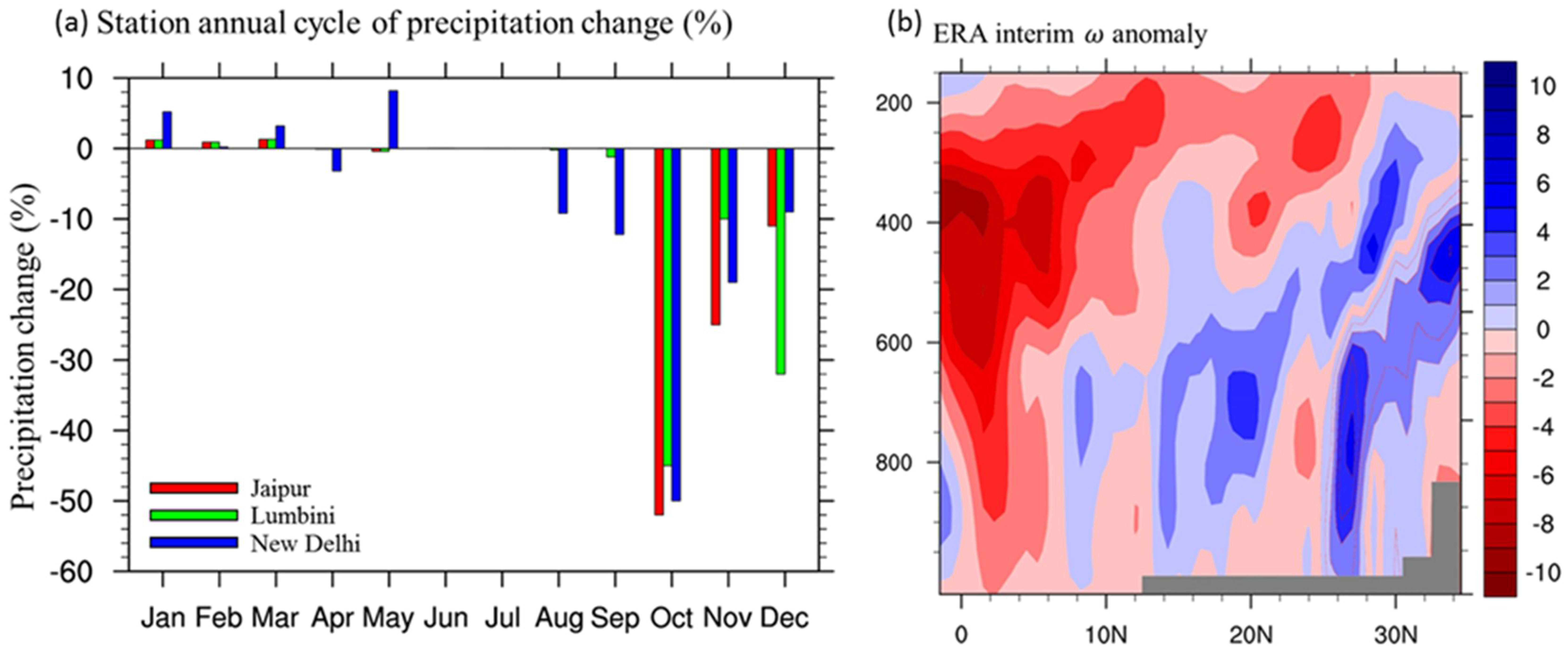
4. Discussion
4.1. Nonlinear Responses to the Concurrent Aerosol and irrigation Effects
4.2. The Local Meridional Circulation Change and the Earlier Withdrawal of the South Asia Summer Monsoon
5. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Adler, R.F.; Huffman, G.J.; Chang, A.; Ferraro, R.; Xie, P.-P.; Janowiak, J.; Rudolf, B.; Schneider, U.; Curtis, S.; Bolvin, D.; et al. The version-2 global precipitation climatology project (GPCP) monthly precipitation analysis (1979–present). J. Hydrometeorol. 2003, 4, 1147–1167. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Gu, G. Improving the global precipitation record: GPCP version 2.1. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Wang, S.-Y.; Yoon, J.-H.; Gillies, R.R.; Cho, C. What caused the winter drought in western nepal during recent years? J. Clim. 2013, 26, 8241–8256. [Google Scholar] [CrossRef]
- Kar, S.C.; Rana, S. Interannual variability of winter precipitation over northwest India and adjoining region: Impact of global forcings. Theor. Appl. Climatol. 2014, 116, 609–623. [Google Scholar] [CrossRef]
- Barlow, M.; Cullen, H.; Lyon, B. Drought in central and southwest Asia: La niña, the warm pool, and Indian Ocean precipitation. J. Clim. 2002, 15, 697–700. [Google Scholar] [CrossRef]
- Wey, H.; Lo, M.; Lee, S.; Yu, J.; Hsu, H. Potential impacts of wintertime soil moisture anomalies from agricultural irrigation at low latitudes on regional and global climates. Geophys. Res. Lett. 2015, 42, 8605–8614. [Google Scholar] [CrossRef] [Green Version]
- Rodell, M.; Velicogna, I.; Famiglietti, J.S. Satellite-based estimates of groundwater depletion in India. Nature 2009, 460, 999–1002. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wisser, D.; Frolking, S.; Douglas, E.M.; Fekete, B.M.; Vörösmarty, C.J.; Schumann, A.H. Global irrigation water demand: Variability and uncertainties arising from agricultural and climate data sets. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef] [Green Version]
- Seneviratne, S.I.; Corti, T.; Davin, E.L.; Hirschi, M.; Jaeger, E.B.; Lehner, I.; Orlowsky, B.; Teuling, A.J. Investigating soil moisture–climate interactions in a changing climate: A review. Earth-Sci. Rev. 2010, 99, 125–161. [Google Scholar] [CrossRef]
- Douglas, E.M.; Niyogi, D.; Frolking, S.; Yeluripati, J.B.; Pielke, R.A.; Niyogi, N.; Vörösmarty, C.J.; Mohanty, U.C. Changes in moisture and energy fluxes due to agricultural land use and irrigation in the Indian Monsoon Belt. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef] [Green Version]
- Bonfils, C.; Lobell, D. Empirical evidence for a recent slowdown in irrigation-induced cooling. Proc. Natl. Acad. Sci. USA 2007, 104. [Google Scholar] [CrossRef] [PubMed]
- Roy, S.S.; Mahmood, R.; Niyogi, D.; Lei, M.; Foster, S.A.; Hubbard, K.G.; Douglas, E.; Pielke, R. Impacts of the agricultural green revolution—Induced land use changes on air temperatures in India. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef]
- Sacks, W.J.; Cook, B.I.; Buenning, N.; Levis, S.; Helkowski, J.H. Effects of global irrigation on the near-surface climate. Clim. Dyn. 2009, 33, 159–175. [Google Scholar] [CrossRef]
- DeAngelis, A.; Dominguez, F.; Fan, Y.; Robock, A.; Kustu, M.D.; Robinson, D. Evidence of enhanced precipitation due to irrigation over the Great Plains of the United States. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef] [Green Version]
- Puma, M.J.; Cook, B.I. Effects of irrigation on global climate during the 20th century. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef] [Green Version]
- Shukla, S.P.; Puma, M.J.; Cook, B.I. The response of the South Asian Summer Monsoon circulation to intensified irrigation in global climate model simulations. Clim. Dyn. 2014, 42, 21–36. [Google Scholar] [CrossRef]
- Lo, M.-H.; Famiglietti, J.S. Irrigation in California’s Central Valley strengthens the southwestern U.S. water cycle. Geophys. Res. Lett. 2013, 40, 301–306. [Google Scholar] [CrossRef]
- Im, E.; Eltahir, E.A.B. Enhancement of rainfall and runoff upstream from irrigation location in a climate model of West Africa. Water Resour. Res. 2014, 50, 8651–8674. [Google Scholar] [CrossRef] [Green Version]
- Holben, B.N.; Tanré, D.; Smirnov, A.; Eck, T.F.; Slutsker, I.; Abuhassan, N.; Newcomb, W.W.; Schafer, J.S.; Chatenet, B.; Lavenu, F.; et al. An emerging ground-based aerosol climatology: Aerosol optical depth from AERONET. J. Geophys. Res. 2001, 106, 12067–12097. [Google Scholar] [CrossRef] [Green Version]
- Jin, Q.; Wei, J.; Yang, Z. Positive response of Indian summer rainfall to Middle East dust. Geophys. Res. Lett. 2014, 41, 4068–4074. [Google Scholar] [CrossRef]
- Lamarque, J.-F.; Bond, T.C.; Eyring, V.; Granier, C.; Heil, A.; Klimont, Z.; Lee, D.; Liousse, C.; Mieville, A.; Owen, B.; et al. Historical (1850–2000) gridded anthropogenic and biomass burning emissions of reactive gases and aerosols: Methodology and application. Atmos. Chem. Phys. 2010, 10, 7017–7039. [Google Scholar] [CrossRef] [Green Version]
- Ramanathan, V.; Chung, C.; Kim, D.; Bettge, T.; Buja, L.; Kiehl, J.T.; Washington, W.M.; Fu, Q.; Sikka, D.R.; Wild, M. Atmospheric brown clouds: Impacts on South Asian climate and hydrological cycle. Proc. Natl. Acad. Sci. USA 2005, 102. [Google Scholar] [CrossRef] [PubMed]
- Meywerk, J.; Ramanathan, V. Observations of the spectral clear-sky aerosol forcing over the tropical Indian Ocean. J. Geophys. Res. 1999, 104, 24359–24370. [Google Scholar] [CrossRef] [Green Version]
- Lau, K.-M.; Kim, K.-M. Observational relationships between aerosol and Asian monsoon rainfall, and circulation. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef] [Green Version]
- Lau, K.M.; Kim, M.K.; Kim, K.M. Asian summer monsoon anomalies induced by aerosol direct forcing: The role of the Tibetan Plateau. Clim. Dyn. 2006, 26, 855–864. [Google Scholar] [CrossRef]
- Bollasina, M.A.; Ming, Y.; Ramaswamy, V. Anthropogenic aerosols and the weakening of the South Asian Summer Monsoon. Science 2011, 334, 502–505. [Google Scholar] [CrossRef] [PubMed]
- Ganguly, D.; Rasch, P.J.; Wang, H.; Yoon, J. Climate response of the South Asian monsoon system to anthropogenic aerosols. J. Geophys. Res. 2012, 117. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Kim, D.; Ekman, A.M.L.; Barth, M.C.; Rasch, P.J. Impact of anthropogenic aerosols on Indian summer monsoon. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef] [Green Version]
- Guo, L.; Highwood, E.J.; Shaffrey, L.C.; Turner, A.G. The effect of regional changes in anthropogenic aerosols on rainfall of the East Asian Summer Monsoon. Atmos. Chem. Phys. 2013, 13, 1521–1534. [Google Scholar] [CrossRef]
- Chen, J.-P.; Chen, I.-J.; Tsai, I.-C. Dynamic feedback of aerosol effects on the East Asian Summer Monsoon. J. Clim. 2016, 29, 6137–6149. [Google Scholar] [CrossRef]
- Schneider, U.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Rudolf, B.; Ziese, M. GPCC full data reanalysis version 6.0 at 1.0°: Monthly land-surface precipitation from rain-gauges built on GTS-based and historic data. 2011. Available online: https://www.esrl.noaa.gov/psd/data/gridded/data.gpcc.html (accessed on 8 August 2018). [CrossRef]
- Xie, P.; Arkin, P.A. Global precipitation: A 17-year monthly analysis based on gauge observations, satellite estimates, and numerical model outputs. Bull. Am. Meteorol. Soc. 1997, 78, 2539–2558. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Nelkin, E.J. The TRMM multi-satellite precipitation analysis (TMPA). In Satellite Rainfall Applications for Surface Hydrology; Gebremichael, M., Hossain, F., Eds.; Springer: Dordrecht, The Netherlands, 2010. [Google Scholar]
- Remer, L.A.; Kleidman Richard, G.; Levy Robert, C.; Kaufman Yoram, J.; Didier, T.; Shana, M.; Vanderlei, M.J.; Charles, I.; Ilan, K.; Yu, H.; et al. Global aerosol climatology from the MODIS satellite sensors. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef] [Green Version]
- Deng, J.; Xu, H. Nonlinear effect on the East Asian summer monsoon due to two coexisting anthropogenic forcing factors in eastern China: An AGCM study. Clim. Dyn. 2016, 46, 3767–3784. [Google Scholar] [CrossRef]
- Neale, R.B.; Chen, C.-C.; Gettelman, A.; Lauritzen, P.H.; Park, S.; Williamson, D.L.; Conley, A.J.; Garcia, R.; Kinnison, D.; Lamarque, J.-F.; et al. Description of the NCAR Community Atmosphere Model (CAM 5.0); NCAR Tech. Note NCAR/TN-486+STR. 2012. Available online: http://www.cesm.ucar.edu/models/cesm1.0/cam/docs/description/cam5_desc.pdf (accessed on 8 August 2018).
- Liu, X.; Easter, R.C.; Ghan, S.J.; Zaveri, R.; Rasch, P.; Shi, X.; Lamarque, J.-F.; Gettelman, A.; Morrison, H.; Vitt, F.; et al. Toward a minimal representation of aerosols in climate models: description and evaluation in the Community Atmosphere Model CAM5. Geosci. Model Dev. 2012, 5, 709–739. [Google Scholar] [CrossRef]
- Henderson-Sellers, A.; Pitman, A.J.; Love, P.K.; Irannejad, P.; Chen, T.H. The project for intercomparison of land surface parameterization schemes (PILPS): Phases 2 and 3*. Bull. Am. Meteorol. Soc. 1995, 76, 489–504. [Google Scholar] [CrossRef]
- Lo, M.; Famiglietti, J.S. Precipitation response to land subsurface hydrologic processes in atmospheric general circulation model simulations. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef] [Green Version]
- Chou, C.; Neelin, J.D. Mechanisms of global warming impacts on regional tropical precipitation. J. Clim. 2004, 17, 2688–2701. [Google Scholar] [CrossRef]
- Chou, C.; Neelin, J.D.; Chen, C.-A.; Tu, J.-Y. Evaluating the “rich-get-richer” mechanism in tropical precipitation change under global warming. J. Clim. 2009, 22, 1982–2005. [Google Scholar] [CrossRef]
- Chou, C.; Tu, J.-Y.; Tan, P.-H. Asymmetry of tropical precipitation change under global warming. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef] [Green Version]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Wang, B. LinHo rainy season of the Asian–Pacific summer monsoon. J. Clim. 2002, 15, 386–398. [Google Scholar] [CrossRef]
- Goswami, B.N.; Xavier, P.K. ENSO control on the south Asian monsoon through the length of the rainy season. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef] [Green Version]
- Sabeerali, C.T.; Rao, S.A.; Ajayamohan, R.S.; Murtugudde, R. On the relationship between Indian summer monsoon withdrawal and Indo-Pacific SST anomalies before and after 1976/1977 climate shift. Clim. Dyn. 2012, 39, 841–859. [Google Scholar] [CrossRef]
- Li, J.; Wang, B. How predictable is the anomaly pattern of the Indian summer rainfall? Clim. Dyn. 2016, 46, 2847–2861. [Google Scholar] [CrossRef]
- Li, J.; Wang, B.; Yang, Y.-M. Retrospective seasonal prediction of summer monsoon rainfall over West Central and Peninsular India in the past 142 years. Clim. Dyn. 2017, 48, 2581–2596. [Google Scholar] [CrossRef]
| Simulations | Aerosol and Precursor Emissions | Irrigation | Climate Responses |
|---|---|---|---|
| Control | Year 1850 | No | |
| AERO | Year 2000 | No | ΔA = AERO–Control |
| IRRI | Year 1850 | Yes | ΔI = IRRI–Control |
| BOTH | Year 2000 | Yes | ΔAI = BOTH–Control |
| Variables | ΔA | ΔI | ΔAI | ΔAI − (ΔA + ΔI) ii |
|---|---|---|---|---|
| Aerosol optical depth | 0.21 | 0.00 | 0.32 | 0.11 * |
| Shortwave flux (W m−2) | −5.98 | −0.01 | −8.52 | −2.53 * |
| Longwave flux (W m−2) | 1.07 | 2.88 | 3.03 | −0.92 |
| Latent heat flux (W m−2) | 0.02 | −8.97 | −10.1 | −1.15 * |
| Sensible heat flux (W m2) | 0.11 | 4.21 | 5.41 | 1.09 * |
| Surface temperature (K) | −0.31 | −0.61 | −1.12 | −0.20 * |
| Variables | ΔA | ΔI | ΔAI | ΔAI − (ΔA + ΔI) ii |
|---|---|---|---|---|
| Total precipitation, ΔP | −16.32 (−52%) | −7.66 (−24%) | −22.10 (−70%) | 1.88 (+6%) |
| Vertical moisture convergence by changed vertical motion, | −10.94 | −5.93 | −19.11 | −2.24 * |
| Vertical moisture convergence by changed moisture profile, | −6.45 | −2.79 | −6.19 | 3.05 |
| Horizontal moisture convergence, | 1.05 | 0.02 | 0.30 | −0.77 |
| Evaporation, ΔET | −0.01 | 1.04 | 2.90 | 1.87 * |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, W.-T.; Huang, K.-T.; Lo, M.-H.; LinHo, L.H. Post-Monsoon Season Precipitation Reduction over South Asia: Impacts of Anthropogenic Aerosols and Irrigation. Atmosphere 2018, 9, 311. https://doi.org/10.3390/atmos9080311
Chen W-T, Huang K-T, Lo M-H, LinHo LH. Post-Monsoon Season Precipitation Reduction over South Asia: Impacts of Anthropogenic Aerosols and Irrigation. Atmosphere. 2018; 9(8):311. https://doi.org/10.3390/atmos9080311
Chicago/Turabian StyleChen, Wei-Ting, Kung-Tzu Huang, Min-Hui Lo, and L. H. LinHo. 2018. "Post-Monsoon Season Precipitation Reduction over South Asia: Impacts of Anthropogenic Aerosols and Irrigation" Atmosphere 9, no. 8: 311. https://doi.org/10.3390/atmos9080311





