On the Current and Future Dry Spell Characteristics over Africa
Abstract
:1. Introduction
2. Model, Experimental Configuration, Datasets and Methods
2.1. Model and Experimental Configuration
2.2. Observational Data
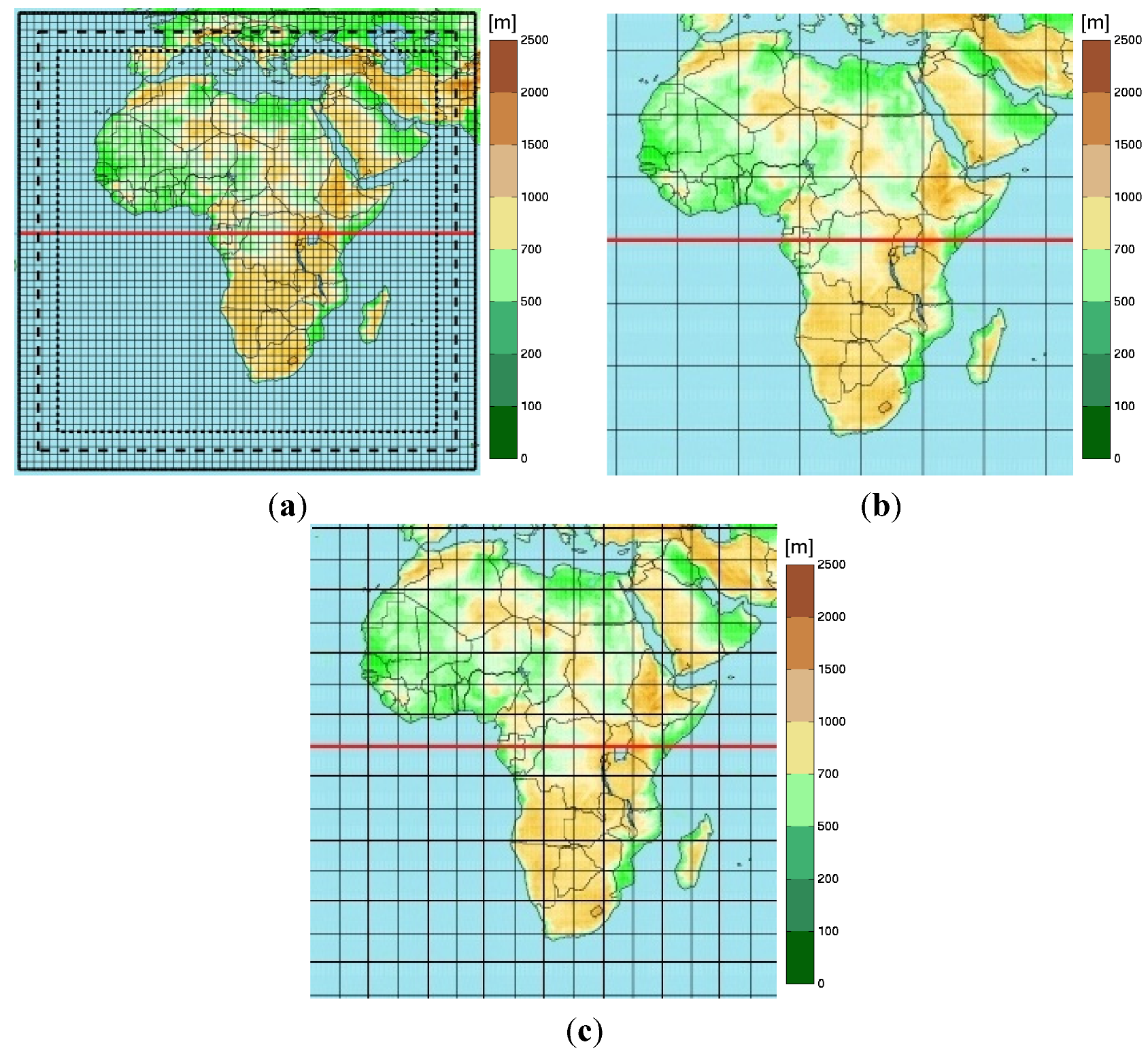
2.3. Methods
2.3.1. Performance Errors
2.3.2. Boundary Forcing Errors
2.3.3. Added Value
2.3.4. Projected Changes
3. Results
3.1. Assessment of Errors and Added Value
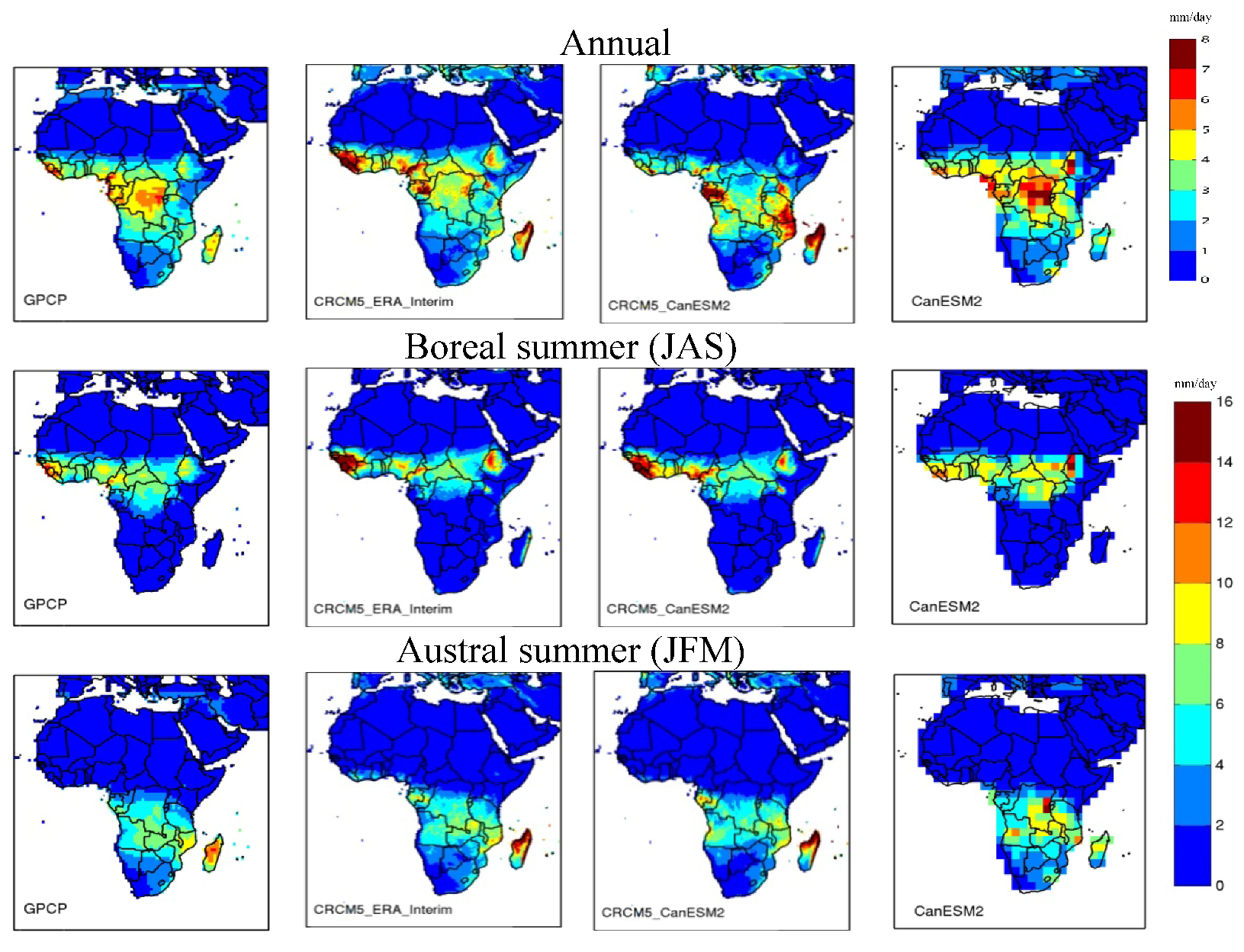
3.1.1. Performance Errors



3.1.2. Boundary Forcing Errors
3.1.3 Added Value
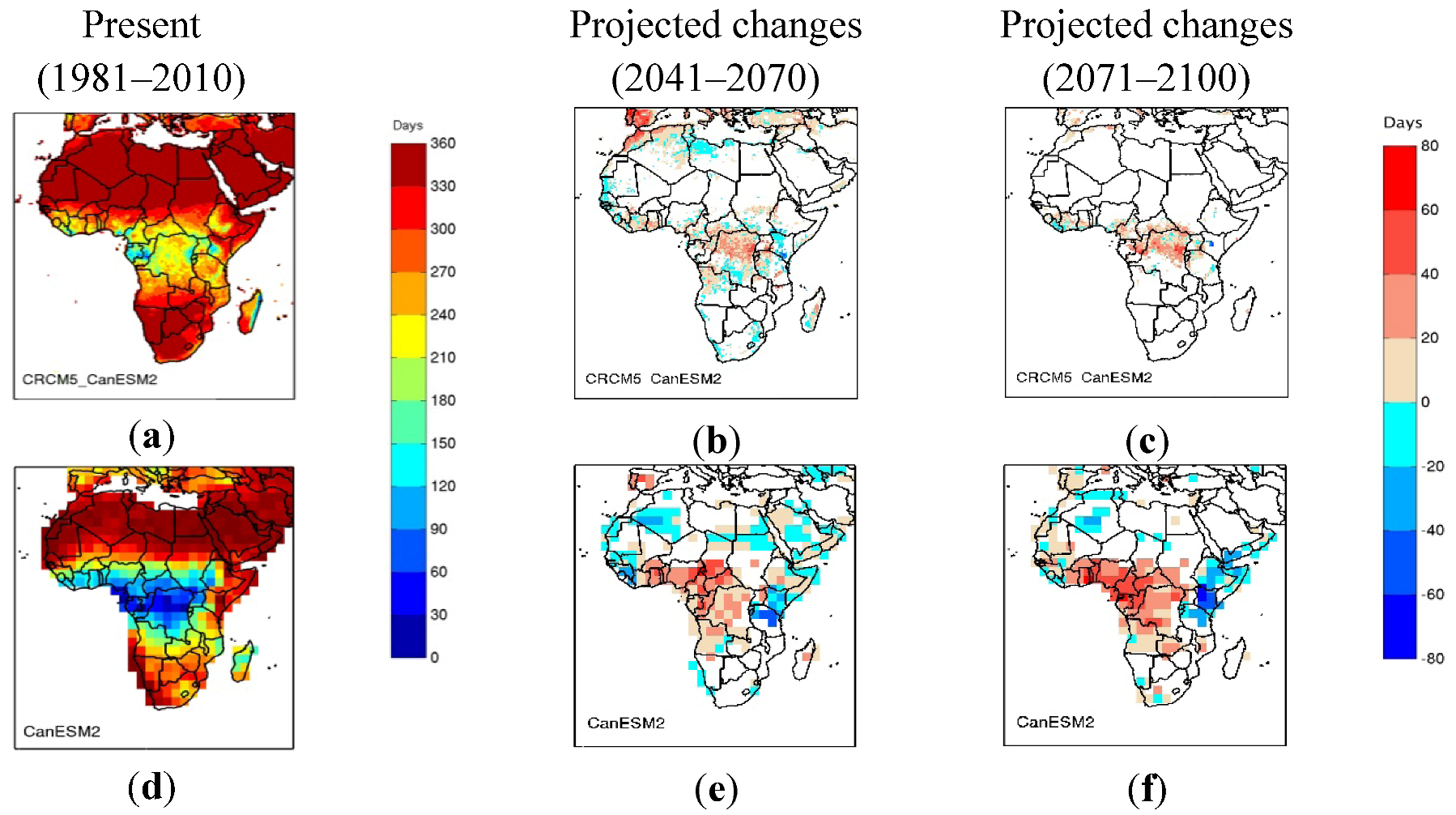
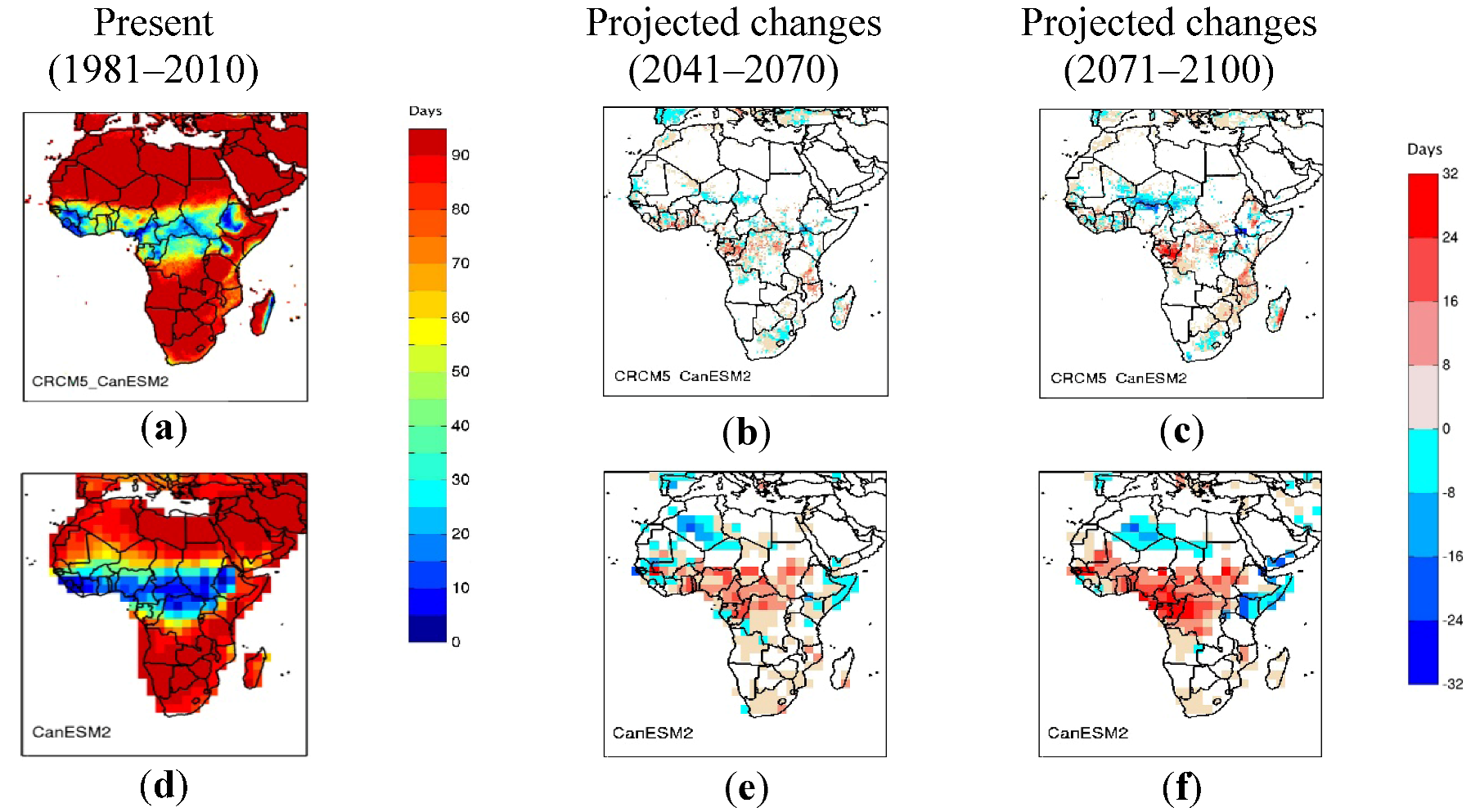
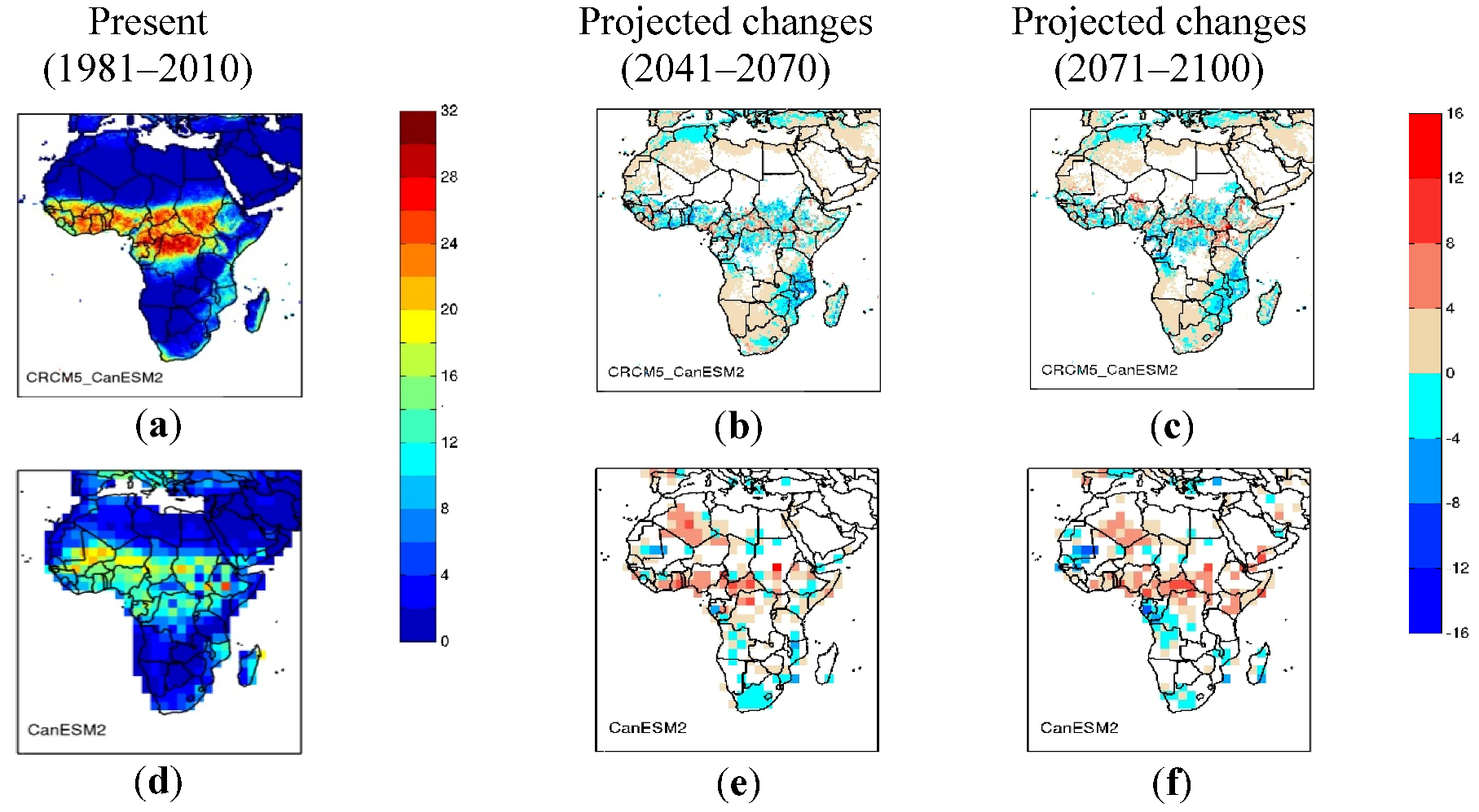
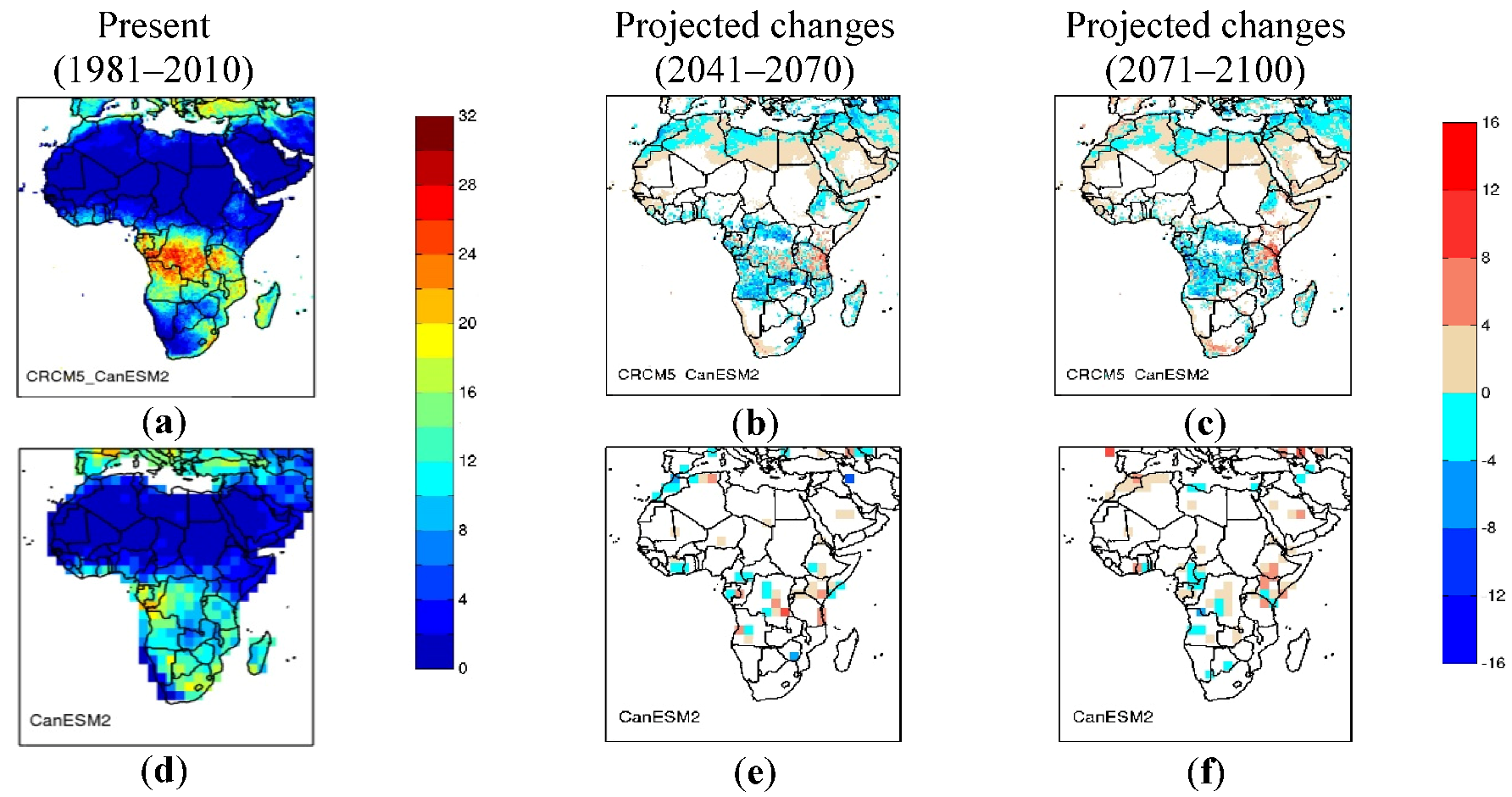
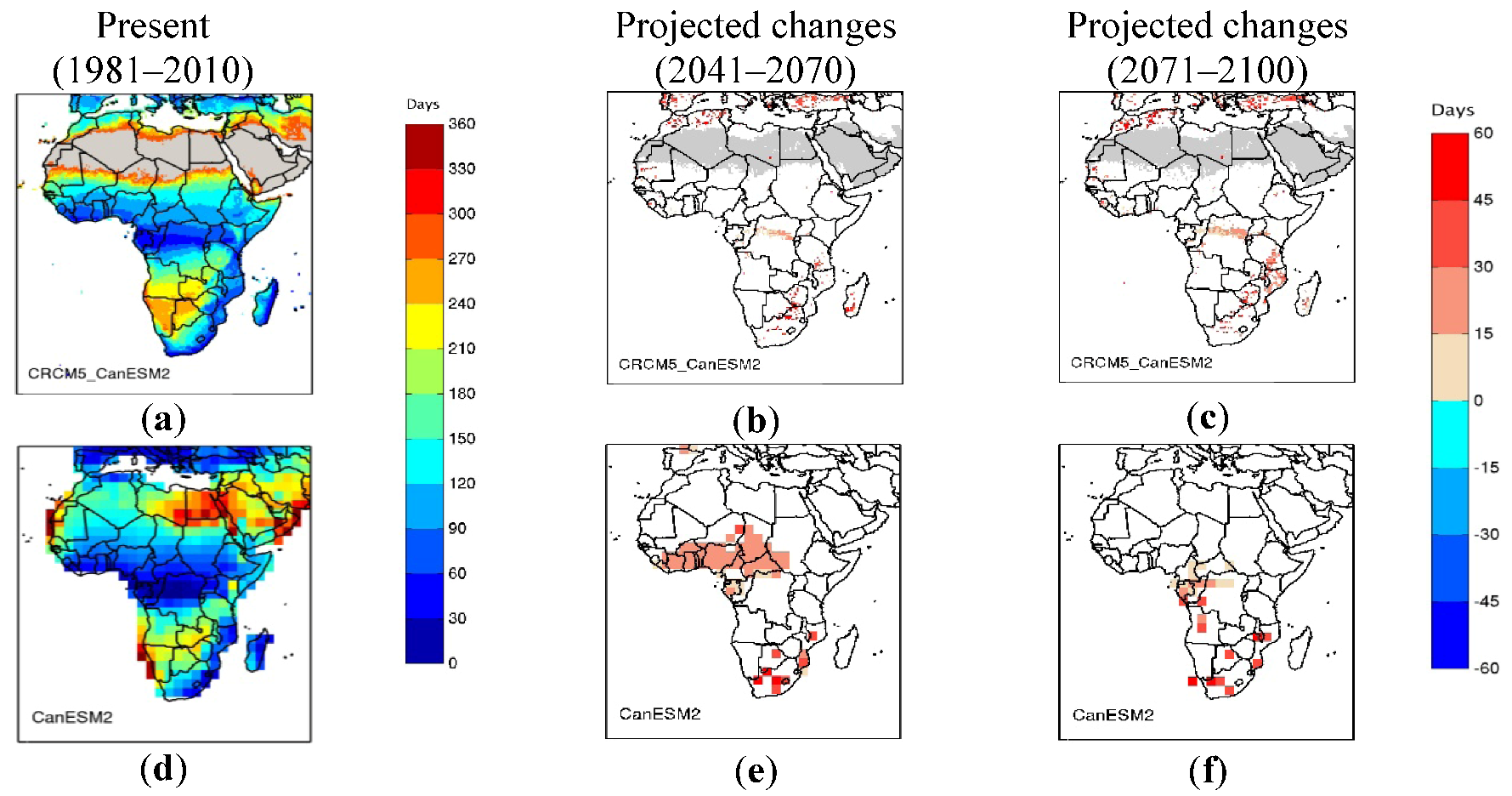
3.2. Projected Changes to Dry Spell Characteristics




4. Discussion and Conclusions
- ▪
- The ability of CRCM5 in simulating dry spell characteristics in current climate is evaluated prior to the assessment of projected changes. The results for the various precipitation thresholds were similar (0.5 mm, 1 mm, 2 mm and 3 mm). Results suggest that the annual (seasonal) numbers of dry days are generally overestimated (underestimated) by CRCM5_ERA_Interim, i.e., positive (negative) performance errors, particularly for North Equatorial Central Africa and Central Southern Africa regions, compared to GPCP. This overestimation in the annual mean number of dry days decreases with increasing precipitation thresholds. Consistent with these results, the annual (seasonal) number of dry spells are underestimated (overestimated) by CRCM5_ERA_Interim over the same regions. The five-year return levels of annual and seasonal maximum dry spell duration computed using the POT approach is generally overestimated by CRCM5_ERA_Interim.
- ▪
- Results suggest that, in general, the performance errors are larger than the lateral boundary forcing errors. Performance errors can be reduced by further improving the representation of processes in the model such as convection, land-atmospheric interactions, West African Monsoon (WAM), while reduction of lateral boundary forcing errors require improved quality of the GCM data used as boundary conditions. CRCM5 reproduces the West African Monsoon, but fails to bring the precipitation far enough north into Sahel due to a weaker monsoonal flow associated with a cold bias in the Sahara as was also reported in Hernández-Díaz et al. [30]. This is the reason for the overestimation of dry days in that region. As for the tropics, it was noted that the soil moisture is generally underestimated in the model due to increased drainage in comparison with the Global Land Data Assimilation System (GLDAS) [62] database, which leads to less evaporation and therefore, a reduced number of precipitation days. Thus, better representation of land-surface processes is important as was pointed out by Taylor et al. [63] in their study over West Africa.
- ▪
- The added value analysis showed that for many regions in Africa, CRCM5_CanESM2 improves local representation of the dry spell characteristics compared to CanESM2. In fact, CRCM5 driven by CanESM2 provides realistic spatial detail in the tropics since the regional model is able to capture the convection cells in the monsoon region more realistically, which is the main source of precipitation, due to its higher resolution compared to CanESM2.
- ▪
- Analysis of the projected changes to dry spell characteristics revealed, that annually and seasonally in the tropics, CRCM5_CanESM2 shows significant increases in the number of dry days and in the five-year return levels of maximum dry spell durations. Analysis also showed significant decreases in the number of dry spells for the 2041–2070 and 2071–2100 periods. In other words, dry spells of longer durations can be expected in future climate with increasing magnitude from 2041–2070 to 2071–2100. For both periods, CanESM2 projections are similar to that of CRCM5_CanESM2 for the annual number of dry days and five-year return levels of annual maximum dry spell duration. However, conflicting climate change signal can be noted for the number of dry spells for the annual and boreal summer, where CRCM5_CanESM2 shows a significant increase while CanESM2 shows a significant decrease. This difference can partly be explained by the fact that CanESM2 is unable to reproduce the dry spell characteristics at lower precipitation thresholds.
- ▪
- Projected changes to dry spell characteristics for the Horn of Africa are in general not found to be significant. However, CRCM5_CanESM2 shows some significant increase in the number of dry spells for boreal summer for the 2071–2100 periods. Similarly, for the Sahel region, projected changes to dry spell characteristics are not found significant, except for some significant decreases in the number of dry days for the boreal summer for the 2041–2070 and 2071–2100 periods for CRCM5_CanESM2.
Acknowledgements
Conflict of Interest
References and Notes
- Solomon, S.; Qin, D.; Manning, M.; Chen, Z.; Marquis, M.; Averyt, K.B.; Tignor, M.; Miller, H.L. Climate Change 2007: The Physical Science Basis; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Barron, J.; Rockström, J.; Gichuki, F.; Hatibu, N. Dry spell analysis and maize yields for two semi-arid locations in East Africa. Agric. For. Meteorol. 2003, 117, 23–37. [Google Scholar] [CrossRef]
- Shongwe, M.E.; Van Oldenborgh, G.J.; Van Den Hurk, B.; Van Aalst, M.K. Projected changes in mean and extreme precipitation in Africa under global warming. Part II: East Africa. J. Clim. 2010, 24, 3718–3733. [Google Scholar]
- Barnett, D.N.; Brown, S.J.; Murphy, J.M.; Sexton, D.M.H.; Webb, M.J. Quantifying uncertainty in changes in extreme event frequency in response to doubled CO2 using a large ensemble of GCM simulations. Clim. Dyn. 2006, 26, 489–511. [Google Scholar] [CrossRef]
- Dai, A. Precipitation characteristics in eighteen coupled climate models. J. Clim. 2006, 19, 4605–4630. [Google Scholar] [CrossRef]
- Tebaldi, C.J.; Arblaster, M.; Hayhoe, K.; Meehl, G.A. Going to the extremes: An intercomparison of model-simulated historical and future changes in extreme events. Clim. Change 2006, 79, 185–211. [Google Scholar] [CrossRef]
- Hudson, D.A.; Jones, R.G. Regional Climate Model Simulations of Present-Day and Future Climates of Southern Africa; Met Office Hadley Center: Exeter, UK, 2002. [Google Scholar]
- Sun, Y.; Solomon, S.; Dai, A.; Portmann, R. How often does it rain? J. Clim. 2005, 19, 916–934. [Google Scholar]
- Kundzewicz, Z.W.; Mata, L.J.; Arnell, N.; Döll, P.; Kabat, P.; Jiménez, B.; Miller, K.; Oki, T.; Sen, Z.; Shiklomanov, I. Freshwater Resources and Their Management. In Climate Change Impacts, Adaptation and Vulnerability. Contribution of Working Group II to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2007; pp. 173–210. [Google Scholar]
- Sushama, L.; Khaliq, M.N.; Laprise, R. Dry spell characteristics over Canada in a changing climate as simulated by the Canadian RCM. Glob. Planet. Change 2010, 74, 1–14. [Google Scholar] [CrossRef]
- Gao, X.; Pal, J.S.; Giorgi, F. Projected changes in mean and extreme precipitation over the Mediterranean region from a high resolution double nested RCM simulation. Geophys. Res. Lett. 2006. [Google Scholar] [CrossRef]
- Heinrich, G.; Gobiet, A. The future of dry and wet spells in Europe : A comprehensive study based on the ENSEMBLES regional climate models. Int. J. Climatol. 2012, 32, 1951–1970. [Google Scholar] [CrossRef]
- May, W. Potential future changes in the characteristics of daily precipitation in Europe simulated by the HIRHAM regional climate model. Clim. Dyn. 2008, 30, 581–603. [Google Scholar] [CrossRef]
- Sanchez, E.; Dominguez, M.; Romera, R.; Lopez De la Franca, N.; Gaertner, M.A.; Gallardo, C.; Castro, M. Regional modeling of dry spells over the Iberian Peninsula for present climate and climate change conditions. Clim. Change 2011, 107, 625–634. [Google Scholar] [CrossRef]
- Hulme, M.; Doherty, R.; Ngara, T.; New, M.; Lister, D. African climate change: 1900–2100. Clim. Res. 2001, 17, 145–168. [Google Scholar] [CrossRef]
- Sun, L.; Semazzi, F.H.M.; Giorgi, F.; Ogallo, L. Application of the NCAR regional climate model to eastern Africa. 1. Simulation of the short rains of 1988. J. Geophys. Res. 1999, 104, 6529–6548. [Google Scholar] [CrossRef]
- Sun, L.; Semazzi, F.H.M.; Giorgi, F.; Ogallo, L. Application of the NCAR regional climate model to eastern Africa. 2. Simulation of interannual variability of short rains. J. Geophys. Res. 1999, 104, 6549–6562. [Google Scholar] [CrossRef]
- Patricola, C.M.; Cook, K.H. Dynamics of the West African monsoon under mid-holocene precessional forcing: Regional climate model simulations. J. Clim. 2006, 20, 694–716. [Google Scholar] [CrossRef]
- Ibrahim, B.; Polcher, J.; Karambiri, H.; Rockel, B. Characterization of the rainy season in Burkina Faso and its representation by regional climate models. Clim. Dyn. 2012, 39, 1287–1302. [Google Scholar] [CrossRef] [Green Version]
- Joubert, A.M.; Katzfey, J.J.; McGregor, J.L.; Nguyen, K.C. Simulating midsummer climate over southern Africa using a nested regional climate model. J. Geophys. Res. 1999, 104, 19015–19025. [Google Scholar] [CrossRef]
- Hudson, D.A.; Jones, R.G. Simulations of Present-day and Future Climate over Southern Africa Using HadAM3H; Met Office Hadley Center: Exeter, UK, 2002. [Google Scholar]
- Hewitson, B. Developing perturbations for climate change impact assessments. EOS Trans. AGU 2003, 84, 337–339. [Google Scholar] [CrossRef]
- Anyah, R.O.; Qiu, W. Characteristic 20th and 21st century precipitation and temperature patterns and changes over the Greater Horn of Africa. Int. J. Climatol. 2011, 32, 347–363. [Google Scholar] [CrossRef]
- Redelsperger, J.-L.; Thorncroft, C.D.; Lebel, T.; Douglas, J.P.; Polcher, J. African monsoon multidisciplinary analysis: An international research project and field campaign. Bull. Am. Meteorol. Soc. 2006, 87, 1739–1746. [Google Scholar] [CrossRef]
- Sultan, B.; Janicot, S. La variabilité climatique en Afrique de l’Ouest aux échelles intra-saisonnières. I: mise en place de la mousson et variabilité intra-saisonnière de la convection. Sécheresse 2004, 15, 321–330. [Google Scholar]
- Van der Linden, P.; Mitchell, J.F.B. ENSEMBLES: Climate Change and its Impacts: Summary of research and results from the ENSEMBLES Project; Met Office Hadley Centre: Exeter, UK, 2009. [Google Scholar]
- Xue, Y.; De Sales, F.; Lau, W.K.M.; Boone, A.; Feng, J.; Dirmeyer, P.; Guo, Z.; Kim, K.-M.; Kitoh, A.; Kumar, V.; et al. Intercomparison and analyses of the climatology of the West African monsoon in the West African Monsoon Modeling and Evaluation project (WAMME) first model intercomparison experiment. Clim. Dyn. 2010, 35, 3–27. [Google Scholar] [CrossRef]
- Druyan, L.M.; Feng, J.; Cook, K.H.; Xue, Y.; Fulakeza, M.; Hagos, S.M.; Konaré, A.; Moufouma-Okia, W.; Rowell, D.P.; Vizy, E.K.; et al. The WAMME regional model intercompariason study. Clim. Dyn. 2010, 35, 175–192. [Google Scholar] [CrossRef]
- Giorgi, F.; Jones, C.; Asrar, G. Addressing climate information needs at the regional level: The CORDEX framework. WMO Bull. 2009, 58, 175–183. [Google Scholar]
- Hernández-Díaz, L.; Laprise, R.; Sushama, L.; Martynov, A.; Winger, K.; Dugas, B. Climate simulation over CORDEX Africa domain using the fifth-generation Canadian Regional Climate Model (CRCM5). Clim. Dyn. 2013, 40, 1415–1433. [Google Scholar] [CrossRef]
- Laprise, R.; Hernandez-Diaz, L.; Tete, K.; Sushama, L.; Separovic, L.; Martynov, A.; Winger, K.; Valin, M. Climate projections over CORDEX Africa domain using the fifth-generation Canadian Regional Climate Model. Clim. Dyn. 2013. [Google Scholar] [CrossRef]
- Meinshausen, M.; Smith, S.J.; Calvin, K.; Daniel, J.S.; Kainuma, M.L.T.; Lamarque, J.-F.; Matsumoto, K.; Montzka, S.A.; Raper, S.C.B.; Riahi, K.; et al. The RCP greenhouse gas concentrations and their extensions from 1765 to 2300. Clim. Change 2011. [Google Scholar] [CrossRef]
- Zadra, A.; Caya, D.; Cote, J.; Dugas, B.; Jones, C.; Laprise, R.; Winger, K.; Caron, L.-P. The next canadian regional climate model. Phys. Can. 2008, 64, 75–83. [Google Scholar]
- Côté, J.; Gravel, S.; Méthot, A.; Patoine, A.; Roch, M.; Staniforth, A. The operational CMC–MRB Global Environmental Multiscale (GEM) model. Part I: Design considerations and formulation. Mon. Weather Rev. 1998, 126, 1373–1395. [Google Scholar] [CrossRef]
- Côté, J.; Desmarais, J.-G.; Gravel, S.; Méthot, A.; Patoine, A.; Roch, M.; Staniforth, A. The operational CMC–MRB Global Environmental Multiscale (GEM) model. Part II: Results. Mon. Weather Rev. 1998, 126, 1397–1418. [Google Scholar] [CrossRef]
- Yeh, K.; Côté, J.; Gravel, S.; Méthot, A.; Patoine, A.; Roch, M.; Staniforth, A. The CMC–MRB Global Environmental Multiscale (GEM) model. Part III: Nonhydrostatic formulation. Mon. Weather Rev. 2002, 130, 339–356. [Google Scholar] [CrossRef]
- Laprise, R. The EULER equations of motion with hydrostatic pressure as an independent variable. Mon. Weather Rev. 1992, 120, 197–207. [Google Scholar] [CrossRef]
- Kain, J.S.; Fritsch, J.M. A one-dimensional entraining/detraining plume model and its application in convective parameterization. J. Atmos. Sci. 1990, 47, 2784–2802. [Google Scholar] [CrossRef]
- Kuo, H.L. On formation and intensification of tropical cyclone through latent heat release by cumulus convection. J. Atmos Sci. 1965, 22, 40–63. [Google Scholar] [CrossRef]
- Bélair, S.; Mailhot, J.; Girard, C.; Vaillancourt, P. Boundary-layer and shallow cumulus clouds in a medium-range forecast of a large-scale weather system. Mon. Wea. Rev. 2005, 133, 1938–1960. [Google Scholar] [CrossRef]
- Sundqvist, H.; Berge, E.; Kristjansson, J.E. Condensation and cloud parameterization studies with a Mesoscale numerical weather prediction model. Mon. Wea. Rev. 1989, 117, 1641–1657. [Google Scholar] [CrossRef]
- Li, J.; Barker, H.W. A radiation algorithm with correlated-k distribution. Part I: Local thermal equilibrium. J. Atmos. Sci. 2005, 62, 286–309. [Google Scholar] [CrossRef]
- McFarlane, N.A. The effect of orographically excited gravity wave drag on the general circulation of the lower stratosphere and troposphere. J. Atmos. Sci. 1987, 44, 1775–1800. [Google Scholar] [CrossRef]
- Zadra, A.; Roch, M.; Laroche, S.; Charron, M. The subgrid scale orographie blocking parametrization of the GEM model. Atmos.-Ocean 2003, 41, 155–170. [Google Scholar] [CrossRef]
- Benoit, R.; Cote, J.; Mailhot, J. Inclusion of a TKE boundary layer parameterization in the Canadian regional finite-element model. Mon. Wea. Rev. 1989, 117, 1726–1750. [Google Scholar] [CrossRef]
- Delage, Y.; Girard, C. Stability functions correct at the free convection limit and consistent for both the surface and Ekman layers. Bound. Layer Meteor. 1992, 58, 19–31. [Google Scholar] [CrossRef]
- Delage, Y. Parameterising sub-grid scale vertical transport in atmospheric models under statically stable conditions. Bound.-Layer Meteor. 1997, 82, 23–48. [Google Scholar] [CrossRef]
- Verseghy, L.D. The Canadian Land Surface Scheme (CLASS): Its history and future. Atmos. Ocean 2000, 38, 1–13. [Google Scholar] [CrossRef]
- Simmons, A.S.; Uppala, D.D.; Kobayashi, S. ERA-interim: new ECMWF reanalysis products from 1989 onwards. ECMWF Newsl. 2007, 110, 29–35. [Google Scholar]
- Uppala, S.; Dee, D.; Kobayashi, S.; Berrisford, P.; Simmons, A. Towards a climate data assimilation system: status update of ERA-interim. ECMWF Newsl. 2008, 115, 12–18. [Google Scholar]
- Huffman, G.J.; Adler, R.F.; Morrissey, M.M.; Curtis, S.; Joyce, R.; McGavock, B.; Susskind, J. Global precipitation at one-degree daily resolution from multisatellite observations. J. Hydrometeor. 2001, 2, 36–50. [Google Scholar] [CrossRef]
- Nikulin, G.; Jones, C.; Giorgi, F.; Asrar, G.; Büchner, M.; Cerezo-Mota, R.; Christensen, O.B.; Déqué, M.; Fernandez, J.; Hänsler, A.; et al. Precipitation climatology in an ensemble of CORDEX-Africa regional climate simulations. J. Clim. 2012. [Google Scholar] [CrossRef]
- Beniston, M.; Stephenson, D.B.; Christenson, O.B.; Ferro, C.A.T.; Frei, C.; Goyette, S.; Halsnaes, K.; Holt, T.; Jylhä, K.; Koffi, B.; et al. Future extreme events in European climate: an exploration of regional climate model projections. Clim. Change 2007, 81, 71–95. [Google Scholar]
- Lana, X.; Martínez, M.D.; Burgueño, A.; Serra, C. Statistical distribution and sampling strategies for the analysis of extreme dry spells in Catalonia (NE Spain). J. Hydrol. 2006. [Google Scholar] [CrossRef]
- She, D.; Xia, J.; Song, J.; Du, H.; Chen, J.; Wan, L. Spatio-temporal variation and statistical characteristic of extreme dry spell in Yellow River, China. Theor. Appl. Climatol. 2012. [Google Scholar] [CrossRef]
- Coles, S. An Introduction to Statistical Modeling of Extreme Values; Springer: New York, NY, USA, 2001. [Google Scholar]
- Christensen, J.H.; Machenhauer, B.; Jones, R.G.; Schär, C.; Ruti, P.M.; Castro, M.; Visconti, G. Validation of present regional climate simulations over Europe: LAM simulations with observed boundary conditions. Clim. Dyn. 1997, 13, 489–506. [Google Scholar] [CrossRef]
- Walpole, R.E.; Myers, R.H. Probability and Statistics for Engineers and Scientists, 3rd ed.; Macmillan: New York, USA, 1985. [Google Scholar]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap. Monographs on Statistics and Applied Probability; Chapman and Hall: New York, USA, 1993. [Google Scholar]
- GREPHYS. Inter-comparison of regional flood frequency procedure for Canadian rivers. J. Hydrol. 1996, 186, 85–103. [CrossRef]
- Khaliq, M.N.; Ouarda, T.B.M.J.; Gachon, P.; Sushama, L.; St-Hilaire, A. Identification of hydrological trends in the presence of serial and cross correlations: a review of selected methods and their application to annual flow regimes of Canadian rivers. J. Hydrol. 2009, 368, 117–130. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C-J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The global land data assimilation system. Bull. Amer. Meteor. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Taylor, C.M.; Parker, D.J.; Kalthoff, N.; Gaertner, M.A.; Philippon, N.; Bastin, S.; Harris, P.P.; Boone, A.; Guichard, F.; Agustin-Panareda, A.; et al. New perspectives on land-atmosphere feedbacks from the African monsoon multidisciplinary analysis. Atmos. Sci. Lett. 2011, 12, 38–44. [Google Scholar] [CrossRef] [Green Version]
- Mupangwa, W.; Walker, S.; Twomlow, S. Start, end and dry spells of the growing season in semi-arid southern Zimbabwe. J. Arid Environ 2011, 75, 1097–1104. [Google Scholar] [CrossRef]
- Cook, C.; Reason, C.J.C.; Hewitson, B.C. Wet and dry spells within particularly wet and dry summers in the South African summer rainfall region. Clim. Res. 2004, 26, 17–31. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Bouagila, B.; Sushama, L. On the Current and Future Dry Spell Characteristics over Africa. Atmosphere 2013, 4, 272-298. https://doi.org/10.3390/atmos4030272
Bouagila B, Sushama L. On the Current and Future Dry Spell Characteristics over Africa. Atmosphere. 2013; 4(3):272-298. https://doi.org/10.3390/atmos4030272
Chicago/Turabian StyleBouagila, Bessam, and Laxmi Sushama. 2013. "On the Current and Future Dry Spell Characteristics over Africa" Atmosphere 4, no. 3: 272-298. https://doi.org/10.3390/atmos4030272



