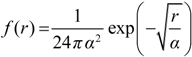1. Introduction
Phenotyping of quantitative disease resistance (QDR) through exposure of plants to pathogens and visual observation of disease symptoms is an important stage in many plant breeding programmes. To ensure an accurate and cost-effective operation, a number of methodological and philosophical issues of critical importance should be considered. The methodological issues include field plot techniques (consideration of edge effects, competition among progenies, plot size and shape), design of trials (based on concepts of replication, control of variation among plots and randomization), and analysis of variety trials. The philosophical issue is primarily whether the testing of experimental cultivars should be conducted in an optimum climatic and agronomic environment, or should be conducted in the target environment, as in multi-environment trials. Although these topics have been extensively discussed in the literature, the inference from
ex-situ assessment of QDR to commercial production settings is generally not clear and often doubtful [
1,
2,
3]. This is because there is an increasing trend towards the use of single plants in pots in artificial environments such as growth cabinets and glasshouses including the latest automated, image analysis-based “phenomics” facilities, due to the ease of controlling stress. In the field there is a trend towards reducing plot size in order to maximize the number of varieties that can be assessed, such as the use of small unbordered “hills” or spaced plants differing in height and maturity, ear rows or short-rod rows containing only a few seeds, or micro-plots arranged in a matrix [
3]. In such cases, the phenotyping of QDR may be confounded by the artificial environment (e.g., high temperatures in glasshouses), or complicated by competition effects from neighbours that do not reproduce the competition experienced by plants grown in canopies in the field, or impaired by unnaturally low or high levels of initial or background inoculum.
In summary, the phenotypic assessment of QDR may be hampered by the failure of experimental efforts to accurately represent agricultural settings. A major cause of this problem is “interplot (inoculum) interference” which can be especially important in experiments with aerially disseminated pathogens [
4,
5]. Negative interference occurs when a large proportion of inoculum produced within a small plot (or pot) is dispersed outwith that plot’s boundaries. The rate of epidemic progress is then reduced since the lost inoculum cannot contribute to further multiplication of disease. Conversely, positive interference occurs when a plot is subjected to an influx of inoculum from external sources (e.g., other plots in the experiment, or surrounding crops), resulting in an increased rate of epidemic progress [
4]. The importance of inoculum interference was pointed out by Vanderplank as early as 1963 [
6], and despite much attention since, a precise, generic means of quantifying interference remains elusive. Some practices, such as adjusting plot size and spacing, are commonly used to reduce inoculum interference, although this is often done in an
ad-hoc manner based on expert opinion (or limited space), as there are no hard and fast quantitative guidelines. Furthermore, in agricultural landscapes, host crop abundance and heterogeneity can affect the magnitude of inoculum dispersal among crops [
5,
7,
8,
9,
10]. Thus, an agricultural landscape may have epidemic suppressive or enhancing effects that confound projections for QDR based on pot experiments or field trials.
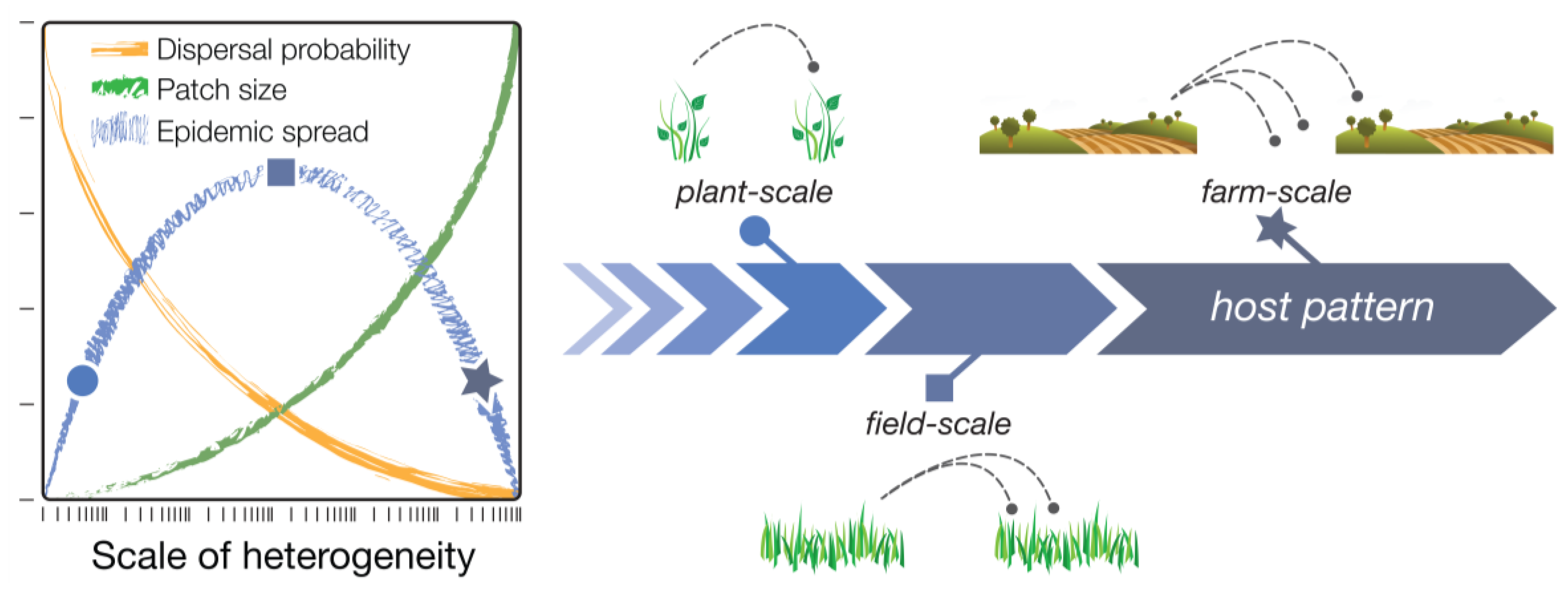
The dispersal scaling hypothesis (DSH) is a new theory in spatial ecology that formalizes the expected relationship between spatial heterogeneity, scale of heterogeneity, and pest or pathogen dispersal/epidemic spread. The DSH therefore provides a framework for quantifying inoculum interference, and its impact on epidemic outcomes. In formal terms: the DSH posits a unimodal (“humpbacked”) relationship between the magnitude of pest or pathogen infestation and the grain size (spatial resolution, or the finest scale of patchiness) of a host distribution [
7,
8]. In other words, the magnitude of dispersal (the number of pests or propagules moving from one patch to another) is predicted to increase with increasing grain size (scale) up to a certain point (the “hump”), after which the magnitude of dispersal declines (
Figure 1; blue line). This is explained as follows. Initially, dispersal of infectious agents among host patches increases with patch size, as larger populations produce more dispersers and larger patches are more attractive or make bigger targets for dispersers (
Figure 1; green line). Eventually, however, a maximum scale of patchiness is reached at which there are no further gains in dispersal, and the magnitude of dispersal instead begins to decline with further increases in grain size. This is because increasing the grain size (scale) of the landscape also increases the size of the gaps—the non-host areas—between patches, which has an overall depressive effect on dispersal (
Figure 1; orange line). In summary, host patchiness can vary over a spectrum of scales (grain sizes), dispersal processes have a characteristic scale (the dispersal range of the pest or pathogen species), and the interplay between these different scales results in a unimodal distribution of dispersal magnitudes, and thus, pest or pathogen infestation. The exact grain size at which dispersal is maximized, however, depends on other aspects of spatial heterogeneity, such as the amount, quality, and distribution of habitat (or hosts) on the landscape [
8].
The DSH has identified a potential for scale-dependent maxima in epidemic outcomes for a large variety of economically important pests and diseases under numerous different disease management scenarios and spatial configurations of host species, using a multi–model approach encompassing analytical and numerical techniques, deterministic and stochastic methods of dispersal, individual– and population–level movements, and multiple generations of spatiotemporal spread in complex landscapes [
7,
8]. As such, the DSH offers a credible new theoretical framework for quantifying the expected inoculum/disease pressure in heterogeneous host distributions at, e.g., plant-, plot-, field-, and landscape-scale. Thus, this sort of analysis could be of predictive value in optimizing the design of experiments to ensure that crop phenotypes are assessed in settings that simulate real agricultural (epidemic) situations. This will broaden their scope of inference to situations that more closely match commercial production settings, in terms of cultivar performance under realistic (natural) levels of inoculum/disease pressure. This is an obvious and desirable goal in the accurate quantification of complex plant phenotypes and selection of elite cultivars with relatively high QDR, or high yield in the presence of disease. In practice it may be the tool used to determine the best compromise or prioritization as pathogens with different and contrasting dispersal scales are frequently assessed together, thus giving a basis on which to determine whether assessments are likely to be over- or under-estimate estimates compared with real agricultural situations.
As originally written, the DSH formalized the expected relationship between the magnitude of a single generation of dispersal and the scale of host patchiness (
i.e., spread from an infected area to a non-infected area), and the end result of many dispersal events and the scale of host patchiness (
i.e., final epidemic extent in a landscape containing many host areas). In the current modelling study we investigated the influence of this scaling relationship on phenotyping of QDR. QDR is characterized by a reduced rate of epidemic development in a host crop variety attributed to various components of partial disease resistance, such as a lower infection frequency [
11]. We therefore considered the temporal evolution of this scaling relationship (DSH) over the course of epidemics in crops with different resistance components. We also explored the influence of the wider environment in a number of scenarios that mimic varietal deployment in commercial production settings. Our objectives were to: (1) characterize the impact of the interaction of spatial heterogeneity and scale of heterogeneity on the progress of plant disease epidemics in crop varieties with varying levels of QDR; and (2) investigate this interaction as a potential confounding factor in the inference from
ex-situ assessment of QDR to commercial production settings. As the generality of the theoretical predictions of the DSH have previously been demonstrated using a wide array of modelling assumptions [
7,
8], here we make a number of classic simplifying assumptions in theoretical epidemiology from which departures resulting from additional complexities can later be evaluated. We describe a simple, spatiotemporal model of the susceptible, exposed, infectious and removed (SEIR) type, which is the standard modelling approach in human disease epidemiology, and is also widely used in plant disease epidemiology, e.g., Skelsey
et al. [
5,
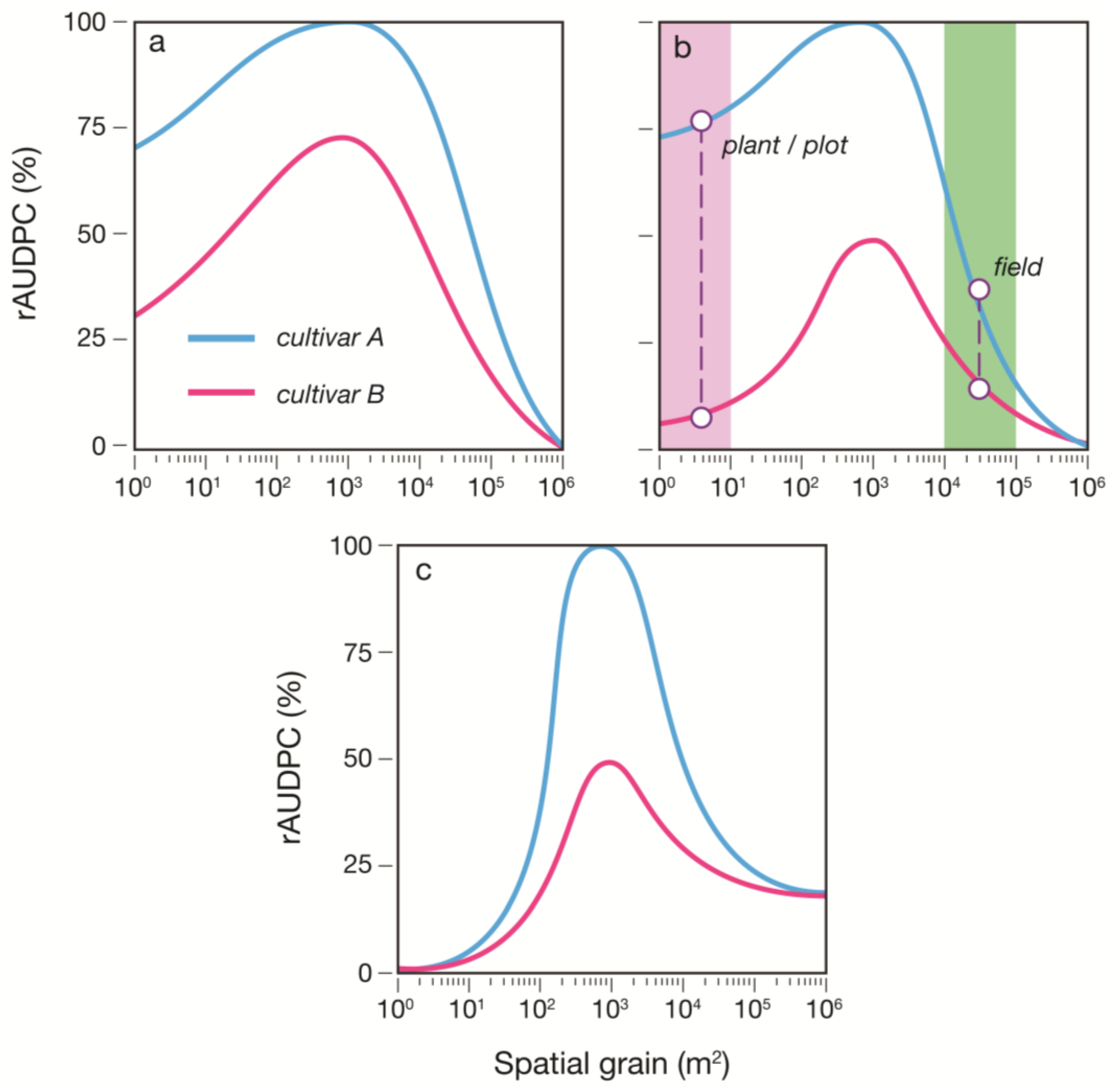
9]. In this approach, the host population is divided into several non-overlapping categories: healthy susceptible, latently infected, infectious, and removed (post-infectious). Space was simulated as a binary raster landscape (Cartesian grid) of host and non-host areas to create spatially heterogeneous landscapes in which various aspects of host pattern, such as host abundance and degree of aggregation, could be altered. The grain size (cell dimensions) of landscapes was varied to investigate the influence of the interaction of spatial heterogeneity and scale on epidemic progress. Grain size ranged over a spectrum of values from plant-, to plot-, to field-, to regional-level. Epidemic progress was characterized at regular intervals using the average number of successfully deposited spores (on healthy or infected tissue, whether within the same host patch or another host patch) per diseased patch,
N (no.), and overall disease severity,
S (%). At the end of each model run (epidemic), the area under the disease progress (
S) curve (AUDPC; % days) was used to assess the impact of heterogeneity and scale on the relative difference in epidemic outcomes between varieties. Insights gained from this study and the recommendations made herein may inform the design of future phenotyping platforms to optimize the scale for QDR assessment.
Figure 1.
Conceptual diagram of the dispersal scaling hypothesis (DSH). Scaling a heterogeneous host distribution relative to the gap–crossing abilities of a pest or pathogen produces a trade-off between the “benefits” (larger patches = more dispersers) and “costs” (dispersal distances become larger and harder to traverse) of increasing grain (patch) size. This results in a unimodal (“humpbacked”) relationship between dispersal or epidemic spread and scale of heterogeneity.
Figure 1.
Conceptual diagram of the dispersal scaling hypothesis (DSH). Scaling a heterogeneous host distribution relative to the gap–crossing abilities of a pest or pathogen produces a trade-off between the “benefits” (larger patches = more dispersers) and “costs” (dispersal distances become larger and harder to traverse) of increasing grain (patch) size. This results in a unimodal (“humpbacked”) relationship between dispersal or epidemic spread and scale of heterogeneity.
4. Conclusions
This study refines and extends new ecological theory (the DSH) by characterising the relationship between host heterogeneity, scale of heterogeneity, and the progress of plant disease epidemics in crop varieties with varying levels of QDR. We conclude that this relationship follows the DSH, with the proviso that sufficient time has elapsed to promote invasive spread. We further conclude that the interaction between host heterogeneity and scale is an important determinant of varietal performance (in terms of relative resistance to disease) under epidemic conditions. We advise that accurate ranking of cultivars or lines according to their relative resistance to disease requires that the level of disease pressure of the designed experiment matches that of the crop in its commercial production setting as closely as possible. To achieve this, we recommend that interplot (inoculum) interference is considered as an experimental variable that could be manipulated to ensure conformity in the level of disease pressure between experiment and deployment. The degree of manipulation required can be determined with minimal knowledge of the pathosystem of interest using the quantitative framework of the DSH. Pot/plot size and spacing, initial inoculum dose, and rate of epidemic progress (using agrochemicals, or a continuous supply of inoculum) can then be adjusted within the parameters defined by the DSH.
Plot trialling designs are always a compromise between costs, equipment constraints, seed quantity and many other operational factors. They are also required to produce data for many and sometimes conflicting purposes. Add to this the conflicting scale demands for assessing the effects of different diseases simultaneously, and the scope for change is often limited. Similarly, the costs and practicality of inoculation are often prohibitive. Use of agrochemicals to control inoculum can introduce pleiotrophic confounding factors. However, even where changes cannot be made, or even where further compromises have to be made for cost or other practical reasons, the DSH provides the rationale and parameterisation for adjusting relative pathogen performance to that likely to be expressed under farm-scale conditions.