The Effect of CFRP Length on the Failure Mode of Strengthened Concrete Beams
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
| Material | Cement | Coarse aggregate | Fine aggregate | Water | Concrete admixture | Fly-ash |
|---|---|---|---|---|---|---|
| Weight per concrete cubic meter (kg) | 300 | 615 | 1210 | 185 | 6.60 | 95 |
| Mass ratio | 1.000 | 2.050 | 4.033 | 0.617 | 0.022 | 0.317 |
| Curing days | Compressive strength (MPa) |
|---|---|
| 3 | 23.4 |
| 7 | 29.9 |
| 28 | 41.4 |
| Material | Concrete | CFRP | Adhesive |
|---|---|---|---|
| Elastic Modulus (GPa) | 32.89 | 165 | 9.60 |
| Poisson’s ratio | 0.28 | 0.25 | 0.30 |
| Density | Tensile strength | Ductility | Typical thickness |
|---|---|---|---|
| 20 g·m−3 | 4640 MPa | 1.7% | 0.111 mm |
2.2. Specifications of the Beams
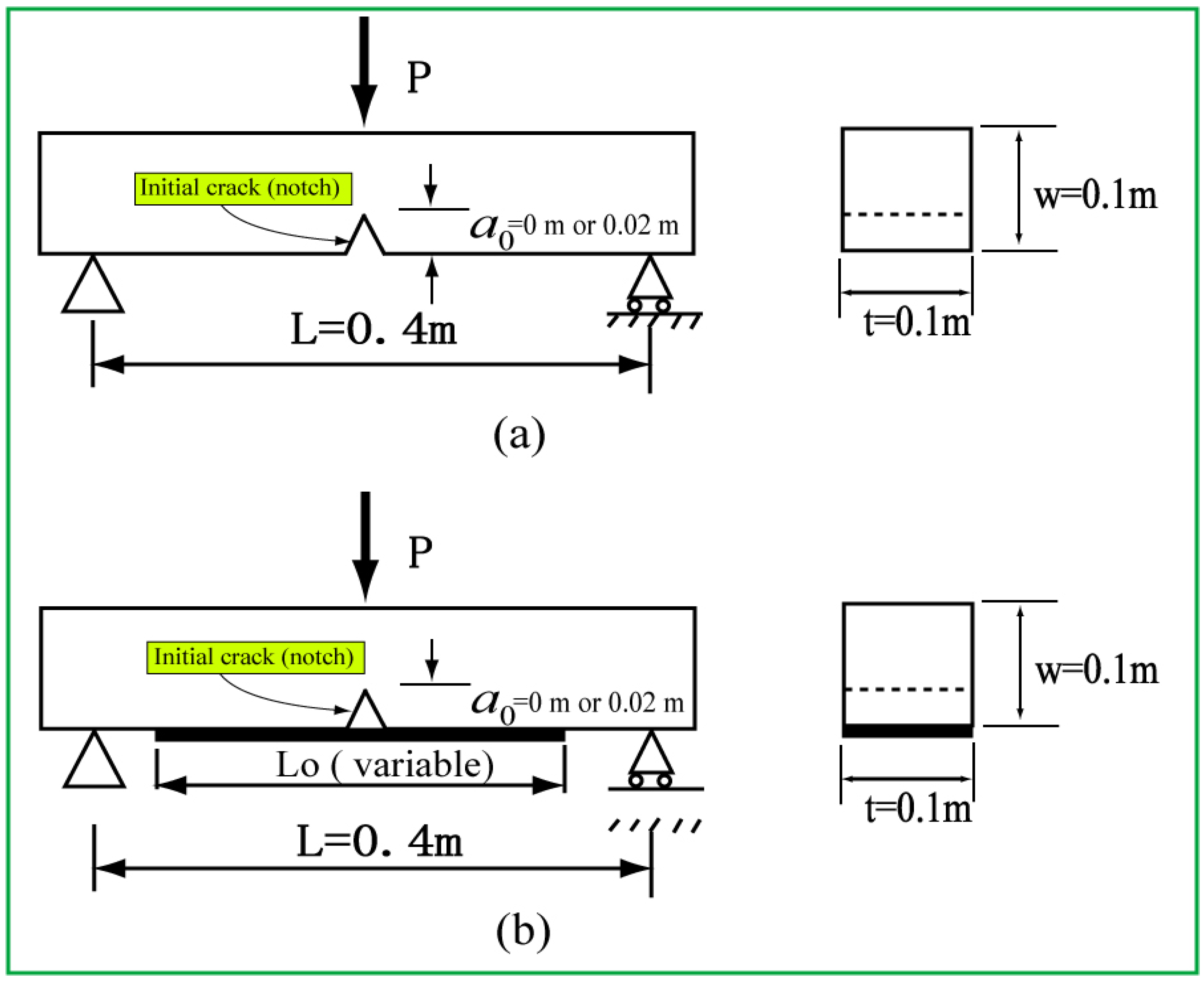
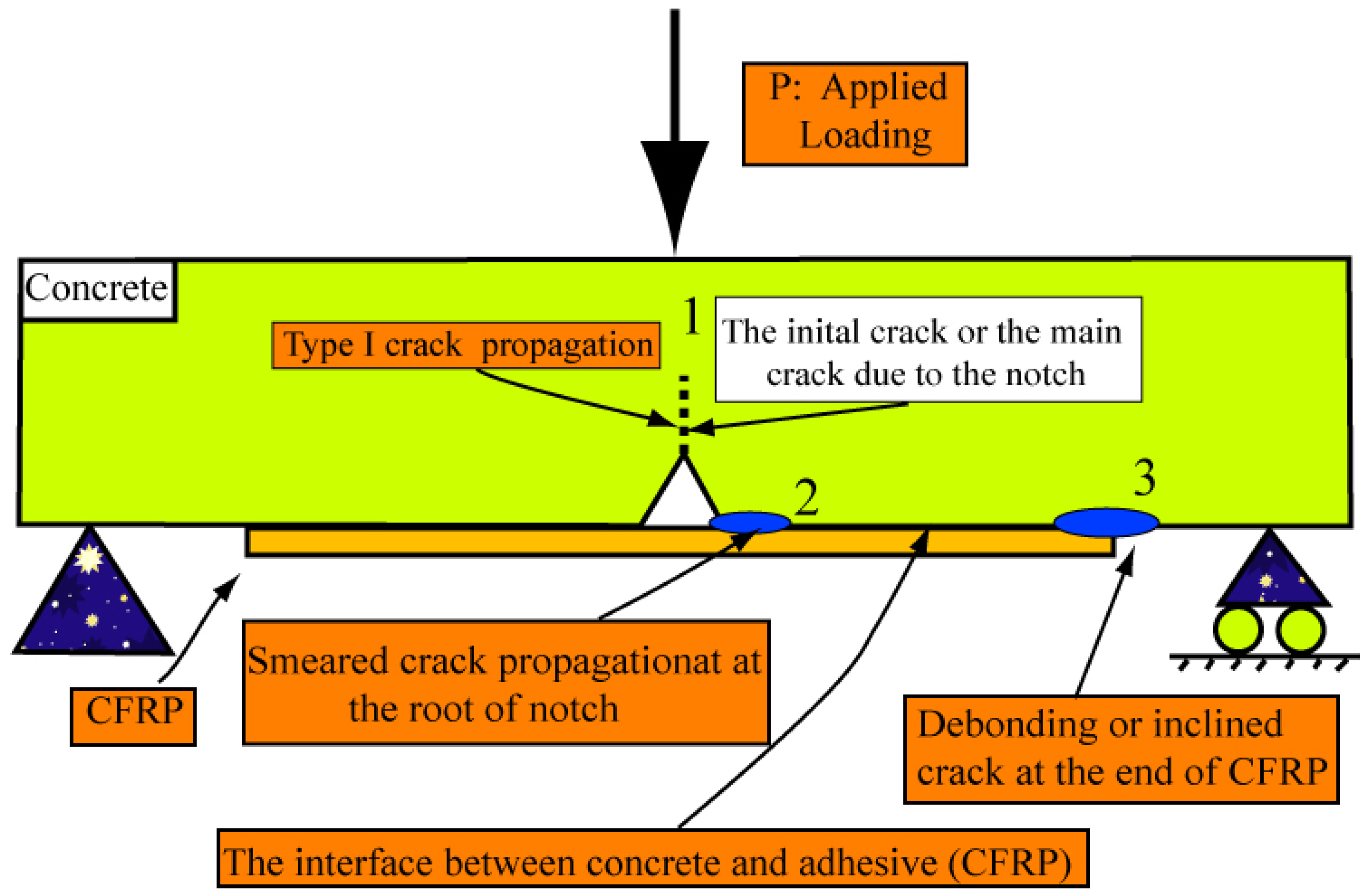
2.3. Test Setup

2.4. Experimental Results
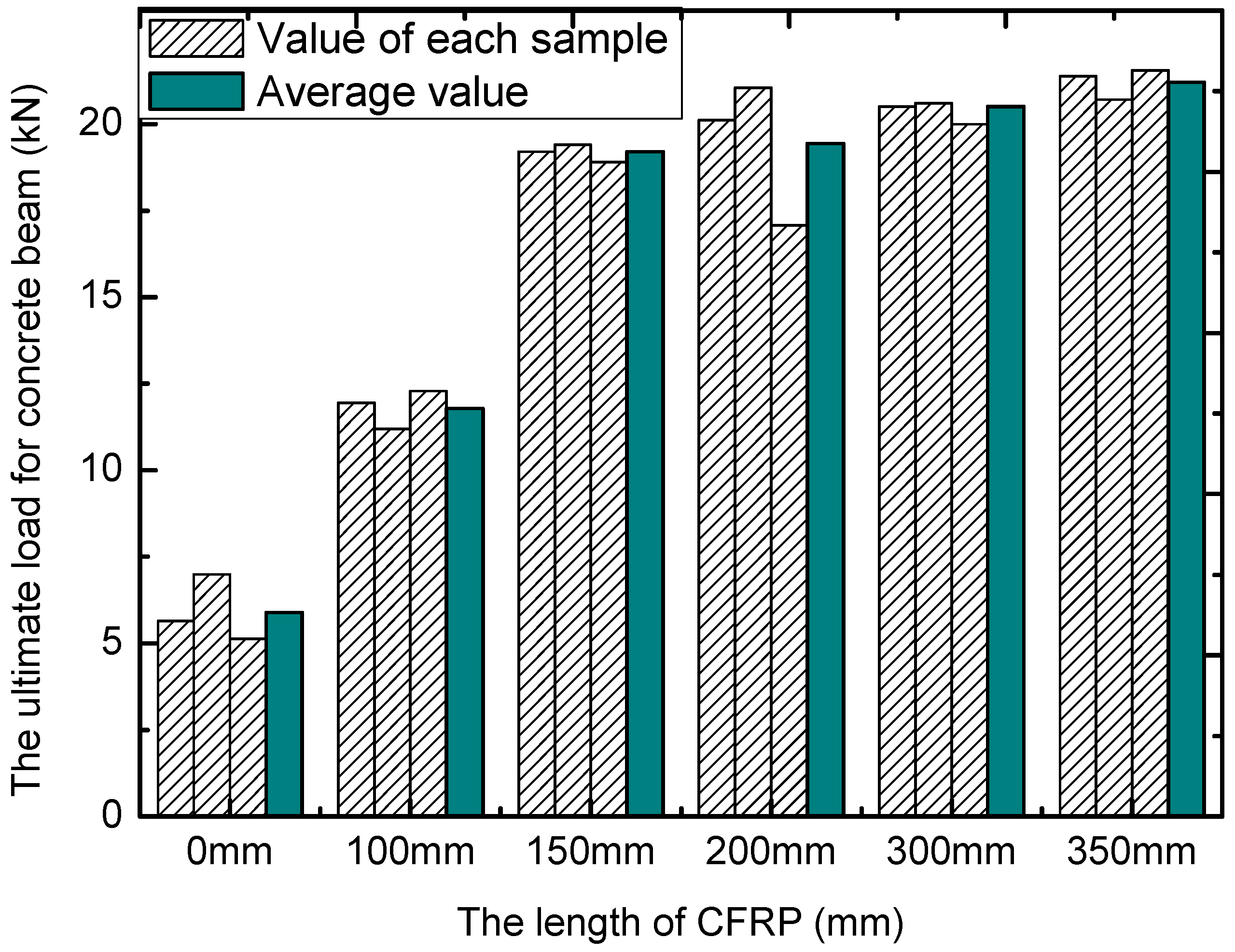


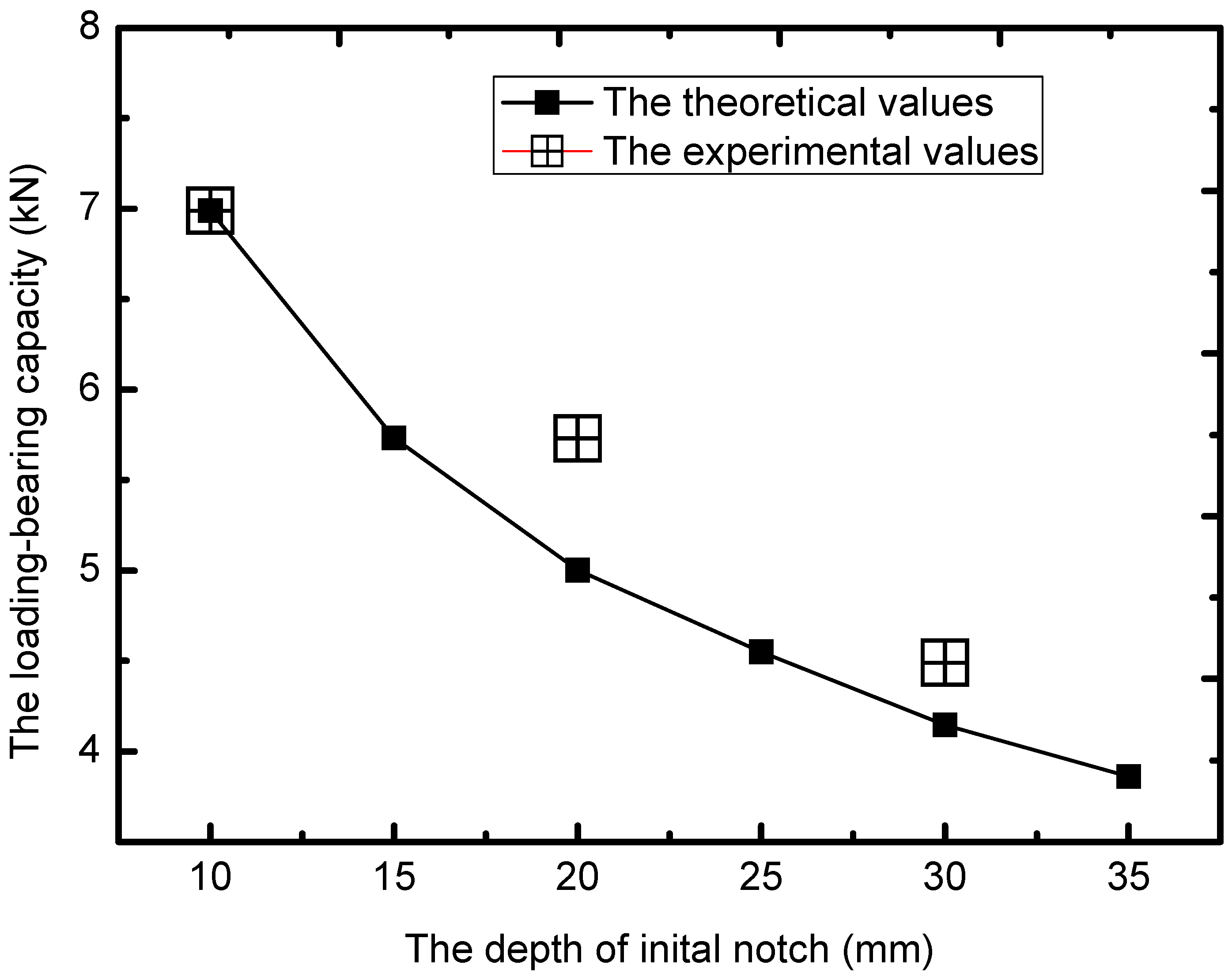

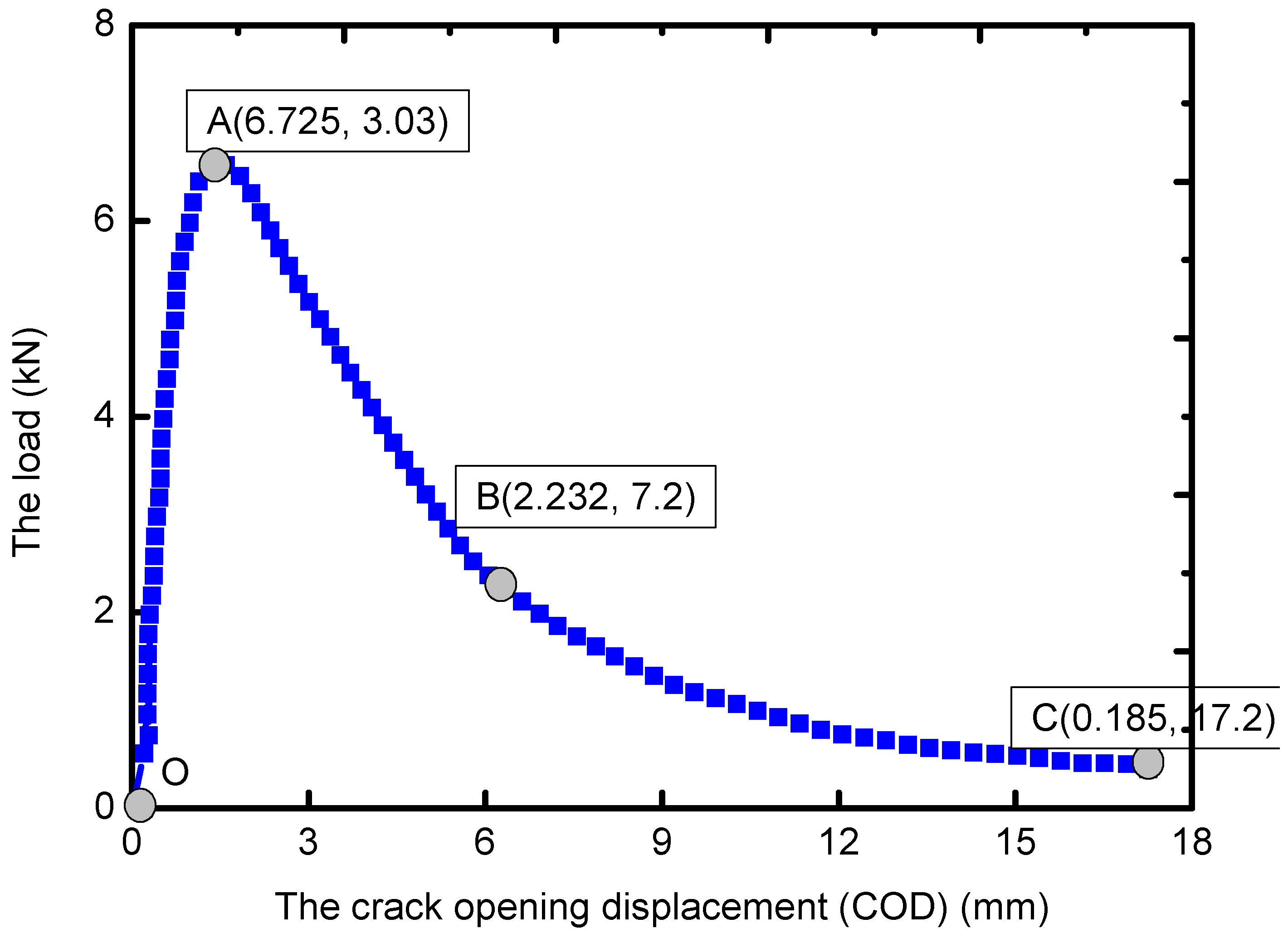

2.5. Numerical Simulation

3. Results and Discussion
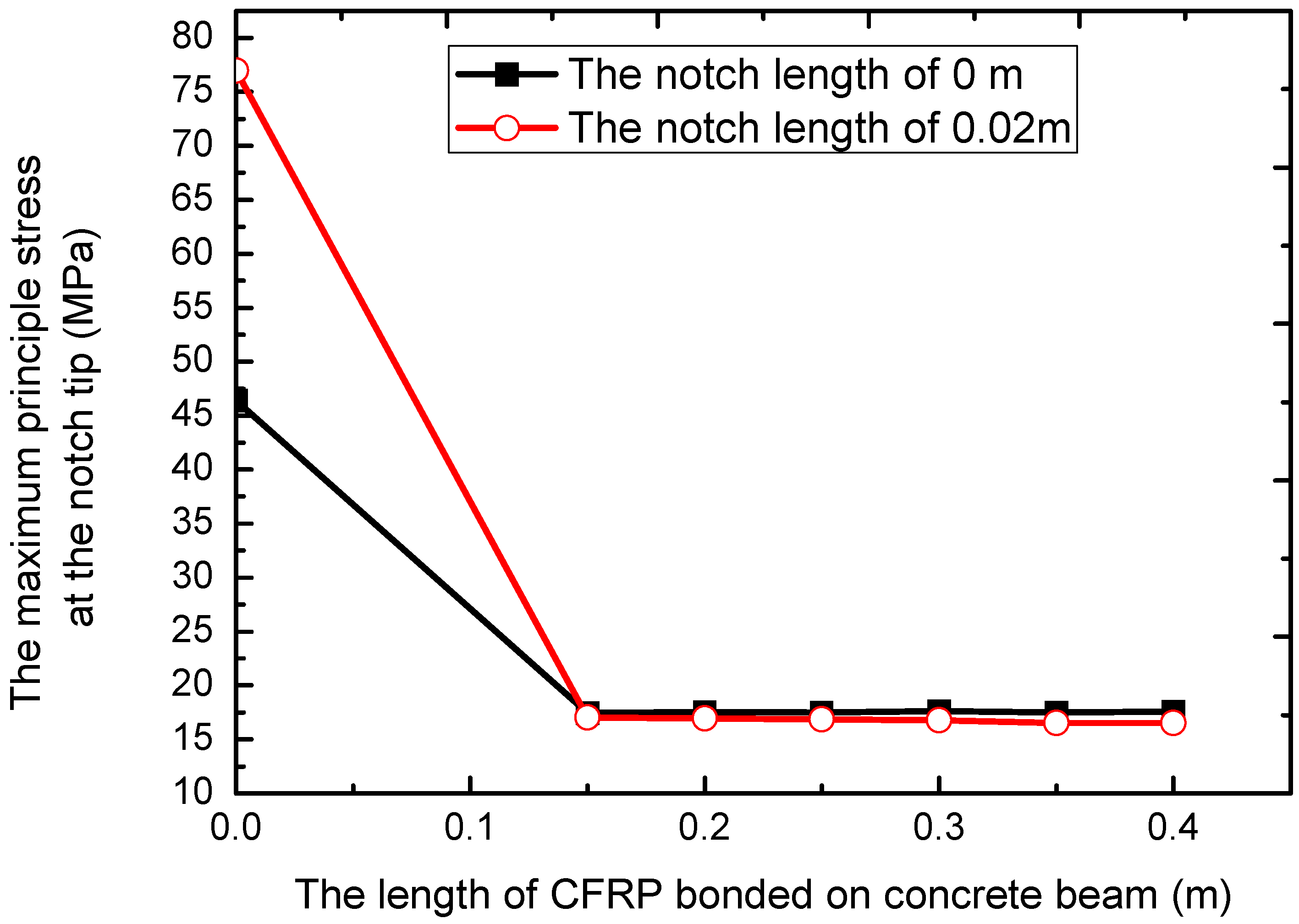
3.1. The Effect of CFRP Length on Stresses around the Crack Tip
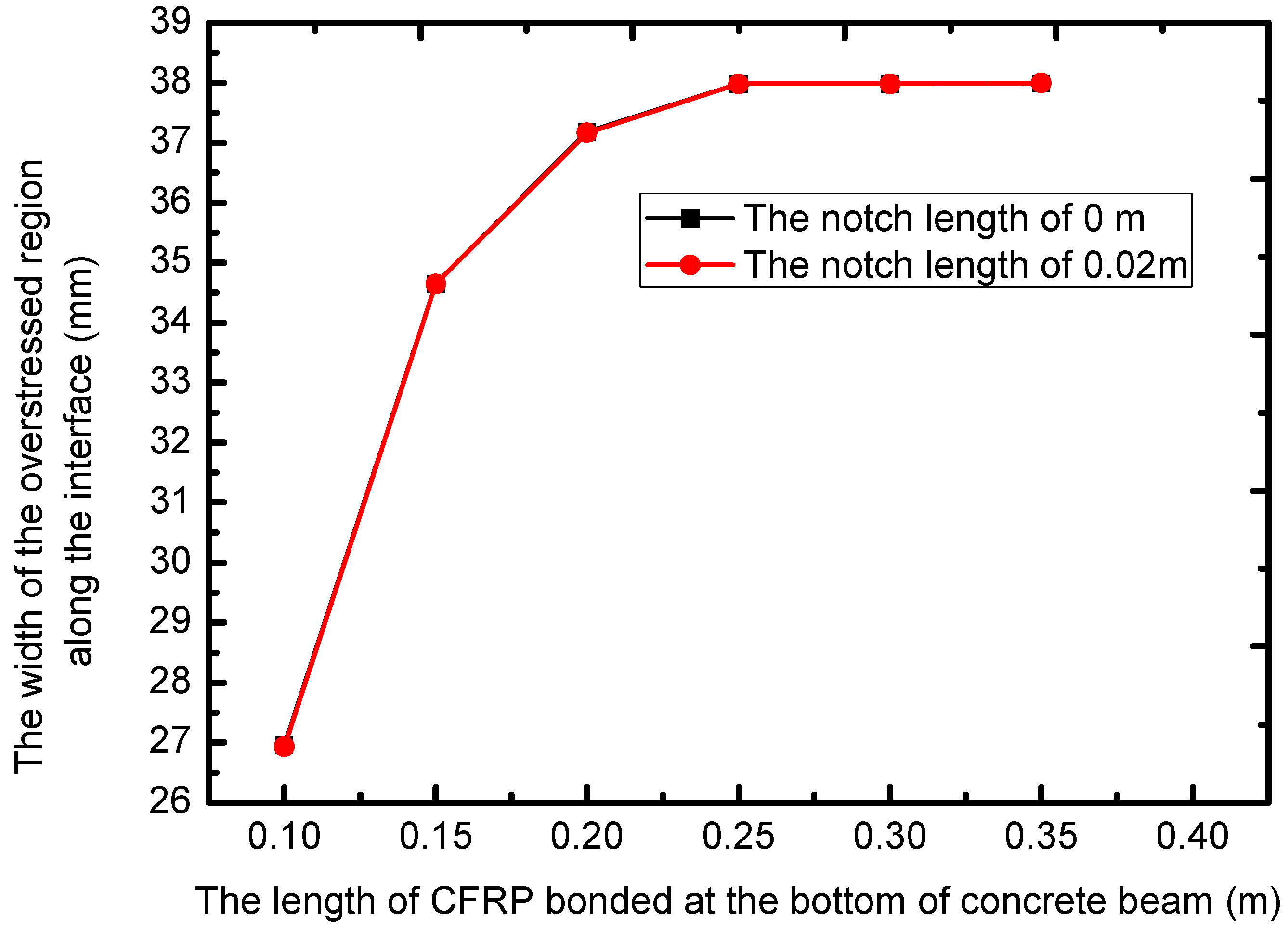
3.2. The Effect of CFRP Length on Stresses at the Interface
3.3. The Effect of CFRP Length on Stresses at the End of CFRP
3.3.1. CFRP Length of 0.10 m

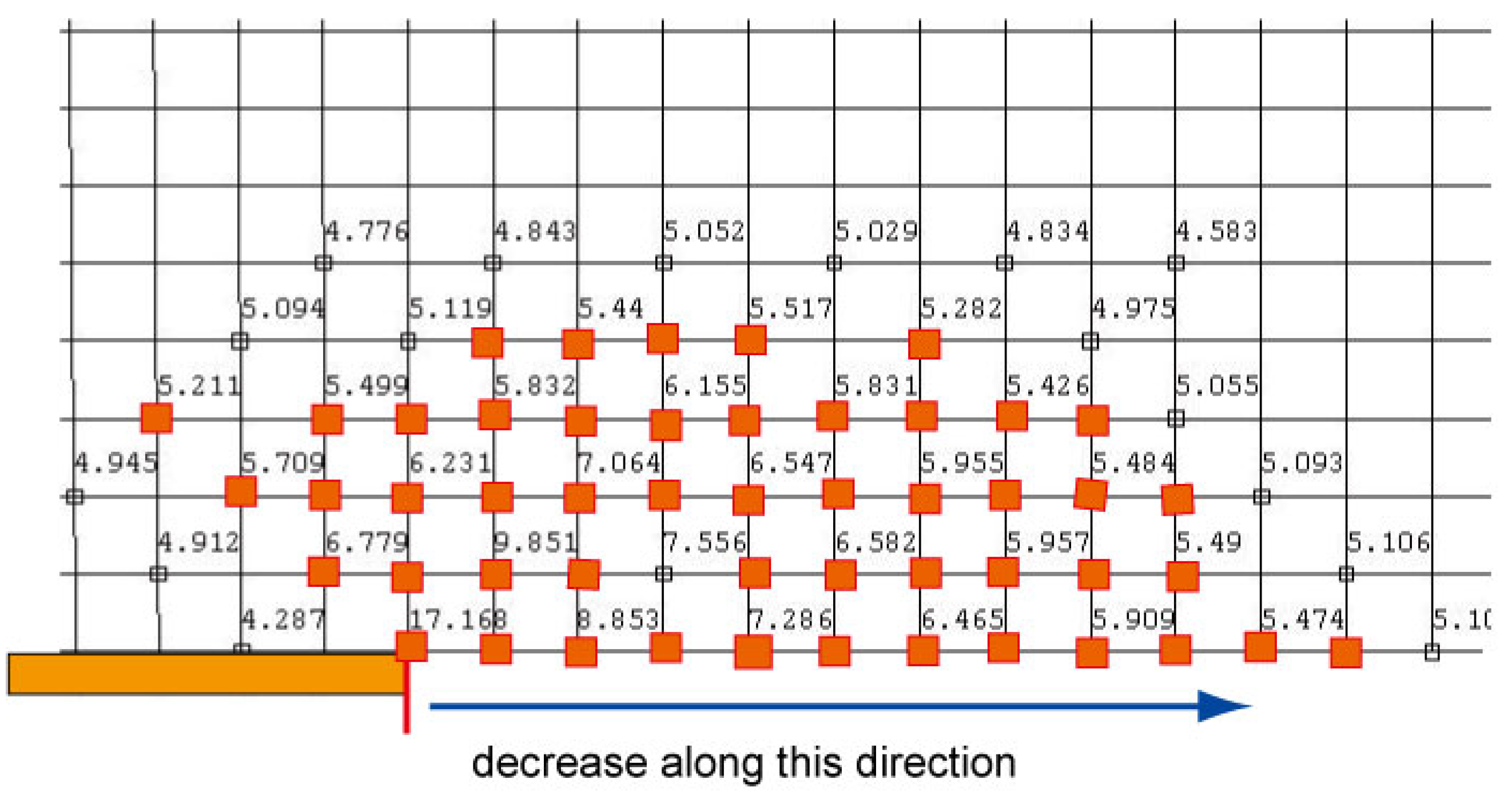
3.3.2. CFRP Length of 0.20 m

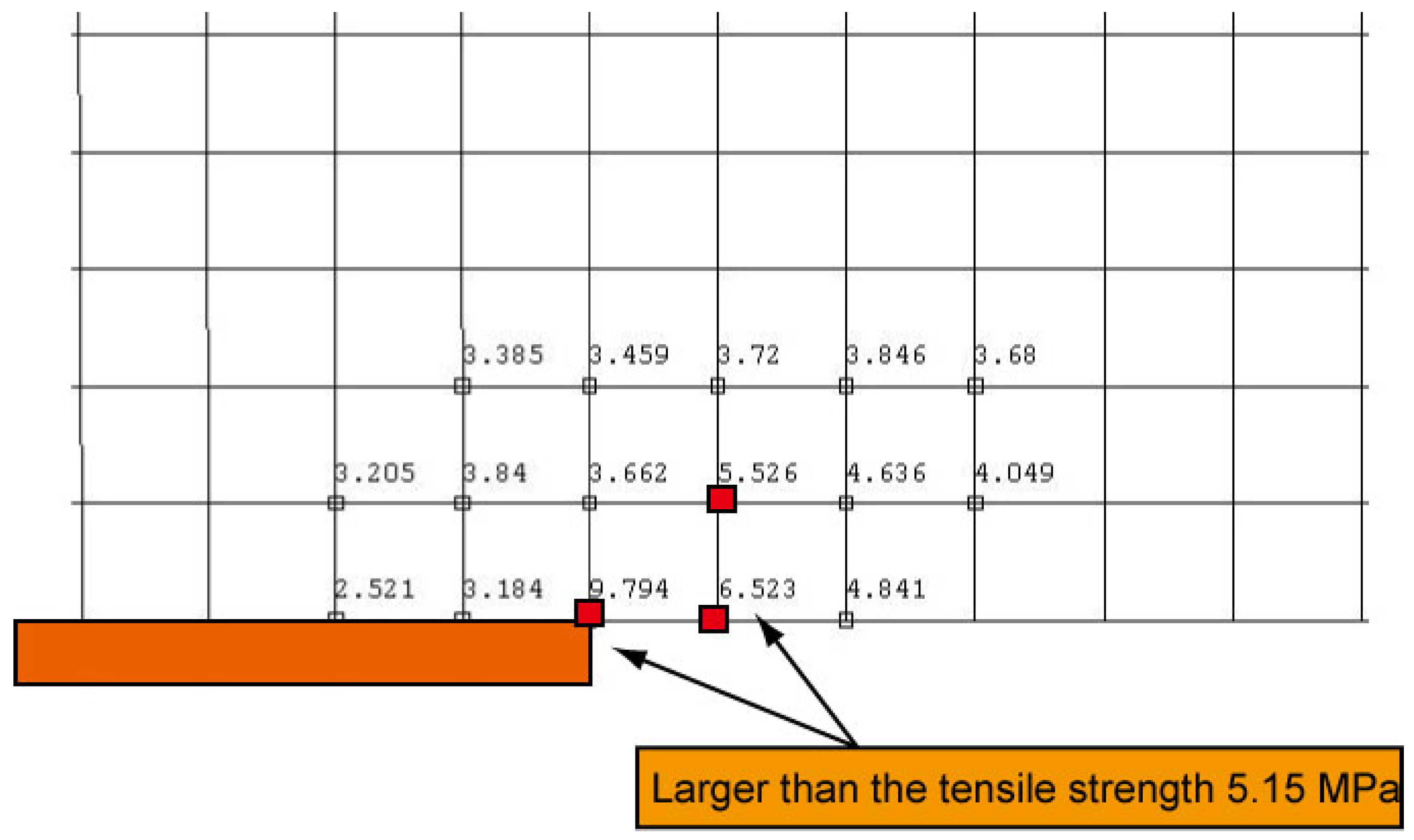
3.3.3. CFRP Length of 0.30 m
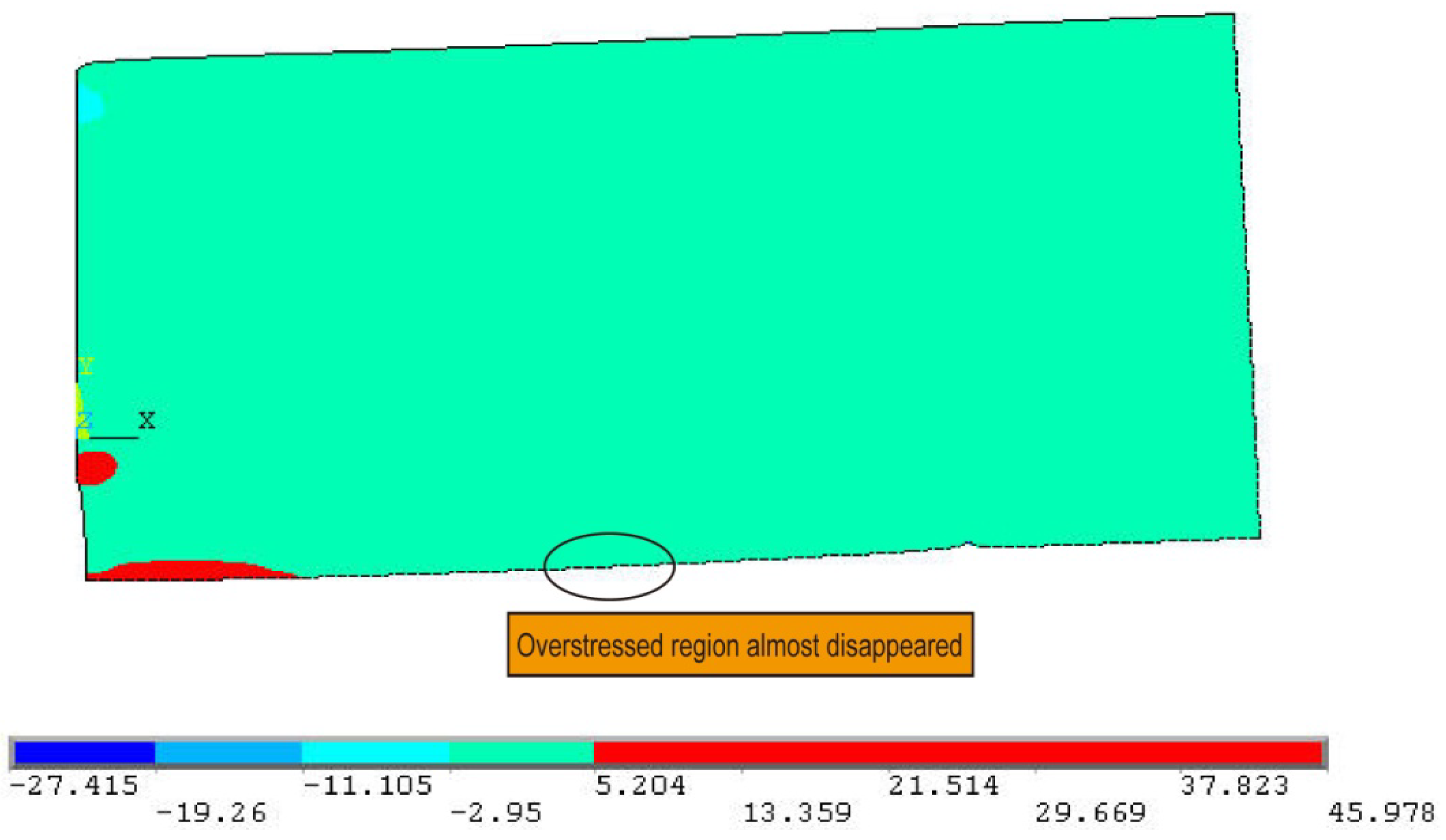
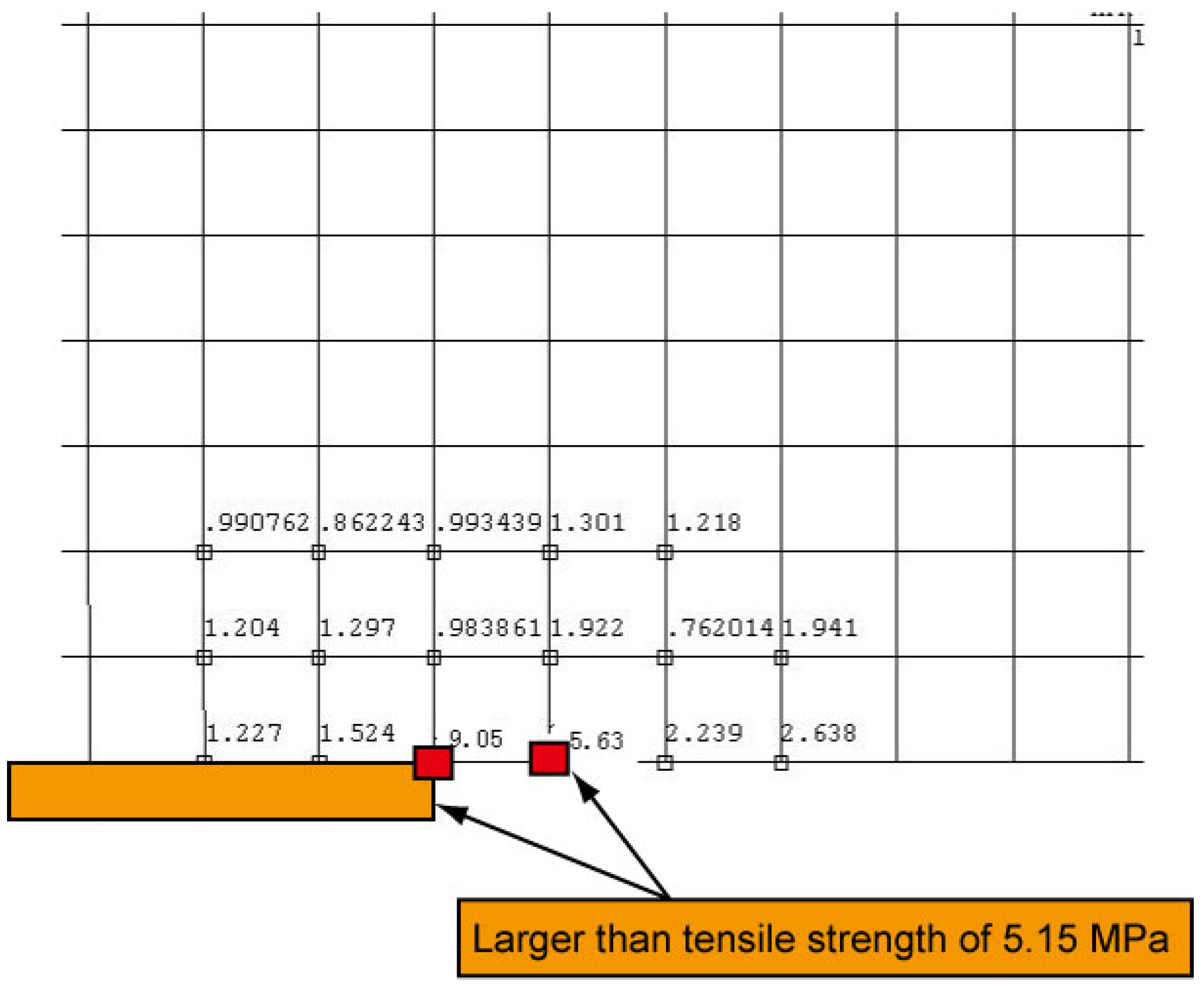
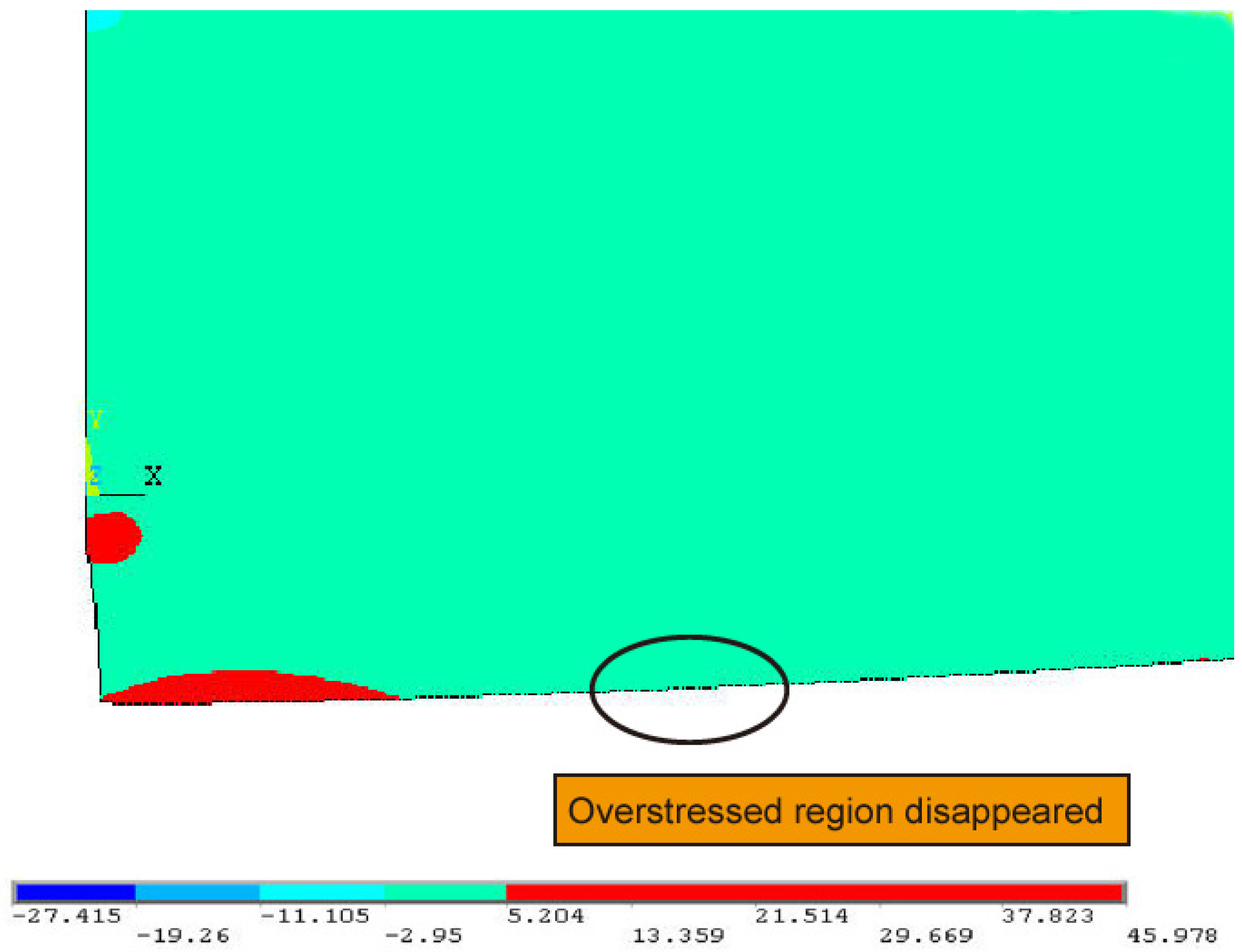
3.3.4. CFRP Length of 0.35 m

4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Anwarul Islam, A.K.M. Effective methods of using CFRP bars in shear strengthening of concrete griders. Eng. Struct. 2009, 31, 709–714. [Google Scholar] [CrossRef]
- Biscaia, H.C.; Chastre, C.; Silva, M.A. Nolinear numerical analysis of the debonding failure process of FRP-to-concrete interfaces. Compos. B Eng. 2010, 50, 210–223. [Google Scholar]
- Michels, J.; Christen, R.; Waldmann, D. Experimental and numerical investigation on postcracking behavior of steel fiber reinforced concrete. Eng. Fract. Mech. 2013, 98, 326–349. [Google Scholar] [CrossRef]
- Sundarraja, M.C.; Rajamohan, S. Strengthening of RC beams in shear using GFRP inclined strips-An experimental study. Construct. Build. Mater. 2009, 23, 856–864. [Google Scholar] [CrossRef]
- Edberg, W.; Mertz, D.; Gillespie, J., Jr. Rehabilitation of steel beams using composites materials. In Proceedings of ASCE Fourth Material Engineering Conference, Washington, D.C., USA, 10–14 November 1996; pp. 502–508.
- Buyle-Bodin, F.; David, E.; Ragneau, E. Finite element modelling of flexual behaviour of externally bonded CFRP reinforced concrete structures. Eng. Struct. 2002, 24, 1423–1429. [Google Scholar]
- Mazzotti, C.; Savoia, M.; Ferracuti, B. An experimental study on delamination of FRP plates bonded to concrete. Constr. Build. Mater. 2008, 22, 1409–1421. [Google Scholar]
- Martinez, X.; Oller, S.; Rastellini, F.; Barbat, A. A numerical procedure simulating RC structures reinforced with FRP using the serial/parallel mixing theory. Comput. Struct. 2008, 86, 1604–1618. [Google Scholar]
- Tavakkolizadeh, M.; Saadatmanesh, H. Fatigue strength of steel girders strengthened with carbon fiber reinforced polymer patch. J. Struct. Eng. 2003, 129, 186–196. [Google Scholar]
- Xue, W.; Zeng, L.; Tan, Y. Experimental studies on bond behavior of high strength CFRP plates. Compos. B Eng. 2008, 39, 592–603. [Google Scholar] [CrossRef]
- Valivonis, J.; Skuturna, T. Cracking and strength of reinforced concrete structures in flexure strengthened with carbon fibre laminates. J. Civ. Eng. Manag. 2007, 4, 317–323. [Google Scholar]
- Deng, J.; Lee, M.M.K.; Moy, S.S.J. Stress analysis of steel beams reinforced with a bonded CFRP plate. Compos. Struct. 2004, 65, 205–215. [Google Scholar] [CrossRef]
- Buyukozturk, O.; Gunes, O.; Karaca, E. Progress on understanding debonding problems in reinforced concrete and steel members strengthened using FRP composites. Constr. Build. Mater. 2004, 18, 9–19. [Google Scholar] [CrossRef]
- Schnerch, D.; Stanford, K.; Sumner, E.; Rizkalla, S. Bond behavior of CFRP strengthened steel bridges and structures. In Proceedings of International Symposium on Bond Behavior of FRP in Structures, Hong Kong, China, 7–9 December 2005.
- Schnerch, D.; Dawood, M.; Rizkalla, S.; Sumner, E.; Stanford, K. Bond behavior of CFRP strengthened steel structures. Adv. Struct. Eng. 2006, 9, 805–817. [Google Scholar] [CrossRef]
- Colombi, P. Reinforcement delamination of metallic beams strengthened by FRP strips: Fracture mechanics based approach. Eng. Fract. Mech. 2006, 73, 1980–1995. [Google Scholar]
- Belachour, A.; Benyoucefa, S.; Tounsi, A.; Adda bedia, E.A. Interfacial stress analysis of steel beams reinforced with bonded prestressed FRP plate. Eng. Struct. 2008, 30, 3305–3315. [Google Scholar] [CrossRef]
- Al-Emarani, M.; Kliger, R. Experimental and numerical investigation of the behavior and strength of composite steel-CFRP members. Adv. Struct. Eng. 2006, 9, 819–831. [Google Scholar] [CrossRef]
- Lu, X.Z.; Jiang, J.J.; Teng, J.G.; Ye, L.P. Finite element simulation of debonding in FRP-to-concrete bonded joints. Constr. Build. Mater. 2006, 20, 412–424. [Google Scholar] [CrossRef]
- Atas, A.; Soutis, C. Strength prediction of bonded joints in CFRP composite laminates using cohesive zone elements. Compos. B Eng. 2014, 58, 25–34. [Google Scholar] [CrossRef]
- Chen, G.M.; Chen, J.F.; Teng, J.G. On the finite element modelling of RC beams shear strengthened with FRP. Constr. Build. Mater. 2012, 32, 13–26. [Google Scholar] [CrossRef]
- Ding, J. Crack failure study of CFRP reinforced concrete beams. Master Thesis, Chongqing University, Chongqing, China, 1 July 2004. [Google Scholar]
- Niu, S.S. The experimental study on concrete beams strengthened with CFRP. Master Thesis, Chongqing University, Chongqing, China, 1 July 2002. [Google Scholar]
- Ding, J.; Huang, X.; Zhu, G.; Chen, S.; Wang, G.C. Mechanical performance evaluation of concrete beams strengthened with CFRP. Adv. Mater. Sci. Eng. 2013, 2013, 1–9. [Google Scholar]
- Concrete Structure Design Specifications; GB50010-2010; China Building Industry Press: Beijing, China, 2011.
- Product Specifications for CFRP; Taiwan Zhongyi Company Press: Taiwan, 2012.
- Chinese Aeronautical Establishment. In The Handbook for Stress Intensity Factors; Beijing Science Press: Beijing, China, 1981.
- ABAQUS, version 6.10, User Documentation; Dassault Systemes: Vélizy-Villacoublay, France, 2010.
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ding, J.; Wang, F.; Huang, X.; Chen, S. The Effect of CFRP Length on the Failure Mode of Strengthened Concrete Beams. Polymers 2014, 6, 1705-1726. https://doi.org/10.3390/polym6061705
Ding J, Wang F, Huang X, Chen S. The Effect of CFRP Length on the Failure Mode of Strengthened Concrete Beams. Polymers. 2014; 6(6):1705-1726. https://doi.org/10.3390/polym6061705
Chicago/Turabian StyleDing, Jun, Fang Wang, Xia Huang, and Song Chen. 2014. "The Effect of CFRP Length on the Failure Mode of Strengthened Concrete Beams" Polymers 6, no. 6: 1705-1726. https://doi.org/10.3390/polym6061705




