A Unified Theoretical Model for the Monotonic and Cyclic Response of FRP Strips Glued to Concrete
Abstract
:1. Introduction
2. Formulation of the Proposed Theoretical Model
- -
- the crack develops at the FRP-to-concrete interface in (pure shear) “mode II”;
- -
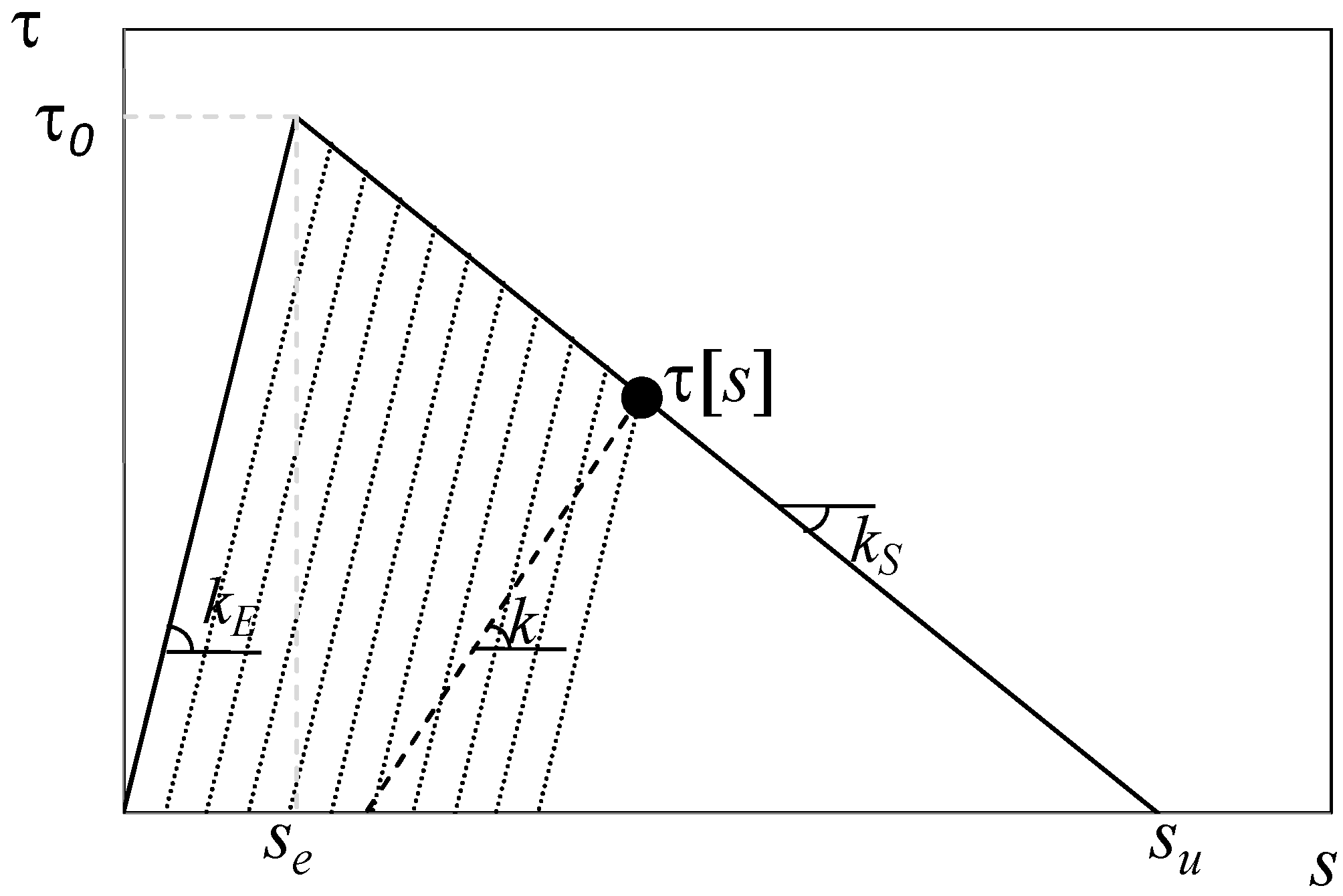
- the analytical expression of the monotonic softening branch of the bond-slip relationship is described “a priori” by assuming an analytical expression (either exponential or linear in shape);
- -
- stiffness degradation in the unloading stages depends upon the actual value of the “fracture work” developed in each interface point;
- -
- “small” displacements are assumed at the interface and axial strains possibly developing in the concrete substrate are neglected.
2.1. Fundamental Assumptions
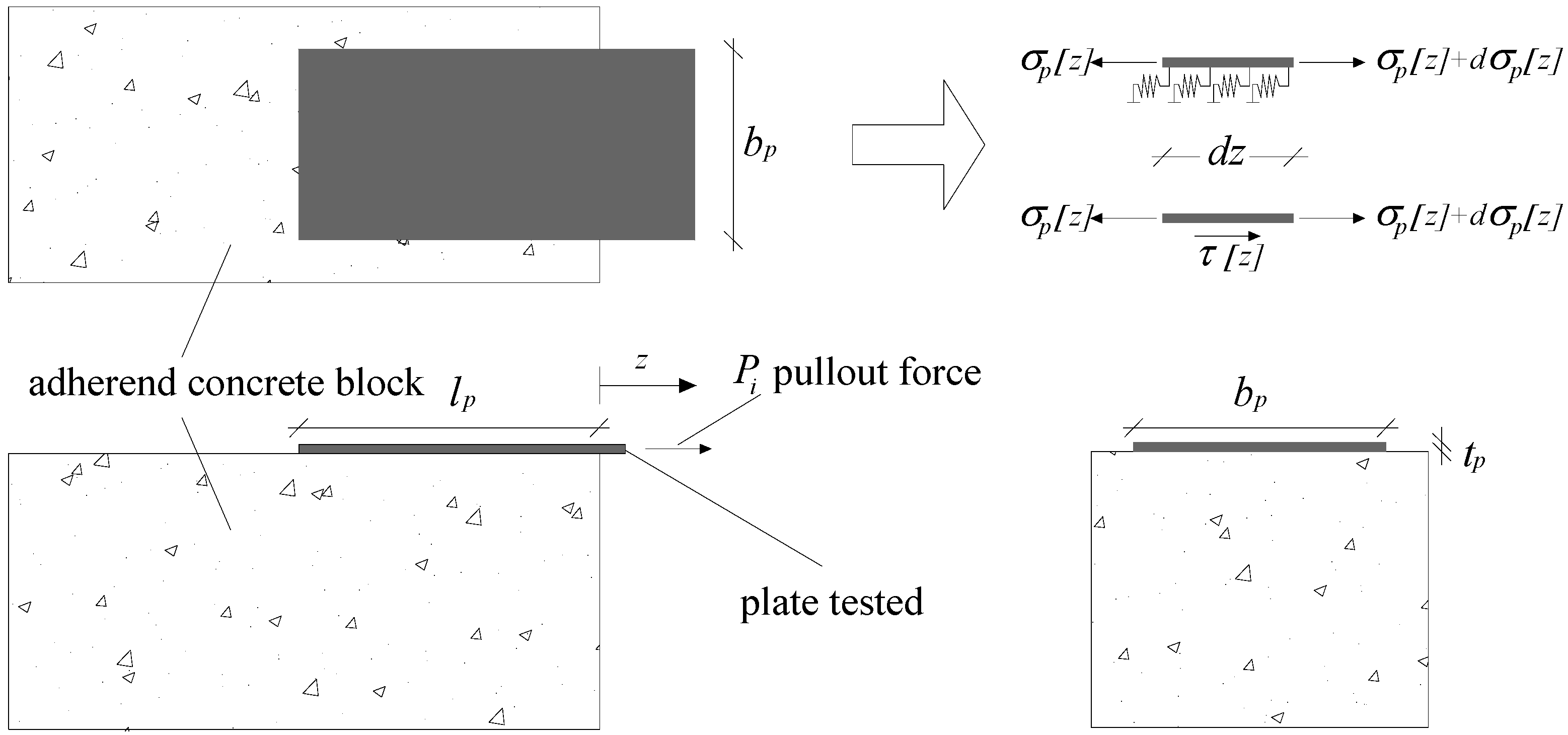
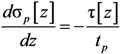
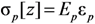

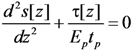
2.2. Fracture-Based Damage Modeling
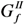 . They both can be determined by assuming “a priori” a bond-slip interface law τ(s); the latter also depends on the actual cracking displacement which is assumed as a state variable. Therefore, assuming “a priori” expressions for the bond-slip laws results in several simplifications and the consistency of the numerical integration process is guaranteed because the value of wsl can be univocally defined in each point of the interface depending on the current value of the local cracking displacement.
. They both can be determined by assuming “a priori” a bond-slip interface law τ(s); the latter also depends on the actual cracking displacement which is assumed as a state variable. Therefore, assuming “a priori” expressions for the bond-slip laws results in several simplifications and the consistency of the numerical integration process is guaranteed because the value of wsl can be univocally defined in each point of the interface depending on the current value of the local cracking displacement.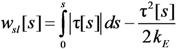
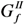 is uniform throughout such a length and depends on the key parameters involved in the bond-slip law under consideration:
is uniform throughout such a length and depends on the key parameters involved in the bond-slip law under consideration:


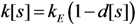
2.2.1. Exponential Softening Bond-Slip Law
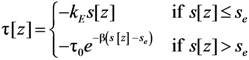
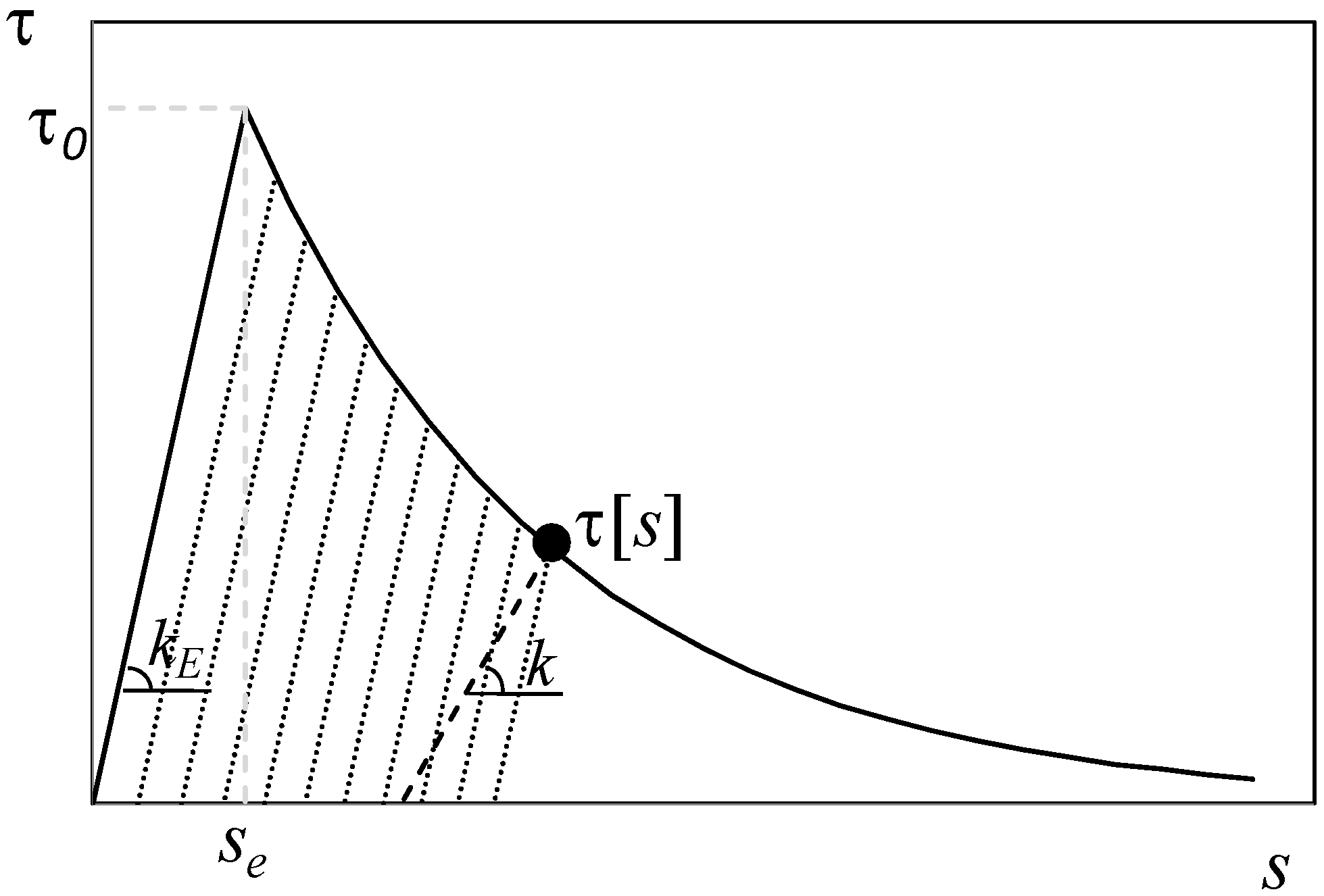

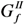 can be expressed as follows, depending on the other parameters which define the assumed bond-slip law (namely kE, se and β):
can be expressed as follows, depending on the other parameters which define the assumed bond-slip law (namely kE, se and β):
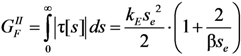
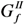 , according to the analytical expressions proposed in Equation (7) and (8).
, according to the analytical expressions proposed in Equation (7) and (8).2.2.2. Linear Softening Bond-Slip Law
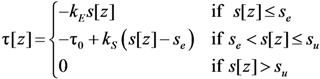
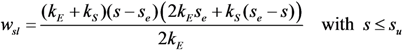
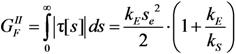
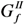 , respectively, within the definition of the parameters d and k provided by Equations (7) and (8).
, respectively, within the definition of the parameters d and k provided by Equations (7) and (8).2.3. Outline of the Numerical Procedure
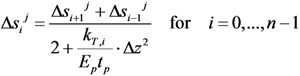
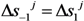

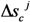 at the loaded end (i.e., node n).
at the loaded end (i.e., node n).
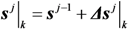
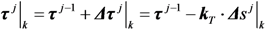
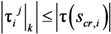
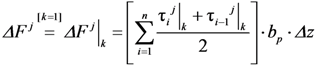
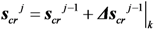
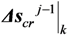 is the vector collecting all the increments of the cracking displacements Δsij|k,cr at convergence. Moreover, the corresponding force increment
is the vector collecting all the increments of the cracking displacements Δsij|k,cr at convergence. Moreover, the corresponding force increment 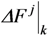 determined through Equation (21) can be added to the previous value of the external force to determine the total external load applied at the end of the j-th analysis step (and nodal displacement increment).
determined through Equation (21) can be added to the previous value of the external force to determine the total external load applied at the end of the j-th analysis step (and nodal displacement increment).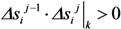
3. Experimental Validation
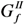 = 0.958 N/mm, are assumed in the following numerical simulations for the mechanical quantities which are relevant for both the bond-slip relationships, according to the average values identified by the cited authors for the specimens A11, A12 and A13, tested under monotonic actions. Regarding the softening branch, it can be consistently derived by the three aforementioned values and taking into account the two expressions of
= 0.958 N/mm, are assumed in the following numerical simulations for the mechanical quantities which are relevant for both the bond-slip relationships, according to the average values identified by the cited authors for the specimens A11, A12 and A13, tested under monotonic actions. Regarding the softening branch, it can be consistently derived by the three aforementioned values and taking into account the two expressions of 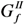 described in Subsection 2.2.1 and Subsection 2.2.2 [namely, those reported as Equations (11) and (14)], which connect the β exponent and the kS slope characterizing the exponential and the linear softening relationships, respectively. Moreover, the unit value is considered for the damage parameter αd.
described in Subsection 2.2.1 and Subsection 2.2.2 [namely, those reported as Equations (11) and (14)], which connect the β exponent and the kS slope characterizing the exponential and the linear softening relationships, respectively. Moreover, the unit value is considered for the damage parameter αd.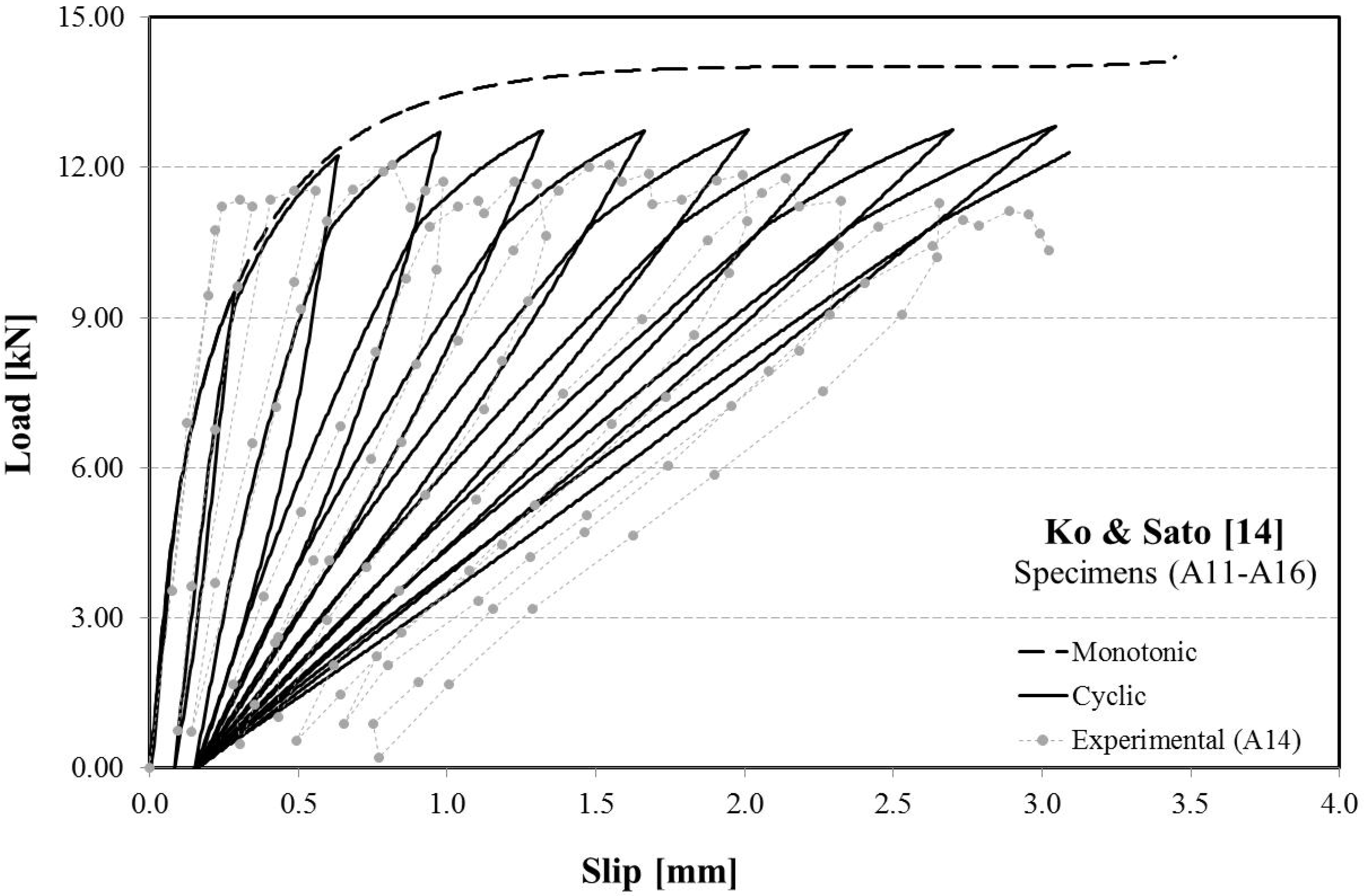
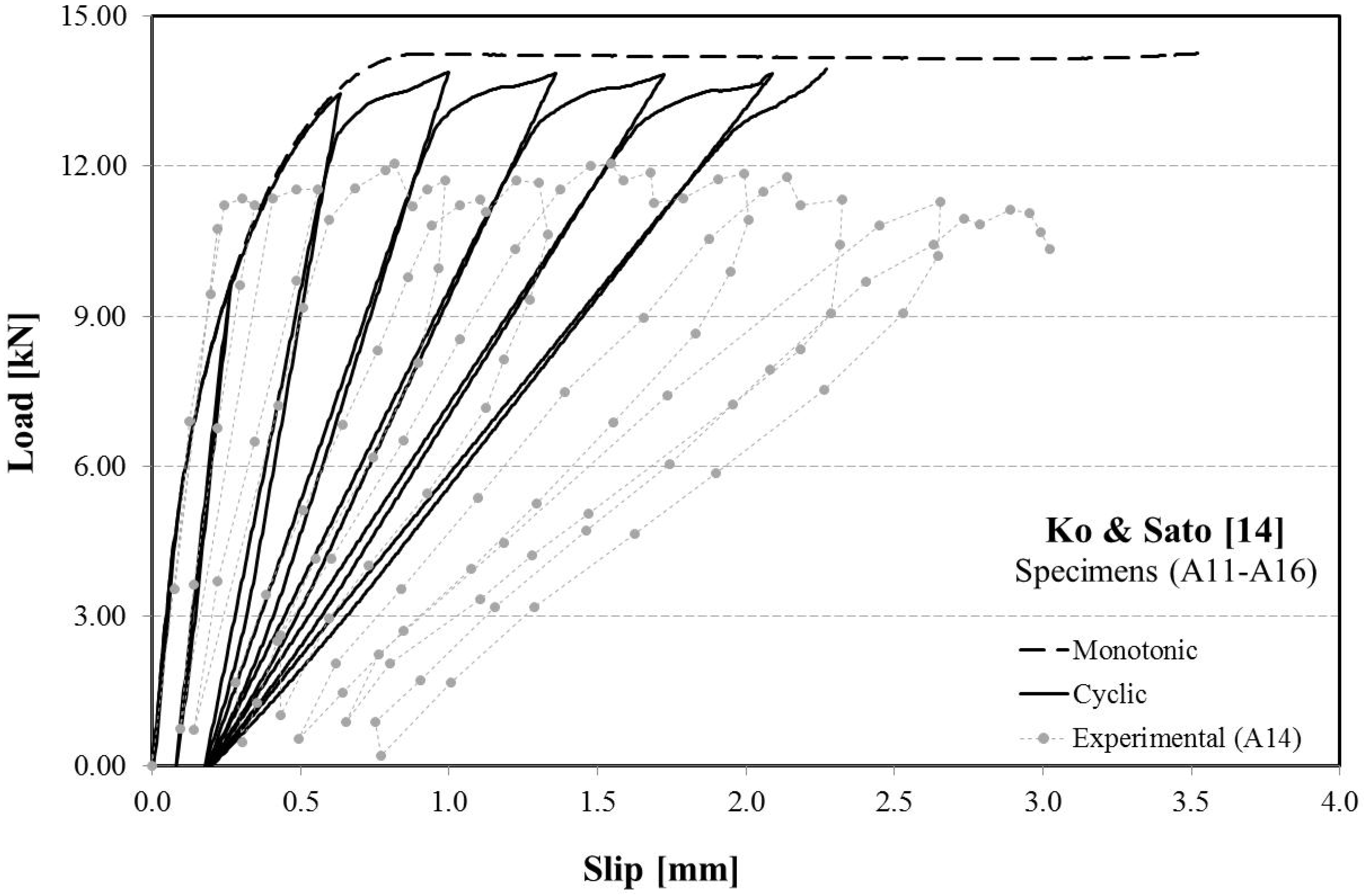
 defined by Equation (11) and this results in an higher stability of the numerical procedure outlined in Section 2.3.
defined by Equation (11) and this results in an higher stability of the numerical procedure outlined in Section 2.3.4. Conclusions
- -
- the proposed model has been formulated within the framework of Fracture Mechanics and assumed two alternative expressions for the softening branch of the bond-slip relationship;
- -
- the closed-form expressions obtained for determining the key fracture-related quantities are among the novel and most attractive features of the present formulation;
- -
- the comparison between some experimental results available in the literature and the numerical simulations performed by means of the present model highlighted its high predictive potential;
- -
- the proposed experimental comparisons pointed out the higher accuracy obtained by assuming an exponential softening branch, with respect to the linear one, generally accepted for simulating the response under monotonic actions;
- -
- the extension of such comparisons to further experimental observation is among the future steps of this research, that finally aims at characterizing the force and displacement capacity of FRP-to-concrete joints subjected to cyclic actions, which are quite common in seismic retrofitting of existing buildings.
Acknowledgments
Conflicts of Interest
References
- Pan, J.L.; Xu, T.; Hu, Z.J. Experimental investigation of load carrying capacity of the slender reinforced concrete columns wrapped with FRP. Constr. Build. Mater. 2007, 21, 1991–1996. [Google Scholar] [CrossRef]
- Corradi, M.; Speranzini, E.; Borri, A.; Vignoli, A. In-plane shear reinforcement of wood beam floors with FRP. Compos. Part B Eng. 2006, 37, 310–319. [Google Scholar] [CrossRef]
- Marcari, G.; Manfredi, G.; Prota, A.; Pecce, M. In-plane shear performance of masonry panels strengthened with FRP. Compos. Part B Eng. 2007, 38, 887–901. [Google Scholar] [CrossRef]
- Chajes, M.; Finch, W.; Januska, T.; Thomson, T. Bond and force transfer of composite material plates bonded to concrete. ACI Struct. J. 1996, 93, 208–217. [Google Scholar]
- Czaderski, C.; Martinelli, E.; Michels, J.; Motavalli, M. Effect of curing conditions on strength development in an epoxy resin for structural strengthening. Compos. Part B Eng. 2012, 43, 398–410. [Google Scholar]
- Ferracuti, B.; Savoia, M.; Mazzotti, C. A numerical model for FRP-concrete delamination. Compos. Part B Eng. 2006, 37, 356–364. [Google Scholar] [CrossRef]
- Cornetti, P.; Carpinteri, A. Modelling the FRP-concrete delamination by means of an exponential softening law. Eng. Struct. 2001, 33, 1988–2001. [Google Scholar] [CrossRef]
- Martinelli, E.; Czaderski, C.; Motavalli, M. Modeling in-plane and out-of-plane displacement fields in pull-off tests on FRP strips. Eng. Struct. 2011, 33, 3715–3725. [Google Scholar] [CrossRef]
- Caggiano, A.; Martinelli, E.; Faella, C. A fully-analytical approach for modelling the response of FRP plates bonded to a brittle substrate. Int. J. Solids Struct. 2012, 49, 2291–2300. [Google Scholar] [CrossRef]
- Caggiano, A.; Martinelli, E. A fracture-based interface model for simulating the bond behaviour of FRP strips glued to a brittle substrate. Compos. Struct. 2013, 99, 397–403. [Google Scholar] [CrossRef]
- Mazzotti, C.; Savoia, M. FRP-concrete bond behaviour under cyclic debonding force. Adv. Struct. Eng. 2009, 12, 771–780. [Google Scholar] [CrossRef]
- Nigro, E.; di Ludovico, M.; Bilotta, A. Experimental investigation of FRP-concrete debonding under cyclic actions. J. Mater. Civil Eng. (ASCE) 2011, 23, 360–371. [Google Scholar] [CrossRef]
- Carloni, C.; Subramaniam, K.V.; Savoia, M.; Mazzotti, C. Experimental determination of FRP-concrete cohesive interface properties under fatigue loading. Compos. Struct. 2012, 94, 1288–1296. [Google Scholar] [CrossRef]
- Ko, H.; Sato, Y. Bond stress-slip relationship between FRP sheet and concrete under cyclic load. J. Compos. Construct. (ASCE) 2007, 11, 419–246. [Google Scholar]
- Fédération Internationale du Béton (FIB). Bulletin 14: Externally Bonded FRP Reinforcement for RC Structures; Technical report, ISBN 978–2-88394–054–3; FIB: Lausanne, Switzerland, 2001. [Google Scholar]
- Martinelli, E.; Bilotta, A.; Faella, C.; Nigro, E. On the Behavior of FRP-to-concrete Adhesive Interface: Theoretical Models and Experimental Results. In Advances in Composite Materials—Ecodesign and Analysis; Attaf, B., Ed.; InTech Open Access Publisher: Rijeka, Croatia, 2011; pp. 517–546. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Martinelli, E.; Caggiano, A. A Unified Theoretical Model for the Monotonic and Cyclic Response of FRP Strips Glued to Concrete. Polymers 2014, 6, 370-381. https://doi.org/10.3390/polym6020370
Martinelli E, Caggiano A. A Unified Theoretical Model for the Monotonic and Cyclic Response of FRP Strips Glued to Concrete. Polymers. 2014; 6(2):370-381. https://doi.org/10.3390/polym6020370
Chicago/Turabian StyleMartinelli, Enzo, and Antonio Caggiano. 2014. "A Unified Theoretical Model for the Monotonic and Cyclic Response of FRP Strips Glued to Concrete" Polymers 6, no. 2: 370-381. https://doi.org/10.3390/polym6020370
APA StyleMartinelli, E., & Caggiano, A. (2014). A Unified Theoretical Model for the Monotonic and Cyclic Response of FRP Strips Glued to Concrete. Polymers, 6(2), 370-381. https://doi.org/10.3390/polym6020370





