Statistical Analysis of the Progressive Failure Behavior for Fiber-Reinforced Polymer Composites under Tensile Loading
Abstract
:1. Introduction
2. Formulation and Algorithm
2.1. Analytical Model
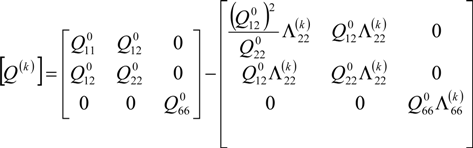
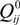 are the stiffness of an intact lamina and Q(k) are the degraded stiffness matrices of the k-th damaged lamina.
are the stiffness of an intact lamina and Q(k) are the degraded stiffness matrices of the k-th damaged lamina. 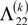 and
and 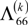 , called in situ damage effective functions (IDEFs), can be expressed as:
, called in situ damage effective functions (IDEFs), can be expressed as:
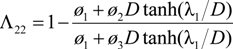
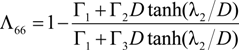
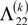 and
and 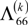 , are determined from the obtained stress field under the framework of shear-lag arguments. They characterize the in-plane stiffness reductions of the constrained, cracked lamina. The findings of some work show that a crack lamina behaves within a laminate in a different manner compared to an infinite effective medium containing many cracks [24].
, are determined from the obtained stress field under the framework of shear-lag arguments. They characterize the in-plane stiffness reductions of the constrained, cracked lamina. The findings of some work show that a crack lamina behaves within a laminate in a different manner compared to an infinite effective medium containing many cracks [24].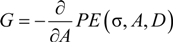
 is the x-axis normal stress in the xy-plane and the superscript, 0, is used to indicate the quantities that belongs to the undamaged state.
is the x-axis normal stress in the xy-plane and the superscript, 0, is used to indicate the quantities that belongs to the undamaged state.  are the in-plane stiffness components of an undamaged lamina. g(L, D) is the normalized energy release rate, which can be expressed as:
are the in-plane stiffness components of an undamaged lamina. g(L, D) is the normalized energy release rate, which can be expressed as:
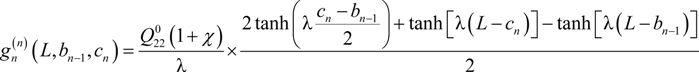
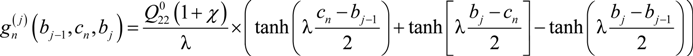
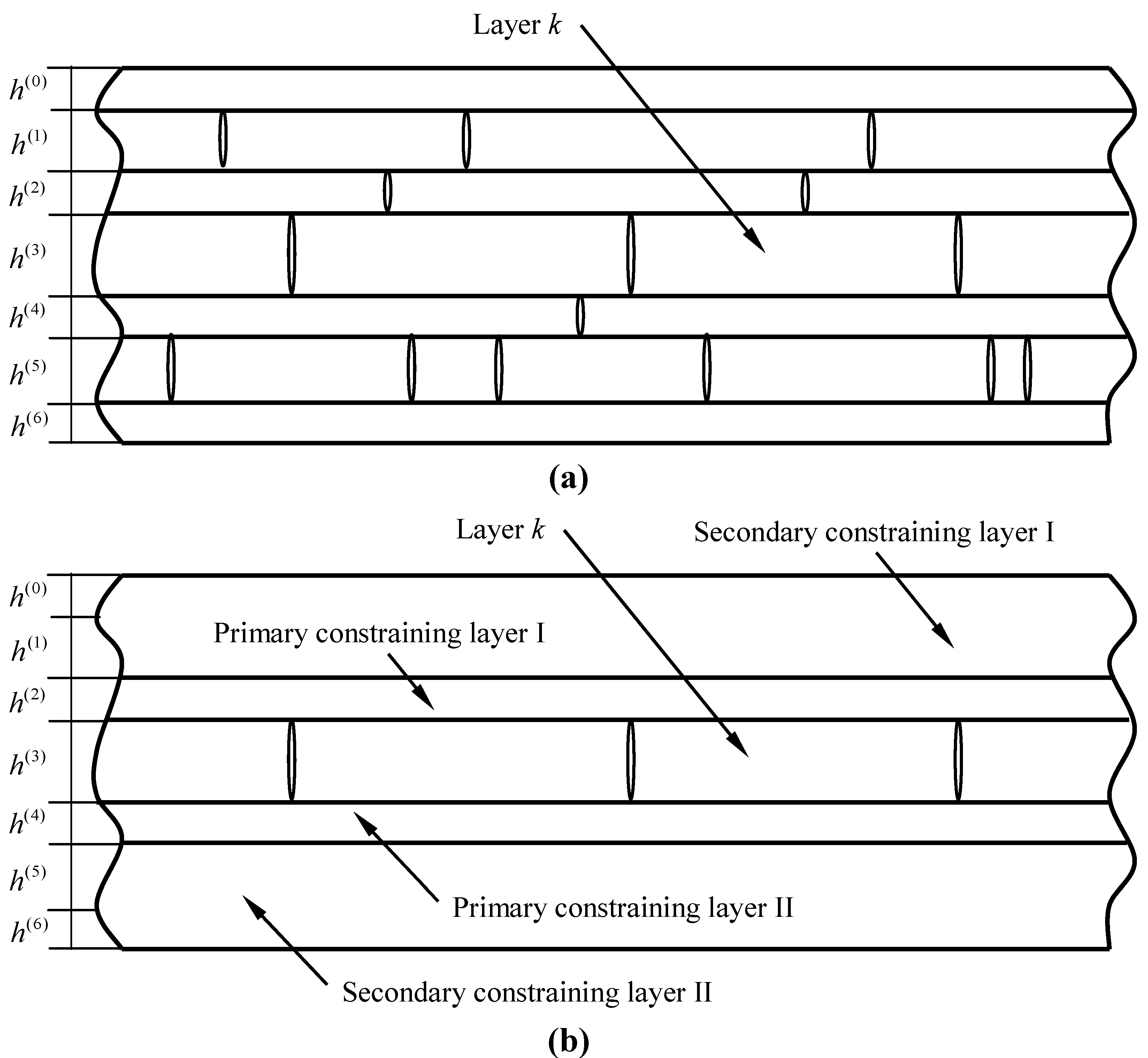
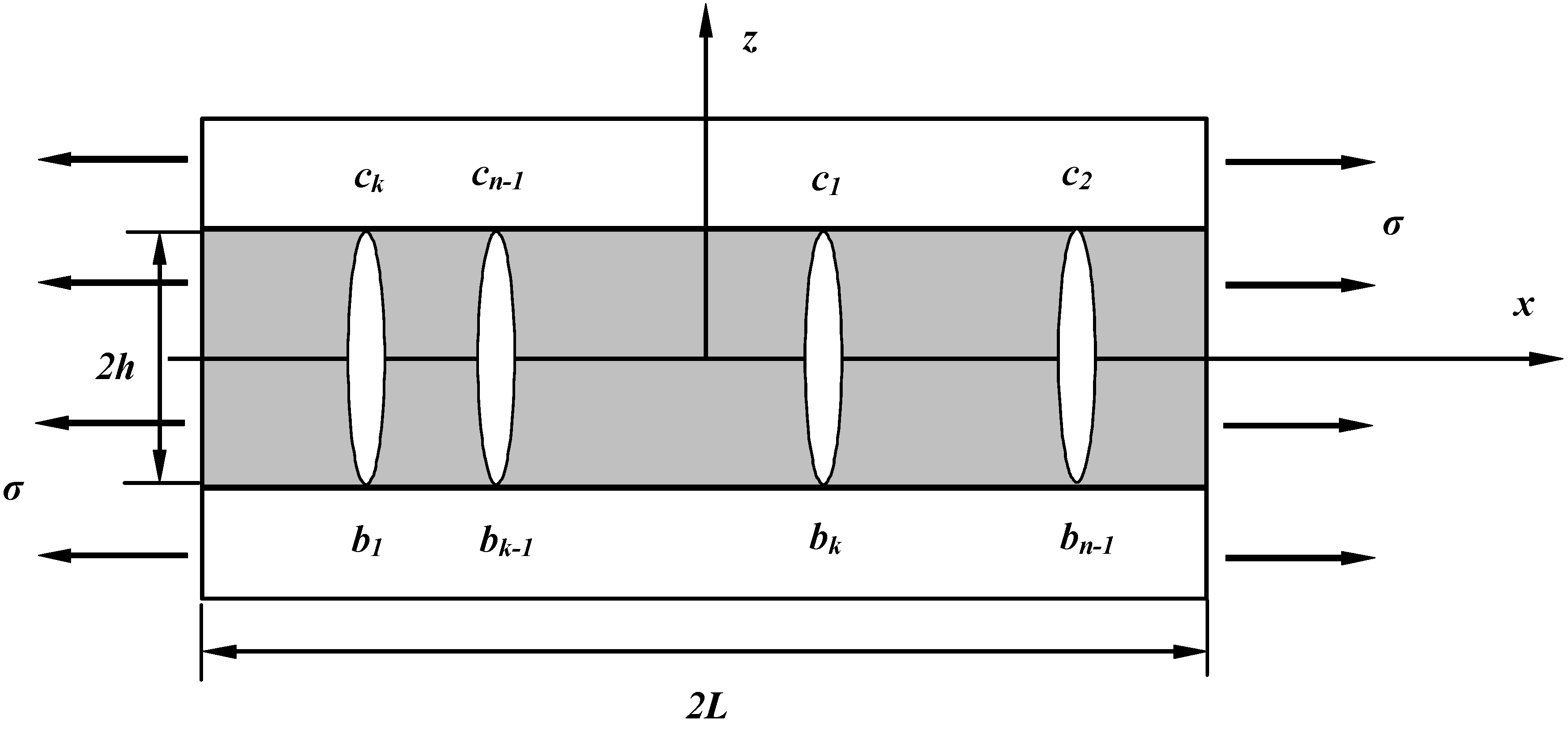
2.2. Modeling of Progressive Cracking
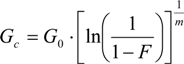
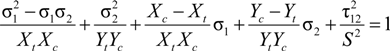
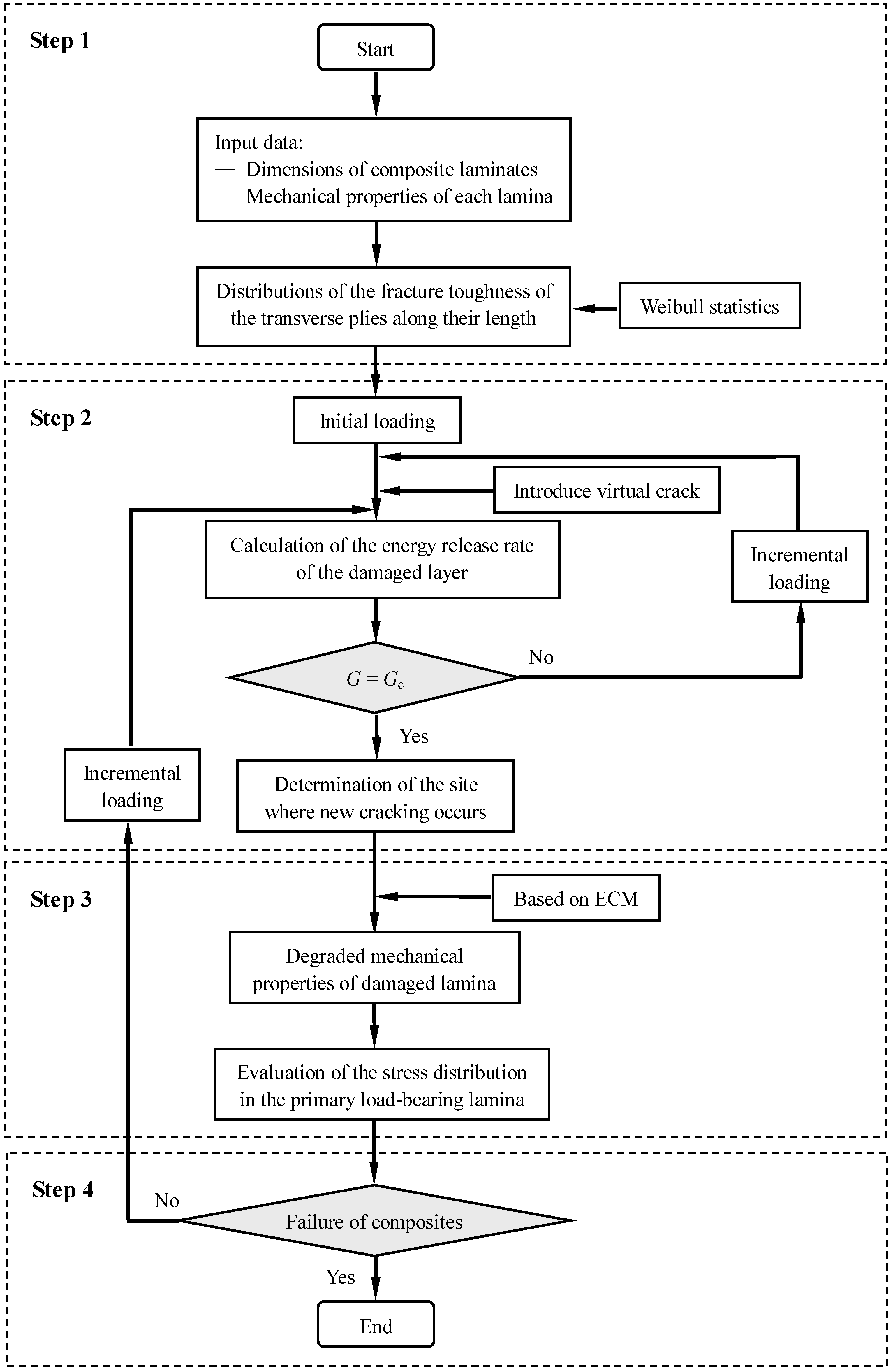
2.3. Numerical Algorithm
3. Results and Discussion
| Fiber Matrix | AS4/3501 | T300/5208 | Glass-fiber epoxy (GFRP) |
|---|---|---|---|
| Elastic properties | |||
| E1 (GPa) | 126 | 132.58 | 44.73 |
| E2 (GPa) | 11 | 10.8 | 12.76 |
| G12 (GPa) | 6.6 | 5.7 | 5.8 |
| γ12 | 0.28 | 0.24 | 0.297 |
| Strength parameters | |||
| XT (MPa) | 1950 | 1515 | 1062 |
| XC (MPa) | 1480 | 1697 | 610 |
| YT (MPa) | 48 | 43.8 | 118 |
| YC (MPa) | 200 | 43.8 | 118 |
| S (MPa) | 79 | 86.9 | 72 |
| Ply thickness | |||
| t (mm) | 0.125 | 0.132 | 0.144 |
| Weibull distribution | |||
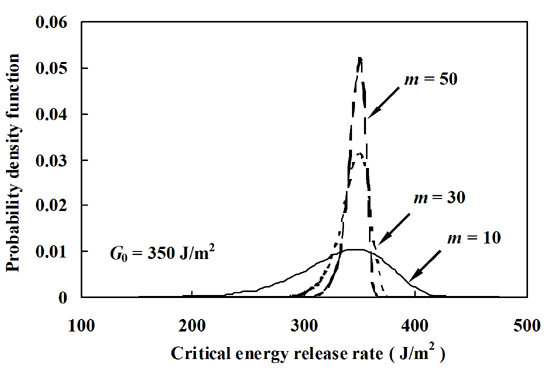
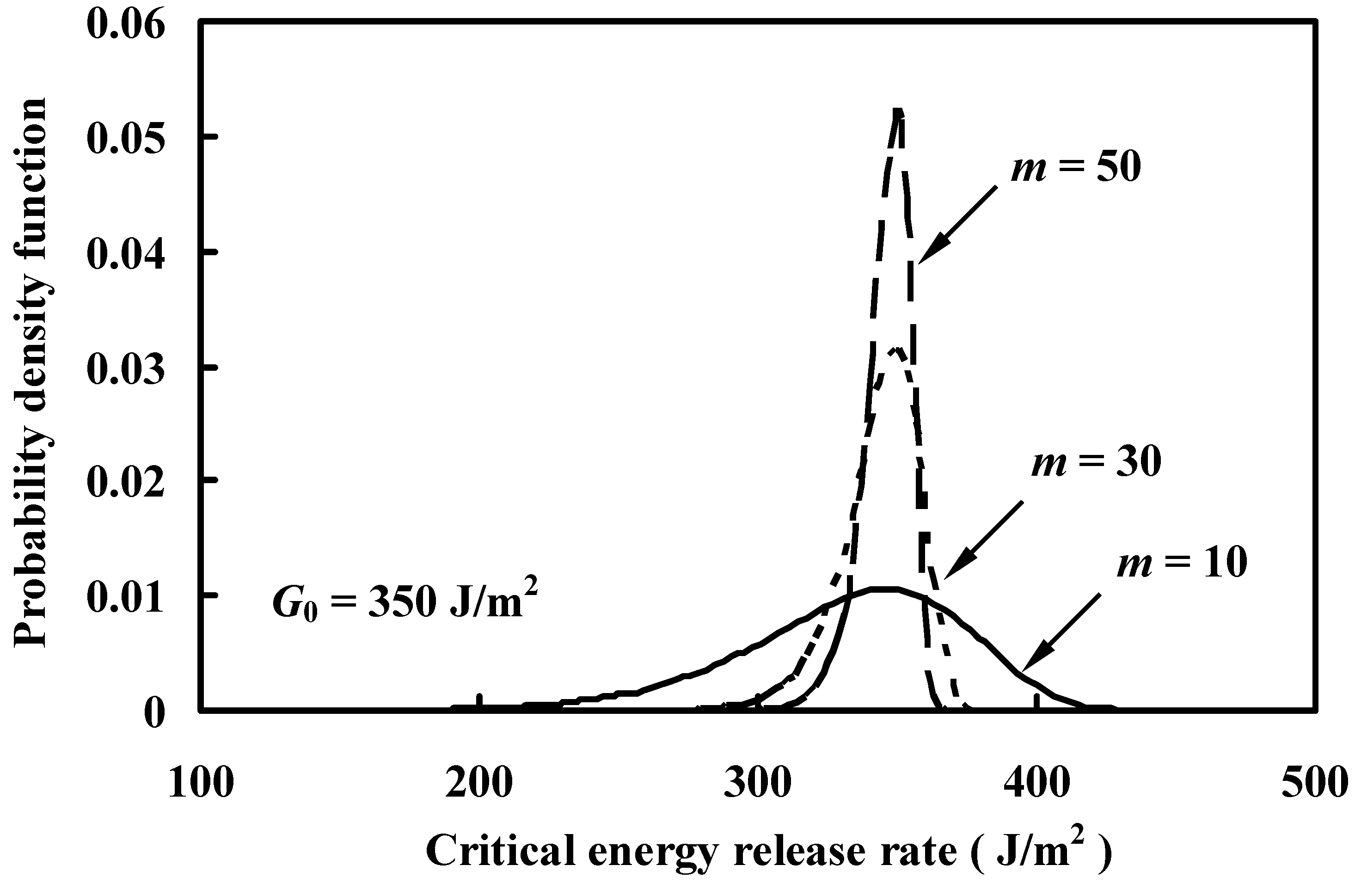
| G0 (J/m2) | 220 | 228 | 750 |
| m | 50 | 50 | 10 |
| Laminate | Configuration | Laminate | Configuration |
|---|---|---|---|
| A | [02/904]S | B | [0/90]S |
| C | [±15/904]S | D | [±30/904]S |
| E | [0/±θ/90]S | F | [0/90/±θ]S |
3.1. Prediction of Stiffness Reduction

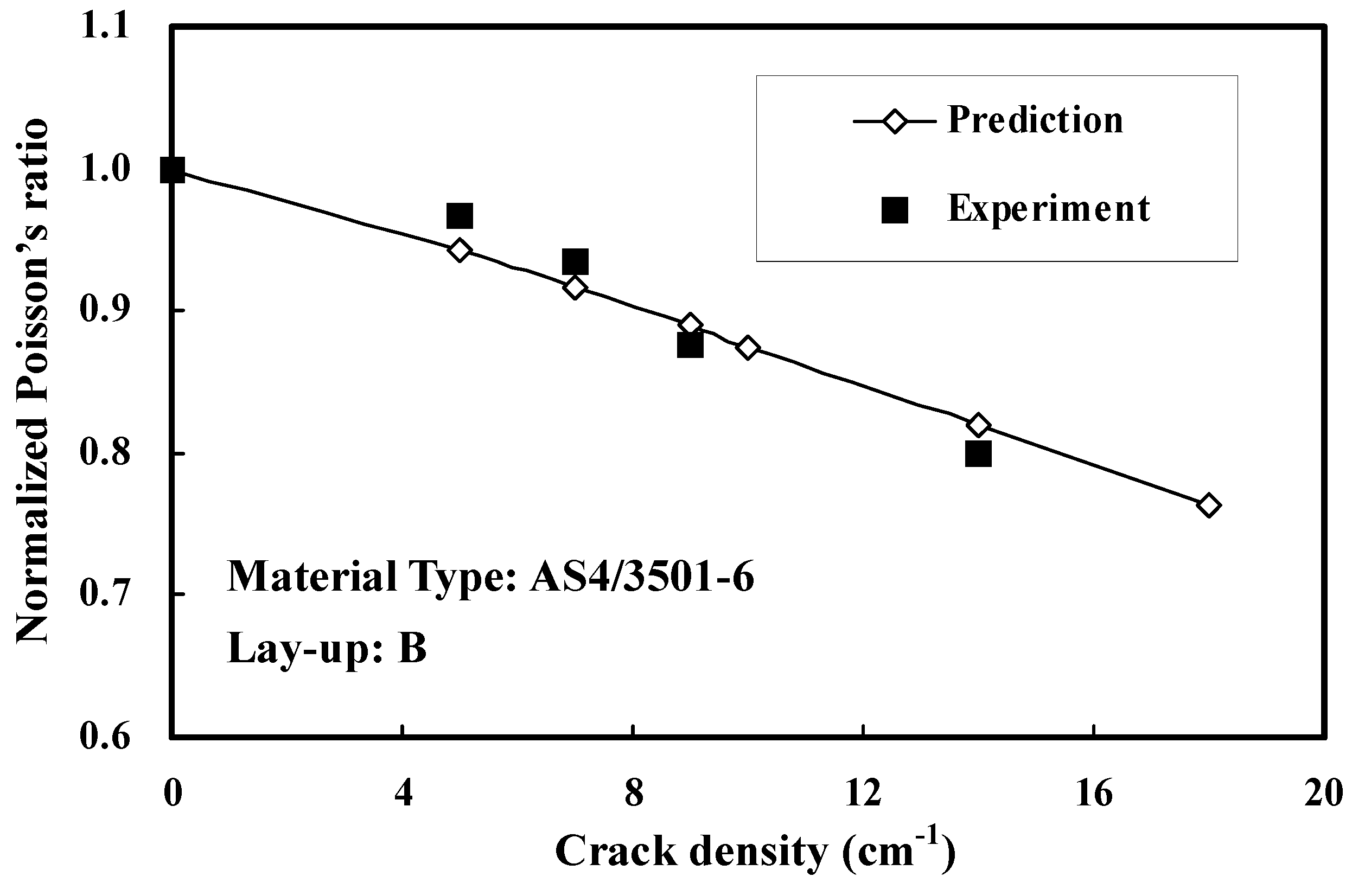
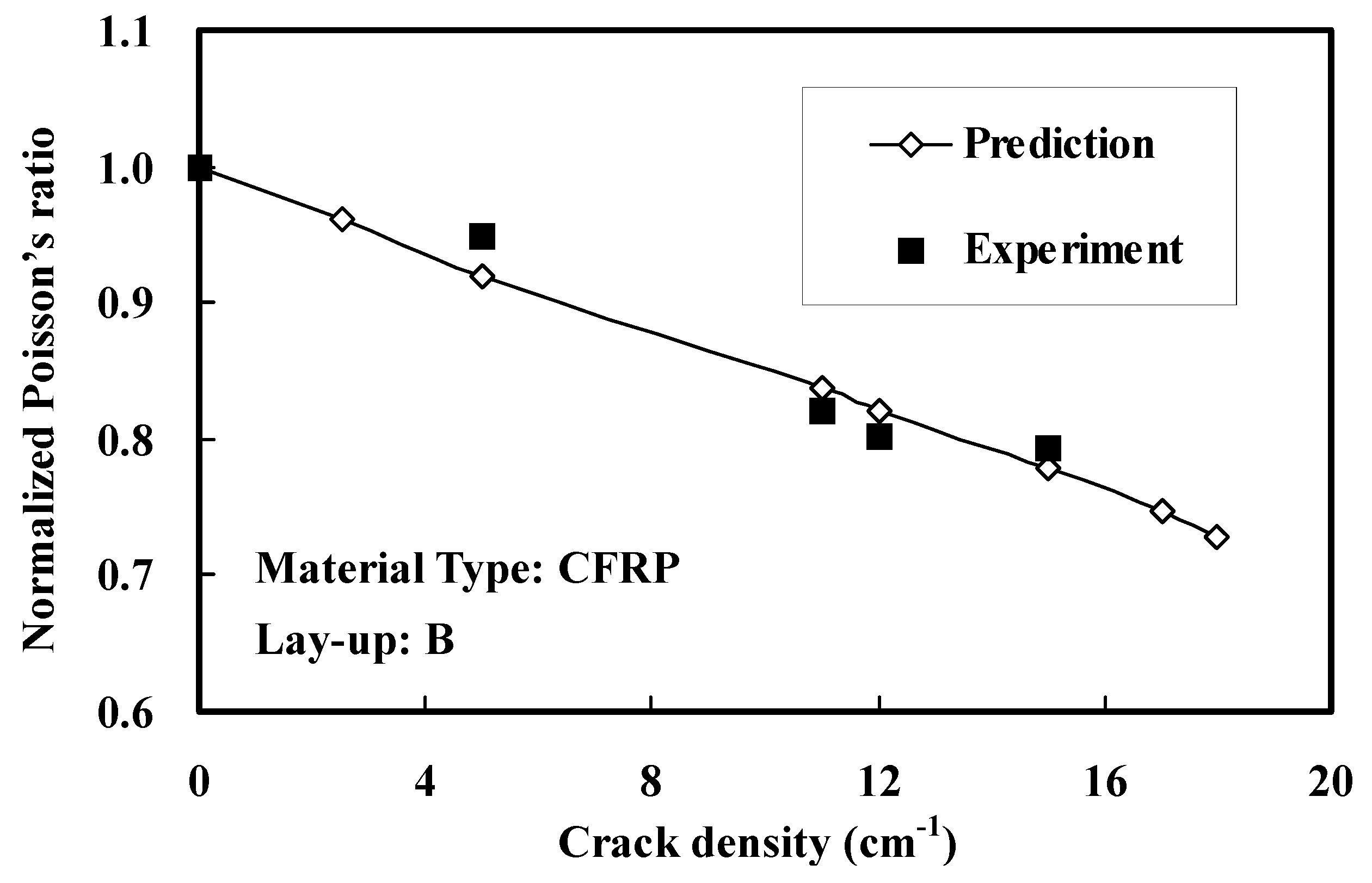
3.2. Analysis of Progressive Cracking
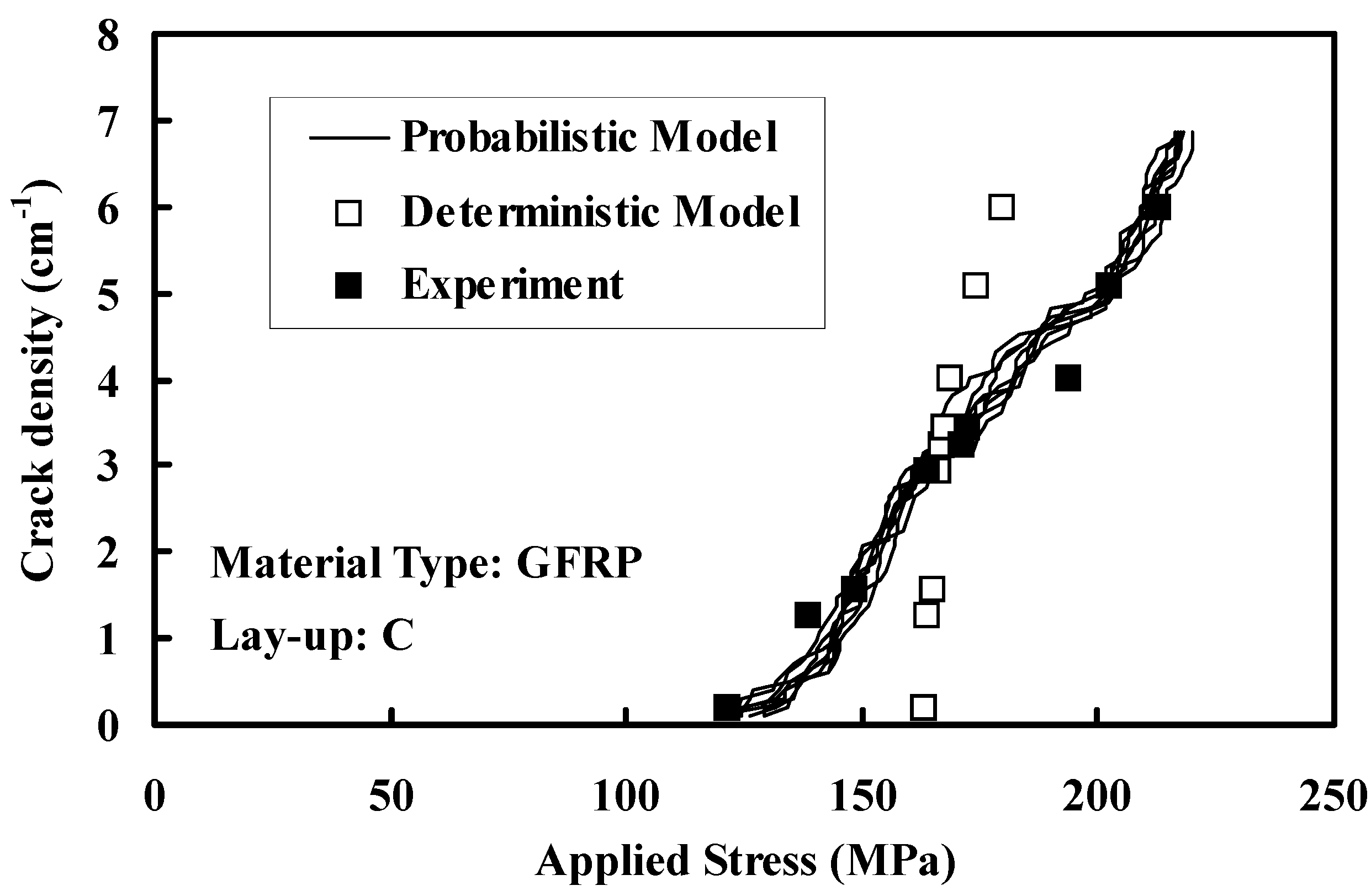
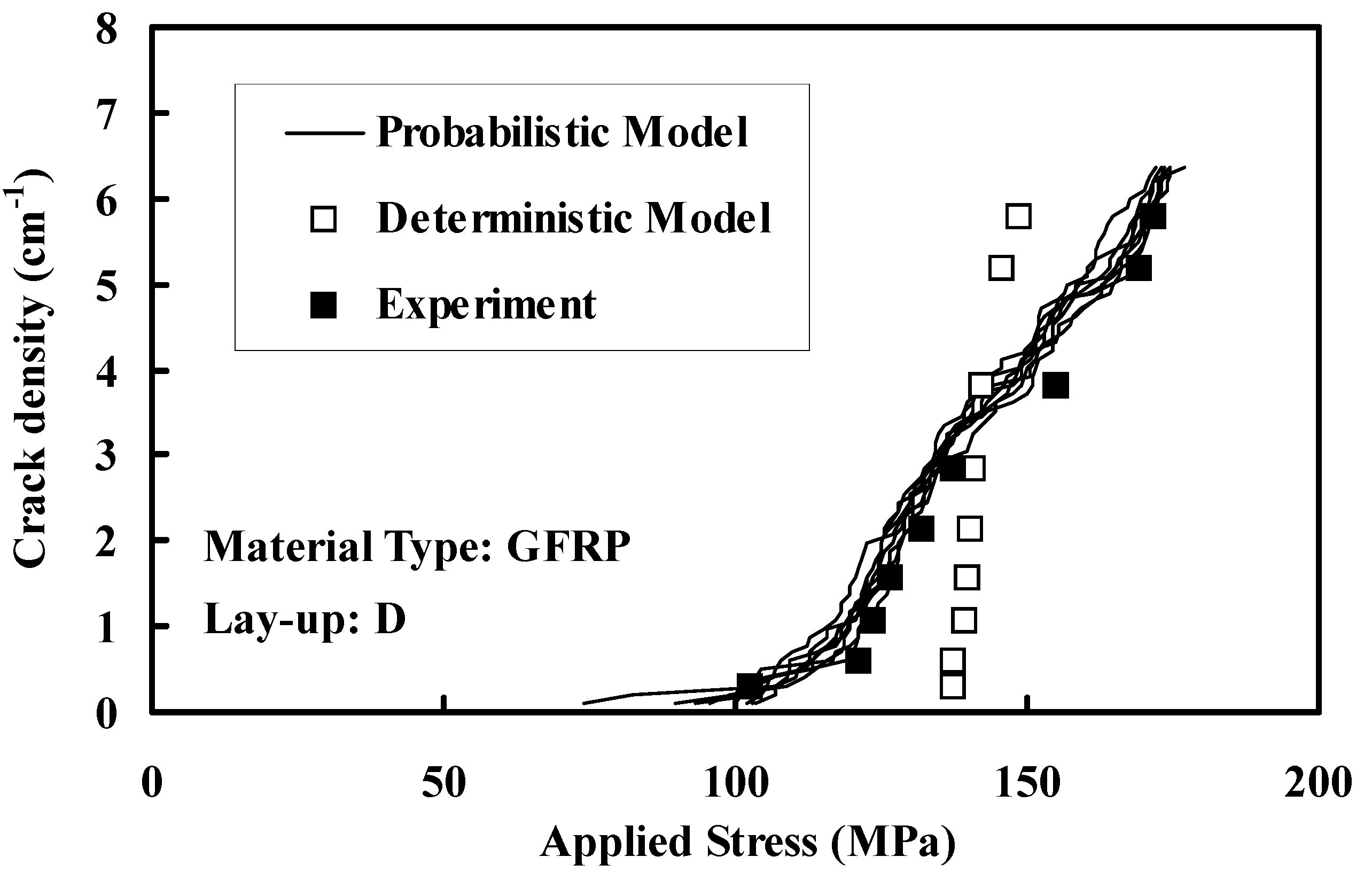
3.3. Estimation of Ultimate Strength
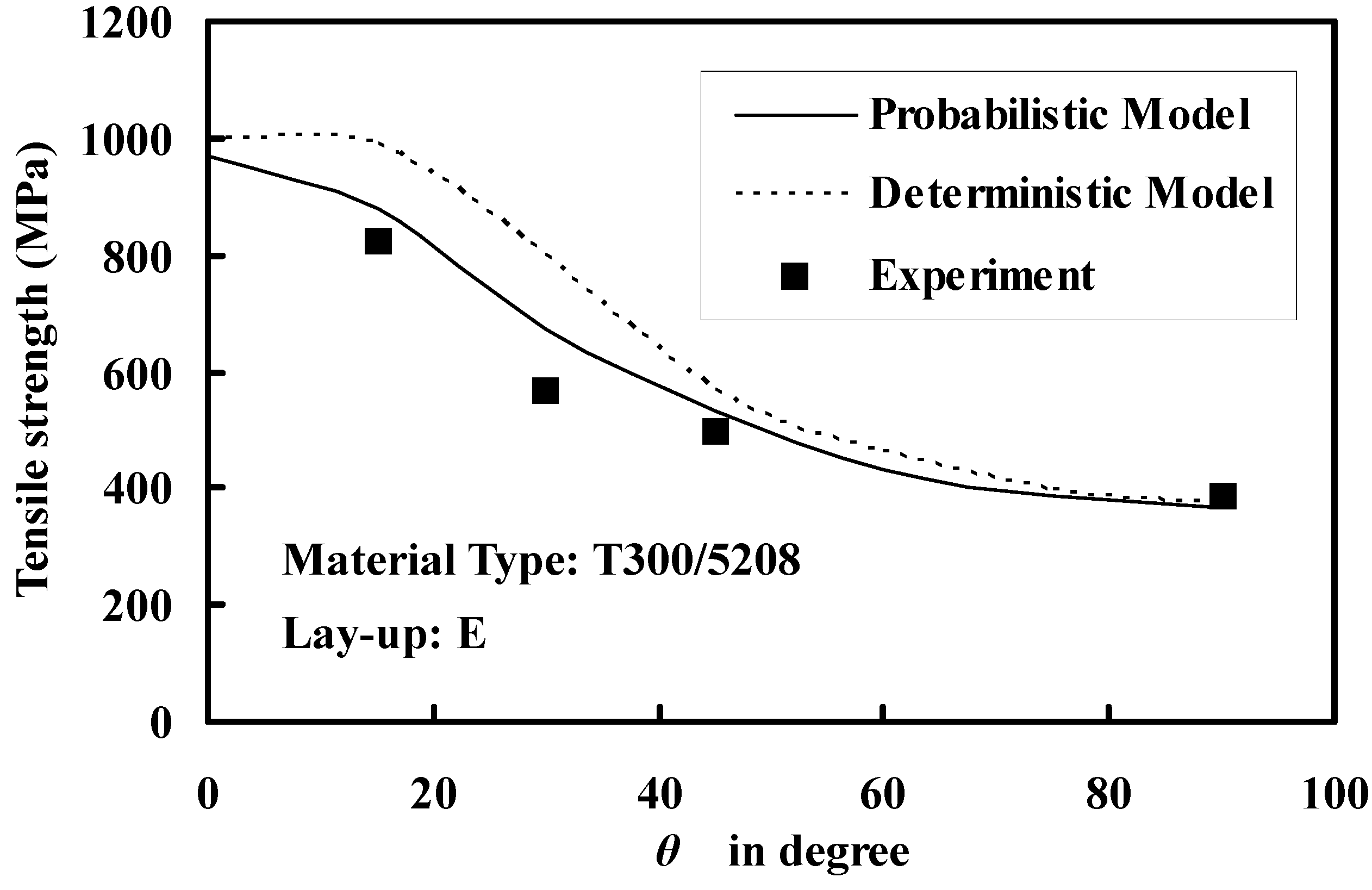
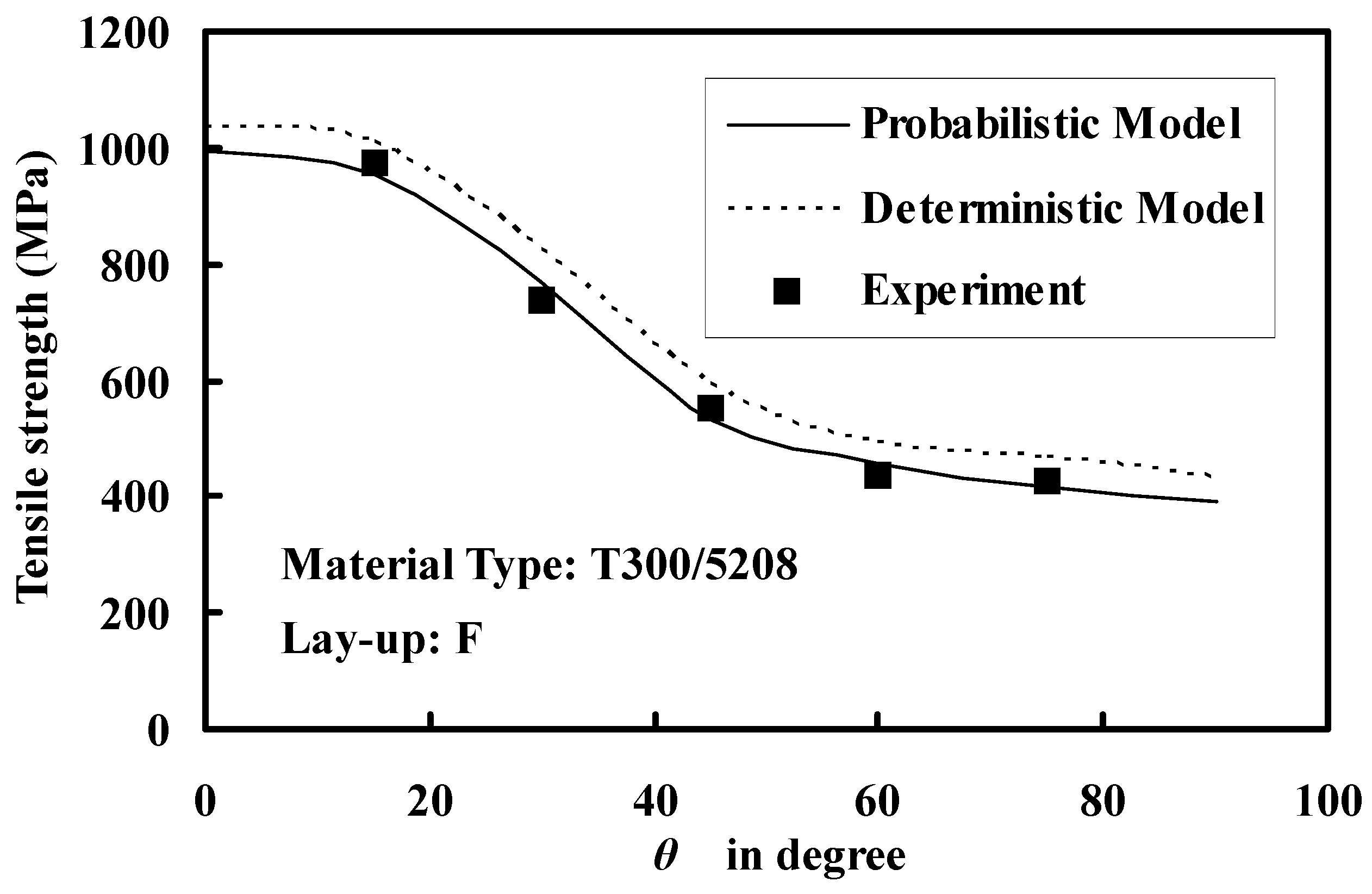
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Kashtalyan, M.; Soutis, C. Stiffness and fracture analysis of laminated composites with off-axis ply matrix cracking. Compos. Part A Appl. Sci. Manuf. 2007, 38, 1262–1269. [Google Scholar] [CrossRef]
- Zhang, J.Q.; Fan, J.H.; Hermann, K.P. Delaminations induced by constrained transverse cracking in symmetric composite laminates. Int. J. Solids Struct. 1999, 36, 813–846. [Google Scholar] [CrossRef]
- Okabe, T.; Nishikawa, M.; Takeda, N. Numerical modeling of progressive damage in fiber reinforced plastic cross-ply laminates. Compos. Sci. Technol. 2008, 68, 2282–2289. [Google Scholar] [CrossRef]
- Reifsnider, K.L.; Stinchcomb, W.W. A Critical-Element Model of the Residual Strength and Life of Fatigue-Loaded Composite Coupons. In Composite Materials: Fatigue and Fracture; Hahn, H.T., Ed.; ASTM STP 907, American Society for Testing and Materials: Philadephia, PA, USA, 1986; pp. 298–313. [Google Scholar]
- Kashtalyan, M.; Soutis, C. The effect of delaminations induced by transverse cracks and splits on stiffness properties of composite laminates. Compos. Part A Appl. Sci. Manuf. 2000, 31, 107–119. [Google Scholar] [CrossRef]
- Hashin, Z. Analysis of cracked laminates: A variational approach. Mech. Mater. 1985, 4, 121–136. [Google Scholar] [CrossRef]
- Kang, K.W.; Lim, D.M.; Kim, J.K. Probabilistic analysis for the fatigue life of carbon/epoxy laminates. Compos. Struct. 2008, 85, 258–264. [Google Scholar] [CrossRef]
- Liu, P.F.; Chu, J.K.; Liu, Y.L.; Zheng, J.Y. A study on the failure mechanism of carbon fiber/epoxy composite laminates using acoustic emission. Mater. Des. 2012, 37, 228–235. [Google Scholar] [CrossRef]
- Alfaro, M.V.C.; Suiker, A.S.J.; Borst, R.D.; Remmers, J.J.C. Analysis of fracture and delamina-tion in laminates using 3D numerical modelling. Eng. Fract. Mech. 2009, 76, 761–780. [Google Scholar] [CrossRef]
- Lee, J.W.; Daniel, I.M. Progressive transverse cracking of cross ply composite laminates. J. Compos. Mater. 1990, 24, 1225–1243. [Google Scholar] [CrossRef]
- Joffe, R.; Krasnikovs, A.; Varna, J. COD-based simulation of transverse cracking and stiffness reduction in [S/90n]s laminates. Compos. Sci. Technol. 2001, 61, 637–656. [Google Scholar] [CrossRef]
- Berthelot, J.M.; Le Corre, J.F. Statistical analysis of the progression of transverse cracking and delamination in cross-ply laminates. Compos. Sci. Technol. 2000, 60, 2659–2669. [Google Scholar] [CrossRef]
- Hinton, M.J.; Kaddour, A.S.; Soden, P.D. Evaluation of failure prediction in composite laminates: Background to ‘part B’ of the exercise. Compos. Sci. Technol. 2002, 62, 1481–1488. [Google Scholar] [CrossRef]
- Soden, P.D.; Hinton, M.J.; Kaddour, A.S. Biaxial test results for strength and deformation of a range of E-glass and carbon fiber reinforced composite laminates: Failure exercise benchmark data. Compos. Sci. Technol. 2002, 62, 1489–1514. [Google Scholar] [CrossRef]
- Liu, K.S.; Tsai, S.W. A progressive quadratic failure criterion for a laminate. Compos. Sci. Technol. 1998, 58, 1023–1032. [Google Scholar] [CrossRef]
- Hinton, M.J.; Kaddour, A.S.; Soden, P.D. A comparison of the predictive capabilities of current failure theories for composite laminates, judged against experimental evidence. Compos. Sci. Technol. 2002, 62, 1725–1797. [Google Scholar] [CrossRef]
- Maimi, P.; Camanho, P.P.; Mayugo, J.A.; Turon, A. Matrix cracking and delamination in laminated composites. Part I: Ply constitutive law, first ply failure and onset of delamination. Mech Mater. 2011, 43, 169–185. [Google Scholar] [CrossRef]
- Zhang, J.Q.; Herrmann, K.P. Stiffness degradation induced by multiplayer intralaminar cracking in composite laminates. Compos. Part A Appl. Sci. Manuf. 1999, 30, 683–706. [Google Scholar] [CrossRef]
- Zhang, J.Q.; Herrmann, K.P.; Fan, J.H. A theoretical model of matrix cracking in composite laminates under thermomechanical loading. Acta Mech. Solida Sinica 2001, 14, 299–305. [Google Scholar]
- Wang, F.; Zhang, J.Q.; Li, L.; Chen, Z.Q. ECM-Based Statistical Simulation of Progressive Failure in Symmetric Laminates Damaged by Transverse Ply Cracking. In Proceedings of the 13th International Conference on Fracture, Beijing, China, 16–21 June 2013; Yu, S.W., Feng, X.Q., Eds.; China Science Literature Publishing House: Hongkong, 2013; p. 226. [Google Scholar]
- Zhang, J.Q.; Soutis, C.; Fan, J.H. Effects of matrix cracking and hygrothermal stresses on the strain energy release rate for edge delamination in composite laminates. Composites 1994, 25, 27–35. [Google Scholar] [CrossRef]
- Zhang, J.Q.; Fan, J.H.; Soutis, C. Analysis of multiple cracking in [±θm/90n]s composite laminates. Part Ι: In-plane stiffness properties. Composites 1992, 23, 291–298. [Google Scholar] [CrossRef]
- Zhang, J.Q.; Fan, J.H.; Soutis, C. Analysis of multiple cracking in [±θm/90n]s composite laminates. Part II: Development of transverse ply crack. Composites 1992, 23, 299–304. [Google Scholar] [CrossRef]
- Kashtalyan, M.; Soutis, C. Stiffness degradation in cross-ply laminates damaged by transverse cracking and splitting. Compos. Part A Appl. Sci. Manuf. 2000, 31, 335–351. [Google Scholar] [CrossRef]
- Herrmann, K.P.; Zhang, J.Q.; Fan, J.H. An energy-based statistical model for multiple fractures in composite laminates. Int. J. Multiscale Comput. Eng. 2003, 1, 327–347. [Google Scholar] [CrossRef]
- Wang, F.; Zeng, X.G.; Zhang, J.Q. Predictive approach to the failure of composite laminates with equivalent constraint model. Acta Mech. Solida Sinica 2010, 23, 230–247. [Google Scholar]
- Irwin, G.R. Fracture. In Handbuch der Physik VI; Flugge, S., Ed.; Springer-Verlag: Berlin, Germany, 1958; pp. 551–590. (in German) [Google Scholar]
- Bažant, Z.P. Size effect on structural strength: A review. Arch. Appl. Mech. 1999, 69, 703–725. [Google Scholar] [CrossRef]
- Sutherland, L.S.; Shenoi, R.A.; Lewis, S.M. Size and scale effects in composites: I. Literature review. Compos. Sci. Technol. 1999, 59, 209–220. [Google Scholar] [CrossRef]
- Joffe, R.; Varna, J. Analytical modeling of stiffness reduction in symmetric and balanced laminates due to cracks in 90° layers. Compos. Sci. Technol. 1999, 59, 1641–1652. [Google Scholar] [CrossRef]
- Han, Y.M.; Hahn, H.T. Ply cracking and property degradations of symmetric balanced laminates under general in-plane loading. Compos. Sci. Technol. 1989, 35, 377–397. [Google Scholar] [CrossRef]
- Smith, P.A.; Wood, J.R. Poisson’s ratio as a damage parameter in the static tensile loading of simple crossply laminates. Compos. Sci. Technol. 1990, 38, 85–93. [Google Scholar] [CrossRef]
- Wang, F.; Li, L.; Chen, Z.Q.; Zeng, X.G. Statistical modeling for the accumulation of transverse matrix cracking in cross-ply laminates. Polym. Compos. 2012, 33, 912–917. [Google Scholar] [CrossRef]
- Zou, Z.H. Structure and Properties of Composites, 1st ed.; Science Press: Beijing, China, 1999; pp. 402–526. [Google Scholar]
- McCartney, L.N. Energy-based prediction of progressive ply cracking and strength of general symmetric laminates using an homogenisation method. Compos. Part A: Appl. Sci. Manuf. 2005, 36, 119–128. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Wang, F.; Ding, J.; Chen, Z. Statistical Analysis of the Progressive Failure Behavior for Fiber-Reinforced Polymer Composites under Tensile Loading. Polymers 2014, 6, 145-159. https://doi.org/10.3390/polym6010145
Wang F, Ding J, Chen Z. Statistical Analysis of the Progressive Failure Behavior for Fiber-Reinforced Polymer Composites under Tensile Loading. Polymers. 2014; 6(1):145-159. https://doi.org/10.3390/polym6010145
Chicago/Turabian StyleWang, Fang, Jun Ding, and Zhiqian Chen. 2014. "Statistical Analysis of the Progressive Failure Behavior for Fiber-Reinforced Polymer Composites under Tensile Loading" Polymers 6, no. 1: 145-159. https://doi.org/10.3390/polym6010145