Diffusion-Enhanced Förster Resonance Energy Transfer in Flexible Peptides: From the Haas-Steinberg Partial Differential Equation to a Closed Analytical Expression

Abstract

In the huge field of polymer structure and dynamics, including intrinsically disordered peptides, protein folding, and enzyme activity, many questions remain that cannot be answered by methodology based on artificial intelligence, X-ray, or NMR spectroscopy but maybe by fluorescence spectroscopy. The theory of Förster resonance energy transfer (FRET) describes how an optically excited fluorophore transfers its excitation energy through space to an acceptor moiety—with a rate that depends on the distance between donor and acceptor. When the donor and acceptor moiety are conjugated to different sites of a flexible peptide chain or any other linear polymer, the pair could in principle report on chain structure and dynamics, on the site-to-site distance distribution, and on the diffusion coefficient of mutual site-to-site motion of the peptide chain. However, the dependence of FRET on distance distribution and diffusion is not defined by a closed analytical expression but by a partial differential equation (PDE), by the Haas-Steinberg equation (HSE), which can only be solved by time-consuming numerical methods. As a second complication, time-resolved FRET measurements have thus far been deemed necessary. As a third complication, the evaluation requires a computationally demanding but indispensable global analysis of an extended experimental data set. These requirements have made the method accessible to only a few experts. Here, we show how the Haas-Steinberg equation leads to a closed analytical expression (CAE), the Haas-Steinberg-Jacob equation (HSJE), which relates a diffusion-diagnosing parameter, the effective donor–acceptor distance, to the augmented diffusion coefficient, J, composed of the diffusion coefficient, D, and the photophysical parameters that characterize the used FRET method. The effective donor–acceptor distance is easily retrieved either through time-resolved or steady-state fluorescence measurements. Any global fit can now be performed in seconds and minimizes the sum-of-square difference between the experimental values of the effective distance and the values obtained from the HSJE. In summary, the HSJE can give a decisive advantage in applying the speed and sensitivity of FRET spectroscopy to standing questions of polymer structure and dynamics.

1. Introduction

There is no question about the significance of fluorescence in multiple molecular investigations; its speed and sensitivity even enable investigations on the level of the single molecule [1]. There is also no question about the significance of Förster resonance energy transfer in structural and dynamic molecular studies as the number of citations to Förster’s original paper approaches 10,000 [2]. We believe that diffusion-enhanced fluorescence resonance energy transfer, or DFRET, on the molecule ensemble can also develop into an influential method but is, as of now, difficult to handle and non-transparent in terms of data acquisition and analytics [3,4,5,6,7,8,9,10,11,12,13,14]. This article aims to make DFRET accessible to any scientist working in one of the many fields of polymer structure and dynamics. Here, we would like to point out that the Supporting Information file we have created contains assisting information in regard to different audiences: the layman, the expert, and, especially, the scientist who wants to put our method to work.

When a protein or peptide, or any molecule, has been modified at two sites with two fluorophoric moieties, one moiety can act as FRET donor and the other as FRET acceptor. When the intermittent chain between these sites is flexible, the optically excited donor and the acceptor can approach each other by diffusional motion. In accordance with Förster’s law (Equation (1)), the probability of energy transfer from donor to acceptor increases. Förster’s law connects the distance-dependent transfer rate constant, k_T(r), with the rate constant of deactivation in the donor-only peptide, k_D, with the Förster distance, R₀, a constant that characterizes the donor-acceptor pair, and with the donor–acceptor distance, R_DA.

$$k_{\mathrm{T}}=k_{\mathrm{D}}{\left(\frac{R_0}{R_{\mathrm{DA}}}\right)}^6$$

(1)

Figure 1 gives a survey of the processes relevant in DFRET.

After excitation, the excited donor (D) can become deactivated in one of three ways: by emitting fluorescence with the rate constant k_rad (“k_radiative”); by being quenched, for instance by iodine ions, with the rate constant k_nrad (“k_{non-radiative}”); or by transferring its excitation energy to the acceptor (A) with the rate constant k_FRET. In experimental measurements, we always use the donor-acceptor peptide (the DA-peptide) together with the “donor-only” peptide (the D-peptide). If no acceptor is present but only the donor, the measured rate of deactivation is k_D = k_rad + k_nrad (Figure 1; (I)). In the donor-acceptor peptide, in presence of an acceptor, the measured rate is k_DA = k_rad + k_nrad + k_FRET (Figure 1, (II)). Subtracting (I) from (II) yields the effective FRET rate, k_FRET, k_FRET = k_DA − k_D (Equation (2)). In any normal situation, k_FRET increases with increasing diffusional motion between donor and acceptor. During the lifetime of the donor fluorescence, donor and acceptor can approach each other, and the probability of the FRET event increases in accordance with Förster’s law (Equation (1)), where k_T is the distance-dependent Förster transfer rate constant at a specific donor–acceptor distance, R_DA. Consequently, k_FRET increases with diffusion, and the effective distance derived from k_FRET (Figure 1, (III), (IV), Equations (3) and (4)) decreases. In summary, the effective distance (Equation (4)) is a suitable diagnostic parameter to measure the diffusion enhancement of FRET. The effective distance serves as the interface between experiment and theory, that is, between the experimental results and the numerical solutions of the Haas-Steinberg equation (HSE). To restate, the effective distance is obtained experimentally from steady-state or time-resolved measurements on the peptide equipped with donor and acceptor, the “DA-peptide” (see Figure 1), and the peptide equipped only with the donor, the “D-peptide”. Measurements on the DA-peptide yield the fluorescence intensity, I_DA, in steady-state experiments or the fluorescence decay rate, k_DA, in time-resolved experiments, while measurements on the D-peptide yield I_D or k_D. Exemplary chemical structures (Figure S1) and kinetics (Figure S2a,b) are given in the Supporting Information, Chapter 3.

$$k_{\mathrm{FRET}}=k_{\mathrm{DA}}-k_{\mathrm{D}}$$

(2)

$$k_{\mathrm{FRET}}=k_{\mathrm{D}}{\left(\frac{R_0}{R_{\mathrm{eff}}}\right)}^6$$

(3)

$$R_{\mathrm{eff}}=k_{\mathrm{D}}{\left(\frac{R_0}{k_{\mathrm{FRET}}}\right)}^{1/6}$$

(4)

Introduction to the Haas-Steinberg Equation

The story of diffusion-enhanced FRET or DFRET started 40 years ago [3]. Since then, the number of published articles based on DFRET has remained small, not for lack of interest but for the method’s complexity [4,5,6,8,10,11,12,13,14]. In 1978, Steinberg derived what we began to call the Haas-Steinberg equation (HSE) [3]. Haas and co-workers developed unique techniques and used the HSE to tackle fundamental biological questions in protein folding, enzyme activity, and, more recently, in regard to intrinsically disordered peptides [3,5,10,11,15].

The HSE allows the calculation of theoretical effective distances. These theoretical or predicted values of HSE-based effective distances can then be fitted to the experimentally observed values in a multivariate analysis; in a global fit, that yields structure, i.e., the distance distribution, p(r), as well as dynamics, i.e., the diffusion coefficient, D.

In this work, we show how the HSE leads to a closed analytical equation, the HSJE (Haas-Steinberg-Jacob equation) by going through four equivalence statements (ES1-4). The HSJE eases and accelerates any global analysis, and, in addition, provides insight into the role of each parameter participating in DFRET.

2. Materials and Methods

The HSE was solved numerically by using the finite element method implemented in the PDE toolbox of MATLAB 2020 (MathWorks). The results from MATLAB calculations were analyzed within MATLAB 2020 and Microsoft Excel (Mac 2011). Figures were produced by using ProFit (QuantumSoft). For the global fits based on the HSJE and presented in the Supporting Information, Chapter 8, Figures S6 and S7, we used Microsoft Excel and its Solver add-in.

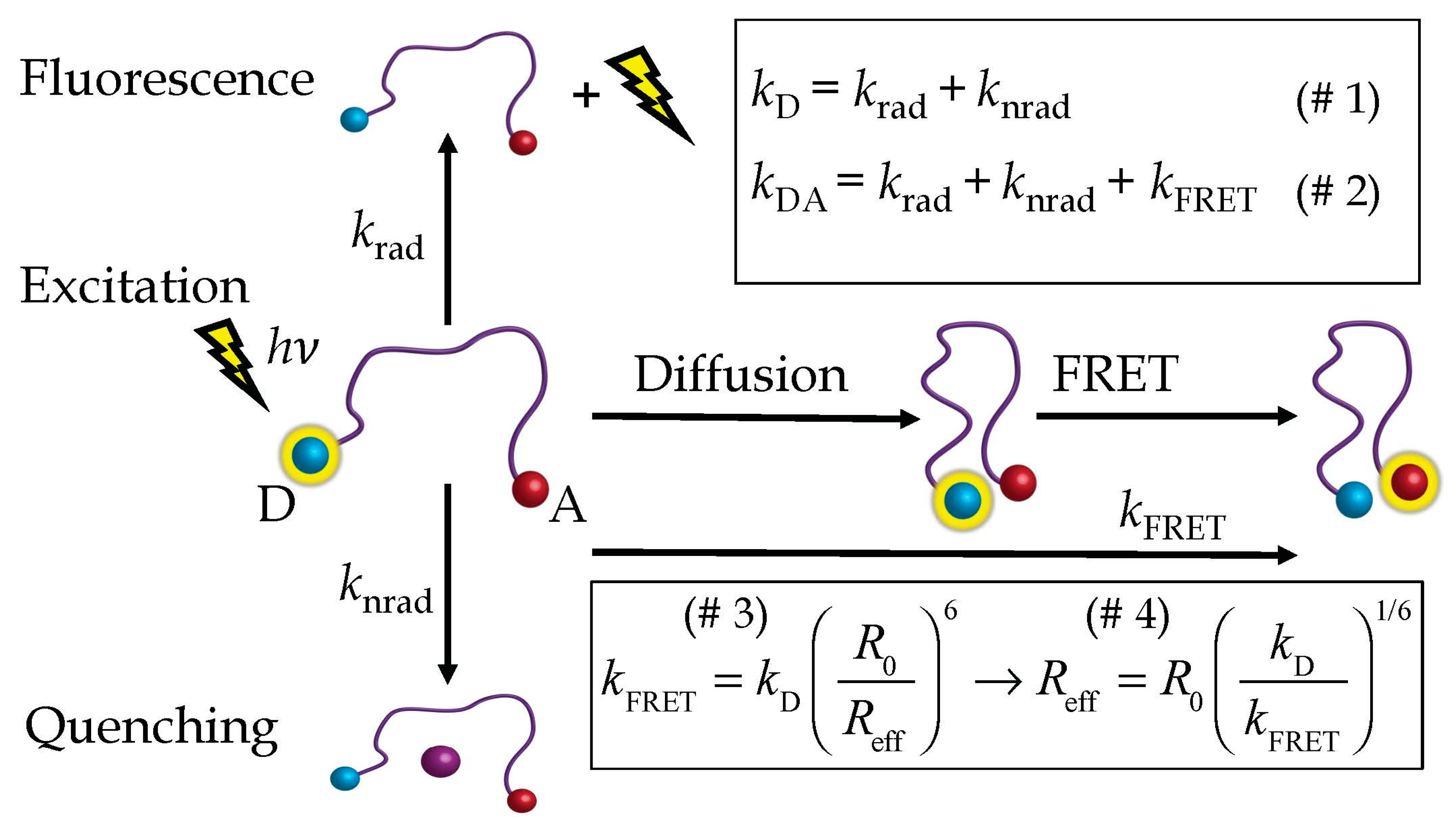
2.1. The HSE

The HSE can be written in various ways; we have specifically chosen the version shown in Equation (5).

$$\frac{\partial N\left(r,t\right)}{\partial t}=-\frac{1}{{\tau }_{\mathrm{D}}}N\left(r,t\right)-\frac{1}{{\tau }_{\mathrm{D}}}\frac{R_0^6}{r^6}N\left(r,t\right)+\frac{\partial }{\partial r}\left(N_0\left(r\right)D\frac{\partial \left(N/N_0\right)}{\partial r}\right)$$

(5)

In Equation (5), we focus on the donor fluorescence lifetime, τ_D, instead of the donor deactivation rate constant, k_D, used in Figure 1 (Equation (I): k_D = k_rad + k_nrad). It is much easier to recall the value of a lifetime, for instance, 100 ns, than that of a rate constant, for instance, 0.01 ns⁻¹. The donor lifetime in the donor-only peptide, τ_D, is simply the inverse of the rate constant, k_D, in this peptide (Equation (6)).

$${\tau }_{\mathrm{D}}=k_{\mathrm{D}}^{-1}$$

(6)

Our shorthand notation for the HSE will simply be “(0) = (1) + (2) + (3)”, which enables us to address the left-hand-side term of the equation with term-(0) and the right-hand-side terms of the equation with terms-(1), -(2), and -(3). The function, N(r,t), on the left-hand side is a measure of the number of chains with excited donor after donor excitation. At a specific donor–acceptor distance, r, this number decreases with time, t. Thus, we have two independent variables, r and t, and, therefore, a partial differential equation, a PDE. N(r,t) is further normalized in a way that N₀ = N(r, t = 0) in term-(3) is the initial probability density distance distribution. Upon irradiation, donors become activated with a probability assumed to be random, to be independent of the presence of an acceptor at various distances. In consequence, N₀ is identical to the equilibrium distance distribution, p(r), of all chains present in the measurement sample. This distance distribution, p(r), as well as the site-to-site diffusion coefficient, D, in term-(3), is what we are interested in. They inform us on the structure and the dynamics of the (bio)polymer under investigation.

In summary, the HSE is a linear partial differential equation of second order: The second derivative becomes better visible on expansion of term-(3). Further, the HSE has constant coefficients that include the parameters, D, τ_D, and R₀. The HSE relates the rate of donor deactivation, term-(0); to the rate of donor deactivation in the absence of FRET, term-(1); plus the additional rate due to FRET, term-(2); plus the additional rate due to diffusion enhanced FRET, term-(3). A numerically obtained solution of the HSE yields the value of the effective distance between donor and acceptor. We elaborate on this calculation in Supporting Information, Chapter 4, Figure S3a–i.

2.2. Steinberg’s Derivation

Steinberg’s derivation of the HSE led him first to the following form (Equation (7)) [3].

$$\frac{\partial N\left(r,t\right)}{\partial t}=-k_{\mathrm{D}}N\left(r,t\right)-k_{\mathrm{D}}\frac{R_0^6}{r^6}N\left(r,t\right)+\frac{\partial }{\partial r}\left(N_0\left(r\right)D\frac{\partial \left(N/N_0\right)}{\partial r}\right)$$

(7)

Here, the diffusion coefficient, D, in term-(3) does not depend on time, t, but it could still depend on the donor–acceptor distance, r: D = f(r). It is, however, even today, challenging to gather sufficient experimental results to investigate this possible dependence. Steinberg was content with an average diffusion coefficient that can be regarded as a constant. Then, D can be written in front of term-(3) (Equation (8)).

$$\frac{\partial N\left(r,t\right)}{\partial t}=-k_{\mathrm{D}}N\left(r,t\right)-k_{\mathrm{D}}{\left(\frac{R_0}{r}\right)}^{6}N\left(r,t\right)+D\frac{\partial }{\partial r}\left(N_0\left(r\right)\frac{\partial \left(N/N_0\right)}{\partial r}\right)$$

(8)

When we apply Equation (6), we again obtain the HSE in the form of Equation (5). In summary, we know how to obtain R_eff from experiments as well as from numerically solving the HSE. We can therefore use the HSE to globally fit the experimental data. This was quite arduous in the past, where the HSE served a bit as a black box [5,6,10,11,12,13,14]. In the Results Section, we develop the Haas-Steinberg–Jacob equation (HSJE), a closed analytical expression (CAE). Any global fit based not on the HSE (PDE) but on the HSJE (CAE) is faster by about two orders of magnitude.

3. Results

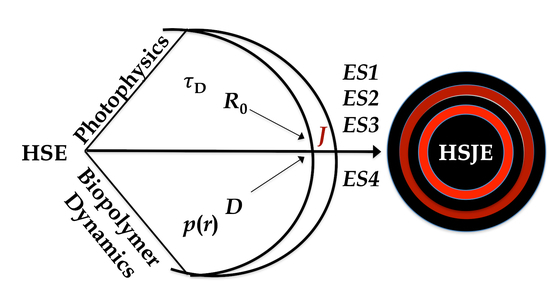
3.1. Ideas and Concepts

We first outline the basic ideas and concepts. Based on a freely selected distance distribution (Figure 2a) and selected values for the donor lifetime and Förster distance, τ_D and R₀, we solved the HSE for a large range of values of the diffusion coefficient reaching from 10⁻³ to 10⁶ Ų/ns. The obtained effective-distance values formed a full diffusion profile, ranging from the “static limit” in the near absence of diffusion to the “dynamic limit” at high diffusion. In figures and graphs, we always plotted the effective distance against the square root of the diffusion coefficient or, later, against the square root of the “augmented diffusion coefficient” to keep the x-axis numbers or labels manageably small and readable (Figure 2b).

We have analytical equations for both extremes of the diffusion influence (Equations (9) and (10)): The “left” value, L, of the effective distance marks the static limit or the case of no diffusion (Equation (9)), as we first derived in the Supporting Information of reference [12]. The “right” value, R, of the effective distance marks the dynamic limit or the case of infinite diffusion (Equation (10)) [12,16] The derivations of the L- and R-equations can be found in this article’s Supporting Information, Chapters 4 and 4a,b. Explanations of the two underlying basic concepts, “the Energy Transfer Efficiency” and “the Average”, can be found in in the Supporting Information, Chapters 3 and 3a,b. At first glance, these equations appear to be quite complex, but, because of their analytical character, L and R are calculated within Matlab or Excel in a fraction of a second. We note that L is a function of the Förster radius and the distance distribution, while R is a function of only the distance distribution. Further, we note that any integration of p(r) takes place from the left-integration limit, r_L, to the right-integration limit, r_R. A physical but oversimplified perspective is to view r_L as the closest possible distance between donor and acceptor.

$$L=R_{\mathrm{eff},D\to 0}=R_0{\left({\left(1-{\displaystyle \underset{r_{\mathrm{L}}}{\overset{r_{\mathrm{R}}}{\int }}p(r)\left(\frac{r^6}{r^6+R_0^6}\right)\mathrm{d}r}\right)}^{-1}-1\right)}^{1/6}$$

(9)

$$R=R_{\mathrm{eff},D\to \infty }={\langle r^{-6}\rangle }^{-1/6}={\left({\displaystyle \underset{r_{\mathrm{L}}}{\overset{r_{\mathrm{R}}}{\int }}\left(1/r^6\right)p(r)\mathrm{d}r}\right)}^{-1/6}$$

(10)

As we have these analytical equations for the static and dynamic limit of the effective distance, the L and R values are supposed to be extremely close to the effective-distance values at the start and end of the numerically obtained diffusion profile (Figure 2b). This demands virtual identity of the analytically and numerically obtained values that always served as the first important control indicating that the numerical simulations were properly executed. We now use the L- and R-values to normalize the diffusion profiles: Equation (11) defines the diffusion influence DI. It goes from 0 or 0%, when R_eff approaches L, to 1 or 100%, when R_eff approaches R (Figure 2c). Thus, we distinguish in Figure 2 between the diffusion profiles, the R_eff(D) or R_eff(D^1/2) profiles (Figure 2b), and the diffusion-influence profiles, the DI(D) or DI(D^1/2) profiles (Figure 2c), or the DI(J), DI(J^1/2), or DI(X) profiles (Figure 2d) after we discovered that the decisive independent variable, the decisive x-variable, is not D but J or its square root, X (Equation (12)).

$$DI=\frac{R_{\mathrm{eff}}-L}{R-L}$$

(11)

In our quest for the HSJE, for an analytic equation that captures all possible diffusion profiles, we systematically varied the initial distance distribution as well as all coefficients of the HSE. Doing that, we found that, as mentioned, the appropriate independent variable is not the diffusion coefficient, D, but what we now call the augmented diffusion coefficient, J, composed of three coefficients: the diffusion coefficient, the donor lifetime, and the Förster radius (Equation (12)). Remarkably, J is dimensionless. To repeat, we address plots of DI versus J or its square root, X = J^1/2, as diffusion-influence profiles, as DI, DI(J), or DI(X) profiles.

$$J=\frac{D{\tau }_{\mathrm{D}}}{R_0^2};X=\sqrt{J}=\frac{\sqrt{D{\tau }_{\mathrm{D}}}}{R_0}$$

(12)

We found that all DI-profiles are sigmoids that can be fitted to Equation (13), where X⁰ = J^1/2. The value X⁰ is the X value where DI = 50%; the M value describes the steepness of the sigmoid.

$$DI\left(X\right)=\frac{{\left(X/X_0\right)}^M}{1+{\left(X/X_0\right)}^M}$$

(13)

The sigmoidal profiles obtained from the HSE solutions appear to be perfectly point symmetrical around the point (X₀, 50%) provided that a logarithmic scale is chosen for the x-axes or, equivalently, that DI is plotted against lnX. The numerically obtained profiles could then be perfectly fitted according to Equation (13). Thus, we are convinced that any DI profile follows a symmetrical sigmoid in accordance with Equation (13). This requirement of sigmoidal symmetry served as the second important control that indicates correctly performed numerical simulations. Equations (12) and (13), in combination, yield Equation (14), a first raw form of the HSJE.

In the course of our investigation, we discovered and formulated four equivalence statements that led us from D as the independent variable in the diffusion profiles, to J or its square root, X, as independent variables in the diffusion-influence profiles. We learned that the parameters X₀ and M in Equation (13) are functions of just a single variable, of the ratio of the Förster radius and the left-integration limit, of R₀/r_L. Thus, in the last step, we completed the HSJE by numerical work to determine how X₀ and M depend on R₀/r_L.

$$R_{\mathrm{eff}}=\frac{{\left(X/X_0\right)}^M}{1+{\left(X/X_0\right)}^M}\cdot \left(R-L\right)+L$$

(14)

3.2. The Equivalence Statements

In the following, we always compare effective-distance and diffusion-influence values and profiles obtained from the HSE used with two different sets of inputs that we distinguish by (1) and (2) as superscript. That is, we compare HSE⁽¹⁾ and HSE⁽²⁾, where HSE⁽¹⁾ uses set⁽¹⁾ that consists of the distance distribution, p⁽¹⁾(r), and the values, D⁽¹⁾, τ_D⁽¹⁾, R₀⁽¹⁾, and r_L⁽¹⁾, while HSE⁽²⁾ uses set⁽²⁾ that consists of the distance distribution, p⁽²⁾(r), and the values, D⁽²⁾, τ_D⁽²⁾, R₀⁽²⁾, and r_L⁽²⁾. Accordingly, the augmented diffusion coefficient J⁽¹⁾ equals D⁽¹⁾τ_D⁽¹⁾/(R₀⁽¹⁾)² and J⁽²⁾ equals D⁽²⁾τ_D⁽²⁾/(R₀⁽²⁾)². We also have to distinguish between the two diffusion-influence profiles obtained from HSE⁽¹⁾ and HSE⁽²⁾, between DI⁽¹⁾ and DI⁽²⁾ as functions of J or X, as they usually stem from different distance distributions, p⁽¹⁾(r) and p⁽²⁾(r), that usually come with different L- and R-values, L⁽¹⁾ and R⁽¹⁾ and L⁽²⁾ and R⁽²⁾ (see Equations (9)–(11)).

3.2.1. The First Equivalence Statement: Variation of the Distance Distribution

To expose what happens if we only vary the distance distribution, we have chosen the three distributions shown in Figure 3a. The diffusion profiles that correspond to these distributions and to the chosen photophysical parameters are given in Figure 3b. These profiles are expectedly very different because any specific distance distribution comes with specific L- and R-values (Equations (9) and (10)). However, when we calculate the DI-values by using the L- and R-values characteristic for each distribution (Equation (11)), and normalize the profiles that way, we obtain perfect overlap of the resulting diffusion-influence profiles (Figure 3c). This normalization, the introduction of the diffusion-influence or DI-value defined by Equation 11 opened our path towards the HSJE.

We now express the first equivalence statement (ES1) as text and, then, in formula.

Equivalence Statement 1 (ES1, Text)

“The diffusion-influence profiles of any two well-behaved probability distributions, p⁽¹⁾(r) and p⁽²⁾(r), coincide if they were obtained with the same values of the donor lifetime, τ_D, the Förster radius, R₀, and the left-integration limit, r_L.”

ES1 (formal):

$$\begin{array}{l}\mathrm{For}\mathrm{any}{p}^{(1)}\left(r\right)\mathrm{and}{p}^{(2)}\left(r\right):\mathrm{If}{D}^{(1)}=D^{(2)},{\tau }_{\mathrm{D}}^{\left(1\right)}={\tau }_{\mathrm{D}}^{\left(2\right)},R_0^{\left(1\right)}=R_0^{\left(2\right)},\mathrm{and}{r}_{\mathrm{L}}^{(1)}=r_{\mathrm{L}}^{(2)}\\ \mathrm{then}D{I}^{(1)}\left(J^{\left(1\right)}\right)=D{I}^{(2)}\left(J^{\left(2\right)}\right)\end{array}$$

(15)

Here and in the three following statements, we always use the augmented diffusion coefficient, J, defined by Equation (12), as the independent variable in diffusion-influence or DI profiles. In this first statement, J⁽¹⁾ and J⁽²⁾ are obviously identical, and using J as the independent variable makes no difference versus using D instead, but it fosters the formal parallelism of the four equivalence statements. Two questions arise:

1.

Why do we demand that r_L⁽¹⁾ = r_L⁽²⁾? Why can ES1 not be applied if the left-integration limit differs in both sets?

In case of a smaller left-integration value, the contribution of diffusion to FRET at infinite diffusion is higher. This can be concluded from term-(2) of the HSE (Equation (5)) that encompasses Förster’s law (Equation (1)): At smaller r_L values, FRET becomes faster. As a consequence, higher values of the augmented diffusion coefficient are necessary to reach the dynamic limit in the diffusion-influence profiles. Therefore, the distribution with smaller r_L will lead to a diffusion-influence profile that only later reaches DI values close to 100%. This is further detailed and illustrated in the Supporting Information, Chapter 7b, Figure S4a–c.

2.

Is ES1 valid for any distance distribution equation or model? Or is it only valid for “well-behaved” models?

Prominent model equations that have been chosen in the past to describe end-to-end distance distributions in flexible peptides have been the one-parameter ideal-chain or random-coil model (Equation (16), parameter b) or the two-parameter 3D-Gaussian or skewed-Gaussian model (Equation (17), parameters a and b). The normalization constant, N, is determined through the normalization condition: The integral over p(r) from left to right integration limit has to be unity (see the Supporting Information, Chapter 7c, Equation (S26)).

$$p(r)=N{r}^2\cdot \left(\frac{3}{2\pi b^2}\right)\cdot \exp \left(-\frac{3r^2}{2b^2}\right);b={\langle r^2\rangle }^{1/2}$$

(16)

$$p(r)=N{r}^2\cdot \exp \left(-a\left(b-r^2\right)\right)$$

(17)

Using Equations (16) or (17), we discovered that sometimes the DI-overlap of the profiles of two such distributions became less perfect in case of large discontinuities of the distributions at the point r = r_L, that is, in the case of large jumps of probability-density values from zero to finite values at this point (Supporting Information, Chapter 7c, Figure S5a). In the transition region of the sigmoidal DI-profiles of two such distributions, the DI-value disagreement can become as large as 10%, undermining our efforts to develop a closed analytic equation with precisely determined constants, the HSJE. Further, such discontinuities can hardly be justified by any physical reasoning. This problem was resolved, and complete overlap was restored for all cases when we modified the distribution equations to display continuity of probability-density values at and around r = r_L (Equations (18) and (19)), (Supporting Information, Chapter 7c, Figure S5b). Thus, we proceeded by using only “well-behaved” distribution equations that, by their very nature, guarantee that p(r = r_L) = 0 and guarantee p(r)-value continuity (Equations (18) and (19)).

$$p(r)=N{r}_0^2\cdot \left(\frac{3}{2\pi b^2}\right)\cdot \exp \left(-\frac{3r_0^2}{2b^2}\right);r_0=r-r_{\mathrm{L}}$$

(18)

$$p(r)=N{r}_0^2\cdot \exp \left(-a\left(b-r_0^2\right)\right);r_0=r-r_{\mathrm{L}}$$

(19)

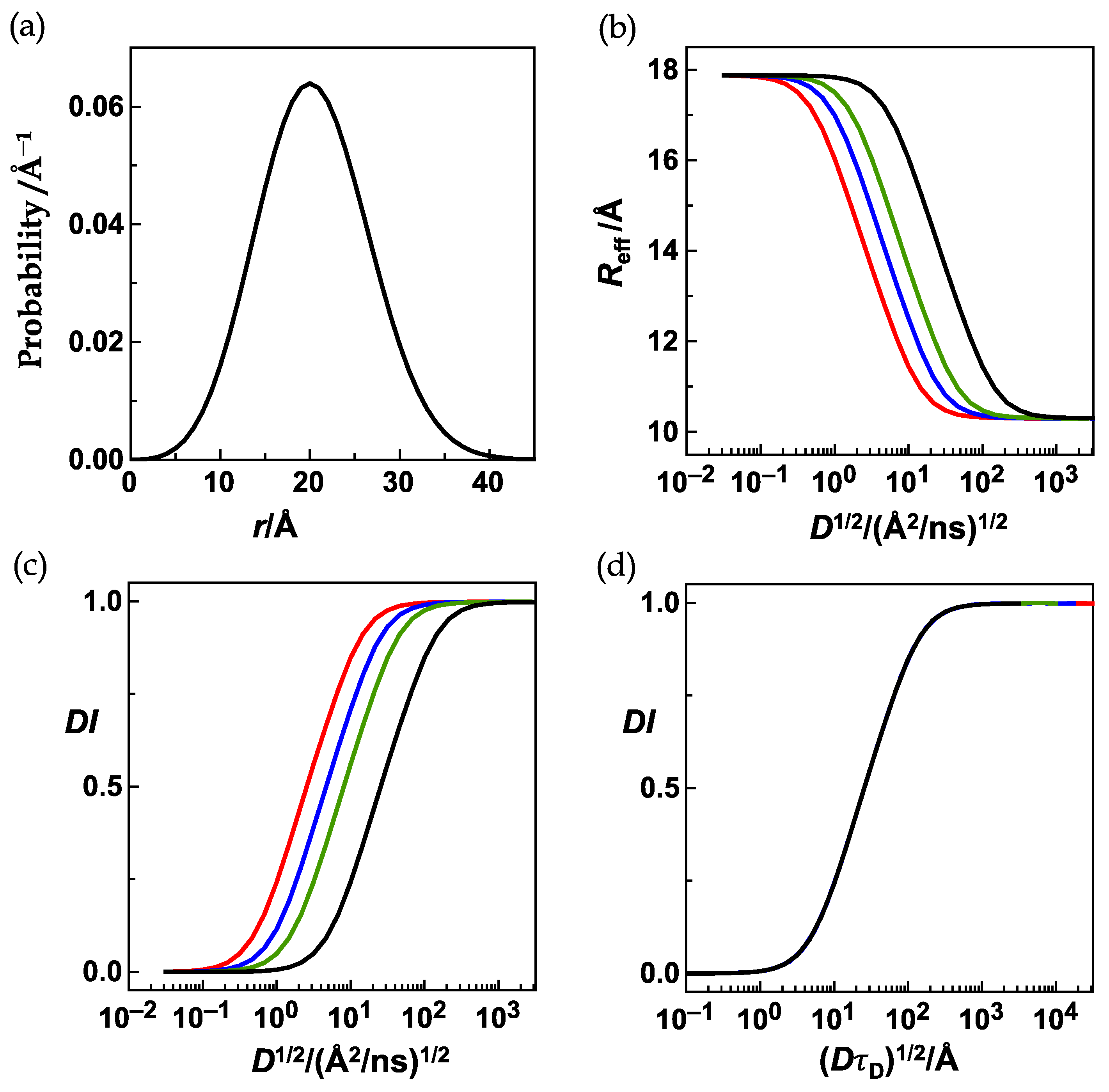
3.2.2. The Second Equivalence Statement: Variation of the Donor Lifetime

Next, we vary the donor lifetime. Figure 4a shows an exemplary distance distribution, and Figure 4b the four diffusion profiles that were obtained for this distribution and for the four donor lifetime values, 100 ns (red curve, left), 30 ns (blue curve), 10 ns (green curve), and 1 ns (black curve, right). All other parameters of the HSE were kept constant. Using the same color code, Figure 4c shows the corresponding diffusion-influence profiles. When we now plot, for each profile, the diffusion-influence value against the product of the diffusion coefficient and the corresponding donor lifetime, 100, 30, 10, or 1 ns, or against the square root of this product, we observe that the four profiles become identical (Figure 4d). Going from the diffusion coefficient, D, to the product D⋅τ_D as the independent variable in diffusion-influence plots is the first of two steps towards the augmented diffusion coefficient, J.

This observed profile identity means that the values of the effective distance obtained from the HSE with input sets, set⁽¹⁾ and set⁽²⁾, that only differ by the diffusion coefficient, D⁽¹⁾ in contrast to D⁽²⁾, and by the donor lifetime, τ_D⁽¹⁾ in contrast to τ_D⁽²⁾, are identical as long as the product D⋅τ_D does not change, that is, as long as it is valid that D⁽¹⁾τ_D⁽¹⁾ = D⁽²⁾τ_D⁽²⁾. We now formulate the second equivalence statement and prove it to be a mathematical consequence of the HSE.

Equivalence Statement 2 (ES2, Text)

“Given any probability distribution: If the diffusion coefficient is varied from D⁽¹⁾ to D⁽²⁾ and the donor lifetime from τ_D⁽¹⁾ to τ_D⁽²⁾, but the product of diffusion coefficient and donor lifetime remains constant, then the diffusion-influence values obtained from the diffusion-influence functions, DI⁽¹⁾(J⁽¹⁾) and DI⁽²⁾(J⁽²⁾), are identical. The corresponding diffusion-influence profiles coincide”.

ES2 (formal):

$$\begin{array}{l}\mathrm{For}\mathrm{any}{p}^{(1)}\left(r\right)=p^{(2)}\left(r\right):\mathrm{If}{D}^{(1)}{\tau }_{\mathrm{D}}^{\left(1\right)}=D^{(2)}{\tau }_{\mathrm{D}}^{\left(2\right)},R_0^{\left(1\right)}=R_0^{\left(2\right)},\mathrm{and}{r}_{\mathrm{L}}^{(1)}=r_{\mathrm{L}}^{(2)}\\ \mathrm{then}D{I}^{(1)}\left(J^{\left(1\right)}\right)=D{I}^{(2)}\left(J^{\left(2\right)}\right)\end{array}$$

(20)

ES2 can be derived in several ways from the HSE (Equation (5)), as detailed in the Supporting Information, Chapter 7d.

Here we opted for a change-of-variable approach applied to the HSE (Equation (5)). We use the fact that any rescaling of time can impossibly affect the value of the effective distance (see Supporting Information, Chapter 7d). We rescale the time with the donor lifetime (Equation (21)) and insert the resulting substitutions into the HSE to arrive at Equation (22) that simplifies to Equation (23).

$$z=\frac{t}{{\tau }_{\mathrm{D}}}\to \partial z=\frac{\partial t}{{\tau }_{\mathrm{D}}}\to \partial t={\tau }_{\mathrm{D}}\partial z$$

(21)

$$\frac{1}{{\tau }_{\mathrm{D}}}\frac{\partial N\left(r,z\right)}{\partial t}=-\frac{1}{{\tau }_{\mathrm{D}}}N\left(r,z\right)-\frac{1}{{\tau }_{\mathrm{D}}}\frac{R_0^6}{r^6}N\left(r,z\right)+D\frac{\partial }{\partial r}\left(N_0\left(r\right)\frac{\partial \left(N/N_0\right)}{\partial r}\right)$$

(22)

$$\frac{\partial N\left(r,z\right)}{\partial z}=-N\left(r,z\right)-\frac{R_0^6}{r^6}N\left(r,z\right)+D{\tau }_{\mathrm{D}}\frac{\partial }{\partial r}\left(N_0\left(r\right)\frac{\partial \left(N/N_0\right)}{\partial r}\right)$$

(23)

We observe that the product of diffusion coefficient and donor lifetime, D⋅τ_D, appears in the rescaled HSE (Equation (23)) at the same place as D does in the initial HSE (Equation (5)). Secondly, neither D nor τ_D appear at any other place of the rescaled HSE (Equation (23)). It is obvious from Equation (23) that any change of the diffusion coefficient and donor lifetime will not change the resulting effective distance, R_eff, if their product, D⋅τ_D, does not change. This is what ES2 expresses.

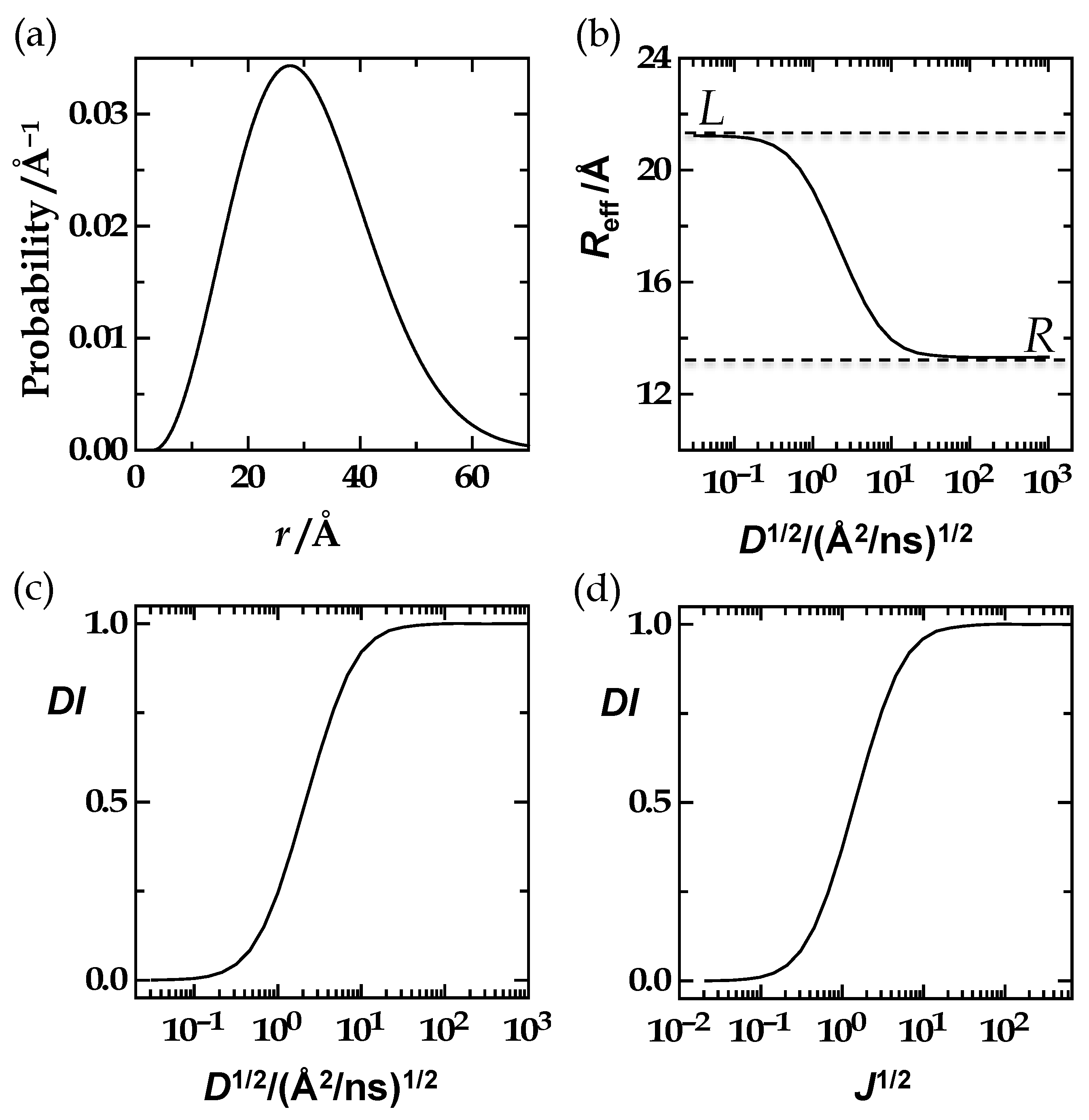
3.2.3. The Third Equivalence Statement: Variation of the Förster Radius and Left-Integration Limit

In the next step, we only change the Förster radius from R₀⁽¹⁾ to R₀⁽²⁾ and the left-integration value from r_L⁽¹⁾ to r_L⁽²⁾. We observe total overlap of the resulting diffusion-influence profiles, DI⁽¹⁾(J⁽¹⁾) and DI⁽²⁾(J⁽²⁾), if the third equivalence statement is obeyed:

Equivalence Statement 3 (ES3, Text)

“Given any probability distribution: If the Förster radius and the left-integration limit are varied but not their ratio, then the diffusion-influence values obtained from the diffusion-influence functions, DI⁽¹⁾(J⁽¹⁾) and DI⁽²⁾(J⁽²⁾), are identical. The corresponding diffusion-influence profiles coincide”.

ES3 (formal):

$$\begin{array}{l}\mathrm{For}\mathrm{any}{p}^{(1)}\left(r\right)=p^{(2)}\left(r\right):\mathrm{If}\frac{D^{(1)}{\tau }_{\mathrm{D}}^{\left(1\right)}}{{\left(R_0^{\left(1\right)}\right)}^2}=\frac{D^{(2)}{\tau }_{\mathrm{D}}^{\left(2\right)}}{{\left(R_0^{\left(2\right)}\right)}^2}\mathrm{and}\frac{R_0^{\left(1\right)}}{r_{\mathrm{L}}^{(1)}}=\frac{R_0^{\left(2\right)}}{r_{\mathrm{L}}^{(2)}}\\ \mathrm{then}D{I}^{(1)}\left(J^{\left(1\right)}\right)=D{I}^{(2)}\left(J^{\left(2\right)}\right)\end{array}$$

(24)

That ES3 holds true with excellent precision is illustrated in Figure 5. Here, we also tested ES1 again: We compared three different distance distributions and their DI-profiles obtained with three different pairs of R₀-and r_L-values where R₀/r_L was always held constant at 3. The three corresponding DI-profiles coincide (Figure 5c, X = J^1/2).

To explain ES3, we continue to use the change-of-variable approach. After rescaling time with the donor lifetime, we now rescale space with the Förster radius. The new space coordinate is defined by Equation (25).

$$s=\frac{r}{R_0}\to \partial s=\frac{\partial r}{R_0}\to \partial r=R_0\partial s$$

(25)

How term-(2) of the HSE (Equation (5)) changes after time rescaling and subsequent space rescaling is shown in Equation (26).

$$-\frac{1}{{\tau }_{\mathrm{D}}}{\left(\frac{R_0}{r}\right)}^{6}N(r,t)=-{\left(\frac{R_0}{r}\right)}^{6}N(r,z)=-\frac{1}{{\left(\frac{r}{R_0}\right)}^6}N(r,z)=-\frac{1}{s^6}N(s,z)$$

(26)

Thus, the HSE, now written not with the old (r,t)-coordinates but with the new (s,z)-coordinates, is expressed by Equation (27) or, when we insert the definition of the augmented diffusion coefficient, J, (Equation (12)), by Equation (28).

$$\frac{\partial N\left(s,z\right)}{\partial z}=-N\left(s,z\right)-\frac{1}{s^6}N\left(s,z\right)+\frac{D{\tau }_{\mathrm{D}}}{R_0^2}\frac{\partial }{\partial s}\left(N_0\left(s\right)\frac{\partial \left(N/N_0\right)}{\partial s}\right)$$

(27)

$$\frac{\partial N\left(s,z\right)}{\partial z}=-N\left(s,z\right)-\frac{1}{s^6}N\left(s,z\right)+J\frac{\partial }{\partial s}\left(N_0\left(s\right)\frac{\partial \left(N/N_0\right)}{\partial s}\right)$$

(28)

When we rescale space, we also rescale the distance distribution, and that also means that we rescale the integration limits of the distance distribution. As discussed, changing the left-integration limit has a strong effect on the diffusion-influence profile. We need to pay less attention to the right-integration limit, r_R, as simulations showed that r_R has only to be chosen to be sufficiently large to enclose the distance distribution up to probability-density values close to zero. Additionally, the changing shape of the distribution caused by rescaling, its expansion or contraction in the x-direction, is of no consequence, as has been demonstrated (ES1, Figure 3 and Figure 6). Nevertheless, we keep in mind, in the ongoing analysis, the validity of ES3 rests on the validity of ES1. After rescaling, in accordance with Equation (26), the new left-integration limit follows Equation (29).

$$s_{\mathrm{L}}=\frac{r_{\mathrm{L}}}{R_0}$$

(29)

Thus, when we change R₀⁽¹⁾ to R₀⁽²⁾ and r_L⁽¹⁾ to r_L⁽²⁾ and apply space rescaling to the corresponding HSE equations, HSE⁽¹⁾ and HSE⁽²⁾, we obtain J⁽¹⁾ and J⁽²⁾ as well as s_L⁽¹⁾ and s_L⁽²⁾. Only if s_L⁽¹⁾ and s_L⁽²⁾ are identical can we expect that the diffusion-influence values DI⁽¹⁾(J⁽¹⁾) and DI⁽²⁾(J⁽²⁾) and corresponding profiles coincide. According to Equation (29), this will be the case if r_L⁽¹⁾/R₀⁽¹⁾ = r_L⁽²⁾/R₀⁽²⁾. This is equivalent to the condition used in ES3: R₀⁽¹⁾/r_L⁽¹⁾ = R₀⁽²⁾/r_L⁽²⁾.

3.2.4. The Fourth Equivalence Statement

Taken together, the three established statements combine into a fourth one.

Equivalence Statement 4 (ES4, Text)

“For any pair of distance distributions, p⁽¹⁾(r) and p⁽²⁾(r): If the diffusion coefficient or the donor lifetime or the Förster radius are varied but not the augmented diffusion coefficient J composed of these parameters, and if the ratio of the Förster radius and left-integration limit is not varied, then the diffusion-influence values obtained from the diffusion-influence functions, DI⁽¹⁾(J⁽¹⁾) and DI⁽²⁾(J⁽²⁾), are identical. The corresponding diffusion-influence profiles coincide.”

ES4 (formal):

$$\begin{array}{l}\mathrm{For}\mathrm{any}{p}^{(1)}\left(r\right)\mathrm{and}{p}^{(2)}\left(r\right):\mathrm{If}\frac{D^{(1)}{\tau }_{\mathrm{D}}^{\left(1\right)}}{{\left(R_0^{\left(1\right)}\right)}^2}=\frac{D^{(2)}{\tau }_{\mathrm{D}}^{\left(2\right)}}{{\left(R_0^{\left(2\right)}\right)}^2}\mathrm{and}\frac{R_0^{\left(1\right)}}{r_{\mathrm{L}}^{(1)}}=\frac{R_0^{\left(2\right)}}{r_{\mathrm{L}}^{(2)}}\\ \mathrm{then}D{I}^{(1)}\left(J^{\left(1\right)}\right)=D{I}^{(2)}\left(J^{\left(2\right)}\right)\end{array}$$

(30)

This means that a fixed R₀/r_L ratio corresponds to a single sigmoidal curve, a single diffusion-influence profile. We slide along that sigmoid when we vary J, that is (see Equation (11)), when we vary the diffusion coefficient, or the donor lifetime, or the Förster radius and the left-integration limit, but latter two only in combinations that keep R₀/r_L constant. Such a sigmoid follows Equation (13) with constant coefficients, X₀ and M.

Thus, if the R₀/r_L ratio is fixed, X₀ and M are constants that can be determined by fitting the numerically obtained sigmoid to Equation (13). As soon as we vary R₀/r_L, we obtain a different sigmoid characterized by different X₀- and M-values. Thus, X₀- and M are functions of R₀/r_L. We need to determine these functions to establish Equation (13) as an equation that covers all possible diffusion-influence profiles. Being content to firstly cover only a small two-dimensional range of R₀ and r_L, we learned that these functions are then simple polynomials of second degree. In the following, the focus shifts from mainly mathematical reasoning to the need to obtain reliable results from numerical HSE-solutions.

3.3. The Grid

We determined these polynomial functions firstly for a limited two-dimensional range of 9–15 Å for R₀ and of 1.5–5 Å for r_L: These are the crucial R₀- and r_L-ranges for short-distance FRET methods applied to flexible peptides or polymers [13,17,18] (see Supporting Information, Chapter 3, Figures S1 and S2). The R₀,r_L-grid, or R₀,r_L-set, was R₀/Å × r_L/Å = {9.0, 10.0, 11.0, 12.0, 13.0, 14.0, 15.0} × {1.5, 2.0, 2.5, 3.0, 3.5, 4,0, 4.5, 5.0} resulting in a total of 56 R₀,r_L-combination. For each combination, we determined the corresponding DI-profile by numerically solving the HSE for at least 28 values of the diffusion coefficient. We then determined the X₀- and M-value of each of these 56 profiles by fitting them to Equation (13). Indeed, the X₀- and M-values coincided for all those R₀,r_L-combinations with a constant ratio R₀/r_L. A selection of results, those for R₀/r_L equal to 3, 4, 5, or 6, are shown in

Table 1. Fitting results for X₀ and M *.

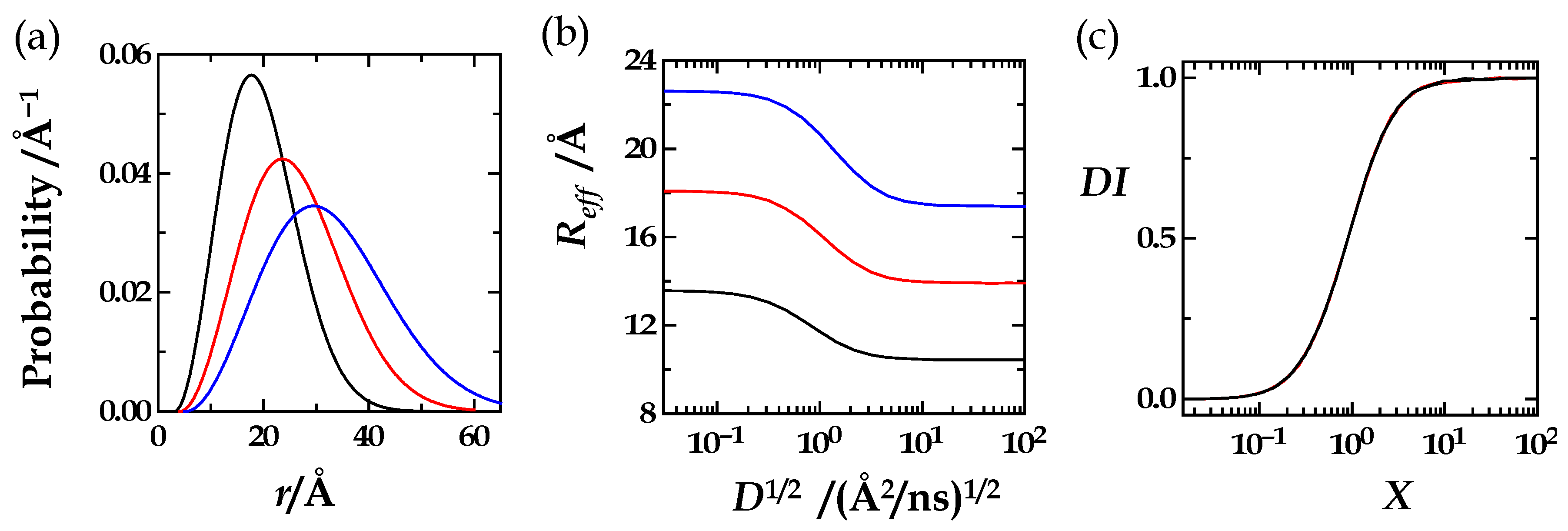
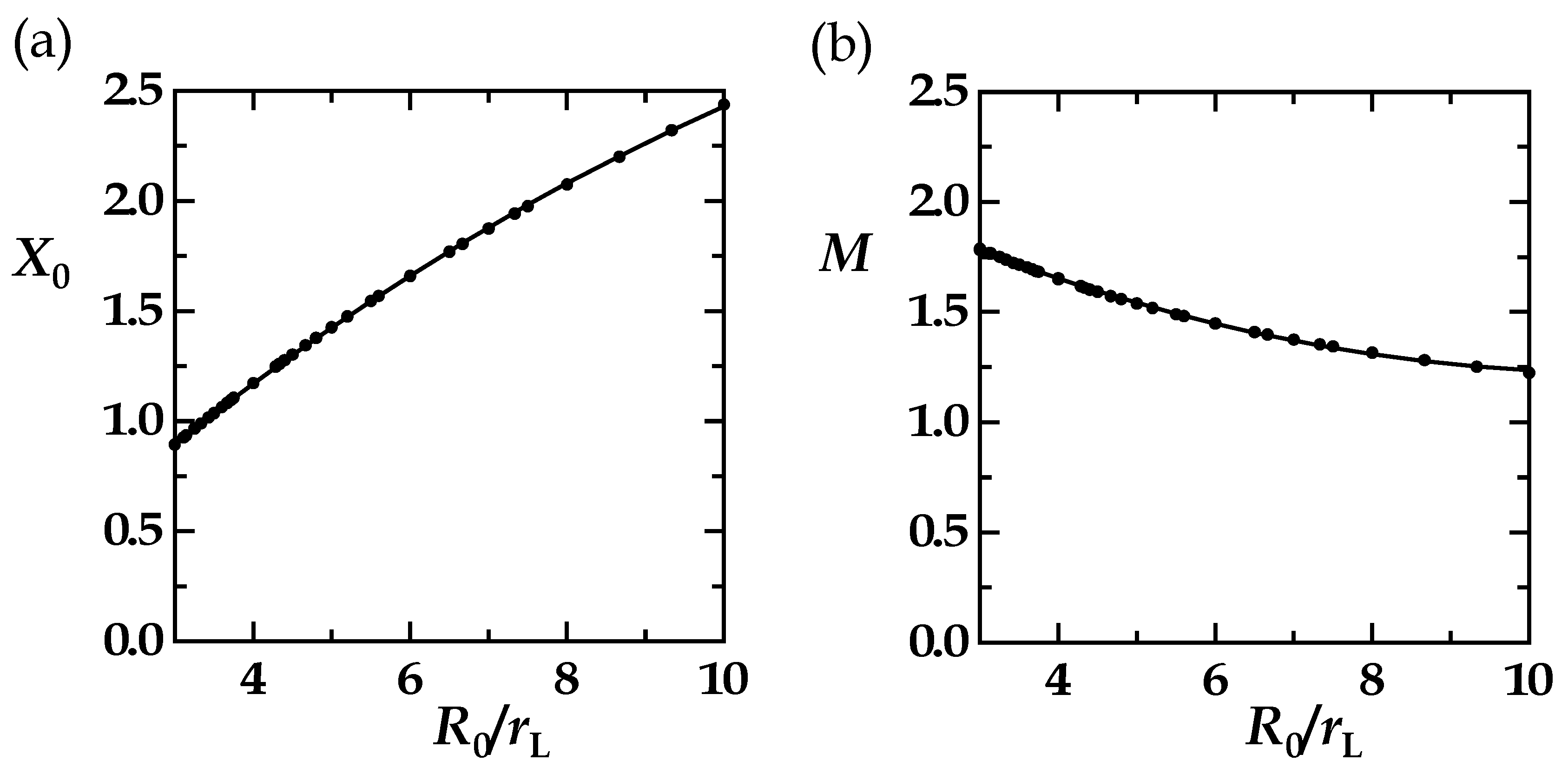
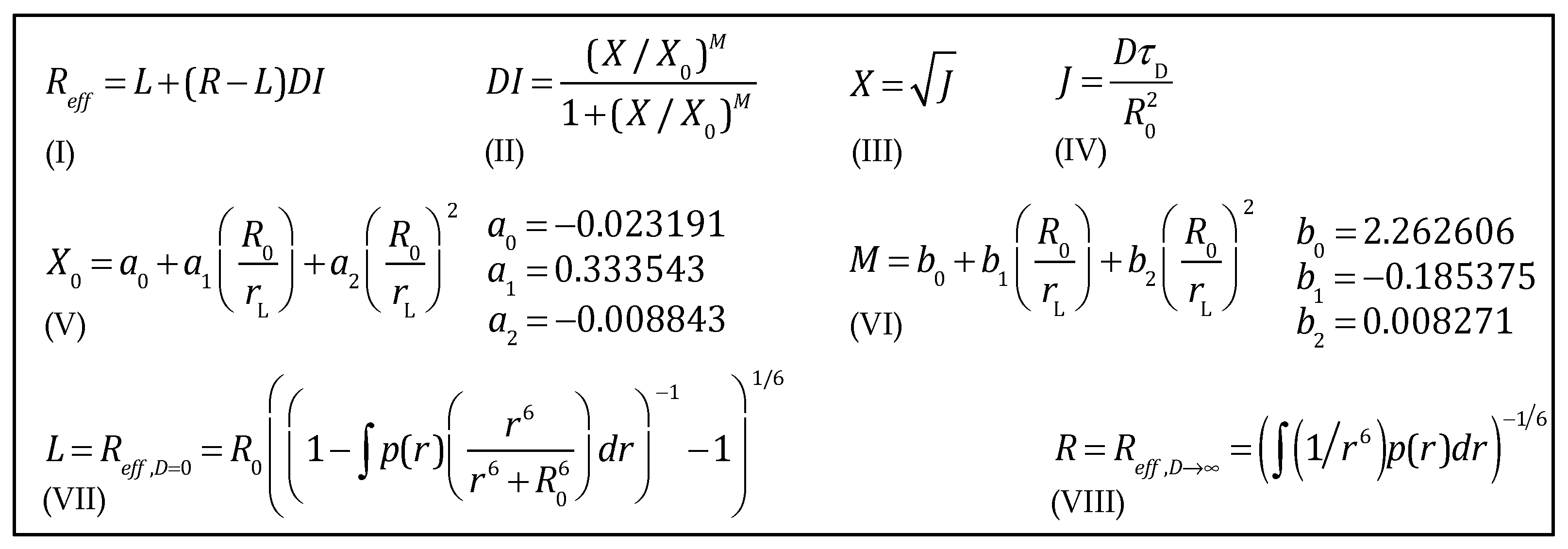
R0/rL	R0	rL	X0	M
3	9	3	0.8935	1.7823
3	12	4	0.8929	1.7876
3	15	5	0.8933	1.7861
4	10	2.5	1.1722	1.6513
4	12	3	1.1719	1.6532
4	14	3.5	1.1724	1.6494
5	10	2	1.4259	1.5387
5	15	3	1.4256	1.5391
6	9	1.5	1.6591	1.4481
6	12	2	1.6592	1.4483
6	15	2.5	1.6587	1.4483

* The test distributions were chosen to follow Equation (18) with b = 2R₀.

. These results clearly corroborate ES3 and, by that, also ES1, on which ES3 rests.

Which distance distributions were used in this analysis? To obtain highly reliable X₀- and M-values from fits of the numerically obtained sigmoids required perfectly symmetrical sigmoids in the first place. Recall, that we argued in the first chapter of Results, “Ideas and Concepts”, that any diffusion-influence profile should be a perfectly symmetrical sigmoid, a condition that when met points to a properly executed numerical simulation. A consequence of the normalization Equation (11) is that sigmoids numerically obtained from the HSE follow Equation (13) less accurately when the difference between the extreme values of the effective distance, L and R, when the amplitude of the sigmoid, ∆R_eff = L − R, becomes smaller. Very narrow distance distributions only allow for accordingly small ∆R_eff-values. It is then almost impossible to numerically obtain well-shaped sigmoids. Luckily, we were free to choose the distance distributions in any way we wanted (ES1) to evaluate the grid. We have chosen the simplest model possible, the ideal-chain or random coil model (Equation (18)). Here, the broadness of the distribution is determined by the parameter, b. Thus, to always guarantee broad distributions and to always guarantee a large difference, ∆R_eff = L − R, when R₀ is varied within the grid, the parameter b was chosen to follow the equation b = 2⋅R₀. An exemplary distribution (R₀ = 10 Å, r_L = 3 Å) of this series is given by the black curve in Figure 6a.

We performed the same analysis with a series of less broad distributions following b = R₀ and b = 1.5⋅R₀. An exemplary distribution (R₀ = 10 Å, r_L = 3 Å) of the latter is given by the blue curve in Figure 6a. Figure 6b compares the diffusion-influence profiles for R₀ = 10 Å, r_L = 3 Å, b = 2⋅R₀ (black curve) and for R₀ = 10 Å, r_L = 3 Å, b = 1.5⋅R₀ (blue curve). Both profiles overlap so well that visual distinction is impossible. This is valid for comparisons at any of the employed R₀-values as is shown in Figure 6c. The M-values were virtually identical, and the X₀-values (lower black and blue data points) were always so close that the corresponding DI-profiles were visually indistinguishable (see Figure 6b).

This comparative analysis confirmed that distributions with b = 2⋅R₀ are sufficiently broad to guarantee accurate numerical results. In addition, at this point, we have gained strong confidence in the validity of ES1 and ES3 and in all of the equivalence statements.

The figure illustrates how X₀ and M vary with R₀ for the two series when r_L is kept at 3 Å. For M, the values obtained for the two series overlap (upper black and blue circles); for X₀, the values (lower black and blue circles) obtained for the two series are so close that the corresponding diffusion profiles (see panel b) are visually indistinguishable.

3.4. The HSJE

We can now analyze the results obtained for X₀ and M for the distribution series with b = 2R₀, the series that guarantees highest numerical accuracy by leading to the largest ∆R_eff = L − R differences or DI(X) amplitudes. We obtained smooth curves that could be fitted to second-degree polynomial functions. Data points and fitting curves coincided (Figure 7). The functions and coefficients are given in

Table 2. X₀ and M as second-degree polynomial functions of R₀/r_L.

X0 = a0 + a1 × (R0/rL) + a2 × (R0/rL)2; M = b0 + b1 × (R0/rL) + b2 × (R0/rL)2
n	X0 =	an-value	M =	bn-value
0	a0	−0.023191	b0	2.262606
1	a1 × (R0/rL)	0.333543	b1 × (R0/rL)	−0.185375
2	a2 × (R0/rL)2	−0.008843	b2 × (R0/rL)2	0.008271

The coefficients a₀, a₁, a₂, and b₀, b₁, b₂ are valid for the conditions R₀ = 9–15 Å, r_L = 1.5–5 Å, R₀/r_L > 3.

.

We are ready to state the HSJE for the given range of R₀ = 9–15 Å and r_L = 1.5–5 Å (see the legend of Figure 7) in Figure 8. For clarity, we have decomposed the HSJE into its simple constituents, equations (I) to (VIII). The HSJE written as a single equation is shown in Supporting Information, Chapter 7e.

We now have a closed analytical expression, a CAE, for a defined parameter range. As with any other equation, it can now be applied to global analyses. The preliminary insights gained from such applications are very interesting but not the main topic of this article. We therefore referred these first applications of the HSJE to the Supporting Information, Chapter 8, Figures S6a–d and S7a–d.

4. Discussion

We have followed the full path from a partial differential equation, the HSE, to a closed analytical expression, the HSJE. Its benefits are of a theoretical but also of a mere practical nature: The HSJE is usually solved in seconds, not in minutes or hours, by two orders of magnitude faster than the HSE. This advantage amplifies when the HSJE is used as the basis of a global analysis that generally requires numerous fitting cycles to reach the best values for the diffusion coefficient, D; the distance distribution, p(r); and the left-integration limit, r_L. Experimental values of the effective distance can be obtained from time-resolved fluorescence measurements but equally well from more widely available steady-state fluorescence spectroscopy. The HSJE is certainly not trivial but is still simple enough that multivariate or global analysis can be performed in commonly available programs such as Microsoft Excel.

DFRET is just one method in a whole range of optical methods for studying the structure and dynamics of polymers [10,11,12,13,14,17,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62]. When we go into detail, we realize that any progress in DFRET can synergistically promote progress in this entire field [13]. The structure and dynamics of polymers are so important that numerous methods based on two optical molecular labels have been developed [2,3,5,6,10,11,13,15,17,22,23,24,25,27,28,29,30,31,32,33,34,35,36,37,38,47,48,49,57,58,59,63,64,65,66,67,68]. These labels are either synthetically conjugated to the chain or naturally present, as, for instance, Trp or Tyr in a peptide or protein. One of the deepest motivations for developing such methods has always been the “protein folding problem”. The “static” folding problem now appears to have been solved by artificial intelligence methods applied to a huge amount of data [69] but countless questions about folding involving dynamics and mechanisms remain open. Examples include misfolding in amyloidosis diseases as well as the sometimes bizarre behavior of intrinsically disordered peptides and proteins [70].

These methods include not only FRET, but also CQ methods (collisional-quenching methods)1 [25,71]. For example, the sdFRET method is based on the excitation of a donor, e.g., the donor FTrp, in combination with Dbo as acceptor. The peculiarity of this FTrp/Dbo pair is that instead of FTrp, one can simply excite Dbo, whose fluorescence is then quenched by collision with FTrp [49]. This particular CQ method is called CIFQ (collision-induced fluorescence quenching). How quickly this quenching proceeds also informs the dynamics and flexibility of the chain. In the past, we have been able to reconcile seemingly contradictory results from different sdFRET, CIFQ, and CQ methods [13]. Therefore, we reiterate our assertion that any progress in DFRET or any of the other methods can synergistically promote progress in the entire field of polymer structure and dynamics. We believe that we have made such progress with the development of the HSJE.

The augmented diffusion coefficient. In addition to the practical benefits of the HSJE, we believe that its structure gives a more lucid insight into parameters whose variation can feed essential information into the needed global analysis. This is first of all the newly defined augmented diffusion coefficient, J. What does J actually mean? If we want to determine the diffusion impact and the diffusion coefficient, D, we need the widest possible range of the diffusion influence, DI, preferably from 0 to 100%. It is clear that any experimental series might cover a range within these limits but can never reach these limits themselves. We established that DI increases with J and that J increases linearly with D and τ_D, the donor lifetime, and decreases with the square root of the Förster radius, R₀ (Equation (18)). All of these variations have been employed in earlier attempts at a global analysis but without knowing which range of the diffusion influence was actually covered [3,7,9,10,14]. In this work, we obtained certainty that our previous variation [14] of the diffusion coefficient by solvent viscosity and variation of the donor lifetime by adding the viscogen ethylene glycol and by going from the donor FTrp to the donor NAla covered a DI range of 8 to 80% (comp. Supporting Information, Chapter 8c). In previous works [12,14], we also investigated and discussed the role of the donor quantum yield, and we continue this discussion in Supporting Information, Chapter 9, because the donor quantum yield can be made part of the HSJE as shown in Equations (S31)–(S33).

Preview. In summary, the diffusion contribution to FRET should not be neglected whenever we are not close to the static limit. Therefore, the question remains up to which R₀-values and under which circumstances are we not close to this limit. Up to which R₀-values should diffusion be included into the analysis, and up to which values should the HSJE be extended?

5. Conclusions

Fluorescence methods and methods based on fluorescence resonance energy transfer have asserted their place in questions of molecular/bio-molecular structure and dynamics simply because their speed and sensitivity are unsurpassed. We believe that also diffusion-enhanced Förster resonance energy transfer or DFRET has the potential to become influential, although the number of publications based on it has been small to date. DFRET ensemble analysis has been based on a partial differential equation, on the HSE. Using the HSE in a global analysis means that profound challenges must first be overcome. Furthermore, even with seemingly successful fits, doubts often remain about the realistic significance of the results obtained. By replacing the PDE with a closed analytical expression, by replacing the HSE with the HSJE, these difficulties can be ended.