Temperature Dependence of the Vacancy Formation Energy in Solid ⁴He

Abstract

We studied the thermal effects on the behavior of incommensurate solid ${}^4$He at low temperatures using the path integral Monte Carlo method. Below a certain temperature, depending on the density and the structure of the crystal, the vacancies delocalize and a finite condensate fraction appears. We calculated the vacancy formation energy as a function of the temperature and observed a behavior compatible with a two-step structure, with a gap of few K appearing at the onset temperature of off-diagonal long-range order. Estimation of the energy cost of creating two vacancies seems to indicate an effective attractive interaction among the vacancies but the large error inherent to its numerical estimation precludes a definitive statement.

1. Introduction

Solid ${}^4$He at very low temperature has been the candidate for achieving the supersolid state of matter for long time [1,2]. Its extreme quantum nature and its stability at relatively low pressures could fit into the desired target. However, the search for a clear signature of it has been extremely elusive despite continued effort. Some years ago there was a big excitement after the announcement of a finite superfluid fraction in solid ${}^4$He observed as a non-conventional moment of inertia of a sample of hcp ${}^4$He grown inside a torsional oscillator [3,4]. Soon after this achievement, it was observed that the elastic constants of the crystal change also at similar temperatures [5]. Initially, the elastic anomaly was assumed to be independent of the mass decoupling in the torsional oscillator [6]. However, improvements in the experimental setup confirmed finally that the change in the response under rotation can be understood in terms of only the elastic anomaly and that the superfluid signal was not present [7].

The interest on the possible supersolid phase of ${}^4$He has motivated intense theoretical studies to better understand the role of defects, as point vacancies [8,9,10,11,12,13,14,15,16,17] and dislocations [18,19], when the limit of zero temperature is reached. Andreev and Lifshitz [20] were the first to postulate that vacancies in solid ${}^4$He should behave as a Bose gas and thus their presence can induce a finite condensate fraction below some critical temperature. More recently, this scenario has been observed in the microscopic simulation of hcp ${}^4$He crystals with the path integral Monte Carlo (PIMC) method [17]. This numerical study has shown that, in the regimes of low temperatures where the off-diagonal long-range order (ODLRO) appears, the zero-point motion of ${}^4$He atoms is particularly large and makes the vacancies delocalized over several lattice sites, giving rise to a supersolid behavior.

However, the possibility of observing vacancy-induced Bose–Einstein condensation in solid ${}^4$He at thermal equilibrium seems very difficult, because these defects have a large activation energy, of the order of ten Kelvin, even in the limit of zero temperature. Therefore, the fraction of vacancies present in the crystal is expected to be exponentially suppressed at the low temperatures needed to reach the supersolid regime. However, this evidence does not exclude the possibility of vacancy-induced supersolidity in metastable conditions out of equilibrium, as recently observed in crystalline samples of ${}^4$He during pulsed vacuum expansion [21], or in quantum crystals other than solid helium [22].

Another relevant question about the behavior of vacancies in solid ${}^4$He concerns the effective interaction arising among these defects. Although several works point out that vacancies tend to attract each other, it is still unclear if this interaction can lead to the formation of bound states between them. Some studies suggest that vacancies should clusterize and evaporate out of the crystal during the annealing process [13,23,24], but other works do not see any evidence of the clusterization of vacancies inside bulk ${}^4$He [25]. This discrepancy can be due to the finite-size effects which unavoidably affect microscopic simulations and therefore do not allow to provide a clear answer about the behavior of the vacancies in a real macroscopic system.

The aim of the present work was to study the vacancy formation energy $E_v$ in quantum solids as a function of its temperature. One should expect, indeed, that the appearance of off-diagonal long range order in incommensurate solid ${}^4$He should present some characteristic signal in the energetic properties of the system, similar to what happens in liquid ${}^4$He across the transition from the normal to the superfluid phase, where the derivative of the energy with respect to the temperature (specific heat) presents a singularity at the critical temperature. Our results show the emergence of two distinct regimes of temperature where $E_v$ assumes different values, in crystals with different lattice structures and different densities. Remarkably, the temperature at which the behavior of $E_v$ changes corresponds to that at which a finite condensate fraction appears in the crystal.

The rest of the paper is organized as follows. In Section 2, we briefly discuss the PIMC method used in the simulations of solid ${}^4$He with (incommensurate solid) and without (commensurate solid) vacancies. In Section 3, we report the results for the vacancy formation energies as a function of the temperature. Finally, in Section 4, we summarize the main conclusions of the work.

2. Method

The PIMC method is nowadays a standard tool to study quantum fluids and solids at finite temperature. It estimates, in a stochastic form, the thermal density matrix of an N particle system [26]. As is well known, the partition function

$$Z=\mathrm{Tr}\left(e^{-\beta \widehat{H}}\right)=\int dR\langle R|e^{-\beta \widehat{H}}|R\rangle$$

(1)

allows for a full microscopic description of the properties of a given system with Hamiltonian $\widehat{H}=\widehat{K}+\widehat{V}$ at a temperature $T={(k_B\beta )}^{-1}$ (we use the position basis $|R\rangle =|{\mathbf{r}}_1,\dots {\mathbf{r}}_N\rangle$, with N the number of particles). In quantum systems, the noncommutativity of the kinetic and potential energy operators (respectively, $\widehat{K}$ and $\widehat{V}$) make impractical a direct calculation of Z using its definition in Equation (1).

PIMC uses the convolution property of the thermal density matrix $\rho (R,R^{\prime };\beta )=\langle R|e^{-\beta \widehat{H}}|R^{\prime }\rangle$ to rewrite the partition function as

$$Z=\int \prod _{i=0}^{M-1}d{R}_i\rho (R_i,R_{i+1};\epsilon ),$$

(2)

with $\epsilon =\beta /M$ and the boundary condition $R_M=R_0$. For sufficiently large M, we recover the high-temperature limit of the thermal density matrix where the kinetic and potential parts factorize (Primitive Approximation). Ignoring the quantum statistics of particles, the distribution law appearing in Equation (2) is positive definite and can be interpreted as a probability distribution function which can be sampled by standard metropolis Monte Carlo methods.

The number M of convolution terms (beads) necessary to reach the convergence of Equation (2) to the exact value of Z is inversely proportional to the temperature of the system. This means that, when approaching the interesting quantum regime at very low temperature, M increases quickly, making simulations hard, if not impossible, due to the very low efficiency in the sampling of the long chains involved. It is therefore important to work out high-order approximation schemes for the density matrix, able to work with larger values of $\epsilon$. The approximation we use in this work is called Chin Approximation (CA) [27]. CA is based on a fourth-order expansion of the operator $e^{-\beta \widehat{H}}$ which makes use of the double commutator $[[\widehat{V},\widehat{K}],\widehat{V}]$, this term being related to the gradient of the interatomic potential.

In the case of bosons such as ${}^4$He, the indistinguishability of particles does not change the positivity of the probability distribution in Equation (2) and the symmetry of $\rho (R,R^{\prime };\beta )$ can be recovered via the direct sampling of permutations. We use the Worm Algorithm (WA) [28] which samples very efficiently the permutation space. This technique works in an extended configuration space, given by the union of the ensemble W, formed by the usual closed-ring configurations, and the ensemble G, which is made up of configurations where all the polymers but one are closed. The G-configurations can be used to compute off-diagonal observables, such as the one-body density matrix ${\rho }_1({\mathbf{r}}_1,{\mathbf{r}}_1^{\prime })$, which is one of the main goals of the present work.

The PIMC approach can be easily extended to simulate Bose systems at strictly zero temperature, in the so-called Path Integral Ground State (PIGS) method [29]. Indeed, the thermal density matrix $\rho (R,R^{\prime };\epsilon )$ can be seen as an imaginary-time propagator and can be used to project a trial wave function ${\Psi }_T(R)$ onto the real ground state ${\Psi }_0(R)$ of the many-body system, according to the formula

$${\Psi }_0(R_M)=\int \prod _{i=0}^{M-1}d{R}_i\rho (R_i,R_{i+1};\epsilon ){\Psi }_T(R_0).$$

(3)

With this assumption, the ground state average of the physical observables can be written in terms of a multidimensional integral, which presents a term equivalent to the probability distribution appearing in Equation (2). The only requirement for the trial wave function ${\Psi }_T$ is to satisfy the symmetry condition imposed by the Bose statistics of the quantum many-body system [30,31]. In this work, we consider an uncorrelated trial wave function ${\Psi }_T(R)=1$. Moreover, we make use of the WA also in the simulation of solid ${}^4$He at zero temperature even if it is not strictly necessary, as it allows for a better sampling of the probability distribution and it provides a simple strategy to guarantee the right normalization of the one-body density matrix ${\rho }_1({\mathbf{r}}_1,{\mathbf{r}}_1^{\prime })$ [31].

3. Results

We have carried out a series of PIMC simulations of solid ${}^4$He at densities close to the melting point and for temperatures $T\le 2$ K, with the main goal of determining the thermal evolution of a quantum crystal with point defects. In particular, we have simulated systems of N and $N-1$ particles interacting with the Aziz potential [32], inside a cubic simulation box with periodic boundary conditions. The number of atoms N is chosen to make the crystal geometry commensurate with the simulation box: we have chosen $N=108$ for the fcc lattice and $N=128$ for the bcc lattice. In these simulations, we focus our attention in the calculation of two observables: the one-body density matrix ${\rho }_1$ and the activation energy of a vacancy $E_v$.

The one-body density matrix (OBDM) is defined as

$${\rho }_1({\mathbf{r}}_1,{\mathbf{r}}_1^{\prime })=\frac{1}{\rho Z}\int d{\mathbf{r}}_2\dots d{\mathbf{r}}_N\rho (R,R^{\prime };\beta ),$$

(4)

where the two configurations $|R\rangle =|{\mathbf{r}}_1,{\mathbf{r}}_2\dots {\mathbf{r}}_N\rangle$ and $|R^{\prime }\rangle =|{\mathbf{r}}_1^{\prime },{\mathbf{r}}_2,\dots {\mathbf{r}}_N\rangle$ differ only for the coordinate of one particle and $\rho$ is the density of the system. In PIMC simulations, ${\rho }_1({\mathbf{r}}_1,{\mathbf{r}}_1^{\prime })$ can be computed by mapping the system of N quantum particles on a classical system made of $N-1$ ring closed polymers and one linear open polymer and by building the histogram of the distances between the extremities of the open chain occurred during the Monte Carlo sampling [26]. Moreover, from the long-range behavior of the OBDM, it is possible to infer the condensate fraction $n_0$ of the system, according to the formula

$$n_0=\underset{|{\mathbf{r}}_1-{\mathbf{r}}_1^{\prime }|\to \infty }{\lim }{\rho }_1({\mathbf{r}}_1,{\mathbf{r}}_1^{\prime }).$$

(5)

It is important to notice that, despite the finite-size effects which unavoidably affect PIMC simulations, this approach allows for very accurate estimations of $n_0$ in liquid ${}^4$He, which are in good agreement with experimental measurements over a wide range of pressures and temperatures [26,33,34].

The activation energy of a vacancy [35]

$$E_v=E(N-1,(N-1/N)V)-\frac{N-1}{N}E(N,V),$$

(6)

where $E(N,V)$ is the total energy of the system made up of N particles inside a box of volume V, is obtained as the difference between the total energy of the crystal presenting a vacancy and that of the commensurate crystal. Notice that, in the calculation of the incommensurate system, we rescale the dimensions of the simulation box to have the same density as in the commensurate solid: thus, our estimation for $E_v$ has to be intended as the vacancy activation energy at constant density. Moreover, as $E_v$ is obtained as a difference between two energies which scale with N, we have restricted our simulations to not very large systems to keep the statistical errors under control.

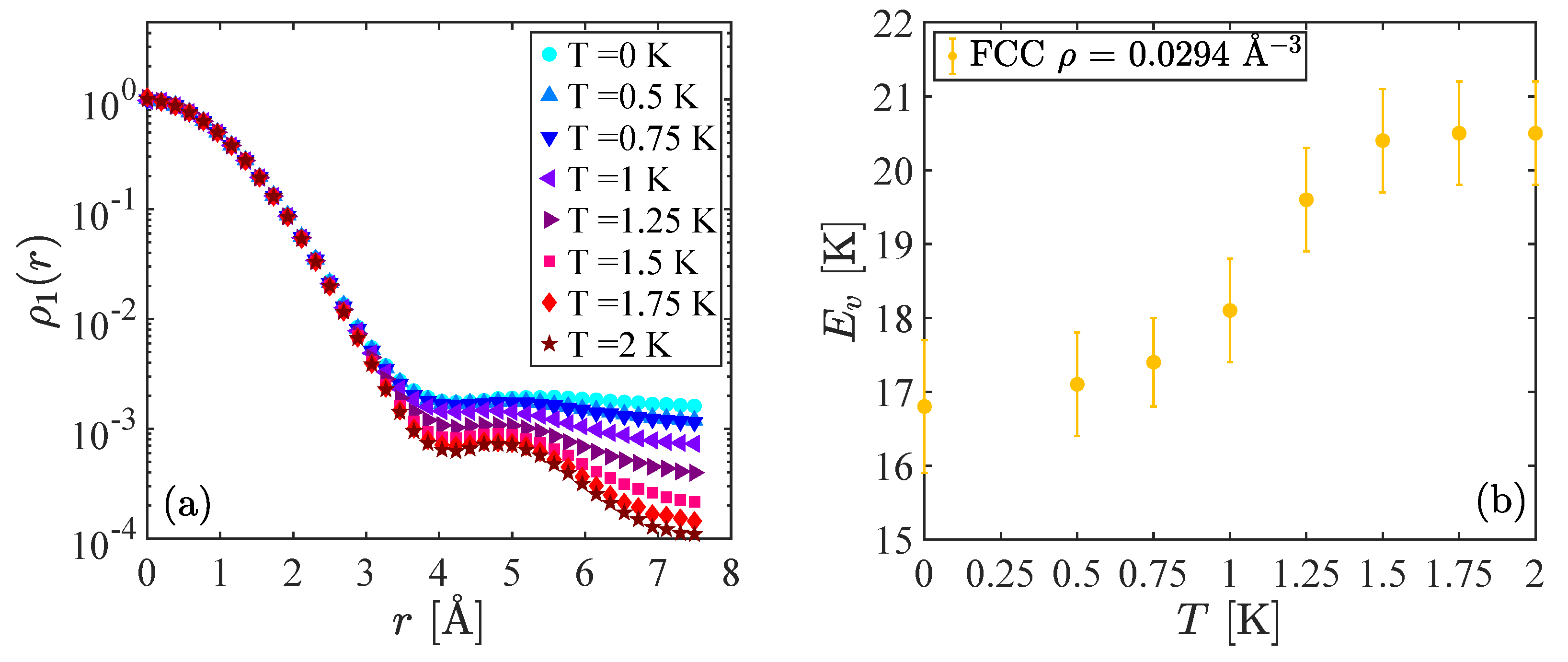
In Figure 1, we show results corresponding to the fcc crystal at the density $\rho =0.0294$ Å${}^{-3}$. Looking at the one-body density matrix ${\rho }_1(r)$ results in Figure 1a, we can see the evolution with temperature. When T is large ($T\ge 1.5$ K), we observe an exponential decay which coincides with the behavior of ${\rho }_1(r)$ of the commensurate crystal at any temperature and corresponds to absence of Bose–Einstein condensation. At these temperatures, the vacancy is localized and the permutations between particles are very rare events. Consequently, the vacancy in this regime behaves in a quasi-classical way. When the temperature decreases, we notice some deviations in the behavior of ${\rho }_1(r)$ at large distances until we reach a regime of small temperature ($T\le 0.75$ K) where the one-body density matrix shows clearly the emergence of ODLRO, pointing to a supersolid behavior where the vacancy is delocalized and induces a finite superfluid fraction in the crystal. For this case, the condensate fraction at zero temperature is $n_0=(1.5\pm 0.2)\times {10}^{-3}$, which is consistent with the variational calculations presented in Ref. [10]. In Figure 1b, we report results for the vacancy formation energy as a function of the temperature. For $T\le 0.75$ K, i.e., where the system presents ODLRO. we find a value $E_v\simeq 17$ K which is almost independent of T. Our numerical results are in agreement with the previous PIGS calculation of Ref. [11]. At higher temperature, we notice at first a steep increase of $E_v$ with T and then a regime where again $E_v$ depends very weakly on T: for $T\ge 1.5$ K, i.e., where ${\rho }_1(r)$ decays exponentially, we estimate $E_v\simeq 20$ K. This behavior shows the emergence of two different phases, according to the temperature of the crystal, and indicates that the delocalization of the vacancies implies a reduction in their activation energy of about 3 K.

It is interesting to notice that Clark and Ceperley [14] claimed that turning on the Bose statistics on a PIMC simulation of solid ${}^4$He does not have any significant effect in commensurate crystals but leads to reduction of the total energy of the system in crystals with a vacancy. This result is plausible with our hypothesis that the delocalization of the vacancies at low temperature, which is allowed by the frequent permutations among ${}^4$He atoms, is at the origin of the behavior of $E_v(T)$ shown in Figure 1.

To investigate the effect of the density of the system and the lattice geometry, we performed the same calculation in different configurations of the crystal. The results obtained for a fcc lattice at a higher density, $\rho =0.0313$ Å${}^{-3}$, are shown in Figure 2. In this case, clear evidence of a finite condensate fraction is found only for $T\le 0.5$ K and the activation energy of the vacancy is larger than in the previous case. The increase of $E_v$ with the density agrees with previous results at zero temperature [8]. However, despite these small quantitative differences, its qualitative behavior is similar to what is shown in Figure 1 and confirms the evidence that the activation energy of a delocalized vacancy is smaller than that of a localized one. At this density, the gap between the energies in the two phases is about 5 K.

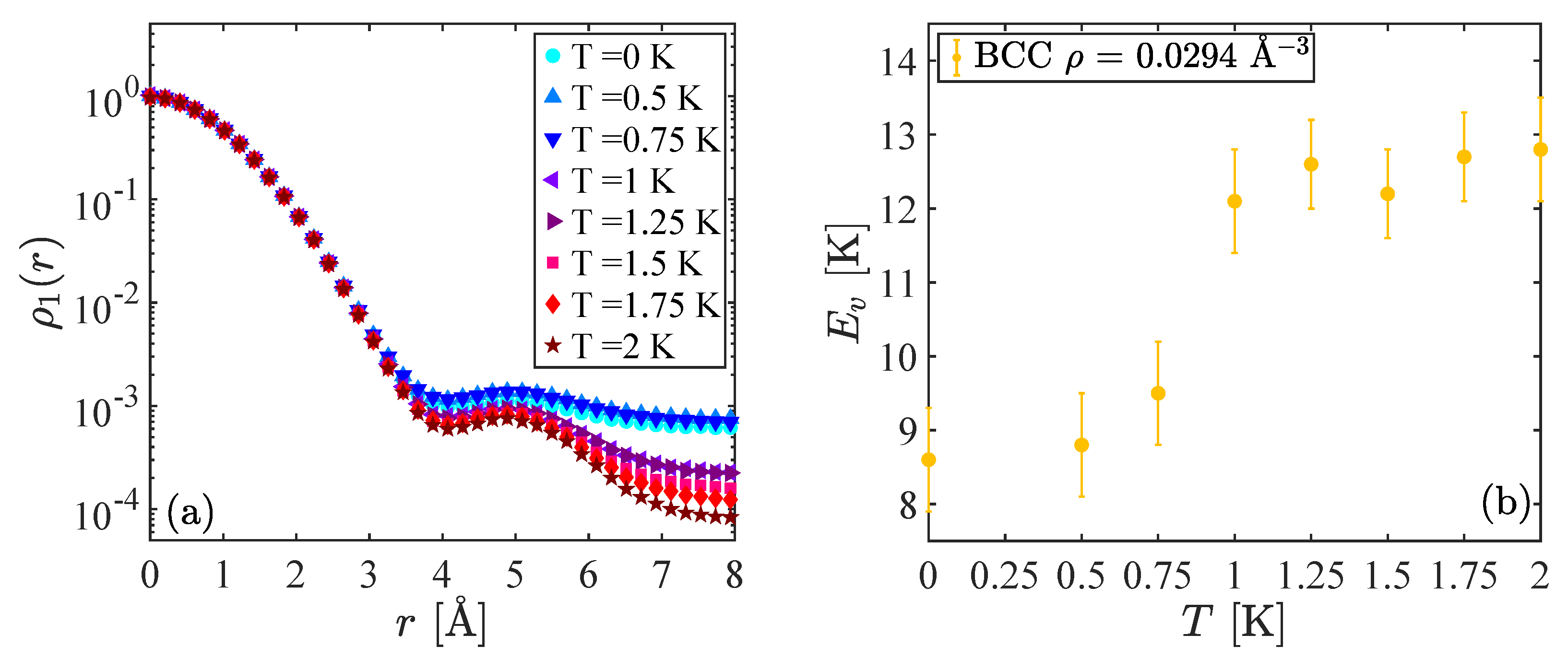
In Figure 3, we show the results obtained for a bcc crystal with $N=128$ sites at a density $\rho =0.0294$ Å${}^{-3}$. The quantitative differences between the activation energy of a vacancy in bcc and fcc crystals have already been observed in Ref. [9] and can be ascribed to the less packed structure of the bcc lattice. Nevertheless, we notice once again a clear two-step behavior in the curve for $E_v(T)$: for $T\le 0.75$ K, where ${\rho }_1(r)$ shows clearly the presence of a condensate fraction $n_0=(7.0\pm 0.8)\times {10}^{-4}$, the activation energy of the vacancy is $E_v\simeq 8.5$ K; instead, in the regimes of large temperatures, a larger value $E_v\simeq 12.5$ K is found.

Finally, for the specific case of the fcc crystal at the lowest density, we calculated the energy cost of introducing two vacancies in the system, $E_{2v}$. To do this, we performed PIMC simulations of $N-2$${}^4$He atoms, in a box commensurate with a fcc lattice of N sites. The activation energy of the bi-vacancy can be computed with the formula $E_{2v}=E(N-2,(N-2/N)V)-(N-2)E(N,V)/N$ (i.e., the same as for $E_v$ in Equation (6) but changing $N-1$ to $N-2$). In

Table 1. Vacancy formation energy for a single vacancy $E_v$, and for two vacancies $E_{2v}$ in a fcc ${}^4$He crystal with $N=108$ sites, at density $\rho =0.0294$ Å${}^{-3}$.

T	${\mathit{E}}_{\mathit{v}}$	${\mathit{E}}_{2\mathit{v}}$
0.5	$17.1\pm 0.7$	$31.9\pm 0.5$
0.75	$17.4\pm 0.6$	$33.6\pm 0.5$
1.0	$18.1\pm 0.7$	$35.6\pm 0.7$
1.25	$19.6\pm 0.7$	$36.5\pm 0.7$
1.5	$20.4\pm 0.7$	$38.1\pm 0.7$
1.75	$20.5\pm 0.7$	$38.7\pm 0.7$
2.0	$20.5\pm 0.7$	$40.5\pm 0.7$

, we report the results obtained as a function of the temperature, for both $E_v$ and $E_{2v}$. The comparison between these two quantities can give some insight into the discussion about the stability of vacancies inside the bulk crystal and its possible aggregation and posterior evaporation. Indeed, the condition $E_{2v}<2E_v$ should indicate the tendency for the two vacancies to approach each other, in order to reduce their energy cost. Although a precise estimation of the difference $\Delta =E_{2v}-2E_v$ is not feasible due to the large error bars of our data, we see that the activation energy of the bi-vacancy is systematically lower that twice the energy of a single vacancy: in particular, this effect is clearer at low temperature, where the vacancies delocalize.

4. Conclusions

We performed a set of PIMC simulations to investigate the behavior of point defects (vacancies) in solid samples of ${}^4$He at low temperatures. Our results confirm the old conjecture firstly proposed by Andreev and Lifshitz [20], according to which vacancies in quantum crystals, below a certain temperature, are delocalized over several lattice sites and can turn the system into a supersolid phase. Indeed, we notice that the behavior of the one-body density matrix of a defected crystal at high temperature is comparable with that of a perfect one. On the contrary, at low temperature, ${\rho }_1(r)$ at large distances presents a plateau, which signifies a finite condensation fraction in the many-body system ($n_0\sim {10}^{-3}$).

Moreover, a clear signal of the delocalization of the vacancies can be found in their energetic properties. The behavior of the activation energy $E_v$ of a single vacancy as a function of the temperature shows a characteristic two-step structure indicating that, whenever the vacancies are delocalized, their energy cost is reduced by an amount of few Kelvin. This behavior is independent of the density and the lattice geometry of the simulated crystal. Both the emergence of ODLRO and the two-step behavior of $E_v$ points to the existence of a second-order phase transition between the normal and superfluid crystals. However, we cannot determine the critical temperature with precision since that would require a finite-size scaling study, which would be extremely demanding in computer time, and that it is out of the scope of the present work.

We have also calculated the energetic properties of the solid sample when two vacancies are present. The comparison between the activation energy of the bi-vacancy $E_{2v}$ with that of a single vacancy $E_v$ seems to indicate an effective attraction between the defects, for the whole range of temperatures studied here. However, it is difficult to get a deeper insight into the question about the spatial clusterization of vacancies, due to the large error bars of our estimations that hinders any firm statement.