σ-Hole Interactions: Perspectives and Misconceptions
Abstract
:1. A Brief History of the σ-Hole
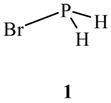
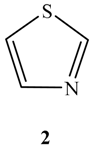
2. Characteristics of σ-Holes: Some Common Misconceptions
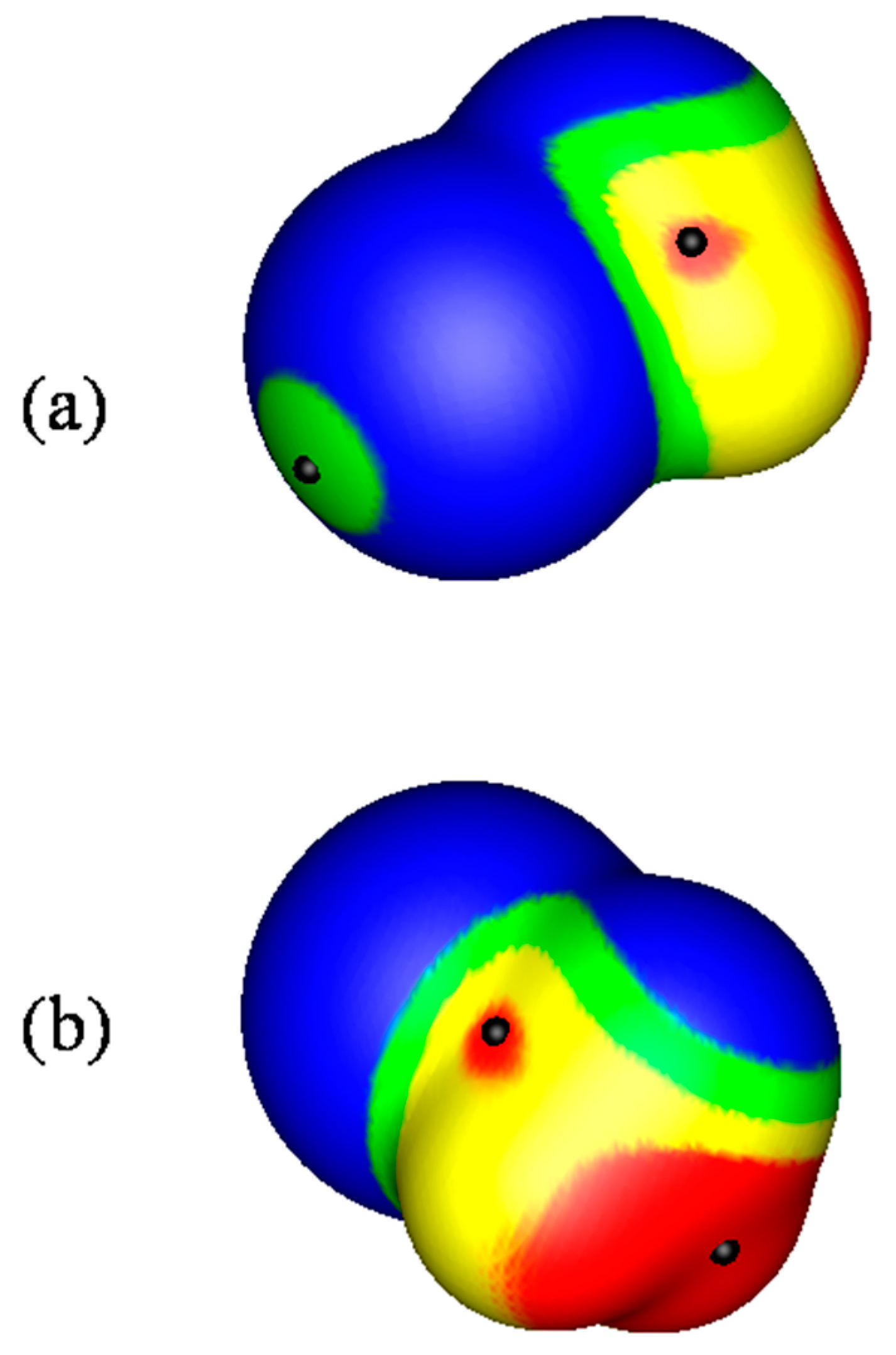
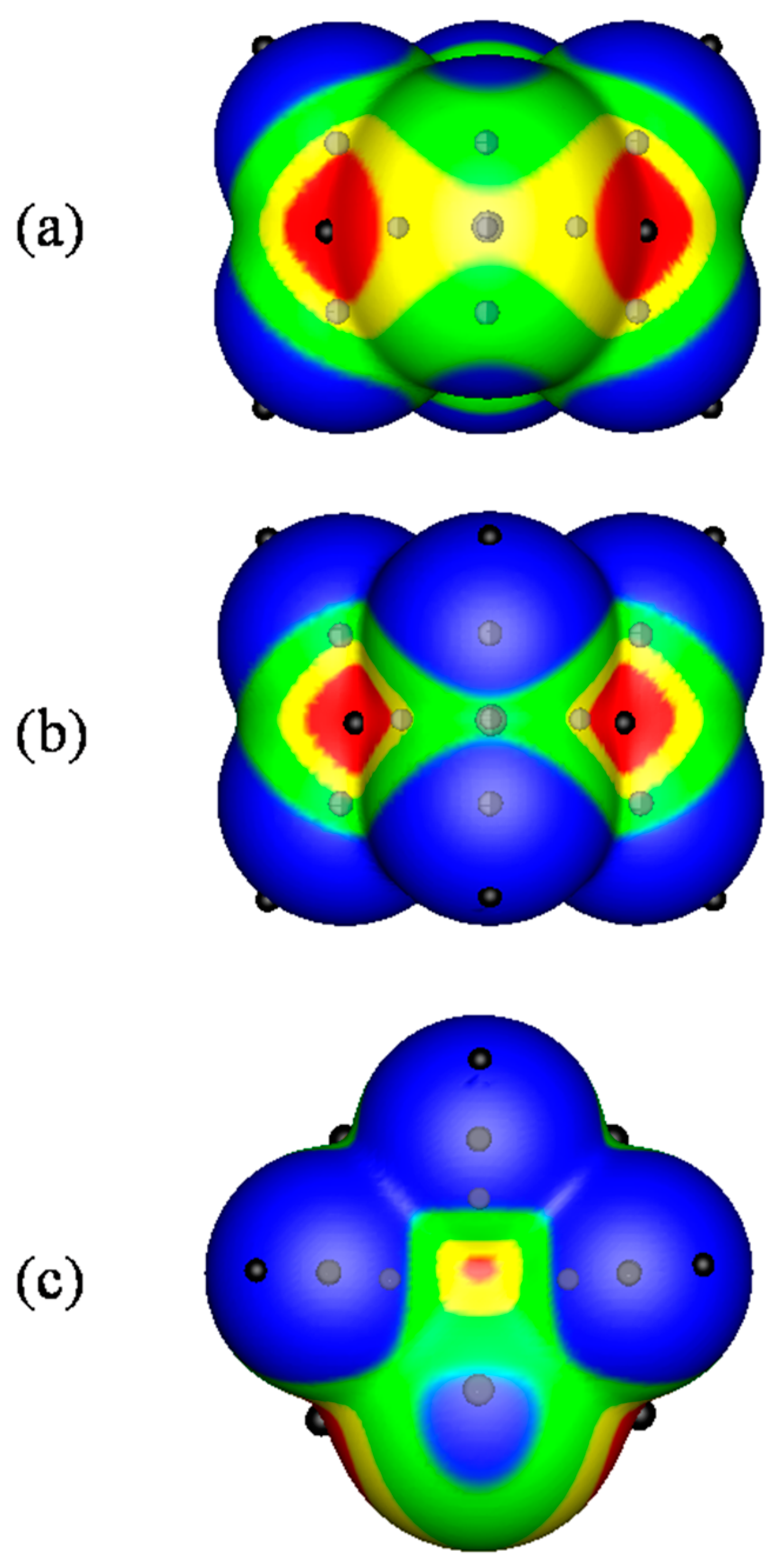
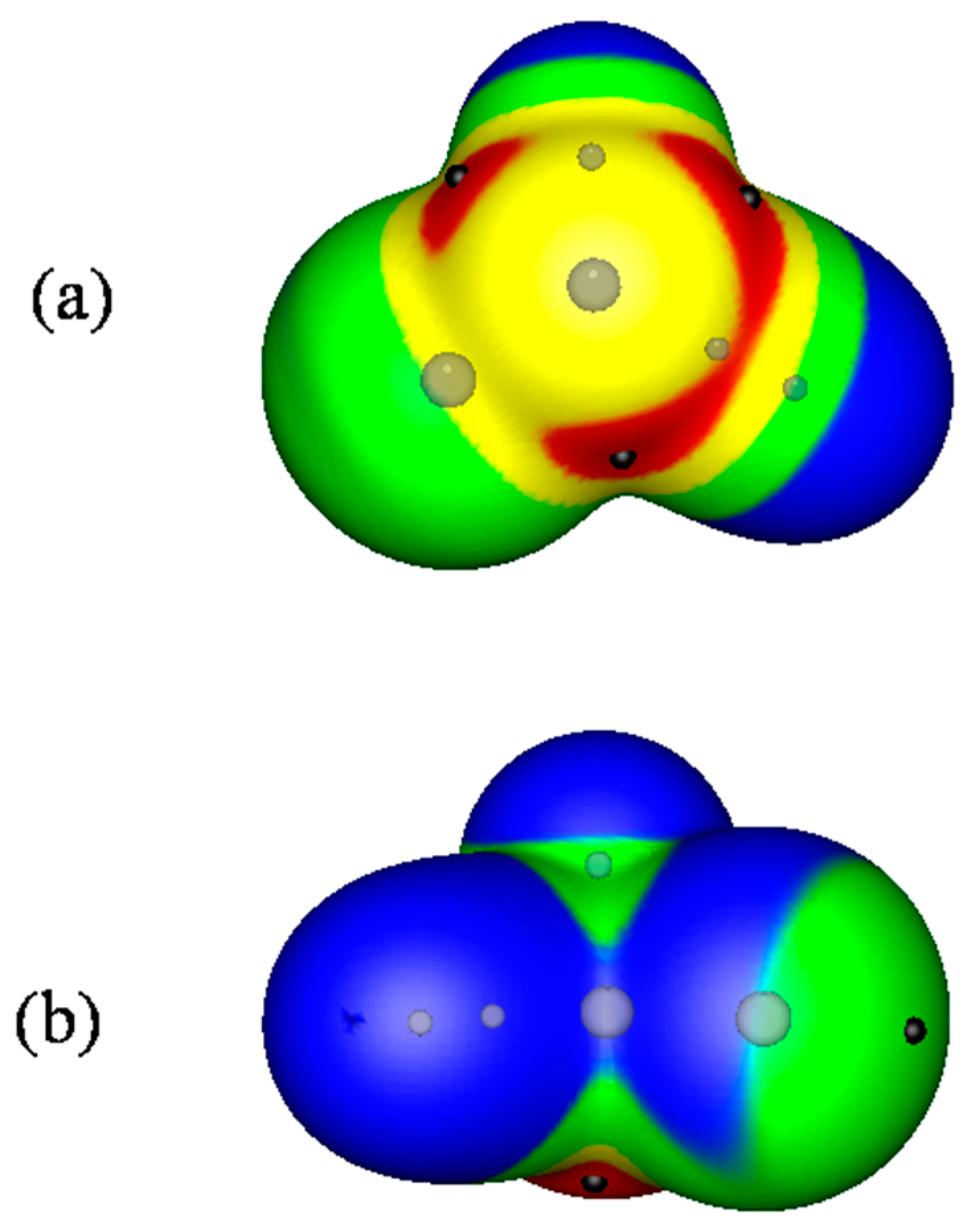
2.1. Locations and Strengths of Positive Potentials
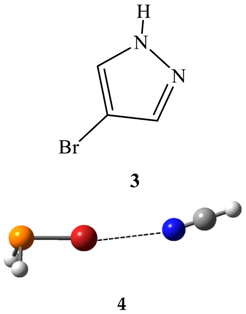
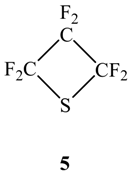
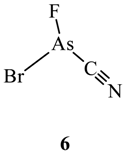

2.2. Van der Waals Radii and Close Contacts


3. Discussion and Summary
- It cannot be assumed that, in general, regions of higher electronic density will have negative electrostatic potentials and that regions of lower electronic density will have positive ones. The electrostatic potential reflects the effects of the nuclei as well as the electrons.
- A corollary to this is that the electrostatic potential in a given region is not determined only by the electrons and nuclei in that region but also by those in the remainder of the molecule, particularly those in neighboring portions.
- A σ-hole is a region of lower electronic density on the extension of a covalent bond, not a region of electrostatic potential.
- Noncovalent interactions are between positive and negative regions, and these may not be associated with specific atoms. Accordingly, close contacts between atoms are not always a reliable indicator of the actual interactions.
Author Contributions
Conflicts of Interest
References
- Workshop on Modeling Interactions in Biomolecules II, Prague, 5–9 September 2005. Available online: http://physics.mff.cuni.cz/kchfo/workshop05/ (accessed on 23 June 2017).
- Clark, T.; Hennemann, M.; Murray, J.S.; Politzer, P. Halogen bonding: The σ-hole. J. Mol. Model. 2007, 13, 291–296. [Google Scholar] [CrossRef] [PubMed]
- Guthrie, F. XXVIII. On the iodide of iodammonium. J. Chem. Soc. 1863, 16, 239–244. [Google Scholar] [CrossRef]
- Remsen, I.; Norris, J.F. The action of the halogens on the methylamines. Am. Chem. J. 1896, 18, 90–95. [Google Scholar]
- Benesi, H.A.; Hildebrand, J.H. Ultraviolet absorption bands of iodine in aromatic hydrocarbons. J. Am. Chem. Soc. 1948, 70, 2832–2833. [Google Scholar] [CrossRef]
- Benesi, H.A.; Hildebrand, J.H. A spectrophotometric investigation of the interaction of iodine with aromatic hydrocarbons. J. Am. Chem. Soc. 1949, 71, 2703–2707. [Google Scholar] [CrossRef]
- Slifkin, M.A. Charge Transfer Interactions of Biomolecules; Academic Press: London, UK, 1971. [Google Scholar]
- Di Paolo, T.; Sandorfy, C. On the hydrogen bond breaking ability of fluorocarbons containing higher halogens. Can. J. Chem. 1974, 52, 3612–3622. [Google Scholar] [CrossRef]
- Dumas, J.-M.; Kern, M.; Janier-Dubry, J.L. Cryoscopic and Calorimetric Study of MX4-Polar Organic Base Interactions (M = C, Si, X = Cl, Br)—Influence of Element and of Halogen. Bull. Soc. Chim. Fr. 1976, 11, 1785–1790. [Google Scholar]
- Blackstock, S.C.; Lorand, J.P.; Kochi, J.K. Charge-Transfer Interactions of Amines with Tetrahalomethanes. X-ray Crystal Structures of the Donor-Acceptor Complexes of Quinuclidine and Diazabicyclo[2.2.2]octane with Carbon Tetrabromide. J. Org. Chem. 1987, 52, 1451–1460. [Google Scholar] [CrossRef]
- Hassel, O.; Rømming, C. Direct Structural Evidence for Weak Charge Transfer Bonds in Solids Containing Chemically Saturated Molecules. Quart. Rev. Chem. Soc. 1962, 16, 1–18. [Google Scholar] [CrossRef]
- Bent, H.A. Structural Chemistry of Donor-Acceptor Interactions. Chem. Rev. 1968, 68, 587–648. [Google Scholar] [CrossRef]
- Ramasubbu, N.; Parthasarathy, R.; Murray-Rust, P. Angular Preferences of Intermolecular Forces around Halogen Centers: Preferred Directions of Approach of Electrophiles and Nucleophiles around Carbon-Halogen Bond. J. Am. Chem. Soc. 1986, 108, 4308–4314. [Google Scholar] [CrossRef]
- Mulliken, R.S. Molecular Compounds and Their Spectra. II. J. Am. Chem. Soc. 1952, 74, 811–824. [Google Scholar] [CrossRef]
- Flurry, R.L., Jr. Molecular Orbital Theory of Electron Donor-Acceptor Complexes. I. A Simple Semiempirical Treatment. J. Phys. Chem. 1969, 69, 1927–1933. [Google Scholar] [CrossRef]
- Flurry, R.L., Jr. Molecular Orbital Theory of Electron Donor-Acceptor Complexes. II. Charged Donors and Acceptors. J. Phys. Chem. 1969, 73, 2111–2117. [Google Scholar] [CrossRef]
- Dewar, M.J.S.; Thompson, C.C. Π-Molecular complexes—III: A critique for charge-transfer, and stability constants for some TCNE-hydrocarbon complexes. Tetrahedron 1966, 7, 97–114. [Google Scholar] [CrossRef]
- Stewart, R.F. On the mapping of electrostatic properties from bragg diffraction data. Chem. Phys. Lett. 1979, 65, 335–342. [Google Scholar] [CrossRef]
- Politzer, P.; Truhlar, D.G. (Eds.) Chemical Applications of Atomic and Molecular Electrostatic Potentials; Plenum Press: New York, NY, USA, 1981. [Google Scholar]
- Klein, C.L.; Stevens, E.D. Charge Density Studies of Drug Molecules. In Structure and Reactivity; Liebman, J.F., Goldberg, A., Eds.; VCH Publishers: New York, NY, USA, 1988; pp. 26–64. [Google Scholar]
- Stone, A.J.; Price, S.L. some new ideas in the theory of intermolecular forces: Anisotropic atom-atom potentials. J. Phys. Chem. 1988, 92, 3325–3335. [Google Scholar] [CrossRef]
- Price, S.L. Applications of realistic electrostatic modelling to molecules in complexes, solids and proteins. J. Chem. Soc. Faraday Trans. 1996, 92, 2997–3008. [Google Scholar] [CrossRef]
- Wiberg, K.B.; Rablen, P.R. Comparison of atomic charges derived via different procedures. J. Comput. Chem. 1993, 14, 1504–1518. [Google Scholar] [CrossRef]
- Murray, J.S.; Politzer, P. The electrostatic potential: An overview. WIREs Comput. Mol. Sci. 2011, 1, 153–163. [Google Scholar] [CrossRef]
- Kollman, P. A general analysis of noncovalent intermolecular interactions. J. Am. Chem. Soc. 1977, 99, 4875–4894. [Google Scholar] [CrossRef]
- Stevens, E.D. Experimental electron density distributions of molecular chlorine. Mol. Phys. 1979, 37, 27–45. [Google Scholar] [CrossRef]
- Tsirelson, V.G.; Zou, P.F.; Tang, T.-H.; Bader, R.F.W. Topological definition of crystal structure determination of the bonded interactions in solid molecular chlorine. Acta Cryst. A 1995, 51, 143–153. [Google Scholar] [CrossRef]
- Brinck, T.; Murray, J.S.; Politzer, P. Surface electrostatic potentials of halogenated methanes as indicators of directional intermolecular interactions. Int. J. Quantum Chem. 1992, 44, 57–64. [Google Scholar] [CrossRef]
- Brinck, T.; Murray, J.S.; Politzer, P. Molecular electrostatic potentials and local ionization energies of group V–VII hydrides and their anions. Relationships for aqueous and gas-phase acidities. Int. J. Quantum Chem. 1993, 48, 73–88. [Google Scholar] [CrossRef]
- Bader, R.F.W.; Carroll, M.T.; Cheeseman, J.R.; Chang, C. Properties of atoms in molecules: Atomic volumes. J. Am. Chem. Soc. 1987, 109, 7968–7979. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S.; Concha, M.C. σ-Hole bonding between like atoms. A fallacy of atomic charges. J. Mol. Model. 2008, 14, 659–665. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09; Revision A.1; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Bulat, F.A.; Toro-Labbé, A.; Brinck, T.; Murray, J.S.; Politzer, P. Quantitative analysis of molecular surface properties. J. Mol. Model. 2010, 16, 1679–1691. [Google Scholar] [CrossRef] [PubMed]
- Riley, K.E.; Tran, K.; Lane, P.; Murray, J.S.; Politzer, P. Comparative analysis of electrostatic potential maxima and minima on molecular surfaces, as determined by three methods and a variety of basis sets. J. Comput. Sci. 2016, 17, 273–284. [Google Scholar] [CrossRef]
- Row, T.N.G.; Parthasarathy, R. Directional preferences of nonbonded atomic contacts with divalent sulfur in terms of its orbital orientations. 2. S---S interactions and nonspherical shape of sulfur in crystals. J. Am. Chem. Soc. 1981, 103, 477–479. [Google Scholar] [CrossRef]
- Nyburg, S.C.; Faerman, C.H. A revision of van der waals atomic radii for molecular crystals: N, O, F, S, Cl, Se, Br and I bonded to carbon. Acta Crystallogr. Sect. B Struct. Sci. 1985, 41, 274–279. [Google Scholar] [CrossRef]
- Ramasubbu, N.; Parthasarathy, R. Stereochemistry of incipient electrophilic and nucleophilic reactions at divalent selenium center: Electrophilic-nucleophilic pairing and anisotropic shape of Se in Se---Se interactions. Phosphorus Sulfur 1987, 31, 221–229. [Google Scholar] [CrossRef]
- Ikuta, S. Anisotropy of electron density distribution around atoms in molecules: N, P, O and S atoms. J. Mol. Struct. (Theochem) 1990, 205, 191–201. [Google Scholar] [CrossRef]
- Awwadi, F.F.; Willett, R.D.; Peterson, K.A.; Twamley, B. The nature of halogen-halogen synthons: crystallographic and theoretical studies. Chem. Eur. J. 2006, 12, 8952–8960. [Google Scholar] [CrossRef] [PubMed]
- Eramian, H.; Tian, Y.-H.; Fox, Z.; Beneberu, H.Z.; Kertesz, M. On the anisotropy of van der waals atomic radii of O, S, Se, F, Cl, Br, and I. J. Phys. Chem. A 2013, 117, 14184–14190. [Google Scholar] [CrossRef] [PubMed]
- Murray, J.S.; Lane, P.; Clark, T.; Politzer, P. σ-Hole bonding: molecules containing group VI atoms. J. Mol. Model. 2007, 13, 1033–1038. [Google Scholar] [CrossRef] [PubMed]
- Murray, J.S.; Lane, P.; Politzer, P. A predicted new type of directional noncovalent interaction. Int. J. Quantum Chem. 2007, 107, 2286–2292. [Google Scholar] [CrossRef]
- Murray, J.S.; Lane, P.; Politzer, P. Expansion of the σ-hole concept. J. Mol. Model. 2009, 15, 723–729. [Google Scholar] [CrossRef] [PubMed]
- Rosenfield, R.E., Jr.; Parthasarathy, R.; Dunitz, J.D. Directional preferences of nonbonded atomic contacts with divalent sulfur. 1. electrophiles and nucleophiles. J. Am. Chem. Soc. 1977, 99, 4860–4862. [Google Scholar] [CrossRef]
- Burling, F.T.; Goldstein, B.M. Computational studies of nonbonded sulfur-oxygen and selenium-oxygen interactions in the thiazole and selenazole nucleosides. J. Am. Chem. Soc. 1992, 114, 2313–2320. [Google Scholar] [CrossRef]
- Cozzolino, A.F.; Vargas-Baca, I.; Mansour, S.; Mahmoudkhani, A.H. The nature of the supramolecular association of 1,2,5-chalcogenadiazoles. J. Am. Chem. Soc. 2005, 127, 3184–3190. [Google Scholar] [CrossRef] [PubMed]
- Politzer, P.; Murray, J.S.; Clark, T. Halogen bonding and other σ-hole interactions: A perspective. Phys. Chem. Chem. Phys. 2013, 15, 11178–11189. [Google Scholar] [CrossRef] [PubMed]
- Politzer, P.; Murray, J.S.; Janjić, G.V.; Zarić, S.D. σ-Hole interactions of covalently-bonded nitrogen, phosphorus and arsenic: A survey of crystal structures. Crystals 2014, 4, 12–31. [Google Scholar] [CrossRef]
- Bauzá, A.; Mooibroek, T.J.; Frontera, A. The bright future of unconventional σ/π-hole interactions. ChemPhysChem 2015, 16, 2496–2517. [Google Scholar] [CrossRef] [PubMed]
- Politzer, P.; Murray, J.S. Molecular Electrostatic Potentials and Chemical Reactivity. In Reviews in Computational Chemistry; Lipkowitz, K.B., Boyd, D.B., Eds.; VCH Publishers: New York, NY, USA, 1991; Volume 2, pp. 273–312. [Google Scholar]
- Wheeler, S.E.; Houk, K.N. Through-space effects of substituents dominate molecular electrostatic potentials of substituted arenes. J. Chem. Theory Comput. 2009, 5, 2301–2312. [Google Scholar] [CrossRef] [PubMed]
- Murray, J.S.; Shields, Z.P.-I.; Seybold, P.G.; Politzer, P. Intuitive and counterintuitive noncovalent interactions of aromatic π regions with the hydrogen and the nitrogen of HCN. J. Comput. Sci. 2015, 10, 209–216. [Google Scholar] [CrossRef]
- Murray, J.S.; Politzer, P. Molecular electrostatic potentials and noncovalent interactions. WIREs Comput. Mol. Sci. 2017, in press. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S. σ-Holes and π-Holes: Similarities and differences. J. Comput. Chem. 2017, in press. [Google Scholar] [CrossRef]
- Sen, K.D.; Politzer, P. Characteristic features of the electrostatic potentials of singly-negative monoatomic ions. J. Chem. Phys. 1989, 90, 4370–4372. [Google Scholar] [CrossRef]
- Coppens, P. Experimental electron densities and chemical bonding. Angew. Chem. Int. Ed. 1977, 16, 32–40. [Google Scholar] [CrossRef]
- Feil, D. The electron density distribution in molecular crystals: Exploring the boundary between X-ray diffraction and quantum chemistry. Chem. Scr. 1986, 26, 395–408. [Google Scholar]
- Politzer, P.; Daiker, K.C. Models for Chemical Reactivity. In The Force Concept in Chemistry; Deb, B.M., Ed.; Van Nostrand Reinhold: New York, NY, USA, 1981; pp. 294–387. [Google Scholar]
- Nayak, S.K.; Kumar, V.; Murray, J.S.; Politzer, P.; Terraneo, G.; Pilati, T.; Metrangolo, P.; Resnati, G. Fluorination promotes chalcogen/tetrel bonding in crystalline solids. CrystEngComm 2017, in press. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S. Halogen bonding: An interim discussion. ChemPhysChem 2013, 14, 278–294. [Google Scholar] [CrossRef] [PubMed]
- Murray, J.S.; Macaveiu, L.; Politzer, P. Factors affecting the strengths of σ-hole electrostatic potentials. J. Comput. Sci. 2014, 5, 590–596. [Google Scholar] [CrossRef]
- Metrangolo, P.; Neukirch, H.; Pilati, T.; Resnati, G. Halogen bonding based recognition processes: A world parallel to hydrogen bonding. Acc. Chem. Res. 2005, 38, 386–395. [Google Scholar] [CrossRef] [PubMed]
- Halogen Bonding: Fundamentals and Applications; Metrangolo, P.; Resnati, G. (Eds.) Springer: Berlin, Germany, 2008. [Google Scholar]
- Politzer, P.; Murray, J.S.; Concha, M.C. Halogen bonding and the design of new materials: Organic bromides, chlorides and even fluorides as donors. J. Mol. Model. 2007, 13, 643–650. [Google Scholar] [CrossRef] [PubMed]
- Chopra, D.; Row, T.N.G. Role of organic fluorine in crystal engineering. CrystEngComm 2011, 13, 2175–2186. [Google Scholar] [CrossRef]
- Metrangolo, P.; Murray, J.S.; Pilati, T.; Politzer, P.; Resnati, G.; Terraneo, G. Fluorine-centered halogen bonding: A factor in recognition phenomena and reactivity. Cryst. Growth Des. 2011, 11, 4238–4246. [Google Scholar] [CrossRef]
- March, J. Advanced Organic Chemistry, 3rd ed.; Wiley: New York, NY, USA, 1985; p. 247. [Google Scholar]
- Bundhun, A.; Ramasami, P.; Murray, J.S.; Politzer, P. Trends in σ-hole strengths and interactions of F3MX molecules (M = C, Si, Ge and X = F, Cl, Br, I). J. Mol. Model. 2013, 19, 2739–2746. [Google Scholar] [CrossRef] [PubMed]
- Dance, I. Distance criteria for crystal packing analysis of supramolecular motifs. New J. Chem. 2003, 27, 22–27. [Google Scholar] [CrossRef]
- Alvarez, S. A cartography of the van der waals territories. Dalton Trans. 2013, 42, 8617–8636. [Google Scholar] [CrossRef] [PubMed]
- Murray, J.S.; Politzer, P. In search of the “impenetrable” volume of a molecule in a noncovalent complex. Mol. Phys. 2017, in press. [Google Scholar]
- Rowland, R.S.; Taylor, R. Intermolecular nonbonded contact distances in organic crystal structures: Comparison with distances expected from van der waals radii. J. Phys. Chem. 1996, 100, 7384–7391. [Google Scholar] [CrossRef]
- Politzer, P.; Resnati, G.; Murray, J.S. Close contacts and noncovalent interactions in crystals. Faraday Disc. 2017. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S. Quantitative analyses of molecular surface electrostatic potentials in relation to hydrogen bonding and Co-crystallization. Cryst. Growth Des. 2015, 15, 3767–3774. [Google Scholar] [CrossRef]
- Cavallo, G.; Murray, J.S.; Politzer, P.; Pilati, T.; Ursini, M.; Resnati, G. Halogen bonding in hypervalent iodine and bromine derivatives: Halonium salts. IUCrJ 2017, 4, 411–419. [Google Scholar] [CrossRef]
- Etter, M.C.; Urbanczyk-Lipkowska, Z.; Zia-Ebrahimi, M.; Panunto, T.W. Hydrogen bond directed cocrystallization and molecular recognition properties of diarylureas. J. Am. Chem. Soc. 1990, 112, 8415–8426. [Google Scholar] [CrossRef]
- Näther, C.; Döring, C.; Jess, I.; Jones, P.G.; Taouss, C. Thermodynamic and structural relationships between the two polymorphs of 1,3-dimethylurea. Acta Crystallogr. Sect. B Struct. Sci. 2013, 69, 70–76. [Google Scholar] [CrossRef]
- Feynman, R.P. Forces in molecules. Phys. Rev. 1939, 56, 340–343. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S.; Clark, T. σ-Hole bonding: A physical interpretation. Top. Curr. Chem. 2015, 358, 19–42. [Google Scholar] [PubMed]
- Clark, T.; Politzer, P.; Murray, J.S. Correct electrostatic treatment of noncovalent interactions: The importance of polarisation. WIREs Comput. Mol. Sci. 2015, 5, 169–177. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S.; Clark, T. Mathematical modeling and physical reality in noncovalent interactions. J. Mol. Model. 2015, 21, 52. [Google Scholar] [CrossRef] [PubMed]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Politzer, P.; Murray, J.S. σ-Hole Interactions: Perspectives and Misconceptions. Crystals 2017, 7, 212. https://doi.org/10.3390/cryst7070212
Politzer P, Murray JS. σ-Hole Interactions: Perspectives and Misconceptions. Crystals. 2017; 7(7):212. https://doi.org/10.3390/cryst7070212
Chicago/Turabian StylePolitzer, Peter, and Jane S. Murray. 2017. "σ-Hole Interactions: Perspectives and Misconceptions" Crystals 7, no. 7: 212. https://doi.org/10.3390/cryst7070212





