Pb(In1/2Nb1/2)O3–Pb(Mg1/3Nb2/3)O3–PbTiO3 Piezoelectric Single-Crystal Rectangular Beams: Mode-Coupling Effect and Its Application to Ultrasonic Array Transducers
Abstract
:1. Introduction
2. Results and Discussion
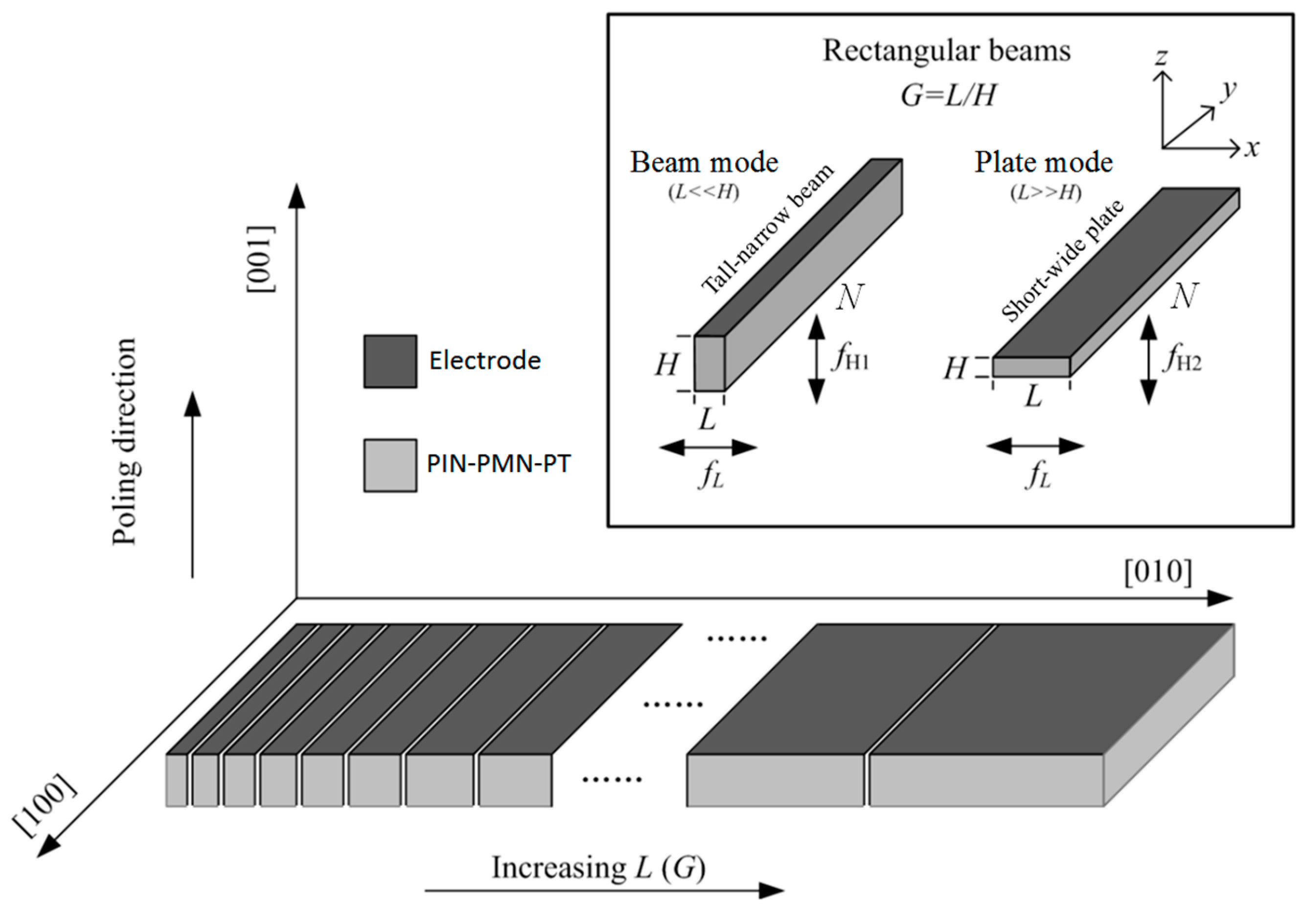
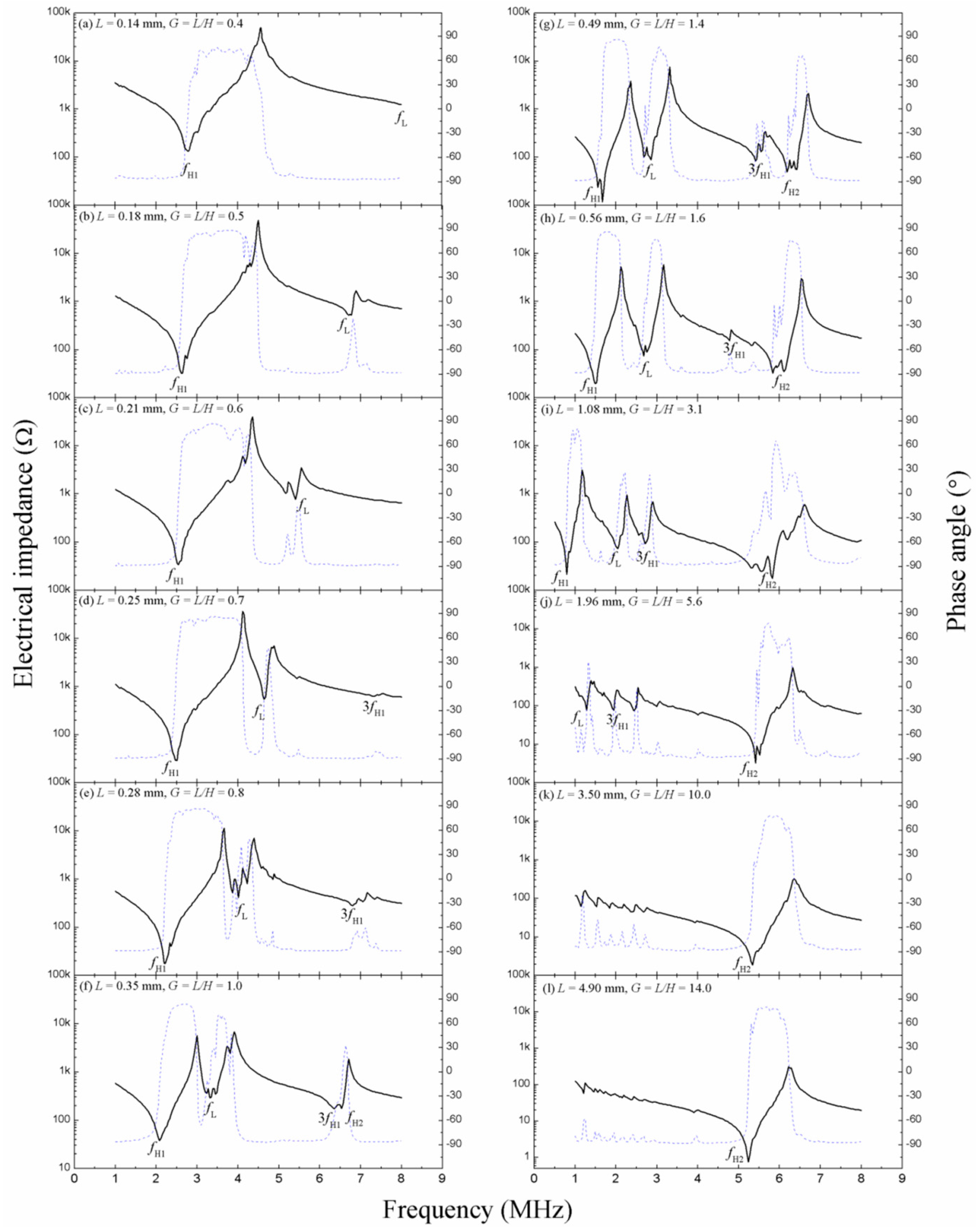
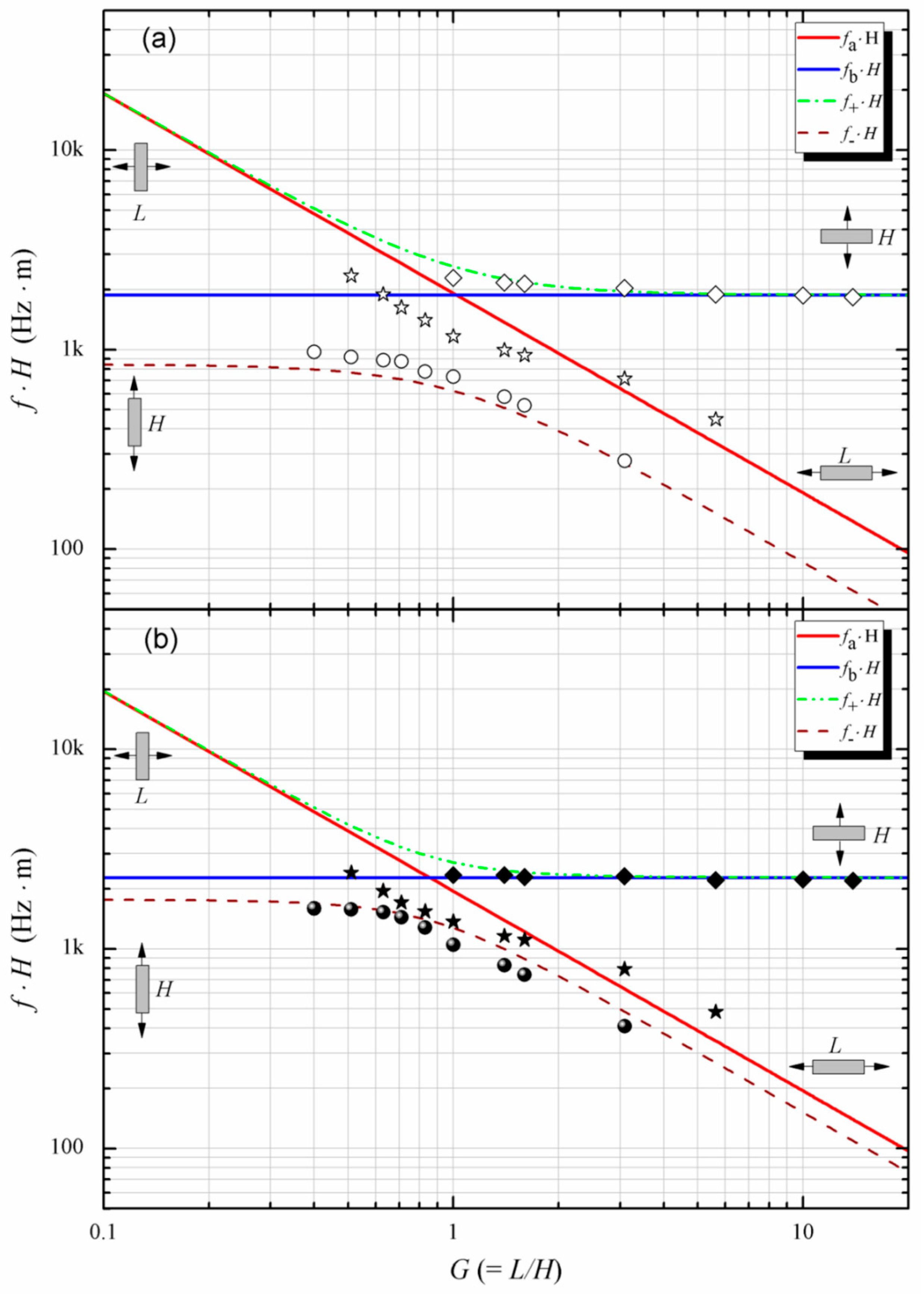
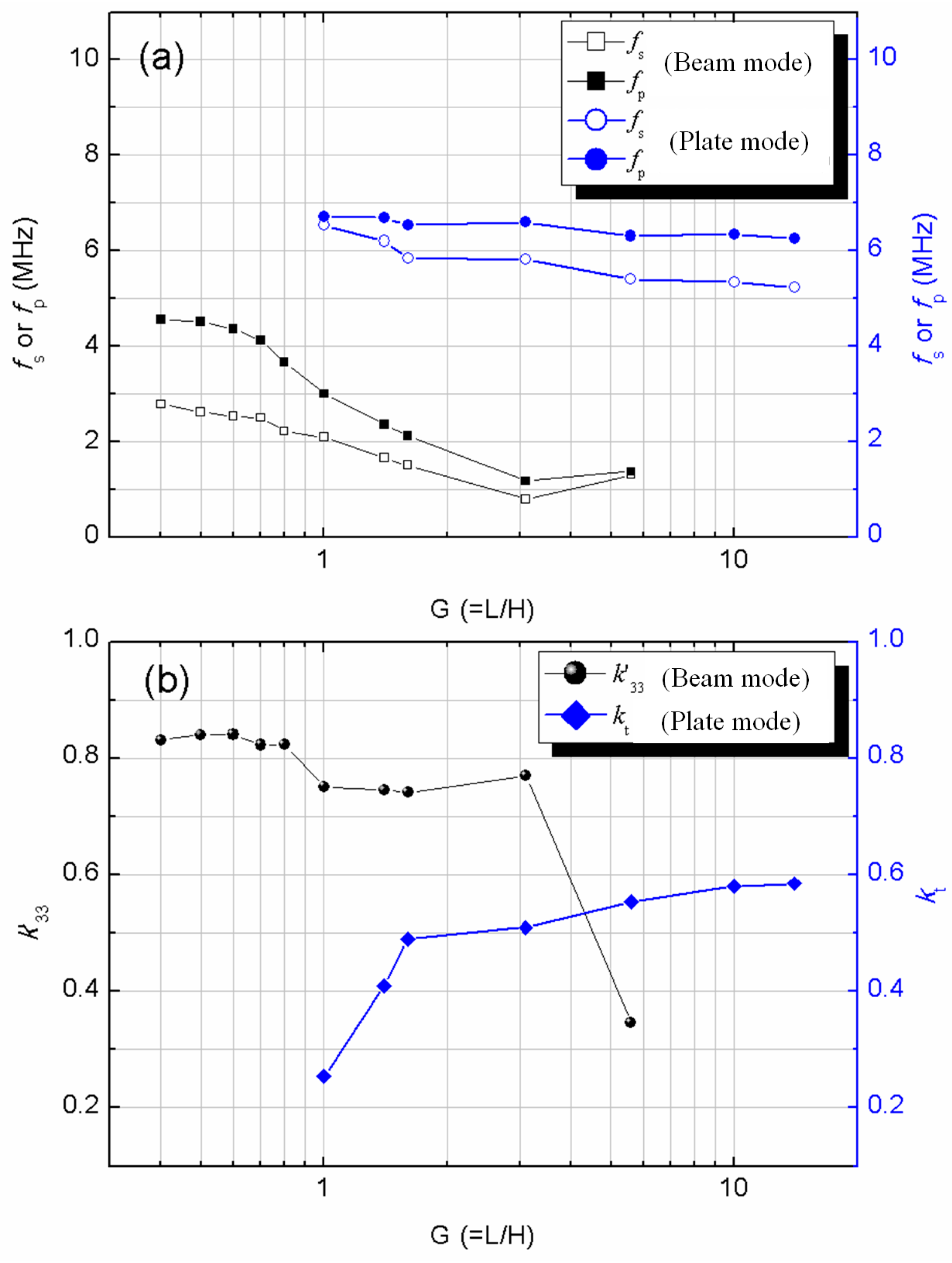
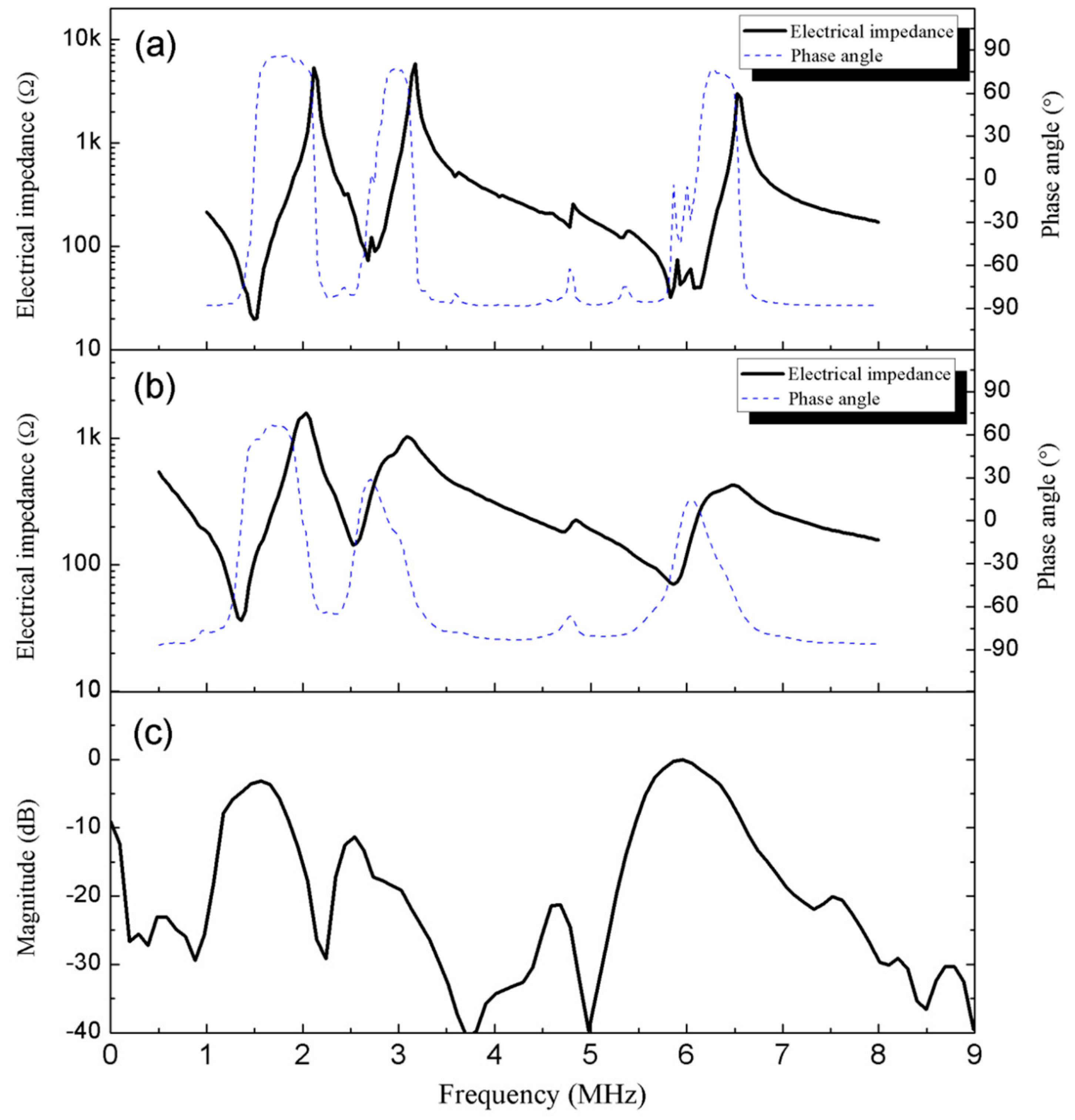
2.1. Mode Coupling Effect in PIN–PMN–PT Rectangular Beams
- (1)
- The height-extensional (beam) mode. When L << H such that G is small, the PIN–PMN–PT rectangular beams become tall-narrow beams and operate in beam mode. The beam mode frequency fH1 is essentially determined by the height H of the PIN–PMN–PT rectangular beams.
- (2)
- The thickness-extensional (plate) mode. When L >> H such that G is large, the PIN–PMN–PT rectangular beams become short-wide plates and operate in plate mode. The plate mode frequency fH2 is determined by the thickness of the short-wide plates which, in turn, corresponds to the height H of the PIN–PMN–PT rectangular beams.
- (3)
- The width (lateral) mode. The lateral mode frequency fL is determined by the width L of the PIN–PMN–PT rectangular beams. When L is comparable with H, coupling of the modes fH1, fH2, and fL occurs. This mode-coupling effect can be predicted using the mode-coupling theory described in the following paragraph [14,15].
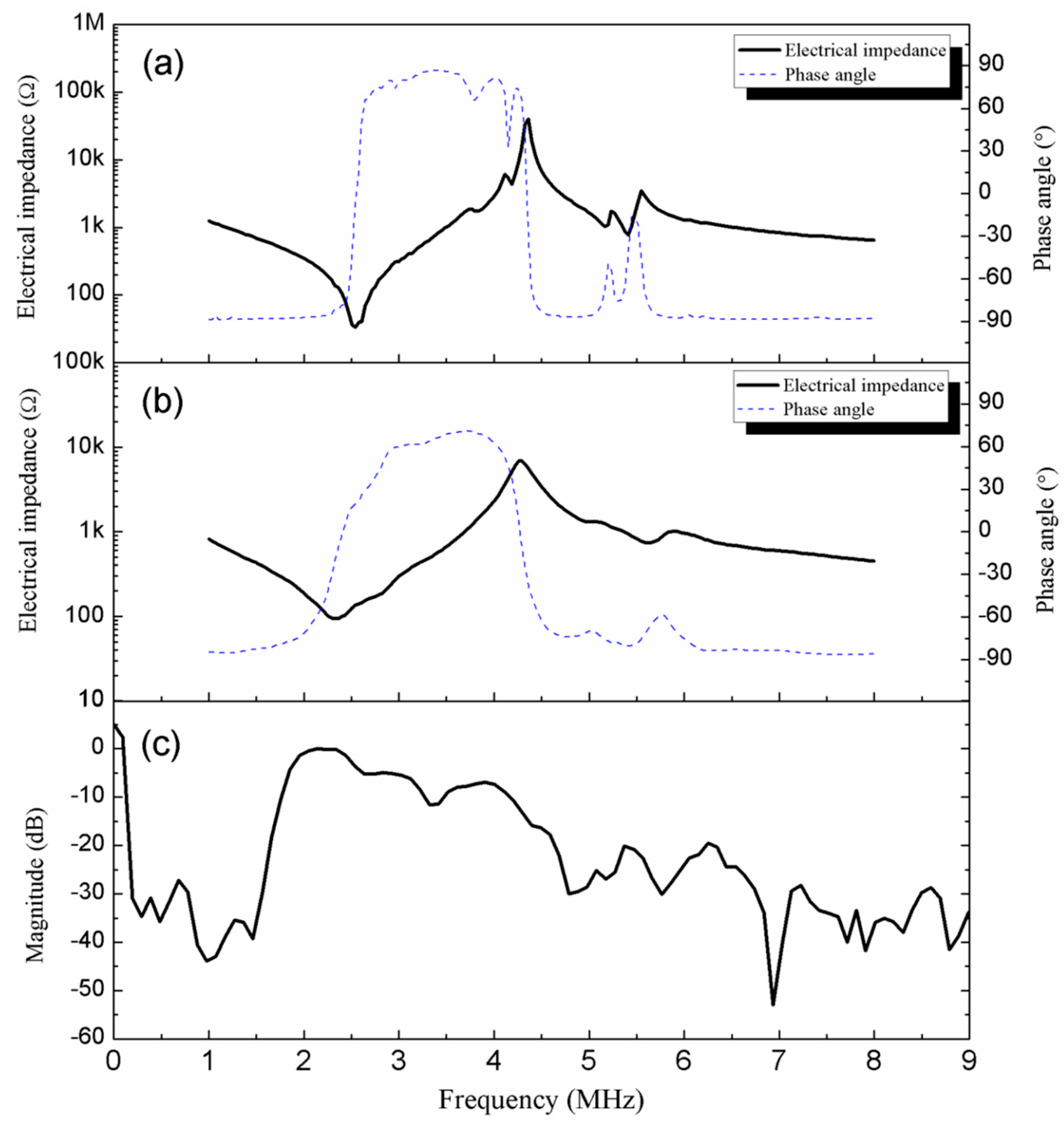
2.2. Performance of PIN–PMN–PT Multifrequency and Single-Frequency Ultrasonic Array Transducers
3. Experiments for Materials and Transducers
3.1. Preparation of PIN–PMN–PT Rectangular Plates and Their Rectangular Beams
3.2. Evaluation of PIN–PMN–PT Rectangular Beams
3.3. Fabrication of PIN–PMN–PT Multifrequency and Single-Frequency Ultrasonic Array Transducers
3.4. Evaluation of PIN–PMN–PT Multifrequency and Single-Frequency Ultrasonic Array Transducers
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhou, D.; Cheung, K.F.; Lam, K.H.; Chen, Y.; Chiu, Y.C.; Dai, J.Y.; Chan, H.L.W.; Luo, H.S. Broad-band and high-temperature ultrasonic transducer fabricated using a Pb(In1/2Nb1/2)O3–Pb(Mg1/3Nb2/3)O3–PbTiO3 single crystal∕epoxy 1–3 composite. Rev. Sci. Instrum. 2011, 82, 055110. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.Y.; Zhao, X.Y.; Wang, W.; Ren, B.; Liu, D.A.; Luo, H.S. Fabrication of PIMNT/epoxy 1–3 composites and ultrasonic transducer for nondestructive evaluation. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2011, 58, 1774–1781. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Wang, S.; Zhang, Y.Y.; Zhao, X.Y.; Luo, H.S. Beam-mode piezoelectric properties of ternary Pb(In1/2Nb1/2)O3–Pb(Mg1/3Nb2/3)O3–PbTiO3 single crystals for medical linear array applications. J. Electron. Mater. 2011, 40, 2228–2233. [Google Scholar] [CrossRef]
- Chen, J.; Panda, R.; Rafter, P.G.; Gururaja, T.R. Wideband Piezoelectric Transducer for Harmonic Imaging. U.S. Patent 6532819 B1, 18 March 2003. [Google Scholar]
- Chen, J.; Panda, R. Review: Commercialization of piezoelectric single crystals for medical imaging applications. IEEE Ultrason. Symp. Proc. 2005, 1, 235–240. [Google Scholar]
- Service, R.F. Shape-changing crystals get shiftier. Science 1997, 275, 1878. [Google Scholar] [CrossRef]
- Lee, H.J.; Zhang, S.J.; Luo, J.; Li, F.; Shrout, T.R. Thickness-dependent properties of relaxor-PbTiO3 ferroelectrics for ultrasonic transducers. Adv. Funct. Mater. 2010, 20, 3154–3162. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Q.F.; Lam, K.H.; Zheng, H.R.; Qiu, W.B.; Shung, K.K. Piezoelectric single crystal ultrasonic transducers for biomedical applications. Prog. Mater. Sci. 2014, 66, 87–111. [Google Scholar] [CrossRef] [PubMed]
- Xu, G.S.; Chen, K.; Yang, D.F.; Li, J.B. Growth and electrical properties of large size Pb(In1/2Nb1/2)O3–Pb(Mg1/3Nb2/3)O3–PbTiO3 crystals prepared by the vertical Bridgeman technique. Appl. Phys. Lett. 2007, 90, 032901. [Google Scholar] [CrossRef]
- Zhang, S.J.; Luo, J.; Hackenberger, W.; Sherlock, N.P.; Meyer, R.J., Jr.; Shrout, T.R. Electromechanical characterization of Pb(In0.5Nb0.5)O3–Pb(Mg1/3Nb2/3)O3–PbTiO3 crystals as a function of crystallographic orientation and temperature. J. Appl. Phys. 2009, 105, 104506. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Zhao, X.Y.; Or, S.W.; Leung, C.M.; Zhang, Y.Y.; Jiao, J.; Luo, H.S. Broadband ultrasonic linear array using ternary PIN–PMN–PT single crystal. Rev. Sci. Instrum. 2012, 83, 095001. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Or, S.W.; Yue, Q.W.; Zhang, Y.Y.; Jiao, J.; Ren, B.; Lin, D.; Leung, C.M.; Zhao, X.Y.; Luo, H.S. Cylindrically shaped ultrasonic linear array fabricated using PIMNT/epoxy 1–3 piezoelectric composite. Sens. Actuators A Phys. 2013, 192, 69–75. [Google Scholar] [CrossRef]
- Wang, W.; Or, S.W.; Yue, Q.W.; Zhang, Y.Y.; Jiao, J.; Leung, C.M.; Zhao, X.Y.; Luo, H.S. Ternary piezoelectric single-crystal PIMNT based 2–2 composite for ultrasonic transducer applications. Sens. Actuators A Phys. 2013, 196, 70–77. [Google Scholar] [CrossRef]
- Bui, T.; Chan, H.L.W.; Unsworth, J. A multifrequency composite ultrasonic transducer system. IEEE Ultrason. Symp. 1988, 2, 627–630. [Google Scholar]
- Or, S.W.; Chan, H.L.W. Mode coupling in lead zirconate titanate/epoxy 1–3 piezocomposite rings. J. Appl. Phys. 2001, 90, 4122–4129. [Google Scholar] [CrossRef]
- Selfridge, A.R. Design and Fabrication of Ultrasonic Transducer Arrays. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1982. [Google Scholar]
- Onoe, M.; Tiersten, H.F. Resonant frequencies of finite piezoelectric ceramic vibrators with high electromechanical coupling. IEEE Trans. Ultrason. Eng. 1963, 10, 32–38. [Google Scholar] [CrossRef]
- Luo, J.; Hackenberger, W.; Zhang, S.J.; Shrout, T.R. Elastic, piezoelectric and dielectric properties of PIN–PMN–PT crystals grown by Bridgman method. IEEE Ultrason. Symp. Proc. 2008, 1–4, 261–264. [Google Scholar]
- Zhang, Y.Y.; Li, X.B.; Liu, D.A.; Zhang, Q.H.; Wang, W.; Ren, B.; Lin, D.; Zhao, X.Y.; Luo, H.S. The compositional segregation, phase structure and properties of Pb(In1/2Nb1/2)O3–Pb(Mg1/3Nb2/3)O3–PbTiO3 single crystal. J. Cryst. Growth 2011, 318, 890–894. [Google Scholar] [CrossRef]
- Wang, W.; Li, X.B.; Or, S.W.; Leung, C.M.; Jiao, J.; Zhang, Y.Y.; Zhao, X.Y.; Luo, H.S. Temperature dependence of dielectric polarization and strain behaviors for rhombohedral PIMNT single crystal with different crystallographic orientations. J. Alloys Compd. 2012, 545, 57–62. [Google Scholar] [CrossRef]
- ANSI/IEEE Std. 176-1987, IEEE Standard on Piezoelectricity; The Institute of Electrical and Electronics Engineers: New York, NY, USA, 1987.
- Kim, M.; Kim, J.S.; Cao, W.W. Aspect ratio dependence of electromechanical coupling coefficient of piezoelectric resonators. Appl. Phys. Lett. 2005, 87, 132901. [Google Scholar] [CrossRef]
- Desilets, C.S.; Fraser, J.D.; Kino, G.S. The design of efficient broad-band piezoelectric transducers. IEEE Trans. Sonics Ultrason. 1978, 25, 115–125. [Google Scholar] [CrossRef]

| kg/m3 | |
| GN/m2 | GN/m2 |
| GN/m2 | GN/m2 |
| GN/m2 | GN/m2 |
| GN/m2 | GN/m2 |
| Design Features and Performance Data | Multifrequency Ultrasonic Array Transducer | Beam-Mode Single-Frequency Ultrasonic Array Transducer | Plate-Mode Single-Frequency Ultrasonic Array Transducer |
|---|---|---|---|
| Width-to-height ratio G | 1.6 | 0.6 | 10.0 |
| Operational mode(s) | Coupled/coexistent beam mode fH1, lateral mode fL, plate mode fH2 | Uncoupled beam mode fH1 | Uncoupled plate mode fH2 |
| Center frequency fC (MHz) | 1.52, 2.60, 6.01 | 2.24 | 5.75 |
| −6 dB bandwidth BW−6dB (%) | 46.5, 18.8, 15.2 | 38.7 | 15.8 |
| Backing layer | Araldite GY251/HY956 (100:18) epoxy layer | ||
| Front matching layer | Nil | ||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Or, S.W.; Luo, H. Pb(In1/2Nb1/2)O3–Pb(Mg1/3Nb2/3)O3–PbTiO3 Piezoelectric Single-Crystal Rectangular Beams: Mode-Coupling Effect and Its Application to Ultrasonic Array Transducers. Crystals 2017, 7, 101. https://doi.org/10.3390/cryst7040101
Wang W, Or SW, Luo H. Pb(In1/2Nb1/2)O3–Pb(Mg1/3Nb2/3)O3–PbTiO3 Piezoelectric Single-Crystal Rectangular Beams: Mode-Coupling Effect and Its Application to Ultrasonic Array Transducers. Crystals. 2017; 7(4):101. https://doi.org/10.3390/cryst7040101
Chicago/Turabian StyleWang, Wei, Siu Wing Or, and Haosu Luo. 2017. "Pb(In1/2Nb1/2)O3–Pb(Mg1/3Nb2/3)O3–PbTiO3 Piezoelectric Single-Crystal Rectangular Beams: Mode-Coupling Effect and Its Application to Ultrasonic Array Transducers" Crystals 7, no. 4: 101. https://doi.org/10.3390/cryst7040101







