Atomistic Studies of Nanoindentation—A Review of Recent Advances
Abstract
:1. Introduction
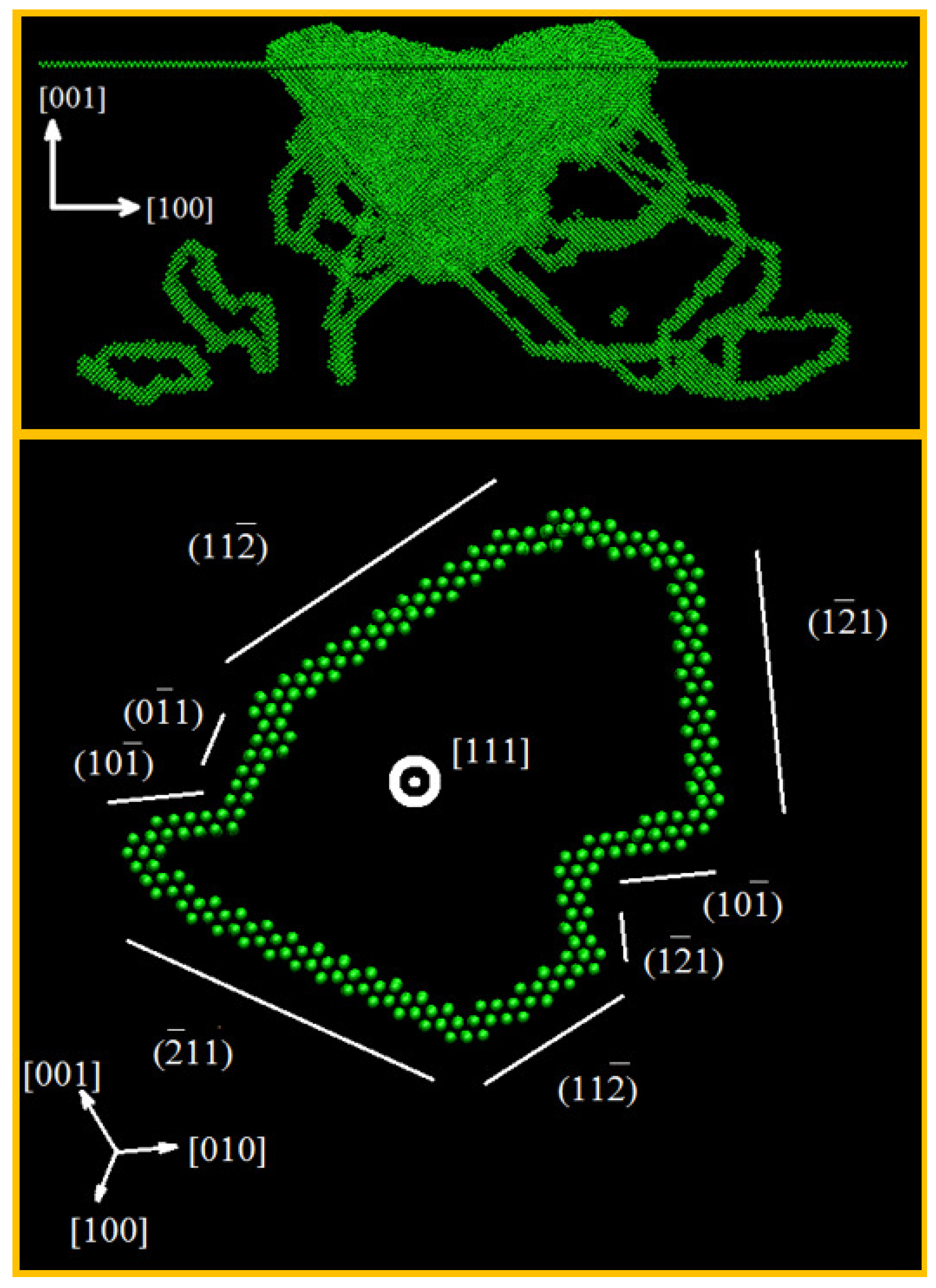
2. Ideal Crystals, Effect of Surface Orientation and Crystallography
2.1. Fcc Metals
2.2. Bcc Metals
2.3. Hcp Metals
2.4. Si
2.5. Other Materials
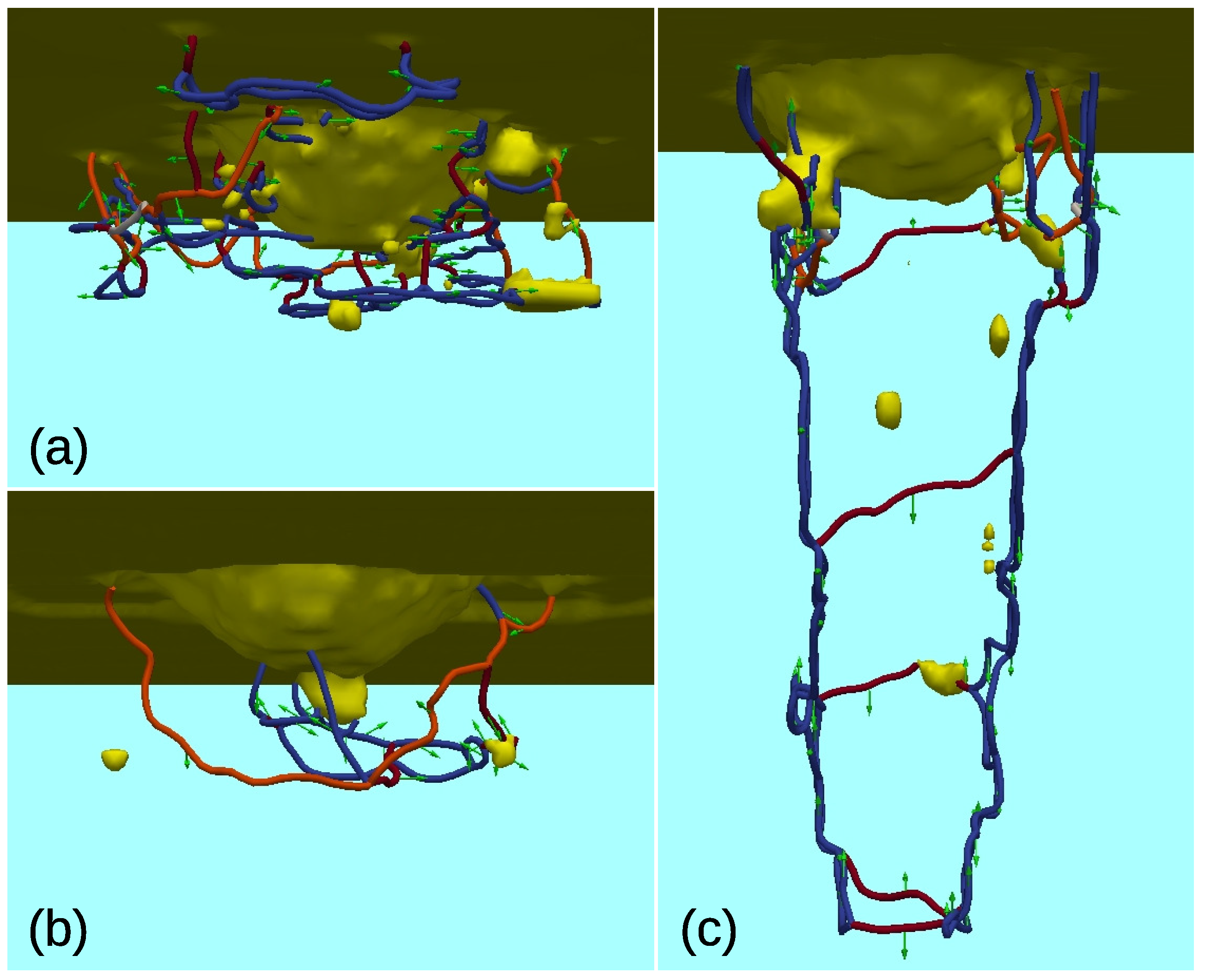
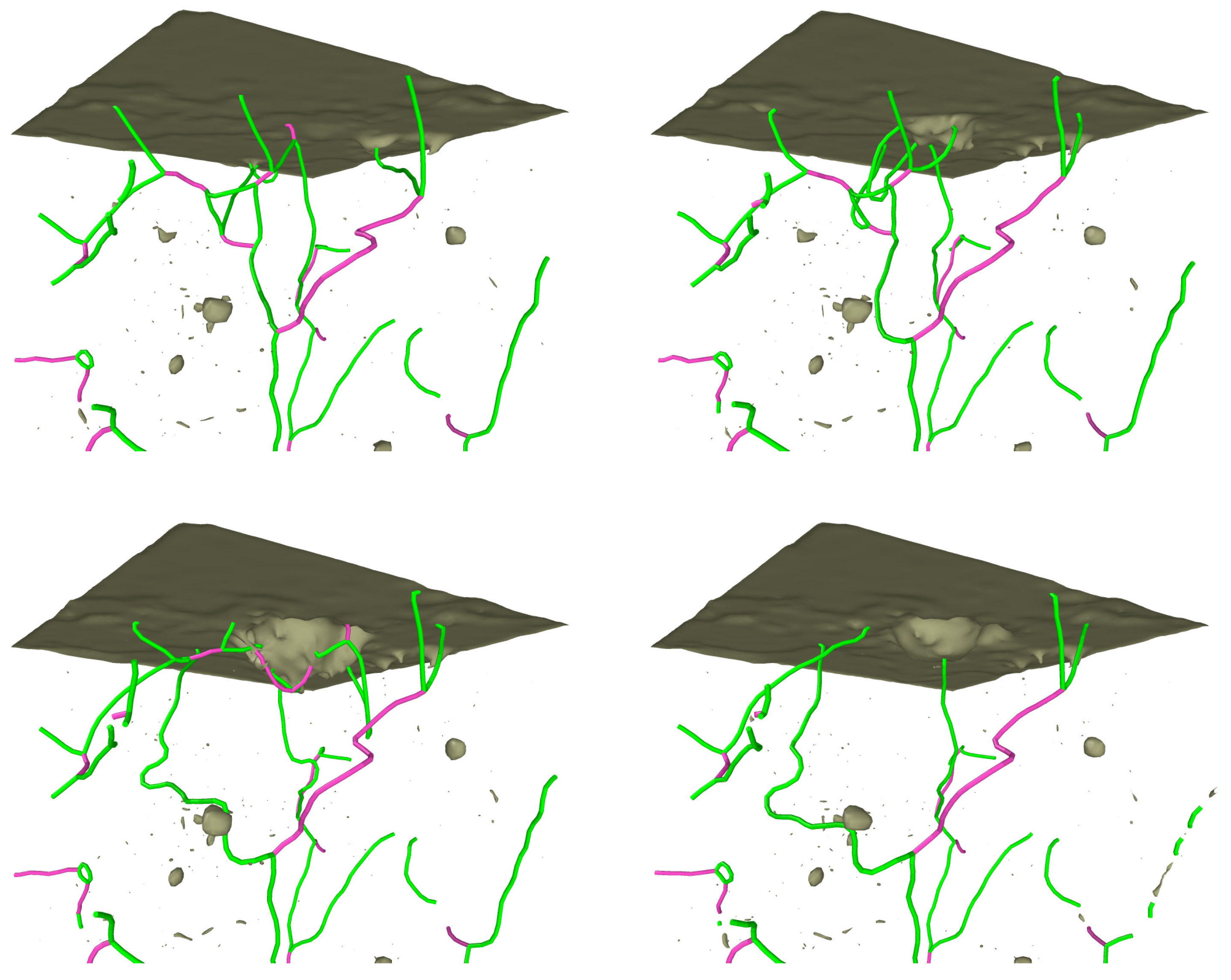
3. Effect of Surface and Bulk Defects on Plasticity
4. Multiple (Sequential, Cyclic) Indentation
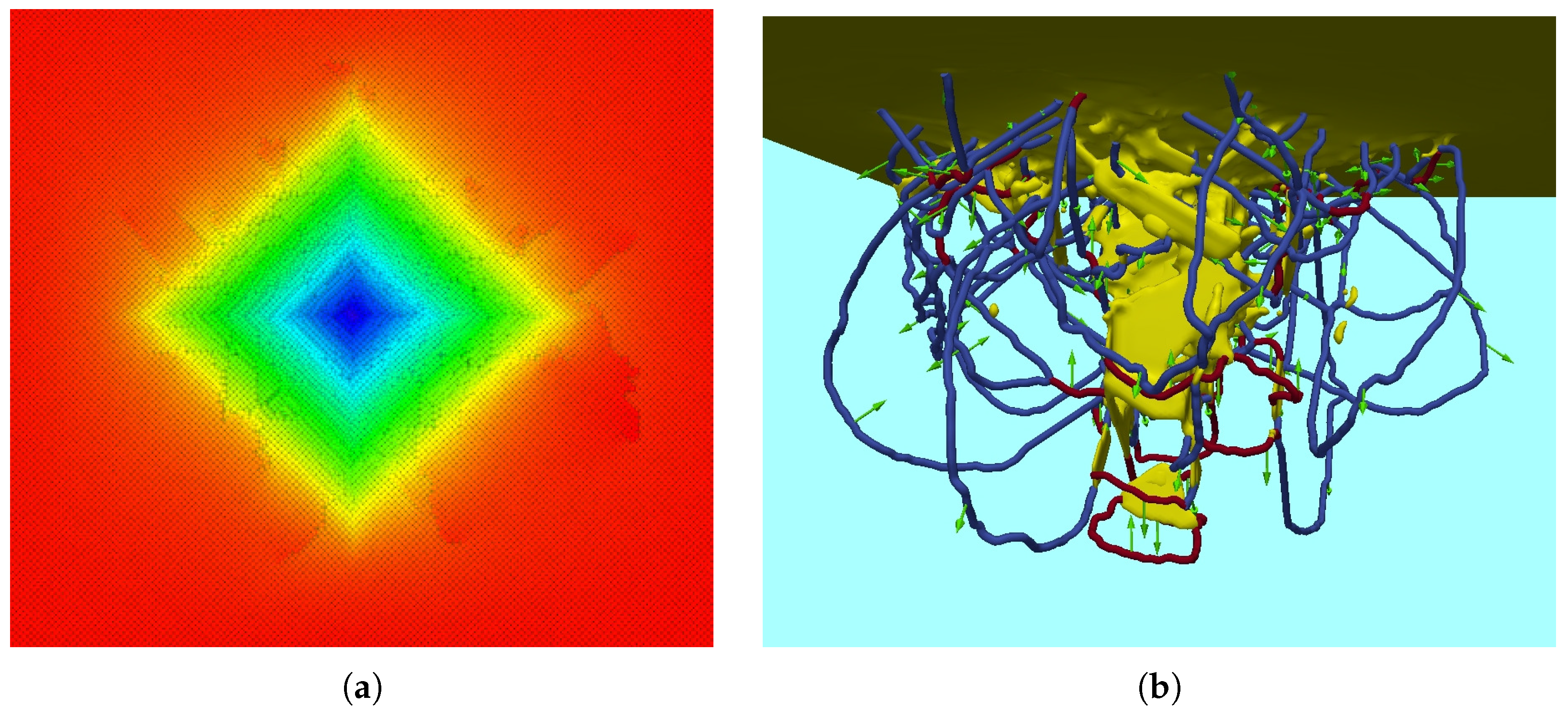
5. Tip Geometry
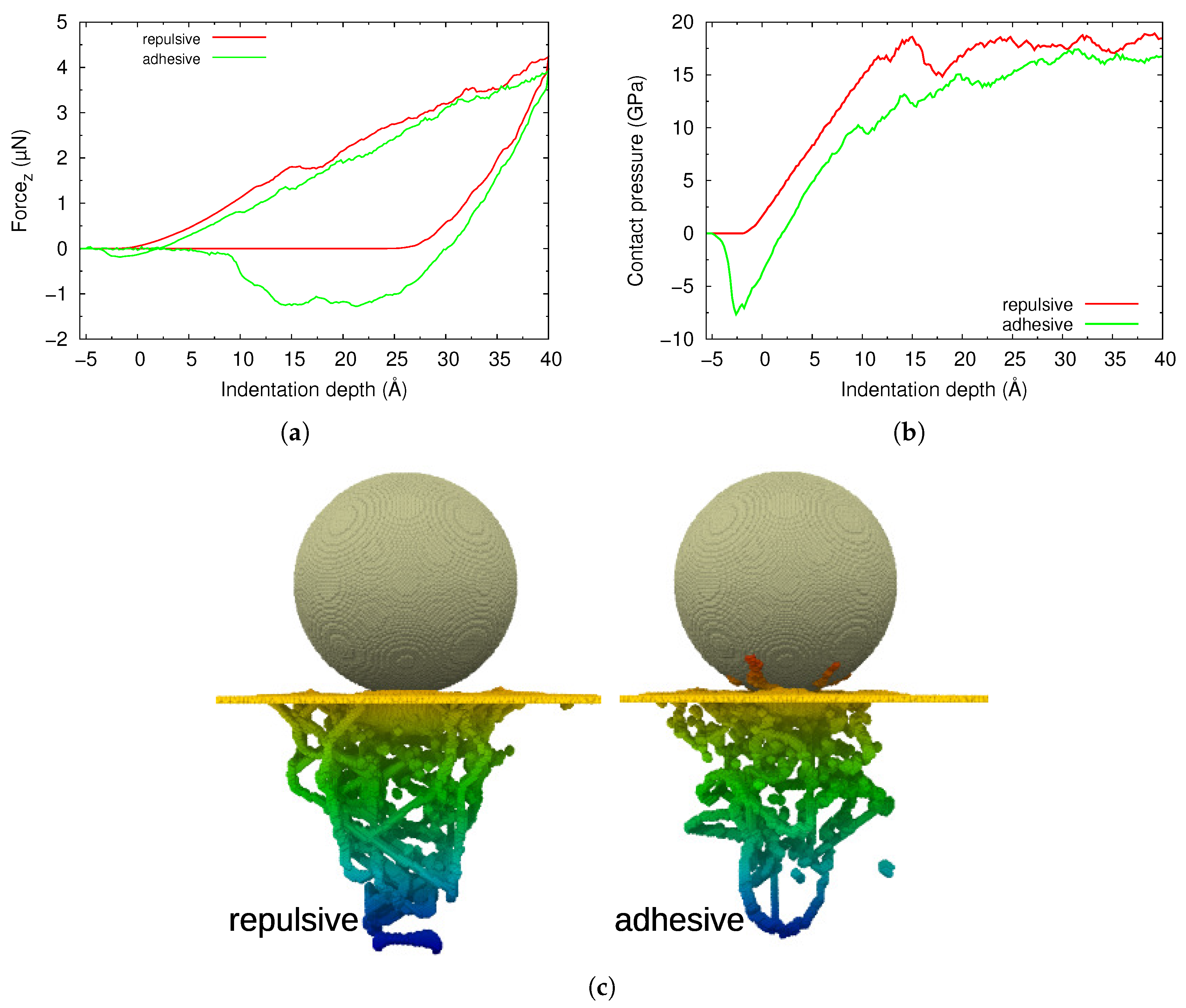
6. Role of Adhesive Forces and Tip Wetting
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| bcc | body centered cubic |
| fcc | face centered cubic |
| hcp | hexagonal close packed |
| nc | nanocrystalline |
| nt | nanotwinned |
| sc | single-crystalline |
| GB | grain boundary |
| MD | molecular dynamics |
| SFE | stacking fault energy |
| TB | twin boundary |
References
- Fischer-Cripps, A.C. Nanoindentation, 2nd ed.; Mechanical Engineering Series; Springer: New York, NY, USA, 2004. [Google Scholar]
- Armstrong, R.W.; Elban, W.L.; Walley, S.M. Elastic, Plastic, Cracking Aspects of the Hardness of Materials. Int. J. Mod. Phys. B 2013, 27, 1330004. [Google Scholar] [CrossRef]
- Weppelmann, E.; Wittling, M.; Swain, M.V.; Munz, D. Indentation Cracking of Brittle Thin Films on Brittle Substrates. In Fracture Mechanics of Ceramics; Bradt, R.C., Hasselman, D.P.H., Munz, D., Sakai, M., Shevchenko, V.Y., Eds.; Springer: Boston, MA, USA, 1996; pp. 475–486. [Google Scholar]
- Volinsky, A.A.; Vella, J.B.; Gerberich, W.W. Fracture toughness, adhesion and mechanical properties of low-K dielectric thin films measured by nanoindentation. Thin Solid Films 2003, 429, 201–210. [Google Scholar] [CrossRef]
- Yang, B.; Riester, L.; Nieh, T. Strain hardening and recovery in a bulk metallic glass under nanoindentation. Scr. Mater. 2006, 54, 1277–1280. [Google Scholar] [CrossRef]
- Bendavid, A.; Martin, P.; Takikawa, H. Deposition and modification of titanium dioxide thin films by filtered arc deposition. Thin Solid Films 2000, 360, 241–249. [Google Scholar] [CrossRef]
- Veprek, S. The search for novel, superhard materials. J. Vac. Sci. Technol. A Vac. Surf. Films 1999, 17, 2401–2420. [Google Scholar] [CrossRef]
- Cuy, J.L.; Mann, A.B.; Livi, K.J.; Teaford, M.F.; Weihs, T.P. Nanoindentation mapping of the mechanical properties of human molar tooth enamel. Arch. Oral Biol. 2002, 47, 281–291. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Palacio, M.L.B.; Bhushan, B. Depth-sensing indentation of nanomaterials and nanostructures. Mater. Charact. 2013, 78, 1–20. [Google Scholar] [CrossRef]
- Luan, B.; Robbins, M.O. The breakdown of continuum models for mechanical contacts. Nature 2005, 435, 929. [Google Scholar] [CrossRef] [PubMed]
- Luan, B.; Robbins, M.O. Hybrid atomistic/continuum study of contact and friction between rough solids. Tribol. Lett. 2009, 36, 1–16. [Google Scholar] [CrossRef]
- Sinnott, S.B.; Heo, S.J.; Brenner, D.W.; Harrison, J.A.; Irving, D.L. Computer Simulations of Nanometer-Scale Indentation and Friction. In Springer Handbook of Nanotechnology; Springer: Berlin/Heidelberg, Germany, 2010; pp. 955–1011. [Google Scholar]
- Landman, U.; Luedtke, W.D.; Burnham, N.A.; Colton, R.J. Atomistic mechanisms and dynamics of adhesion, nanoindentation, and fracture. Science 1990, 248, 454–461. [Google Scholar] [CrossRef] [PubMed]
- Hoover, W.G.; De Groot, A.J.; Hoover, C.G.; Stowers, I.F.; Kawai, T.; Holian, B.L.; Boku, T.; Ihara, S.; Belak, J. Large-scale elastic-plastic indentation simulations via nonequilibrium molecular dynamics. Phys. Rev. A 1990, 42, 5844. [Google Scholar] [CrossRef] [PubMed]
- Harrison, J.A.; White, C.T.; Colton, R.J.; Brenner, D.W. Nanoscale investigation of indentation, adhesion and fracture of diamond (111) surfaces. Surf. Sci. 1992, 271, 57–67. [Google Scholar] [CrossRef]
- Sinnott, S.B.; Colton, R.J.; White, C.T.; Shenderova, O.A.; Brenner, D.W.; Harrison, J.A. Atomistic simulations of the nanometer-scale indentation of amorphous-carbon thin films. J. Vac. Sci. Technol. A Vac. Surf. Films 1997, 15, 936–940. [Google Scholar] [CrossRef]
- Kelchner, C.; Plimpton, S.; Hamilton, J. Dislocation nucleation and defect structure during surface indentation. Phys. Rev. B 1998, 58, 11085–11088. [Google Scholar] [CrossRef]
- Ruestes, C.J.; Bringa, E.M.; Gao, Y.; Urbassek, H.M. Molecular dynamics modeling of nanoindentation. In Applied Nanoindentation in Advanced Materials; Tiwari, A., Natarajan, S., Eds.; Wiley: Chichester, UK, 2017; Chapter 14; pp. 313–345. [Google Scholar]
- Van Vliet, K.; Li, J.; Zhu, T.; Yip, S.; Suresh, S. Quantifying the early stages of plasticity through nanoscale experiments and simulations. Phys. Rev. B 2003, 67, 104105. [Google Scholar] [CrossRef]
- Lee, Y.; Park, J.Y.; Kim, S.Y.; Jun, S.; Im, S. Atomistic simulations of incipient plasticity under Al (111) nanoindentation. Mech. Mater. 2005, 37, 1035–1048. [Google Scholar] [CrossRef]
- Zimmerman, J.A.; Kelchner, C.L.; Klein, P.A.; Hamilton, J.C.; Foiles, S.M. Surface Step Effects on Nanoindentation. Phys. Rev. Lett. 2001, 87, 165507. [Google Scholar] [CrossRef] [PubMed]
- Ziegenhain, G.; Urbassek, H.M. Effect of material stiffness on hardness: A computational study based on model potentials. Philos. Mag. 2009, 89, 2225–2238. [Google Scholar] [CrossRef]
- Ziegenhain, G.; Hartmaier, A.; Urbassek, H.M. Pair vs. many-body potentials: Influence on elastic and plastic behavior in nanoindentation of fcc metals. J. Mech. Phys. Solids 2009, 57, 1514–1526. [Google Scholar] [CrossRef]
- Ziegenhain, G.; Urbassek, H.M.; Hartmaier, A. Influence of crystal anisotropy on elastic deformation and onset of plasticity in nanoindentation: A simulational study. J. Appl. Phys. 2010, 107, 061807. [Google Scholar] [CrossRef]
- Gao, Y.; Ruestes, C.J.; Tramontina, D.R.; Urbassek, H.M. Comparative simulation study of the structure of the plastic zone produced by nanoindentation. J. Mech. Phys. Solids 2015, 75, 58–75. [Google Scholar] [CrossRef]
- Li, Y.; Goyal, A.; Chernatynskiy, A.; Jayashankar, J.S.; Kautzky, M.C.; Sinnott, S.B.; Phillpot, S.R. Nanoindentation of gold and gold alloys by molecular dynamics simulation. Mater. Sci. Eng. A 2016, 651, 346–357. [Google Scholar]
- Begau, C.; Hua, J.; Hartmaier, A. A novel approach to study dislocation density tensors and lattice rotation patterns in atomistic simulations. J. Mech. Phys. Solids 2012, 60, 711–722. [Google Scholar] [CrossRef]
- Yaghoobi, M.; Voyiadjis, G.Z. Atomistic simulation of size effects in single-crystalline metals of confined volumes during nanoindentation. Comput. Mater. Sci. 2016, 111, 64–73. [Google Scholar] [CrossRef]
- Hagelaar, J.H.A.; Bitzek, E.; Flipse, C.F.J.; Gumbsch, P. Atomistic simulations of the formation and destruction of nanoindentation contacts in tungsten. Phys. Rev. B 2006, 73, 045425. [Google Scholar] [CrossRef]
- Alcalá, J.; Dalmau, R.; Franke, O.; Biener, M.; Biener, J.; Hodge, A. Planar Defect Nucleation and Annihilation Mechanisms in Nanocontact Plasticity of Metal Surfaces. Phys. Rev. Lett. 2012, 109, 075502. [Google Scholar] [CrossRef] [PubMed]
- Remington, T.P.; Ruestes, C.J.; Bringa, E.M.; Remington, B.A.; Lu, C.H.; Kad, B.; Meyers, M.A. Plastic deformation in nanoindentation of tantalum: A new mechanism for prismatic loop formation. Acta Mater. 2014, 78, 378–393. [Google Scholar] [CrossRef]
- Ruestes, C.J.; Stukowski, A.; Tang, Y.; Tramontina, D.R.; Erhart, P.; Remington, B.A.; Urbassek, H.M.; Meyers, M.A.; Bringa, E.M. Atomistic simulation of tantalum nanoindentation: Effects of indenter diameter, penetration velocity, and interatomic potentials on defect mechanisms and evolution. Mater. Sci. Eng. A 2014, 613, 390–403. [Google Scholar] [CrossRef]
- Goel, S.; Beake, B.; Chan, C.W.; Faisal, N.H.; Dunne, N. Twinning anisotropy of tantalum during nanoindentation. Mater. Sci. Eng. A 2015, 627, 249–261. [Google Scholar] [CrossRef] [Green Version]
- Zambaldi, C.; Zehnder, C.; Raabe, D. Orientation dependent deformation by slip and twinning in magnesium during single crystal indentation. Acta Mater. 2015, 91, 267–288. [Google Scholar] [CrossRef]
- Sánchez-Martín, R.; Zambaldi, C.; Pérez-Prado, M.T.; Molina-Aldareguia, J.M. High temperature deformation mechanisms in pure magnesium studied by nanoindentation. Scr. Mater. 2015, 104, 9–12. [Google Scholar] [CrossRef]
- Somekawa, H.; Tsuru, T.; Singh, A.; Miura, S.; Schuh, C.A. Effect of crystal orientation on incipient plasticity during nanoindentation of magnesium. Acta Mater. 2017, 139, 21–29. [Google Scholar] [CrossRef]
- Lu, Z.; Chernatynskiy, A.; Noordhoek, M.J.; Sinnott, S.B.; Phillpot, S.R. Nanoindentation of Zr by Molecular Dynamics Simulation. J. Nucl. Mater. 2015, 467, 742–757. [Google Scholar]
- Alabd Alhafez, I.; Ruestes, C.J.; Gao, Y.; Urbassek, H.M. Nanoindentation of hcp metals: A comparative simulation study of the evolution of dislocation networks. Nanotechnology 2016, 27, 045706. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.E.; Oh, S.I. Atomistic simulation of structural phase transformations in monocrystalline silicon induced by nanoindentation. Nanotechnology 2006, 17, 2259. [Google Scholar] [CrossRef]
- Mylvaganam, K.; Zhang, L.C.; Eyben, P.; Mody, J.; Vandervorst, W. Evolution of metastable phases in silicon during nanoindentation: mechanism analysis and experimental verification. Nanotechnology 2009, 20, 305705. [Google Scholar] [CrossRef] [PubMed]
- Goel, S.; Faisal, N.H.; Luo, X.; Yan, J.; Agrawal, A. Nanoindentation of polysilicon and single crystal silicon: Molecular dynamics simulation and experimental validation. J. Phys. D 2014, 47, 275304. [Google Scholar] [CrossRef]
- Du, X.; Zhao, H.; Zhang, L.; Yang, Y.; Xu, H.; Fu, H.; Li, L. Molecular dynamics investigations of mechanical behaviours in monocrystalline silicon due to nanoindentation at cryogenic temperatures and room temperature. Sci. Rep. 2015, 5, 16275. [Google Scholar] [CrossRef] [PubMed]
- Mylvaganam, K.; Zhang, L. Effect of crystal orientation on the formation of bct-5 silicon. Appl. Phys. A 2015, 120, 1391–1398. [Google Scholar] [CrossRef]
- Zhang, Z.; Stukowski, A.; Urbassek, H.M. Interplay of dislocation-based plasticity and phase transformation during Si nanoindentation. Comput. Mater. Sci. 2016, 119, 82–89. [Google Scholar] [CrossRef]
- Zhang, Z.; Urbassek, H.M. Comparative study of interatomic interaction potentials for describing indentation into Si using molecular dynamics simulation. Appl. Mech. Mater. 2017, 869, 3–8. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, J.; Wang, Z.; Hartmaier, A.; Yan, Y.; Sun, T. Interaction between phase transformations and dislocations at incipient plasticity of monocrystalline silicon under nanoindentation. Comput. Mater. Sci. 2017, 131, 55–61. [Google Scholar] [CrossRef]
- Abram, R.; Chrobak, D.; Nowak, R. Origin of a Nanoindentation Pop-in Event in Silicon Crystal. Phys. Rev. Lett. 2017, 118, 095502. [Google Scholar] [CrossRef] [PubMed]
- Stillinger, F.H.; Weber, T.A. Computer simulation of local order in condensed phases of Si. Phys. Rev. B 1985, 31, 5262–5271. [Google Scholar] [CrossRef]
- Tersoff, J. New emprirical approach for the structure and energy of covalent systems. Phys. Rev. B 1988, 37, 6991. [Google Scholar] [CrossRef]
- Chrobak, D.; Kim, K.H.; Kurzydlowski, K.J.; Nowak, R. Nanoindentation experiments with different loading rate distinguish the mechanism of incipient plasticity. Appl. Phys. Lett. 2013, 103, 072101. [Google Scholar] [CrossRef]
- Chrobak, D.; Tymiak, N.; Beaber, A.; Ugurlu, O.; Gerberich, W.W.; Nowak, R. Deconfinement leads to changes in the nanoscale plasticity of silicon. Nat. Nanotechnol. 2011, 6, 480–484. [Google Scholar] [CrossRef] [PubMed]
- Goel, S.; Luo, X.; Agrawal, A.; Reuben, R.L. Diamond machining of silicon: A review of advances in molecular dynamics simulation. Int. J. Mach. Tools Manuf. 2015, 88, 131–164. [Google Scholar] [CrossRef]
- Erhart, P.; Albe, K. Analytical potential for atomistic simulations of silicon, carbon, and silicon carbide. Phys. Rev. B 2005, 71, 035211. [Google Scholar] [CrossRef]
- Richter, A.; Ries, R.; Smith, R.; Henkel, M.; Wolf, B. Nanoindentation of diamond, graphite and fullerene films. Diam. Relat. Mater. 2000, 9, 170–184. [Google Scholar] [CrossRef]
- Szlufarska, I.; Nakano, A.; Vashishta, P. A crossover in the mechanical response of nanocrystalline ceramics. Science 2005, 309, 911–914. [Google Scholar] [CrossRef] [PubMed]
- Walsh, P.; Kalia, R.K.; Nakano, A.; Vashishta, P.; Saini, S. Amorphization and anisotropic fracture dynamics during nanoindentation of silicon nitride: A multimillion atom molecular dynamics study. Appl. Phys. Lett. 2000, 77, 4332–4334. [Google Scholar] [CrossRef]
- Chen, Y.C.; Nomura, K.I.; Kalia, R.K.; Nakano, A.; Vashishta, P. Molecular dynamics nanoindentation simulation of an energetic material. Appl. Phys. Lett. 2008, 93, 171908. [Google Scholar] [CrossRef]
- Imran, M.; Hussain, F.; Rashid, M.; Cai, Y.; Ahmad, S.A. Mechanical behavior of Cu-Zr bulk metallic glasses (BMGs): A molecular dynamics approach. Chin. Phys. B 2013, 22, 096101. [Google Scholar] [CrossRef]
- Qiu, C.; Zhu, P.; Fang, F.; Yuan, D.; Shen, X. Study of nanoindentation behavior of amorphous alloy using molecular dynamics. Appl. Surf. Sci. 2014, 305, 101–110. [Google Scholar] [CrossRef]
- Zhao, D.; Zhao, H.; Zhu, B.; Wang, S. Investigation on hardening behavior of metallic glass under cyclic indentation loading via molecular dynamics simulation. Appl. Surf. Sci. 2017, 416, 14–23. [Google Scholar] [CrossRef]
- Feng, Q.; Song, X.; Xie, H.; Wang, H.; Liu, X.; Yin, F. Deformation and plastic coordination in WC-Co composite—Molecular dynamics simulation of nanoindentation. Mater. Des. 2017, 120, 193–203. [Google Scholar] [CrossRef]
- Zhang, Z.; Urbassek, H.M. Indentation into an Al/Si composite: Enhanced dislocation mobility at interface. J. Mater. Sci. 2017, 1–15. [Google Scholar] [CrossRef]
- Li, J.; Fang, Q.; Liu, B.; Liu, Y.; Liu, Y. Atomic-scale analysis of nanoindentation behavior of high-entropy alloy. J. Micromech. Mol. Phys. 2016, 1, 1650001. [Google Scholar] [CrossRef]
- Zhao, Y.; Peng, X.; Fu, T.; Huang, C.; Feng, C.; Yin, D.; Wang, Z. Molecular dynamics simulation of nano-indentation of (111) cubic boron nitride with optimized Tersoff potential. Appl. Surf. Sci. 2016, 382, 309–315. [Google Scholar] [CrossRef]
- Xu, S.; Wan, Q.; Sha, Z.; Liu, Z. Molecular dynamics simulations of nano-indentation and wear of the gamma-Ti-Al alloy. Comput. Mater. Sci. 2015, 110, 247–253. [Google Scholar] [CrossRef]
- Javaid, F.; Stukowski, A.; Durst, K. 3D Dislocation structure evolution in strontium titanate: Spherical indentation experiments and MD simulations. J. Am. Ceram. Soc. 2017, 100, 1134–1145. [Google Scholar] [CrossRef]
- Van Swygenhoven, H.; Derlet, P.M.; Hasnaoui, A. Atomic mechanism for dislocation emission from nanosized grain boundaries. Phys. Rev. B 2002, 66, 024101. [Google Scholar] [CrossRef]
- Van Vliet, K.J.; Tsikata, S.; Suresh, S. Model experiments for direct visualization of grain boundary deformation in nanocrystalline metals. Appl. Phys. Lett. 2003, 83, 1441–1443. [Google Scholar] [CrossRef]
- Feichtinger, D.; Derlet, P.M.; Van Swygenhoven, H. Atomistic simulations of spherical indentations in nanocrystalline gold. Phys. Rev. B 2003, 67, 024113. [Google Scholar] [CrossRef]
- Ma, X.L.; Yang, W. Molecular dynamics simulation on burst and arrest of stacking faults in nanocrystalline Cu under nanoindentation. Nanotechnology 2003, 14, 1208. [Google Scholar] [CrossRef]
- Hasnaoui, A.; Derlet, P.M.; Van Swygenhoven, H. Interaction between dislocations and grain boundaries under an indenter–a molecular dynamics simulation. Acta Mater. 2004, 52, 2251–2258. [Google Scholar] [CrossRef]
- Jang, H.; Farkas, D. Interaction of lattice dislocations with a grain boundary during nanoindentation simulation. Mater. Lett. 2007, 61, 868–871. [Google Scholar] [CrossRef]
- Liu, X.; Yuan, F.; Wei, Y. Grain size effect on the hardness of nanocrystal measured by the nanosize indenter. Appl. Surf. Sci. 2013, 279, 159–166. [Google Scholar] [CrossRef]
- Huang, C.C.; Chiang, T.C.; Fang, T.H. Grain size effect on indentation of nanocrystalline copper. Appl. Surf. Sci. 2015, 353, 494–498. [Google Scholar] [CrossRef]
- Li, J.; Guo, J.; Luo, H.; Fang, Q.; Wu, H.; Zhang, L.; Liu, Y. Study of nanoindentation mechanical response of nanocrystalline structures using molecular dynamics simulations. Appl. Surf. Sci. 2016, 364, 190–200. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Yaghoobi, M. Role of grain boundary on the sources of size effects. Comput. Mater. Sci. 2016, 117, 315–329. [Google Scholar] [CrossRef]
- Guleryuz, E.; Mesarovic, S.D. Dislocation nucleation on grain boundaries: Low angle twist and asymmetric tilt boundaries. Crystals 2016, 6, 77. [Google Scholar] [CrossRef]
- Talaei, M.S.; Nouri, N.; Ziaei-Rad, S. Grain boundary effects on nanoindentation of Fe bicrystal using molecular dynamic. Mech. Mater. 2016, 102, 97–107. [Google Scholar] [CrossRef]
- Dupont, V.; Sansoz, F. Grain Boundary Structure Evolution in Nanocrystalline Al by Nanoindentation Simulations. MRS Online Proc. Libr. Arch. 2005, 903, 0903–Z06–05. [Google Scholar] [CrossRef]
- Faghihi, D.; Voyiadjis, G.Z. Determination of nanoindentation size effects and variable material intrinsic length scale for body-centered cubic metals. Mech. Mater. 2012, 44, 189–211. [Google Scholar] [CrossRef]
- Esqué-de los Ojos, D.; Pellicer, E.; Sort, J. The Influence of Pore Size on the Indentation Behavior of Metallic Nanoporous Materials: A Molecular Dynamics Study. Materials 2016, 9, 355. [Google Scholar] [CrossRef] [PubMed]
- Ukwatta, A.; Achuthan, A. A molecular dynamics (MD) simulation study to investigate the role of existing dislocations on the incipient plasticity under nanoindentation. Comput. Mater. Sci. 2014, 91, 329–338. [Google Scholar] [CrossRef]
- Ziegenhain, G.; Urbassek, H.M. Nanostructured surfaces yield earlier: Molecular dynamics study of nanoindentation into adatom islands. Phys. Rev. B 2010, 81, 155456. [Google Scholar] [CrossRef]
- Van Vliet, K.J.; Suresh, S. Simulations of cyclic normal indentation of crystal surfaces using the bubble-raft model. Philos. Mag. A 2002, 82, 1993–2001. [Google Scholar] [CrossRef]
- Gouldstone, A.; Van Vliet, K.J.; Suresh, S. Nanoindentation: Simulation of defect nucleation in a crystal. Nature 2001, 411, 656. [Google Scholar] [CrossRef] [PubMed]
- Zarudi, I.; Zhang, L.C.; Swain, M.V. Microstructure evolution in monocrystalline silicon in cyclic microindentations. J. Mater. Res. 2003, 18, 758–761. [Google Scholar] [CrossRef]
- Komvopoulos, K.; Yan, W. Molecular dynamics simulation of single and repeated indentation. J. Appl. Phys. 1997, 82, 4823–4830. [Google Scholar] [CrossRef]
- Cheong, W.C.D.; Zhang, L. Effect of repeated nano-indentations on the deformation in monocrystalline silicon. J. Mater. Sci. Lett. 2000, 19, 439–442. [Google Scholar] [CrossRef]
- Shiari, B.; Miller, R.E. Multiscale modeling of ductile crystals at the nanoscale subjected to cyclic indentation. Acta Mater. 2008, 56, 2799–2809. [Google Scholar] [CrossRef]
- Cordill, M.J.; Lund, M.S.; Parker, J.; Leighton, C.; Nair, A.K.; Farkas, D.; Moody, N.R.; Gerberich, W.W. The Nano-Jackhammer effect in probing near-surface mechanical properties. Int. J. Plast. 2009, 25, 2045–2058. [Google Scholar] [CrossRef]
- Deng, C.; Schuh, C.A. Atomistic mechanisms of cyclic hardening in metallic glass. Appl. Phys. Lett. 2012, 100, 251909. [Google Scholar] [CrossRef]
- Imran, M.; Hussain, F.; Rashid, M.; Ahmad, S.A. Dynamic characteristics of nanoindentation in Ni: A molecular dynamics simulation study. Chin. Phys. B 2012, 21, 116201. [Google Scholar] [CrossRef]
- Salehinia, I.; Wang, J.; Bahr, D.F.; Zbib, H.M. Molecular dynamics simulations of plastic deformation in Nb/NbC multilayers. Int. J. Plast. 2014, 59, 119–132. [Google Scholar] [CrossRef]
- Wang, N.; Yan, F.; Li, L. Mesoscopic examination of cyclic hardening in metallic glass. J. Non-Cryst. Solids 2015, 428, 146–150. [Google Scholar] [CrossRef]
- Göring, G.; Dietrich, P.I.; Blaicher, M.; Sharma, S.; Korvink, J.G.; Schimmel, T.; Koos, C.; Hölscher, H. Tailored probes for atomic force microscopy fabricated by two-photon polymerization. Appl. Phys. Lett. 2016, 109, 063101. [Google Scholar] [CrossRef]
- Commercial Diamond Tips from SCD Probe (D300 Series). Available online: www.scdprobes.com/D300.pdf (accessed on 5 September 2017).
- Alabd Alhafez, I.; Brodyanski, A.; Kopnarski, M.; Urbassek, H.M. Influence of Tip Geometry on Nanoscratching. Tribol. Lett. 2017, 65, 26. [Google Scholar] [CrossRef]
- Fischer-Cripps, A.C. Critical review of analysis and interpretation of nanoindentation test data. Surf. Coat. Technol. 2006, 200, 4153–4165. [Google Scholar] [CrossRef]
- Oliver, D.J.; Paul, W.; El Ouali, M.; Hagedorn, T.; Miyahara, Y.; Qi, Y.; Grütter, P.H. One-to-one spatially matched experiment and atomistic simulations of nanometre-scale indentation. Nanotechnology 2013, 25, 025701. [Google Scholar] [CrossRef] [PubMed]
- Paul, W.; Oliver, D.; Grütter, P. Indentation-formed nanocontacts: An atomic-scale perspective. Phys. Chem. Chem. Phys. 2014, 16, 8201–8222. [Google Scholar] [CrossRef] [PubMed]
- Tavazza, F.; Senftle, T.P.; Zou, C.; Becker, C.A.; van Duin, A.C.T. Molecular Dynamics Investigation of the Effects of Tip-Substrate Interactions during Nanoindentation. J. Phys. Chem. C 2015, 119, 13580–13589. [Google Scholar] [CrossRef]
- Tavazza, F.; Levine, L.E. DFT Investigation of Early Stages of Nanoindentation in Ni. J. Phys. Chem. C 2016, 120, 13249–13255. [Google Scholar] [CrossRef]
- Tavazza, F.; Kuhr, B.; Farkas, D.; Levine, L.E. Ni Nanoindentation at the Nanoscale: Atomic Rearrangements at the Ni-C Interface. J. Phys. Chem. C 2017, 121, 2643–2651. [Google Scholar] [CrossRef]
- Gao, Y.F.; Yang, Y.; Sun, D.Y. Wetting of Liquid Iron in Carbon Nanotubes and on Graphene Sheets: A Molecular Dynamics Study. Chem. Phys. Lett. 2011, 28, 036102. [Google Scholar] [CrossRef]
- Spearot, D.E.; Sangid, M.D. Insights on slip transmission at grain boundaries from atomistic simulations. Curr. Opin. Solid State Mater. Sci. 2014, 18, 188–195. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruestes, C.J.; Alhafez, I.A.; Urbassek, H.M. Atomistic Studies of Nanoindentation—A Review of Recent Advances. Crystals 2017, 7, 293. https://doi.org/10.3390/cryst7100293
Ruestes CJ, Alhafez IA, Urbassek HM. Atomistic Studies of Nanoindentation—A Review of Recent Advances. Crystals. 2017; 7(10):293. https://doi.org/10.3390/cryst7100293
Chicago/Turabian StyleRuestes, Carlos J., Iyad Alabd Alhafez, and Herbert M. Urbassek. 2017. "Atomistic Studies of Nanoindentation—A Review of Recent Advances" Crystals 7, no. 10: 293. https://doi.org/10.3390/cryst7100293





