Strategies to Approach Stabilized Plasticity in Metals with Diminutive Volume: A Brief Review
Abstract
:1. Introduction
2. Onset of the Strain Bursts and Softening in Metals with Diminutive Volume during Deformation
3. Early Extrinsic Strategies to Stabilize Plasticity and Limits
4. Suppressing Strain Burst by Intrinsic Defects
4.1. Effect of the Interaction between Dislocations and the Grain Boundary on Plasticity
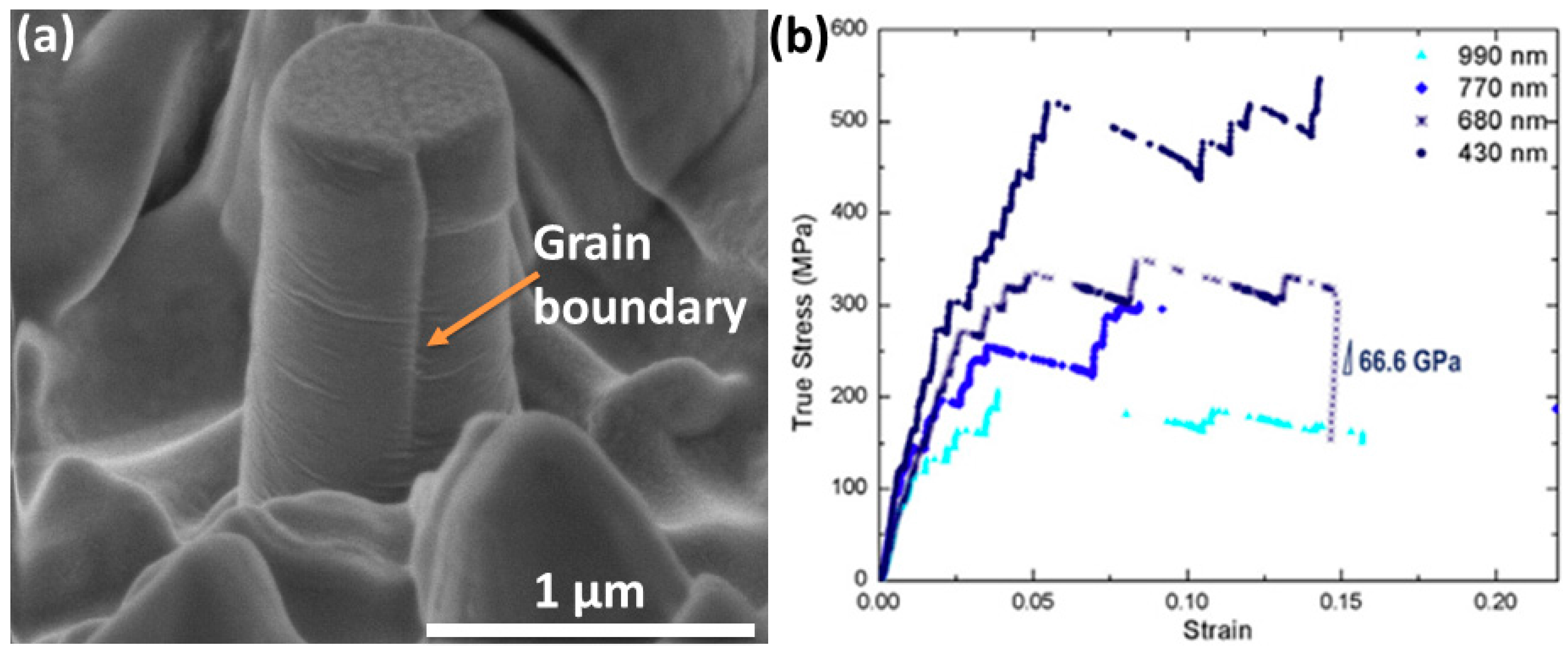
4.2. Effect of Grain Boundary Sliding on the Plasticity
4.3. Incorporating Nanoscale Second Phase Particles and Multiple Grain Boundaries
5. Concluding Remarks and Future Directions
- (1)
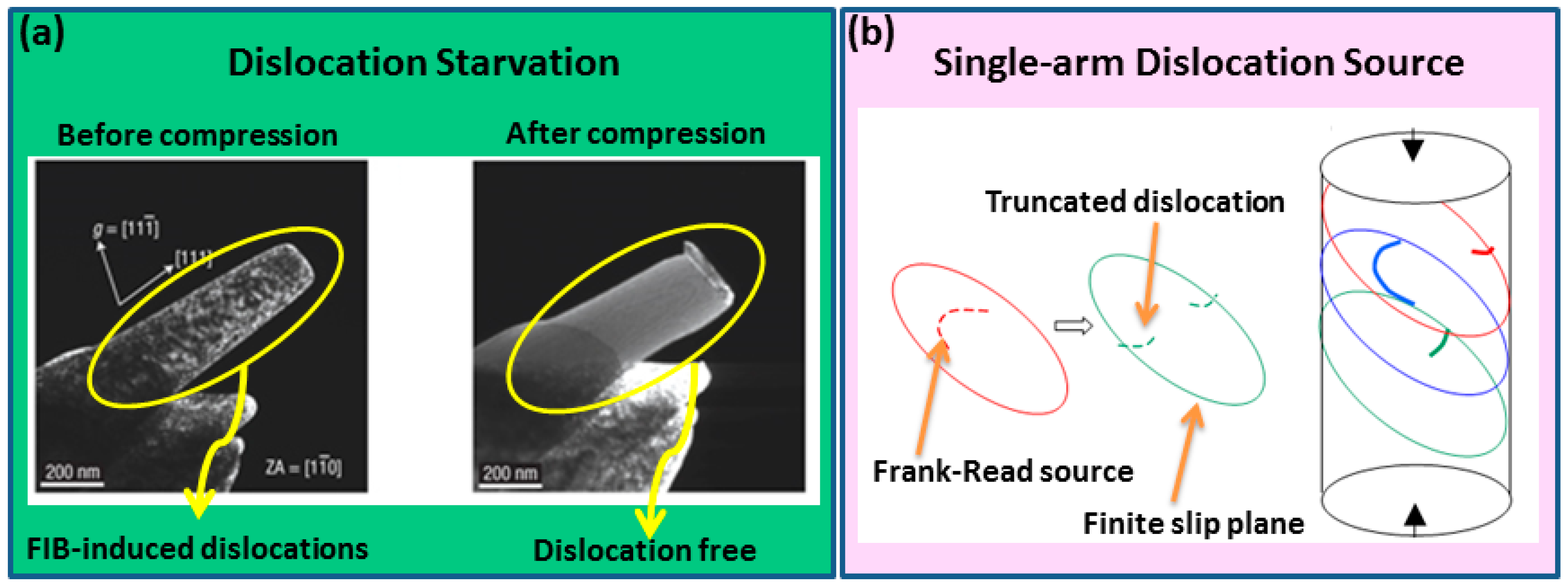
- To attain stabilized plasticity, extrinsic routes were developed, including W coating deposition and a center-cavity with filled W material in a pillar. The W coating or filling on the pillar trapped the dislocations inside the pillar, which stopped the abrupt escape of the dislocations.
- (2)
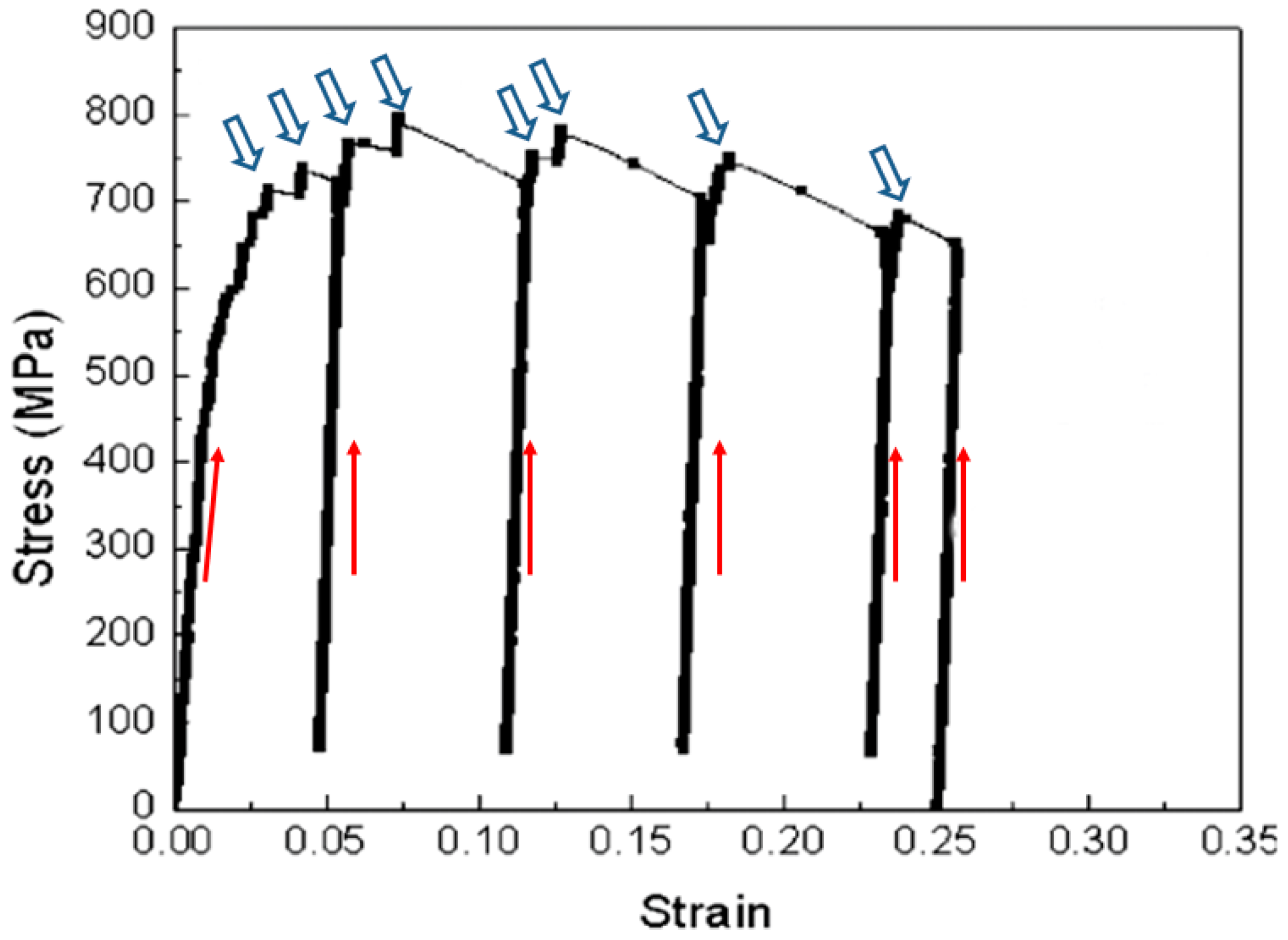
- By introducing a single GB perpendicular to the top surface, strain bursts in micrometer-sized pillars were suppressed. It is suggested that this perpendicular GB piled up dislocations and resulted in dislocation accumulation inside the pillar. However, when the pillar size was decreased down to the submicron scale, this phenomenon failed to appear.
- (3)
- Alternatively, a single GB located in the pillar with an inclined angle normal to the axis could lead to a stable plastic flow, yet with strain softening. The continuous plastic flow is due to the fact that the deformation is driven by GB sliding rather than dislocation-mediated deformation. However, the shear stress to activate the GB sliding is higher than that during the sliding. Therefore, further sliding yields strain softening.
- (4)
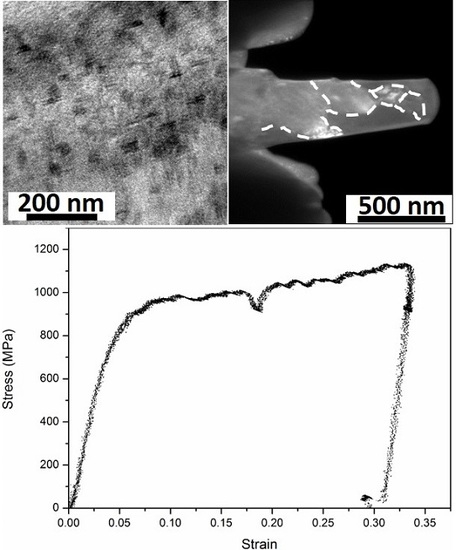
- Submicron pillars containing multiple GBs and nanoscale coherent second phase particles exhibit continuous plastic flow, as well as considerable strain hardening. The highly dense second phase particles effectively pin the dislocations at the early stage of the deformation. This mechanism suppresses the strain bursts and also results in considerable strain hardening. Further deformation will trigger the GB-mediated deformation and give the dislocations no chance to escape from the pillar surface. A dynamic balance between dislocation storing and GB activities was achieved during the late stage of the compression, causing a stabilized plasticity and work hardening.
- Further research should focus on the influence of other defects, such as twins, stacking faults and thermally-stable precipitates, on the plastic stability. By introducing these defects into the micrometer-sized and/or submicrometer-sized metals in an ordered or disordered manner, the plastic flow of the materials at such length scales will be influenced substantially. The revealing of the deformation mechanisms induced by each type of defect will provide insights to tailor the mechanical behavior.
- The atomic mechanism of strain bursts occurring in micrometer-sized and/or submicrometer-sized crystals needs more investigation. The jamming of dislocations and avalanche-like escaping phenomenon are still unclear. In situ high resolution TEM observation with high speed recording will be employed for experimental purpose. Molecular dynamics (MD) simulation is also required to reveal the atomic mechanism;
- While introducing the bulk defects, GBs also need to be tailored via element segregation. The GB activities, e.g., GB sliding, migration and rotation, will thus be modified in a controllable manner to achieve stabilized plasticity.
Acknowledgments
Conflicts of Interest
References
- Uchic, M.D.; Dimiduk, D.M.; Florando, J.N.; Nix, W.D. Sample dimensions influence strength and crystal plasticity. Science 2004, 305, 986–989. [Google Scholar] [CrossRef] [PubMed]
- Shan, Z.; Mishra, R.K.; Asif, S.A.S.; Warren, O.L.; Minor, A. Mechanical annealing and source-limited deformation in submicrometre-diameter Ni crystals. Nat. Mater. 2008, 7, 115–119. [Google Scholar] [CrossRef] [PubMed]
- Greer, J.R.; Oliver, W.C.; Nix, W.D. Size dependence of mechanical properties of gold at the micron scale in the absence of strain gradients. Acta Mater. 2005, 53, 1821–1830. [Google Scholar] [CrossRef]
- Greer, J.R.; de Hosson, J.T.M. Plasticity in small-sized metallic systems: Intrinsic versus extrinsic size effect. Prog. Mater. Sci. 2011, 56, 654–724. [Google Scholar] [CrossRef]
- Shan, Z.W. In-situ TEM investigation of the mechanical behavior of micronanoscaled metal pillars. JOM 2012, 64, 1229–1234. [Google Scholar] [CrossRef]
- Brenner, S.S. Tensile strength of whiskers. J. Appl. Phys. 1956, 27, 1484–1491. [Google Scholar] [CrossRef]
- Greer, J.R.; Kim, J.; Burek, M.J. The in-situ mechanical testing of nanoscale single-crystalline nanopillars. JOM 2009, 61, 19–25. [Google Scholar] [CrossRef]
- Legros, M.; Gianola, D.S.; Motz, C. Quantitative in-situ mechanical testing in electron microscopes. MRS Bull. 2010, 35, 354–360. [Google Scholar] [CrossRef]
- Rinaldi, A.; Peralta, P.; Friesen, C.; Sieradzki, K. Sample-size effects in the yield behavior of nanocrystalline nickel. Acta Mater. 2008, 56, 511–517. [Google Scholar] [CrossRef]
- Volkert, C.A.; Lilleodden, E.T. Size effects in the deformation of submicron Au columns. Philos. Mag. 2006, 86, 5567–5579. [Google Scholar] [CrossRef]
- Kiener, D.; Minor, A.M. Source-controlled yield and hardening of Cu (1 0 0) studied by in situ transmission electron microscopy. Acta Mater. 2011, 59, 1328–1337. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Q.; Shan, Z.; Li, J.; Sun, J.; Ma, E. Sample size effects on the large strain bursts in submicron aluminum pillars. Appl. Phys. Lett. 2012, 100, 071906. [Google Scholar] [CrossRef]
- Yu, Q.; Shan, Z.; Li, J.; Huang, X.; Xiao, L.; Sun, J.; Ma, E. Strong crystal size effect on deformation twinning. Nature 2010, 463, 335–338. [Google Scholar] [CrossRef] [PubMed]
- Ye, J.; Mishra, R.K.; Sachdev, A.K.; Minor, A.M. In-situ TEM compression testing of Mg and Mg–0.2 wt.% Ce single crystals. Scr. Mater. 2011, 64, 292–295. [Google Scholar] [CrossRef]
- Huang, L.; Li, Q.; Shan, Z.; Li, J.; Sun, J.; Ma, E. A new regime for mechanical annealing and strong sample-size strengthening in body centred cubic molybdenum. Nat. Commun. 2011, 2, 547. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Jang, D.; Greer, J.R. Tensile and compressive behavior of tungsten, molybdenum, tantalum and niobium at the nanoscale. Acta Mater. 2010, 58, 2355–2363. [Google Scholar] [CrossRef]
- Kim, J.; Greer, J.R. Size-dependent mechanical properties of molybdenum nanopillars. Appl. Phys. Lett. 2008, 93, 101916. [Google Scholar] [CrossRef]
- Kim, J.; Jang, D.; Greer, J.R. Insight into the deformation behavior of niobium single crystals under uniaxial compression and tension at the nanoscale. Scr. Mater. 2009, 61, 300–303. [Google Scholar] [CrossRef]
- Burek, M.J.; Jin, S.; Leung, M.C.; Jahed, Z.; Wu, J.; Budiman, A.S.; Tamura, N.; Kunz, M.; Tsui, T.Y. Grain boundary effects on the mechanical properties of bismuth nanostructures. Acta Mater. 2011, 59, 4709–4718. [Google Scholar] [CrossRef]
- Nix, W.D.; Lee, S. Micropillar plasticity controlled by dislocation nucleation at surfaces. Philos. Mag. 2011, 91, 1084–1096. [Google Scholar] [CrossRef]
- Zuo, L.; Ngan, A.H.; Zheng, G.P. Size dependent of incipient dislocation plasticity in Ni3Al. Phys. Rev. Lett. 2005, 94, 095501. [Google Scholar] [CrossRef] [PubMed]
- Parthasarathy, T.A.; Rao, S.I.; Dimiduk, D.M.; Uchic, M.D.; Trinkle, D.R. Contribution to size effect of yield strength from the stochastic of dislocation source lengths in finite samples. Scr. Mater. 2007, 56, 313–316. [Google Scholar] [CrossRef]
- Rao, S.I.; Dimiduk, D.M.; Parthasarathy, T.A.; Uchic, M.D.; Tang, M.; Woodward, C. Athermal mechanisms of size-dependent crystal flow gleaned from three-dimensional discrete dislocation simulations. Acta Mater. 2008, 56, 3245–3259. [Google Scholar]
- Zheng, K.; Han, X.; Wang, L.; Zhang, Y.; Yue, Y.; Qin, Y.; Zhang, X.; Zhang, Z. Atomic mechanisms governing the elastic limit and the incipient plasticity of bending Si nanowires. Nano Lett. 2009, 9, 2471–2476. [Google Scholar] [CrossRef] [PubMed]
- Han, X.; Zheng, K.; Zhang, Y.; Zhang, X.; Zhang, Z.; Wang, Z. Low-temperature in situ large-strain plasticity of Si nanowires. Adv. Mater. 2007, 19, 2112–2118. [Google Scholar] [CrossRef]
- Csikor, F.F.; Motz, C.; Weygand, D.; Zaiser, M.; Zapperi, S. Dislocation avalanches, strain bursts, and the problem of plastic forming at the micrometer scale. Science 2007, 318, 251–254. [Google Scholar] [CrossRef] [PubMed]
- Oh, S.; Legros, M.; Kiener, D.; Dehm, G. In-situ observation of dislocation nucleation and escape in a submicrometer aluminum single crystal. Nat. Mater. 2009, 8, 95–100. [Google Scholar] [CrossRef] [PubMed]
- Maaß, R.; Derlet, P.M.; Greer, J.R. Small-scale plasticity, Insights into dislocation avalanche velocities. Scr. Mater. 2013, 69, 586–589. [Google Scholar] [CrossRef]
- Meyers, M.A.; Chawla, K. Mechanical Behavior of Materials; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Sun, Q.; Guo, Q.; Yao, X.; Xiao, L.; Greer, J.R.; Sun, J. Size effects in strength and plasticity of single-crystalline titanium micropillars with prismatic slip orientation. Scr. Mater. 2011, 65, 473–476. [Google Scholar] [CrossRef]
- Kheradmand, N.; Vehoff, H.; Barnoush, A. An insight into the role of the grain boundary in plastic deformation by means of a bicrystalline pillar compression test and atomistic simulation. Acta Mater. 2013, 61, 7454–7465. [Google Scholar] [CrossRef]
- Girault, B.; Schneider, A.S.; Frick, C.P.; Arzt, E. Strength effects in micropillars of a dispersion strengthened superalloy. Adv. Eng. Mater. 2012, 12, 385–388. [Google Scholar] [CrossRef]
- Ng, K.S.; Ngan, A.H.W. Effects of trapping dislocations within small crystals on their deformation behavior. Acta Mater. 2009, 57, 4902–4910. [Google Scholar] [CrossRef]
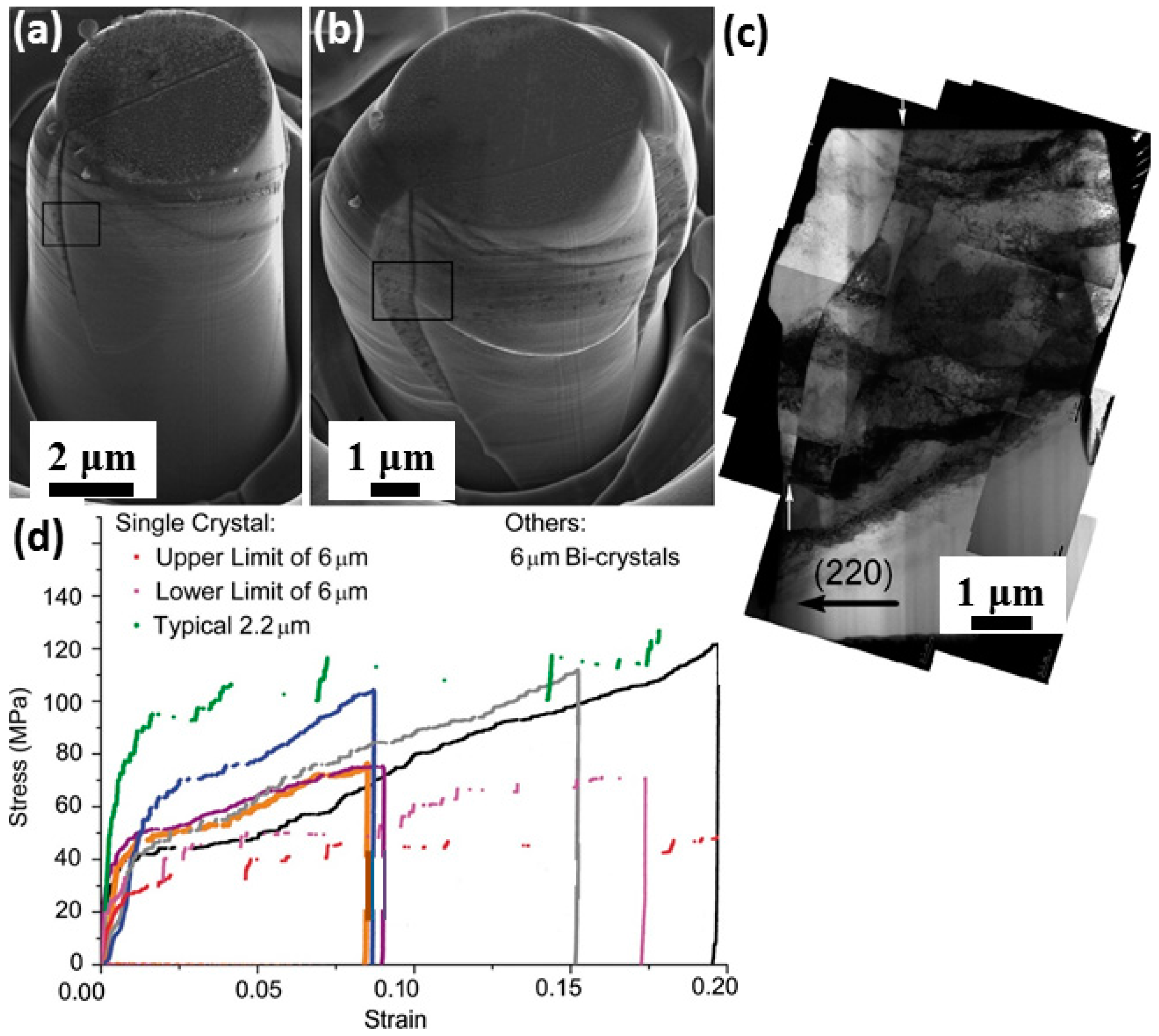
- Ng, K.S.; Ngan, A.H.W. Deformation of micron-sized aluminum bi-crystal pillars. Philos. Mag. 2009, 89, 3013–3026. [Google Scholar] [CrossRef]
- Kunz, A.; Pathak, S.; Greer, J.R. Size effects in Al nanopillars: Single crystalline vs. bicrystalline. Acta Mater. 2011, 59, 4416–4424. [Google Scholar] [CrossRef]
- Aitken, Z.H.; Jang, D.; Weinberger, C.R.; Greer, J.R. Grain boundary sliding in aluminum nano-bi-crystals deformed at room temperature. Small 2014, 10, 100–108. [Google Scholar] [CrossRef] [PubMed]
- Gu, X.W.; Loynachan, C.N.; Wu, Z.; Zhang, Y.; Srolovitz, D.J.; Greer, J.R. Size-dependent deformation of nanocrystalline Pt nanopillars. Nano Lett. 2012, 12, 6385–6392. [Google Scholar] [CrossRef] [PubMed]
- Hirouchi, T.; Shibutani, Y. Mechanical responses of copper bicrystalline micro pillars with sigma-3 coherent twin boundaries by uniaxial compression tests. Mater. Trans. 2015, 55, 52–57. [Google Scholar] [CrossRef]
- Ng, K.S.; Ngan, A.H.W. Breakdown of Schmid’s law in micropillars. Scr. Mater. 2008, 59, 796–799. [Google Scholar] [CrossRef]
- DeIasi, R.; Adler, P.N. Calorimetric studies of 7000 series aluminum alloys: I. matrix precipitate characterization of 7075. Metall. Mater. Trans. A 1977, 8, 1177–1183. [Google Scholar]
- Hu, T.; Jiang, L.; Yang, H.; Ma, K.; Topping, T.D.; Yee, J.; Li, M.; Mukherjee, A.K.; Schoenung, J.M.; Lavernia, E.J. Stabilized plasticity in ultrahigh strength, submicron Al crystals. Acta Mater. 2015, 94, 46–58. [Google Scholar] [CrossRef]
- Tao, N.; Wang, Z.; Tong, W.; Sui, M.; Lu, J.; Lu, K. An investigation of surface nanocrystallization mechanism in Fe induced by surface mechanical attrition treatment. Acta Mater. 2002, 50, 4603–4616. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, H.; Lu, K. Strain-induced ultrahard and ultrastable nanolaminated structure in nickel. Science 2013, 342, 337–340. [Google Scholar] [CrossRef] [PubMed]
- Rupert, T.J.; Gianola, D.S.; Gan, Y.; Hemker, K.J. Experimental observations of stress-driven grain boundary migration. Science 2009, 326, 1686–1690. [Google Scholar] [CrossRef] [PubMed]



© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, T.; Jiang, L.; Mukherjee, A.K.; Schoenung, J.M.; Lavernia, E.J. Strategies to Approach Stabilized Plasticity in Metals with Diminutive Volume: A Brief Review. Crystals 2016, 6, 92. https://doi.org/10.3390/cryst6080092
Hu T, Jiang L, Mukherjee AK, Schoenung JM, Lavernia EJ. Strategies to Approach Stabilized Plasticity in Metals with Diminutive Volume: A Brief Review. Crystals. 2016; 6(8):92. https://doi.org/10.3390/cryst6080092
Chicago/Turabian StyleHu, Tao, Lin Jiang, Amiya K. Mukherjee, Julie M. Schoenung, and Enrique J. Lavernia. 2016. "Strategies to Approach Stabilized Plasticity in Metals with Diminutive Volume: A Brief Review" Crystals 6, no. 8: 92. https://doi.org/10.3390/cryst6080092