Magnetism and Pressure-Induced Superconductivity of Checkerboard-Type Charge-Ordered Molecular Conductor β-(meso-DMBEDT-TTF)2X (X = PF6 and AsF6)
Abstract
:1. Introduction
2. Results and Discussion
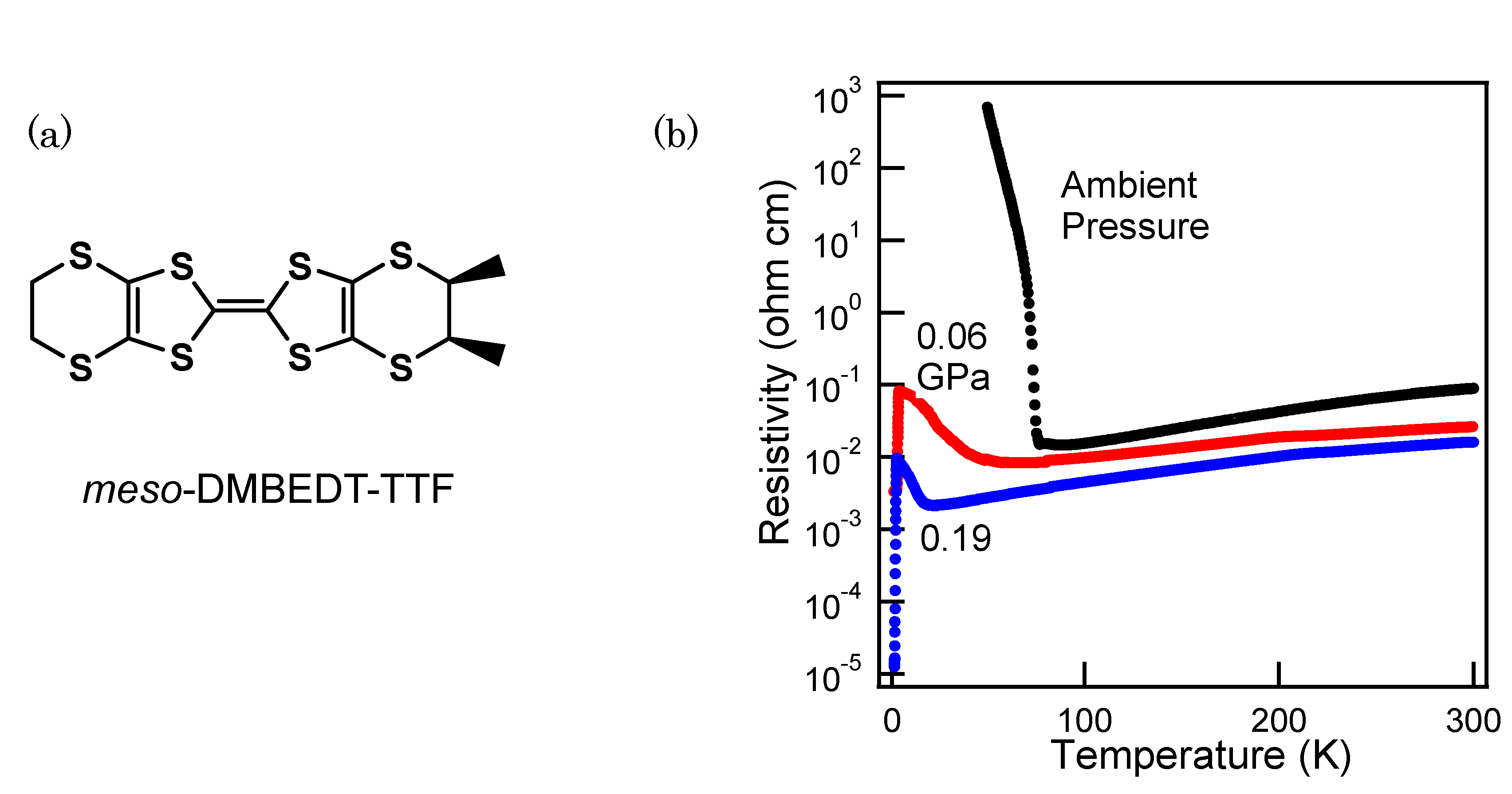
2.1. Metallic State at 298 K to Charge-Ordered State at 30 K for β-(meso-DMBEDT-TTF)2AsF6

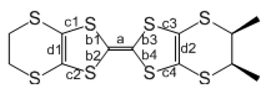
| a (Å) | b1 (Å) b2 (Å) b3 (Å) b4 (Å) | c1 (Å) c2 (Å) c3 (Å) c4 (Å) | d1 (Å) d2 (Å) | δ1 | δ2 | |
|---|---|---|---|---|---|---|
| charge-rich donor | 1.379(4) | 1.735(3) 1.728(3) 1.722(3) 1.741(2) | 1.748(3) 1.743(3) 1.752(3) 1.751(3) | 1.354(4) 1.350(4) | +0.76(3) | +0.65(3) [=0.76(3)/ (0.76(3)+0.41(3)) ] |
| charge-poor donor | 1.354(4) | 1.745(2) 1.751(3) 1.753(4) 1.740(2) | 1.749(4) 1.757(3) 1.760(3) 1.757(4) | 1.357(4) 1.350(4) | +0.41(3) | +0.35(3) [=0.41(3)/ (0.76(3)+0.41(3))] |
| Direction | 298 K | Direction | 11.5 K | 30 K | |
|---|---|---|---|---|---|
| PF6 | AsF6 | PF6 | AsF6 | ||
| r1 | 8.24 | 9.86 | r1 | 12.6 | 12.9 |
| r 2 | 22.6 | 20.9 | r2 | 25.3 | 25.1 |
| r 3 | - | - | r3 | 18.2 | 18.7 |
| r 4 | - | - | r4 | 25.3 | 25.1 |
| p1 | −4.75 | −4.89 | p1 | −4.4 | −4.3 |
| p2 | - | - | p2 | −6.1 | −6.1 |
| q1 | 4.38 | 4.03 | q1 | 3.7 | 3.7 |
| q2 | 11.5 | 10.7 | q2 | 10.7 | 10.6 |
| q3 | - | - | q3 | 4.2 | 4.3 |
| q4 | - | - | q4 | 10.7 | 10.6 |
| r2/r1 | 2.74 | 2.12 | r2/r1 | 2.01 | 1.94 |
| r4/r3 | - | - | r4/r3 | 1.39 | 1.34 |
| Ref. | [4] | this work | - | [6] | this work |
| WU | WL | W | Eg | ∆E | WU/∆E | ref. | |
|---|---|---|---|---|---|---|---|
| β-(meso-DMBEDT-TTF)2PF6 | 0.50 | 0.40 | 0.93 | 0.02 | 0.45 | 1.11 | [4] |
| β-(meso-DMBEDT-TTF)2AsF6 | 0.51 | 0.43 | 0.92 | 0 | 0.42 | 1.23 | this work |
| κ-(BEDT-TTF)2Cu(NCS)2 | 0.57 | 0.36 | 1.08 | 0.16 | 0.46 | 1.24 | [11,12,13] |
| κ-(BEDT-TTF)2Cu2(CN)3 | 0.50 | 0.33 | 1.00 | 0.17 | 0.45 | 1.11 | 13] |
2.2. Pressure-Induced Superconductivity of β-(meso-DMBEDT-TTF)2AsF6
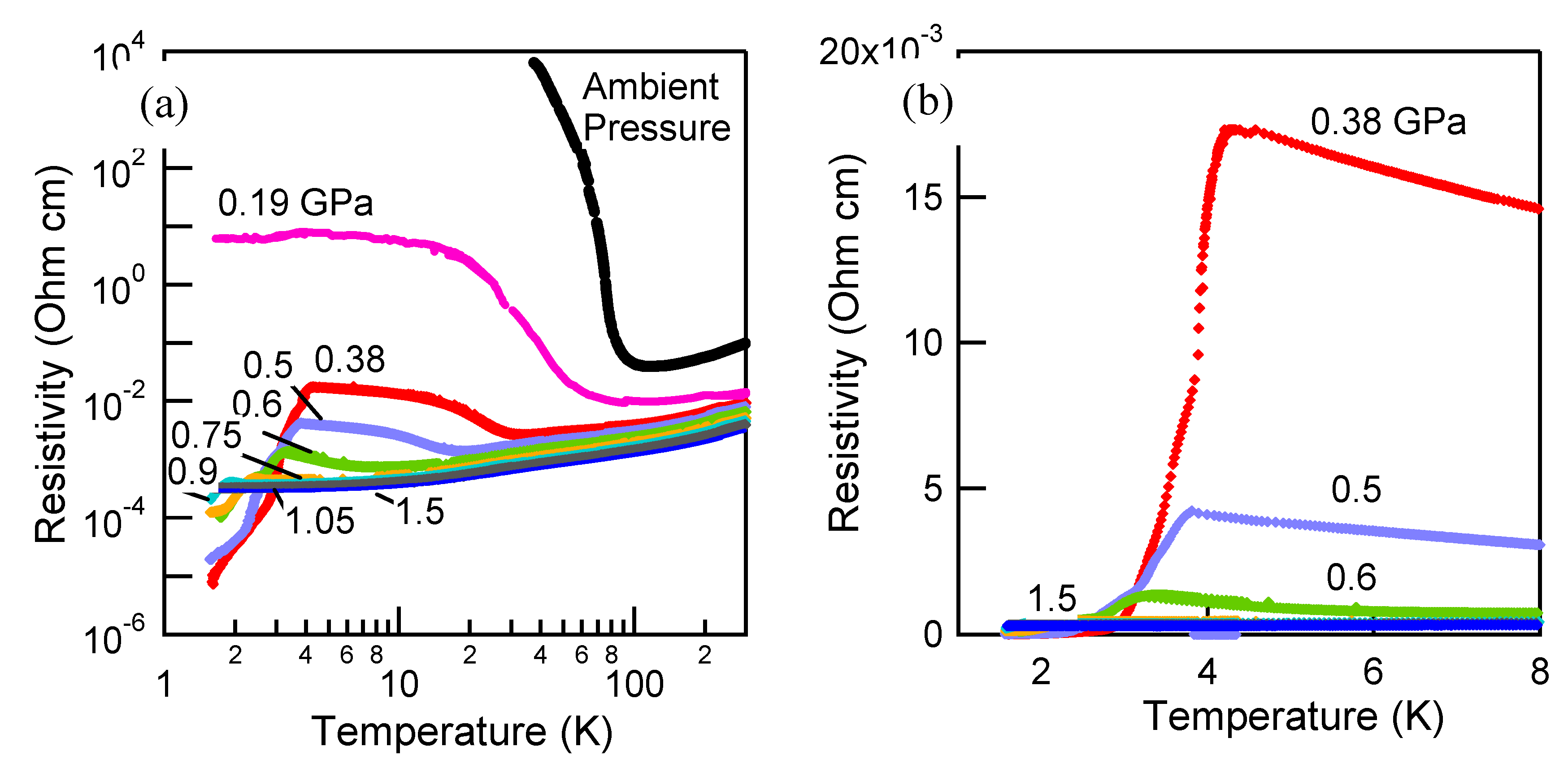
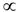 Tα was carried out under several pressures in the temperature range of 2 < T < 20 K. The exponent α is 2 when the electronic state is in the Fermi liquid nature. Near the superconducting state, α is calculated to be 1.3 under 0.9 GPa. The power α increases almost linearly with application of pressure. The pressure dependence is dα/dP = 0.6 K/GPa, which is much faster than those of (TMTTF)2X (X = PF6, AsF6) with 0.15–0.19 K/GPa [16]. The system at 1.5 GPa is non-Fermi liquid (NFL) with α = 1.7 and might be realized to be the Fermi liquid above 2.5 GPa if the linear extrapolation of the pressure dependence is assumed.
Tα was carried out under several pressures in the temperature range of 2 < T < 20 K. The exponent α is 2 when the electronic state is in the Fermi liquid nature. Near the superconducting state, α is calculated to be 1.3 under 0.9 GPa. The power α increases almost linearly with application of pressure. The pressure dependence is dα/dP = 0.6 K/GPa, which is much faster than those of (TMTTF)2X (X = PF6, AsF6) with 0.15–0.19 K/GPa [16]. The system at 1.5 GPa is non-Fermi liquid (NFL) with α = 1.7 and might be realized to be the Fermi liquid above 2.5 GPa if the linear extrapolation of the pressure dependence is assumed.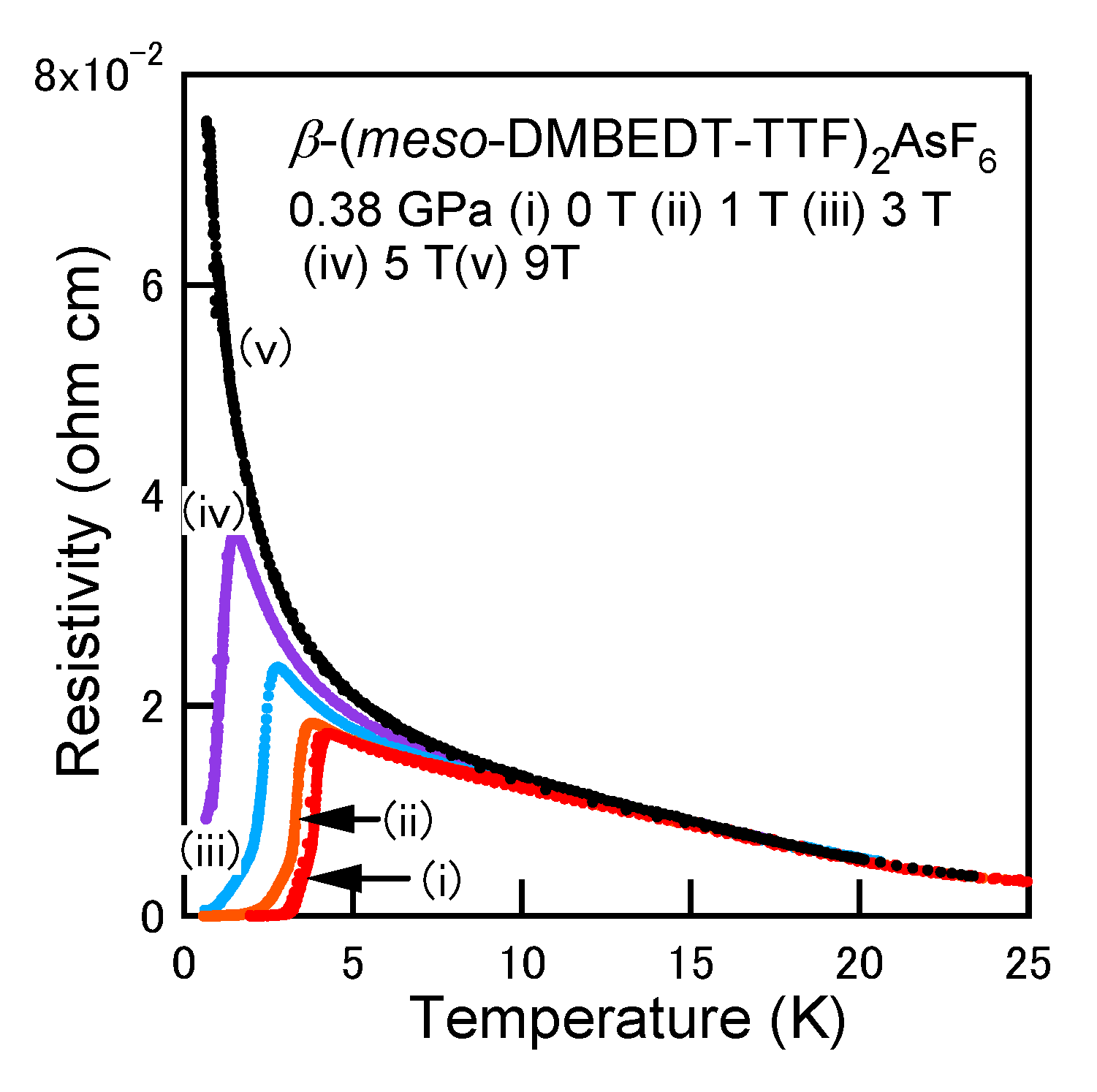
 Tα in Figure 5(a)] for β-(meso-DMBEDT-TTF)2AsF6. In (b) CO and SC denote the charge-ordered state and the superconducting state.
Tα in Figure 5(a)] for β-(meso-DMBEDT-TTF)2AsF6. In (b) CO and SC denote the charge-ordered state and the superconducting state.
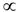 Tα in Figure 5(a)] for β-(meso-DMBEDT-TTF)2AsF6. In (b) CO and SC denote the charge-ordered state and the superconducting state.
Tα in Figure 5(a)] for β-(meso-DMBEDT-TTF)2AsF6. In (b) CO and SC denote the charge-ordered state and the superconducting state.
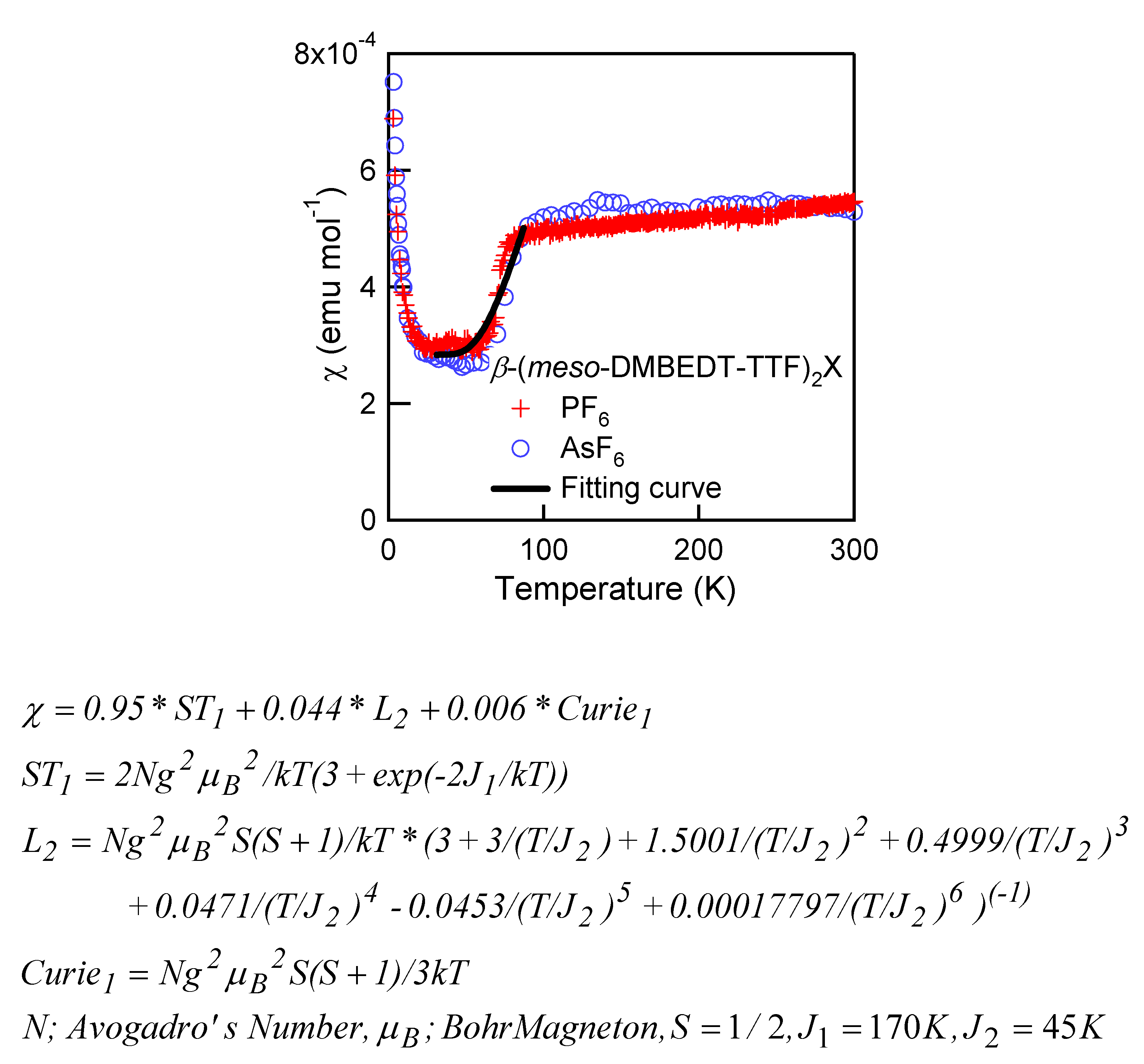
2.3. Magnetic Susceptibility of β-(meso-DMBEDT-TTF)2X (X = PF6 and AsF6)
3. Experimental Section
4. Conclusions
Acknowledgments
References
- Fukuyama, H. Physics of Molecular Conductors. J. Phys. Soc. Jpn. 2006, 75. [Google Scholar] [CrossRef]
- Seo, H.; Hotta, C.; Fukuyama, H. Toward Systematic Understanding of Diversity of Electronic Properties in Low-dimensional Molecular Solids. Chem. Rev. 2004, 104, 5005–5056. [Google Scholar]
- Kimura, S.; Suzuki, H.; Maejima, T.; Suto, M.; Yamashita, K.; Ichikawa, S.; Mori, H.; Moriyama, H.; Mochida, T.; Nishio, Y.; Kajita, K. Crystal Structures and Electrical Conductivities Controlled by CH/n interactions. J. Phys. IV Fr. 2004, 114, 521–522. [Google Scholar] [CrossRef]
- Kimura, S.; Maejima, T.; Suzuki, H.; Chiba, R.; Mori, H.; Kawamoto, T.; Mori, T.; Moriyama, H.; Nishio, Y.; Kajita, K. A New Organic Superconductor β-(meso-DMBEDT-TTF)2PF6. Chem. Commun. 2004, 2454–2455. [Google Scholar]
- Kimura, S.; Suzuki, H.; Maejima, T.; Mori, H.; Yamaura, J.; Kakiuchi, T.; Sawa, H.; Moriyama, H. Checkerboard-Type Charge-Ordered State of a Pressure-Induced Superconductor, β-(meso-DMBEDT-TTF)2PF6. J. Am. Chem. Soc. 2006, 128, 1456–1457. [Google Scholar]
- Mori, H. Materials Viewpoint of Organic Superconductors. J. Phys. Soc. Jpn. 2006, 75. [Google Scholar] [CrossRef]
- Morinaka, N.; Takahashi, K.; Chiba, R.; Yoshikane, F.; Niizeki, S.; Tanaka, M.; Yakushi, K.; Koeda, M.; Hedo, M.; Fujiwara, T.; et al. Superconductivity Competitive with Checkerboard-type Charge Ordering in Organic Conductor beta-(meso-DMBEDT-TTF)2PF6. Phys. Rev. B 2009, 80. [Google Scholar] [CrossRef]
- Niizeki, S.; Yoshikane, F.; Kohno, K.; Takahashi, K.; Mori, H.; Bando, Y.; Kawamoto, T.; Mori, T. Dielectric Response and Electric-Field-Induced Metastable State in an Organic Conductor β-(meso-DMBEDT-TTF)2PF6. J. Phys. Soc. Jpn. 2008, 77. [Google Scholar] [CrossRef]
- Tanaka, M.; Yamamoto, K.; Uruichi, M.; Yamamoto, T.; Yakushi, K.; Kimura, S.; Mori, H. Infrared and Raman Study of the Charge-Ordered State in the Vicinity of the Superconducting State in the Organic Conductor β-(meso-DMBEDT-TTF)2PF6. J. Phys. Soc. Jpn. 2008, 77. [Google Scholar] [CrossRef]
- Guionneau, P.; Kepert, C.J.; Bravic, G.; Chasseau, D.; Truter, M.R.; Kurmoo, M.; Day, P. Determining the Charge Distribution in BEDT-TTF Salts. Synth. Metals 1997, 86, 1973–1974. [Google Scholar]
- Oshima, K.; Mori, T.; Inokuchi, H.; Urayama-Mori, H.; Yamochi, H.; Saito, G. Shubnikov-de Haas Effect and the Fermi Surface in an Ambient Pressure Organic Superconductor [bis(ethylenedithiolo)tetrathiafulvalene]2Cu(NCS)2. Phys. Rev. B 1988, 38, 938–941. [Google Scholar]
- Mori, H. Overview of Organic Superconductors. Int. J. Mod. Phys. B 1994, 8. [Google Scholar] [CrossRef]
- Komatsu, T.; Matsukawa, N.; Inoue, T.; Saito, G. Realization of Superconductivity at Ambient Pressure by Band-filling Control of κ-(BEDT-TTF)2Cu2(CN)3. J. Phys. Soc. Jpn. 1996, 65, 1340–1365. [Google Scholar]
- Okazaki, R.; Terasaki, I.; Mori, H. The University of Tokyo, Japan. Private communication, 2012.
- Takahide, Y.; Konoike, T.; Enomoto, K.; Nishimura, M.; Terashima, T.; Uji, S.; Yamamoto, H.M. Large Positive Magnetoresistance of Insulating Organic Crystals in the Non-Ohmic Region. Phys. Rev. Lett. 2007, 98. [Google Scholar] [CrossRef]
- Itoi, M.; Araki, C.; Hedo, M.; Uwatoko, Y.; Nakamura, T. Anomalously Wide Superconducting Phase of One-Dimensional Organic Conductor (TMTTF)2SbF6. J. Phys. Soc. Jpn. 2008, 77. [Google Scholar] [CrossRef]
- Kanoda, K. Metal-Insulator Transition in κ-(ET)2X and (DCNQI)2M: Two Contrasting Manifestation of Electron Correlation. J. Phys. Soc. Jpn. 2006, 75. [Google Scholar] [CrossRef]
- Mori, H.; Tanaka, S.; Mori, T. Systematic Study of the Electronic State in θ-type BEDT-TTF Organic Conductors by Changing the Electronic Correlation. Phys. Rev. B 1998, 57, 12023–12029. [Google Scholar]
- Carlin, R.L. Magnetochemistry; Springer-Verlag: Berlin, Germany, 1986. [Google Scholar]
- Lines, M.E. The Quadratic-Layer Antiferromagnet. J. Phys. Chem. Solids 1970, 31, 101–116. [Google Scholar] [CrossRef]
- Miyagawa, K.; Kanoda, K.; Mori, H. The University of Tokyo, Japan.Private communication, 2012.
- Dayal, S.; Clay, R.T.; Li, H.; Mazumdar, S. Paired Electron Crystal: Order from Frustration in the Quarter-Filled Band. Phys. Rev. B 2011, 83. [Google Scholar] [CrossRef]
- Radaelli, P.G.; Horibe, Y.; Gutmann, M.J.; Ishibashi, H.; Chen, C.H.; Ibberson, R.M.; Koyama, Y.; Hor, Y.-S.; Kiryukhin, V.; Cheong, S.-W. Formation of isomorphic Ir3+ and Ir4+ Octamers and Spin Dimerization in the spinel CuIr2S4. Nature 2002, 416, 155–158. [Google Scholar]
- Yamamoto, T.; Nakazawa, Y.; Tamura, M.; Nakao, A.; Ikemoto, Y.; Moriwaki, T.; Fukaya, A.; Kato, R.; Yakushi, K. Intradimer Charge Disproportionation in Triclinic-EtMe3P[Pd(dmit)2]2 (dmit: 1,3-Dithiole-2-thione-4,5-dithiolate). J. Phys. Soc. Jpn. 2011, 80. [Google Scholar] [CrossRef]
- Mori, T.; Kobayashi, A.; Sasaki, Y.; Kobayashi, H.; Saito, G.; Inokuchi, H. The Intermolecular Interaction of Tetrathiafulvalene and Bis(ethylenedithio)tetrathiafulvalene in Organic Metals. Calculation of Orbital Overlaps and Models of Energy-band Structures. Bull. Chem. Soc. Jpn. 1984, 57, 627–633. [Google Scholar]
- Eiling, A.; Schilling, J.S. Pressure and Temperature Dependence of Electrical Resistivity of Pb and Sn from 1–300 K and 0–10 GPa-Use as Continuous Resistive Pressure Monitor Accurate Over Wide Temperature Range; Superconductivity Under Pressure in Pb, Sn and In. J. Phys. F 1981, 11, 623–639. [Google Scholar]
- Iwasawa, Y. Kagaku Binran Kisohen II, Version 5; Maruzen: Tokyo, 2004; p. 508. [Google Scholar]
- Nozawa, K.; Sugano, T.; Urayama-Mori, H.; Yamochi, H.; Saito, G.; Kinoshita, M. Meissner Effect in an Organic Superconductor (BEDT-TTF)2[Cu(NCS) 2]. Chem. Lett. 1988, 17, 617–620. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Shikama, T.; Shimokawa, T.; Lee, S.; Isono, T.; Ueda, A.; Takahashi, K.; Nakao, A.; Kumai, R.; Nakao, H.; Kobayashi, K.; et al. Magnetism and Pressure-Induced Superconductivity of Checkerboard-Type Charge-Ordered Molecular Conductor β-(meso-DMBEDT-TTF)2X (X = PF6 and AsF6). Crystals 2012, 2, 1502-1513. https://doi.org/10.3390/cryst2041502
Shikama T, Shimokawa T, Lee S, Isono T, Ueda A, Takahashi K, Nakao A, Kumai R, Nakao H, Kobayashi K, et al. Magnetism and Pressure-Induced Superconductivity of Checkerboard-Type Charge-Ordered Molecular Conductor β-(meso-DMBEDT-TTF)2X (X = PF6 and AsF6). Crystals. 2012; 2(4):1502-1513. https://doi.org/10.3390/cryst2041502
Chicago/Turabian StyleShikama, Takahisa, Tatsuya Shimokawa, Sanguchul Lee, Takayuki Isono, Akira Ueda, Kazuyuki Takahashi, Akiko Nakao, Reiji Kumai, Hironori Nakao, Kensuke Kobayashi, and et al. 2012. "Magnetism and Pressure-Induced Superconductivity of Checkerboard-Type Charge-Ordered Molecular Conductor β-(meso-DMBEDT-TTF)2X (X = PF6 and AsF6)" Crystals 2, no. 4: 1502-1513. https://doi.org/10.3390/cryst2041502