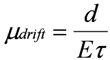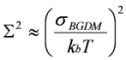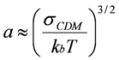2.1. Time-of-Flight Photoconductivity Measurement of Polymer Hole Drift Mobility in MEH-PPV/CdSe Hybrid Nanocomposites
An example of the measured TOF transients for the 80:20 MEH-PPV:CdSe CQD sample (
i.e., the overall heterostructure transient and the reference pure polymer transient) is shown in
Figure 2. It is important to note that the appearance of the observed shoulders for all measured transients vary in shape from a plateau to a sharp shoulder. Therefore, the transit time is best defined as the roll-off point of the transient current when plotted on a log(I)-log(time) scale, as shown in the inset to
Figure 2. It is also important to note that several factors must be considered for the TOF measurement to yield useful data: first, the RC time constant of the entire circuit must be significantly less than the transient decay time; second, the absorption coefficient of the active layer must be large enough such that the laser energy is absorbed in a shallow depth relative to the total thickness of the film; and third, the generated sheet of carriers must be sufficiently thin such that nearly all of the carriers arrive at the far contact (Al contact) at the same time. These factors were considered in selecting the film thickness for the measured samples, as described in the Experimental Section.
The measured transit times for the nanocomposites (τnanocomposite) are used to determine the associated hole drift mobilities according to the following equation:
where
µdrift is the hole drift mobility,
d is the sample thickness, and
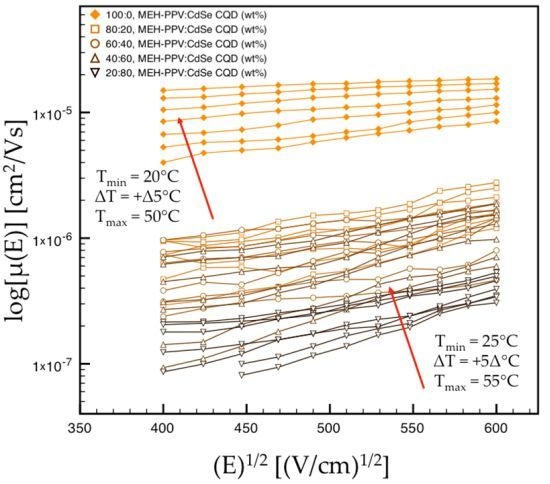
E is the applied electric field. The hole drift mobilities determined using Equation (1) for MEH-PPV-CdSe CQD nanocomposites with different concentration ratios are shown in
Figure 3 as a function of the square root of the applied electric field for each measurement temperature. It is important to note that the mobility is plotted against
E1/2 because it is advantageous for the disorder model analysis used to correlate mobility to internal morphology. In this figure, the general trend is that as the CdSe CQD content in the hybrid nanocomposite films increases, the hole drift mobility decreases [from ~5.9 × 10
−6 cm
2/Vs in MEH-PPV films to ~8.1 × 10
−8 cm
2/Vs in a 20:80 (wt%) MEH-PPV:CdSe CQD nanocomposite film at 25 °C and an applied field of ~2 × 10
5 V/cm].
Figure 2.
TOF transients for the entire 80:20 MEH-PPV:CdSe CQD (CdSe colloidal quantum dot) heterostructure and for the pure polymer laser absorption layer at 30 °C and an applied field of 2.6 × 105 V/cm.
Figure 2.
TOF transients for the entire 80:20 MEH-PPV:CdSe CQD (CdSe colloidal quantum dot) heterostructure and for the pure polymer laser absorption layer at 30 °C and an applied field of 2.6 × 105 V/cm.
Figure 3.
Hole drift mobility vs. temperature and electric field for nanocomposite thin films with different MEH-PPV:CdSe CQD ratios.
Figure 3.
Hole drift mobility vs. temperature and electric field for nanocomposite thin films with different MEH-PPV:CdSe CQD ratios.
2.2. Amorphous Film Disorder Models
The measured mobility values are related to the polymer internal morphology of each film by using the BGDM and the CDM [
12,
13,
14]. For each disorder model, it is assumed that interchain hopping conduction occurs in a polymer film when charge carriers hop between energy levels associated with two adjacent sites. According to the BGDM, the energy distribution of such hopping states is Gaussian and the energy levels of adjacent sites are uncorrelated. The primary difference in the CDM is that the energy distribution of hopping states for adjacent molecules is correlated with the spatial positions of chain sites. Each disorder model yields a corresponding energy disorder parameter,
σ, which describes the energy required for a charge carrier to hop between adjacent sites in the polymer film. Therefore, smaller values of σ indicate more intimately interacting polymer chains. Specifically, according to the BGDM, the hole drift mobility in disordered materials is described by [
7]:
where
T is temperature,
µ∞ is the zero-field drift mobility at
T = ∞,
σBGDM is the energy disorder parameter,
kb is Boltzmann’s constant,
Σ is the positional disorder parameter, and
C is a constant, which is approximately 2.9 × 10
−4 (cm/V)
1/2 for MEH-PPV [
12]. The positional disorder parameter,
Σ, describes the fluctuation in the distance and orientation of the hopping sites associated with hopping charge carriers. Therefore, decreasing values of
Σ indicate increasing film homogeneity on a sub-nanometer scale. Similarly, according to the CDM, the hole drift mobility in disordered materials is described by [
8]:
where σCDM is the energy disorder parameter,e is the charge of an electron, and a is the hopping distance between two adjacent sites. Smaller values of a also indicate more relaxed polymer chains. Thus, in order to extract information about the MEH-PPV film internal morphology from the measured hole drift mobility data, the BGDM is used to calculate the energy disorder parameter, σBGDM, and the positional disorder parameter, Σ, while the CDM is used to calculate σCDM and the hopping distance, a. By determining the disorder parameters using both models, a more complete picture of the polymer film internal morphology is obtained.
2.3. Disorder Model Parameters
It is important to note that according to Equations (2) and (3), the zero-field drift mobilities should follow the so-called non-Arrhenius temperature dependence for the BDGM and the CDM, respectively [
15]:
and
These zero-field mobilities,
µ0, are determined from the measured electric field-dependent mobilities by extrapolating the measured data to the
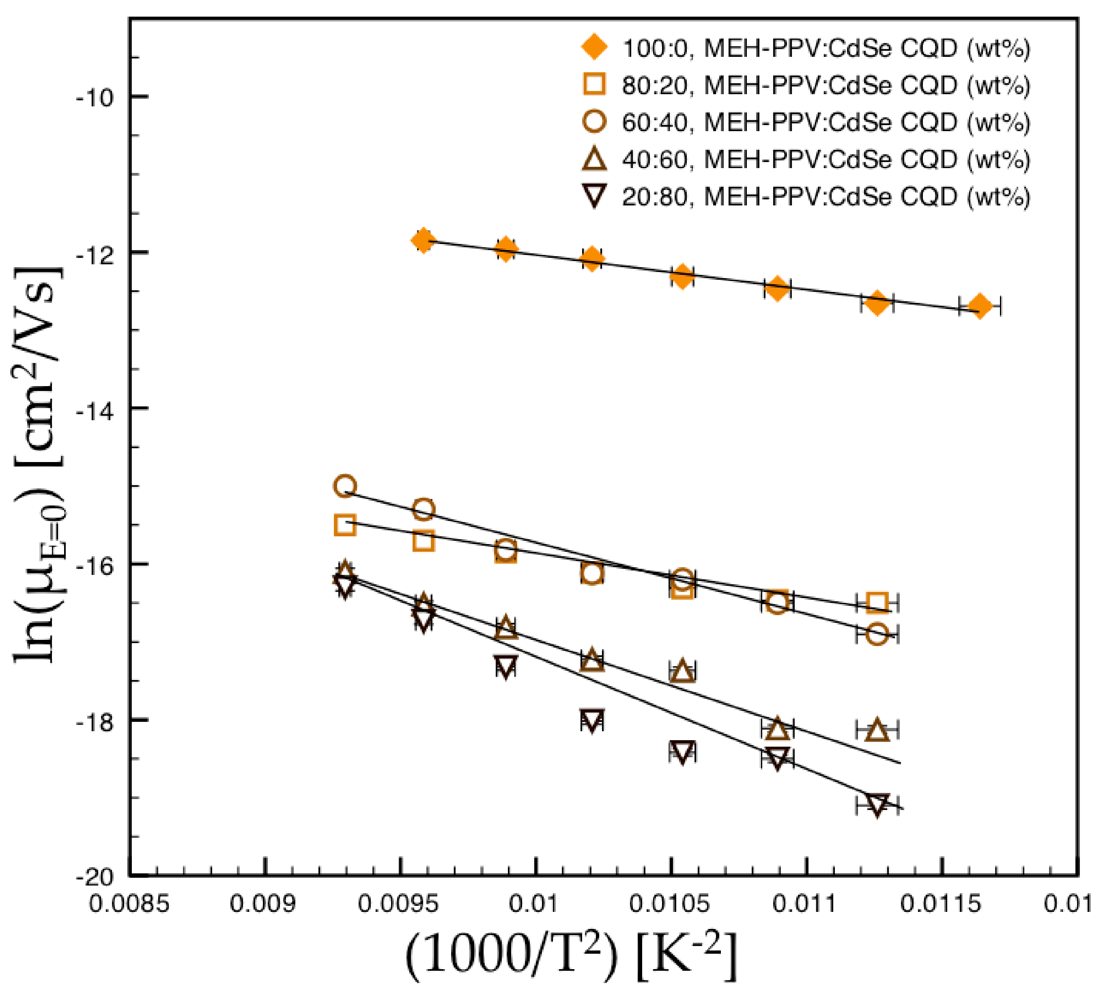
E = 0 value for each temperature and each nanocomposite concentration. The resultant plot of the non-Arrhenius temperature dependence is shown in
Figure 4 for the MEH-PPV-CdSe nanocomposite films of different CQD concentration over the entire range of investigated temperatures. The energy disorder parameters for both the BGDM(
σBGDM) and the CDM (
σCDM) can then be obtained from the gradient of the resultant plot in accordance with Equations (4) and (5), respectively. These energy disorder parameters indicate that the average energy required for holes to hop between two adjacent sites within the MEH-PPV polymer film increases as the CdSe CQD content increases, indicating that the presence of CdSe CQDs in the nanocomposite bulk decreases interchain transport.
Figure 4.
Non-Arrhenius plot of the hole drift mobility at zero-field [μ(E = 0)] as a function of inverse temperature.
Figure 4.
Non-Arrhenius plot of the hole drift mobility at zero-field [μ(E = 0)] as a function of inverse temperature.
The hole drift mobility data presented in
Figure 3 is also used to determine the BGDM positional disorder parameter,
Σ, and the CDM hopping distance,
a. In order to calculate these parameters, it is first necessary to recognize that the electric field- and temperature-dependent mobilities depicted in
Figure 3 follow the Poole-Frenkel relationship [
12]:
where
µ0(
T) is the temperature-dependent zero-field mobility determined experimentally from
Figure 3 and
Y is a pre-factor corresponding to the slope of the natural log of the measured electric field-dependent mobility.
Y can also be determined experimentally from
Figure 3 for each temperature and each deposition technique.
In order to extract the BGDM positional disorder parameter,
Σ, Equations (2) and (6) are used along with the temperature-dependent
Y pre-factors from
Figure 3 and the energy disorder parameters from
Figure 4. The expression for the positional disorder parameter is:
Thus, the BGDM positional disorder parameter,
Σ, is determined by plotting the
Υpre-factors for each temperature and nanocomposite concentration (from
Figure 3) as a function of (
σBGDM/kbT)
2, where
σBGDM is determined from
Figure 4.
Figure 5 shows the resultant linear plots of the BDGM
Υ pre-factor for the films with different MEH-PPV:CdSe ratios. The value of the x-intercept (
Y = 0) for each plot is equal to
Σ2. The positional disorder parameters increase as a function of increasing CdSe content in the nanocomposite, indicating an increasingly disordered state of the polymer component of the nanocomposite as more CdSe CQDs are added.
Figure 5.
The Bässler’s Gaussian disorder model (BGDM) pre-factor, ΥBGDM, as a function of the second power of the energy disorder parameter normalized to kbT.
Figure 5.
The Bässler’s Gaussian disorder model (BGDM) pre-factor, ΥBGDM, as a function of the second power of the energy disorder parameter normalized to kbT.
A similar procedure is used to extract the CDM hopping distance, a, the expression for which is:
Thus, the CDM hopping distance is determined by plotting the
Υpre-factorsfor each temperature and nanocomposite concentration (from
Figure 3) as a function of
(σCDM/kbT)3/2, where
σCDM is determined from
Figure 4.
Figure 6 shows the resultant linear plots of the CDM
Υ pre-factor for the pure polymer and nanocomposite samples. The value of the x-intercept (
Y = 0) for each plot is equal to
a. The hopping distance increases as a function of increasing CdSe CQD content, which indicates that the polymer chains are less relaxed as more CQDs are incorporated into the nanocomposites.
Figure 6.
The correlated disorder model (CDM) pre-factor, ΥCDM, as a function of the 3/2-power of the energy disorder parameter normalized to kbT.
Figure 6.
The correlated disorder model (CDM) pre-factor, ΥCDM, as a function of the 3/2-power of the energy disorder parameter normalized to kbT.
The BGDM and CDM energy disorder parameters (
σBGDM and
σCDM), BGDM positional disorder parameters (
Σ), and CDM hopping distances (
a) extracted from the measured hole drift mobilities are summarized in
Table 1. The overall picture provided by the disorder parameters in
Table 1 is that increasing the incorporation of CdSe CQDs into the polymer bulk reduces interchain interaction because the polymer chains exhibit more disorder and less relaxation, and the corresponding hole hopping conduction decreases. It is important to point out that surface traps on the CQD are likely to have little influence on hole transport through the nanocomposite in this system. First, holes do not enter the CQD due to the Type-II band line-up between MEH-PPV and CdSe CQDS of this size [
4]. Second, theCdSe CQDs are passivated with relatively long ligands (octadecylamine, approximately 2.2 nm in length).
Table 1.
The BGDM and CDM disorder model parameters of MEH-PPV-CdSe CQD thin films with different MEH-PPV:CdSe ratios.
Table 1.
The BGDM and CDM disorder model parameters of MEH-PPV-CdSe CQD thin films with different MEH-PPV:CdSe ratios.
| MEH-PPV:CdSe ratio (%) | BGDM energy disorder parameter (σ, eV) | CDM energy disorder parameter (σ, eV) | BGDM positional disorder parameter (Σ) | CDM hopping distance (a, Å) |
| 100:0 | 0.085 | 0.094 | 2.64 | 4.7 |
| 80:20 | 0.106 | 0.118 | 3.46 | 6.3 |
| 60:40 | 0.126 | 0.140 | 3.74 | 8.2 |
| 40:60 | 0.134 | 0.149 | 4.44 | 9.5 |
| 20:80 | 0.153 | 0.170 | 4.91 | 13.1 |
The hole drift mobility measurements for polymer-CQD nanocomposites reported herein could have important implications for the use of semiconductor nanocrystals in optoelectronic devices. It has been established that the electron percolation threshold for hopping conduction in nanocomposites is approximately 50 vol% to 65 vol% of the electron transporting material (in this case, the CdSe CQDs) relative to the polymer bulk [
6]; hence, in the context of this study, a 50:50 MEH-PPV:CdSevol% ratio is approximately 15:85 MEH-PPV:CdSewt% (MEH-PPV, density of 0.98 g/cm and CdSe, density of 5.82 g/cm), which is still slightly more CdSe-rich than the maximum MEH-PPV:CdSe ratio (20:80) investigated in this TOF measurement. As a result, in order to incorporate enough CdSe CQDs into the MEH-PPV so as to achieve electron transport through the CQDs, the MEH-PPV hole transport is markedly degraded. This property of charge conduction in polymer-CQD hybrid nanocomposites is extremely relevant to the performance of optoelectronic devices (especially photovoltaics), and could be a contributing factor to the comparatively lower device performances demonstrated using these materials [
2].