Fairness in Risky Environments: Theory and Evidence
Abstract
:1. Introduction
2. Theoretical Predictions for Fairness in Risky Environments
2.1. Risk Attitude and Inequality Aversion
- Hypothesis 1D: In the Dictator game, those with higher risk aversion give more than those with lower risk aversion, independent of the degree of risk in the environment.
- Hypothesis 1U: In the Ultimatum game, those with higher risk aversion set higher thresholds than those with lower risk aversion, independent of the degree of risk in the environment.
2.2. Consistency within Games
 ) be additively separable in utility (
) be additively separable in utility (  ) and inequality aversion (
) and inequality aversion (  ):
):
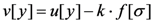
 if n = 2 (i.e., the decision maker’s disutility from his relative payoff is minimized when his payoff equals the other player’s payoff), and k > 0. The parameter k quantifies how much he cares about his relative payoff. As k approaches 0, he increasingly cares less about his relative standing in society and becomes, at the limit, a selfish decision maker whose utility function u mimics standard economic theory.
if n = 2 (i.e., the decision maker’s disutility from his relative payoff is minimized when his payoff equals the other player’s payoff), and k > 0. The parameter k quantifies how much he cares about his relative payoff. As k approaches 0, he increasingly cares less about his relative standing in society and becomes, at the limit, a selfish decision maker whose utility function u mimics standard economic theory.  for r≠0,
for r≠0,  for r = 0. We further assumed that a constant-relative-inequality-aversion function is a good approximation for fairness preferences:
for r = 0. We further assumed that a constant-relative-inequality-aversion function is a good approximation for fairness preferences:  . Substituting these functions into (1), the ERC formula becomes:
. Substituting these functions into (1), the ERC formula becomes:
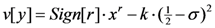
 ), where r <(>) 1 indicates risk-averse (risk-loving) preferences. A dictator who gives proportion p of an ex ante unknown realization of S (and thus keeps percentage 1-p) is assumed to have a motivation function given by Equation (2) where
), where r <(>) 1 indicates risk-averse (risk-loving) preferences. A dictator who gives proportion p of an ex ante unknown realization of S (and thus keeps percentage 1-p) is assumed to have a motivation function given by Equation (2) where  is substituted for x and 1-p for σ:
is substituted for x and 1-p for σ:
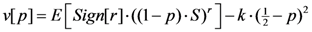
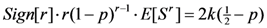
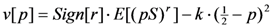
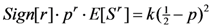
 , where SH is the high- and SL the low-risk lottery. An increase in risk thus lowers the value of the expected motivation function. This makes the left-hand side of Equations (4) and (4’) smaller. For the Dictator (Ultimatum) scenario, increasing p can restore the equality as the right-hand can be made arbitrarily small by letting p approach ½, while the left-hand side stays bounded below by a strictly positive number for any p ≤ ½. The model thus predicts an increase in giving (threshold) when risk is increased. For highly risk-averse (r < 0) and risk-loving (r > 1) preferences, the relationship is rather complicated and we thus exclude subjects with these preferences.11
, where SH is the high- and SL the low-risk lottery. An increase in risk thus lowers the value of the expected motivation function. This makes the left-hand side of Equations (4) and (4’) smaller. For the Dictator (Ultimatum) scenario, increasing p can restore the equality as the right-hand can be made arbitrarily small by letting p approach ½, while the left-hand side stays bounded below by a strictly positive number for any p ≤ ½. The model thus predicts an increase in giving (threshold) when risk is increased. For highly risk-averse (r < 0) and risk-loving (r > 1) preferences, the relationship is rather complicated and we thus exclude subjects with these preferences.11- Hypothesis 2: For people that have typical risk-averse preferences (
), the risk of the endowment does not have a significant effect:
- D. On giving in the Dictator game
- U. On the threshold in the Ultimatum game
2.3. Consistency across Games
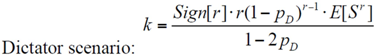
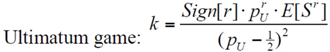
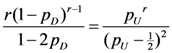

- Hypothesis 3: The choices in Dictator game (scenarios) and Ultimatum game (scenarios) are consistent.
3. Experimental Design and Implementation
 that realized a mean-preserving spread:
that realized a mean-preserving spread:  . In the low-risk condition, the lottery SL takes the value of 900 or 1100, with ½ probability each. In the high-risk condition, the lottery SH takes the value of 300 or 1700, with ½ probability each. In the no-risk condition, the lottery SN is fixed at 1000. SH is thus a mean-preserving spread of SL, which is in turn a mean-preserving spread of SN. Table 1 summarizes the different endowment risks.
. In the low-risk condition, the lottery SL takes the value of 900 or 1100, with ½ probability each. In the high-risk condition, the lottery SH takes the value of 300 or 1700, with ½ probability each. In the no-risk condition, the lottery SN is fixed at 1000. SH is thus a mean-preserving spread of SL, which is in turn a mean-preserving spread of SN. Table 1 summarizes the different endowment risks.| Possible realizations of the pie sizes Si (Dictator and Ultimatum) | |||
|---|---|---|---|
| Games | No-risk condition SN | Low-risk condition SL | High-risk condition SH |
| Dictator | - | 900 or 1100 | 300 or 1700 |
| Ultimatum | 1000 | 900 or 1100 | 300 or 1700 |
| Session | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | Total |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Type of subjects | CTU | CTU | CTU | CTU | CTU | CTU | CTU | CTU | CTUR | CTUR | CH | CH | CH | CH | |
| Number of subjects | 14 | 12 | 16 | 14 | 12 | 16 | 16 | 16 | 16 | 16 | 10 | 8 | 16 | 10 | 192 |
| Safer option | EV | Riskier option | EV | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Choice 1: | 1000 | if n> | 40 | , | 1250 | otherwise | 1100 | 60 | if n> | 40 | , | 2400 | Otherwise | 996 |
| Choice 2: | 1000 | if n> | 50 | , | 1250 | otherwise | 1125 | 60 | if n> | 50 | , | 2400 | Otherwise | 1230 |
| Choice 3: | 1000 | if n> | 60 | , | 1250 | otherwise | 1150 | 60 | if n> | 60 | , | 2400 | Otherwise | 1464 |
| Choice 4: | 1000 | if n> | 70 | , | 1250 | otherwise | 1175 | 60 | if n> | 70 | , | 2400 | Otherwise | 1698 |
| Choice 5: | 1000 | if n> | 80 | , | 1250 | otherwise | 1200 | 60 | if n> | 80 | , | 2400 | Otherwise | 1932 |
| Number of safe choices | Range of Relative Risk Aversion
r for  | Risk Preference Classification | |
|---|---|---|---|
| 0 | 1.15 | ∞ | Risk-loving |
| 1 | 0.86 | 1.15 | Risk-neutral |
| 2 | 0.60 | 0.86 | Somewhat Risk-averse |
| 3 | 0.33 | 0.60 | Intermediately Risk-averse |
| 4 | 0.04 | 0.33 | Very Risk-averse |
| 5 | –∞ | 0.04 | Highly Risk-averse |
4. Results
 , we need to determine risk preferences precisely to test our hypotheses. We thus excluded inconsistent subjects from our sample in the regressions. Table A1 in Appendix A.1 shows the implied interval for risk aversion for all patterns of choice.
, we need to determine risk preferences precisely to test our hypotheses. We thus excluded inconsistent subjects from our sample in the regressions. Table A1 in Appendix A.1 shows the implied interval for risk aversion for all patterns of choice.| Variables | Effects |
|---|---|
| Income | –0.11** (0.06) |
| Age | 0.05 (0.03) |
| Female | 0.67 * (0.37) |
| Time_to_answer | 0.06 (0.04) |
| City_Hall_employee | –0.63 (0.82) |
| CTUR | 0.07 (0.50) |
| Constant | 2.23 *** (0.75) |
4.1. Risk Attitude and Inequality Aversion (Hypothesis 1: Those with Higher Risk Aversion Show Higher Inequality Aversion in Their Responses.)
| Dictator | Ultimatum | |||||||
|---|---|---|---|---|---|---|---|---|
| Model 1D1 | Model 1D2 | Model 1D3 | Model 1D4 | Model 1U1 | Model 1U2 | Model 1U3 | Model 1U4 | |
| Dummy: Somewhat_versus_highly_risk_averse | 9.59*** | 6.01* | 10.49*** | 6.91* | 5.81 | 4.68 | 6.73 | 5.59 |
| (3.60) | (3.46) | (3.92) | (3.92) | (3.96) | (4.08) | (4.10) | (4.24) | |
| High_endowment_risk | −0.97 | −0.97 | 0.30 | 0.30 | 3.71*** | 3.71*** | 5.40* | 5.40* |
| (1.81) | (1.83) | (3.58) | (3.62) | (1.24) | (1.25) | (2.93) | (2.95) | |
| Low_endowment_risk | 1.39 | 1.39 | 1.63 | 1.63 | ||||
| (0.86) | (0.86) | (1.41) | (1.42) | |||||
| Interaction Dummy: Somewhat_versus_highly_risk_averse x High_endowment_risk | −1.80 | −1.80 | −2.40 | −2.40 | ||||
| (4.15) | (4.19) | (3.19) | (3.21) | |||||
| Interaction Dummy: Somewhat_versus_highly_risk_averse x High_endowment_risk | −0.34 | −0.34 | ||||||
| (1.77) | (1.78) | |||||||
| Income | −0.00 | −0.00 | −0.64 | −0.64 | ||||
| (0.49) | (0.50) | (0.51) | (0.51) | |||||
| Age | −0.32 | −0.32 | −0.21 | −0.21 | ||||
| (0.32) | (0.32) | (0.27) | (0.27) | |||||
| Female | 3.81 | 3.81 | −1.95 | −1.95 | ||||
| (3.65) | (3.66) | (3.52) | (3.53) | |||||
| Time_to_answer | 1.80*** | 1.80*** | 0.61* | 0.61* | ||||
| (0.37) | (0.38) | (0.32) | (0.32) | |||||
| City_Hall_employees | 8.73* | 3.98 | 8.73* | 3.98 | −2.93 | 2.67 | −2.93 | 2.67 |
| (4.62) | (6.36) | (4.63) | (6.38) | (4.08) | (7.08) | (4.09) | (7.10) | |
| CTUR | −3.87 | −6.46 | −3.87 | −6.46 | −4.38 | −5.26 | −4.38 | −5.26 |
| (5.16) | (4.57) | (5.18) | (4.58) | (4.94) | (4.95) | (4.96) | (4.97) | |
| Constant | 10.55*** | 12.70* | 9.91*** | 12.06* | 20.18*** | 25.67*** | 19.53*** | 25.03*** |
| (3.27) | (7.45) | (3.51) | (7.20) | (3.71) | (7.28) | (3.80) | (7.28) | |
| N | 204 | 204 | 306 | 306 | ||||
| (Independent clusters) | (102) | (102) | 204 | 204 | (102) | (102) | 306 | 306 |
| R-squared | 0.08 | 0.21 | 0.08 | 0.21 | 0.04 | 0.07 | 0.04 | 0.08 |
4.2. Consistency within Games (Hypothesis 2: Increasing Endowment Risk does not have a Significant Effect)
| Dictator | Ultimatum | |||||
|---|---|---|---|---|---|---|
| Model 2D1 | Model 2D2 | Model 2D3(Tobit) | Model 2D4(Tobit) | Model2U1 | Model2U2 | |
| High_endowment_risk | −0.83 | −0.83 | −0.92 | −0.93 | 4.78*** | 4.78*** |
| (1.96) | (2.02) | (2.52) | (2.50) | (1.65) | (1.68) | |
| Low_endowment_risk | 3.18* | 3.18* | ||||
| (1.73) | (1.76) | |||||
| Income | 1.16 | 2.09 | −2.05 | |||
| (1.17) | (1.42) | (1.55) | ||||
| Age | −0.49 | −0.86 | −0.08 | |||
| (0.43) | (0.59) | (0.54) | ||||
| Female | 5.32 | 9.48 | −1.20 | |||
| (5.88) | (7.71) | (6.69) | ||||
| Time_to_answer | 2.06** | 2.95** | 0.55 | |||
| (0.89) | (1.25) | (1.36) | ||||
| City_Hall_employees | 14.90* | 2.19 | 18.80* | −3.74 | −4.21 | 16.33 |
| (7.99) | (12.07) | (9.62) | (15.63) | (8.58) | (17.12) | |
| CTUR | −3.53 | −10.71 | −8.78 | −20.01 | −1.88 | −1.23 |
| (7.14) | (7.88) | (12.71) | (13.97) | (6.80) | (7.80) | |
| Constant | 15.59*** | 15.67 | 10.04* | 12.45 | 24.47*** | 30.28* |
| (3.22) | (10.53) | (5.18) | (13.50) | (3.86) | (15.00) | |
| N | 80 | 80 | 80 | 80 | 120 | 120 |
| (Independent clusters) | (40) | (40) | (40) | (40) | 60 | 60 |
| R-squared (pseudo R-squared) | 0.11 | 0.22 | (0.02) | (0.04) | 0.02 | 0.09 |
4.3. Consistency across Games (Hypothesis 3: Subjects Are Consistent between Games)
| Successful | Unsuccessful | Total | |
|---|---|---|---|
| Predict D from U and visa versa | 8 (10%) | 75 (90%) | 83 (100%) |

5. Concluding Discussion
- 1.A reasonable intuition for that finding could be this: encountering states of inequality in the world makes one aware of the danger that one self may end up in some such state. This is likely to be the more threatening for a person the more s/he is risk-averse. This threat might activate, or intensify, inequality aversion.
- 2.Cherry et al. [7] have demonstrated persuasively that the experimental results reported in the literature are dependent on both the degree of asset legitimacy and social distance. When the pie was not provided by the experimenter but had to be earned by their student dictators first (“asset legitimacy”), and when the game was also played under double anonymity (maximal “social distance”; see Hoffman et al. [12]), giving was as predicted by the standard economic assumption of selfishness. Bekkers [13] provides similar evidence through a field experiment. Smith [14] argues that asset legitimacy is an important challenge that experimental economists need to address.
- 3.Engelmann & Strobel [15] presented an experimental test of the Bolton & Ockenfels and Fehr & Schmidt models which suggests that people, following Rawls’s theory of justice (Rawls [1]), want to maximize the welfare of the person who is the worst off (a form of other-regarding behavior); these authors (see also Engelmann & Strobel [16] for a balanced review of the literature and Engelmann [17] for an important caveat regarding the appropriate modeling of welfare maximization) identify the importance of efficiency concerns (defined as the sum of all payoffs in the game) as an explanatory variable. In their theory section, Charness & Rabin [18] use a social welfare criterion, which is defined as a weighted combination of minimal payoff (again, a form of other-regarding behavior) and the sum of all payoffs in the game. Cox & Sadiraj [19] provide a non-linear generalization of that model.
- 4.Recent experimental work conducted in parallel by Güth et al. [21], Cappelen et al. [22], and Krawczyk & Le Lec [23], introduce theories or experimental results of distributive choice under risk. Güth et al. [21], continuing the work of Brennan et al. [24] and, using a within-subject design and incentive-compatible elicitation of valuations of 16 different prospects, find that individuals are self-oriented towards the social allocation of risk and delay and other-regarding with respect to expected payoffs. Cappelen et al. [22] use a two-stage dictator game to study to what extent, and under what circumstances, ex-ante fairness under risk is robust to ex-post redistribution. Krawzcyk & Le Lec [23] use a within-subject design and probabilistic versions of the dictator game that are manipulated along two dimensions (the relative cost of giving and the nature of the lottery) to try to tease out the relative merits of outcome-based and intention-based models of fairness under risk. All the models mentioned above were constructed under the assumption of pie sizes that are known ex ante.
- 5.In addition, we also studied the so-called Trust game in such an environment (see Appendices A.5, A.6, and A.8). Assuming self-regarding preferences, the situation for responders in the Trust game is theoretically equivalent to that of dictators in a standard Dictator scenario. However, responders in our design and implementation of the Trust game cannot infer precisely the proposer’s initial decision (because the amount sent is multiplied by an unknown random factor X), and proposers cannot foresee the responders’ reaction. Proposers probably developed beliefs about responders’ behavior, but we were not able, given time constraints, to control for these during the experiment. We are therefore not able to theoretically derive the effects of risk preferences for proposing and responding in the Trust game and therefore decided not to include the Trust game in our analysis. We note that none of the relationships turned out significant for the Trust game.
- 6.In principle, the recipient’s proposed share can also be determined in absolute terms. There are three reasons why we did not use absolute terms. First, in theories of fairness and reciprocity only relative terms matter. Second, an ex-ante allocation in absolute terms could result in a negative outcome for the decision maker (when the realized pie is small), which might trigger loss aversion and confound our results. Third, in the present paper we are not interested in optimal contract design (this could solve the preceding problem, but would also complicate our design beyond what seems feasible to implement.)
- 7.Note that we have not used the ERC formulation to derive our hypotheses regarding the relation between risk aversion and inequality aversion in the Dictator and Ultimatum game, as this formulation is moot on the possible effects of risk aversion on inequality aversion. Predictions could be derived for people with different risk preferences, if the inequality aversion parameter k could be assumed to remain constant between different people with different risk preferences but with equal inequality aversion. This assumption does not hold as the inequality aversion parameter k conveys both an inequality aversion and an (unknown) rescaling effect. An increase in risk aversion is modeled by a transformation that results in a more concave utility function. This transformation also rescales the magnitude and the slope of the utility function and the parameter k needs to change to correct for this rescaling effect, making it impossible to deduce the individual inequality aversion effect. For example, using formula (4) below to estimate the parameter k shows that in our sample it ranges from an average of 0.2 (for highly risk-averse subjects) to 100 (for somewhat risk-averse subjects) to 5500 (for risk-loving subjects).
- 9.For standard stakes (such as the ones in our experiment) the constant-relative-risk-aversion form of the utility function can be rationalized experimentally by the results of Holt & Laury [5], p.1652, who suggest that it works as a “good approximation” of human behavior. This approximation simplifies our theoretical arguments considerably.
- 10.Note that always
. For any c,
, any proportion of giving equal to
is dominated by
, as the latter proportion of giving results in higher utility, u[y], and equal inequality,
.
- 11.For risk-loving (r > 1) preferences, the relationship is inverted in the Ultimatum game, and depends on the values of k and r in the Dictator game. For highly risk-averse (r < 0) preferences, the relationship is inverted in the Dictator game and undefined in the Ultimatum game.
- 12.See Appendix A.3.
- 13.Note that for certain Ultimatum threshold levels no prediction of positive Dictator giving exists. For example, for Highly Risk-averse subjects, an Ultimatum threshold of 0.23 predicts zero Dictator giving. Ultimatum thresholds lower than 0.23 then predict negative Dictator giving, or “Dictator taking”. As Dictator taking was not a choice option in the experiment, the 14 observations where the Ultimatum threshold predicts Dictator taking were excluded from the analysis.
- 14.We ran, at the tail end of the CTU sessions, two control sessions with an additional 32 CTU student subjects (sessions 9 and 10, indicated by CTUR in Table 2). The subjects in the control group read the same instructions but were given a different ordering of decisions: all low-risk treatments were switched to high-risk treatments and vice versa. This control group, which did not take part in any of the other sessions, was conducted to control for order effects. Two-sample Kolmogorov-Smirnov tests suggest that the control group differs statistically significantly from the CTU group in at least two respects (age and the measure of cognitive ability that we will discuss below). It is not clear to us why we find these differences in age and cognitive ability, although it might be due to the fact that we ran those sessions at the tail end of the CTU sessions. In addition, using again two-sample Kolmogorov-Smirnov tests, we found the following significant differences in the decisions of the control group: they gave less in the Dictator game, made a lower offer in the Trust game, and sent less back in the Trust game. We include the data in our analysis below to determine the extent of the estimated treatment effects attributable to decision-order effects with a dummy variable, CTUR. This dummy is not significant in any of the regressions in the results section.
- 15.Each session contained an even number of participants, and was constrained by the maximum lab capacity of 16 people. We attempted to have at least 12 participants in each session but scheduling the four CH sessions turned out to be difficult. There is no a-priori reason that we can think of that would suggest this was more than a logistic inconvenience.
- 16.Subjects were thus paid twice as recipients in the Dictator game (once for the low-risk and once for the high-risk condition).
- 17.In the Trust game, subjects were informed of the amount they received once they were asked at the end of a session to make a decision as responder.
- 18.When the experimental sessions were conducted, the exchange rate was about 23 CZK/1 USD, implying that our subjects—not counting appearance fees—earned on average 17–18 USD. The local purchasing power of these payoffs was about twice as much. Thus, it seems fair to say that the stakes were considerable for both students and City Hall employees. Since CH employees (and students) were told ex ante what average earning they could expect, we believe that only subjects that thought the money was worth their troubles signed up forthe experiment.
- 19.Sessions lasted from 60 to 100 minutes, with student sessions typically being in the lower half and the CH sessions in the upper half of the interval.
- 20.As in Holt & Laury [5], subjects were not told the expected value of the options they were given.
- 21.We were aware ex ante (based, for example, on evidence reported in Hey & Orme [28]) that our procedure was likely to induce at least 25% inconsistent choices. Since we did not give our subjects the five risk-aversion measurement choices back to back, and did not give our subjects the EV of their options, with the benefit of hindsight, the fairly high percentage of inconsistent choices (not observed in the pilots in which we employed CERGE-EI students) is arguably not that surprising. It might simply reflect (as does also recent evidence on the stability of risk attitude assessment measures; see Dickhaut & Wilcox [29]) that other forms of elicitation may be confounded by subjects’ attempts to be consistent. Harrison et al. [30] interpret inconsistent choices as an indication that subjects are indifferent between the different gambles and that their risk preference is thus part of a “fatter” interval.
- 22.The average number of safe choices is 3.5 for students and 3.2 for City Hall employees. This result is not out of line with other evidence (e.g., [5]), which suggests the vast majority of subjects are rather risk-averse. Given the considerable stakes in our experiment, our risk-attitude results seem sensible.
- 23.We ran, as a robustness test, ordered logistic regressions with the number of safe choices as the independent variable: Signs are unaffected and the significance levels are roughly the same. The effect of being female, however, is no longer significant (p = 0.12). The difference between City Hall employees and students is not significant (p > 0.42).
- 24.As robustness tests, we rerun the regressions using, to capture the difference in risk preferences, the variable safe, the number of safe choices a subject made, instead of the dummy Somewhat_versus_highly_risk_averse. With the variable safe, the significance is overall lower: the relationship for Dictator giving in Model 1 stays significant (p < 0.042), but not in Model 2 (p < 0.311).
- 25.Running a Tobit regression, to account for the left-censoring of Dictator giving, gives the same significance levels for Models 1D1 and 1D3, and slightly higher ones for Models 1D2 and 1D4.
- 26.Note that subjects with one safe choice include subjects who lean towards being somewhat risk-averse (0.86 < r < 1), subjects who are risk-neutral (r = 1), and subjects who lean towards being risk-loving (1 < r < 1.15); see Table 4. Since theory predicts that an increase in risk aversion has an effect for risk-loving subjects (decrease giving) that is opposite to that for risk-averse subjects (increase giving), the inclusion of these subjects should lead us to underestimate the increase in giving. However, effects on giving are very small round the point where risk-loving changes to risk aversion (r = 1), and we can thus expect that the resulting underestimation will be small. Indeed, running a regression excluding also the subjects with 1 safe choice does not change the results qualitatively.
- 27.An F-test shows that the dummies for high and low endowment risk are not significantly different (p = 0.42).
- 28.The success percentages are symmetric by design. The analysis in Table 8 excluded the 14 responses where the choice for the Ultimatum threshold predicted Dictator taking (giving a negative amount, which was not a possible choice in the experiment). Including these 14 responses, and accepting the closest possible Dictator giving choice, zero, as a correct prediction, increases the correct percentage of predictions somewhat, from the 10% reported in Table 8 to 20%.
- 29.For each of the levels of risk aversion we studied, we created a grid of values for the inequality aversion parameter k and, using formula (4), calculated the optimal giving for each of the values of k, given the level of risk aversion and the level of risk. We use these coordinates to draw the figures in Figure A.2. We used a likewise procedure, using formula (4’) for drawing the figures in Figure A.3 for the Ultimatum games. We programmed the algorithms in Mathematica.
Acknowledgments
Conflict of Interest
References
- Rawls, J. A Theory of Justice; Belknap Press of Harvard University Press: Cambridge, MA, USA, 1971. [Google Scholar]
- Chambers, C.P. Inequality aversion and risk aversion. J. Econ. Theory 2012, 147, 1642–1651. [Google Scholar] [CrossRef]
- Ferrer-i-Carbonell, A.; Ramos, X. Inequality aversion and risk attitudes. SOEP papers 271; DIW Berlin: Berlin, Germany, 2010. [Google Scholar]
- Carlsson, F.; Daruvala, D.; Johansson-Stenman, O. Are people inequality-averse, or just risk-averse? Economica 2005, 72, 375–396. [Google Scholar] [CrossRef]
- Holt, C.; Laury, S. Risk aversion and incentive effects. Am. Econ. Rev. 2002, 92, 1644–1655. [Google Scholar] [CrossRef]
- Harrison, G.W.; Johnson, E.; McInnes, M.M.; Rutström, E.E. Risk aversion and incentive effects: Comment. Am. Econ. Rev. 2005, 95, 897–901. [Google Scholar] [CrossRef]
- Cherry, T.; Frykblom, P.; Shogren, J. Hardnose the dictator. Am. Econ. Rev. 2002, 92, 1218–1221. [Google Scholar] [CrossRef]
- Camerer, C.F. Behavioral Game Theory; Princeton University Press: Princeton, NJ, USA, 2003. [Google Scholar]
- Güth, W.; Ortmann, A.A. Behavioral approach to distribution and bargaining. In Foundations and Extensions of Behavioral Economics: A Handbook; Altman, M., Ed.; Sharpe Publishers: New York, NY, USA, 2006; pp. 405–422. [Google Scholar]
- Bolton, G.; Ockenfels, A. ERC: A theory of equity, reciprocity and competition. Am. Econ. Rev. 2000, 90, 166–193. [Google Scholar] [CrossRef]
- Fehr, E.; Schmidt, K.A. Theory of fairness, competition and cooperation. Quart. J. Econ. 1999, 114, 817–868. [Google Scholar] [CrossRef]
- Hoffman, E.; McCabe, K.; Smith, V.L. Social distance and other-regarding behavior in Dictator games. Am. Econ. Rev. 1996, 86, 653–660. [Google Scholar]
- Bekkers, R. Measuring altruistic behavior in surveys: The all-or-nothing Dictator game. Surv. Res. Methods 2007, 1, 139–144. [Google Scholar]
- Smith, V. Theory and experiment: What are the questions? J. Econ. Behav. Organ. 2010, 73, 3–15. [Google Scholar] [CrossRef]
- Engelmann, D.; Strobel, M. Inequality aversion, efficiency and maximin preferences in simple distribution experiments. Am. Econ. Rev. 2004, 94, 857–869. [Google Scholar] [CrossRef]
- Engelmann, D.; Strobel, M. Preference over income distributions—Experimental evidence. Public Finance Rev. 2007, 35, 285–310. [Google Scholar] [CrossRef]
- Engelmann, D. How not to extend models of inequality aversion. J. Econ. Behav. Organ. 2012, 81, 599–605. [Google Scholar] [CrossRef]
- Charness, G.; Rabin, M. Understanding social preferences with simple tests. Quart. J. Econ. 2002, 117, 817–869. [Google Scholar] [CrossRef]
- Cox, J.; Sadiraj, V. Direct tests of individual preferences for efficiency and equity. Econ. Inquiry 2010, 50, 920–931. [Google Scholar]
- Blanco, M.; Engelmann, D.; Normann, H.T. A within-subject analysis of other-regarding preferences. Games Econ. Behav. 2011, 72, 321–338. [Google Scholar] [CrossRef]
- Güth, W.; Levati, M.V.; Ploner, M. On the social dimension of time and risk preferences. Econ. Inquiry 2008, 64, 261–272. [Google Scholar]
- Cappelen, A.W.; Konow, J.; Sorensen, E.; Tungodden, B. Just luck: An experimental study of risk taking and fairness. Am. Econ. Rev. forthcoming.
- Krawczyk, M.; Le Lec, F. “Give me a chance!” And experiment in social decision under risk. Exper. Econ. 2010, 13, 500–511. [Google Scholar] [CrossRef]
- Brennan, G.; González, L.G.; Güth, W.; Levati, M.V. Attitudes toward private and collective risk in individual and strategic choice situations. J. Econ. Behav. Organ. 2008, 67, 253–262. [Google Scholar] [CrossRef]
- Babicky, V. Fairness under risk: Insights from dictator games. CERGE-EI Working paper 2004, No. 217; The Center for Economic Research and Graduate Education, Economic Institute: Prague, Czech Republic, 2003. [Google Scholar]
- Fischbacher, U. Z-Tree, Zurich toolbox for ready-made economic experiments. Exp. Econ. 2007, 10, 171–178. [Google Scholar] [CrossRef]
- Weber, R.A. “Learning” with no feedback in a competitive guessing game. Games Econ. Behav. 2003, 44, 134–144. [Google Scholar] [CrossRef]
- Hey, J.; Orme, C. Investigating Generalizations of expected utility theory using experimental data. Econometrica 1994, 62, 1291–1326. [Google Scholar] [CrossRef]
- Dickhaut, J.; Wilcox, N. Elicitation of risk attitudes, a new assessment battery. 2010. Mimeo. [Google Scholar]
- Harrison, G.W.; Lau, M.I.; Rutström, E.E.; Sullivan, M.B. Eliciting risk and time preferences using field experiments: Some methodological issues. In Field Experiments in Economics: Research in Experimental Economics; Harrison, G.W., Carpenter, J., List, J.A., Eds.; Emerald Group Publishing Limited: Bingley, UK, 2005; Volume 12, pp. 125–218. [Google Scholar]
- Harrison, G.W.; Rutström, E.E. Risk aversion in the laboratory. In Research in Experimental Economics; Cox, J.C., Harrison, G.W., Eds.; Emerald: Bingley, UK, 2008; Volume 12, pp. 41–196. [Google Scholar]
- Froot, K.A. Consistent covariance matrix estimation with cross-sectional dependence and heteroskedasticity in financial data. J. Finan. Quant. Anal. 1989, 24, 301–312. [Google Scholar] [CrossRef]
- Rydval, O.; Ortmann, A. How financial incentives and cognitive abilities affect task performance in laboratory settings: An illustration. Econ. Lett. 2004, 85, 315–320. [Google Scholar] [CrossRef]
Appendix
A.1. Overview of Responses on the Holt-Laury Test
| 1st | 2nd | 3rd | 4th | 5th | Interval | Risk aversion | Occurrence |
|---|---|---|---|---|---|---|---|
| Subjects that were consistent in their choices | |||||||
| RISKY | RISKY | RISKY | RISKY | RISKY | [1.15; +∞] | Risk-loving | 9% |
| SAFE | RISKY | RISKY | RISKY | RISKY | [0.86; 1.15] | Risk-neutral | 4% |
| SAFE | SAFE | RISKY | RISKY | RISKY | [0.60; 0.86] | Somewhat Risk-averse | 4% |
| SAFE | SAFE | SAFE | RISKY | RISKY | [0.33; 0.60] | Intermediately Risk-averse | 4% |
| SAFE | SAFE | SAFE | SAFE | RISKY | [0.04; 0.33] | Very Risk-averse | 9% |
| SAFE | SAFE | SAFE | SAFE | SAFE | [−∞; 0.04] | Highly Riskaverse | 24% |
| Subjects that had fat risk aversion intervals | |||||||
| SAFE | RISKY | RISKY | RISKY | SAFE | [−∞; 1.15] | Undeterminable | 2% |
| SAFE | RISKY | RISKY | SAFE | RISKY | [0.04; 1.15] | Undeterminable | 2% |
| SAFE | RISKY | RISKY | SAFE | SAFE | [−∞; 1.15] | Undeterminable | 3% |
| SAFE | RISKY | SAFE | RISKY | RISKY | [0.33; 1.15] | Undeterminable | 2% |
| SAFE | RISKY | SAFE | RISKY | SAFE | [−∞; 1.15] | Undeterminable | 1% |
| SAFE | RISKY | SAFE | SAFE | RISKY | [0.04; 1.15] | Undeterminable | 2% |
| SAFE | RISKY | SAFE | SAFE | SAFE | [−∞; 1.15] | Undeterminable | 3% |
| SAFE | SAFE | RISKY | SAFE | RISKY | [0.04; 0.86] | Undeterminable | 3% |
| SAFE | SAFE | RISKY | SAFE | SAFE | [−∞; 0.86] | Undeterminable | 1% |
| SAFE | SAFE | SAFE | RISKY | SAFE | [−∞; 0.60] | Undeterminable | 2% |
| RISKY | RISKY | RISKY | SAFE | RISKY | [0.04; +∞] | Undeterminable | 4% |
| RISKY | RISKY | SAFE | RISKY | RISKY | [0.33; +∞] | Undeterminable | 3% |
| RISKY | SAFE | RISKY | SAFE | RISKY | [0.04; +∞] | Undeterminable | 4% |
| RISKY | SAFE | SAFE | RISKY | RISKY | [0.33 ; +∞] | Undeterminable | 1% |
| Subjects that made contradictory choices | |||||||
| RISKY | RISKY | RISKY | RISKY | SAFE | [−∞; +∞] | Undeterminable | 3% |
| RISKY | RISKY | RISKY | SAFE | SAFE | [−∞; +∞] | Undeterminable | 4% |
| RISKY | RISKY | SAFE | SAFE | SAFE | [−∞; +∞] | Undeterminable | 1% |
| RISKY | SAFE | RISKY | RISKY | SAFE | [−∞; +∞] | Undeterminable | 1% |
| RISKY | SAFE | RISKY | SAFE | SAFE | [−∞; +∞] | Undeterminable | 1% |
| RISKY | SAFE | SAFE | RISKY | SAFE | [−∞; +∞] | Undeterminable | 1% |
| RISKY | SAFE | SAFE | SAFE | SAFE | [−∞; +∞] | Undeterminable | 7% |
A.2. Overview of the Socio-demographic Characteristics of the Subjects

A.3. Simulations on the Effect of Risk in the Dictator and Ultimatum Games on Decisions
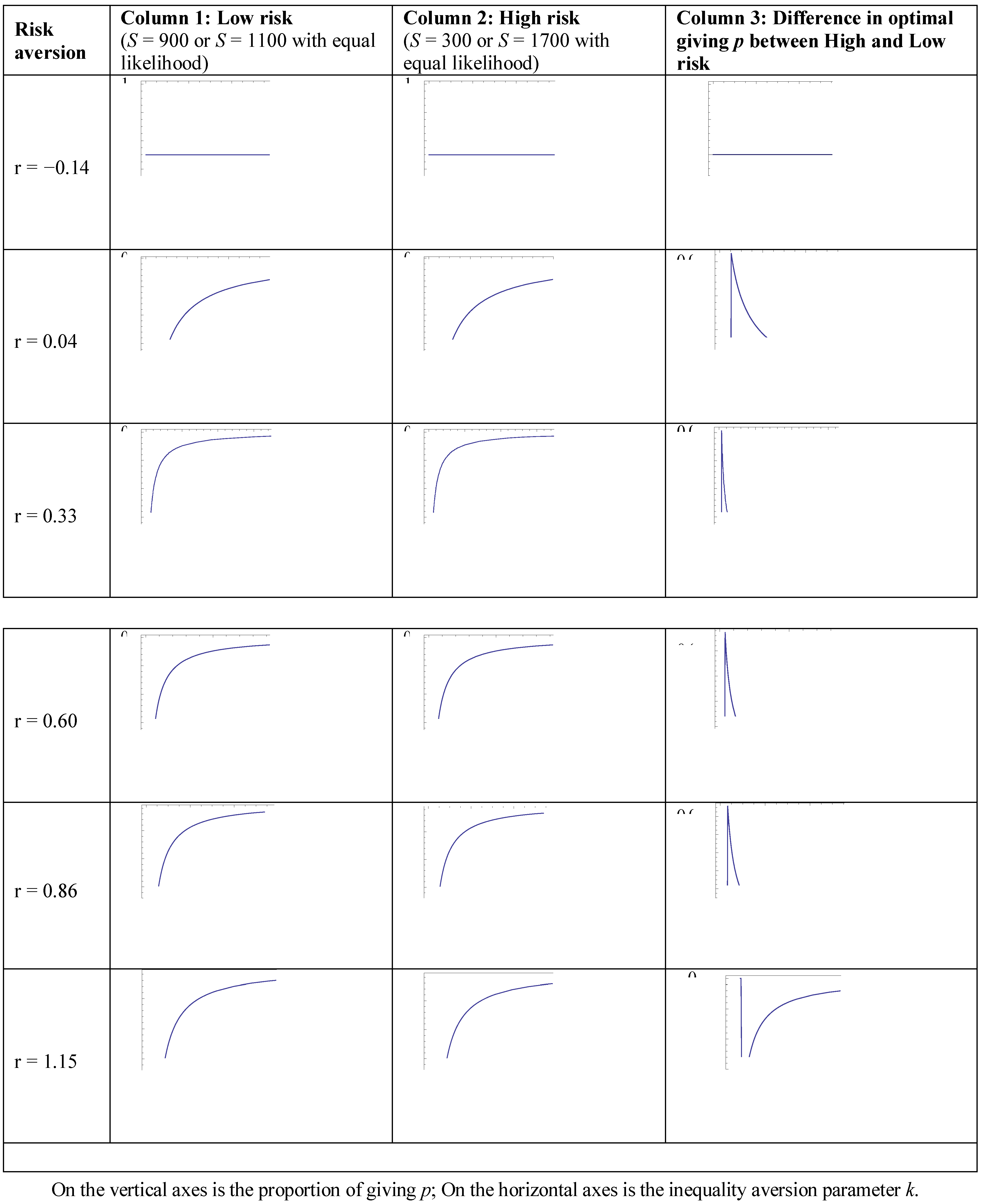
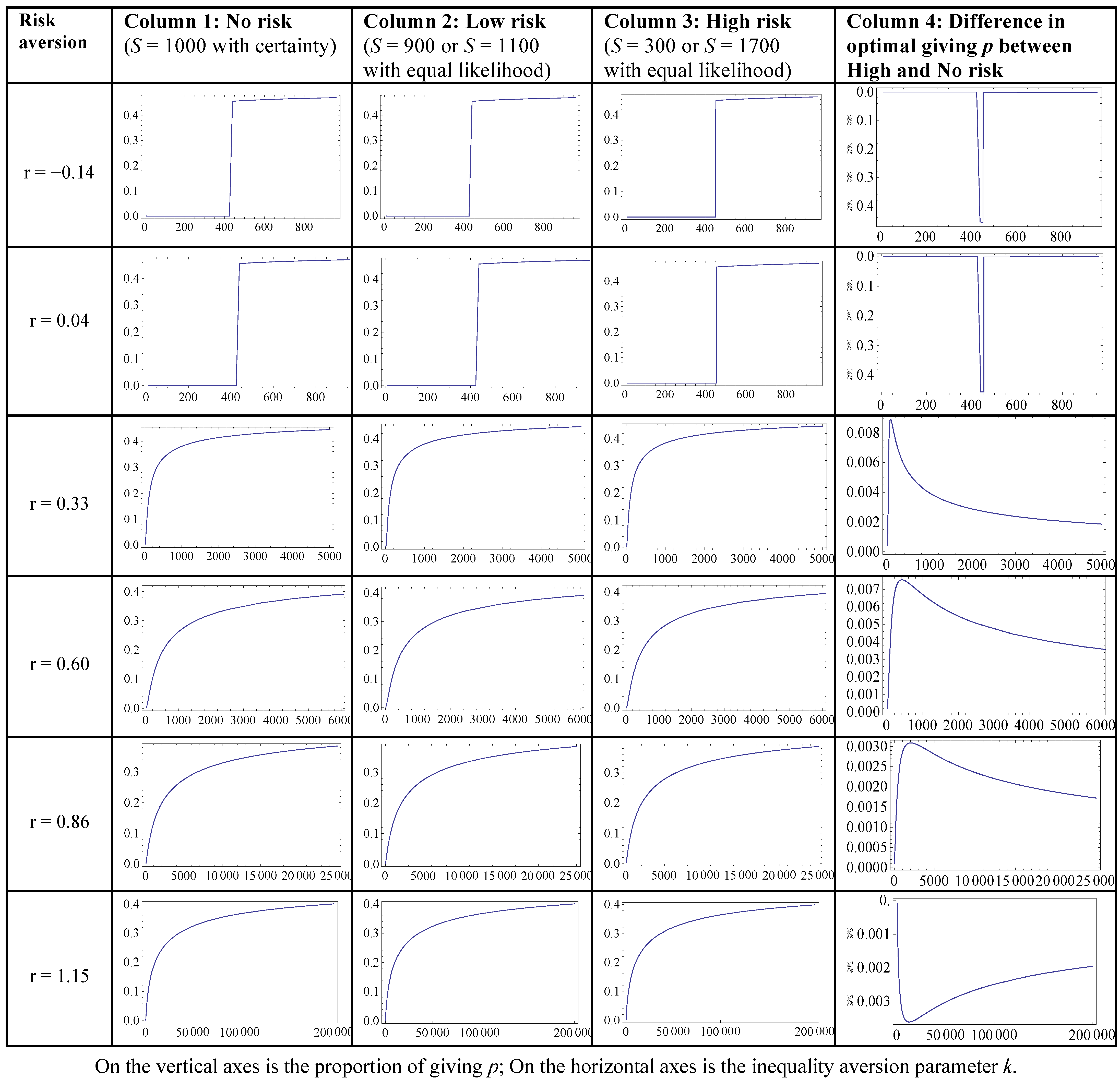
A.4. Prediction Errors on the Individual Level

A.5. Scripted Instructions
A.6. Sequencing of decisions
- Decision 1: Ultimatum proposal with no risk (pie size 1000)
- Decision 2: Risk attitude measurement (n>40, i.e., Choice 1)
- Decision 3: Dictator with low risk (pie size 900 or 1100)
- Decision 4: Trust game sending with high risk (factor 1.2 or 2.8)
- Decision 5: Ultimatum proposal with high risk (pie size 300 or 1700)
- Decision 6: Risk attitude measurement (n>50, i.e., Choice 2)
- Decision 7: Ultimatum threshold with high risk (pie size 300 or 1700)
- Decision 8: Trust game sending with low risk (factor 1.8 or 2.2)
- Decision 9: Ultimatum proposal with low risk (pie size 900 or 1100)
- Decision 10: Risk attitude measurement (n>60, i.e., Choice 3)
- Decision 11: Ultimatum threshold with low risk (pie size 900 or 1100)
- Decision 12: Risk attitude measurement (n>70, i.e., Choice 4)
- Decision 13: Dictator with high risk (pie size 300 or 1700)
- Decision 14: Ultimatum threshold with no risk (pie size 1000)
- Decision 15: Trust game return with high risk (factor 1.2 or 2.8)
- Decision 16: Risk attitude measurement (n>80, i.e., Choice 5)
- Decision 17: Trust game return with low risk (factor 1.8 or 2.2)
A.7. Control Questions
- Question 1: What are your earnings from this scenario?
- Question 2: What are the earnings of participant B, who has been selected randomly and assigned to you for this scenario. Please fill out your answer in the space above and confirm.
A.8. Instructions in the z-Tree Program
Abbreviations used
| D | Dictator Scenario |
| P | Proposer role |
| none | no-risk condition |
| U | Ultimatum Game |
| R | Respondent role |
| low | low-risk condition |
| T | Trust Game |
| high | high-risk condition |
| HL | Holt-Laury task |
| Original (Czech) | English translation |
|---|---|
| [Questionnaire] Nyni overime, ze vsichni porozumeli zakladnim scenarum, ktere popisuji instrukce. Odpovedi na nasledujici dve otazky nebudou mit dopad na Vasi vyplatu z experimentu, ale pokracovat budete moci jen po jejich spravnem zodpovezeni. Mate-li otazku, zvednete ruku a experimentator Vam prijde odpovedet. Uvazujte scenar Jedna s celkovou castkou S=200 ECU. (Pokud potrebujete, vratte se k tistenym instrukcim, ktere tento scenar popisuji.) Jste v roli ucastnika A a sve rozhodnuti jste vyjadril cislem 84. Otazka 1: Kolik je Vas zisk z pouziti tohoto scenare? Otazka 2: Kolik je zisk ucastnika B, ktery k Vam byl pro pouziti tohoto scenare nahodne prirazen? Vase odpovedi prosim vyplnte v jednotkach ECU do okenek vyse a potvrdte! | [Questionnaire] We will now ensure that everybody understood the basic scenarios from the instructions. Your answers on the two following questions will not have any effect on your earnings from the experiment, but you will be able to continue only after you have answered them correctly If you have an answer, please raise your hand and an experimenter will come. Consider scenario One with the total S=200 ECU (If you need to, you may return to the written instruction that describes this scenario) You have the role of participant A and you made a choice of 84. Question 1: What are your earnings from this scenario? Question 2: What are the earnings of participant B, who has been selected randomly and assigned to you for this scenario? Please fill out your answer in ECUs in the space above and confirm! |
| [U_P-none] Od nynejska budou mit vsechna Vase rozhodnuti dusledky na vysi Vasi vyplaty z tohoto experimentu. Proto davejte dobry pozor na ukoly, o ktere Vas budeme zadat. Uvazujte Scenar Dva s celkovou castkou S= 1000 ECU. (Pokud potrebujete, vratte se k tistenym instrukcim, ktere tento scenar popisuji.) Jste v roli ucastnika C a pro ucely scenare jste byl pocitacem nahodne prirazen k jinemu ucastnikovi experimentu. Rozhodnuti 1: Jaka je Vase nabidka? Prosim vyplnte Vasi odpoved do okenka a potvrdte! | [U_P-none] From now on, all your decisions will affect your earnings from this experiment. Therefore, pay close attention to the tasks we will present to you. Consider Scenario Two with the total S=200 ECU (If you need to, you may return to the written instruction that describes this scenario) You have the role of participant C and for this scenario you have been randomly assigned to another participant in this experiment. Decision 1: What is your proposal? Please fill out your answer in the space above and confirm! |
| [HL-40] Uvazujte scenar Ctyri. (Pokud potrebujete, vratte se k tistenym instrukcim, ktere tento scenar popisuji.) Volba "+": Ziskate 1000 ECU pokud N>40, jinak ziskate 1250 ECU Volba "*": Ziskate 60 ECU pokud N>40, jinak ziskate 2400 ECU Rozhodnuti 2: Kterou volbu preferujete? | [HL-40] Consider scenario Four (If you need to, you may return to the written instruction that describes this scenario) Choice “+”: You receive 1000 ECU when N>40, otherwise you receive 1250 ECU Choice “*”: You receive 60 ECU when N>40, otherwise you receive 2400 ECU Decision 2: What choice do you prefer? |
| [D] Nyni uvazujte scenar Jedna. (Pokud potrebujete, vratte se k tistenym instrukcim, ktere tento scenar popisuji.) Celkova castka S je nahodna a se stejnou pravdepodobnosti je bud S=900 ECU nebo S=1100 ECU. Jste v roli ucastnika A a pro ucely scenare jste byl pocitacem nahodne prirazen k jinemu ucastnikovi experimentu. Rozhodnuti 3: Jake je Vase rozhodnuti, kolik procent prevest? | [D] Now consider Scenario One. (If you need to, you may return to the written instruction that describes this scenario) The total amount S is random and is, with equal likelihood, equal to either S=900 ECU or S=1100 ECU. You have the role of participant A and for this scenario you have been randomly assigned to another participant in this experiment. Decision 3: What is your decision, how much as a percentage will you transfer? |
| [T_P] Uvazujte nyni scenar Tri. (Pokud potrebujete, vratte se k tistenym instrukcim, ktere tento scenar popisuji.) Faktor X je nahodne cislo a se stejnou pravdepodobnosti je bud X=1.2 nebo X=2.8. Jste v roli ucastnika E a pro ucely scenare jste byl pocitacem nahodne prirazen k jinemu ucastnikovi experimentu. Rozhodnuti 4: Kolik ECU posilate ucastnikovi F? | [T_P] Consider Scenario Three. (If you need to, you may return to the written instruction that describes this scenario) Factor X is a random number and is, with equal likelihood, equal to either X=1.2 or X=2.8. You have the role of participant E and for this scenario you have been randomly assigned to another participant in this experiment. Decision 4: How much ECU will you send to participant F? |
| [U_P-high] Uvazujte Scenar Dva. (Pokud potrebujete, vratte se k tistenym instrukcim, ktere tento scenar popisuji.) Celkova castka S je nahodna a se stejnou pravdepodobnosti je bud S=300 ECU nebo S=1700 ECU. Jste v roli ucastnika C a pro ucely scenare jste byl pocitacem nahodne prirazen k jinemu ucastnikovi experimentu. Rozhodnuti 5: Jaka je Vase nabidka? Prosim vyplnte Vasi odpoved do okenka a potvrdte! | [U_P-high] Consider Scenario Two. (If you need to, you may return to the written instruction that describes this scenario) The total amount S is random and is, with equal likelihood, equal to either S=300 ECU or S=1700 ECU. You have the role of participant C and for this scenario you have been randomly assigned to another participant in this experiment. Decision 5: What is your proposal?Please fill out your answer in the space above and confirm! |
| [HL-50] Uvazujte scenar Ctyri. (Pokud potrebujete, vratte se k tistenym instrukcim, ktere tento scenar popisuji.) Volba "+": Ziskate 1000 ECU pokud N>50, jinak ziskate 1250 ECU Volba "*": Ziskate 60 ECU pokud N>50, jinak ziskate 2400 ECU Rozhodnuti 6: Kterou volbu preferujete? | [HL-50] Consider scenario Four (If you need to, you may return to the written instruction that describes this scenario) Choice “+”: You receive 1000 ECU when N>50, otherwise you receive 1250 ECU Choice “*”: You receive 60 ECU when N>50, otherwise you receive 2400 ECU Decision 6: What choice do you prefer? |
| [U_R-high] Uvazujte Scenar Dva. (Pokud potrebujete, vratte se k tistenym instrukcim, ktere tento scenar popisuji.) Celkova castka S je nahodna a se stejnou pravdepodobnosti je budS=300 ECU nebo S=1700 ECU. Jste v roli ucastnika D a pro ucely scenare jste byl pocitacem nahodne prirazen k jinemu ucastnikovi experimentu. Rozhodnuti 7: Jaky je Vas prah akceptovatelnosti? Prosim vyplnte Vasi odpoved do okenka a potvrdte! | [U_R-high] Consider Scenario Two. (If you need to, you may return to the written instruction that describes this scenario) The total amount S is random and is, with equal likelihood, equal to either S=300 ECU or S=1700 ECU. You have the role of participant D and for this scenario you have been randomly assigned to another participant in this experiment. Decision 7: What is your proposal?Please fill out your answer in the space above and confirm! |
| [T_P-high] Uvazujte nyni scenar Tri. (Pokud potrebujete, vratte se k tistenym instrukcim, ktere tento scenar popisuji.) Faktor X je nahodne cislo a se stejnou pravdepodobnosti je bud X=1.8 nebo X=2.2. Jste v roli ucastnika E a pro ucely scenare jste byl pocitacem nahodne prirazen k jinemu ucastnikovi experimentu. Rozhodnuti 8: Kolik ECU posilate ucastnikovi F? | [T_P-high] Consider Scenario Three. (If you need to, you may return to the written instruction that describes this scenario) Factor X is a random number and is, with equal likelihood, equal to either X=1.8 or X=2.2. You have the role of participant E and for this scenario you have been randomly assigned to another participant in this experiment. Decision 8: How much ECU will you send to participant F? |
| [U_P-low] Uvazujte Scenar Dva. (Pokud potrebujete, vratte se k tistenym instrukcim, ktere tento scenar popisuji.) Celkova castka S je nahodna a se stejnou pravdepodobnosti je budS=900 ECU nebo S=1100 ECU. Jste v roli ucastnika C a pro ucely scenare jste byl pocitacem nahodne prirazen k jinemu ucastnikovi experimentu. Rozhodnuti 9: Jaka je Vase nabidka? Prosim vyplnte Vasi odpoved do okenka a potvrdte! | [U_P-low] Consider Scenario Two. (If you need to, you may return to the written instruction that describes this scenario) The total amount S is random and is, with equal likelihood, equal to either S=900 ECU or S=1100 ECU. You have the role of participant C and for this scenario you have been randomly assigned to another participant in this experiment. Decision 9: What is your proposal? Please fill out your answer in the space above and confirm! |
| [HL-60] Uvazujte scenar Ctyri. (Pokud potrebujete, vratte se k tistenym instrukcim, ktere tento scenar popisuji.) Volba "+": Ziskate 1000 ECU pokud N>60, jinak ziskate 1250 ECU Volba "*": Ziskate 60 ECU pokud N>60, jinak ziskate 2400 ECU Rozhodnuti 10: Kterou volbu preferujete? | [HL-60] Consider scenario Four (If you need to, you may return to the written instruction that describes this scenario) Choice “+”: You receive 1000 ECU when N>60, otherwise you receive 1250 ECU Choice “*”: You receive 60 ECU when N>60, otherwise you receive 2400 ECU Decision 10: What choice do you prefer? |
| [U_R-low] Uvazujte Scenar Dva. (Pokud potrebujete, vratte se k tistenym instrukcim, ktere tento scenar popisuji.) Celkova castka S je nahodna a se stejnou pravdepodobnosti je bud S=900 ECU nebo S=1100 ECU. Jste v roli ucastnika D a pro ucely scenare jste byl pocitacem nahodne prirazen k jinemu ucastnikovi experimentu. Rozhodnuti 11: Jaky je Vas prah akceptovatelnosti? Prosim vyplnte Vasi odpoved do okenka a potvrdte! | [U_R-low] Consider Scenario Two. (If you need to, you may return to the written instruction that describes this scenario) The total amount S is random and is, with equal likelihood, equal to either S=900 ECU or S=1100 ECU. You have the role of participant D and for this scenario you have been randomly assigned to another participant in this experiment. Decision 11: What is your acceptance threshold?Please fill out your answer in the space above and confirm! |
| [HL-70] Uvazujte scenar Ctyri. (Pokud potrebujete, vratte se k tistenym instrukcim, ktere tento scenar popisuji.) Volba "+": Ziskate 1000 ECU pokud N>70, jinak ziskate 1250 ECU Volba "*": Ziskate 60 ECU pokud N>70, jinak ziskate 2400 ECU Rozhodnuti 12: Kterou volbu preferujete? | [HL-70] Consider scenario Four (If you need to, you may return to the written instruction that describes this scenario) Choice “+”: You receive 1000 ECU when N>70, otherwise you receive 1250 ECU Choice “*”: You receive 60 ECU when N>70, otherwise you receive 2400 ECU Decision 12: What choice do you prefer? |
| [D-high] Nyni uvazujte scenar Jedna. (Pokud potrebujete, vratte se k tistenym instrukcim, ktere tento scenar popisuji.) Celkova castka S je nahodna a se stejnou pravdepodobnosti je bud S=300 ECU nebo S=1700 ECU. Jste v roli ucastnika A a pro ucely scenare jste byl pocitacem nahodne prirazen k jinemu ucastnikovi experimentu. Rozhodnuti 13: Jake je Vase rozhodnuti, kolik procent prevest? | [D-high] Now consider Scenario One. (If you need to, you may return to the written instruction that describes this scenario) The total amount S is random and is, with equal likelihood, equal to either S=300 ECU or S=1700 ECU. You have the role of participant A and for this scenario you have been randomly assigned to another participant in this experiment. Decision 13: What is your decision, how much as a percentage will you transfer? |
| [U_R-none] Uvazujte Scenar Dva s celkovou castkou S= 1000 ECU. (Pokud potrebujete, vratte se k tistenym instrukcim, ktere tento scenar popisuji.) Jste v roli ucastnika D a pro ucely scenare jste byl pocitacem nahodne prirazen k jinemu ucastnikovi experimentu. Rozhodnuti 14: Jaky je Vas prah akceptovatelnosti? Prosim vyplnte Vasi odpoved do okenka a potvrdte! | [U_R-none] Consider Scenario Two. With the amount S=1000 ECU. (If you need to, you may return to the written instruction that describes this scenario) You have the role of participant D and for this scenario you have been randomly assigned to another participant in this experiment. Decision 14: What is your acceptance threshold? Please fill out your answer in the space above and confirm! |
| [T_R-high] Uvazujte nyni scenar Tri. (Pokud potrebujete, vratte se k tistenym instrukcim, ktere tento scenar popisuji.) Faktor X je nahodne cislo a se stejnou pravdepodobnosti je bud X=1.2 nebo X=2.8. Jste v roli ucastnika F a pro ucely scenare jste byl pocitacem nahodne prirazen k jinemu ucastnikovi experimentu. Obdrzel jste castku ECU (to je X krat mnozstvi poslane ucastnikem E, ktery k Vam byl pro toto rozhodnuti nahodne prirazen.) Rozhodnuti 15: Kolik ECU prevadite zpet na ucastnika E? | [T_R-high] Consider Scenario Three. (If you need to, you may return to the written instruction that describes this scenario) Factor X is a random number and is, with equal likelihood, equal to either X=1.2 or X=2.8. You have the role of participant F and for this scenario you have been randomly assigned to another participant in this experiment. You received the amount ECU: … (this is X times the amount send by the participant E, who was for this decision randomly assigned to you.) Decision 15: How much ECU will you send back to participant E? |
| [HL-80] Uvazujte scenar Ctyri. (Pokud potrebujete, vratte se k tistenym instrukcim, ktere tento scenar popisuji.) Volba "+": Ziskate 1000 ECU pokud N>80, jinak ziskate 1250 ECU Volba "*": Ziskate 60 ECU pokud N>80, jinak ziskate 2400 ECU Rozhodnuti 16: Kterou volbu preferujete? | [HL-80] Consider scenario Four (If you need to, you may return to the written instruction that describes this scenario) Choice “+”: You receive 1000 ECU when N>80, otherwise you receive 1250 ECU Choice “*”: You receive 60 ECU when N>80, otherwise you receive 2400 ECU Decision 16: What choice do you prefer? |
| [T_R-low] Uvazujte nyni scenar Tri. (Pokud potrebujete, vratte se k tistenym instrukcim, ktere tento scenar popisuji.) Faktor X je nahodne cislo a se stejnou pravdepodobnosti je bud X=1.8 nebo X=2.2. Jste v roli ucastnika F a pro ucely scenare jste byl pocitacem nahodne prirazen k jinemu ucastnikovi experimentu. Obdrzel jste castku ECU(to je X krat mnozstvi poslane ucastnikem E, ktery k Vam byl pro toto rozhodnuti nahodne prirazen.) Rozhodnuti 17: Kolik ECU prevadite zpet na ucastnika E? | [T_R-low] Consider Scenario Three. (If you need to, you may return to the written instruction that describes this scenario) Factor X is a random number and is, with equal likelihood, equal to either X=1.8 or X=2.2. You have the role of participant F and for this scenario you have been randomly assigned to another participant in this experiment. You received the amount ECU: … (this is X times the amount send by the participant E, who was for this decision randomly assigned to you.) Decision 17: How much ECU will you send back to participant E? |
| [Demographics] Zatimco my a pocitacovy program urcujeme celkove vydelky z dnesniho experimentu, prosime Vas odpovedet na nekolik otazek o Vas. Vsechna data budou povazovana za prisne duverna a budou pouzita pouze pro tuto studii. Po vyplneni a az Vas experimentator pozada, predstupujte jednotlive s Vasim obcanskym prukazem (pripadne jinou ID kartou) k vyplate. -Vase rodne cislo -Kolik je Vas mesicni disponibilni prijem (to je, kolik penez muzete utratit pote, co zaplatite za sve ubytovani)? | [Demographics] While we an the computer program are calculating the total earnings from todays experiment, we would like to ask you to answer some questions. All data will be considered as strictly confidential a will be used only for this study. After you have filled out the questionnaire and once the experimenter ask you to, please come one by one to the pay desk with your identity card (or with another form of ID). -Your birth number -How much is your monthly disposable income (that is, how much can you spend after you have paid for lodging?) |
| [Results] Vase N bylo Z rozhodnuti 2,6,10,12,16 bylo nahodne vybrano rozhodnuti Z toho rozhodnuti Vas vydelek cinil ECU Z rozhodnuti 1 jste vydelal ECU Z rozhodnuti 3 jste vydelal ECU V roli ucastnika B jste z rozhodnuti 3 Vam nahodne prirazeneho ucastnika A vydelal ECU Z rozhodnuti 4 jste vydelal ECU Z rozhodnuti 5 jste vydelal ECU Z rozhodnuti 7 jste vydelal ECU Z rozhodnuti 8 jste vydelal ECU Z rozhodnuti 9 jste vydelal ECU Z rozhodnuti 11 jste vydelal ECU Z rozhodnuti 13 jste vydelal ECU V roli ucastnika B jste z rozhodnuti 13 Vam nahodne prirazeneho ucastnika A vydelal ECU Z rozhodnuti 14 jste vydelal ECU Z rozhodnuti 15 jste vydelal ECU Z rozhodnuti 17 jste vydelal ECU | [Results] Your N was From decisions 2, 6, 10, 12, 16 has been randomly chosen decision: … From this decision you earning is in ECU: … From decision 1 you earned in ECU: … From decision 3 you earned in ECU: … In the role of participant B, you have for decision 3 received from a randomly assigned participant A in ECU: … From decision 4 you earned in ECU: … From decision 5 you earned in ECU: … From decision 7 you earned in ECU: … From decision 8 you earned in ECU: … From decision 9 you earned in ECU: … From decision 11 you earned in ECU: … From decision 13 you earned in ECU: … In the role of participant B, you have for decision 3 received from a randomly assigned participant A in ECU: … From decision 14 you earned in ECU: … From decision 15 you earned in ECU: … From decision 17 you earned in ECU: … |
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Van Koten, S.; Ortmann, A.; Babicky, V. Fairness in Risky Environments: Theory and Evidence. Games 2013, 4, 208-242. https://doi.org/10.3390/g4020208
Van Koten S, Ortmann A, Babicky V. Fairness in Risky Environments: Theory and Evidence. Games. 2013; 4(2):208-242. https://doi.org/10.3390/g4020208
Chicago/Turabian StyleVan Koten, Silvester, Andreas Ortmann, and Vitezslav Babicky. 2013. "Fairness in Risky Environments: Theory and Evidence" Games 4, no. 2: 208-242. https://doi.org/10.3390/g4020208










