A Scent of Lemon—Seller Meets Buyer with a Noisy Quality Observation
Abstract
: We consider a market for lemons in which the seller is a monopolistic price setter and the buyer receives a private noisy signal of the product's quality. We model this as a game and analyze perfect Bayesian equilibrium prices, trading probabilities and gains of trade. In particular, we vary the buyer's signal precision, from being completely uninformative, as in standard models of lemons markets, to being perfectly informative. We show that high quality units are sold with positive probability even in the limit of uninformative signals, and we identify some discontinuities in the equilibrium predictions at the boundaries of completely uninformative and completely informative signals, respectively.1. Introduction
In many markets, prospective buyers are imperfectly informed about the quality of the items for sale. Sellers, on the other hand, often know much about the quality of their products. In his classical “market for lemons” paper, George Akerlof showed that such informational asymmetry, when taken to the extreme, can lead to adverse selection. Although there is room for gains of trade in all qualities if only buyers were able to distinguish these from each other, the complete lack of such discriminatory power—the usual assumption—may imply crowding-out of high quality items, leaving only the “lemons” in the market; see Akerlof [1]. That paper initiated a surge of economic analyses of markets with asymmetric information, where typically the seller has better information than the buyer. For example, a used-car owner usually knows more about his car than the prospective buyer and a job applicant usually knows more about her ability than the employer.1
In this paper, we introduce a fairly rich form of asymmetric information in such situations of bilateral trade. In addition to observing the price posted by the seller, the buyer receives a noisy private signal about the product's quality. The noisy signal has a given precision, known also to the seller, and a continuum of different values. The actual value is known only to the buyer. In the metaphorical language of our title: we endow buyers with some capability to detect the scent of lemon. We believe this is a realistic and relevant extension. Consumers typically have the opportunity to study the object for sale, thus getting an impression of its quality, and employers usually interview job candidates, thus obtaining an impression of the candidates' abilities, etc. The impression may be more or less strong, and hence the consumer or employer may be more or less convinced of the quality of the object or the ability of the job candidate. So even if the signal precision is fixed and there are only two levels of quality or ability, as we here assume, the continuum signal assumption allows for a continuum range of degrees of confidence, represented as a continuum range of posterior probabilities that the object is of high quality (or the job candidate is of the high-ability type).
By varying the precision of the signal, the present model spans the whole continuum of consumer capabilities to recognize quality, from one extreme to the other. At the one end, when the signal precision is maximal, consumers recognize the true quality without mistake. At the other end, when the signal precision is minimal, it is as if all consumers have no sense of smell and are completely unable to recognize quality. Instead, they have to base their purchasing decision on their prior belief and the price chosen by the seller. This is the case treated in Akerlof's classical model. Central questions in the present study are what happens to the set of equilibria when one varies the signal precision, and, in particular, how robust the standard predictions are for the two extreme cases of “symmetric” information (maximal signal precision) and “one-sided” asymmetric information (minimal signal precision—as in Akerlof's approach).
Our starting point is a standard lemons model: an indivisible unit is available in two qualities, low and high. Buyers are interested in buying at most one unit. The seller knows the quality of the unit for sale. For each quality, the seller's valuation is lower than buyers' willingness to pay, so there are potential gains of trade in both qualities. When the seller and buyer meet, the seller sets a take-it-or-leave-it price for his unit. The buyer observes this price and receives a noisy quality signal. The seller knows the conditional probability distribution for signals, conditional upon the true quality, but does not know the buyer's signal. For the sake of clarity and transparency we focus on an “elementary” situation—only one seller facing one buyer. As the reader will see, even an analysis of such simple situations requires substantial work. We analyze the corresponding non-cooperative game, using pure-strategy (weak) perfect Bayesian equilibrium as solution concept. We characterize equilibrium prices and trading probabilities for all degrees of signal precision.
Our main results are the following. The equilibria are either separating or pooling. Separating equilibria come in two varieties. In partial adverse-selection equilibria, high-quality items are traded with positive probability below one and low quality units are sold with probability one. There is a continuum of such equilibria, even in the limit as the buyer's signal precision is taken down to zero. Hence, high-quality units are sold with positive probability also when buyers have no information at all about the quality of the unit at hand. By contrast, in total-adverse equilibria, high quality units are not sold at all. However, those equilibria are not robust to the elimination of weakly dominated strategies. In pooling equilibria, buyers purchase at the going price only if their quality signal exceeds a certain threshold (determined in equilibrium). Sellers with low-quality units thus have a lower probability of selling than sellers with high-quality goods. In our metaphorical language: a scent of lemon is more likely to come from a low-quality item than from a high-quality item. The equilibrium selling probability for low quality is sufficiently high to deter such sellers from lowering their price. In general, there is a continuum of pooling equilibrium prices. Also here, some discontinuities arise. Firstly, price-pooling at buyers' average valuation—an equilibrium in the classical adverse-selection model (no sense of smell)—need not be an equilibrium outcome if the buyer has even the slightest sense of smell. Secondly, even when this is an equilibrium outcome, there is a discontinuity in trading probabilities. In the classical adverse-selection model, both low and high quality are traded with probability one, while here even a very noisy negative quality signal will deter a buyer from purchase.
Although there certainly is a related literature, to the best of our knowledge the present model is new. In Milgrom and Roberts [4], sellers signal their quality by way of a posted price and observed expenditures on advertisement. The seller knows the combined price-advertisement signal received by buyers, so also that is a model of incomplete information on only one side of the market. Bagwell and Riordan [5] develop a model with informed and uninformed consumers, where the latter update their initial beliefs about quality on the basis of the price posted by the seller. Hence, again the seller knows the buyer's signal. Schlee [6] considers a model in which there is quality uncertainty on both sides of the market, but where buyers and sellers are symmetrically informed; quality information is public. Hence, none of these models has two-sided incomplete information as we have in the present model: the seller does not know the quality signal received by the buyer and the buyer does not know the quality of the item for sale. The studies that are closest to our analysis appear to be Ellingsen [7] and Bester and Ritzberger [8]. A discussion of how our model and results are related to theirs is given in Section 3.5.
It should also be mentioned that the model is different from Spence's [9] signalling model, again a model of “one-sided” incomplete information—the seller knows the signal received by the buyer. Moreover, the signal in Spence's model is chosen by the seller and the signal need not (and in most applications does not) affect the value to the buyer of the unit for sale. By contrast, in our model the seller cannot, by assumption, affect the signal, and the signal is positively correlated with the value of the unit to the buyer. Of related interest are two recent papers on signalling games á la Spence [9]. Feltovich et al. [10] consider a model with three types and costly signalling. Interestingly, if the receiver, in addition to observing the signal of the sender, receives an exogenous quality signal, there arise equilibria where medium types make an effort to signal that they are not of low quality, whereas high types make no such effort, relying on the exogenous signal to reveal their exclusivity. Alós-Ferrer and Prat [11] consider a dynamic signalling model where education plays a role as quality signal and worker productivity is revealed on the job as the result of firms' updating. This gives rise to a large set of equilibria and the Riley equilibrium is no longer uniquely selected by the Intuitive Criterion.
In our model, the seller is a monopolist who offers an indivisible item for sale at a take-it-or-leave-it (TOL) price. TOL pricing is known to be an expected-profit maximizing mechanism in situations of quotation marks “one-sided” incomplete information when there is only one buyer, granted the item is of a given, and to the seller known, quality; see Riley and Samuelson [12]. Therefore, we find a study of TOL pricing relevant also in present context. To the best of our knowledge, the mechanism literature has not yet provided an answer to the question whether TOL pricing is optimal also in settings with two-sided incomplete information, such as here (see Maskin and Tirole [13]).
The paper is organized as follows. Section 2 formalizes the model and provides certain necessary conditions on prices to be consistent with pure-strategy perfect Bayesian equilibrium. Section 3 contains the equilibrium analysis including a study of the boundary cases of completely uninformative and fully informative signals, respectively. Section 4 illustrates some points, and provides some additional results, for the special case of normally distributed error terms. Section 5 concludes. All proofs are in the appendix.
2. Model
An indivisible good is available in two qualities, low and high, denoted qL and qH, where 0 < qL < qH. Buyers are ex ante identical. Without loss of generality, we take the buyers' valuation of (or willingness to pay for) the two qualities to be vL = qL and vH = qH, respectively. The seller has one unit of the good for sale, and knows the quality of his or her unit. The seller's valuation (or reservation price) is wL < vL for a low-quality item and wH < vH for a high-quality item, where wH ≥ wL. The probability that the seller's unit is of low quality is λ ∈ (0, 1). Let q ∈ {qL, qH} be the quality of his product, and let q̅ denote the average quality: q̅ = λqL + (1 − λ) qH. Thus, this is also the buyer's average valuation, v̅ = q̅.
The seller sets a take-it-or-leave-it price p for his unit, and he may condition the price on its quality. The buyer is informed of the price p, but cannot observe the quality q of the item at hand. Instead, the buyer observes a signal q̃ that is positively correlated with quality. We parameterize this relationship in such a way that the traditional cases of symmetric information and the classical adverse-selection model become special cases. More precisely, the buyer observes the noisy signal
Given F, the parameter α thus determines the precision of buyers' information about the quality of the unit at hand: the higher α is, the more precise is the buyer's signal q̃ about the unit's quality. In particular, when α = 1, then we have the classical case of symmetric information when buyers observe quality without error. In the opposite extreme case, α = 0, buyers observe pure noise, q̃ = ε, and thus have no information at all about the quality of the unit at hand. This corresponds to the standard model of adverse selection, pioneered by Akerlof [1], in which the uninformed party receives no signal at all.3 In all cases between these two extremes, buyers make imperfect observations of quality, and the seller knows this. However, the seller does not know the quality signal q̃ received by the buyer.4
The seller is an expected-profit maximizer, where π = p − w is the profit to a seller with valuation w ∈ {wL, wH} who sells his unit at price p. Likewise, the buyers are risk-neutral utility maximizers, where u = v − p is the utility to a buyer when paying p for a unit of value v ∈ {vL, vH} to the buyer. The buyer's utility and the seller's profit are both normalized to zero if no trade takes place.
Under the assumptions made above, there are positive potential gains of trade in both cases: vL − wL> 0 and vH − wH > 0. Expected potential gains of trade are
One of the main concerns from a welfare viewpoint is to what extent these potential gains are realized in equilibrium, and how the realized gains of trade depend on the parameters in the model, in particular on the precision α of buyers' information.
2.1. The Seller-Buyer Game
Formally, we model the interaction outlined above as an extensive-form game with incomplete information between a seller, player 1, and a buyer, player 2, as follows:
Nature chooses θ ∈ {L, H}, where L has probability λ and H probability 1 − λ. Nature also chooses ε ∈ ℝ, according to the distribution F, and these two moves by nature are statistically independent.
The seller observes θ and chooses a price pθ ∈ ℝ. A pure strategy for the seller is thus a pair s = (pL, pH) ∈ ℝ2 of prices, where pL is the price when θ = L and pH the price when θ = H.
The buyer observes the price-signal pair (pθ, q̃), where q̃ = αqθ + (1 − α)ε, and decides whether to buy the item or not. A pure strategy for the buyer is thus a (Borel-measurable) function b: ℝ2 → {0, 1}, where b (p, q̃) = 1 means “buy” and b (p, q̃) = 0 means “don't buy,” given any price p and quality signal q̃.5
The game ends and the players receive their payoffs,
A decision node for the seller in the infinite game tree is thus a pair (θ, ε), but the seller does not observe ε, the noise term in the buyer's perception of the quality of the item at hand. The seller thus has two (infinite) information sets (or “seller types”), namely {(L, ε) : ε ∈ ℝ} and {(H, ε) : ε ∈ ℝ}, depending on whether his item is of low or high quality Likewise, a decision node for the buyer is a triplet (θ, ε, p), but the buyer observes only the seller's price p and the signal q̃. The buyer thus has infinitely many information sets (or “buyer types”). Each of the buyer's information sets is characterized by a pair (p, q̃) ∈ ℝ2, specifying the seller's price p and the received quality signal q̃. For α < 1, each such information set contains exactly two nodes of the game tree, namely (L, εL, p) and (H, εH, p), where
By contrast, for α = 1 the quality signal q̃ always coincides with the true quality: q̃ ∈ {qL, qH}. Hence, in this case the buyer information set (p, qθ) contains infinitely many nodes of the game tree, namely (θ, ε, p) for all ε ∈ ℝ. However, in this classical boundary case of perfect precision, the random variable ε is irrelevant to the buyer's decision making.
As noted above, this game differs from the standard “lemons model” (as, for example, presented in chapter 13 in Mas-Colell et al. [3]), in two respects: (a) the seller is a price setter rather than price taker, and (b) there is incomplete information on both sides of the market—the buyer does not know the quality of the item for sale and the seller does not know the buyer's quality signal. Note also that seller and buyer “types” are correlated: the buyer's “type” is the random variable q̃ = αqθ + (1 − α) ε, where θ ∈ {L, H} is the seller's “type.”
2.2. Equilibrium
We solve this game by adapting the usual notion of (weak) perfect Bayesian equilibrium to the present setting (see, e.g., Fudenberg and Tirole [14] or Mas-Colell et al. [3]). Such an equilibrium specifies a strategy for each player and beliefs for each player over the nodes in the player's information sets, such that (a) beliefs are consistent with all players' strategies and the probabilities for nature's moves along the induced path of play, and (b) at each information set, the strategy of the concerned player is optimal, given the player's belief at the information set and the strategies of all other players (there is no future move by nature in our game). As it requires best replies also off the induced path of play, this concept is more stringent than (Bayesian) Nash equilibrium, but is weaker than sequential equilibrium since it imposes no constraints on beliefs at information sets off its path.6 We will focus on pure strategies.
In the case of an imprecise signal, α < 1, this equilibrium requirement can be broken down to four conditions (the case α = 1 is analyzed in Section 3.1). Following Kreps and Wilson [15], let a belief system be a function μ that assigns to each information set a probability distribution over the nodes in that information set. A pure strategy for the seller is a pair s = (pL, pH) ∈ ℝ2, and a pure strategy for the buyer is a (Borel measurable) function b : ℝ2 → {0, 1}. We will call such a triplet (μ, s, b) an equilibrium if it meets conditions [B1]-[B3] and [SR] below.
- [B1]
At each seller information set {(θ, ε) : ε ∈ ℝ}, and for every x ∈ ℝ, μ assigns probability F (x) to the subset of nodes {(θ, ε) : ε ≤ x}.
- [B2]
If pL ≠ pH: at each buyer information set (pθ, q̃), μ assigns probability 1 to the node (θ, εθ, pθ), where εθ is defined in (4).
- [B3]
If pL = pH: at each buyer information set (p, q̃) where p = pL, μ assigns probability
to the node (L, εL, p) (and thus probability μH(q̃) = 1 − μL(q̃) to the node (H, εH, p)).7- [SR]
At all information sets: the concerned player's strategy is a best response to the other player's strategy, under the belief induced by μ at that information set.
Consistency condition [B1] is met if the seller knows the quality of his item and knows the c.d.f. F of the buyer's noise term ε. At each of his two information sets, {(L, ε) : ε ∈ ℝ} and {(H, ε) : ε ∈ ℝ}, the seller's beliefs are then given by the distribution function F for ε. Conditions [B2] and [B3] are met if, at every information set of the buyer that can be reached with positive probability under the strategy profile (s, b), the buyer's beliefs are consistent with (s, b) in the sense of Bayesian updating. More exactly, condition [B2] requires that if the seller charges different prices, pL and pH, depending on the quality of his good, an incompletely informed buyer should believe that the item is of low (high) quality if he price is pL (pH). Similarly, condition [B3] requires that if the seller charges the same price for high and low-quality items, the buyer's belief about which of the two nodes was reached should be consistent with Bayes' rule applied to the information set in question.8 The posterior probability μH(q̃) can be thought of as the buyer's degree of confidence, after inspection, that the item is of high quality. Finally, condition [SR] requires sequential rationality, as defined in Kreps and Wilson [15].
In any equilibrium (μ, (pL, pH), b), let ρL and ρH denote the trading probabilities for low and high quality units, that is,
An equilibrium (μ, (pL, pH), b) is called separating if pL ≠ pH and pooling if pL = pH.
2.3. Necessary Conditions for Equilibrium
The following lemma provides necessary conditions for equilibrium that follow from first principles. For instance, it is sequentially rational for the buyer to buy if the seller asks a price below the buyer's willingness to pay for a low-quality unit, and it is sequentially rational not to buy if the seller asks a price above the buyer's willingness to pay for a high-quality unit:
These simple observations rule out a wide range of price pairs from equilibrium:
Lemma 1
For α < 1 there are no equilibria (μ, (pL, pH), b) where
min {pL, pH} < vL
pL ≠ pH and pL > vL
pL = vL and pH ∈ (vL, vH)
pL= pH ≥ vH
It follows from this lemma that, in separating equilibria, the price of low-quality units equals buyers' willingness to pay for such units (by (a) and (b)), and the price of high-quality units is never below the buyers' willingness to pay for such units (by (c)). Hence, when trade occurs in separating equilibria, the seller reaps all the gains of trade. This is not surprising, since by assumption the seller is a monopolist who can commit to take-it or leave-it offers. Moreover, in pooling equilibria the price is never below buyers' willingness to pay for low-quality units but always lower than buyers' willingness to pay for high-quality units (by (a) and (d)). In sum:
Remark 1
The only remaining candidates for pure-strategy equilibria, when α < 1, are separating equilibria with pL = vL and pH ≥ vH, and pooling equilibria with pL = pH ∈ [vL, vH).
3. Analysis
In this section we analyze the game's equilibria and come to our main purpose: an investigation of the robustness of the equilibria—in particular the equilibrium prices and trading probabilities—in the classical boundary cases of uninformative signals (α = 0) and fully revealing signals (α = 1) via a systematic study of the equilibria near these boundaries. We proceed as follows: section 3.1 describes the equilibria when α = 1. Moving on to the case where α < 1, we establish conditions for the existence of separating equilibria and investigate their nature. In particular, we will show that low-quality items are sold with probability one in all separating (pure-strategy) equilibria, and we will identify two varieties of such equilibria. In one variety, high-quality units are not sold at all, while in the other variety they are sold with positive probability below one. We will refer to the first variety, studied in Subsection 3.2, as total adverse selection. These are equilibria in which high-quality sellers outprice themselves, and thereby “leave the market,” just as in “classical” adverse selection. The second variety, studied in subsection 3.3, will be called partial adverse selection. Subsection 3.4 characterizes the game's pooling equilibria, and Subsection 3.5, finally, discusses related models.
3.1. Symmetric Information
Under symmetric information, i.e., when α = 1, buyers know exactly the quality of the goods they buy. Pure-strategy perfect Bayesian equilibrium then requires the buyer to make a purchase if and only if the posted price does not exceed the quality signal q̃ = qθ, where qθ is the quality of the unit at hand.9 At price p = q̃, the seller is indifferent between buying and not buying. The seller's best reply to the buyer's strategy is thus to set the price equal to the buyer's willingness to pay if the buyer strategy is to buy, and otherwise to set any price that is not lower than that. However, it is inconsistent with pure-strategy equilibrium that the buyer does not buy, since in this case the seller could marginally reduce the price and make a positive profit. Hence, the buyer always buys at the price p = q̃ and the seller sets prices (pL, pH) = (vL, vH). Consequently, both qualities are traded with probability one in equilibrium, ρL = ρH = 1, and the seller absorbs all gains of trade.
3.2. Separating Equilibria with Total Adverse Selection
If vL ≤ wH, then a seller with a high-quality unit cannot make a profit by selling at buyers' willingness to pay for low quality. Indeed, in this case, and only then, do there exist separating equilibria in which the price of high-quality items exceeds buyers' willingness to pay for high quality, vH. Since it is suboptimal to buy at such prices, there is no trade in high-quality goods in such equilibria. The reason why sellers with high-quality units do not lower their price is that, in these equilibria, buyers believe that such a seller may well hold a low-quality item, and therefore buyers do not “bite” unless the seller sets the price as low as vL, resulting in non-positive profits. In these equilibria, it is as if sellers with high-quality units left the market—as in Akerlof's [1] model of adverse selection.
Proposition 1
Suppose α < 1. Prices pL = vL and pH > vH constitute an equilibrium price pair if and only if vL < wH. In all such equilibria, ρL = 1 and ρH = 0.
This type of outpricing can occur for any degree of buyer signal precision α < 1. Consequently, such equilibria exist even as buyers' information is made arbitrarily precise, that is, in the limit as α → 1, despite the fact that no such equilibria exist under symmetric information, that is, when α = 1 (see Section 3.1). In this sense, the classical result for symmetric equilibrium is non-robust: the slightest noise in buyers' quality observations allows for equilibria where adverse selection hits at full force. At the other end of the information spectrum, when α = 0, proposition 1 establishes that outpricing equilibria exist whenever wH > vL. In particular, this result allows for equilibria with complete adverse selection even when vL ≤ wH < v̅, that is, when a pooling equilibrium would result in positive profits to sellers with high quality units. Such pooling equilibria do exist in standard adverse-selection models; see Section 3.4 for an analysis of pooling equilibria in the present model.
We should add that we do not find these separating equilibria plausible. For a seller with a high-quality couldn't lose, but might gain, by deviating to a price p ∈ (wH, vH). More formally, the equilibria in Proposition 1 do not survive two rounds of elimination of weakly dominated strategies. To see this, note that any buyer strategy b that assigns b (p, q̃) > 0 to some p > vH and q̃ ∈ ℝ is weakly dominated by the buyer strategy b′ that agrees with b everywhere except at the information set (p, q), where b′ instead takes the value zero. After all such weakly dominated buyer strategies have been eliminated, all seller strategies s = (pL, pH) with pH > vH become weakly dominated by any seller strategy s′ = (pL, p) with p ∈ (wH, vH].
3.3. Separating Equilibria with Partial adverse Selection
We here consider pure-strategy separating equilibria in which the seller's strategy is s = (vL, vH). We first outline the main arguments and then make the conclusions precise in a lemma and a proposition.
It follows from first principles that in equilibrium buyers always buy at the low price, p = vL. For had they not done so, then a seller with a low quality unit could make a marginal price cut and sell for sure (since this would be the buyer's unique optimal reaction), thus increasing his profit. Moreover, in equilibrium, buyers buy at the high price, p = vH, with a probability that is less than one. For had they bought for sure at the high price from a seller with a high-quality unit, then they would also have bought for sure from a seller with a low-quality unit who posted that price.10 If this were the case, low-quality sellers would profitably deviate to the high price. Hence, the realization probability ρH is necessarily strictly less than one.
What can be said about the upper bound on the realization probability ρH? Note first that ρH = E [b (pH, q̃) ∣ θ = H]. Suppose that the seller has a low-quality unit but posts the high price. The probability that the buyer will purchase the unit is then
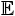
Hence, the upper bound on the equilibrium realization probability ρH is
If wH < vL, so that a seller with a high-quality unit would make a (positive) profit by deviating to the low price, then another necessary condition for equilibrium is that
For had the realization probability ρH been lower, then a seller with a high-quality unit would earn vL − wH by deviating to the low price, thus exceeding his expected equilibrium profit, ρH (vH − wH).
It remains to establish existence of equilibria and to find an operational representation of ρ̂H. Let
We note that t1 > t0, since, by hypothesis, qL < qH and wL < wH. Let
Lemma 2
If α < 1, then t ∈ T if and only if the following two conditions hold:
We use this lemma to establish the existence of partially separating equilibria. In these equilibria, the buyer's strategy is to buy from a seller who posts the low price, pL = vL, irrespective of the perceived quality q̃, and to buy from a seller who posts the high price, pH = vH, if and only if the perceived quality exceeds a certain threshold. More exactly:
Proposition 2
Suppose α < 1. All equilibria with s = (vL, vH) have ρL = 1 and . For each t ∈ T there exists such an equilibrium, with b (pH, q̃) = 1 if and only if q̃ > t, and with
We would like to make some comments to this proposition. First, the continuum of parameterized equilibria is Pareto ranked: the lower the threshold t ∈ T, the higher is the equilibrium probability ρH for trade in high-quality items, and thus the higher is the expected equilibrium profit to the seller. The expected utility to buyers being zero in all equilibria, this means that the equilibrium gains of trade, W*, decrease with t and the equilibrium at t0 Pareto dominates the others.
Secondly, step-functions of the kind used by the buyers in the above equilibria are optimal decision rules in a variety of decision problems related to the one faced by the buyer in the present model. Suppose, for instance, that a decision-maker in a non-strategic environment observes a signal of the form (1), where the true quality q and the noise term ε are statistically independent random variables. Then the signal distribution from a high-quality unit stochastically dominates those from units with lower quality. Moreover, if the probability distribution of the noise term has (a version of) the monotone likelihood ratio property (shared by, for instance, the normal distribution), then the conditionally expected quality,
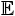
Thirdly, we examine some comparative statics properties of these separating equilibria with respect to the precision α of the buyer's signal. By (13), the realization probability ρH is, for each α < 1, bounded from above by
The upper bound ρ̅H increases continuously with α, from a positive value when α is zero, towards one as α → 1. In other words, the more precise the signal is, the higher can be the equilibrium trading probability for high-quality units, and in the limit, as buyer information tends to perfection, the maximal trading probability for high-quality units tends to one.
What may appear as a surprise is that the present model allows for some trade in high-quality units even when buyers have no information at all about the quality of the unit at hand:
Although buyers receive only a non-informative signal, low-quality sellers do not have an incentive to deviate to the high price, since the trading probability at that price is too low. Until relatively recently, it was commonly presumed that, in classical adverse-selection models, high-quality units are not traded when wH > v̅. However, here they are traded with positive probability, and this is indeed even possible in the absence of a signal, a fact established by Ellingsen [7].12
In sum, the set of equilibrium trading probabilities for high-quality units contains the interval
Fourthly, recall from our second comment that the threshold functions in Proposition 2—where the item is purchased if the quality signal is sufficiently high—are optimal in a wide range of non-strategic circumstances. If the set B in the definition of the theoretical upper bound ρ̂H in (11) is restricted to pure strategies that are weakly increasing functions of quality signal, then the upper bound ρ̅H in (19) in fact equals the theoretical upper bound:
Proposition 3
Suppose α < 1. If buyers use weakly increasing pure strategies, then ρ̂H = ρ̅H.
3.4. Pooling Equilibria
We saw in Section 3.1 that pooling equilibria do not exist in the boundary case α = 1 of symmetric information. We here focus on the case α < 1. By Remark 1, it suffices to consider prices p in the half-open interval [vL, vH).
Consider the decision problem faced by a buyer who receives a quality signal q̃ ∈ ℝ. The conditionally expected value to the buyer of the unit at hand, given her signal, is
If pL = pH = p, then consistency [B3] and sequential rationality [SR] together imply that it is optimal for the buyer to make a purchase if and only if his signal q̃ belongs to A(p).14 This set will be called the buyer's acceptance set at price p.
The following proposition characterizes the set of prices that can be supported in pooling equilibria.
Proposition 4
Suppose α < 1. A price p ∈ [vL, vH) is a pooling equilibrium price if and only if (25) and (26) hold.
The first (second) condition in the proposition guarantees that a seller with a low (high) quality unit does not have an incentive to deviate. We note that condition (26) fails if p < wH. Hence, not surprisingly, such prices can not be supported in pooling equilibria—a seller with a high-quality unit is then better off keeping his unit. By contrast, the same condition, (26), is trivially met if vL ≤ wH ≤ p. In such cases, sellers with high-quality units make a nonnegative profit at the going price p, and cannot make positive profits by deviating to prices p ≤ vL—prices at which it is rational for buyers to buy irrespective of their signal. An immediate consequence of this proposition is that if wH ≤ vL, then p = vL is a pooling equilibrium price, irrespective of α (as long as α < 1). For in this case the seller is willing to part with a high-quality unit, and it is rational for buyers to buy irrespective of the signal (their valuation cannot be lower than the going price). Formally: A (vL) = ℝ, and the probabilities on the left-hand sides of (25) and (26) are both one, and thus both conditions are met for p = vL.15
For the boundary case α = 0, equation (5) implies that μL(q̃) = λ for all signals q̃. Consequently,
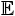
Hence, the set of pooling equilibrium prices is non-empty at α = 0 if and only if wH < v̅, just as in standard adverse-selection models. Moreover, when α = 0, then all pooling equilibria are efficient—they all realize the full potential gains of trade: ρL = ρH = 1 and W* = Ŵ.
Is the equilibrium correspondence that maps buyers' precision α to the corresponding set of pooling equilibrium prices p continuous at α = 0? Assume that α > 0 and wH < v̅, and consider any price p < v̅ satisfying (27). As α → 0, μL(q̃) → λ for all quality signals q̃, by (4) and (5). Hence,
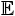
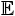
3.5. Related Models
The case α = 0, though closely related to standard models with adverse selection, is technically distinct from these. For in our model there is incomplete information on both sides of the market even when α = 0, in the trivial sense that the seller does not know the buyer's uninformative signal. The signal makes the outcome of the buyer's pure strategies randomized. In the boundary case α = 0, our model is close to those of Ellingsen [7] and Bester and Ritzberger [8]. The differences are that in Ellingsen's model (a) the set of feasible prices is finite, (b) the seller may randomize over these, (c) the gains of trade are the same for both qualities (in our notation: vL − wL = vH − wH), and (d) he also analyzes the case of more than two qualities, distributed over a finite quality grid with fixed grid size. Bester and Ritzberger [8] endow the buyer with the option to inspect the true quality at a cost, an action that the seller is assumed not to observe. Hence, like our model, also their model has incomplete information on both sides of the market. The differences are that (a) in their model buyers either have no signal or a perfect signal, (b) it combines incomplete information (hidden information) with imperfect information (hidden action).
The model in Akerlof [1] is equivalent with the non-strategic variant of our model where the seller is a price taker and the buyer has no quality signal. Akerlof asks at what market prices p, the same for all qualities, trade is possible. If each of the two qualities is offered with probability λ and 1 − λ, respectively, then the buyer's willingness to pay will be v̅: the buyer is willing to buy if and only if p ≤ v̅. Similarly, sellers are willing to sell both qualities if and only if p ≥ max{wL, wH} = wH. Thus, a necessary and sufficient condition for trade in both low and high quality is p ∈ [wH, v̅]. At all such prices, the full gains of trade are realized. On the other hand, if wH > v̅, total adverse selection arises: high quality is driven out of the market and trade occurs only in low quality, at prices p ∈ [wL, vL].
4. Normally Distributed Noise
In the final lines of subsection 3.4, we mentioned a discontinuity in the set of pooling equilibria: although p = v̅ is a pooling equilibrium price when α = 0, this may or may not be the case when α → 0. To make this explicit (indeed, see (30) below), this section studies the particular case of normally distributed error terms. The necessary and sufficient conditions (25) and (26) for pooling equilibrium can then be written explicitly in terms of the primitives of the model. Suppose that α ∈ (0, 1), and define the function φ : (vL, vH) → ℝ by
Clearly φ is increasing, with φ (p) → −∞ as p → vL and φ (p) → +∞ as p → vH.
Proposition 5
If α ∈ (0, 1) and ε ∼ N (q̅, σ2), then p ∈ ℝ is a pooling equilibrium price if and only if max {vL, wH} ≤ p ≤ vH and
We would like to make some comments to this proposition. Firstly, in our model, pooling equilibrium is possible even when wH > v̅, but only if buyers' signal carries some (and not too much) information about the true quality (α is positive but small). The reason why such equilibria require buyers' quality signal to have some precision is that otherwise the buyers would expect all units to be of average quality, and thus would be willing to pay only v. Indeed, the reader may verify that for parameter values wL = 0, qL = 1, qH = 3, λ = 0.25, σ = 1, and α close to 0.1, pooling is possible at a price exceeding the average valuation v̅.
Secondly, the set of pooling equilibrium prices, if non-empty, is an interval. This interval has max{ vL, wH} as its left endpoint, while inspection of equation (28) shows that its right endpoint is decreasing in λ. Thus, the larger the share of “lemons,” the lower is the highest pooling price.
Thirdly, by (28) and (29), the set of pooling equilibrium prices approaches the set
Fourthly, no price above vL is a pooling price in the limit as buyers' signal precision α goes to one. To see this, note that, for any p ∈ (vL, vH), φ(p) is continuous in α and tends to +∞ as α approaches 1. Hence, as α tends to 1, the left-hand side in (29) tends to zero, and thus any such price p ceases to be a pooling equilibrium price.
On a somewhat different note, let us compare the equilibrium profit to the seller in pooling equilibria with the maximal expected profit in separating equilibria with partial adverse selection. The expected profit in a pooling equilibrium with price p equals
We compare this with the expected profit in separating equilibria. Since the prices are the same in all such equilibria, vL for low quality and vH for high, expected profits are maximal in the separating equilibrium with the maximal selling probability for high quality By proposition 3 and (19), the maximal expected profit in separating equilibrium (see Appendix for a derivation) is
These equations are useful when comparing the expected profit in pooling and separating equilibria in the limit case when the signal precision α tends to zero. Recalling that the set P0 of pooling equilibrium prizes in this limit case is empty if wH > v̅ and non-empty if wH < v̅, we focus on the latter case. Let w̅ = λwL + (1 − λ) wH be the seller's average reservation price. The following result establishes that, for all α > 0 sufficiently small, there exist pooling equilibria with higher expected profit than in all separating equilibria, and that there are pooling equilibrium profits arbitrarily close to v̅ − w̅ as α → 0. Formally:
Proposition 6
If wH < v̅, then
In other words, if the buyer's average willingness to pay exceeds the seller's valuation of high quality, then the seller prefers pooling equilibria over separating equilibria. Moreover, in the limit as the buyer's quality signal becomes uninformative, potential gains of trade are virtually realized. The qualifier “virtually” refers to the fact (established in the proof of the proposition) that while there exist pooling equilibria that result in profits arbitrarily close to v̅ − w̅, no equilibrium actually achieves this lowest upper bound exactly. Note, however, that this ambiguity is artificial; it hinges on the assumption that a price can be any real number, while in practice prices are quoted in some smallest monetary unit. In the latter case, the supremum in the statement of the proposition should be taken over the corresponding discrete set of prices, and this supremum profit will indeed be achieved by some pooling price, namely, the largest multiple of the monetary unit that does not exceed the buyer's willingness to pay. In sum: the welfare loss due to asymmetric information is virtually zero in the limit as the buyer's quality signal becomes uninformative. By contrast, some gains of trade are lost in all equilibria at any intermediate level α ∈ (0, 1) of signal precision.
We finally note that when the buyer's quality signal is virtually perfect, α → 1, the best partially separating equilibrium gives a higher expected profit than all pooling equilibria, and this separating equilibrium realizes the potential gains of trade:
In other words, the welfare loss due to asymmetric information vanishes in the limit as the buyer's quality signal becomes perfect.
5. Conclusion
The goal of this paper was to study equilibria when noisy inspection is introduced in an otherwise standard “lemons” model; more specifically, when the buyer does not know the quality of the unit for sale but receives a noisy signal about its quality while the seller knows the quality but not the buyer's signal. We believe that this extension is relevant and provides a more realistic description of asymmetric information in markets. A prospective buyer of a used car may walk around it, take a look under the hood, check whether the bumper falls off when it receives a slight kick etc. and thus get at least some impression of the car's quality, rather than, as in Akerlof's seminal analysis, no impression at all. Although the seller knows the quality of his car, he usually can only guess at the exact impression on the prospective buyer. We chose to study an elementary situation—only one seller facing one buyer at a time—devoid of all the bells and whistles that could make the model richer and more realistic, for the sake of clarity and transparency. Moreover, we focussed on pure-strategy equilibria. In the present model, this is a rich set of strategies, offering a continuum of options for the seller and allowing the buyer to condition the purchasing decision on signal values in a continuum. Arguably, this provides a behaviorally plausible form of randomization—in the form of hesitation in face of quality uncertainty.
While the focus of this paper is admittedly narrow, we felt it natural to first establish a clear-cut and transparent analysis of the set of pure strategies, before embarking on studies of richer, and thus more complex, market settings. Evidently, there are numerous relevant directions for further research. We here briefly name two:
Equilibrium selection
The model allows for multiple equilibria with distinct outcomes. This raises the question whether there are relevant refinements or stability conditions that one could impose in order to cut down the equilibrium set. This is a very interesting avenue for future research, although non-trivial, since standard refinements are defined only for finite games, while the present game is infinite.
Generalizations and extensions
Highly relevant extensions would be to analyze cases of multiple quality levels, multiple sellers and/or buyers, and a variety of pricing mechanisms.
We are currently working on a few such directions, in joint work with Yukio Koriyama. The analysis being quite demanding, it appears that generalization in one dimension typically requires simplification in another. We hope that the present study will inspire future research on market interactions in which some or all parties have noisy signals about product quality.
Acknowledgments
We thank Carlos Alós-Ferrer, Tore Ellingsen, Yukio Koriyama, Lars-Göran Mattsson, Jianjun Miao, and Zvika Neeman, and two anonymous referees for comments. Voorneveld thanks the Wallander/Hedelius Foundation and the Netherlands Organization for Scientific Research for financial support.
Appendix
Proof of Lemma 1
If a seller of type θ ∈ {L, H} sets a price below vL, then, by (8), his expected payoff can be increased from p − wθ to p′ − wθ by deviating to a price p′ ∈ (p, vL)
Suppose pL ≠ pH and pL > vL. Consider an information set (pL, q̃) of the buyer. By [B2], he believes that the item is of low quality, with probability one. Since pL > vL, the optimal decision, according to [SR], is not to buy. So b(pL, q̃) = 0 for all q̃ ∈ ℝ. Hence, the expected payoff to a seller with a low-quality unit equals zero, while (8) implies that the seller can deviate to a price p ∈ (wL, vL) and obtain a positive payoff, p − wL.
Suppose pL = vL and pH ∈ (vL, vH). Consider an information set (pH, q) of the buyer. By [B2], he believes with probability one that the item is of high quality. Since pH < vH, the optimal decision, by [SR], is to buy. So b(pH, q̃) = 1 for all q̃ ∈ R. The low-quality seller can then increase his expected payoff from (qL − wL) · Pr [q̃ ∈ ℝ ∣ b(qL, q̃) = 1] to pH − wL by charging price pH instead of qL.
Suppose first pL = pH > vH. By (9), the good is not sold at this price, so the expected payoff to the low-quality seller equals zero, while (8) implies that he can deviate to a price p ∈ (wL, vL) and make profit p − wL > 0. Suppose now that pL = pH = vH, and consider an information set (pH, q̃) of the buyer. By [B3], he believes with positive probability (5) that the item is of low quality, in which case a purchase would give negative utility (vL − pH = vL − vH < 0), and with the residual probability that the item is of high quality, in which case a purchase would give zero utility (vH − pH = 0). The expected payoff thus being negative, the optimal decision, by [SR], is not to buy The expected payoff of the seller with a low-quality unit hence equals zero, while (8) implies that such a seller can deviate to a price p ∈ (wL, vL) and guarantee himself a positive payoff p − wL.
Proof of Proposition 1
To prove necessity, suppose (μ, (vL, pH), b) is such an equilibrium. Condition (9) implies that sellers with high-quality units obtain zero profit. By condition (8), a deviation from pH to a price p < vL sufficiently close to vL guarantees a profit arbitrarily close to vL − wH. Hence, for pH > vH to be an equilibrium price, it must be that vL − wH ≤ 0. As for sufficiency, assume vL ≤ wH. Let (μ, s, b) be such that pL = vL, pH > vH, let
To establish the last claim in the proposition, consider any equilibrium (μ, s, b) with pL = vL and pH > vH. It follows as in the proof of the preceding proposition that b(vL, q̃) = 1 for almost every q̃ ∈ ℝ, and from (9) that b(pH, q̃) = 0 for every q̃ ∈ ℝ.
Proof of Lemma 2
Recall that the c.d.f. for ε is F, and notice that, for any t ∈ ℝ,
If wH < vL, then t ∈ ℝ satisfies (36) and (37) if and only if
If wH ≥ vL, then the right-hand side of (37) is at least 1, and hence (37) is met.
Proof of Proposition 2
In order to prove that ρL = 1, suppose (μ, s, b) is an equilibrium with (pL, pH) = (vL, vH). By [B2] and [SR], the buyer buys with probability 1 at all prices p < vL, irrespective of her signal q̃. Hence, by choosing p < vL arbitrarily close to vL, a seller with a low-quality item can guarantee himself a profit arbitrarily close to vL − wL. Hence, for pL = vL to be optimal for the seller, it must be that b(vL, q̃) = 1 for almost every q̃ ∈ ℝ. The inequality is trivially met if wH ≥ vL, so suppose wH < vL. If , then a seller with a high-quality unit would earn a higher profit by deviating to any price p < vL sufficiently close to vL, since the buyer would surely buy at such a price and this the deviation profit would be arbitrarily close to vL − wH. The inequality ρH < 1 was established in the text.
To prove the second claim, let (pL, pH) = (vL, vH), let t ∈ T, and let
This defines a pure-strategy pair, (s, b), with
Let μ be any belief system satisfying [B1] and [B2] ([B3] has no bite in separating equilibria). At information sets (p, q̃) of the buyer off the path of (s, b), that is, where p ∉ {vL, vH}, let μ assign probability 1 to the node (L, εL, p). In other words, the buyer then believes the item is of low quality. We verify that (μ, s, b) is an equilibrium in three steps. First, consider the buyer's information sets. At information sets (vL, q̃) and (vH, q̃), the buyer's expected payoff is zero regardless of her choice, for any q̃ ∈ ℝ. Hence, b is a best reply at all information sets on the path of (s, b). At information sets (p, q̃) off the path, the buyer believes the item is of low quality, so buying at a price p ≤ vL and not buying at a price p > vL is a best reply also at such information sets. Secondly, consider the information set {(L, ε): ε ∈ ℝ} of the seller. A price p ≤ vL would yield profit p − wL, so in this price range the optimal price is vL, yielding profit vL − wL > 0. A price p > vL, differing from vH, would result in no trade, and hence profit zero. The price p = vH, by contrast, would result in trade with probability Pr [q̃ > t ∣ θ = L]. However, using (16), the resulting expected profit would not exceed
Hence charging the price vL is indeed a best reply at this information set. Thirdly, consider the information set {(H, ε): ε ∈ ℝ} of the seller. A price p ≤ vL would yield the profit p − wH, so in this price range the optimal price is vL, yielding profit vL − wH. A price p > vL, differing from vH, would result in no trade, and hence profit zero. The price p = vH, by contrast, results in trade with probability Pr [q̃ > t ∣ θ = H]. Using (17), the resulting expected profit does not fall short of
Hence charging price vH is indeed a best reply at this information set.
Proof of Proposition 3
Assume the buyer's strategy at price pH is a threshold function: there is a t ∈ ℝ such that b(pH, x) = 0 if x ≤ t and b(pH, x) = 1 otherwise. Then the problem (11) becomes
Since these probabilities are decreasing in t, the constraint will hold with equality:
Solving this equation for t yields that t = t0 and that ρ̂H, the value of the maximization problem (11), equals the trading probability in high quality if buyers purchase at price qH if the signal exceeds t0, which is exactly ρ̅H.
Proof of Proposition 4
To prove necessity, let (μ, s, b) be a pooling equilibrium with price p ∈ [vL, vH). By sequential rationality, [SR], b(p, q̃) = 0 if q̃ ∉ A(p). Hence, a low-quality seller's expected profit, πL, satisfies
Moreover, such a seller can guarantee himself a profit arbitrarily close to vL − wL by choosing prices p′ < vL. Hence,
Moreover, such a seller can guarantee himself zero profit by setting p′ > vH and a profit arbitrarily close to vL − wH by choosing price p′ < vL. Hence,
Proof of Proposition 5
Condition (26) is violated if p < wH, so no such price is a pooling equilibrium price. We observed earlier that p = vL is a pooling equilibrium price for all α ∈ (0, 1) if vL ≥ wH. To see that p = vL satisfies inequality (29), note that its left-hand side then equals 1 and so does the right-hand side.
It thus only remains to study prices p ∈ (vL, vH) ∩ [wH, +∞). Using (5), we note that q̃ ∈ A(p) iff
The exponential function being strictly increasing, the inequality above holds iff
Using (1), we obtain
As expected, ρH > ρL. For any p ∈ (vL, vH) ∩ [wH, +∞), inequality (26) is met whenever inequality (25) is met. Thus, a necessary and sufficient condition for such a price to be a pooling equilibrium price is
Derivation of Equation (34)
Notice that, with F denoting the error c.d.f.:
Hence
Proof of Proposition 6
It follows from (28) and (32) that φ(p) and ψ(p) have identical limits as α → 0. This limit value depends on whether the term
If p < v̅, β(p) < 0, so φ(p), ψ(p) → −∞ as α → 0. Conclude from (31) that
If p = v̅, β(p) = 0, so φ(p), ψ(p) → 0 as α → 0. Conclude from (31) that
If p = v̅, β(p) = 0, so φ(p), ψ(p) → +∞ as α → 0. Conclude from (31) that
Let p ∈ (vL, v̅). Then φ(p) → −∞ as α → 0, so condition (29) for p ∈ (vL, v̅) being a pooling equilibrium price is satisfied for sufficiently small α > 0. Together with the first observation above, this implies that
References
- Akerlof, G. The market for lemons: Quality uncertainty and the market mechanism. Quart. J. Econ. 1970, 84, 488–500. [Google Scholar]
- Riley, J. Silver signals: Twenty-five years of screening and signaling. J. Econ. Lit. 2001, 39, 432–478. [Google Scholar]
- Mas-Colell, A.; Whinston, M.D.; Green, J.R. Microeconomic Theory; Oxford University Press: New York, NY, USA, 1995. [Google Scholar]
- Milgrom, P.; Roberts, J. Price and advertising signals of product quality. J. Polit. Econ. 1986, 94, 796–821. [Google Scholar]
- Bagwell, K.; Riordan, M.H. High and declining prices signal product quality. Amer. Econ. Rev. 1991, 81, 224–239. [Google Scholar]
- Schlee, E.E. The value of information about product quality. RAND J. Econ. 1996, 27, 803–815. [Google Scholar]
- Ellingsen, T. Price signals quality: The case of perfectly inelastic demand. Int. J. Ind. Organ. 1997, 16, 43–61. [Google Scholar]
- Bester, H.; Ritzberger, K. Strategic pricing, signalling, and costly information acquisition. Int. J. Ind. Organ. 2001, 19, 1347–1361. [Google Scholar]
- Spence, M.A. Job market signaling. Quart. J. Econ. 1973, 87, 355–374. [Google Scholar]
- Feltovich, N.; Harbaugh, R.; To, T. Too cool for school? Signalling and countersignalling. RAND J. Econ. 2002, 33, 630–649. [Google Scholar]
- Alós-Ferrer, C.; Prat, J. Job market signalling and employer learning. In IZA Discussion Paper Series; No. 3285; Institute for the Study of Labor: Bonn, Germany, 2008. [Google Scholar]
- Riley, J.G.; Samuelson, W.F. Optimal auctions. Amer. Econ. Rev. 1981, 71, 381–392. [Google Scholar]
- Maskin, E.; Tirole, J. The principal-agent relationship with an informed principal, II: Common values. Econometrica 1992, 60, 1–42. [Google Scholar]
- Fudenberg, D.; Tirole, J. Game Theory; MIT Press: Cambridge, MA, USA, 1991. [Google Scholar]
- Kreps, D.M.; Wilson, R. Sequential equilibria. Econometrica 1982, 50, 863–894. [Google Scholar]
- Mattsson, L.G.; Voorneveld, M.; Weibull, J.W. Better may be worse: Some monotonicity results and paradoxes in discrete choice under uncertainty. Theor. Decis. 2007, 63, 121–151. [Google Scholar]
- 1We cannot possibly do justice to this rich literature here. The interested reader is referred to Riley [2] for a survey and to Mas-Colell et al. [3] for a textbook treatment.
- 2To be more precise, we assume F to be absolutely continuous: . Note also that the game would remain infinite even if one were to restrict the signal to be binary.
- 3See section 3.5 for a discussion of the subtle difference between pure noise and no signal.
- 4The alternative and more conventional representation q̃ = q + ε of a noisy signal does not permit “pure noise” as a well-defined boundary case.
- 5More generally, the buyer may randomize, in which case the range of the function b is expanded to [0, 1]. However, we here focus on pure strategies.
- 6The present game has infinitely many information sets and thus departs from the usual setting for sequential equilibrium. For exact definitions, see Fudenberg and Tirole [14] and Mas-Colell et al. [3].
- 7In the boundary case α = 0, εθ = q̃ for both θ = L and θ = H, and thus μL(q̃) = λfor all q̃, by (5).
- 8Expressed differently, [B3] requires the probability μL(q̃) to be consistent with the conditional likelihood of the true quality, given the observed quality q̃.
- 9The buyer's information sets then are of the form (p, qθ) and each such set consists of the nodes {(θ, ε, p) : ε ∈ ℝ}. Perfect Bayesian equilibrium requires that the belief system μ assigns probability F(x) to each subset of nodes {(θ, ε, pθ) : ε ≤ x}. However, this consistency requirement is only cosmetic: the error term ε is irrelevant to the buyer when α = 1.
- 10In order to buy from a high-quality seller with probability one the buyer has to buy irrespective of the quality signal, since the error term has full support.
- 11See Mattsson, Voorneveld and Weibull [16] for an investigation of a class of such decision problems.
- 12Notice, however, that this requires that the parties deliberately randomize. In our model, the required randomization is obtained by pure strategies conditioned on the random signal.
- 13Recall that if α = 0, then μL(q̃) → λ for all q.
- 14Indeed, it is the buyer's unique best reply to buy if
[v ∣ q̃] > p.
- 15This is true even when α = 0.
© 2011 by the authors; licensee MDPI, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Voorneveld, M.; Weibull, J.W. A Scent of Lemon—Seller Meets Buyer with a Noisy Quality Observation. Games 2011, 2, 163-186. https://doi.org/10.3390/g2010163
Voorneveld M, Weibull JW. A Scent of Lemon—Seller Meets Buyer with a Noisy Quality Observation. Games. 2011; 2(1):163-186. https://doi.org/10.3390/g2010163
Chicago/Turabian StyleVoorneveld, Mark, and Jörgen W. Weibull. 2011. "A Scent of Lemon—Seller Meets Buyer with a Noisy Quality Observation" Games 2, no. 1: 163-186. https://doi.org/10.3390/g2010163



