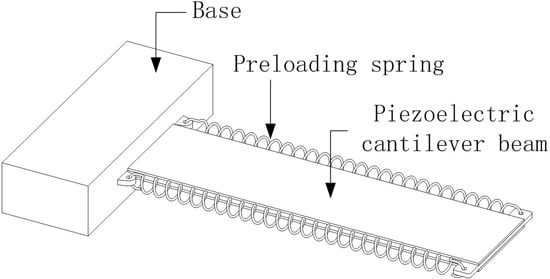
Non-Linear Piezoelectric Actuator with a Preloaded Cantilever Beam
Abstract
:1. Introduction
2. Preloaded Piezoelectric Actuators
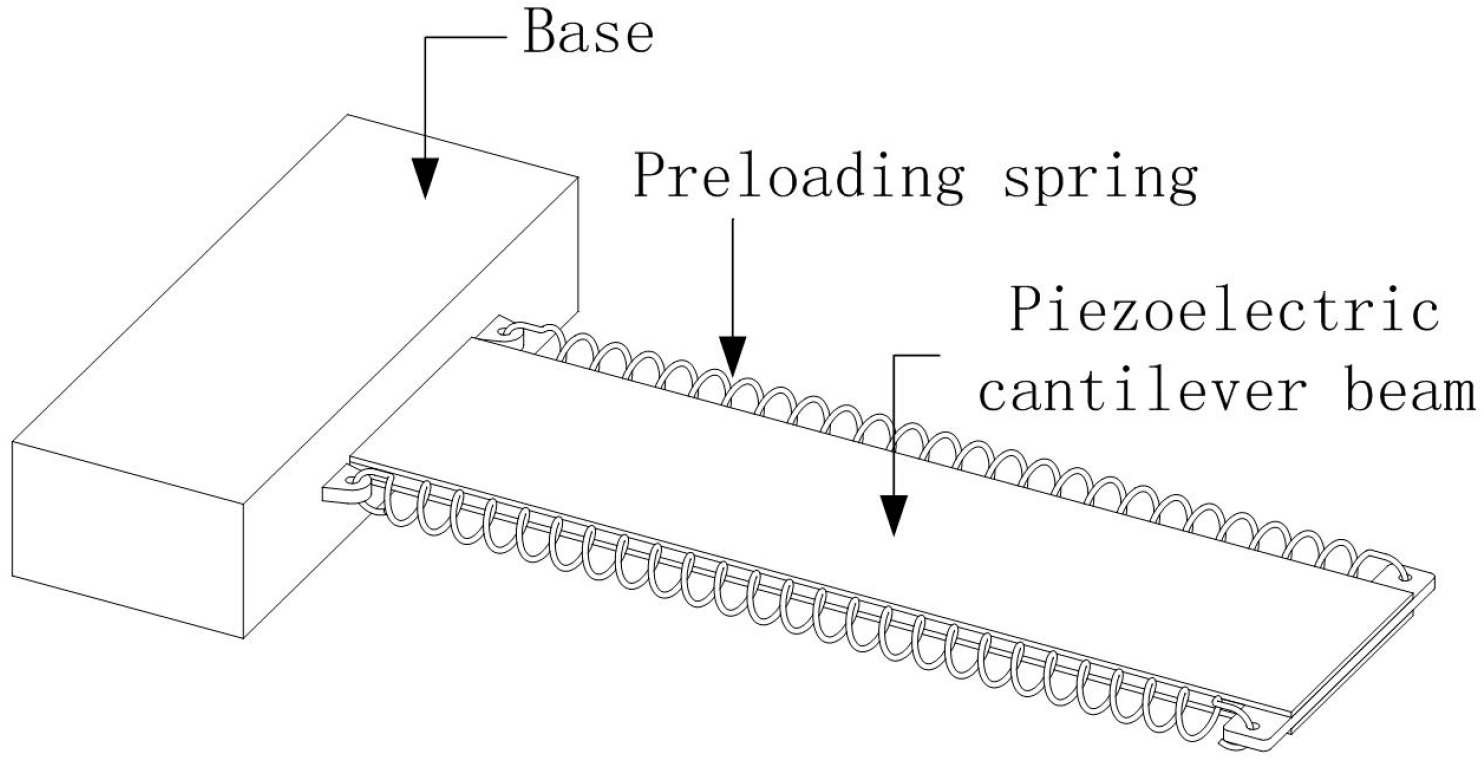
3. Mathematical Model of Preloaded Piezoelectric Actuators
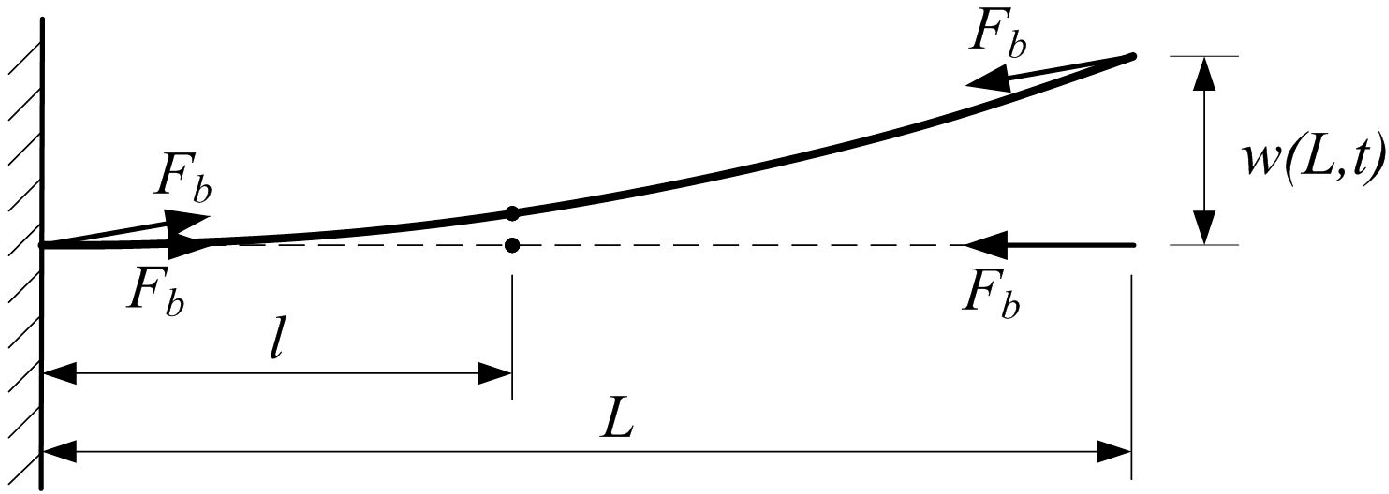
| Parameter | Symbol | Value |
|---|---|---|
| Substrate properties | ||
| Length | la | 120 mm |
| Width | b | 20 mm |
| Thickness | hs | 0.2 mm |
| Density | ρs | 8650 kg/m3 |
| Young’s modulus | Es | 112 GPa |
| Damping ratio | ζ | 0.01 |
| Piezoelectric laminate properties | ||
| Thickness | hp | 0.25 mm |
| Density | ρp | 7700 kg/m3 |
| Young’s modulus | Ep | 63 GPa |
| Coupling coefficient | d31 | −630 × 10−12 C/N |
| Laminate permittivity | εsxx | 3200 ε0 |
| Permittivity of free space | ε0 | 8.854 × 10−12 F/m |
| Loading spring properties | ||
| Stiffness | kb | 10 kN/m |
| Length | lb,0 | 100 mm |
| Pretension | Δlb | 1 mm |
4. Numerical Investigation of the Actuator for Nonlinear Oscillations
4.1. The Nonlinear Elastic Energy of the Actuator
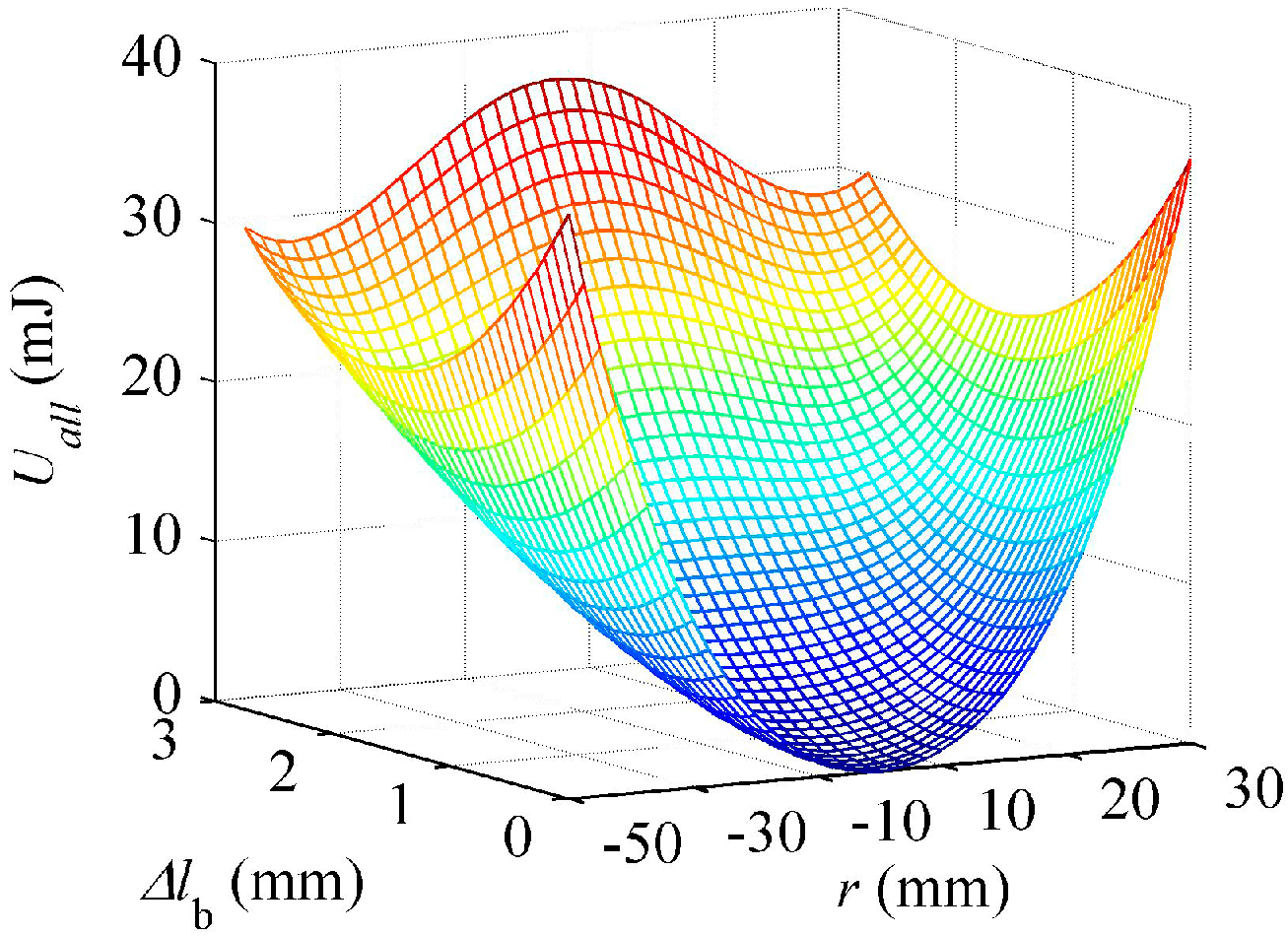
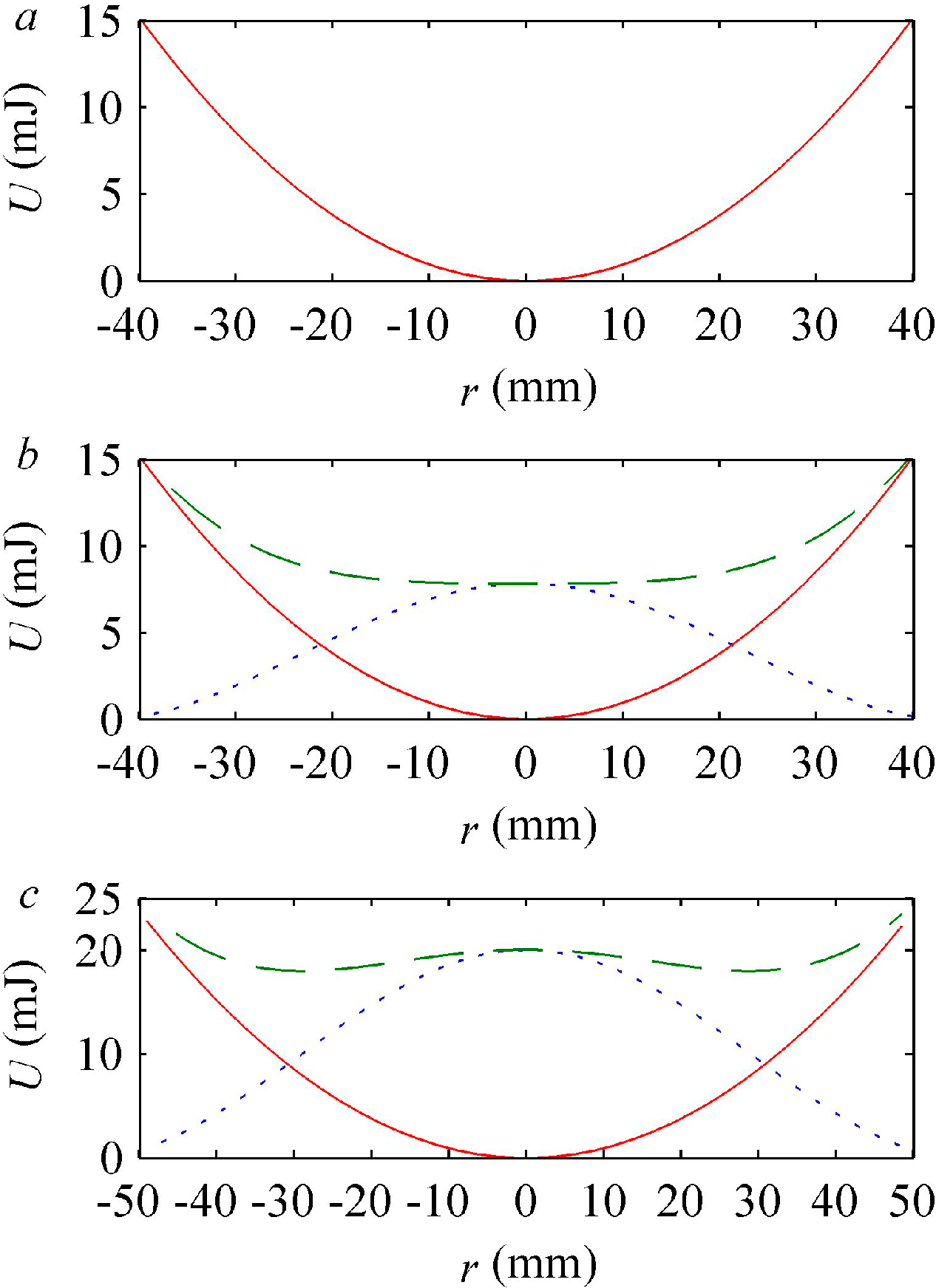

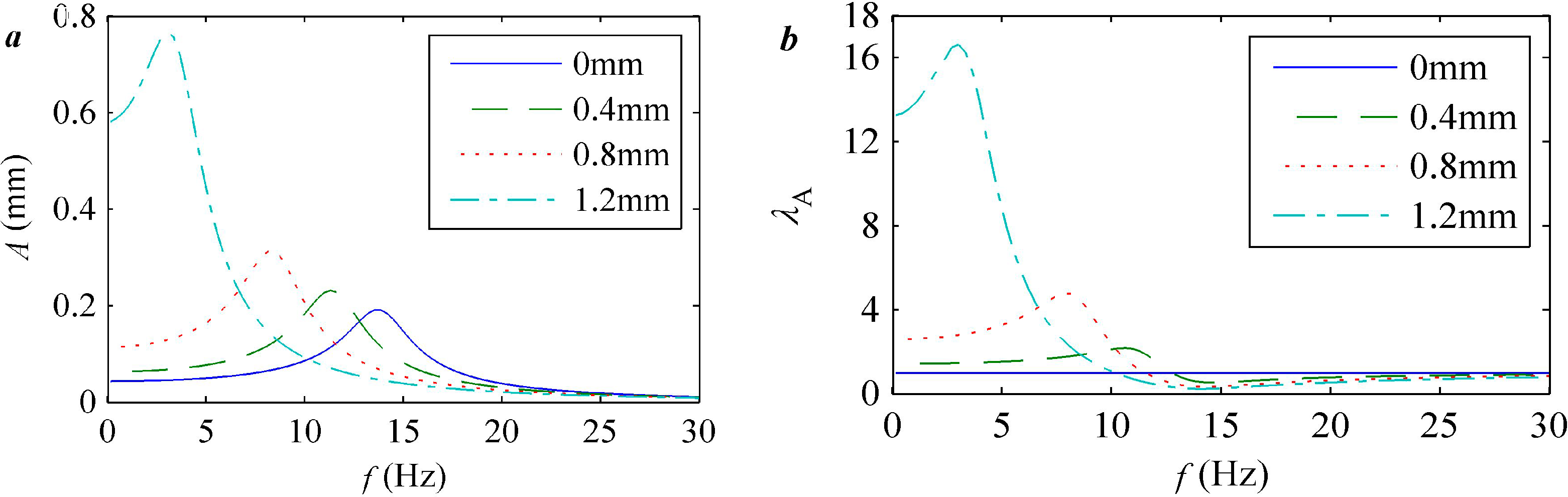
4.2. Pre-Buckled Response
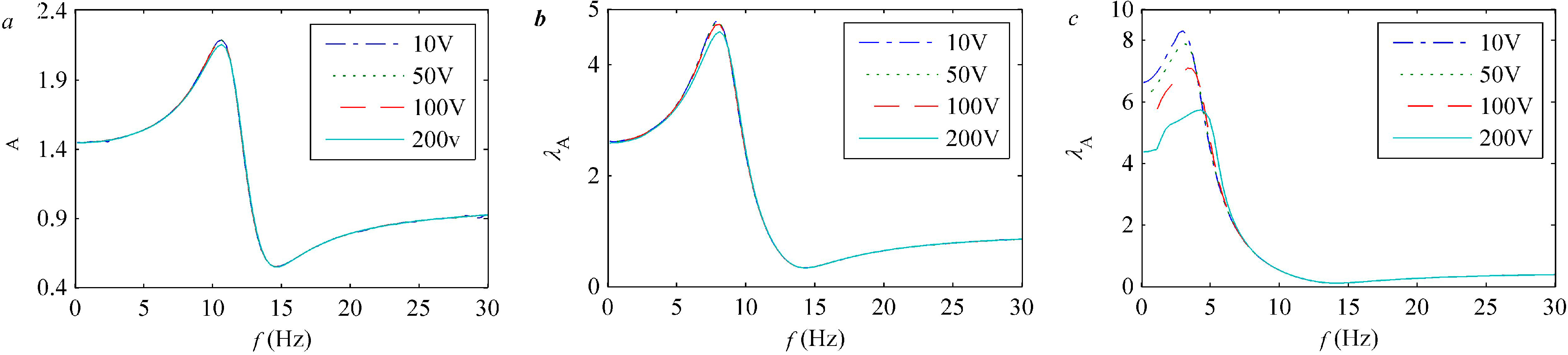
4.3. Post-Buckled Response
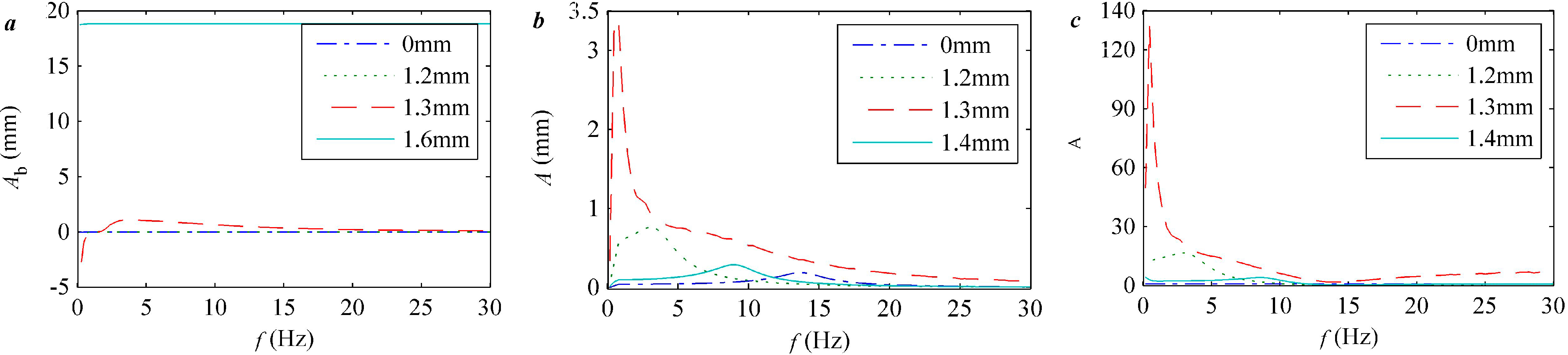
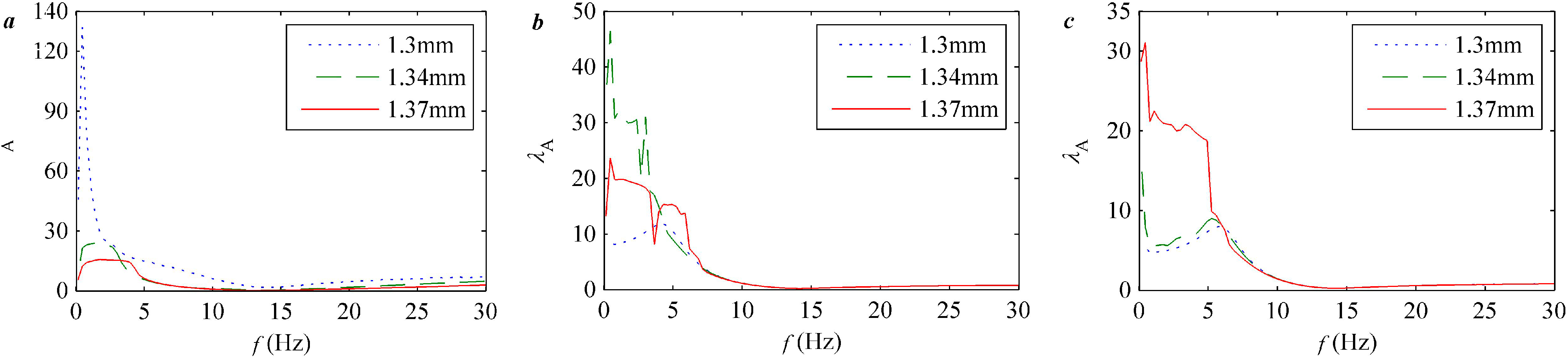
5. Experimental Results and Discussion
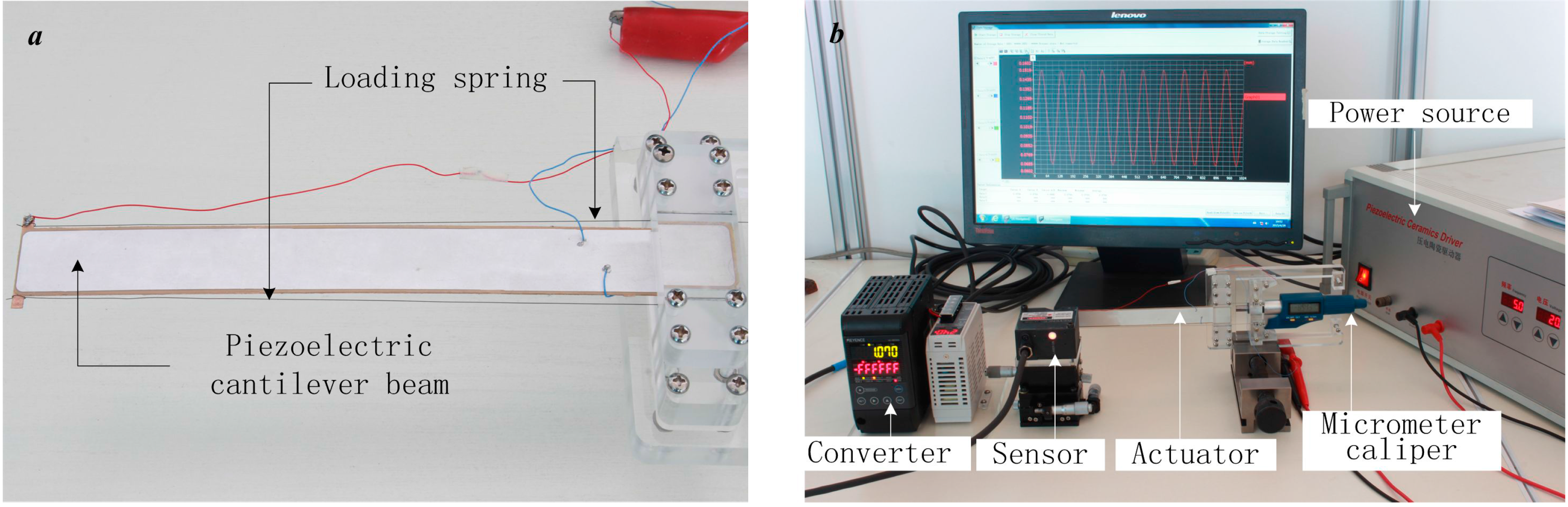
5.1. Measurement and Instrumentation
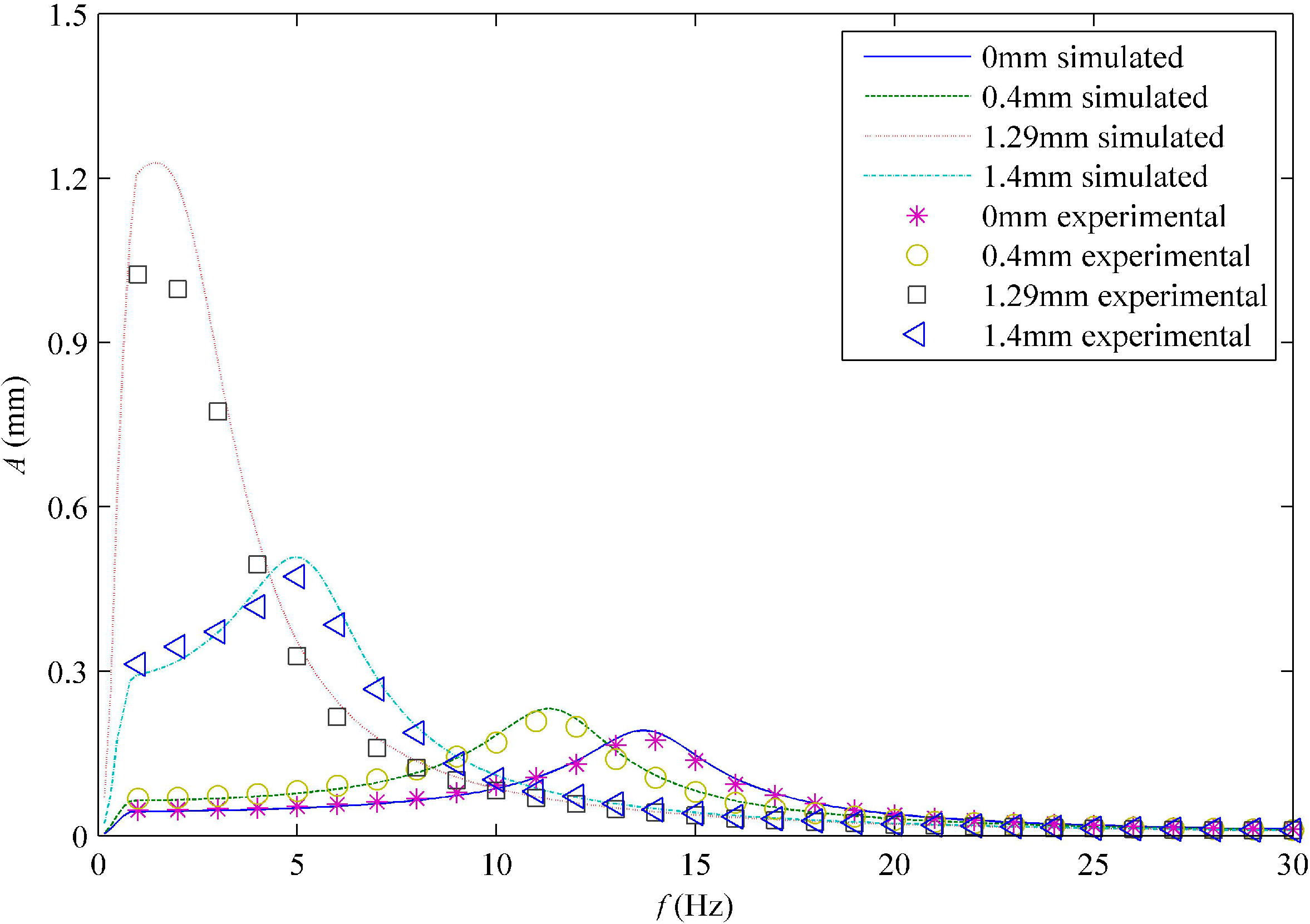
5.2. Comparisons of Experiment with Theory
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Aksel, E.; Jones, J.L. Advances in lead-free piezoelectric materials for sensors and actuators. Sensors 2010, 10, 1935–1954. [Google Scholar] [PubMed]
- Abuzaid, A.; Hrairi, M.; Dawood, M.S.I. Survey of active structural control and repair using piezoelectric patches. Actuators 2015, 4, 77–98. [Google Scholar]
- Gómez Alvarez-Arenas, T. Air-coupled piezoelectric transducers with active polypropylene foam matching layers. Sensors 2013, 13, 5996–6013. [Google Scholar] [PubMed]
- Goldfarb, M.; Celanovic, N. Modeling piezoelectric stack actuators for control of micromanipulation. IEEE Control Syst. 1997, 17, 69–79. [Google Scholar]
- Jakiela, S.; Debski, P.; Dabrowski, B.; Garstecki, P. Generation of nanoliter droplets on demand at hundred-Hz frequencies. Micromachines 2014, 5, 1002–1011. [Google Scholar]
- Furuta, A.; Uchino, K. Dynamic observation of crack propagation in piezoelectric multilayer actuators. J. Am. Ceram. Soc. 1993, 76, 1615–1617. [Google Scholar]
- Low, T.; Guo, W. Modeling of a three-layer piezoelectric bimorph beam with hysteresis. J. Microelectromech. Syst. 1995, 4, 230–237. [Google Scholar] [CrossRef]
- Dogan, A.; Xu, Q.; Onitsuka, K.; Yoshikawa, S.; Uchino, K.; Newnham, R.E. High displacement ceramic metal composite actuators (moonies). Ferroelectrics 1994, 156, 1–6. [Google Scholar] [CrossRef]
- Ochoa, P.; Villegas, M.; Rodriguez, M.; Fernandez, J. Statistic analysis of electromechanical response in cymbal piezocomposites. J. Eur. Ceram. Soc. 2006, 27, 4173–4176. [Google Scholar] [CrossRef]
- Sun, C.L.; Lam, K.H.; Chan, H.L.W.; Zhao, X.-Z.; Choy, C.L. A Novel Drum Piezoelectric-Actuator. Appl. Phys. A 2006, 84, 385–390. [Google Scholar] [CrossRef]
- Her, S.-C.; Lin, C.-S. Vibration analysis of composite laminate plate excited by piezoelectric actuators. Sensors 2013, 13, 2997–3013. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; Zhang, S.; Bar-Cohen, Y.; Sherrit, S. High temperature, high power piezoelectric composite transducers. Sensors 2014, 14, 14526–14552. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Li, M.; Qin, L.; Liu, J. Active design method for the static characteristics of a piezoelectric six-axis force/torque sensor. Sensors 2014, 14, 659–671. [Google Scholar] [CrossRef] [PubMed]
- Dong, X.; Peng, Z.; Hua, H.; Meng, G. Modeling of the through-the-thickness electric potentials of a piezoelectric bimorph using the spectral element method. Sensors 2014, 14, 3477–3492. [Google Scholar] [CrossRef] [PubMed]
- El-Sayed, A.; Abo-Ismail, A.; El-Melegy, M.; Hamzaid, N.; Osman, N. Development of a micro-gripper using piezoelectric bimorphs. Sensors 2013, 13, 5826–5840. [Google Scholar] [CrossRef] [PubMed]
- El-Sayed, A.; Hamzaid, N.; Abu Osman, N. Piezoelectric bimorphs’ characteristics as in-socket sensors for transfemoral amputees. Sensors 2014, 14, 23724–23741. [Google Scholar] [CrossRef] [PubMed]
- Tian, X.; Yang, Z.; Liu, Y.; Shen, Y.; Chen, S. Structural design and experimental analysis of a piezoelectric vibration feeder with a magnetic spring. Micromachines 2014, 5, 547–557. [Google Scholar] [CrossRef]
- Zhang, J.; Wu, Z.; Jia, Y.; Kan, J.; Cheng, G. Piezoelectric bimorph cantilever for vibration-producing-hydrogen. Sensors 2012, 13, 367–374. [Google Scholar] [CrossRef] [PubMed]
- Mann, B.P.; Sims, N.D. Energy harvesting from the nonlinear oscillations of magnetic levitation. J. Sound Vib. 2009, 319, 515–530. [Google Scholar] [CrossRef]
- Erturk, A.; Hoffmann, J.; Inman, D. A piezomagnetoelastic structure for broadband vibration energy harvesting. Appl. Phys. Lett. 2009, 94, 254102. [Google Scholar] [CrossRef]
- Burrow, S.; Clare, L.; Carrella, A.; Barton, D. Vibration Energy Harvesters with Non-linear Compliance. Proc. SPIE 2008, 6928, 692807. [Google Scholar]
- Guyomar, D.; Lallart, M. Recent progress in piezoelectric conversion and energy harvesting using nonlinear electronic interfaces and issues in small scale implementation. Micromachines 2011, 2, 274–294. [Google Scholar] [CrossRef]
- Priya, S.; Ryu, J.; Park, C.-S.; Oliver, J.; Choi, J.-J.; Park, D.-S. Piezoelectric and magnetoelectric thick films for fabricating power sources in wireless sensor nodes. Sensors 2009, 9, 6362–6384. [Google Scholar] [CrossRef] [PubMed]
- Stanton, S.C.; McGehee, C.C.; Mann, B.P. Nonlinear dynamics for broadband energy harvesting: Investigation of a bistable piezoelectric inertial generator. Phys. D Nonlinear Phenom. 2010, 239, 640–653. [Google Scholar] [CrossRef]
- Zhou, S.; Cao, J.; Inman, D.J.; Lin, J.; Liu, S.; Wang, Z. Broadband tristable energy harvester: Modeling and experiment verification. Appl. Energy 2014, 133, 33–39. [Google Scholar] [CrossRef]
- Bilgen, O.; Ali, S.F.; Friswell, M.I.; Litak, G.; de Angelis, M. Non-linear piezoelectric vibration energy harvesting from a vertical cantilever beam with tip mass. In Proceedings of the ASME 2013 Conference on Smart Materials, Adaptive Structures and Intelligent Systems, Snowbird, UT, USA, 16–18 September 2013.
- Friswell, M.I.; Ali, S.F.; Bilgen, O.; Adhikari, S.; Lees, A.W.; Litak, G. Non-linear piezoelectric vibration energy harvesting from a vertical cantilever beam with tip mass. J. Intell. Mater. Syst. Struct. 2012, 23, 1505–1521. [Google Scholar] [CrossRef]
- Kim, P.; Bae, S.; Seok, J. Resonant behaviors of a nonlinear cantilever beam with tip mass subject to an axial force and electrostatic excitation. Int. J. Mechan. Sci. 2012, 64, 232–257. [Google Scholar] [CrossRef]
- Caliò, R.; Rongala, U.; Camboni, D.; Milazzo, M.; Stefanini, C.; de Petris, G.; Oddo, C. Piezoelectric energy harvesting solutions. Sensors 2014, 14, 4755–4790. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hagood, N.W.; Chung, W.H.; Von Flotow, A. Modelling of piezoelectric actuator dynamics for active structural control. J. Intell. Mater. Syst. Struct. 1990, 1, 327–354. [Google Scholar] [CrossRef]
- Wang, Q.-M.; Eric Cross, L. Constitutive equations of symmetrical triple layer piezoelectric benders. IEEE Trans. Ultrason. Ferroelectr. Frequency Control 1999, 46, 1343–1351. [Google Scholar] [CrossRef] [PubMed]
- Sodano, H.A.; Park, G.; Inman, D. Estimation of electric charge output for piezoelectric energy harvesting. Strain 2004, 40, 49–58. [Google Scholar] [CrossRef]
- Dutoit, N.E.; Wardle, B.L.; Kim, S.-G. Design considerations for mems-scale piezoelectric mechanical vibration energy harvesters. Integr. Ferroelectr. 2005, 71, 121–160. [Google Scholar] [CrossRef]
- Stanton, S.; Mann, B. Harvesting energy from the nonlinear oscillations of a bistable piezoelectric inertial energy generator. In Proceedings of the ASME 2009 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, San Diego, CA, USA, 30 August–2 September 2009.
- Meitzler, A.; Tiersten, H.F.; Warner, A.W.; Berlincourt, D.; Couqin, G.A.; Welsh, F.S., III. ANSI/IEEE Std 176-1987: IEEE Standard on Piezoelectricity; IEEE: Piscataway, NJ, USA, 1988. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Dong, J.; Li, X.; Yang, Z.; Liu, Q. Non-Linear Piezoelectric Actuator with a Preloaded Cantilever Beam. Micromachines 2015, 6, 1066-1081. https://doi.org/10.3390/mi6081066
Wu Y, Dong J, Li X, Yang Z, Liu Q. Non-Linear Piezoelectric Actuator with a Preloaded Cantilever Beam. Micromachines. 2015; 6(8):1066-1081. https://doi.org/10.3390/mi6081066
Chicago/Turabian StyleWu, Yue, Jingshi Dong, Xinbo Li, Zhigang Yang, and Qingping Liu. 2015. "Non-Linear Piezoelectric Actuator with a Preloaded Cantilever Beam" Micromachines 6, no. 8: 1066-1081. https://doi.org/10.3390/mi6081066