1. Introduction
Valves are common fluid flow control components which are used in many macro- and microfluidic applications. They are used to regulate and switch liquid flows in continuous flow devices [
1,
2] or for ejection of droplets or jets in non-contact dispensing applications [
3]. Such dispensing valves are facing demanding requirements in terms of minimal volume and volumetric precision and accuracy [
3,
4]. Especially for biomedical applications, dispensing valves usually need to be normally closed, requiring rather complex closing or return mechanisms. Additionally, the avoidance of cross-contamination is crucial giving preference to non-contact dispensing systems that transfer liquids as free flying jets or droplets. To eject free droplets or jets of small volume, the dispensing valve needs to feature high dynamics to overcome surface tension and viscous dissipation.
Piezo actuated or solenoid dispensing valves are the preferred technologies to address these requirements, due to their highly dynamic and precise behavior [
5,
6]. Most of the commercially available systems feature complex and expensive designs, materials and actuation mechanisms and therefore need to be cleaned and reused many times. Such washing procedures are expensive, decrease throughput and increase the risk of cross-contamination.
We have developed a dispensing valve addressing these requirements and overcoming the limitations described above. That is to say, we developed a highly dynamic and precise dispensing valve which features a very simple (i.e. disposable) normally closed design. The solenoid actuation principle features opening times down to 1 ms, depending on the viscosity of the liquid to be dispensed and is therefore well-suited for non-contact dispensing of small volumes. The valve is normally closed by a simple and effective ferromagnetic closing mechanism. Due to the simple design and the low-cost materials, the valve presented hereafter can be considered as a disposable enabling carry-over free liquid dispensing without expensive and time-consuming washing steps.
2. Working Principle
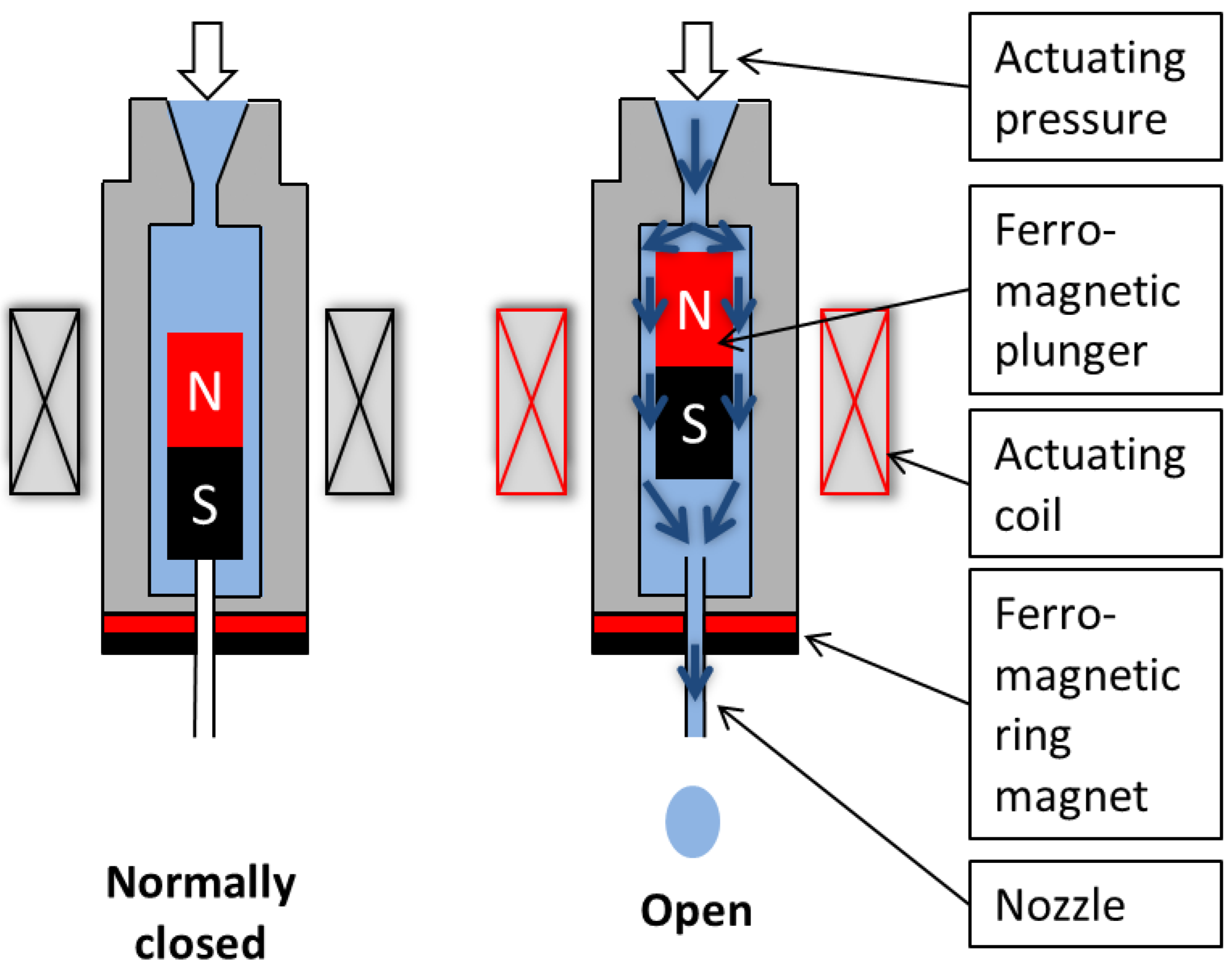
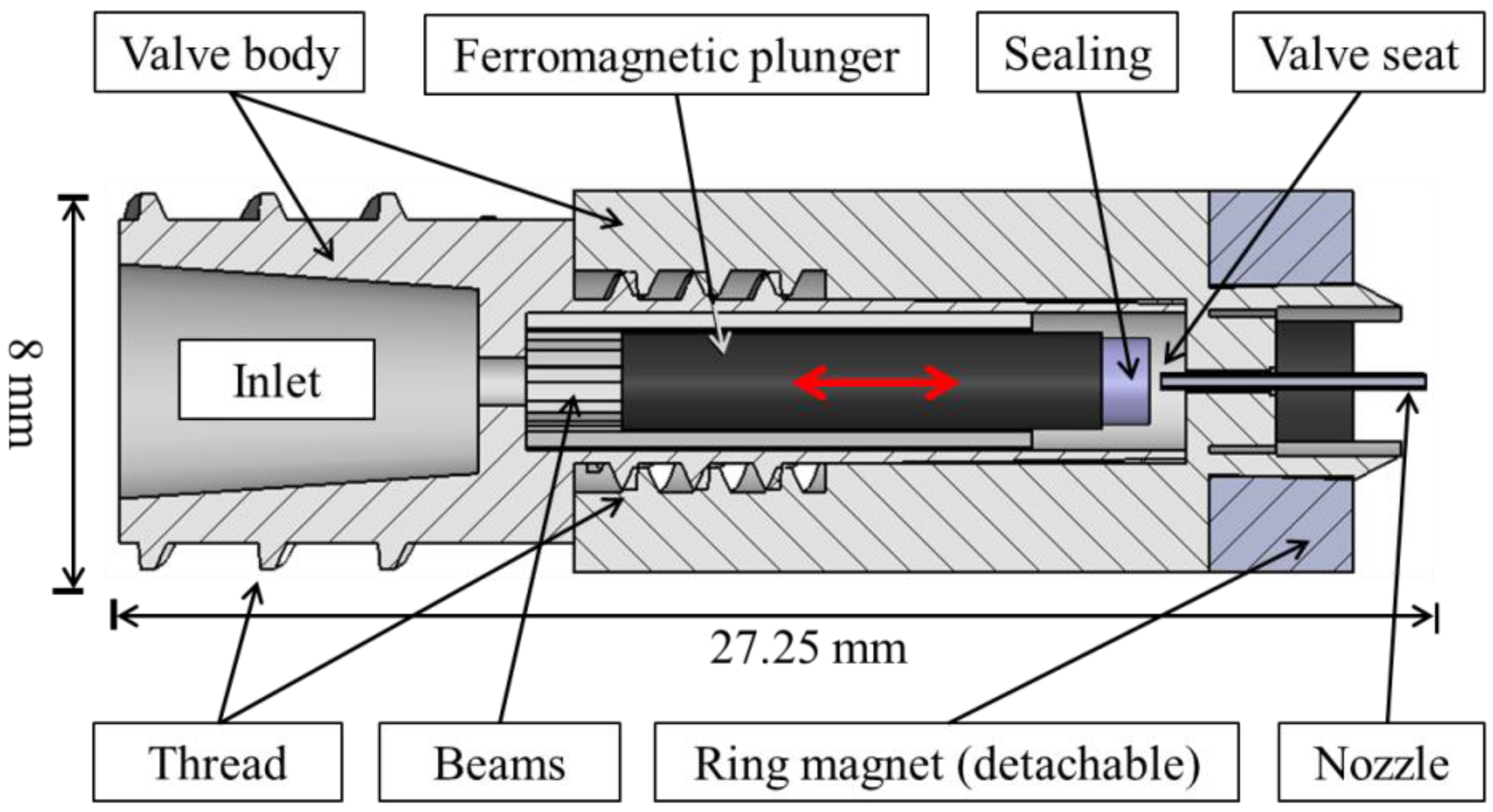
The disposable part of the solenoid valve consists of the main elements as sketched in
Figure 1: A valve body containing a ferromagnetic plunger that can engage with a valve seat to close the nozzle. The valve is normally closed,
i.e. when no electrical current is applied to the actuating coil the ferromagnetic ring magnet attracts the ferromagnetic plunger and pulls it downwards to close the valve (see left hand side of
Figure 1). The inlet of the valve is pressurized at a constant actuating pressure level of typically 200 to 1000 mbar, which are typical values to drive dispensing valves. This actuating pressure is released when the valve is opened. Opening is achieved by moving the ferromagnetic plunger upwards to open the upper end of a metal capillary, which forms the valve seat. To achieve this, an electrical current is applied to the actuating coil which induces a magnetic field to overcome the attractive force of the two permanent magnets to open the valve (see right hand side of
Figure 1).
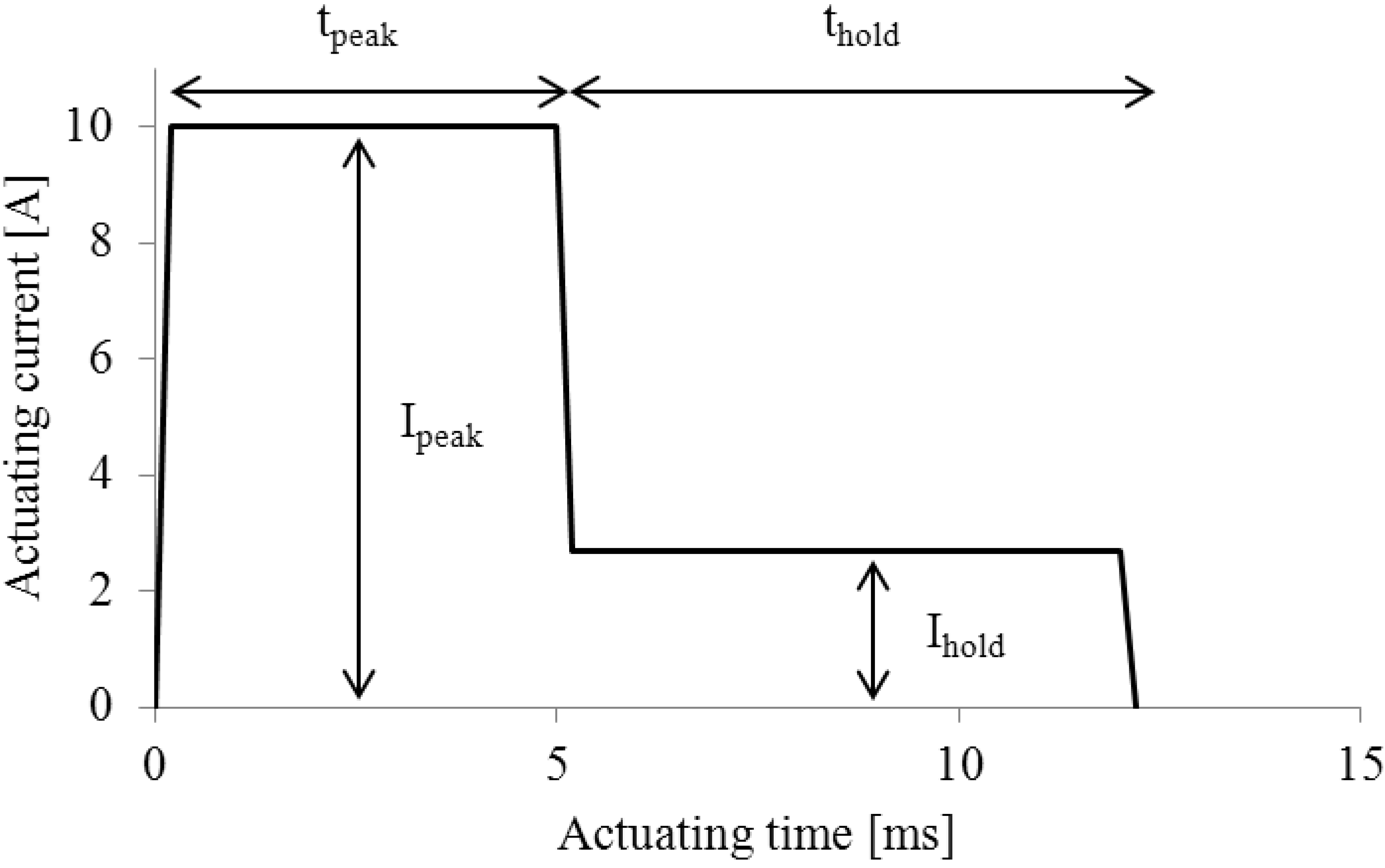
The electrical current has the form of a peak and hold signal [
7], as depicted in
Figure 2, to reduce energy consumption and Joule heating of the valve. The signal starts with a peak current (
Ipeak = 10 A), which is reduced to a hold current (
Ihold = 2.7 A) after
tpeak = 5 ms. For actuating times smaller than 5 ms no hold current is applied.
Figure 1.
Working principle of the dispensing valve. Left: In its normally closed state, the ring magnet attracts the plunger and the valve seat is closed. Right: The actuating coil overcomes the attractive force between the ring magnet and the plunger to open the valve.
Figure 1.
Working principle of the dispensing valve. Left: In its normally closed state, the ring magnet attracts the plunger and the valve seat is closed. Right: The actuating coil overcomes the attractive force between the ring magnet and the plunger to open the valve.
Figure 2.
Scheme of the peak and hold actuation pulse, adapted from [
7]. The peak current is 10 A and the hold current is 2.7 A. The duration of the peak current does not exceed 5 ms.
Figure 2.
Scheme of the peak and hold actuation pulse, adapted from [
7]. The peak current is 10 A and the hold current is 2.7 A. The duration of the peak current does not exceed 5 ms.
Applying a high peak current at the beginning of the actuation pulse allows for a dynamic movement of the plunger. This elevated peak current is important especially at the beginning of the pulse, where the inductivity of the solenoid in addition to the attractive force of the magnets needs to be overcome. The lower hold current reduces heat coupling effects that can lead to heating of the reagent, decreasing its viscosity, which results in higher flow rates and thus a reduced accuracy and precision.
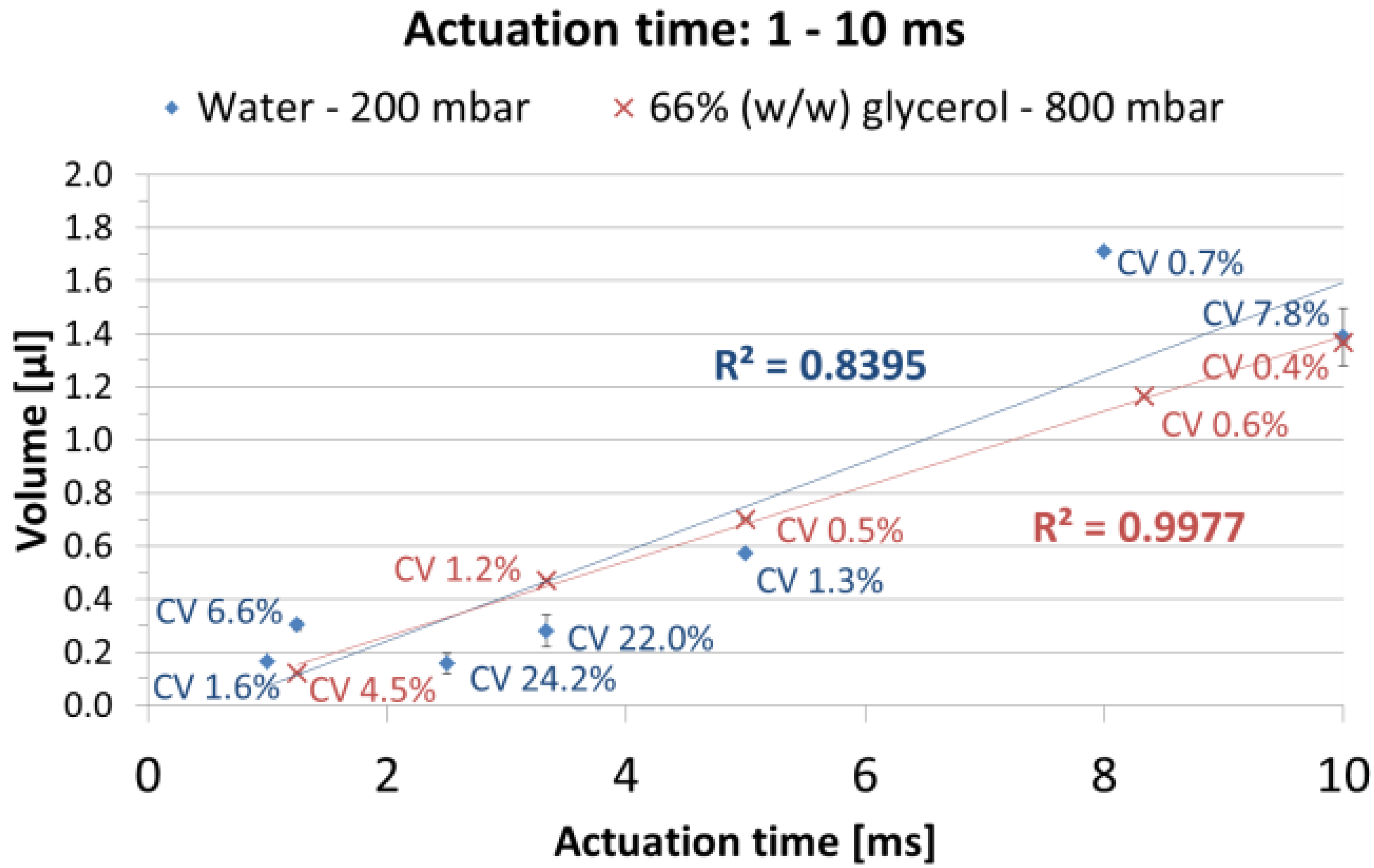
It should be mentioned that the actuation time (
i.e. the time the coil is energized) does not necessarily equal the opening time of the valve. Especially for very small actuation times (e.g. <10ms), the precise control of the time delay between the electrical actuating current and the actual opening time of the valve can be very difficult as described by Shvets
et al. [
8]. The effects described hereafter all have this problem of reproducibly defining the actual opening time of a valve in common.
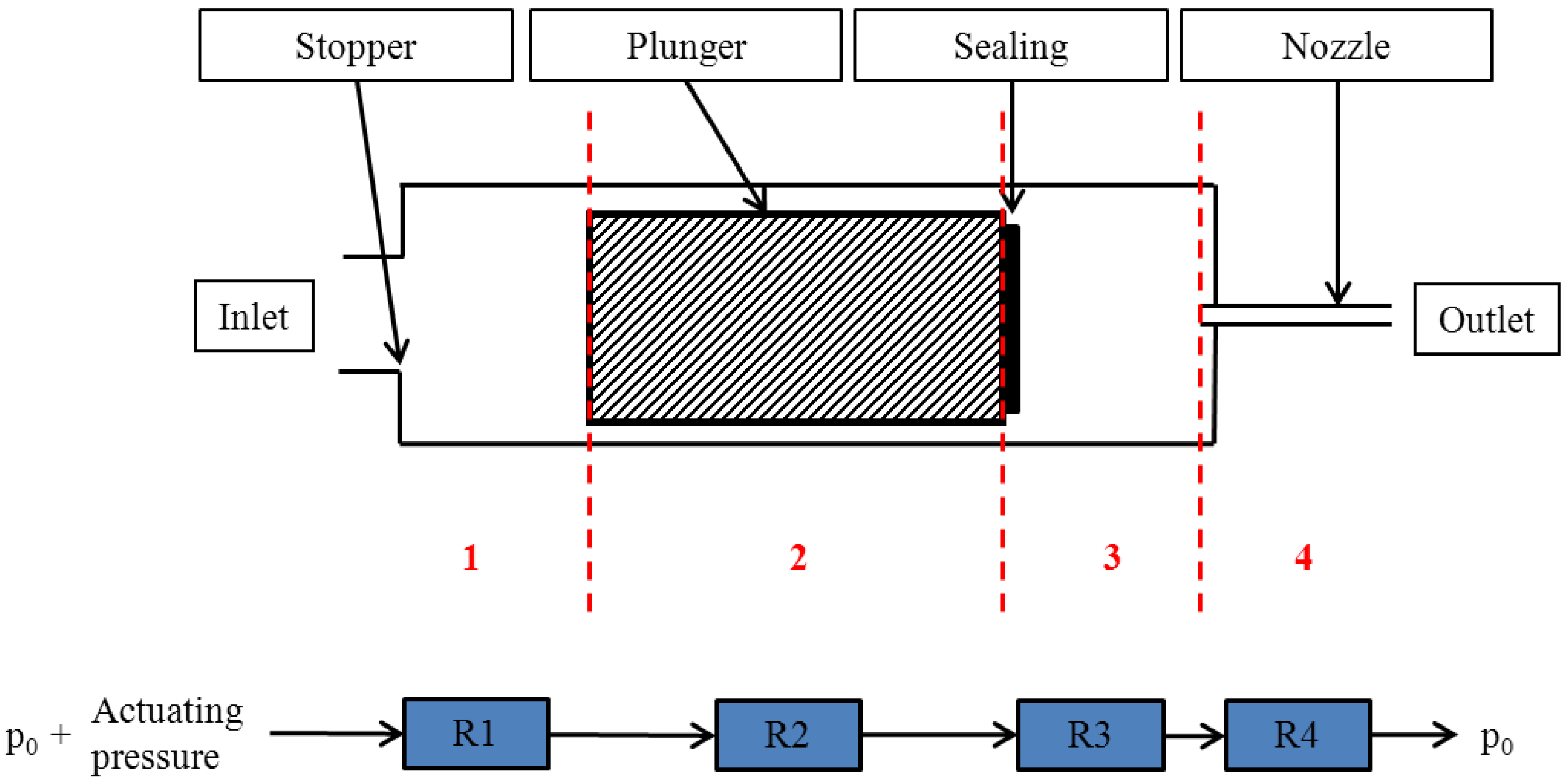
A first source of uncertainty concerning the exact control of the opening time is the soft sealing layer between the plunger and the valve seat (see
Figure 3). Since the sealing is compressed while the valve is closed, a movement of the plunger away from the valve seat does not open the valve immediately but with a small but hardly reproducible time delay.
Secondly, the time delay between actuation and opening time depends on the viscosity of the liquid since the liquid has to be displaced for moving the plunger. The viscosity in turn depends critically on the temperature of the liquid. Thus, temperature variations due to e.g. heat coupling effects of the coil (described above) influence the actual opening time also.
Figure 3.
Scheme of the different subsections of the dispensing valve and the corresponding fluidic resistances. The total fluidic resistance equals the sum of the individual resistances R1 to R4.
Figure 3.
Scheme of the different subsections of the dispensing valve and the corresponding fluidic resistances. The total fluidic resistance equals the sum of the individual resistances R1 to R4.
Additionally, the plunger might bounce when hitting against the stopper (valve opens) or the valve seat (valve closes) [
8]. Both bouncing movements can affect precision negatively. For a confined range of actuation time, the bouncing of the plunger off the stopper can decrease the actual volume (
i.e. accuracy) significantly. The bouncing against the stopper imparts a momentum to the plunger which decreases the valve’s actual opening time. Accordingly, the bouncing against the valve seat can increase the actual volume and accuracy by opening the valve for an additional amount of time.
Lastly, for very small actuation times, the position of the plunger is very hard to predict or control since it does not move far enough to come at rest against the stopper. Again, this behavior makes a reproducible control of the opening time difficult which diminishes dispensing precision.
The effects described above become more significant for small actuation times or target volumes since the relative timing inaccuracies increase for small actuation times [
8].
A vital characteristic of a dispensing valve is its fluidic resistance since it substantially determines the valve’s flow rate, i.e. the volume which is dispensed per unit of time when the valve is opened. In order to investigate the effects of mechanical tolerance on the dispensing performance an approximate formula for the flow rate is derived in the following.
The fluidic resistances of the various subsections inside the valve are outlined in
Figure 3. Subsection one is located in-between the inlet of the valve and the movable plunger. The fluidic resistance of subsection two is determined by the gap in between the plunger and the body of the valve. Subsection three is located in between the plunger and the upper end of the nozzle. The fluidic resistance of the nozzle equals the fluidic resistance of the last subsection. However, due to the small radius of the nozzle of 100 µm, the total fluidic resistance of the dispensing valve is mainly dominated by the fluidic resistance
R4 of the nozzle, which is given by [
9]:
where
h and
r represent the length and the radius of the nozzle and
η represents the viscosity of the reagent (see also the nomenclature at
Table 1). The flow rate
q is inversely proportional to the fluidic resistance:
which indicates a very strong effect of the geometrical tolerances of the radius of the nozzle on the flow rate and therefore on the volumetric dispensing accuracy as discussed further in the Results section.
Table 1.
Nomenclature of the symbols used throughout this paper.
3. Design
The valve’s modular low-cost design consists of “dry parts” which are not in contact with the reagent and “wet parts” which are contaminated by the liquid to be dispensed (see
Table 2).
Table 2.
List of components of the dispensing valve, including the approximate material costs.
Table 2.
List of components of the dispensing valve, including the approximate material costs.
| Component | Source | Application | Approx. Costs |
|---|
| Valve body | Printed (Project HD300, 3D Systems) | Wet part: Contaminated | ≈1 $ |
| Plunger | IBS Magnet | Wet part: Contaminated | 0.6 $ |
| Sealing | RALICKS | Wet part: Contaminated | 0.1 $ |
| Nozzle | Nordson EFD | Wet part: Contaminated | 0.8 $ |
| Ring Magnet | IBS Magnet | Dry part: Reused | 0.3 $ |
| Coil | Imetron | Dry part: Reused | ≈2 $ |
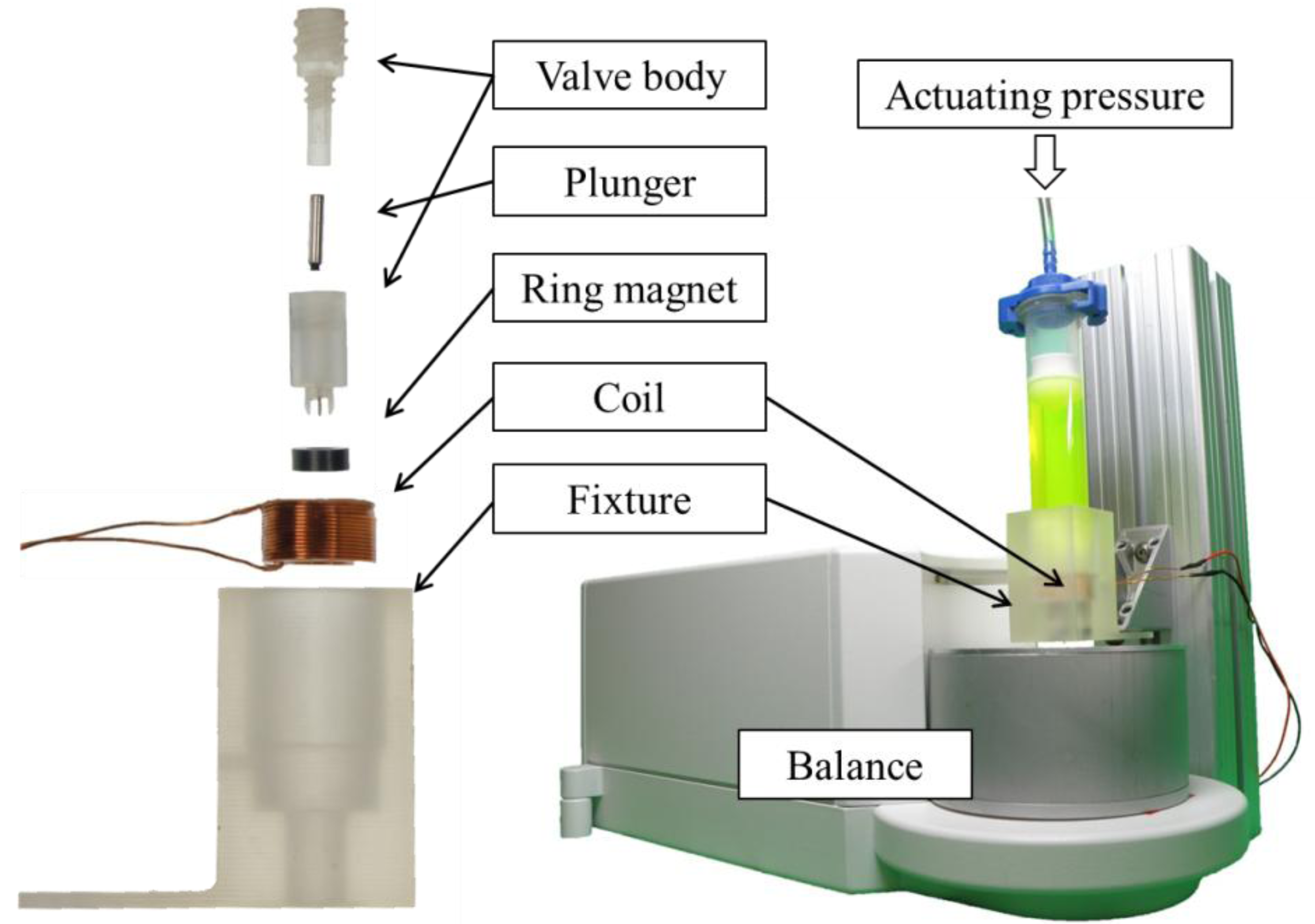
The dry parts comprise the actuating coil (2.2 Ω, 0.47 mH) and the ring magnet (hard ferrite, 380–400 mT), which functions as a normally closing magnetic attraction mechanism (see
Figure 1). The control electronics generating the peak and hold actuating current is custom made with an integrated circuit “LM1949” [
10] from Texas Instruments, Inc. as a key element.
The wet parts consist of a two-part valve body, a ferromagnetic plunger and a metal capillary. The valve body is fabricated by 3D printing (material “Visijet EX 200”) but is designed to be injection-moldable. It consists of two separate parts which are connected by a thread enabling the insertion of the plunger for an easy manufacturing process of the valve. Beams on the inner wall of the body work as guiding structures for the movement of the plunger which has a travel of 2.3 mm (see
Figure 4). The beams allow fluid to flow around the plunger through ducts separating the beams. The gap in between the plunger and the wall of the valve body is 0.45 mm. The inlet of the valve body is equipped with a Luer-Lock thread providing a standard interface for straight forward connections of the valve to e.g. commercial syringes.
Figure 4.
Cross-section through the dispensing valve with the movable plunger (red arrow).
Figure 4.
Cross-section through the dispensing valve with the movable plunger (red arrow).
The ferromagnetic plunger (NdFeB, 1170–1250 mT) has a diameter of 2.0 mm and a length of 10.0 mm. It is coated with Parylene C to ensure biocompatibility. A circular piece of silicone or EPDM (ethylene propylene diene monomer (M-class) rubber, OD × h = 1.8 × 1.0 mm) is attached to the lower end of the plunger forming the sealing layer at the valve seat. The durometer of the sealing can be varied between 50A to 70A depending on the specific dispensing application. The best results were obtained with a durometer of 60 A. The ring magnet at the very end of the valve is attached to the valve body by a simple clipping fixture (see
Figure 4). It is therefore detachable and can be reused since it is not contaminated by the liquid.
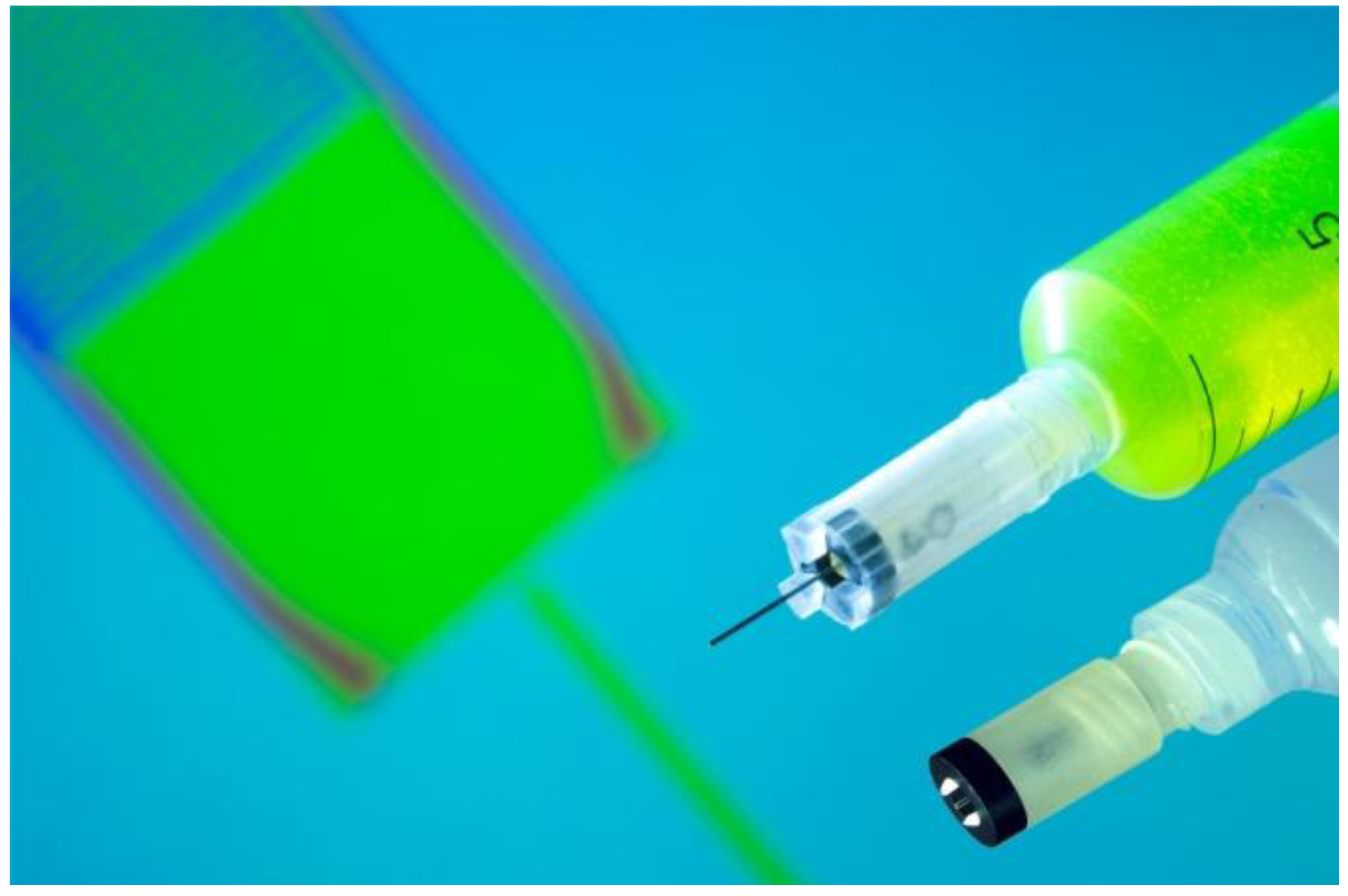
The metal capillary has an inner diameter of 0.2 mm and a length of either 16.5 mm or 5.5 mm (see
Figure 5). The shorter nozzle is the standard nozzle which is also suitable for dispensing high viscosity fluids (up to
ca. 30 mPas). The longer nozzle is suitable for dispensing e.g. low viscous fluids or is used when aspiration of liquid is desired. The upper end of the metal capillary protrudes beyond the valve body by 0.5 mm and forms the valve seat. The lower end functions as the nozzle of the valve.
Figure 5.
The dispensing valve with its black ring magnet attracting the inner plunger to its normally closed position. Foreground: two valves mounted on commercial syringes. Upper valve: long nozzle (16.5 mm) and external ring magnet fixture. Lower valve: short nozzle (5.5 mm) and ring magnet attached by clamping fixture. Background: a screenshot of numerical simulations of the fluid dynamics within the valve as presented in [
11].
Figure 5.
The dispensing valve with its black ring magnet attracting the inner plunger to its normally closed position. Foreground: two valves mounted on commercial syringes. Upper valve: long nozzle (16.5 mm) and external ring magnet fixture. Lower valve: short nozzle (5.5 mm) and ring magnet attached by clamping fixture. Background: a screenshot of numerical simulations of the fluid dynamics within the valve as presented in [
11].
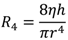
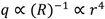






 of one run of N = 24 individually measured aliquots Vn:
of one run of N = 24 individually measured aliquots Vn:

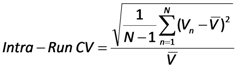
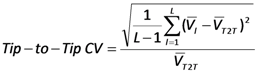
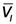 represents the mean volume of one run with one valve l and
represents the mean volume of one run with one valve l and 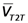 represents the mean volume of all runs performed with L = 4 valves. The Tip-to-Tip CV measures the volumetric precision of the different valves’ mean volume if all parameters (actuation time and pressure) are kept constant. Thus, it evaluates the influence of the fabrication tolerances, in particular variations of the inner diameter of the nozzle, on the dispensing accuracy of the individual valves as described in Section 2.
represents the mean volume of all runs performed with L = 4 valves. The Tip-to-Tip CV measures the volumetric precision of the different valves’ mean volume if all parameters (actuation time and pressure) are kept constant. Thus, it evaluates the influence of the fabrication tolerances, in particular variations of the inner diameter of the nozzle, on the dispensing accuracy of the individual valves as described in Section 2.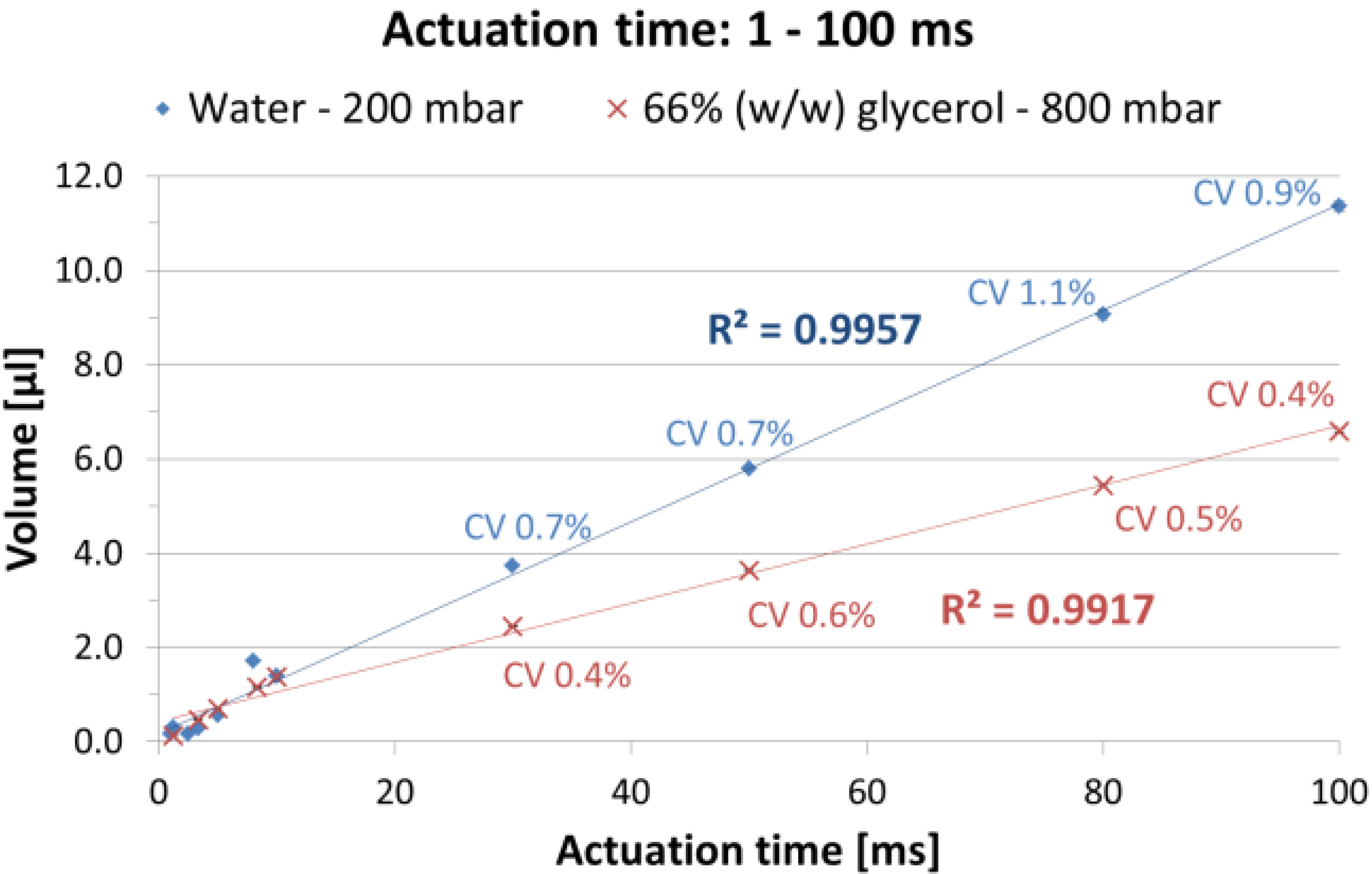
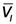 (µL)
(µL)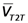 = 1.02
= 1.02




