Nonlinear Thermal/Mechanical Buckling of Orthotropic Annular/Circular Nanoplate with the Nonlocal Strain Gradient Model
Abstract
:1. Introduction
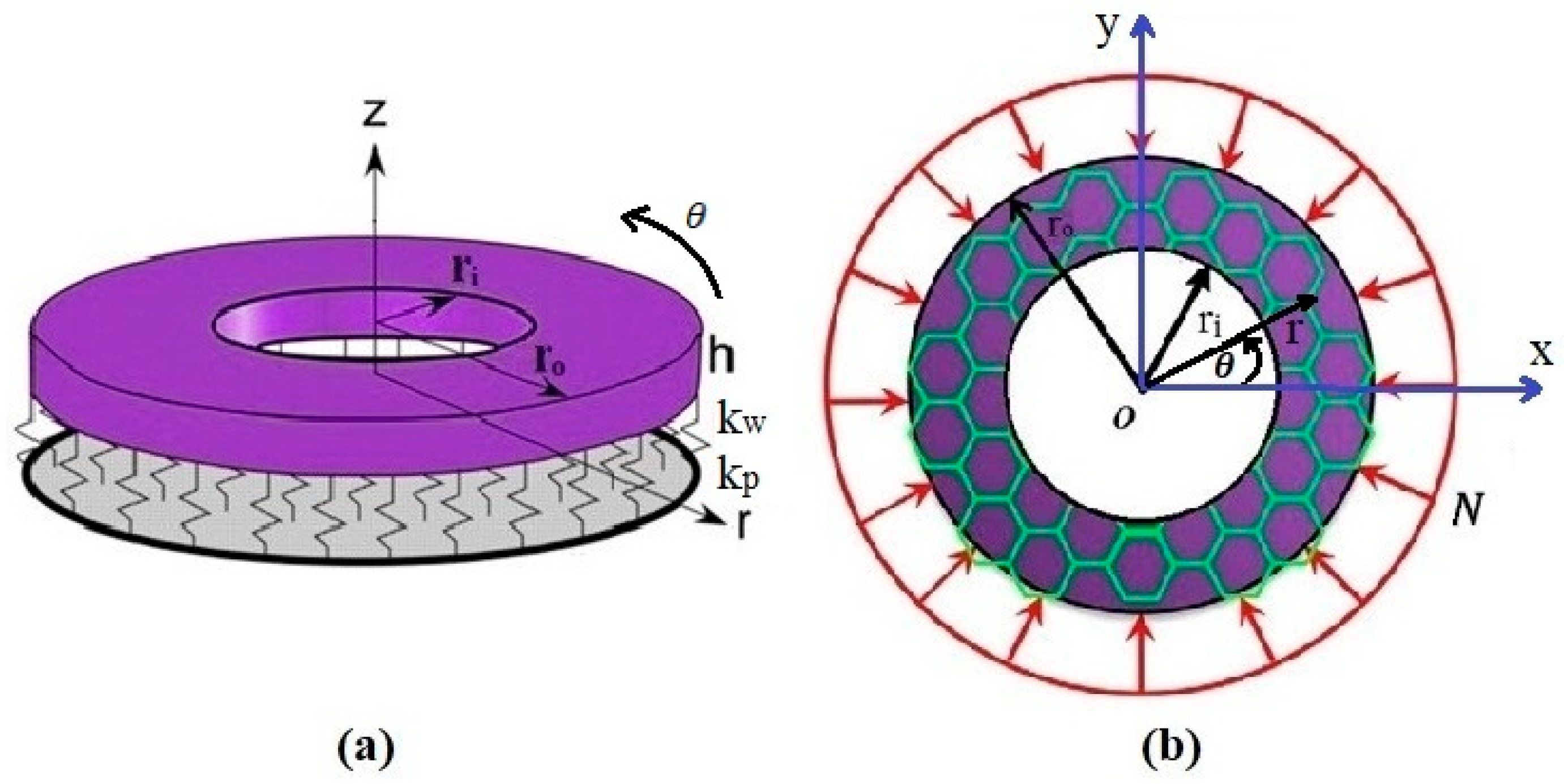
2. Theory and Formulation
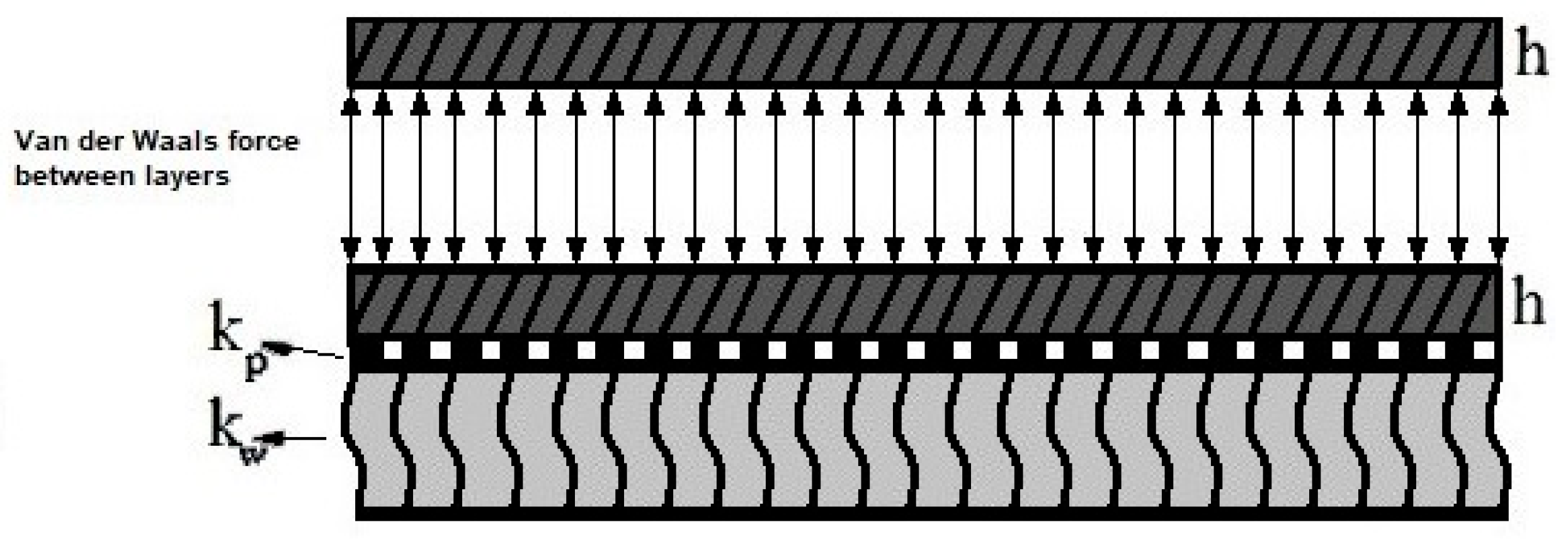
2.1. Derivation of the Governing Equations for the Bilayer Annular/Circular Nanoplate
2.2. Equations of Thermal Stability for a Bilayer Annular/Circular Plate
2.3. Boundary Conditions
2.4. Nondimensional Assumptions
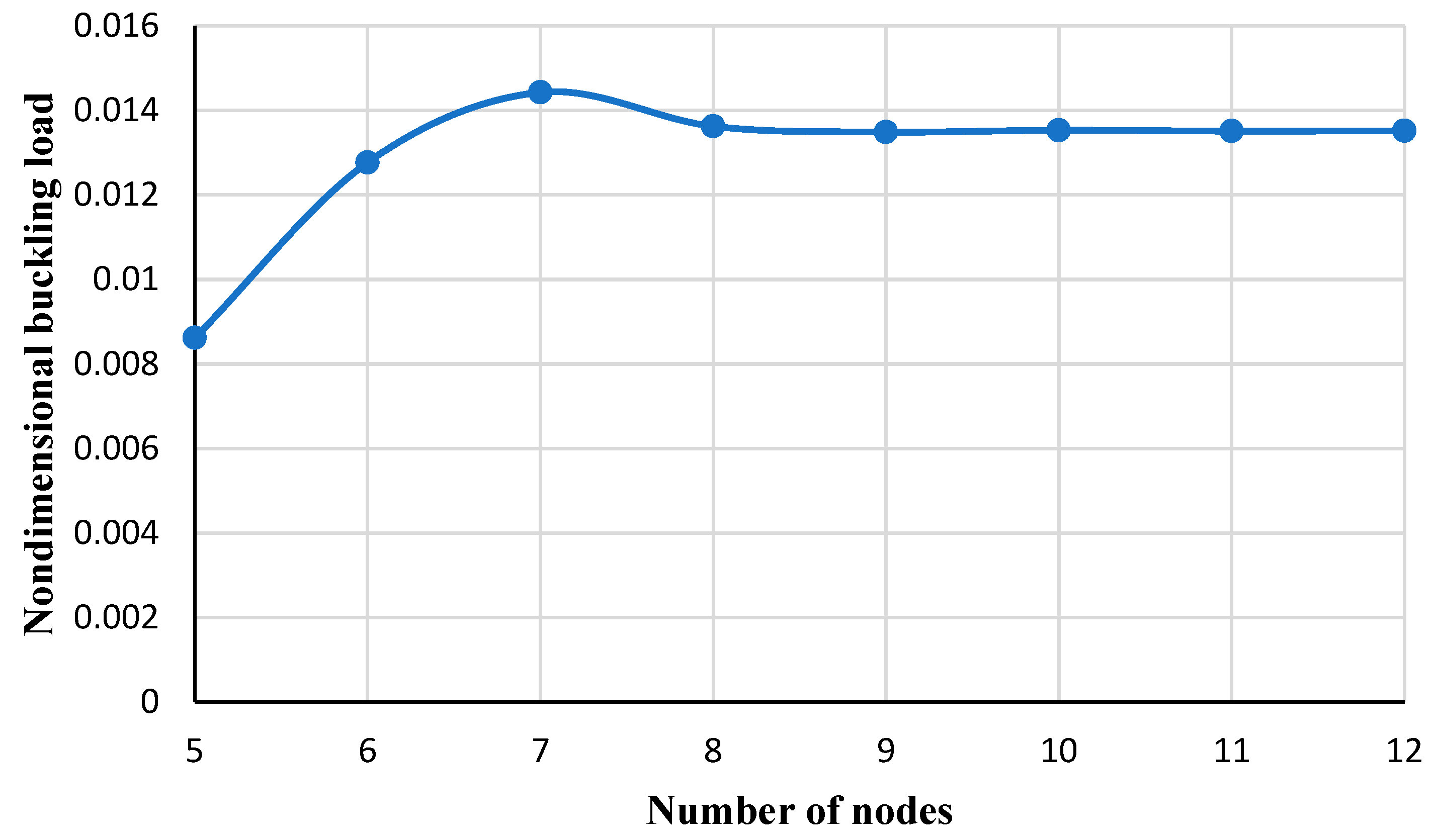
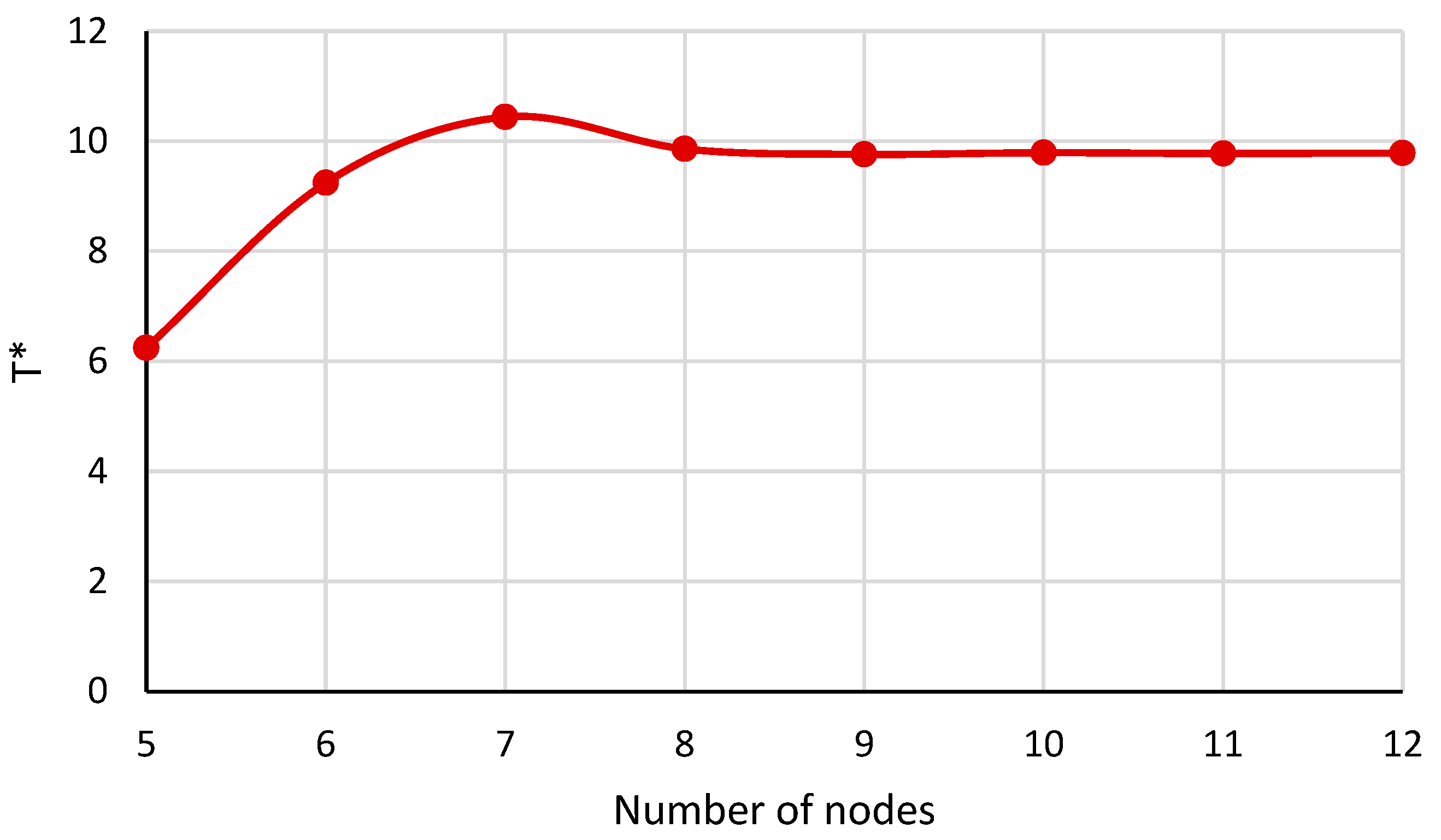
3. Numerical Procedure
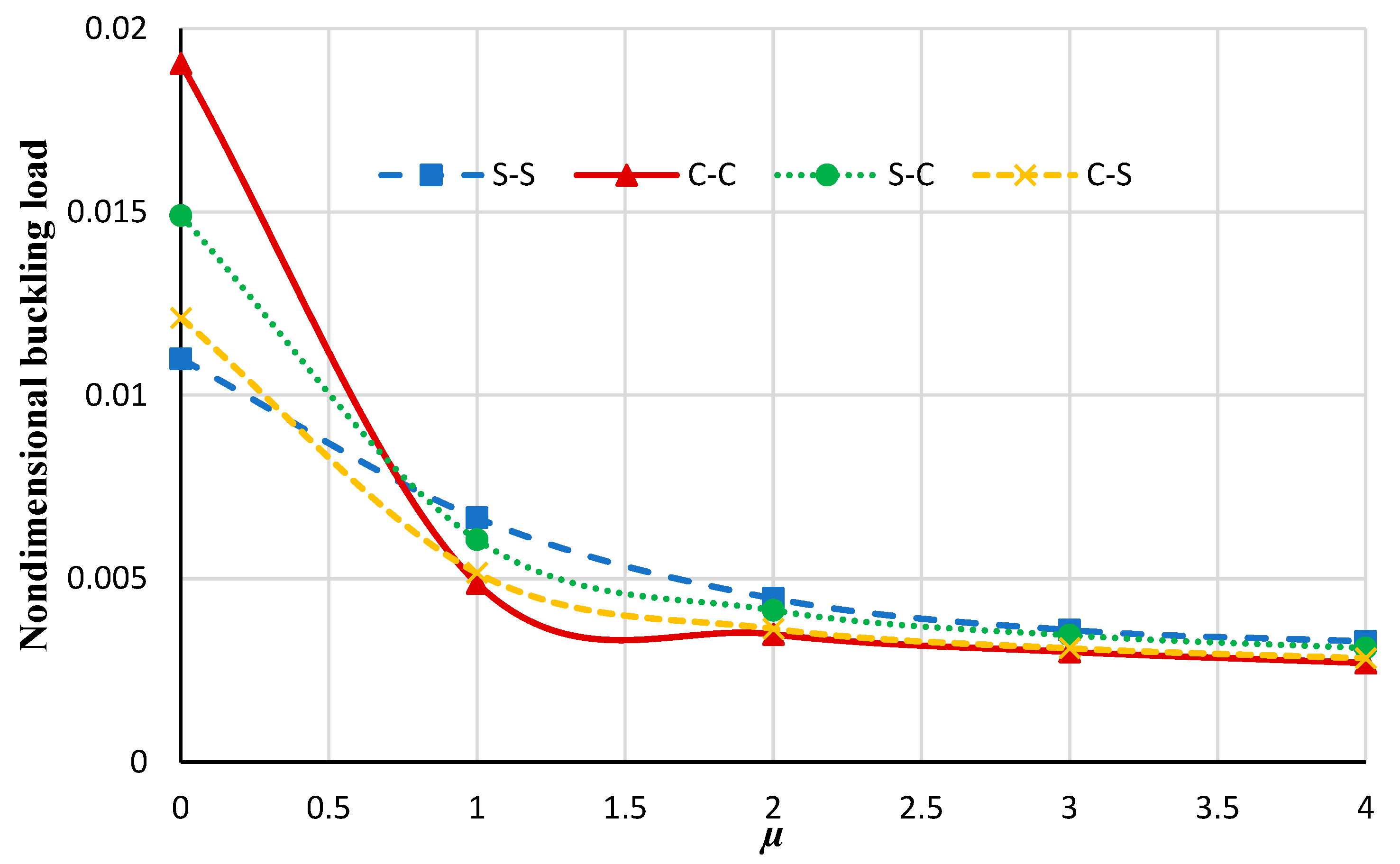
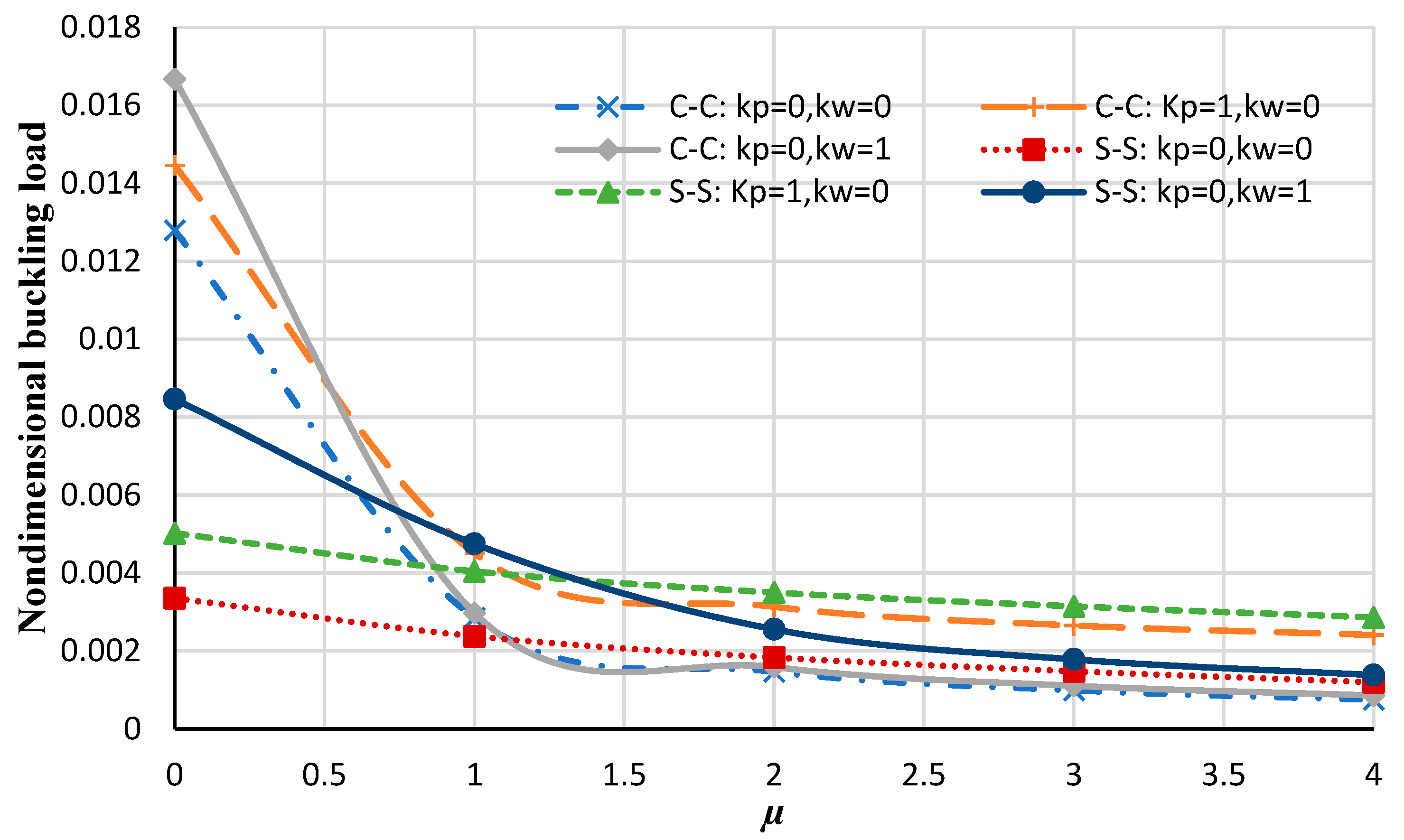
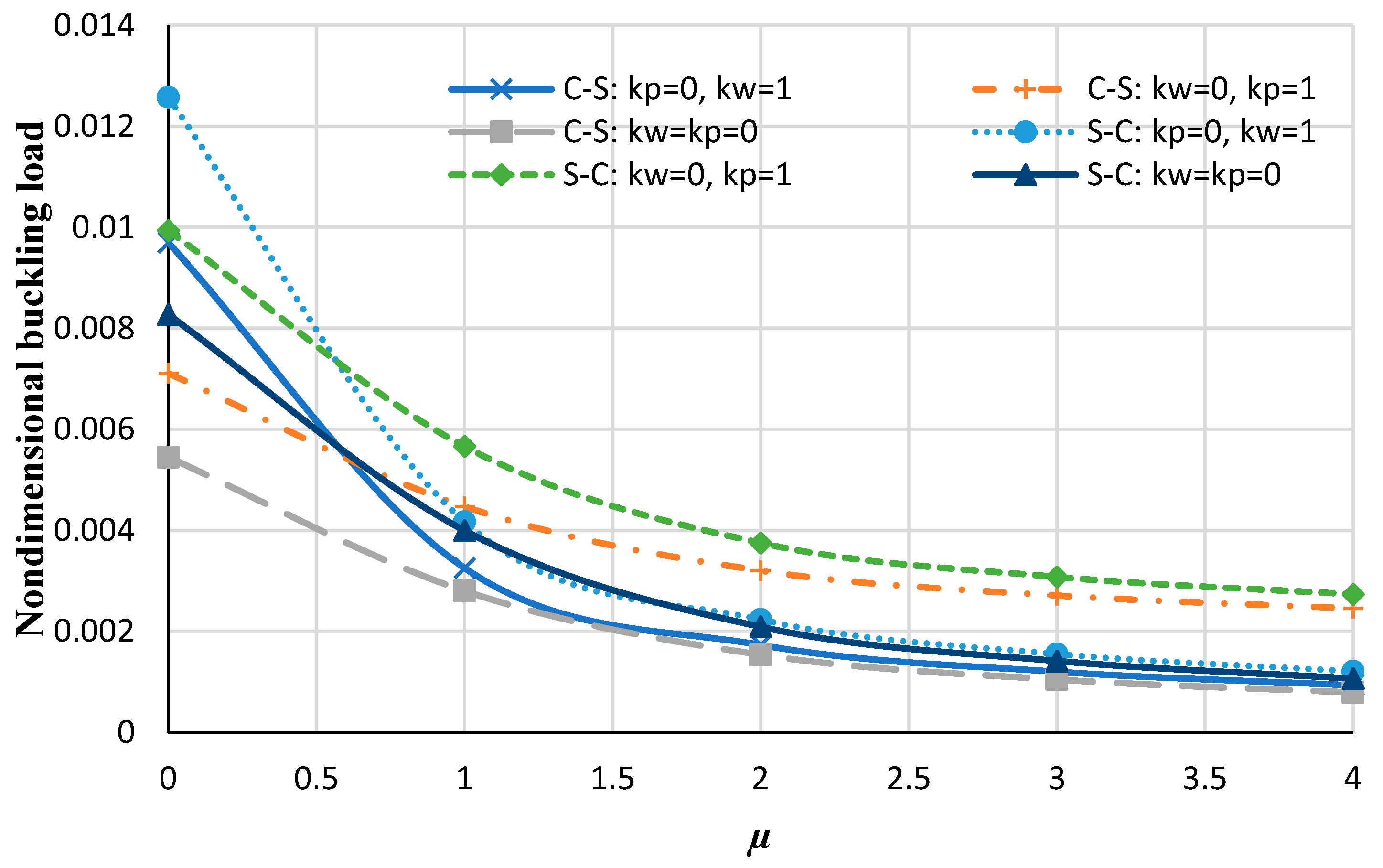
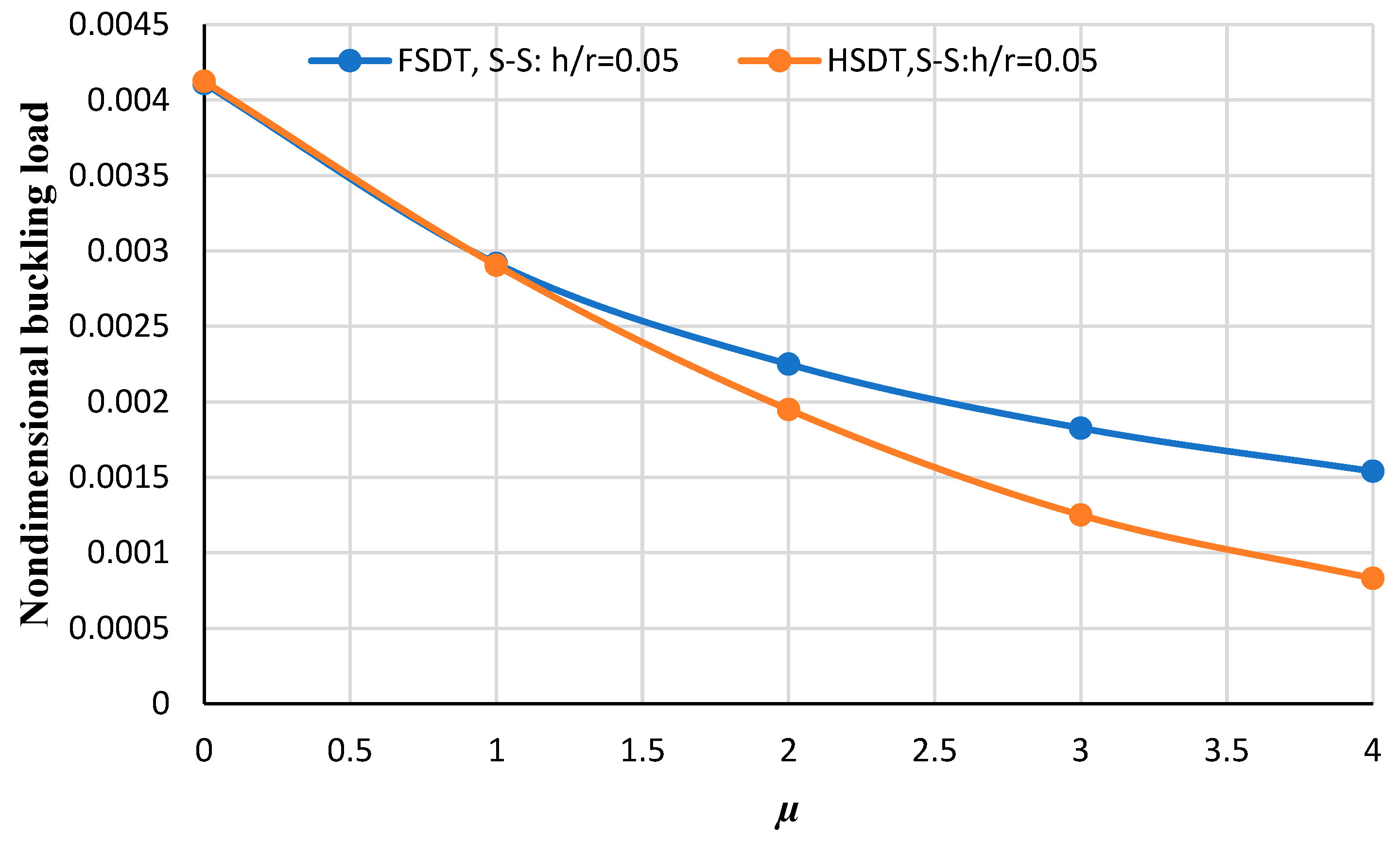
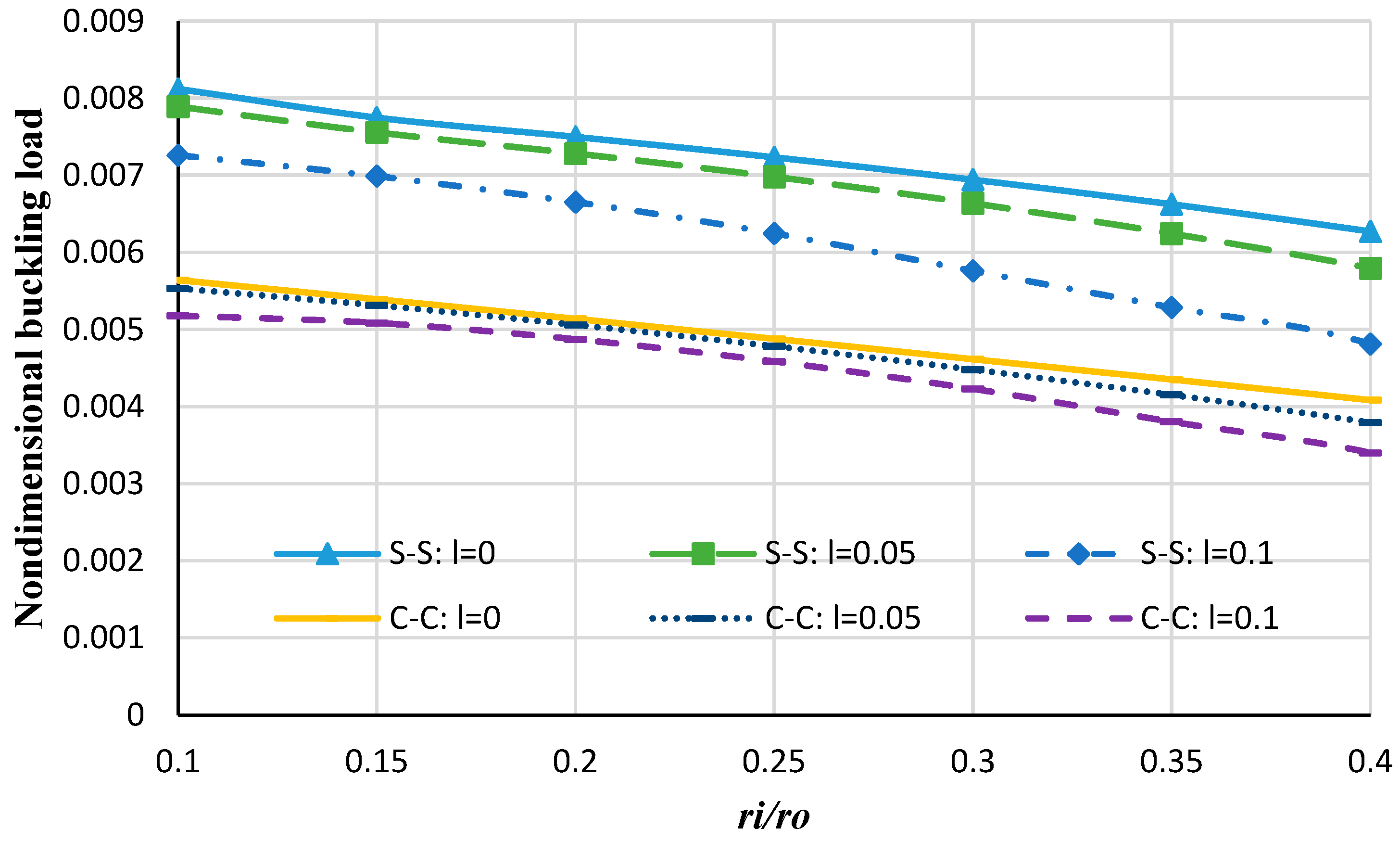
4. Results and Discussion
4.1. Thermal Analysis
4.2. Bilayer Analysis
5. Conclusions
- In the higher thickness-to-radius ratios, the difference between FSDT and HSDT increases more significantly.
- The influence of the nonlocal coefficient on the buckling analysis of circular/annular nanoplate is more significant than the types of boundary conditions or elastic foundations.
- A bilayer nanoplate cannot be considered an equivalent single-layer nanoplate (with the same thickness as the bilayer nanoplate) to obtain the results of the buckling analysis of nanoplate. Furthermore, the results obtained from the equivalent single-layer nanoplate with double thickness overestimate the real results gained using a bilayer nanoplate.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Ji, Y.; Choe, M.; Cho, B.; Song, S.; Yoon, J.; Ko, H.C.; Lee, T. Organic nonvolatile memory devices with charge trapping multilayer graphene film. Nanotechnology 2012, 23, 105202. [Google Scholar] [CrossRef]
- Bunch, J.S.; van der Zande, A.M.; Verbridge, S.S.; Frank, I.W.; Tanenbaum, D.M.; Parpia, J.M.; Craighead, H.G.; McEuen, P.L. Electromechanical Resonators from Graphene Sheets. Science 2007, 315, 490–493. [Google Scholar] [CrossRef] [PubMed]
- Sakhaee-Pour, A.; Ahmadian, M.T.; Vafai, A. Applications of single-layered graphene sheets as mass sensors and atomistic dust detectors. Solid State Commun. 2008, 145, 168–172. [Google Scholar] [CrossRef]
- Lu, G.; Ocola, L.E.; Chen, J. Reduced graphene oxide for room-temperature gas sensors. Nanotechnology 2009, 20, 445502. [Google Scholar] [CrossRef] [PubMed]
- Krishna, S.; Sreedhar, I.; Patel, C.M. Molecular dynamics simulation of polyamide-based materials—A review. Comput. Mater. Sci. 2021, 200, 110853. [Google Scholar] [CrossRef]
- Roudbari, M.A.; Jorshari, T.D.; Lü, C.; Ansari, R.; Kouzani, A.Z.; Amabili, M. A review of size-dependent continuum mechanics models for micro- and nano-structures. Thin-Walled Struct. 2022, 170, 108562. [Google Scholar] [CrossRef]
- Li, L.; Tang, H.; Hu, Y. The effect of thickness on the mechanics of nanobeams. Int. J. Eng. Sci. 2018, 123, 81–91. [Google Scholar] [CrossRef]
- Eringen, A.C. Nonlocal polar elastic continua. Int. J. Eng. Sci. 1972, 10, 1–16. [Google Scholar] [CrossRef]
- Triantafyllidis, N.; Aifantis, E.C. A gradient approach to localization of deformation. I. Hyperelastic materials. J. Elast. 1986, 16, 225–237. [Google Scholar] [CrossRef]
- Lim, C.W.; Zhang, G.; Reddy, J.N. A higher-order nonlocal elasticity and strain gradient theory and its applications in wave propagation. J. Mech. Phys. Solids 2015, 78, 298–313. [Google Scholar] [CrossRef]
- Narendar, S. Buckling analysis of micro-/nano-scale plates based on two-variable refined plate theory incorporating nonlocal scale effects. Compos. Struct. 2011, 93, 3093–3103. [Google Scholar] [CrossRef]
- Jamalpoor, A.; Ahmadi-Savadkoohi, A.; Hosseini, M.; Hosseini-Hashemi, S. Free vibration and biaxial buckling analysis of double magneto-electro-elastic nanoplate-systems coupled by a visco- Pasternak medium via nonlocal elasticity theory. Eur. J. Mech.-A/Solids 2017, 63, 84–98. [Google Scholar] [CrossRef]
- Li, L.; Hu, Y. Buckling analysis of size-dependent nonlinear beams based on a nonlocal strain gradient theory. Int. J. Eng. Sci. 2015, 97, 84–94. [Google Scholar] [CrossRef]
- Shaban, M.; Alibeigloo, A. Three dimensional vibration and bending analysis of carbon nanotubes embedded in elastic medium based on theory of elasticity. Lat. Am. J. Solids Struct. 2014, 11, 2122–2140. [Google Scholar] [CrossRef]
- Taher, H.R.D.; Omidi, M.; Zadpoor, A.A.; Nikooyan, A.A. Free vibration of circular and annular plates with variable thickness and different combinations of boundary conditions. J. Sound Vib. 2006, 296, 1084–1092. [Google Scholar] [CrossRef]
- Shaban, M.; Mazaheri, H. Size-dependent electro-static analysis of smart micro-sandwich panels with functionally graded core. Acta Mech. 2021, 232, 111–133. [Google Scholar] [CrossRef]
- Shaban, M.; Alipour, M.M. Semi-analytical solution for free vibration of thick functionally graded plates rested on elastic foundation with elastically restrained edge. Acta Mech. Solida Sin. 2011, 24, 340–354. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farajpour, A. Nonlinear mechanics of nanoscale tubes via nonlocal strain gradient theory. Int. J. Eng. Sci. 2018, 129, 84–95. [Google Scholar] [CrossRef]
- Gui, Y.; Wu, R. Buckling analysis of embedded thermo-magneto-electro-elastic nano cylindrical shell subjected to axial load with nonlocal strain gradient theory. Mech. Res. Commun. 2023, 128, 104043. [Google Scholar] [CrossRef]
- Tanzadeh, H.; Amoushahi, H. Buckling analysis of orthotropic nanoplates based on nonlocal strain gradient theory using the higher-order finite strip method (H-FSM). Eur. J. Mech.-A/Solids 2022, 95, 104622. [Google Scholar] [CrossRef]
- Cuong-Le, T.; Nguyen, K.D.; Hoang-Le, M.; Sang-To, T.; Phan-Vu, P.; Wahab, M.A. Nonlocal strain gradient IGA numerical solution for static bending, free vibration and buckling of sigmoid FG sandwich nanoplate. Phys. B Condens. Matter 2022, 631, 413726. [Google Scholar] [CrossRef]
- Wang, P.; Gao, Z.; Pan, F.; Moradi, Z.; Mahmoudi, T.; Khadimallah, M.A. A couple of GDQM and iteration techniques for the linear and nonlinear buckling of bi-directional functionally graded nanotubes based on the nonlocal strain gradient theory and high-order beam theory. Eng. Anal. Bound. Elem. 2022, 143, 124–136. [Google Scholar] [CrossRef]
- Wang, S.; Kang, W.; Yang, W.; Zhang, Z.; Li, Q.; Liu, M.; Wang, X. Hygrothermal effects on buckling behaviors of porous bi-directional functionally graded micro-/nanobeams using two-phase local/nonlocal strain gradient theory. Eur. J. Mech.-A/Solids 2022, 94, 104554. [Google Scholar] [CrossRef]
- Esen, I.; Özmen, R. Thermal vibration and buckling of magneto-electro-elastic functionally graded porous nanoplates using nonlocal strain gradient elasticity. Compos. Struct. 2022, 296, 115878. [Google Scholar] [CrossRef]
- Tang, Y.; Qing, H. Elastic buckling and free vibration analysis of functionally graded Timoshenko beam with nonlocal strain gradient integral model. Appl. Math. Model. 2021, 96, 657–677. [Google Scholar] [CrossRef]
- Al-Furjan, M.S.H.; Farrokhian, A.; Keshtegar, B.; Kolahchi, R.; Trung, N.-T. Higher order nonlocal viscoelastic strain gradient theory for dynamic buckling analysis of carbon nanocones. Aerosp. Sci. Technol. 2020, 107, 106259. [Google Scholar] [CrossRef]
- Chwał, M.; Muc, A. Buckling and Free Vibrations of Nanoplates—Comparison of Nonlocal Strain and Stress Approaches. Appl. Sci. 2019, 9, 1409. [Google Scholar] [CrossRef]
- Fan, F.; Safaei, B.; Sahmani, S. Buckling and postbuckling response of nonlocal strain gradient porous functionally graded micro/nano-plates via NURBS-based isogeometric analysis. Thin-Walled Struct. 2021, 159, 107231. [Google Scholar] [CrossRef]
- Sadeghian, M.; Palevicius, A.; Janusas, G. Nonlocal Strain Gradient Model for the Nonlinear Static Analysis of a Circular/Annular Nanoplate. Micromachines 2023, 14, 1052. [Google Scholar] [CrossRef]
- Timoshenko, S.; Woinowsky-Krieger, S. Theory of Plates and Shells; McGraw-Hill: New York, NY, USA, 1959; Volume 2. [Google Scholar]
- Zghal, S.; Trabelsi, S.; Dammak, F. Post-buckling behavior of functionally graded and carbon-nanotubes based structures with different mechanical loadings. Mech. Based Des. Struct. Mach. 2022, 50, 2997–3039. [Google Scholar] [CrossRef]
- Zghal, S.; Dammak, F. Buckling responses of porous structural components with gradient power-based and sigmoid material variations under different types of compression loads. Compos. Struct. 2021, 273, 114313. [Google Scholar] [CrossRef]
- Trabelsi, S.; Zghal, S.; Dammak, F. A Finite Element Procedure for Thermal Buckling Analysis of Functionally Graded Shell Structures. In Design and Modeling of Mechanical Systems—IV; Springer International Publishing: Cham, Switzerland, 2020; pp. 409–416. [Google Scholar]
- Mehar, K.; Kumar Panda, S.; Devarajan, Y.; Choubey, G. Numerical buckling analysis of graded CNT-reinforced composite sandwich shell structure under thermal loading. Compos. Struct. 2019, 216, 406–414. [Google Scholar] [CrossRef]
- Do, V.N.V.; Lee, C.-H. Quasi-3D higher-order shear deformation theory for thermal buckling analysis of FGM plates based on a meshless method. Aerosp. Sci. Technol. 2018, 82–83, 450–465. [Google Scholar] [CrossRef]
- Szekrényes, A. Application of differential quadrature method to delaminated first-order shear deformable composite plates. Thin-Walled Struct. 2021, 166, 108028. [Google Scholar] [CrossRef]
- Duryodhana, D.; Waddar, S.; Bonthu, D.; Pitchaimani, J.; Powar, S.; Doddamani, M. Buckling and free vibrations behaviour through differential quadrature method for foamed composites. Results Eng. 2023, 17, 100894. [Google Scholar] [CrossRef]
- Han, J.; Li, L.; Jin, G.; Ma, W.; Feng, J.; Jia, H.; Chang, D. Qualitative Identification of the Static Pull-In and Fundamental Frequency of One-Electrode MEMS Resonators. Micromachines 2018, 9, 614. [Google Scholar] [CrossRef]
- Ren, Y.; Huo, R.; Zhou, D. Thermo-mechanical buckling analysis of non-uniformly heated rectangular plates with temperature-dependent material properties. Thin-Walled Struct. 2023, 186, 110653. [Google Scholar] [CrossRef]
- Thai, H.-T.; Kim, S.-E. A simple higher-order shear deformation theory for bending and free vibration analysis of functionally graded plates. Compos. Struct. 2013, 96, 165–173. [Google Scholar] [CrossRef]
- Sreehari, V.M. A detailed comparison study of first order and higher order shear deformation theories in the analysis of laminated composite plate. IOP Conf. Ser. Mater. Sci. Eng. 2017, 225, 012018. [Google Scholar] [CrossRef]
- Ambartsumian, S. On the theory of bending plates. Q. Appl. Math. 1958, 5, 69–77. [Google Scholar]
- Reddy, J.N. A Simple Higher-Order Theory for Laminated Composite Plates; American Society of Mechanical Engineers (ASME): New York, NY, USA, 1984. [Google Scholar]
- Reissner, E. On Tranverse Bending of Plates, Including the Effect of Transverse Shear Deformation; National Academy of Sciences, Engineering and Medicine: Washington, DC, USA, 1974. [Google Scholar]
- Touratier, M. An efficient standard plate theory. Int. J. Eng. Sci. 1991, 29, 901–916. [Google Scholar] [CrossRef]
- Soldatos, K. A transverse shear deformation theory for homogeneous monoclinic plates. Acta Mech. 1992, 94, 195–220. [Google Scholar] [CrossRef]
- Aydogdu, M. A new shear deformation theory for laminated composite plates. Compos. Struct. 2009, 89, 94–101. [Google Scholar] [CrossRef]
- Mantari, J.; Oktem, A.; Soares, C.G. A new higher order shear deformation theory for sandwich and composite laminated plates. Compos. Part B Eng. 2012, 43, 1489–1499. [Google Scholar] [CrossRef]
- Li, Q.; Wu, D.; Chen, X.; Liu, L.; Yu, Y.; Gao, W. Nonlinear vibration and dynamic buckling analyses of sandwich functionally graded porous plate with graphene platelet reinforcement resting on Winkler–Pasternak elastic foundation. Int. J. Mech. Sci. 2018, 148, 596–610. [Google Scholar] [CrossRef]
- Farajpour, A.; Arab Solghar, A.; Shahidi, A. Postbuckling analysis of multi-layered graphene sheets under non-uniform biaxial compression. Phys. E Low-Dimens. Syst. Nanostructures 2013, 47, 197–206. [Google Scholar] [CrossRef]
- Pradhan, S.C.; Phadikar, J.K. Small scale effect on vibration of embedded multilayered graphene sheets based on nonlocal continuum models. Phys. Lett. A 2009, 373, 1062–1069. [Google Scholar] [CrossRef]
- Bellman, R.; Casti, J. Differential quadrature and long-term integration. J. Math. Anal. Appl. 1971, 34, 235–238. [Google Scholar] [CrossRef]
- Farajpour, A.; Mohammadi, M.; Shahidi, A.R.; Mahzoon, M. Axisymmetric buckling of the circular graphene sheets with the nonlocal continuum plate model. Phys. E Low-Dimens. Syst. Nanostructures 2011, 43, 1820–1825. [Google Scholar] [CrossRef]
- Xu, X.-J.; Wang, X.-C.; Zheng, M.-L.; Ma, Z. Bending and buckling of nonlocal strain gradient elastic beams. Compos. Struct. 2017, 160, 366–377. [Google Scholar] [CrossRef]
- Sepahi, O.; Forouzan, M.R.; Malekzadeh, P. Thermal buckling and postbuckling analysis of functionally graded annular plates with temperature-dependent material properties. Mater. Des. 2011, 32, 4030–4041. [Google Scholar] [CrossRef]






| Model | Function |
|---|---|
| Ambartsumian [42] | |
| Reddy [43] | |
| Reissner [44] | |
| Touratier [45] | |
| Soldatos [46] | |
| Aydogdu [47] | |
| Mantari [48] |
| Radius | Reference | The Percentage of the Nondimensional Buckling Loads | ||||
|---|---|---|---|---|---|---|
| μ = 0 | μ = 0.25 | μ = 1 | μ = 2.25 | μ = 4 | ||
| 4 | Ref. [53] | 0.9430 | 0.7671 | 0.4918 | 0.3077 | 0.2019 |
| Present FSDT results | 0.9353 | 0.7554 | 0.4794 | 0.3008 | 0.1943 | |
| Present HSDT results | 0.9211 | 0.7435 | 0.3433 | 0.2432 | 0.0913 | |
| 6 | Ref. [53] | 0.4191 | 0.3803 | 0.2977 | 0.2186 | 0.1593 |
| Present FSDT results | 0.4222 | 0.3822 | 0.2975 | 0.2173 | 0.1577 | |
| Present HSDT results | 0.41593 | 0.3768 | 0.2938 | 0.2107 | 0.1446 | |
| 8 | Ref. [53] | 0.2358 | 0.2230 | 0.1918 | 0.1555 | 0.1229 |
| Present FSDT results | 0.2378 | 0.2255 | 0.1933 | 0.1562 | 0.1231 | |
| Present HSDT results | 0.2352 | 0.2223 | 0.1909 | 0.1545 | 0.1218 | |
| 10 | Ref. [53] | 0.1509 | 0.1455 | 0.1316 | 0.1134 | 0.0951 |
| Present FSDT results | 0.1532 | 0.1476 | 0.1332 | 0.1145 | 0.0957 | |
| Present HSDT results | 0.1509 | 0.1455 | 0.1314 | 0.1132 | 0.0947 | |
| Condition | Function | μ = 0 | μ = 1 | μ = 2 | μ = 3 | μ = 4 |
|---|---|---|---|---|---|---|
| C | g1(z) | 0.01296 | 0.00720 | 0.00485 | 0.00400 | 0.00355 |
| g2(z) | 0.01295 | 0.00709 | 0.00480 | 0.00396 | 0.00353 | |
| g3(z) | 0.01296 | 0.00717 | 0.00484 | 0.00399 | 0.00355 | |
| g4(z) | 0.01297 | 0.00722 | 0.00486 | 0.00400 | 0.00356 | |
| g5(z) | 0.01292 | 0.00706 | 0.00478 | 0.00395 | 0.00352 | |
| S | g1(z) | 0.01096 | 0.00775 | 0.00521 | 0.00426 | 0.00377 |
| g2(z) | 0.01096 | 0.00767 | 0.00517 | 0.00423 | 0.00375 | |
| g3(z) | 0.01096 | 0.007732 | 0.00520 | 0.00426 | 0.00377 | |
| g4(z) | 0.01096 | 0.007763 | 0.00522 | 0.00427 | 0.00377 | |
| g5(z) | 0.01095 | 0.00760 | 0.00513 | 0.00421 | 0.00373 |
| Ref. [55] | Present Study (HSDT) | Present Study (FSDT) | Ref. [55] | Present Study (HSDT) | Present Study (FSDT) | Ref. [55] | Present Study (HSDT) | Present Study (FSDT) | ||
|---|---|---|---|---|---|---|---|---|---|---|
| S–S | 0.05 | 18.547 | 18.496 | 18.515 | 28.641 | 28.64 | 28.642 | 60.198 | 60.202 | 60.198 |
| 0.1 | 17.725 | 17.650 | 17.680 | 26.921 | 26.922 | 26.921 | 53.251 | 53.283 | 53.252 | |
| 0.15 | 16.510 | 16.427 | 16.468 | 24.472 | 24.482 | 24.472 | 44.663 | 44.755 | 44.663 | |
| 0.2 | 15.069 | 14.987 | 15.035 | 21.709 | 21.737 | 21.709 | 36.436 | 36.618 | 36.436 | |
| S–C | 0.05 | 40.717 | 40.687 | 40.638 | 61.167 | 61.107 | 61.166 | 122.304 | 121.893 | 122.302 |
| 0.1 | 37.445 | 37.428 | 37.386 | 53.960 | 53.889 | 53.961 | 95.933 | 95.160 | 95.934 | |
| 0.15 | 33.022 | 33.023 | 32.979 | 45.108 | 45.001 | 45.108 | 70.612 | 68.085 | 70.613 | |
| 0.2 | 28.337 | 28.340 | 28.306 | 36.689 | 35.867 | 36.689 | 51.606 | 51.539 | 51.606 | |
| C–S | 0.05 | 27.967 | 26.9487 | 27.933 | 49.956 | 48.898 | 49.956 | 109.571 | 107.756 | 109.574 |
| 0.1 | 25.911 | 24.356 | 25.948 | 44.226 | 42.689 | 44.228 | 86.188 | 83.332 | 86.189 | |
| 0.15 | 23.085 | 21.294 | 23.133 | 37.136 | 35.24 | 37.138 | 63.635 | 60.696 | 63.636 | |
| 0.2 | 20.033 | 18.184 | 20.078 | 30.349 | 28.46 | 30.350 | 46.674 | 46.299 | 46.674 | |
| S–S | 0.05 | 0.2749 | 0.1725 | 0.0034 | 0.0034 | 0.0066 | 0 |
| 0.1 | 0.4231 | 0.2538 | 0.0037 | 0 | 0.0600 | 0.0018 | |
| 0.15 | 0.5027 | 0.2543 | 0.0408 | 0 | 0.2059 | 0 | |
| 0.2 | 0.5441 | 0.2256 | 0.1289 | 0 | 0.4995 | 0 | |
| S–C | 0.05 | 0.0736 | 0.1940 | 0.0980 | 0.0016 | 0.3360 | 0.0016 |
| 0.1 | 0.0453 | 0.1575 | 0.1315 | 0.0018 | 0.8057 | 0.0010 | |
| 0.15 | 0.0030 | 0.1302 | 0.2372 | 0 | 3.5787 | 0.0014 | |
| 0.2 | 0.0105 | 0.1093 | 2.2404 | 0 | 0.1298 | 0 | |
| C–S | 0.05 | 3.6410 | 0.1215 | 2.1178 | 0 | 1.6564 | 0.0027 |
| 0.1 | 6.0013 | 0.1427 | 3.4753 | 0.0045 | 3.3136 | 0.0011 | |
| 0.15 | 7.7582 | 0.2079 | 5.1055 | 0.0053 | 4.6185 | 0.0015 | |
| 0.2 | 9.2297 | 0.2246 | 6.2242 | 0.0032 | 0.8034 | 0 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sadeghian, M.; Palevicius, A.; Janusas, G. Nonlinear Thermal/Mechanical Buckling of Orthotropic Annular/Circular Nanoplate with the Nonlocal Strain Gradient Model. Micromachines 2023, 14, 1790. https://doi.org/10.3390/mi14091790
Sadeghian M, Palevicius A, Janusas G. Nonlinear Thermal/Mechanical Buckling of Orthotropic Annular/Circular Nanoplate with the Nonlocal Strain Gradient Model. Micromachines. 2023; 14(9):1790. https://doi.org/10.3390/mi14091790
Chicago/Turabian StyleSadeghian, Mostafa, Arvydas Palevicius, and Giedrius Janusas. 2023. "Nonlinear Thermal/Mechanical Buckling of Orthotropic Annular/Circular Nanoplate with the Nonlocal Strain Gradient Model" Micromachines 14, no. 9: 1790. https://doi.org/10.3390/mi14091790







