A Multi-Electrode Pixel Structure for Quick-Response Electrowetting Displays
Abstract
:1. Introduction
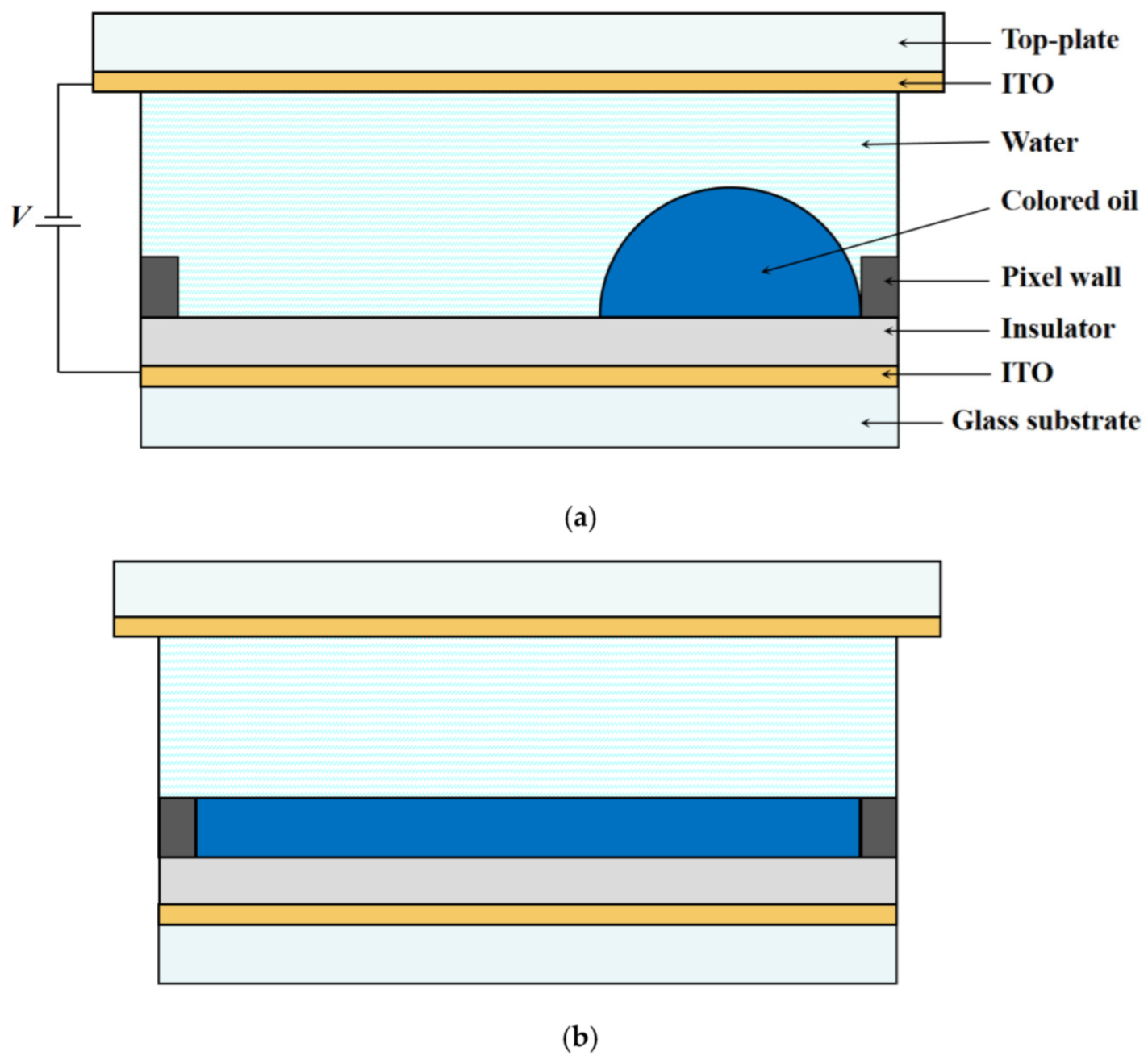
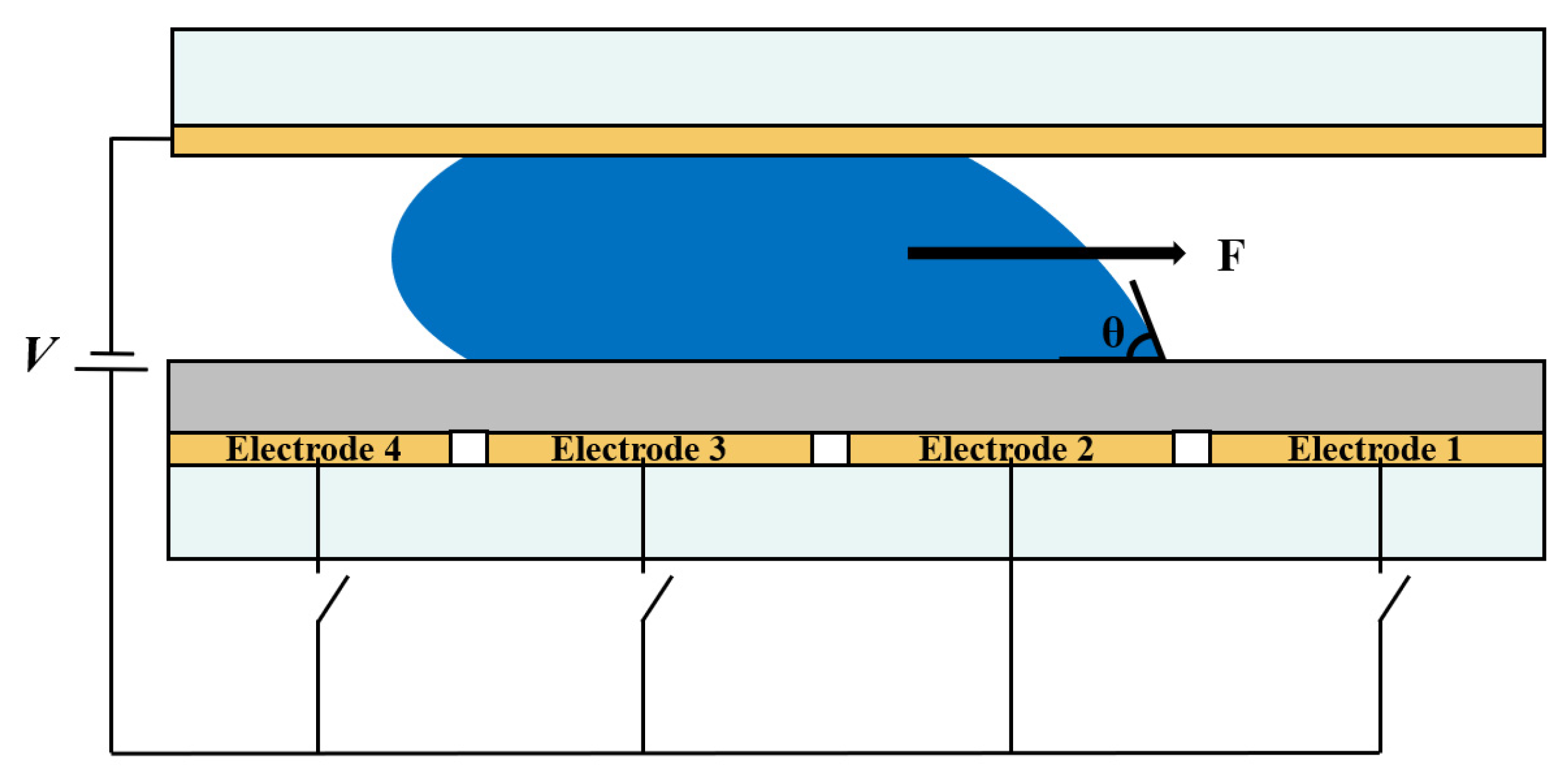
2. Principles of EWDs
3. Numeric Methodology and Modeling
3.1. Numeric Methodology
3.2. Boundary Conditions
4. Results and Discussion
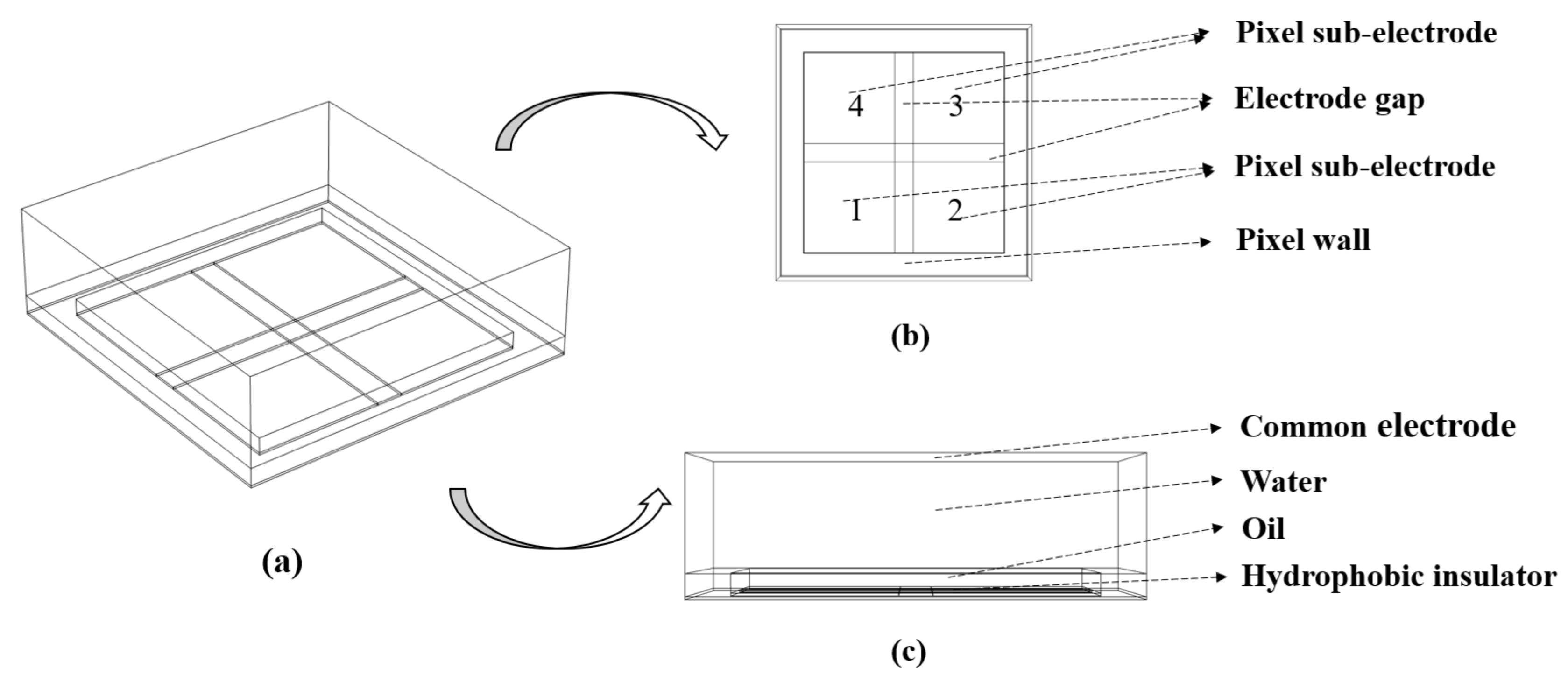
4.1. Multi Electrode Pixel Structure Model Design
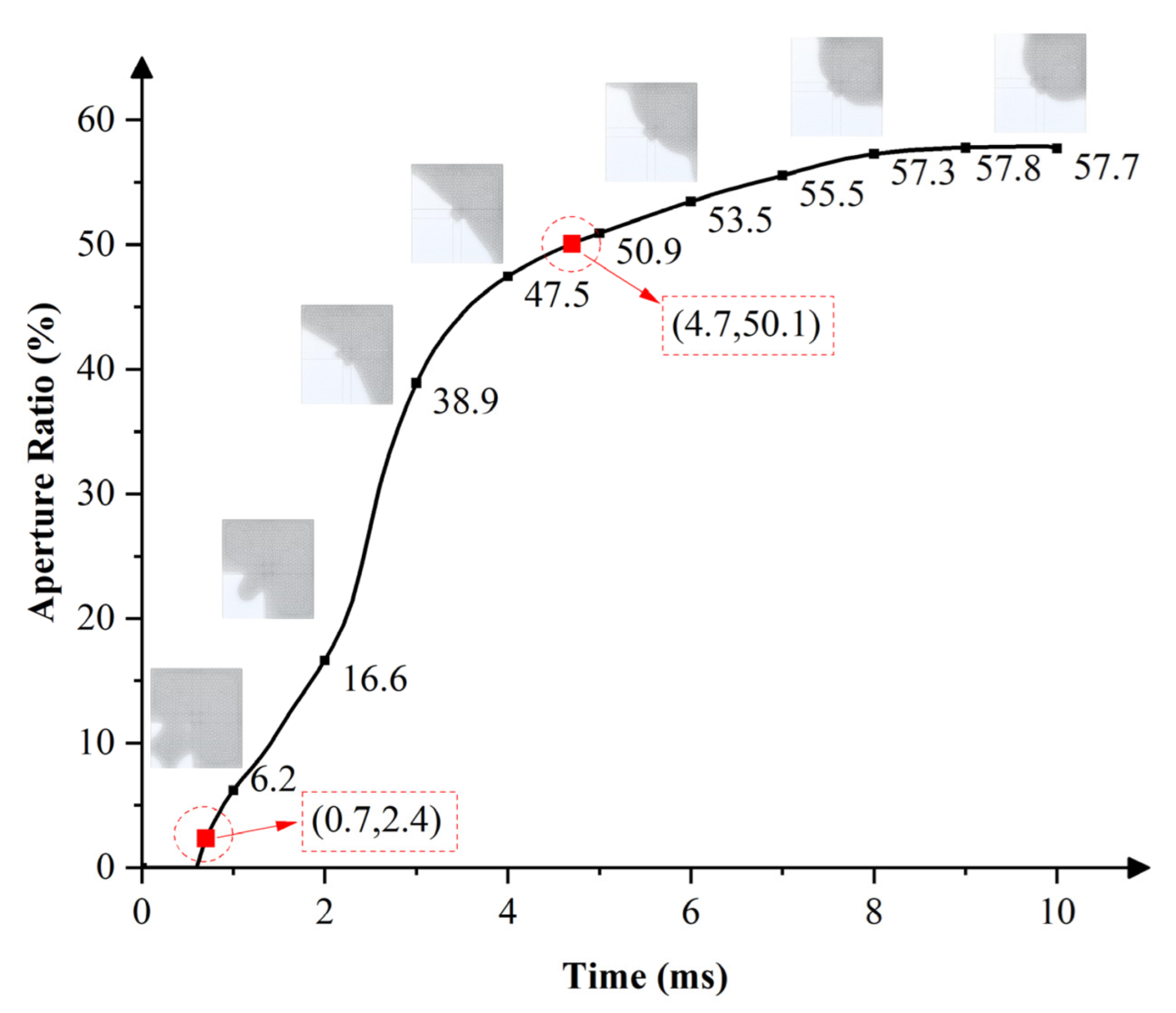
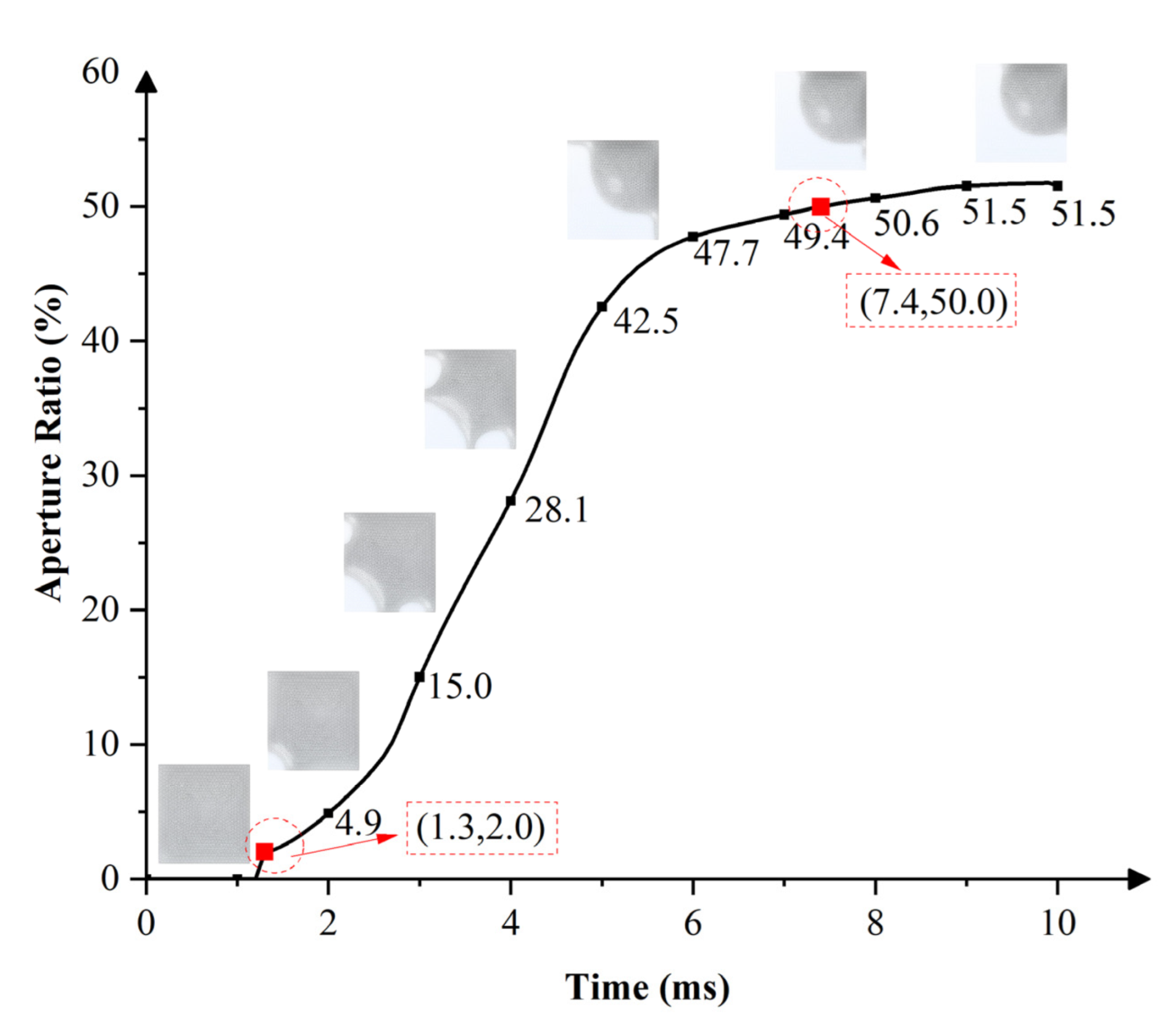
4.2. Effects of Pixel Electrode Structure on Response Speed and Aperture Ratio
4.3. Effects of Pixel Electrode Structure on Oil Acceleration Capacity
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hayes, R.A.; Feenstra, B.J. Video-speed electronic paper based on electrowetting. Nature 2003, 425, 383–385. [Google Scholar] [CrossRef]
- Bai, P.; Hayes, R.A.; Jin, M.; Shui, L.; Yi, Z.; Wang, L.; Zhang, X.; Zhou, G. Review of paper-like display technologies. Prog. Electromagn. Res. 2014, 147, 95–116. [Google Scholar] [CrossRef] [Green Version]
- Roques-Carmes, T.; Hayes, R.A.; Schlangen, L.J.M. A physical model describing the electro-optic behavior of switchable optical elements based on electrowetting. J. Appl. Phys. 2004, 96, 6267–6271. [Google Scholar] [CrossRef]
- Tian, L.; Bai, P. A Combined Pulse Driving Waveform with Rising Gradient for Improving the Aperture Ratio of Electrowetting Displays. Front. Phys. 2021, 9, 709151. [Google Scholar] [CrossRef]
- Yi, Z.; Shui, L.; Wang, L.; Jin, M.; Hayes, R.A.; Zhou, G. A novel driver for active matrix electrowetting displays. Displays 2015, 37, 86–93. [Google Scholar] [CrossRef]
- Chiu, Y.H.; Liang, C.C.; Chen, Y.C.; Lee, W.Y.; Chen, H.Y.; Wu, S.H. Accurate-gray-level and quick-response driving methods for high-performance electrowetting displays. J. Soc. Inf. Disp. 2011, 19, 741–748. [Google Scholar] [CrossRef]
- Yi, Z.; Liu, L.; Wang, L.; Li, W.; Shui, L.; Zhou, G. A Driving System for Fast and Precise Gray-Scale Response Based on Amplitude-Frequency Mixed Modulation in TFT Electrowetting Displays. Micromachines 2019, 10, 732. [Google Scholar] [CrossRef] [Green Version]
- Hsieh, W.; Lin, C.; Lo, K.; Lee, K.; Cheng, W.; Chen, K. 3D electrohydrodynamic simulation of electrowetting displays. J. Micromechanics Microengineering 2014, 24, 125024. [Google Scholar] [CrossRef]
- Zhou, M.; Zhao, Q.; Tang, B.; Groenewold, J.; Hayes, R.A.; Zhou, G. Simplified dynamical model for optical response of electrofluidic displays. Displays 2017, 49, 26–34. [Google Scholar] [CrossRef]
- Giraldo, A.; Vermeulen, P.; Figura, D.; Spreafico, M.; Meeusen, J.A.; Hampton, M.W.; Novoselov, P. Improved Oil Motion Control and Hysteresis-Free Pixel Switching of Electrowetting Displays. SID Symp. Dig. Tech. Pap. 2012, 43, 625–628. [Google Scholar] [CrossRef]
- Dou, Y.; Tang, B.; Groenewold, J.; Li, F.; Yue, Q.; Zhou, R.; Li, H.; Shui, L.; Henzen, A.; Zhou, G. Oil motion control by an extra pinning structure in electro-fluidic display. Sensors 2018, 18, 1114. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dou, Y.; Chen, L.; Li, H.; Tang, B.; Henzen, A.; Zhou, G. Photolithography Fabricated Spacer Arrays Offering Mechanical Strengthening and Oil Motion Control in Electrowetting Displays. Sensors 2020, 20, 494. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Feenstra, J. Video-Speed Electrowetting Display Technology. In Handbook of Visual Display Technology; Springer: Cham, Switzerland, 2016; pp. 1–13. [Google Scholar] [CrossRef]
- Mugele, F.; Baret, J.-C. Electrowetting: From basics to applications. J. Phys. Condens. Matter 2005, 17, 705–774. [Google Scholar] [CrossRef]
- Jin, M.; Shen, S.; Yi, Z.; Zhou, G.; Shui, L. Optofluid-Based reflective displays. Micromachines 2018, 9, 159. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Feenstra, B.J.; Hayes, R.A.; Camps, I.G.J.; Hage, L.M.; Johnson, M.T.; Roques-Carmes, T.; Schlangen, L.J.M.; Franklin, A.R.; Valdes, A.F.; Ford, R.A. A video-speed reflective display based on electrowetting: Principle and properties. J. Soc. Inf. Disp. 2004, 12, 293–299. [Google Scholar] [CrossRef]
- Kang, K.H. How electrostatic fields change contact angle in electrowetting. Langmuir 2002, 18, 10318–10322. [Google Scholar] [CrossRef]
- Brabcova, Z.; McHale, G.; Wells, G.G.; Brown, C.V.; Newton, M.I. Electric field induced reversible spreading of droplets into films on lubricant impregnated surfaces. Appl. Phys. Lett. 2017, 110, 121603. [Google Scholar] [CrossRef]
- Zeng, J.; Korsmeyer, T. Principles of droplet electro-hydrodynamics for lab-on-chip. Lab A Chip 2004, 4, 265–277. [Google Scholar] [CrossRef]
- Datta, S.; Kumar, P.; Das, A.K. Manipulation of Droplets by Electrostatic Actuation and the Related Hydrodynamics. J. Indian Inst. Sci. 2019, 99, 121–141. [Google Scholar] [CrossRef]
- Li, J.; Ha, N.S.; Liu, T.; van Dam, R.M.; Kim, C.J. Ionic-surfactant-mediated electro-dewetting for digital microfluidics. Nature 2019, 572, 507–510. [Google Scholar] [CrossRef]
- Hong, R.; Richard, B.F.; Michael, G.P.; Edward, J.S. Dynamics of electro-wetting droplet transport. Sens. Actuators B Chem. 2002, 87, 201–206. [Google Scholar] [CrossRef]
- Walker, S.W.; Shapiro, B. Modeling the fluid dynamics of electrowetting on dielectric (EWOD). J. Microelectromechanical Syst. 2006, 15, 986–1000. [Google Scholar] [CrossRef] [Green Version]
- Kim, J. Phase-Field Models for Multi-Component Fluid Flows. Commun. Comput. Phys. 2012, 12, 613–661. [Google Scholar] [CrossRef]
- Arzpeyma, A.; Bhaseen, S.; Dolatabadi, A.; Wood-Adams, P. A coupled electro-hydrodynamic numerical modeling of droplet actuation by electrowetting. Colloids Surf. A. Physicochem. Eng. Asp. 2008, 323, 28–35. [Google Scholar] [CrossRef]
- Cahn, J.W.; Hilliard, J.E. Free Energy of a Nonuniform System. I. Interfacial Free Energy. J. Chem. Phys. 1958, 28, 258–267. [Google Scholar] [CrossRef]
- Yue, P.T.; Feng, J.J.; Liu, C.; Shen, J. A diffuse-interface method for simulating two-phase flows of complex fluids. J. Fluid Mech. 2004, 515, 293–317. [Google Scholar] [CrossRef] [Green Version]
- Zhu, G.; Yao, J.; Zhang, L.; Sun, H.; Li, A.F. The investigation of dynamic contact angle using a direct numerical simulation method. Langmuir 2016, 32, 11736–11744. [Google Scholar] [CrossRef]
- Yurkiv, V.; Yarin, A.L.; Mashayek, F. Modeling of Droplet Impact onto Polarized and Nonpolarized Dielectric Surfaces. Langmuir 2018, 34, 10169–10180. [Google Scholar] [CrossRef]
- Lai, S.; Zhong, Q.; Sun, H. Driving Waveform Optimization by Simulation and Numerical Analysis for Suppressing Oil-Splitting in Electrowetting Displays. Front. Phys. 2021, 9, 720515. [Google Scholar] [CrossRef]





| Parameters | Quantity | Symbol | Value | Unit |
|---|---|---|---|---|
| Material | Density of oil | 900 | kg/m3 | |
| Density of water | 1000 | kg/m3 | ||
| Viscosity of oil | 0.004 | Pa·s | ||
| Viscosity of water | 0.001 | Pa·s | ||
| Dielectric constant of oil | 4 | 1 | ||
| Dielectric constant of water | 80 | 1 | ||
| Dielectric constant of hydrophobic dielectric layer | 1.287 | 1 | ||
| Dielectric constant of grid | 3.28 | 1 | ||
| Structure | Thickness of pixel | 50 | μm | |
| Width of pixel | 160 | μm | ||
| Thickness of grid | 8 | μm | ||
| Width of grid | 15 | μm | ||
| Thickness of hydrophobic dielectric layer | 1 | μm | ||
| Thickness of oil | 7 | μm | ||
| Interfacial | Surface tension coefficient of oil and water | 0.02 | N/m | |
| Contact angle of grid | 140 | deg | ||
| Contact angle of hydrophobic surface | 160 | deg | ||
| Contact angle of top substrate | 30 | deg |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, L.; Lai, S.; Zhang, T.; Li, W.; Tang, B.; Zhou, G. A Multi-Electrode Pixel Structure for Quick-Response Electrowetting Displays. Micromachines 2022, 13, 1103. https://doi.org/10.3390/mi13071103
Tian L, Lai S, Zhang T, Li W, Tang B, Zhou G. A Multi-Electrode Pixel Structure for Quick-Response Electrowetting Displays. Micromachines. 2022; 13(7):1103. https://doi.org/10.3390/mi13071103
Chicago/Turabian StyleTian, Lixia, Shufa Lai, Taiyuan Zhang, Wei Li, Biao Tang, and Guofu Zhou. 2022. "A Multi-Electrode Pixel Structure for Quick-Response Electrowetting Displays" Micromachines 13, no. 7: 1103. https://doi.org/10.3390/mi13071103





