Studying the Bulk and Contour Ice Nucleation of Water Droplets via Quartz Crystal Microbalances
Abstract
:1. Introduction
2. Materials and Methods
2.1. Soot Deposition
2.2. QCM Based Sensing Platform for Analyzing the Dynamics of Ice Nucleation on Super-Nonwettable Carbon Soot Coatings
2.3. Icing Assays
3. Results and Discussion
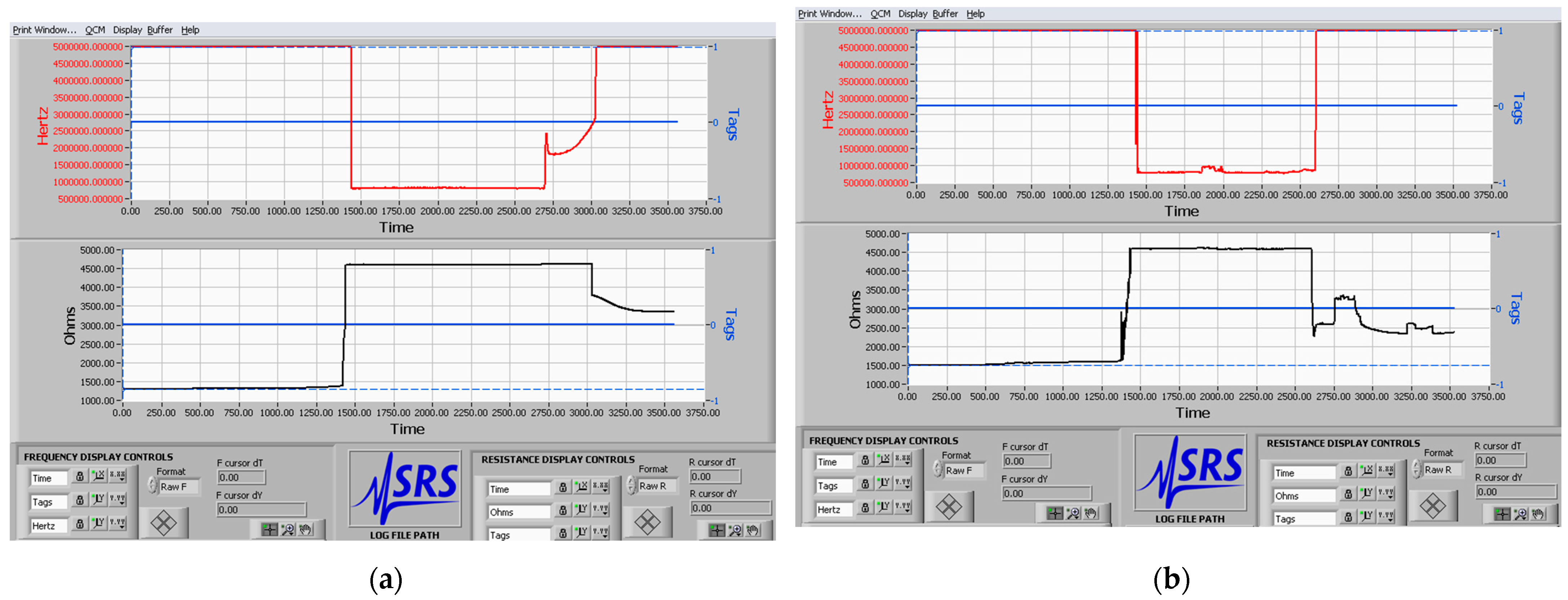
3.1. Detecting Bulk and Contour Ice Nucleation Modes through Soot Coated QCMs
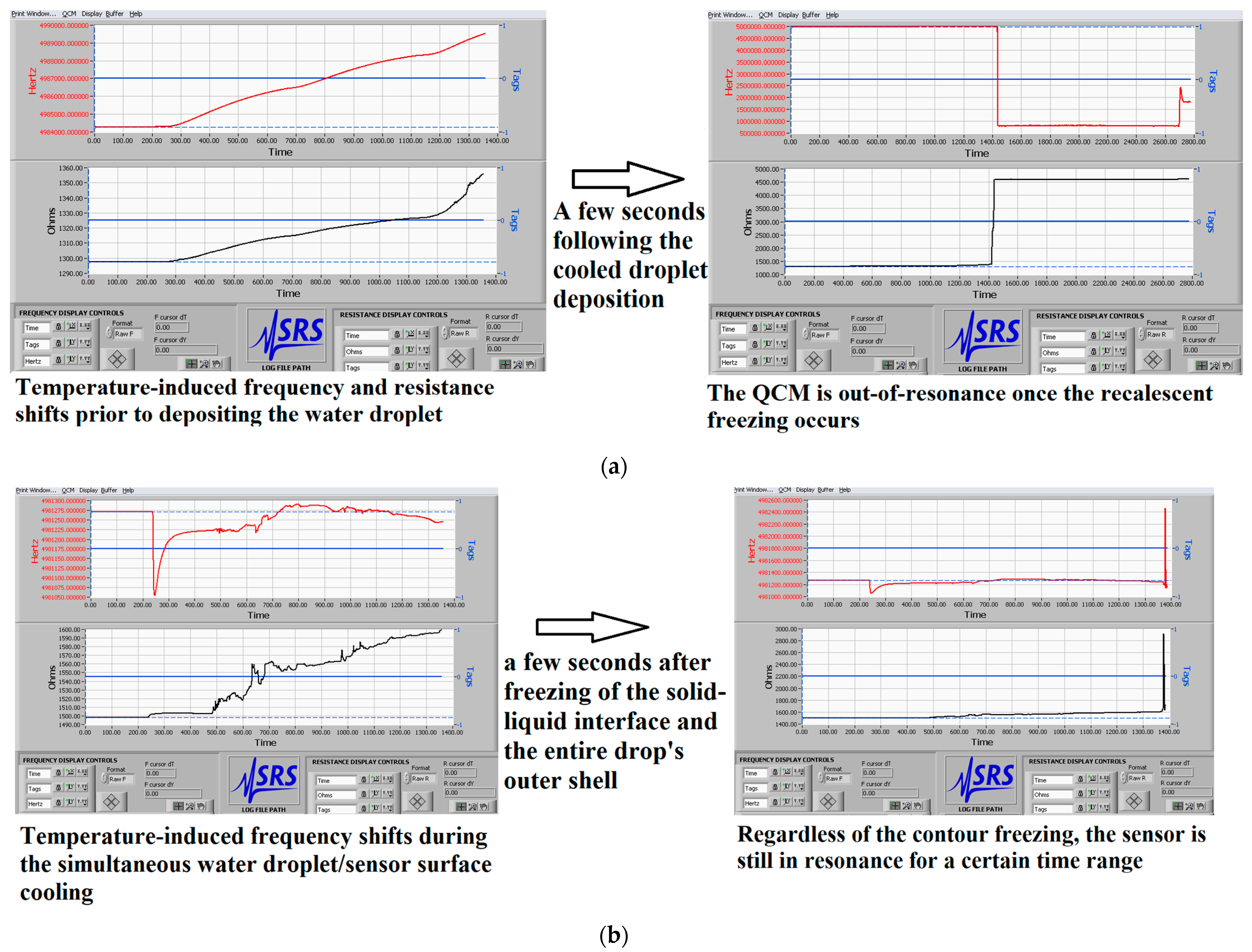
3.2. Insights into the Physical Origin of the Sensor Responses
4. Conclusions
5. Patents
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, H.; Wu, Y.; Xia, H.; Jing, B.; Zhang, Q. Review of ice-pavement adhesion study and development of hydrophobic surface in pavement deicing. J. Traffic Transp. Eng. 2018, 5, 224–238. [Google Scholar] [CrossRef]
- Cao, Y.; Tan, W.; Wu, Z. Aircraft icing: An ongoing threat to aviation safety. Aerosp. Sci. Technol. 2018, 75, 353–385. [Google Scholar] [CrossRef]
- Sullivan, C.R.; Petrenko, V.F.; McCurdy, J.D.; Kozliouk, V. Breaking the ice: De-icing power transmission lines with high-frequency, high-voltage excitation. IEEE Ind. Appl. Mag. 2003, 9, 49–54. [Google Scholar] [CrossRef]
- Parent, O.; Ilinca, A. Anti-icing and de-icing techniques for wind turbines: Critical review. Cold Reg. Sci. Technol. 2011, 65, 88–96. [Google Scholar] [CrossRef]
- Boyina, K.S.; Mahvi, A.J.; Chavan, S.; Park, D.; Kumar, K.; Lira, M.; Yu, Y.; Gunay, A.A.; Wang, X.; Miljkovic, N. Condensation frosting on meter-scale superhydrophobic and superhydrophilic heat exchangers. Int. J. Heat Mass Transf. 2019, 145, 118694. [Google Scholar] [CrossRef]
- Mulherin, N.D. Atmospheric icing and communication tower failure in the United States. Cold Reg. Sci. Technol. 1998, 27, 91–104. [Google Scholar] [CrossRef]
- Koehler, K.A.; DeMott, P.J.; Kreidenweis, S.M.; Popovicheva, O.B.; Petters, M.D.; Carrico, C.M.; Kireeva, E.D.; Khokhlova, T.D.; Shonija, N.K. Cloud condensation nuclei and ice nucleation activity of hydrophobic and hydrophilic soot particles. Phys. Chem. Chem. Phys. 2009, 11, 7906–7920. [Google Scholar] [CrossRef]
- Marcolli, C. Deposition nucleation viewed as homogeneous or immersion freezing in pores and cavities. Atmos. Chem. Phys. 2014, 14, 2071–2104. [Google Scholar] [CrossRef] [Green Version]
- Mahrt, F.; Marcolli, C.; David, R.O.; Grönquist, P.; Barthazy Meier, E.J.; Lohmann, U.; Kanji, Z.A. Ice nucleation abilities of soot particles determined with the horizontal ice nucleation chamber. Atmos. Chem. Phys. 2018, 18, 13363–13392. [Google Scholar] [CrossRef] [Green Version]
- Popovicheva, O.B.; Persiantseva, N.M.; Tishkova, V.; Shonija, N.K.A.; Zubareva, N. Quantification of water uptake by soot particles. Environ. Res. Lett. 2008, 3, 025009. [Google Scholar] [CrossRef]
- Alstadt, V.J.; Dawson, J.N.; Losey, D.J.; Sihvonen, S.K.; Freedman, M.A. Heterogeneous freezing of carbon nanotubes: A model system for pore condensation and freezing in the atmosphere. J. Phys. Chem. A 2017, 121, 8166–8175. [Google Scholar] [CrossRef]
- David, R.O.; Marcolli, C.; Fahrni, J.; Qiu, Y.; Sirkin, Y.A.P.; Molinero, V.; Mahrt, F.; Brühwiler, D.; Lohmann, U.; Kanji, Z.A. Pore condensation and freezing is responsible for ice formation below water saturation for porous particles. Proc. Natl. Acad. Sci. USA 2019, 116, 8184–8189. [Google Scholar] [CrossRef] [Green Version]
- Umo, N.S.; Wagner, R.; Ulrich, R.; Kiselev, A.; Saathoff, H.; Weidler, P.G.; Cziczo, D.J.; Leisner, T.; Möhler, O. Enhanced ice nucleation activity of coal fly ash aerosol particles initiated by ice filled pores. Atmos. Chem. Phys. 2019, 19, 8783–8800. [Google Scholar] [CrossRef] [Green Version]
- Sear, R.P. Nucleation at contact lines where fluid-fluid interfaces meet solid surfaces. J. Phys. Condens. Matter 2007, 19, 466106. [Google Scholar] [CrossRef]
- Gurganus, C.W.; Kostinski, A.B.; Shaw, R.A. High-speed imaging of freezing drops: Still no preference for the contact line. J. Phys. Chem. C 2013, 117, 6195–6200. [Google Scholar] [CrossRef]
- Gurganus, C.W.; Charnawskas, J.C.; Kostinski, A.B.; Shaw, R.A. Nucleation at the contact line observed on nanotextured surfaces. Phys. Rev. Lett. 2014, 113, 235701. [Google Scholar] [CrossRef] [Green Version]
- Ladino Moreno, L.A.; Stetzer, O.; Lohmann, U. Contact freezing: A review of experimental studies. Atmos. Chem. Phys. 2013, 13, 9745–9769. [Google Scholar] [CrossRef] [Green Version]
- Bi, Y.; Cao, B.; Li, T. Enhanced heterogeneous ice nucleation by special surface geometry. Nat. Commun. 2017, 8, 15372. [Google Scholar] [CrossRef] [Green Version]
- Graeber, G.; Schutzius, T.M.; Eghlidi, H.; Poulikakos, D. Spontaneous self-dislodging of freezing water droplets and the role of wettability. Proc. Natl. Acad. Sci. USA 2017, 114, 11040–11045. [Google Scholar] [CrossRef] [Green Version]
- Wildeman, S.; Sterl, S.; Sun, C.; Lohse, D. Fast dynamics of water droplets freezing from the outside. Phys. Rev. Lett. 2017, 118, 084101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Esmeryan, K.D.; Lazarov, Y.; Stamenov, G.S.; Chaushev, T.A. When condensed matter physics meets biology: Does superhydrophobicity benefiting the cryopreservation of human spermatozoa? Cryobiology 2020, 92, 263–266. [Google Scholar] [CrossRef]
- Sauerbrey, G. Verwendung von schwingquarzen zur wägung dünner schichten und zur mikrowägung. Eur. Phys. J. A 1959, 155, 206–222. [Google Scholar]
- Kanazawa, K.K.; Gordon, J.G. Frequency of a quartz microbalance in contact with liquid. Anal. Chem. 1985, 57, 1770–1771. [Google Scholar] [CrossRef]
- Kittle, J.; Levin, J.; Levin, N. Water content of polyelectrolyte multilayer films measured by quartz crystal microbalance and deuterium oxide exchange. Sensors 2021, 21, 771. [Google Scholar] [CrossRef] [PubMed]
- Esmeryan, K.D.; Stamenov, G.S.; Chaushev, T.A. An innovative approach for in-situ detection of postejaculatory semen coagulation and liquefaction using superhydrophobic soot coated quartz crystal microbalances. Sens. Actuators A Phys. 2019, 297, 111532. [Google Scholar] [CrossRef]
- Lin, Z.; Ward, M.D. Determination of contact angles and surface tensions with the quartz crystal microbalance. Anal. Chem. 1996, 86, 1285–1291. [Google Scholar] [CrossRef]
- Su, J.; Esmaeilzadeh, H.; Wang, P.; Ji, S.; Inalpolat, M.; Charmchi, M.; Sun, H. Effect of wetting states on frequency response of a micropillar-based quartz crystal microbalance. Sens. Actuators A Phys. 2019, 286, 115–122. [Google Scholar] [CrossRef]
- Esmeryan, K.D.; Chaushev, T.A. Complex characterization of human urine using super-nonwettable soot coated quartz crystal microbalance sensors. Sens. Actuators A Phys. 2021, 317, 112480. [Google Scholar] [CrossRef]
- Lin, N.; Meng, X.; Nie, J. Dew point calibration system using a quartz crystal sensor with a differential frequency method. Sensors 2016, 16, 1944. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, N.; Huang, Q.; Nie, J.; Meng, X.; Wang, Z.; Wu, Y.; Qi, M.; Liu, Z.; Mi, B.; Lin, L. Dew point measurements using montmorillonite (MTT) and molybdenum disulfide (MoS2) coated QCM sensors. Sens. Actuators B Chem. 2019, 279, 122–129. [Google Scholar] [CrossRef]
- Esmeryan, K.D.; Castano, C.E.; Mohammadi, R.; Lazarov, Y.; Radeva, E.I. Delayed condensation and frost formation on superhydrophobic carbon soot coatings by controlling the presence of hydrophilic active sites. J. Phys. D Appl. Phys. 2018, 51, 055302. [Google Scholar] [CrossRef]
- Lee, M.; Yim, C.; Jeon, S. Anti-icing characteristics of superhydrophobic surfaces investigated by quartz crystal microresonators. J. Chem. Phys. 2015, 142, 041102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Esmeryan, K.D.; Castano, C.E.; Bressler, A.H.; Abolghasemibizaki, M.; Mohammadi, R. Rapid synthesis of inherently robust and stable superhydrophobic carbon soot coatings. Appl. Surf. Sci. 2016, 369, 341–347. [Google Scholar] [CrossRef]
- Stanford Research Systems. Available online: https://www.thinksrs.com/products/qcm200.html (accessed on 1 April 2021).
- Esmeryan, K.D.; Gyoshev, S.D.; Castano, C.E.; Mohammadi, R. Anti-frosting and defrosting performance of chemically modified super-nonwettable carbon soot coatings. J. Phys. D Appl. Phys. 2021, 54, 015303. [Google Scholar] [CrossRef]
- Rocklein, M.N.; George, S.M. Temperature-induced apparent mass changes observed during quartz crystal microbalance measurements of atomic layer deposition. Anal. Chem. 2003, 75, 4975–4982. [Google Scholar] [CrossRef]
- Esmeryan, K.D.; Avramov, I.D.; Radeva, E.I. Temperature behavior of solid polymer film coated quartz crystal microbalance for sensor applications. Sens. Actuators B Chem. 2015, 216, 240–246. [Google Scholar] [CrossRef]
- Li, Q.; Gu, Y.; Xie, B. Hybrid temperature effect on a quartz crystal microbalance resonator in aqueous solutions. Chin. Phys. B 2017, 26, 067704. [Google Scholar] [CrossRef]
- McHale, G.; Roach, P.; Evans, C.R.; Shirtcliffe, N.J.; Elliott, S.J.; Newton, M.I. Sensor response of superhydrophobic quartz crystal resonators. In Proceedings of the IEEE International Frequency Control Symposium., Honolulu HI, USA, 19–21 May 2008; pp. 698–704. [Google Scholar]
- Martin, S.J.; Granstaff, V.E.; Frye, G.C. Characterization of a quartz crystal microbalance with simultaneous mass and liquid loading. Anal. Chem. 1991, 63, 2272–2281. [Google Scholar] [CrossRef]
- Lucklum, R.; Behling, C.; Hauptmann, P. Error analysis of material parameter determination with quartz-crystal resonators. Sens. Actuators A Phys. 1998, 66, 184–192. [Google Scholar] [CrossRef]
- Buttry, D.A.; Ward, M.D. Measurement of interfacial processes at electrode surfaces with the electrochemical quartz crystal microbalance. Chem. Rev. 1992, 92, 1355–1379. [Google Scholar] [CrossRef]
- Songkhla, S.N.; Nakamoto, T. Interpretation of quartz crystal microbalance behavior with viscous film using a mason equivalent circuit. Chemosensors 2021, 9, 9. [Google Scholar] [CrossRef]
- Alizadeh, A.; Yamada, M.; Li, R.; Shang, W.; Otta, S. Dynamics of ice nucleation on water repellent surfaces. Langmuir 2012, 28, 3180–3186. [Google Scholar] [CrossRef]
- Tourkine, P.; Merrer, M.L.; Quere, D. Delayed freezing on water repellent materials. Langmuir 2009, 25, 7214–7216. [Google Scholar] [CrossRef] [PubMed]
- Antonini, C.; Innocenti, M.; Horn, T.; Marengo, M.; Amirfazli, A. Understanding the effect of superhydrophobic coatings on energy reduction in anti-icing systems. Cold Reg. Sci. Technol. 2011, 67, 58–67. [Google Scholar] [CrossRef]
- Peng, C.; Chen, P.; You, Z.; Lv, S.; Xu, F.; Zhang, W.; Yu, J.; Zhang, H. The anti-icing and mechanical properties of a superhydrophobic coating on asphalt pavement. Constr. Build. Mater. 2018, 190, 83–94. [Google Scholar] [CrossRef]
- Ballantine, D.S., Jr.; White, R.M.; Martin, S.J.; Ricco, A.J.; Frye, G.C.; Zellers, E.T.; Wohltjen, H. Performance criteria: Stability, repeatability, reliability and reproducibility. In Acoustic Wave Sensors: Theory, Design and Physico-Chemical Applications; Academic Press: Cambridge, MA, USA, 1996; pp. 245–246. [Google Scholar]
- Parker, T.E.; Montress, G.K. Precision surface-acoustic-wave (SAW) oscillators. IEEE TUFFC 1988, 35, 342–364. [Google Scholar] [CrossRef] [PubMed]



| Freezing mode | ΔfTFC (Hz) | ΔfIF (Hz) | ΔfIT (Hz) | ΔfFT (Hz) | ΔRTFC (Ω) | ΔRIF (Ω) | ΔRIT (Ω) | ΔRFT (Ω) | ΔmTFC (μg/cm2) | ΔmIF (μg/cm2) | ΔmIT (μg/cm2) | ΔmFT (μg/cm2) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| bulk | 5587 | 3110 | 636 | 285 | 81 | 1482 | 2693 | 2039 | −99 | −55 | −11 | −5 |
| 4582 | 3180 | 4305 | 413 | −125 | 531 | 2405 | 905 | −81 | −56 | −76 | −7 | |
| 4427 | 1522 | 2627 | 294 | 3 | 1238 | 2753 | 1852 | −78 | −27 | −46 | −5 | |
| contour | −86 | 750 | 5197 | −393 | 164 | 384 | 2435 | 869 | 1.5 | −13 | −92 | 7 |
| −366 | 4644 | 4922 | −380 | 396 | 844 | 2671 | 803 | 6.5 | −82 | −87 | 7 | |
| −77 | 3235 | 5619 | −308 | 50 | 935 | 2027 | 237 | 1.4 | −57 | −99 | 5.4 |
| Freezing Mode | ΔfIF−ΔfTFC (Hz) | ΔfIT−ΔfTFC (Hz) | ΔfFT−ΔfTFC (Hz) | ΔRIF−ΔRTFC (Ω) | ΔRIT−ΔRTFC (Ω) | ΔRFT−ΔRTFC (Ω) | ΔmIF−ΔmTFC (μg/cm2) | ΔmIT−ΔmTFC (μg/cm2) | ΔmFT−ΔmTFC (μg/cm2) |
|---|---|---|---|---|---|---|---|---|---|
| bulk | −2477 | −4951 | −5302 | 1401 | 2612 | 1958 | 44 | 88 | 94 |
| −1402 | −277 | −4169 | 656 | 2530 | 1030 | 25 | 5 | 74 | |
| −2905 | −1800 | −4133 | 1235 | 2750 | 1849 | 51 | 32 | 73 | |
| contour | 836 | 5283 | −307 | 220 | 2271 | 705 | −14.5 | −93.5 | 5.5 |
| 5010 | 5288 | −14 | 448 | 2275 | 407 | −88.5 | −93.5 | 1.5 | |
| 3312 | 5696 | −231 | 885 | 1977 | 187 | −58.4 | −100.4 | 4 |
| Freezing Mode | tIF (s) | tOR (s) | tIT (s) | tFT (s) | tIT + tFT (s) |
|---|---|---|---|---|---|
| bulk | 12 | 1 | 1598 | 859 | 2457 |
| 24 | 1 | 1090 | 1217 | 2307 | |
| 7 | 2 | 978 | 935 | 1913 | |
| contour | n/a | 62 | 1167 | 1010 | 2177 |
| n/a | 102 | 1149 | 1105 | 2254 | |
| n/a | 149 | 866 | 643 | 1509 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Esmeryan, K.D.; Stoimenov, N.I. Studying the Bulk and Contour Ice Nucleation of Water Droplets via Quartz Crystal Microbalances. Micromachines 2021, 12, 463. https://doi.org/10.3390/mi12040463
Esmeryan KD, Stoimenov NI. Studying the Bulk and Contour Ice Nucleation of Water Droplets via Quartz Crystal Microbalances. Micromachines. 2021; 12(4):463. https://doi.org/10.3390/mi12040463
Chicago/Turabian StyleEsmeryan, Karekin Dikran, and Nikolay Ivanov Stoimenov. 2021. "Studying the Bulk and Contour Ice Nucleation of Water Droplets via Quartz Crystal Microbalances" Micromachines 12, no. 4: 463. https://doi.org/10.3390/mi12040463
APA StyleEsmeryan, K. D., & Stoimenov, N. I. (2021). Studying the Bulk and Contour Ice Nucleation of Water Droplets via Quartz Crystal Microbalances. Micromachines, 12(4), 463. https://doi.org/10.3390/mi12040463






