Liquid-Crystal-Filled Side-hole Fiber for High-Sensitivity Temperature and Electric Field Measurement
Abstract
:1. Introduction
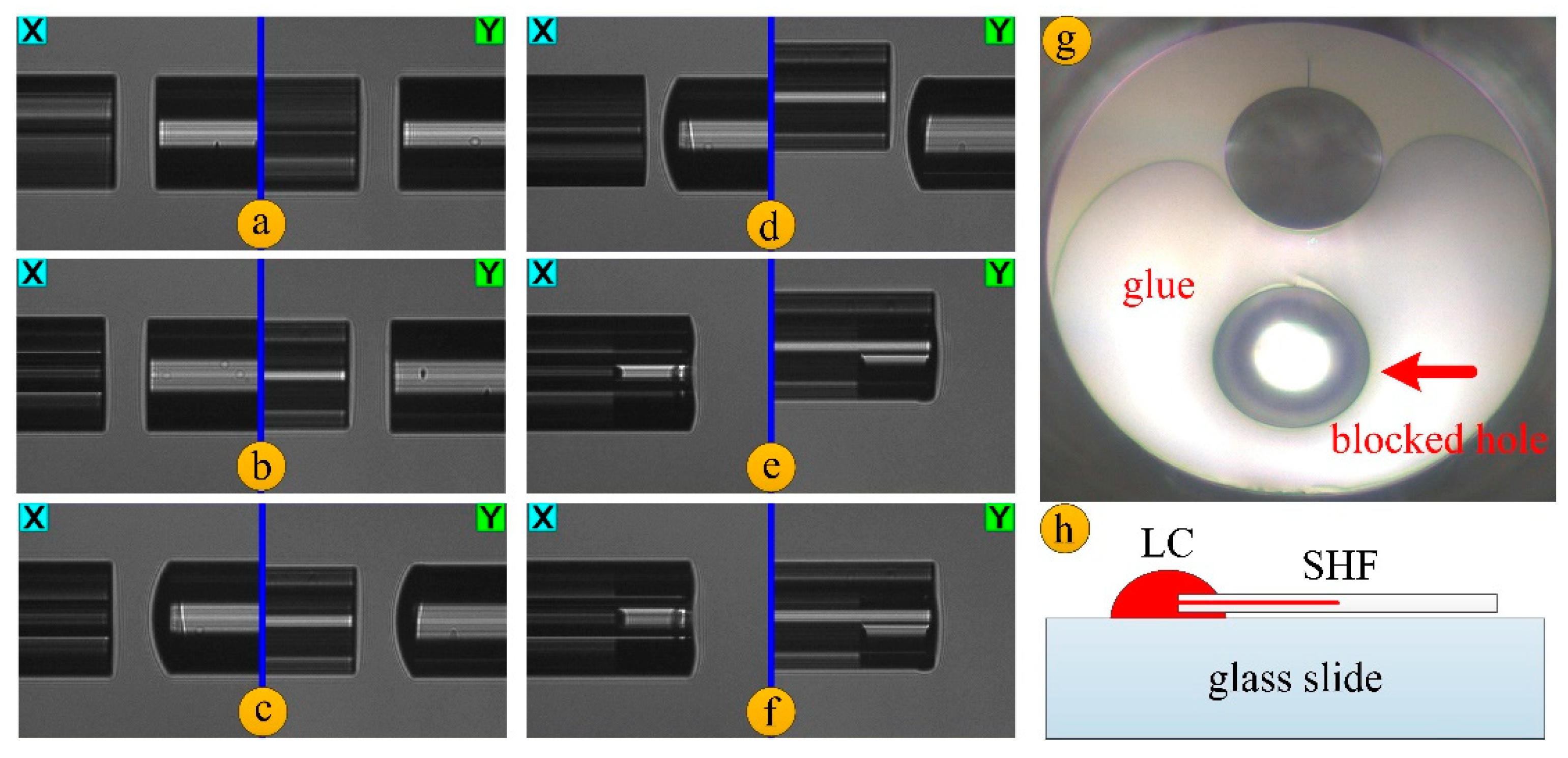
2. Sensor Fabrication and Theoretical Analysis
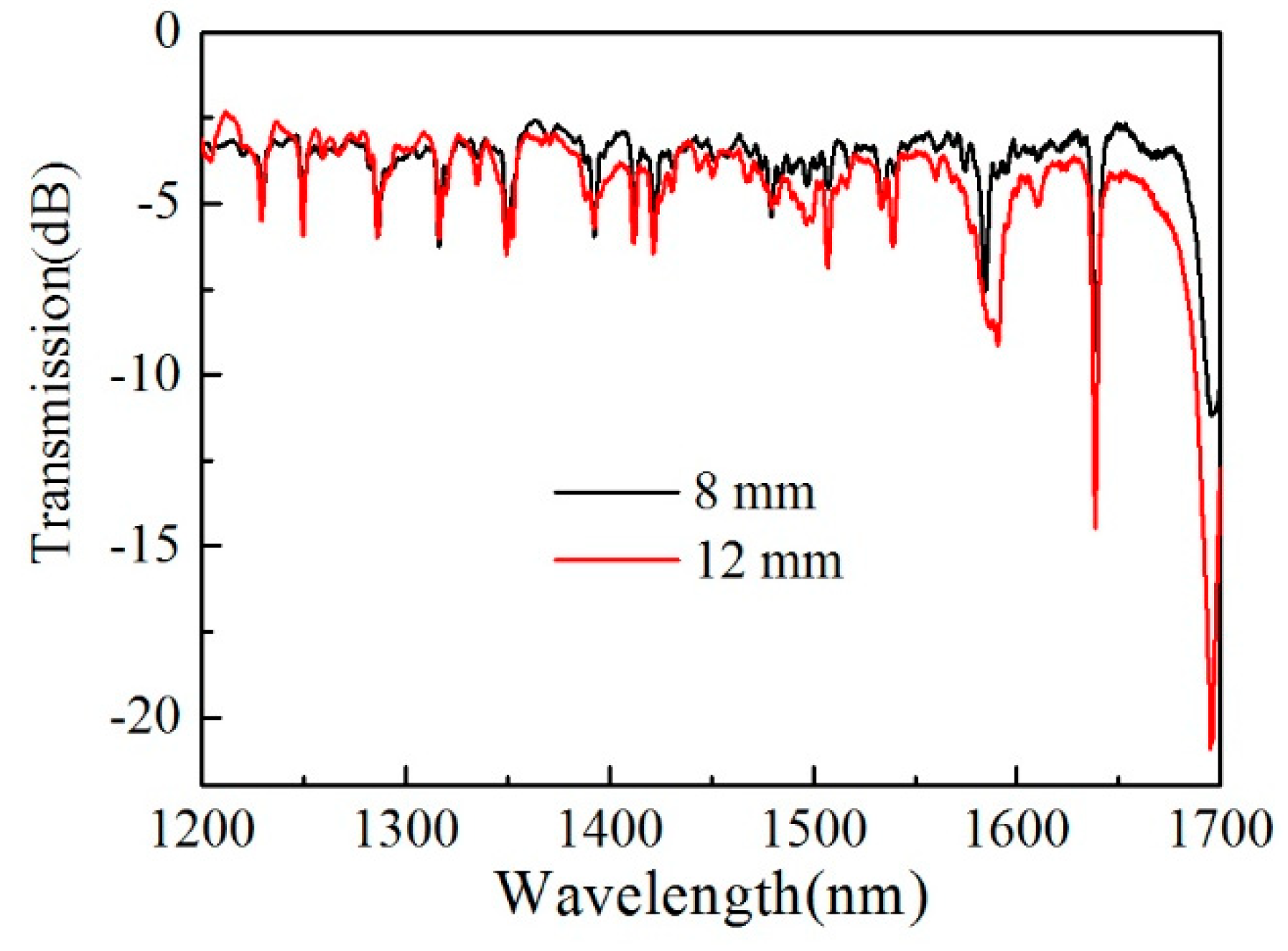
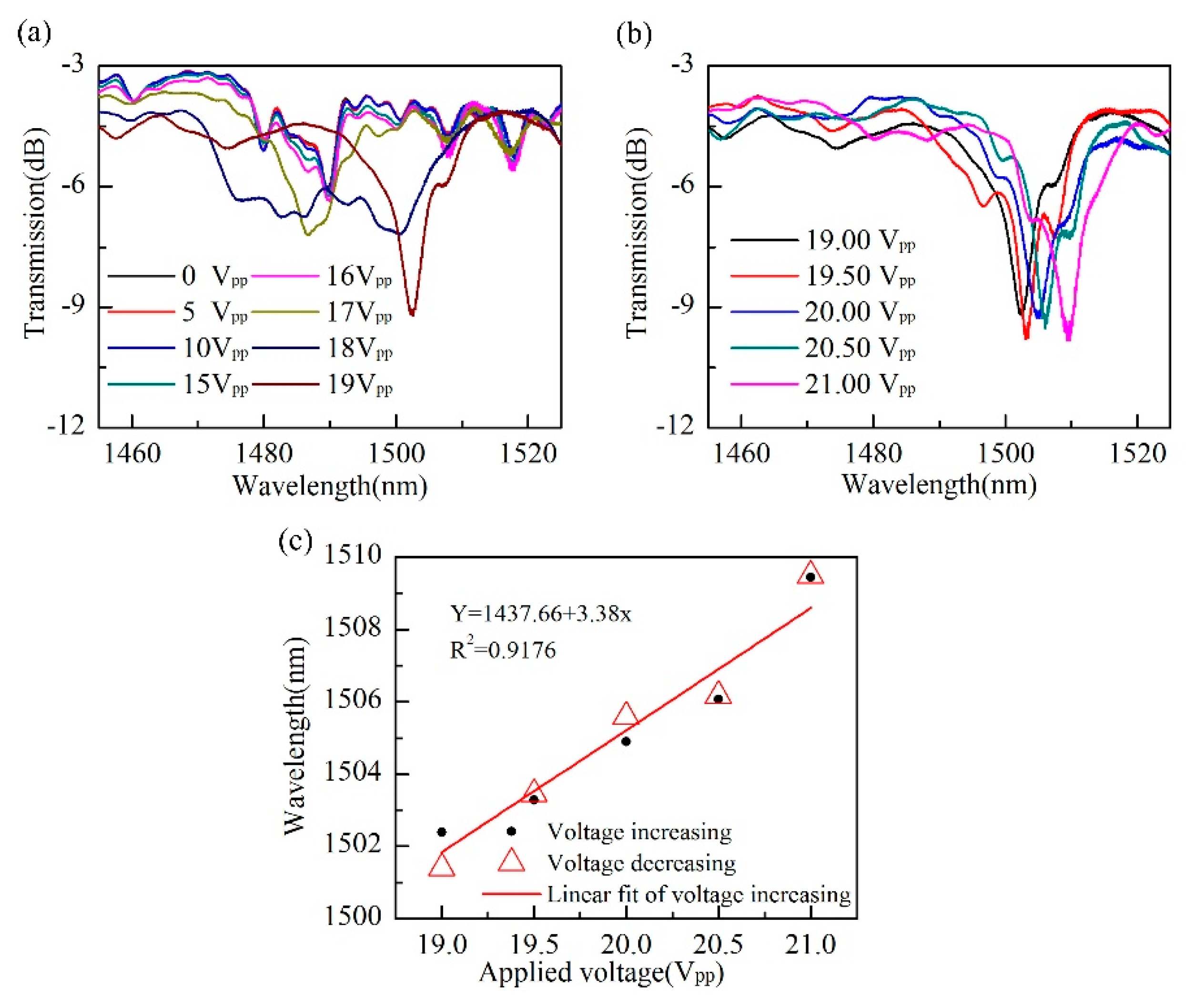
3. Sensing Experiments
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jin, Y.X.; Chan, C.C.; Zhang, Y.F.; Dong, X.Y. Mechanically induced long-period fiber grating in side-hole single-mode fiber for temperature and refractive sensing. Opt. Commun. 2010, 283, 1303–1306. [Google Scholar] [CrossRef]
- Zhang, Q.; Hu, L.; Qi, Y.; Liu, G.; Ianno, N.; Han, M. Fiber-optic refractometer based on a phase-shifted fiber bragg grating on a side-hole fiber. Opt. Express 2015, 23, 16750–16759. [Google Scholar] [CrossRef] [PubMed]
- Xin, Y.; Dong, X.; Meng, Q.; Qi, F.; Zhao, C.-L. Alcohol-filled side-hole fiber sagnac interferometer for temperature measurement. Sens. Actuators A Phys. 2013, 193, 182–185. [Google Scholar] [CrossRef]
- Wu, S.; Yan, G.; Zhou, B.; Lee, E.-H.; He, S. Open-cavity fabry-perot interferometer based on etched side-hole fiber for microfluidic sensing. IEEE Photonics Technol. Lett. 2015, 27, 1813–1816. [Google Scholar]
- Wu, S.; Yan, G.; Lian, Z.; Chen, X.; Zhou, B.; He, S. An open-cavity fabry-perot interferometer with pva coating for simultaneous measurement of relative humidity and temperature. Sens. Actuators B Chem. 2016, 225, 50–56. [Google Scholar] [CrossRef]
- Tian, Y.; Chai, Q.; Tan, T.; Mu, B.; Liu, Q.; Liu, Y.; Ren, J.; Zhang, J.; Oh, K.; Lewis, E.; et al. Directional bending sensor based on a dual side-hole fiber mach-zehnder interferometer. IEEE Photonics Technol. Lett. 2018, 30, 375–378. [Google Scholar] [CrossRef]
- Zhao, Y.J.; Zhou, A.; Guo, H.Y.; Zheng, Z.; Xu, Y.M.; Zhou, C.M.; Yuan, L.B. An integrated fiber michelson interferometer based on twin-core and side-hole fibers for multiparameter sensing. J. Lightwave Technol. 2018, 36, 993–997. [Google Scholar] [CrossRef]
- Lu, Y.Q.; Du, F.; Wu, S.T. Polarization switch using thick holographic polymer-dispersed liquid crystal grating. J. Appl. Phys. 2004, 95, 810–815. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.; Wen, C.-H.; Wu, S.-T. Polarization-independent and submillisecond response phase modulators using a 90 degrees twisted dual-frequency liquid crystal. Appl. Phys. Lett. 2006, 89, 021103. [Google Scholar] [CrossRef]
- Wang, J.; Tian, H.; Wang, Y.; Li, X.Y.; Cao, Y.J.; Li, L.; Liu, J.L.; Zhou, Z.X. Liquid crystal terahertz modulator with plasmon-induced transparency metamaterial. Opt. Express 2018, 26, 5769–5776. [Google Scholar] [CrossRef]
- Dou, H.; Chu, F.; Wang, L.; Tian, L.L.; Li, R.; Hou, W.Y.; Wang, Q.H. A polarisation-free blue phase liquid crystal lens with enhanced tunable focal length range. Liq. Cryst. 2019, 46, 963–969. [Google Scholar] [CrossRef]
- Wang, L.; Urbas, A.M.; Li, Q. Nature-inspired emerging chiral liquid crystal nanostructures: From molecular self-assembly to DNA mesophase and nanocolloids. Adv. Mater. 2018. [Google Scholar] [CrossRef] [PubMed]
- Zhai, F.; Feng, Y.; Zhou, K.; Wang, L.; Zheng, Z.; Feng, W. Graphene-based chiral liquid crystal materials for optical applications. J. Mater. Chem. C 2019, 7, 2146–2171. [Google Scholar] [CrossRef]
- Wang, L.; Li, Q. Stimuli-directing self-organized 3D liquid-crystalline nanostructures: From materials design to photonic applications. Adv. Funct. Mater. 2016, 26, 10–28. [Google Scholar] [CrossRef]
- Wang, L.; Bisoyi, H.K.; Zheng, Z.; Gutierrez-Cuevas, K.G.; Singh, G.; Kumar, S.; Bunning, T.J.; Li, Q. Stimuli-directed self-organized chiral superstructures for adaptive windows enabled by mesogen-functionalized graphene. Mater. Today 2017, 20, 230–237. [Google Scholar] [CrossRef]
- Wang, L.; Li, Q. Photochromism into nanosystems: Towards lighting up the future nanoworld. Chem. Soc. Rev. 2018, 47, 1044–1097. [Google Scholar] [CrossRef] [PubMed]
- Wang, L. Self-activating liquid crystal devices for smart laser protection. Liq. Cryst. 2016, 43, 2062–2078. [Google Scholar] [CrossRef]
- Du, J.; Liu, Y.; Wang, Z.; Zou, B.; Liu, B.; Dong, X. Electrically tunable Sagnac filter based on a photonic bandgap fiber with liquid crystal infused. Opt. Lett. 2008, 33, 2215–2217. [Google Scholar] [CrossRef]
- Chen, X.; Du, F.; Guo, T.; Lao, J.; Zhang, X.; Zhang, Z.; Liu, F.; Li, J.; Chen, C.; Guan, B.-O. Liquid crystal-embedded tilted fiber grating electric field intensity sensor. J. Lightwave Technol. 2017, 35, 3347–3353. [Google Scholar] [CrossRef]
- Du, C.; Wang, Q.; Zhao, Y. Electrically tunable long period gratings temperature sensor based on liquid crystal infiltrated photonic crystal fibers. Sens. Actuators A Phys. 2018, 278, 78–84. [Google Scholar] [CrossRef]
- Yang, C.; Zhang, H.; Liu, B.; Liu, H.; Wang, C.; Lin, S. Electrically tuned whispering gallery modes microresonator based on microstructured optical fibers infiltrated with dual-frequency liquid crystals. Nanophotonics 2018, 7, 1333–1340. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, Y.; Zhang, L.; Shao, Y.; Zhang, F.; Liao, C.; Wang, Y. Tunable electro-optical modulator based on a photonic crystal fiber selectively filled with liquid crystal. J. Lightwave Technol. 2019, 37, 1903–1908. [Google Scholar] [CrossRef]
- Wu, D.K.C.; Kuhlmey, B.T.; Eggleton, B.J. Ultrasensitive photonic crystal fiber refractive index sensor. Opt. Lett. 2009, 34, 322–324. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Wu, S.-T.; Brugioni, S.; Meucci, R.; Faetti, S. Infrared refractive indices of liquid crystals. J. Appl. Phys. 2005, 97, 073501. [Google Scholar] [CrossRef]
- Yang, C.; Zhang, H.; Liu, B.; Lin, S.; Li, Y.; Liu, H. Electrically tunable whispering gallery mode microresonator based on a grapefruit-microstructured optical fiber infiltrated with nematic liquid crystals. Opt. Lett. 2017, 42, 2988–2991. [Google Scholar] [CrossRef]
- Lee, C.-H.; Chen, C.-H.; Kao, C.-L.; Yu, C.-P.; Yeh, S.-M.; Cheng, W.-H.; Lin, T.-H. Photo and electrical tunable effects in photonic liquid crystal fiber. Opt. Express 2010, 18, 2814–2821. [Google Scholar] [CrossRef]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Wang, Y.; Mao, C.; Wang, J.; Wu, H.; Liao, C.; Wang, Y. Liquid-Crystal-Filled Side-hole Fiber for High-Sensitivity Temperature and Electric Field Measurement. Micromachines 2019, 10, 761. https://doi.org/10.3390/mi10110761
Huang Y, Wang Y, Mao C, Wang J, Wu H, Liao C, Wang Y. Liquid-Crystal-Filled Side-hole Fiber for High-Sensitivity Temperature and Electric Field Measurement. Micromachines. 2019; 10(11):761. https://doi.org/10.3390/mi10110761
Chicago/Turabian StyleHuang, Yijian, Ying Wang, Chun Mao, Jingru Wang, Han Wu, Changrui Liao, and Yiping Wang. 2019. "Liquid-Crystal-Filled Side-hole Fiber for High-Sensitivity Temperature and Electric Field Measurement" Micromachines 10, no. 11: 761. https://doi.org/10.3390/mi10110761




