1. Introduction
1.1. The Biogeography of Forest Structure in the Taiga−Tundra Ecotone
The circumpolar taiga (i.e., boreal forest)−tundra ecotone (TTE) covers more than 1.9 million km
2 across northern portions of North America and Eurasia [
1]. It features a gradient of forest structure and species’ composition whose changes may serve as a bellwether for the effects of climate change on terrestrial ecosystems globally [
2,
3,
4]. This biome boundary is among the fastest-warming regions of the planet, where predictions and observations suggest extensive yet site-dependent changes in vegetation cover, structure, and composition [
3,
5,
6,
7]. These rapid temperature changes in and near the TTE will continue to impact the distribution, structure, and function of vegetation, the storage of carbon, the region’s greenhouse gas and energy budget, hydrology, biodiversity and climate in the high northern latitudes [
8,
9,
10,
11,
12,
13,
14,
15,
16].
Scale plays a central role in understanding current TTE extent and how it may change [
7,
17,
18,
19]. Spatial scales of observation control the interpretation of the structurally heterogeneous TTE. Different scales reveal a range of vegetation characteristics and patterns. At the finest scales, the climate-limited portions of the TTE respond to changing climate through the site-specific growth and dieback of trees [
7]. These responses are controlled by a multi-scale suite of factors that, in addition to climate, include topography, edaphic conditions, disturbance history, and current tree species position and extent [
20,
21,
22,
23,
24,
25]. The geographic distribution of these factors may point to how the vulnerability of TTE structure (i.e., the likelihood of changes in spatial patterns and mosaics of trees) to changing climate is cast across the landscape, and the time lags associated with changes in structure. Monitoring the dynamics of this transition zone at multiple spatial and temporal scales is critical for understanding the likelihood of TTE structural change, the causes and consequences of these changes, and the elasticity of those changes [
17,
21,
26,
27]. At each scale of observation, the uncertainty of a mean TTE structure measurement provides the statistical basis upon which the smallest amount of change can be reliably identified. In a region where forest structure is often a critical yet subtle component of the landscape, mean measurements alone of characteristics in discontinuous forests may imply a level of certainty that does not exist at the scale of a single observation, and may result in spurious estimates of changes.
1.2. Spaceborne Mapping of the Taiga−Tundra Ecotone (TTE)
Maps derived from spaceborne data have depicted characteristics of forests in the high northern latitudes at a variety of scales. Plot-scale investigations of TTE forest structure offer detailed site assessments that provide valuable indicators of dynamics locally [
26,
28]. Some continental scale studies rely on scaling up detailed measurements by grouping them across a continuous zone using a sampling approach in place of spatially continuous measurements across the full extent of the biome boundary [
29,
30,
31]. A portion of these studies aggregate pixel measurements into zones or patches to provide mean and variance estimates [
32]. One such study used spaceborne (MODIS) 500 m pixel data to map the TTE at coarse (2.5 km
2 minimum mapping unit) resolution [
1]. This map highlights differences in the general, regional patterns of circumpolar forest structure [
33]. However, the coarse scale of this early dataset was unable to resolve the heterogeneity needed to understand the local constraints and processes governing the northern limit of this ecological transition zone, and is likely to mask near-term (decadal) changes in structure [
14].
A finer-scaled dataset of continuous canopy cover estimates is available through the University of Maryland’s Global Land Cover Facility (GLCF;
www.landcover.org). These canopy cover data, a global 30 m resolution representation of Earth’s forest cover and its change, are reported with estimates of percent tree canopy cover (TCC) [
34]. These data are based on an optimized selection that includes the full USGS collection of Landsat-5 and -7 images in epochs surrounding the nominal years of 2000, 2005, and 2010 [
35]. The GLCF Landsat TCC dataset improved upon MODIS TCC data [
36] because it increased the spatial resolution from 500 m to 30 m and reduced over-prediction of TCC in agricultural areas. However, the seminal version of the data retained the systematic under-estimation of the Hansen et al. [
36] MODIS TCC estimates at 80% cover and suffered from sparse calibration in high-latitude forests [
34].
1.3. Assessing Spaceborne Maps of Tree Cover across the TTE
Independent accuracy assessments of continuous-field (i.e., percent cover) land cover datasets have been scarce. Recent studies have shown that both Landsat- , MODIS- , and MISR-based TCC estimates suffer from confusion between dense herbaceous and discontinuous tree cover and from systematic under-estimation >80% TCC [
33,
34,
37]. The confusion between herbaceous and woody vegetation is ameliorated in the Landsat-based estimates, and a large portion of the uncertainty of Landsat TCC data is systematic and thus can be removed by linear calibration [
34]. Based on light detection and ranging (LiDAR) -derived reference measurements in temperate and tropical forests, post-calibration accuracies have been found to rival or even exceed the 13% precision achieved among multiple expert human observers visually interpreting sub-meter-resolution imagery [
33,
34].
In the current and previous versions of both the Landsat and MODIS TCC datasets, per-pixel uncertainty is quantified as root mean square error (RMSE) within the training sample. This estimate of error is overly optimistic (i.e., the errors are too small) because it only incorporates internal model precision from parameterization and ignores accuracy relative to external reference. In the past, this was necessary because no reliable, external source of reference data was available on a per-pixel basis. As such, the existing Landsat TCC uncertainty estimates may be regarded as preliminary with regard to biome-specific studies.
Now, with increasing coverage worldwide, high-resolution spaceborne imagery (HRSI) as well as LiDAR samples offer additional and often superior means of reference data collection [
38,
39,
40,
41]. Tree cover is estimated from HRSI by visual analysis [
33] or by semi-automated object-oriented methods [
1,
42,
43,
44]. From discrete, small-footprint LiDAR returns, tree cover is calculated by dividing the number of returns above a criterion height by the total number of returns within a given sample [
45,
46]. In accordance with the International Geosphere-Biosphere definition of forests, Sexton et al. specified the height criterion as 5 m, but this parameter may be tuned to biome-specific definitions of tree height [
34,
47].
In the TTE, there is a need for biome-calibrated estimates of Landsat TCC and its uncertainty because of (1) inherent generalizations in what determines tree cover; (2) the underestimation of uncertainty from global Landsat TCC data due to the lack of external reference; (3) the significance of the structure and pattern of trees in defining the TTE; (4) the importance of the TTE as general indicator of the effects of rapidly changing climate; and (5) the need for domain-wide baseline estimates from which change can be monitored.
In this study, we calibrate Landsat TCC estimates across the circumpolar TTE and boreal forest and validate, with external forest structure reference, the calibrated estimates to improve the average per-pixel TCC uncertainty in these forests. We (1) examine the characteristics of the Landsat-based estimates in the circumpolar domain with reference structure estimates; (2) calibrate three Landsat epochs’ TCC estimates to better represent TTE and boreal forest cover by applying a model relating TCC to reference airborne LiDAR canopy cover estimates; and (3) validate the calibrated Landsat TCC estimates from each epoch by updating error estimates that are tuned to the characteristic discontinuous tree cover across the northern boreal forest and TTE.
2. Materials and Methods
2.1. Reference Estimates of Tree Canopy Cover
Two groups of reference estimates of TCC were available for this study. Each group of reference data, collected independently of the other, provided boreal and TTE forest structure reference for previous studies. These reference data serve two distinct purposes. The first group, 425 locations across the entire TTE domain, provides a means to examine the circumpolar consistency of Landsat TCC estimates. The second group, LiDAR-derived estimates of TCC in North America, provides a database of 553,640 samples of tree canopy cover in North America used to calibrate and validate circumpolar Landsat TCC.
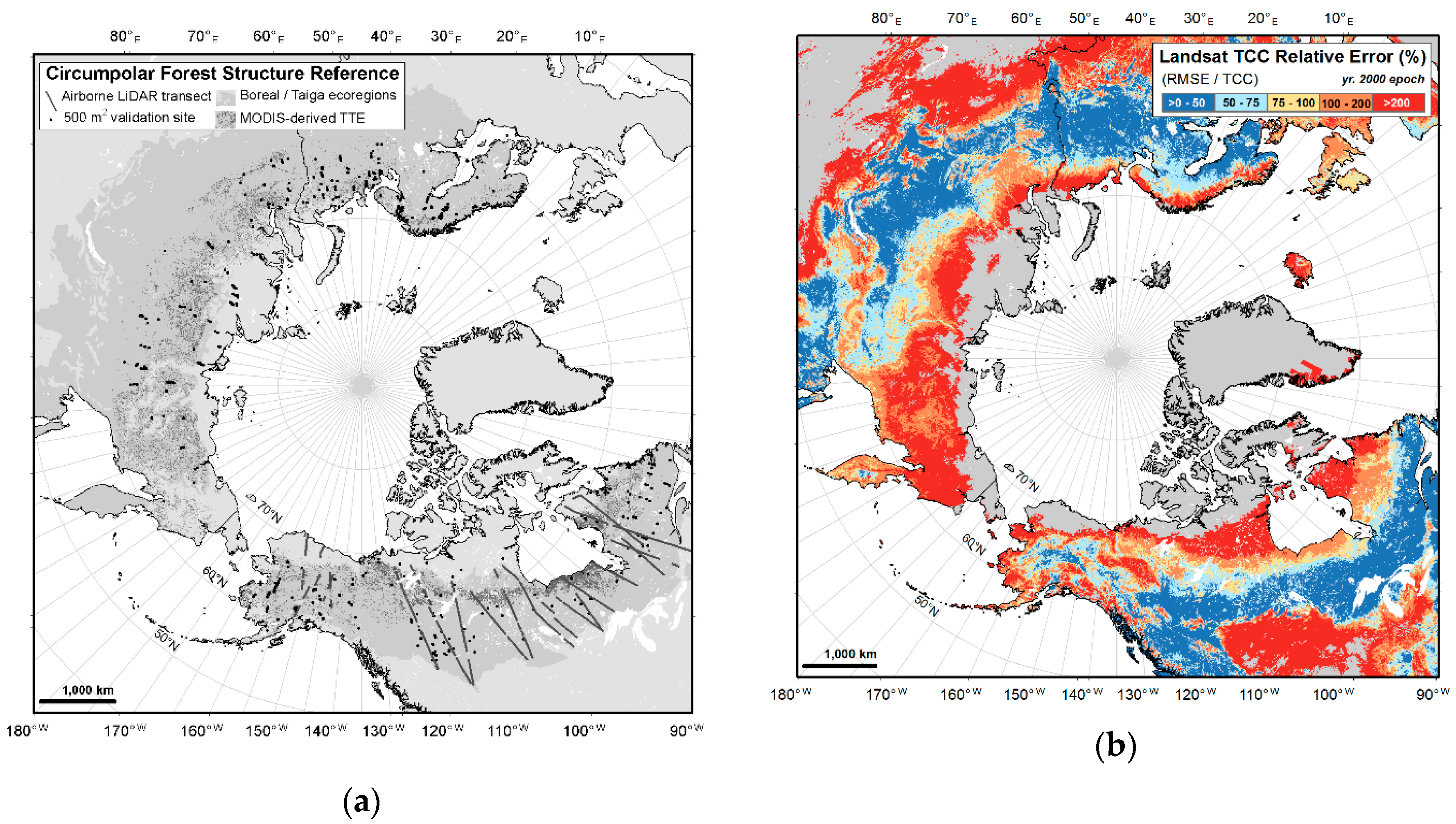
Figure 1a maps both groups of reference estimates with other circumpolar boreal forest structure reference data.
Figure 1b depicts the original pixel-level uncertainty estimates, i.e., Landsat TCC relative error (RMSE/TCC). Although preliminary, these estimates, from Sexton et al. [
34], helped demonstrate the extent to which these reference data sampled the range of boreal and TTE tree canopy cover uncertainty.
2.1.1. High-Resolution Satellite Imagery (HRSI)-Derived Tree Canopy Cover Estimates for the Circumpolar Domain
We used an existing database of 425 sites across the circumpolar domain to provide estimates of reference TCC across all broad-scale regional zones of the boreal forest and TTE. These estimates, available across North America and Eurasia, were made from visual interpretation of the presence or absence of individual tree crown from pan-sharpened color-infrared high-resolution satellite (Quickbird) imagery (HRSI; ~0.6 m/pixel) available in Google Earth (c. 2008). They were made as part of an effort to validate MODIS TCC estimates, and provide a mean tree canopy cover estimate for sites whose extents were nominally 500 m
2, and correspond to a MODIS TCC pixel’s geographic extent [
33]. These HRSI-derived estimates of TCC ranged from 0% to 100% and were collected from cloud-free, primarily growing season imagery acquired from 2001 to 2008. Each HRSI-derived estimate was compared with the mean Landsat TCC value for the set of pixels intersecting each site’s extent. For the preliminary analysis, we divided these sites longitudinally into six coarse circumpolar zones to examine the extent to which comparisons of Landsat TCC and reference TCC varied according to geographic region.
2.1.2. Light Detection and Ranging (LiDAR)-Derived Tree Canopy Cover Estimates for North America
Estimates of forest structure were calculated from individual LiDAR returns from the Portable Airborne Laser System (PALS) [
48]. These samples across boreal and TTE forests were derived from an existing database of 553,640 estimates of forest structure compiled at 30 m intervals along transects traversing a latitudinal gradient in Alaska and Canada. The PALS system records the LiDAR range/amplitude data stream interleaved with location information from GPS. The system’s LiDAR ranging has been used to estimate forest height and canopy cover along the ICESat satellite’s Geoscience Laser Altimeter System orbital transects thousands of km in length throughout North America in a variety of studies [
29,
31].
The nominal flight profile for the Alaska and Canada PALS collection required the pilots to fly ~150 m–200 m above ground at a speed of approximately 50 m·s
−1. Data were collected in the summer of 2005 in Quebec, the summer of 2008 in Alaska, and the summer of 2009 in Ontario and western Canada (Northwest Territories and Saskatchewan). These data were typically acquired at 333 Hz, yielding an effective along-track post spacing of individual LiDAR pulses of 15 cm. The size of the LiDAR pulse at target was ~45 cm, resulting in a planned oversampling along track. Post-flight processing was done to identify ground returns with a spline fit to the ground points to define a ground line, after which canopy height was calculated for every LiDAR pulse. The horizontal location (XY) uncertainty of the individual returns ranges from 5 to 20 m [
45,
48].
Individual LiDAR pulses were aggregated for 30 m segments along each transect. At each 30 m segment, a segment-level canopy height and canopy cover calculation was made. Canopy height (
htc) for each segment was calculated as the average height of canopy returns above a given height threshold for canopy. These canopy returns above a given threshold were also used to calculate canopy cover:
where
TCCthresh,seg refers to percent canopy cover for a given 30 m segment as determined by the number of returns above a given height threshold within that segment (#
returnsthresh,seg) divided by the segment’s total number of returns (#
returnstotal,seg). For each 30 m segment, the mid-point summarized the
TCCthresh,seg estimate along its portion of the LiDAR transect. For this study, two height thresholds (2 m and 5 m above the ground line) were used, providing two estimates of
TCCthresh,seg and
htc for each 30 m interval. These reference canopy cover estimates are determined by the height of the individual LiDAR returns used to compile the 30 m segment estimates. These individual returns have a vertical uncertainty estimated to be ±0.55 m that is likely driven by the XY location uncertainty [
48]. The aggregation of individual returns to 30 m segments likely reduces both the vertical uncertainty and that of the canopy cover estimate.
2.2. Calibrating and Validating Landsat Tree Canopy Cover
The samples of Landsat TCC estimates and their errors covered the domain of boreal forest structure and TTE tree cover. They provided the basis for a pixel-level calibration across the full range of Landsat TCC estimates and the validation of the final calibrated per-pixel Landsat TCC estimates. Specifically, the calibration of Landsat TCC estimates refers to modeling a linear relationship of sampled Landsat TCC estimates with corresponding LiDAR-derived reference estimates within a model training set, and applying the inverted linear model across all original Landsat TCC estimates. A validation on a model testing set of reference data identifies the uncertainty of the calibrated per-pixel results relative to the reference estimates.
2.2.1. Pre-Calibration Sampling of Tree Canopy Cover Estimates and Their Errors
To produce a calibration model appropriate for the entire circumpolar TCC domain, our reference LiDAR estimates were compiled from samples from dense boreal forest south of the TTE up through tundra-dominated regions where no trees were present. These samples traversed the range of estimated, pre-calibration Landsat TCC per-pixel uncertainty from >0%–50% to >200% TCC pixel-level relative error, where relative error was defined as the modeled pixel-level TCC error from Sexton et al. [
34] divided by the TCC estimate. For each reference sample, the corresponding Landsat TCC estimate and error values were linked based on spatial location. All samples with a Landsat TCC flagged as “water” were removed, and 50% of the samples were set aside for calibration model training and the remaining 50% for testing calibrated Landsat TCC estimates.
We calculated the Landsat TCC relative error for each airborne LiDAR sample. The relative error was defined for each sampled pixel as such:
where
TCCthresh,seg is a sample reference estimate of tree canopy cover and
TCCepoch,pix is a Landsat tree canopy cover estimate for a given epoch at a pixel whose location corresponds to that of the reference. The frequency of
Err thresh,seg provided insight into the variation in uncertainty of the TCC estimates across the study area.
2.2.2. Calibrating Landsat TCC Estimates
The calibration equations for each epoch were derived from models comparing
TCCepoch,pix (dependent variable) with
TCCthresh,seg (independent variable) for two height thresholds (2 m and 5 m). These equations are the inverse of the linear models built from the training set of reference and follow the form:
where
b and
m are coefficients of the linear calibration model (y-intercept and slope) and
TCCepoch, cal and
TCCepoch are calibrated and pre-calibrated Landsat TCC estimates, respectively.
2.2.3. Validation: Assessing the Uncertainty of Calibrated Landsat TCC Estimates
Uncertainty metrics follow those described in Sexton et al. [
34]. They are based on average differences between paired model and reference (or training) values [
49], quantified by root mean squared error (RMSE):
where
Mi and
Ri are estimated and reference tree cover values at a location
i in a sample of size
n.
After modeling the relationship between
Mi and
Ri by linear regression, their squared difference was disaggregated into systematic error (
MSES) and unsystematic error (
MSEU) based on the modeled linear relationship [
49]:
where
is the cover value predicted by the modeled relationship [
49]. Accuracy is thus quantified by the difference between the trend of model over reference cover, and precision is quantified by the variation surrounding that trend.
MSES and
MSEU sum to Mean-Squared Error (MSE), and therefore:
To maintain consistency, we report the square roots of MSES and MSEU, i.e., RMSES and RMSEU, in units of percent cover. LiDAR-derived canopy cover reference was used to calibrate Landsat TCC estimates by linear regression. Residual errors in both the Landsat and reference estimates were calculated as the RMSEU and RMSES of the post-calibrated estimates.
3. Results
The results incorporating three epochs of Landsat TCC estimates (2000, 2005, and 2010) are divided into four parts. The preliminary analysis reports (1) the circumpolar consistency of TCCepoch estimates as determined from the 425 HRSI sites and (2) the LiDAR-derived heights used to determine thresholds for tree canopies on which estimates of canopy cover (TCCthresh,seg) were based. Next, we show the comparison of canopy height threshold models relating TCCepoch with reference TCCthresh,seg, and report for each threshold the distribution of TCCepoch errors relative to TCCthresh,seg. Then, we summarize each threshold’s bootstrapped calibration results, which provide a basis for selecting the best calibration model. Finally, we report the results of both thresholds’ calibration models as TCCepoch,cal relative error distributions, summarize the TCC calibration model results, and report both the difference in estimates of TCC uncertainty of pre- and post-calibration and the final TCCepoch,cal uncertainty estimates.
3.1. Preliminary Analysis
3.1.1. Landsat Tree Canopy Cover at Circumpolar HRSI Sites
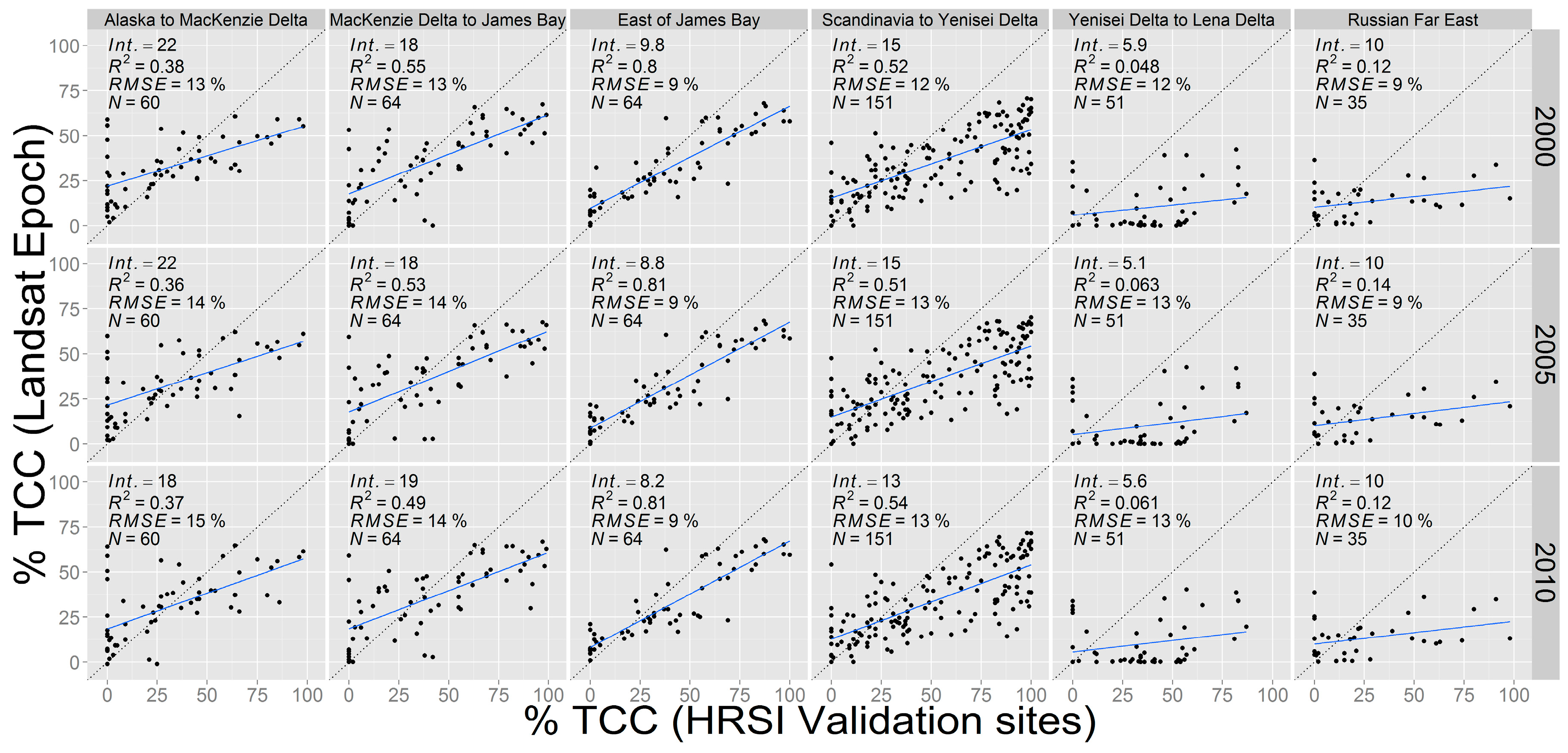
Across the circumpolar TTE, we derived linear models to describe the regional relationships of Landsat TCC with 425 reference HRSI estimates of canopy cover (
Figure 2). Across all epochs, model slopes are similar (0.34–0.59,
p-values <0.001) across North America and from Scandinavia to the Yenisei River in Western Siberia. In these regions Landsat estimates of tree cover show a consistent overestimation at low tree cover (<30%) and an underestimation at higher tree cover, particularly >60%. West of the Yenisei in Central Siberia and the Russian Far East, Landsat tree cover shows poor relationships with reference data, where R
2 < 0.15 and
p-values >0.02 for each slope across all epochs in both regions. For each zone, there were no significant differences in models across all three Landsat epochs (
p-values >0.5), suggesting that Landsat TCC values did not significantly change at the validation sites within the time period covered by this study.
3.1.2. Heights Used in Reporting Reference Tree Canopy Cover
The LiDAR transects across Alaska and Canada provided estimates of forest canopy height. These estimates of height were made from two height thresholds. These thresholds were used to determine which LiDAR returns were classified as being from canopy, and then used to calculate
TCCepoch, seg. An increasing threshold for canopy resulted in a consistently decreasing number of reference estimates of canopy. Applying a 2 m threshold for determining forest canopy resulted in 67% of samples being classified as forest canopy, whereas for the 5 m threshold, the result was 50%, and decreased the average height reported for each sample (
Figure 3).
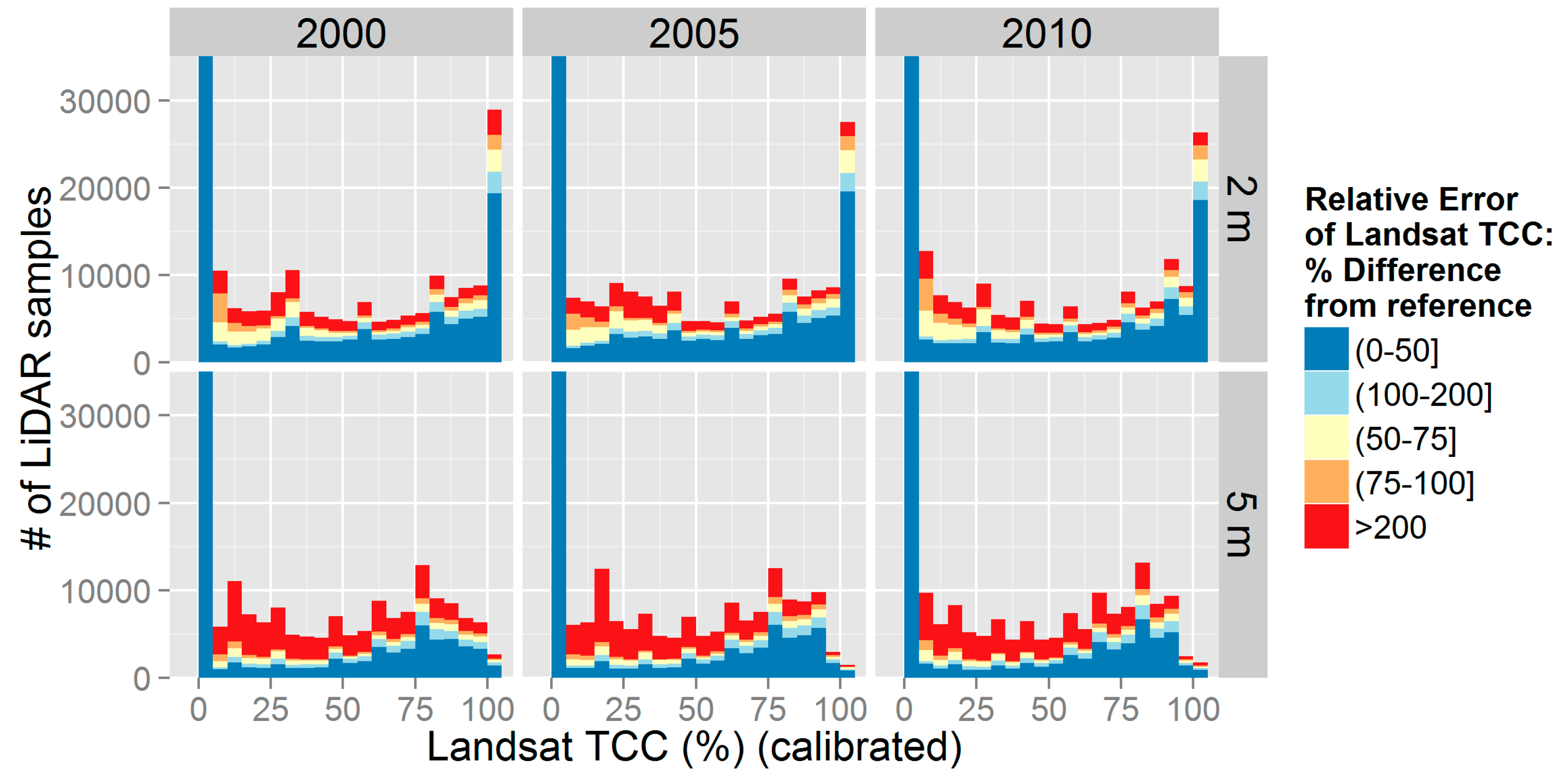
3.2. Pre-Calibrated Landsat TCC Estimates and Their Errors
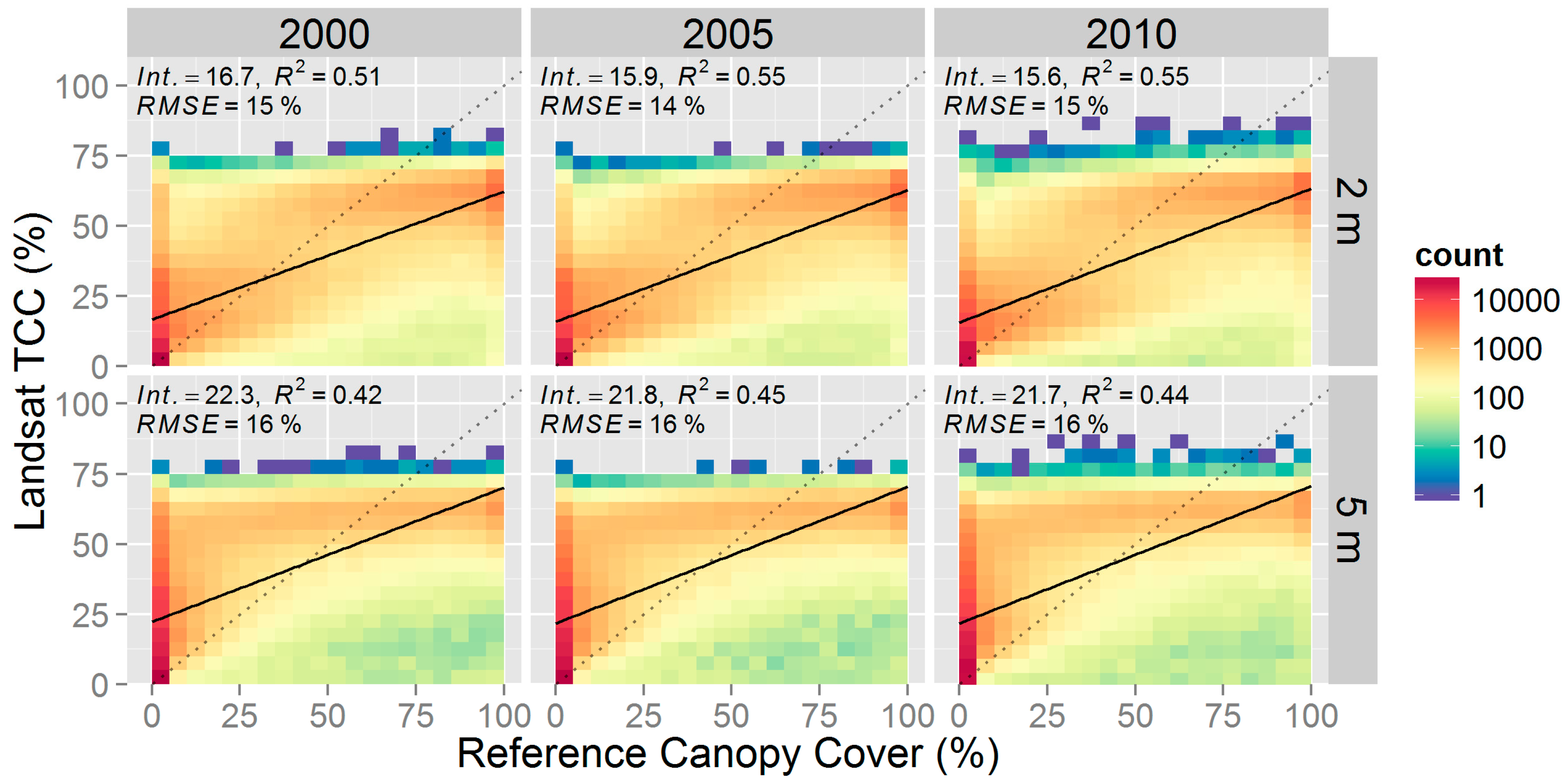
The pre-calibration assessment of Landsat estimates (
TCCepoch) show the nature of scatter relative to reference cover, the similarity between estimates from different epochs, and how uncertainty is distributed across the range of
TCCepoch. Landsat TCC estimates were compared with the training set of reference LiDAR estimates of canopy cover (
Figure 4). These comparisons were made for the 2 m and 5 m canopy height thresholds for reference cover.
Figure 5 shows the distribution of the pre-calibrated Landsat TCC (
TCCepoch) and its categorized errors (
Errthresh,seg). Across the (pre-calibration) range of
TCCepoch,
Err thresh,seg was divided into five general classes to group estimates of error and depict patterns of TCC error across the range of estimates. For all three epochs, compared to the 5 m model, the 2 m model shows a smaller proportion of the
TCCepoch distribution associated with high relative error categories (
Errthresh,seg > 100%; i.e., the error exceeds the magnitude of the estimate. The difference is particularly evident for discontinuous forests (1%–30%
TCCepoch), where low error categories comprise ~40% and ~14% and the reference samples for the 2 m and 5 m thresholds, respectively, for each epoch.
3.3. Selecting a Calibration Model
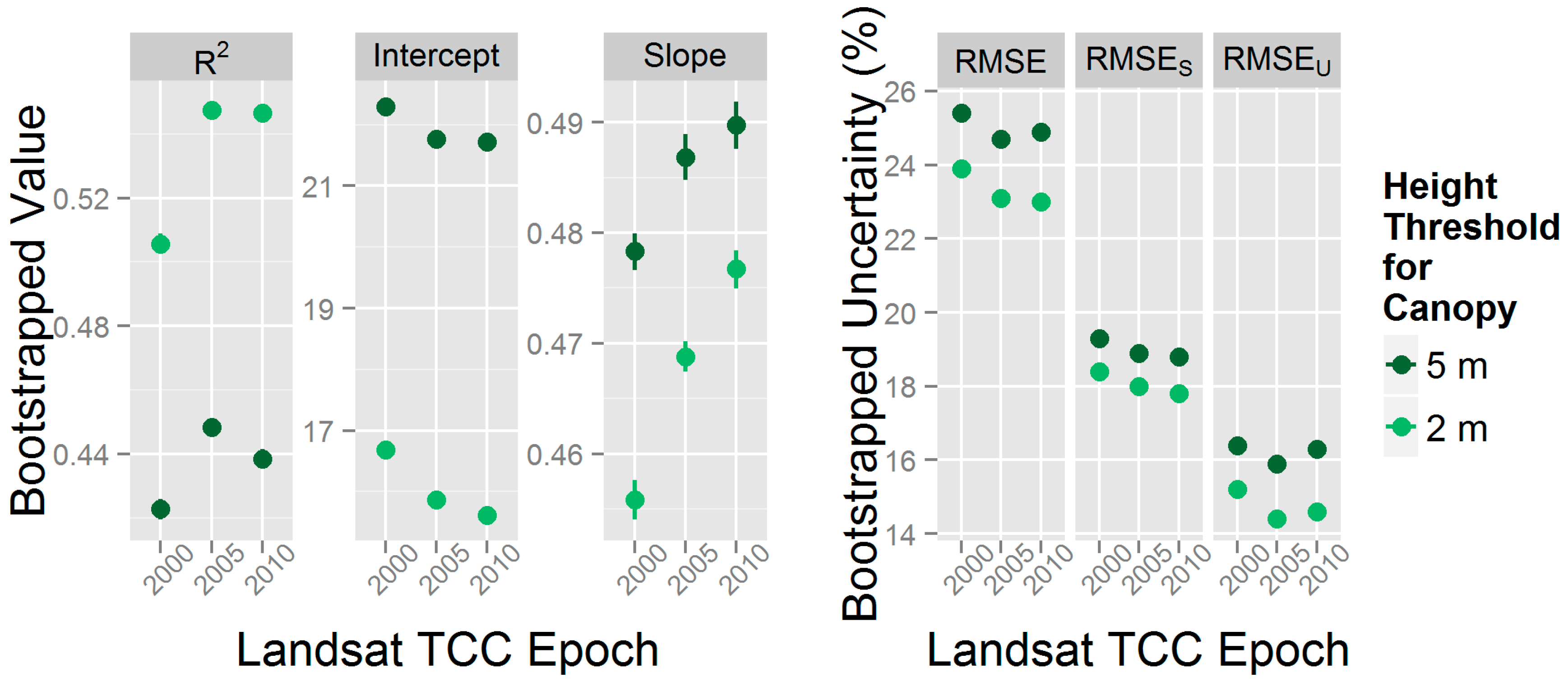
The set of LiDAR reference data was divided so that half was used for model calibration and the other half for model validation. Both model training and testing sets were distinct in that they had no samples in common. The calibration models, specific to epoch and canopy height threshold, were built based on bootstrapped linear model coefficients derived from the set of model training data. These coefficients, because of the large training sample size (
N = ~250,000), had very small confidence intervals at the 95% level (
Figure 6).
The results of the height threshold model summaries formed the basis upon which a final Landsat TCC calibration model was selected. The model from which reference cover estimates were derived from a 2 m canopy height threshold explained the most variation in Landsat TCC and returned the lowest RMSEU and RMSES across all epochs. While not large in terms of magnitude, the differences between model coefficients from the 2 m and 5 m models are statistically significant (p < 0.001).
3.4. Tree Canopy Cover Uncertainty from Validation of Calibrated Landsat Estimates
Models from the testing portion of the reference data validated the calibrated Landsat
TCCepoch estimates. Landsat
TCCepoch estimates were calibrated separately using both the 2 m and 5 m calibration models. The ranges of calibrated estimates from both models are shown in
Figure 7 for each epoch. These calibrated estimates, which extend across the full percent cover range, remove the pre-calibration systematic under-estimation >80%
TCCepoch.
Calibrated estimates feature a greater proportion of samples in low error categories compared to pre-calibrated estimates. For calibrated estimates in discontinuous forests (1%–30% TCCepoch,cal), the proportion of samples in low error categories increased to ~67% (from ~40% for TCCepoch) with the 2 m model, and to ~35% (from ~14% for TCCepoch) for the 5 m model. These results suggest not only that the calibration is reducing relative errors in Landsat TCC estimates in discontinuous forests, but that the 2 m threshold for canopy in these regions provide the most appropriate reference for the calibration. The spike in TCCepoch,cal values at 0% and 100% results from a calibration operation on TCC values for which resulting values of either <0 or >100 were assigned 0 and 100 values, respectively.
Table 1 summarizes the results from the validation of
TCCepoch,cal with model testing samples of
TCCthresh,seg based on 2 m and 5 m height thresholds for canopy. The calibration models, specific to height threshold and epoch, show little variation in model fit and coefficients among epochs, indicating that there was little change at the LiDAR reference sites across this time period. Our estimate of change at these sites, based on the probability that the 2000 TCC estimate was similar to that of 2010, shows that 1.3% of our LiDAR-sampled Landsat TCC estimates changed from 2000−2010 (
p-value <0.1).
For each epoch, reference estimates based on the 2 m height threshold provided the best model fits with Landsat estimates. Compared with the 5 m models, the 2 m models explained a greater proportion of variation between Landsat and reference estimates, as well as featured a higher slope and lower intercept value.
The model summary also reports model uncertainty (RMSE) and its systematic (RMSES) and unsystematic (RMSEU) components. These uncertainty figures provide an estimate of the mean error of the Landsat TCC values. The RMSES (error in the x-direction) and RMSEU (error in the y-direction) show the contribution to overall model error associated from the reference estimates and the Landsat estimates. Each epoch’s 2 m model reports TCC uncertainty (RMSE) of 29.0%, 27.1% and 31.1% for 2000, 2005 and 2010, respectively, with those from the 5 m model report 28.0%, 26.5% and 31.5%.
The differences in
TCCepoch and
TCCepoch,cal systematic (
RMSES) and unsystematic (
RMSEU) uncertainties provide the context needed to compare the overall uncertainties from each epoch’s model.
Figure 8 reports these differences in Landsat TCC uncertainty estimates from comparison with reference estimates based on 2 m and 5 m canopy height thresholds. These pre- and post-calibration results show how the calibration has reduced systematic error and increased the unsystematic error associated with the model residuals of Landsat TCC. For the 2 m models, these differences result in a larger overall
RMSE (increases of 17%–35%) after removing 55%–60% of the systematic contribution to the overall error, resulting in
TCCepoch,cal uncertainties of 29.0%, 27.1% and 31.1% for 2000, 2005 and 2010, respectively, that reflect more closely the uncertainty of TTE tree canopy cover from Landsat relative to the external reference data.
4. Discussion
Using two sets of independent reference tree cover, we examined Landsat TCC estimates in and near the circumpolar TTE, calibrated these estimates with LiDAR-derived canopy height and cover, and validated Landsat TCC to improve estimates of TCC uncertainty for the TTE. Reference estimates show that Landsat exhibits a general circumpolar consistency in its estimates of TCC, which saturates around 80% tree cover. Results show: (1) canopy height can inform estimates of tree canopy cover, (2) calibration can reduce estimates of relative error in areas of low tree cover, and (3) the validation, by reducing systematic error, provides error estimates that better reflect the uncertainty of Landsat TCC in discontinuous forests of the TTE.
4.1. Circumpolar Consistency of Landsat TCC Estimates
The results from the comparison of Landsat TCC estimates with those from HRSI validation sites demonstrate a general consistency in estimating canopy cover across a range of forest structure throughout the TTE domain. While this general consistency holds across the three epochs, it does not appear to extend spatially to the two regions east of the Yenisei River in Siberia. The forests of these regions are dominated by the deciduous conifer
Larix species (
Larix gmelinii in Central Siberia and
Larix cajanderi in the Russian Far East) and constitute the world’s only forest biome on continuous permafrost. Prediction of forest characteristics in this region specifically based on parameters derived for evergreen boreal forests generally may result in underestimation of ecological processes, given this region’s unique relationship between soil type and plant community [
50]. This rule may not apply to the prediction of tree cover, since it is not dependent on soil characteristics. However, the example highlights the region’s distinct features, which, along with its relative under-sampling within our reference data, may in part account for the differences in these regional models relative to the rest of the circumpolar domain.
4.2. The Importance of Height in Estimates of Cover
We found that accounting for canopy height can improve the calibration of Landsat TCC estimates. Pre-calibration models comparing estimates of canopy cover from Landsat with those from reference data show a systematic under-estimation (i.e., saturation) of TCCepoch > 80%. This saturation is well documented in previous studies, and the linear calibration models correct for this saturation in canopy cover. However, comparing model results for reference canopy cover based on 2 m and 5 m height thresholds shows how the added context from vertical forest structure improves reference estimates of cover. Our results show that our reference estimates of canopy cover in the TTE more closely coincide with those from Landsat when we used a 2 m height threshold for calculating canopy cover. Our linear models indicate that TCCepoch is estimating cover that is more closely associated with canopies that include shorter vegetation, rather than canopies that are limited to those that are captured by the conventionally recognized 5 m height threshold, which excludes shorter stature vegetation cover.
The reason why Landsat estimates in the TTE may be incorporating canopy from shorter stature vegetation may include confusion between shrubs and trees. This is a difficulty even for humans visually interpreting tree cover from HRSI (<5 m resolution) data. However, this apparent confusion implies that the definition of what is a tree is of primary importance and spatially consistent [
47]. The TTE, in particular, is a region in which this distinction is blurred. When considering some biophysical processes, it may not be as relevant to remove the low stature canopy component from the overall canopy cover calculation as it otherwise might be in biomes further south. For example, canopy height controls surface energy exchange in the TTE [
16,
51,
52,
53]. The impact of height is thus the key feature in the control of this biophysical process rather than the classification of the canopy components. As such, the results showing Landsat TCC as representing lower stature cover than previously believed may be a useful feature of the dataset for this circumpolar transition zone.
4.3. Improved Estimates of Uncertainty Guide Use of Landsat TCC for Discontinuous Forests
The calibration and validation provided uncertainty estimates that are higher than those from pre-calibration estimates. This increase rose most sharply from the calibration based on a 2 m canopy height threshold because they were accompanied by the greatest reductions in systematic errors. This reduction in systematic error improves the degree to which the unsystematic errors represented the true variability of the Landsat estimates, and is responsible for the overall improvement in our understanding of the degree to which Landsat TCC estimates discontinuous forest cover in the TTE.
Sexton et al. [
34] explained that the original pixel-level uncertainties were likely biased low. This study’s RMSE values of ~30%
TCCepoch,cal across the three epochs (compared to ~23% from pre-calibrated results) support that hypothesis. Furthermore, the calibration resulted in a large proportion of low TCC estimates converting to values of 0%
TCCepoch,cal with pixel-level relative errors (
Errthresh,seg) of 100%. These characteristics underscore the general pixel-level uncertainty of
TCCepoch,cal for discontinuous forests.
This uncertainty, represented by the mean of the distribution of errors captured at the pixel level, is important to consider when examining TCC across a biome for which low tree cover is a defining attribute. In the TTE, small absolute differences in tree cover may have an impact on the ability to interpret the pattern of trees across the landscape and their relationship with other landscape factors. The uncertainty of TCCepoch,cal supports the pixel-level mapping of discontinuous forests in that it provides limits on the magnitude of pixel-level differences in tree cover that can be statistically identified.
These calibrated TCC estimates (TCCepoch,cal) can be used to map discontinuous forest cover characteristics across the circumpolar TTE. First, the mean uncertainty of TCCepoch,cal (RMSE) along with samples of Errthresh,seg can be used to refine models of individual pixel uncertainty, that will be used to map pixel-level uncertainty of TCCepoch,cal. Then, this mapped pixel-level TCCepoch,cal uncertainty can be part of an examination of the optimal spatial scale for aggregating TCCepoch,cal in the TTE, which will inform the extent to which these Landsat-scale data can provide information on the biogeography of forest structure across the circumpolar TTE domain. Furthermore, these calibrated estimates, coupled with the frequent (~5 -year epochs) and circumpolar nature of these spaceborne data, provide for a reliable and systematic characterization of TTE forest structure. In particular, characterizing ecotone form (the horizontal and vertical spatial characteristics of groups of trees) with TCCepoch,cal in the TTE may provide a means for examining the varying potential across the circumpolar domain for forest structure regimes to change to novel states. This opportunity for addressing the horizontal characteristics of ecotone form with calibrated tree canopy cover from Landsat may lie in the ability to link them to forest structure patterns from spatially detailed (<2 m) and continuous (image-based) depictions of the TTE. Such a link will inform which patterns are maintained or disguised from changes of scale, and to what extent those differences impact the ability to predict forest structure dynamics in the TTE.
5. Conclusions
The calibration and validation of Landsat tree canopy cover (TCC) across the boreal forest and taiga−tundra ecotone (TTE) identified the canopy height at which estimates of cover are based and removed TCC systematic under-estimation above 80% cover, thereby improving estimates of TCC uncertainty. These improvements were calculated from reference data for which canopy cover was derived from canopies at least 2 m tall, a height more closely associated with the canopies measured by Landsat across the range of boreal and TTE forest canopy sampled in this study. The improvements were based on the greatest overall reduction in systematic errors (55%, 67%, and 57%) linked to increases in unsystematic (residual) errors and increases in overall uncertainty (21%, 17%, and 35%) for epochs 2000, 2005, and 2010, respectively. This resulted in overall tree canopy cover uncertainties of 29.0%, 27.1% and 31.1% for the 2000, 2005 and 2010 epochs, respectively. Maps from these calibrated data will better represent the uncertainty associated with Landsat tree canopy cover estimates in the discontinuous forests of the circumpolar TTE.
Acknowledgments
Funding for this work was provided by the NASA Terrestrial Ecology Program (NNH13ZDA001N-CARBON).
Author Contributions
Paul Montesano, Christopher Neigh, Joseph Sexton, Min Feng, and Saurabh Channan all contributed to writing, data production, and analysis. K. Jon Ranson and John Townshend assisted with the direction and scope of work.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| TTE | Taiga−tundra ecotone |
| TCC | Tree canopy cover |
| HRSI | High-resolution spaceborne imagery |
| LiDAR | Light detection and ranging |
| PALS | Portable Airborne LiDAR System |
| RMSE | root mean squared error |
References
- Ranson, K.J.; Montesano, P.M.; Nelson, R. Object-based mapping of the circumpolar taiga–tundra ecotone with MODIS tree cover. Remote Sens. Environ. 2011, 115, 3670–3680. [Google Scholar] [CrossRef]
- Timoney, K.P.; LaRoi, G.; Zoltai, S.; Robinson, A. The high subarctic forest-tundra of northwestern Canada: Position, width, and vegetation gradients in relation to climate. Arctic 1992, 45, 1–9. [Google Scholar] [CrossRef]
- Payette, S.; Fortin, M.J.; Gamache, I. The subarctic forest-tundra: The structure of a biome in a changing climate. Bioscience 2001, 51, 709–718. [Google Scholar] [CrossRef]
- MacDonald, G.M.; Edwards, T.W.D.; Moser, K.A.; Pienitz, R.; Smol, J.P. Rapid response of treeline vegetation and lakes to past climate warming. Nature 1993, 361, 243–246. [Google Scholar] [CrossRef]
- Bader, J. Climate science: The origin of regional Arctic warming. Nature 2014, 509, 167–168. [Google Scholar] [CrossRef] [PubMed]
- Post, E.; Forchhammer, M.C.; Bret-Harte, M.S.; Callaghan, T.V.; Christensen, T.R.; Elberling, B.; Fox, A.D.; Gilg, O.; Hik, D.S.; Høye, T.T. Ecological dynamics across the Arctic associated with recent climate change. Science 2009, 325, 1355–1358. [Google Scholar] [CrossRef] [PubMed]
- Holtmeier, F.-K.; Broll, G. Sensitivity and response of northern hemisphere altitudinal and polar treelines to environmental change at landscape and local scales. Glob. Ecol. Biogeogr. 2005, 14, 395–410. [Google Scholar] [CrossRef]
- Evju, M.; Hagen, D.; Hofgaard, A. Effects of disturbance on plant regrowth along snow pack gradients in alpine habitats. Plant Ecol. 2012, 213, 1345–1355. [Google Scholar] [CrossRef]
- Kaarlejärvi, E.; Baxter, R.; Hofgaard, A.; Hytteborn, H.; Khitun, O.; Molau, U.; Sjögersten, S.; Wookey, P.; Olofsson, J. Effects of warming on shrub abundance and chemistry drive ecosystem-level changes in a forest–tundra ecotone. Ecosystems 2012, 15, 1219–1233. [Google Scholar] [CrossRef]
- Pielke, R.A.; Vidale, P.L. The boreal forest and the polar front. J. Geophys. Res. 1995, 100, 755–758. [Google Scholar] [CrossRef]
- Thompson, C.; Beringer, J.; Chapin, F.S.; Mcguire, A.D. Structural complexity and land-surface energy exchange along a gradient from arctic tundra to boreal forest. J. Veg. Sci. 2004, 15, 397–406. [Google Scholar] [CrossRef]
- Bonan, G.B.; Pollard, D.; Thompson, S.L. Effects of boreal forest vegetation on global climate. Nature 1992, 359, 716–718. [Google Scholar] [CrossRef]
- Zhuang, Q.; Melillo, J.M.; Mcguire, A.D. Net emissions of CH4 and CO2 in Alaska: Implications for the region’s greenhouse gas budget. Ecol. Appl. 2007, 17, 203–212. [Google Scholar] [CrossRef]
- Hofgaard, A.; Harper, K.A.; Golubeva, E. The role of the circumarctic forest–tundra ecotone for Arctic biodiversity. Biodiversity 2012, 13, 174–181. [Google Scholar] [CrossRef]
- Wootton, J.; Pfister, C.; Forester, J. Dynamic patterns and ecological impacts of declining ocean pH in a high-resolution multi-year dataset. Proc. Natl. Acad. Sci. USA 2008, 105, 18848–18853. [Google Scholar] [CrossRef] [PubMed]
- Chapin, F., III; Sturm, M.; Serreze, M.; McFadden, J.P.; Key, J.R.; Lloyd, A.H.; McGuire, A.D.; Rupp, T.S.; Lynch, A.H.; Schimel, J.P.; et al. Role of land-surface changes in arctic summer warming. Science 2005, 310, 657–660. [Google Scholar] [CrossRef] [PubMed]
- Callaghan, T.V.; Werkman, B.R.; Crawford, R.M. The tundra-taiga interface and its dynamics: Concepts and applications. Ambio 2002, 12, 6–14. [Google Scholar]
- Timoney, K.P.; Roi, G.H.; Dale, M. Subarctic forest-tundra vegetation gradients: The sigmoid wave hypothesis. J. Veg. Sci. 1993, 4, 387–394. [Google Scholar] [CrossRef]
- Frost, G.V.; Epstein, H.E. Tall shrub and tree expansion in Siberian tundra ecotones since the 1960s. Glob. Chang. Biol. 2014, 20, 1264–1277. [Google Scholar] [CrossRef] [PubMed]
- Harding, R.; Kuhry, P.; Christensen, T.R.; Sykes, M.T.; Dankers, R.; van der Linden, S. Climate feedbacks at the tundra-taiga interface. Ambio 2002, 12, 47–55. [Google Scholar]
- Epstein, H.E.; Beringer, J.; Gould, W.A.; Lloyd, A.H.; Thompson, C.D.; Chapin, F.S.; Michaelson, G.J.; Ping, C.L.; Rupp, T.S.; Walker, D.A. The nature of spatial transitions in the Arctic. J. Biogeogr. 2004, 31, 1917–1933. [Google Scholar] [CrossRef]
- Lloyd, A.H. Ecological histories from Alaskan tree lines provide insight into future change. Ecology 2005, 86, 1687–1695. [Google Scholar] [CrossRef]
- Lloyd, A.H.; Bunn, A.G.; Berner, L.T. A latitudinal gradient in tree growth response to climate warming in the Siberian taiga. Glob. Chang. Biol. 2011, 17, 1935–1945. [Google Scholar] [CrossRef]
- Andreu-Hayles, L.; D’Arrigo, R.; Anchukaitis, K.J.; Beck, P.S.A.; Frank, D.; Goetz, S. Varying boreal forest response to Arctic environmental change at the Firth River, Alaska. Environ. Res. Lett. 2011, 6, 045503, Corrigendum, 2011, 6, 049502. [Google Scholar]
- Berner, L.T.; Beck, P.S.A.; Bunn, A.G.; Goetz, S.J. Plant response to climate change along the forest-tundra ecotone in northeastern Siberia. Glob. Chang. Biol. 2013, 19, 3449–3462. [Google Scholar] [CrossRef] [PubMed]
- Frost, G.V.; Epstein, H.E.; Walker, D.A.; Matyshak, G.; Ermokhina, K. Patterned-ground facilitates shrub expansion in Low Arctic tundra. Environ. Res. Lett. 2013, 8, 015035. [Google Scholar] [CrossRef]
- Macias-Fauria, M.; Forbes, B.C.; Zetterberg, P.; Kumpula, T. Eurasian Arctic greening reveals teleconnections and the potential for structurally novel ecosystems. Nat. Clim. Chang. 2012, 2, 613–618. [Google Scholar] [CrossRef]
- Elmendorf, S.C.; Henry, G.H.R.; Hollister, R.D.; Björk, R.G.; Boulanger-Lapointe, N.; Cooper, E.J.; Cornelissen, J.H.C.; Day, T.A.; Dorrepaal, E.; Elumeeva, T.G.; et al. Plot-scale evidence of tundra vegetation change and links to recent summer warming. Nat. Clim. Chang. 2012, 2, 453–457. [Google Scholar] [CrossRef]
- Margolis, H.A.; Nelson, R.F.; Montesano, P.M.; Beaudoin, A.; Sun, G.; Andersen, H.-E.; Wulder, M.A. Combining satellite lidar, airborne lidar, and ground plots to estimate the amount and distribution of aboveground biomass in the boreal forest of North America 1. Can. J. For. Res. 2015, 838–855. [Google Scholar] [CrossRef]
- Nelson, R.; Ranson, K.J.; Sun, G.; Kimes, D.S.; Kharuk, V.; Montesano, P. Estimating Siberian timber volume using MODIS and ICESat/GLAS. Remote Sens. Environ. 2009, 113, 691–701. [Google Scholar] [CrossRef]
- Neigh, C.S.; Nelson, R.F.; Ranson, K.J.; Margolis, H.A.; Montesano, P.M.; Sun, G.; Kharuk, V.; Næsset, E.; Wulder, M.A.; Andersen, H.-E. Taking stock of circumboreal forest carbon with ground measurements, airborne and spaceborne LiDAR. Remote Sens. Environ. 2013, 137, 274–287. [Google Scholar] [CrossRef]
- Lefsky, M.A. A global forest canopy height map from the Moderate Resolution Imaging Spectroradiometer and the Geoscience Laser Altimeter System. Geophys. Res. Lett. 2010, 37, L15401. [Google Scholar] [CrossRef]
- Montesano, P.; Nelson, R.; Sun, G.; Margolis, H.; Kerber, A.; Ranson, K. MODIS tree cover validation for the circumpolar taiga-tundra transition zone. Remote Sens. Environ. 2009, 113, 2130–2141. [Google Scholar] [CrossRef]
- Sexton, J.O.; Song, X.-P.; Feng, M.; Noojipady, P.; Anand, A.; Huang, C.; Kim, D.-H.; Collins, K.M.; Channan, S.; DiMiceli, C.; et al. Global, 30-m resolution continuous fields of tree cover: Landsat-based rescaling of MODIS vegetation continuous fields with lidar-based estimates of error. Int. J. Digit. Earth 2013, 6, 427–448. [Google Scholar] [CrossRef]
- Channan, S.; Feng, M.; Kim, D.H.; Sexton, J.O. The GLS+: An enhancement of the global land survey datasets. Photogramm. Eng. Remote Sens. 2015, 81, 521–525. [Google Scholar] [CrossRef]
- Hansen, M.; DeFries, R.; Townshend, J. Global percent tree cover at a spatial resolution of 500 meters: First results of the MODIS vegetation continuous fields algorithm. Earth Interact. 2003, 7, 1–15. [Google Scholar] [CrossRef]
- Heiskanen, J. Tree cover and height estimation in the Fennoscandian tundra–taiga transition zone using multiangular MISR data. Remote Sens. Environ. 2006, 103, 97–114. [Google Scholar] [CrossRef]
- Hudak, A.T.; Evans, J.S.; Stuart Smith, A.M. LiDAR utility for natural resource managers. Remote Sens. 2009, 1, 934–951. [Google Scholar] [CrossRef]
- Smith, A.; Falkowski, M.J.; Hudak, A.T. A cross-comparison of field, spectral, and lidar estimates of forest canopy cover. Can. J. Remote Sens. 2009, 35, 447–459. [Google Scholar] [CrossRef]
- Hopkinson, C.; Chasmer, L. Testing LiDAR models of fractional cover across multiple forest ecozones. Remote Sens. Environ. 2009, 113, 275–288. [Google Scholar] [CrossRef]
- Sexton, J.O.; Bax, T.; Siqueira, P.; Swenson, J.J.; Hensley, S. A comparison of lidar, radar, and field measurements of canopy height in pine and hardwood forests of southeastern North America. For. Ecol. Manag. 2009, 257, 1136–1147. [Google Scholar] [CrossRef]
- Platt, R.V.; Schoennagel, T. An object-oriented approach to assessing changes in tree cover in the Colorado Front Range 1938–1999. For. Ecol. Manag. 2009, 258, 1342–1349. [Google Scholar] [CrossRef]
- Moskal, L.M.; Styers, D.M.; Halabisky, M. Monitoring urban tree cover using object-based image analysis and public domain remotely sensed data. Remote Sens. 2011, 3, 2243–2262. [Google Scholar] [CrossRef]
- Hellesen, T.; Matikainen, L. An object-based approach for mapping shrub and tree cover on grassland habitats by use of LiDAR and CIR orthoimages. Remote Sens. 2013, 5, 558–583. [Google Scholar] [CrossRef]
- Nelson, R.; Boudreau, J.; Gregoire, T.G.; Margolis, H.; Næsset, E.; Gobakken, T.; Ståhl, G. Estimating Quebec provincial forest resources using ICESat/GLAS. Can. J. For. Res. 2009, 39, 862–881. [Google Scholar] [CrossRef]
- Korhonen, L.; Korpela, I.; Heiskanen, J.; Maltamo, M. Airborne discrete-return LIDAR data in the estimation of vertical canopy cover, angular canopy closure and leaf area index. Remote Sens. Environ. 2011, 115, 1065–1080. [Google Scholar] [CrossRef]
- Sexton, J.O.; Noojipady, P.; Song, X.-P.; Feng, M.; Song, D.-X.; Kim, D.-H.; Anand, A.; Huang, C.; Channan, S.; Pimm, S.L.; Townshend, J.R. Conservation policy and the measurement of forests. Nat. Clim. Chang. 2015, 6, 192–196. [Google Scholar] [CrossRef]
- Nelson, R.; Parker, G.; Hom, M. A portable airborne laser system for forest inventory. Photogramm. Eng. Remote Sens. 2003, 69, 267–273. [Google Scholar] [CrossRef]
- Willmott, C.J. Some comments on the evaluation of model performance. Bull. Am. Meteorol. Soc. 1982, 63, 1309–1369. [Google Scholar] [CrossRef]
- Zyryanova, O.A.; Abaimov, A.P.; Daimaru, H.; Matsuura, Y. Floristic diversity and its geographical background in Central Siberia. In Permafrost Ecosystems: Siberian Larch Forests; Ecological Studies; Springer Netherlands: Dordrecht, The Netherlands, 2009; Volume 209, pp. 17–39. [Google Scholar]
- Myers-Smith, I.H.; Forbes, B.C.; Wilmking, M.; Hallinger, M.; Lantz, T.; Blok, D.; Tape, K.D.; Macias-Fauria, M.; Sass-Klaassen, U.; Lévesque, E.; et al. Shrub expansion in tundra ecosystems: Dynamics, impacts and research priorities. Environ. Res. Lett. 2011, 6, 045509. [Google Scholar] [CrossRef]
- Loranty, M.M.; Goetz, S.J.; Beck, P.S.A. Tundra vegetation effects on pan-Arctic albedo. Environ. Res. Lett. 2011, 6, 024014. [Google Scholar] [CrossRef]
- Blok, D.; Schaepman-Strub, G.; Bartholomeus, H.; Heijmans, M.M.P.D.; Maximov, T.C.; Berendse, F. The response of Arctic vegetation to the summer climate: Relation between shrub cover, NDVI, surface albedo and temperature. Environ. Res. Lett. 2011, 6, 035502. [Google Scholar] [CrossRef]
Figure 1.
Maps showing circumpolar boreal and TTE forest structure reference data: (
a) The 425 individual validation sites (500 m
2) provided a circumpolar set of reference tree canopy cover and the ~553,640 samples in Alaska and Canada that were collected along boreal-tundra transects with airborne LiDAR that provide tree canopy cover and height estimates at 30 m segments; (
b) Mapped categories of pixel-level uncertainty (TCC relative error) from the year 2000 epoch of Landsat TCC estimates from Sexton et al. [
34] in the circumpolar boreal and TTE regions.
Figure 1.
Maps showing circumpolar boreal and TTE forest structure reference data: (
a) The 425 individual validation sites (500 m
2) provided a circumpolar set of reference tree canopy cover and the ~553,640 samples in Alaska and Canada that were collected along boreal-tundra transects with airborne LiDAR that provide tree canopy cover and height estimates at 30 m segments; (
b) Mapped categories of pixel-level uncertainty (TCC relative error) from the year 2000 epoch of Landsat TCC estimates from Sexton et al. [
34] in the circumpolar boreal and TTE regions.
Figure 2.
Scatterplots showing linear models relating mean Landsat TCC estimates at 425 circumpolar HRSI validation sites. The 425 sites, divided into six regional circumpolar zones, provide reference tree canopy cover for Landsat TCC for three epochs.
Figure 2.
Scatterplots showing linear models relating mean Landsat TCC estimates at 425 circumpolar HRSI validation sites. The 425 sites, divided into six regional circumpolar zones, provide reference tree canopy cover for Landsat TCC for three epochs.
Figure 3.
The distribution of canopy height estimates at two height thresholds for canopy along the airborne LiDAR transects across Alaska and Canada.
Figure 3.
The distribution of canopy height estimates at two height thresholds for canopy along the airborne LiDAR transects across Alaska and Canada.
Figure 4.
The relationship of Landsat tree canopy cover (TCCepoch) with LiDAR-derived reference canopy cover (TCCthresh,seg). For three epochs, the density scatterplots compare the N = ~250,000 training set estimates of Landsat TCC with airborne LiDAR estimates of canopy cover from two height thresholds used to identify canopy. The model fit and one-to-one lines are shown as solid and dotted lines, respectively.
Figure 4.
The relationship of Landsat tree canopy cover (TCCepoch) with LiDAR-derived reference canopy cover (TCCthresh,seg). For three epochs, the density scatterplots compare the N = ~250,000 training set estimates of Landsat TCC with airborne LiDAR estimates of canopy cover from two height thresholds used to identify canopy. The model fit and one-to-one lines are shown as solid and dotted lines, respectively.
Figure 5.
Pre-calibrated estimates (TCCepoch), and their relative error, from models using two height thresholds for tree canopy cover across three epochs. For each epoch, the histograms show both the distribution of pre-calibrated Landsat TCC (x-axis) that was sampled with the training set of reference data, and the relative error of these pre-calibrated samples (the colors represent the relative error class) based on 2 m and 5 m height thresholds for canopy.
Figure 5.
Pre-calibrated estimates (TCCepoch), and their relative error, from models using two height thresholds for tree canopy cover across three epochs. For each epoch, the histograms show both the distribution of pre-calibrated Landsat TCC (x-axis) that was sampled with the training set of reference data, and the relative error of these pre-calibrated samples (the colors represent the relative error class) based on 2 m and 5 m height thresholds for canopy.
Figure 6.
Summary plots comparing each thresholds’ bootstrapped linear calibration model results. Models were built on model training samples where TCCepoch was the dependent variable and TCCthresh,seg was the independent variable. Due to the large training sample size, 95% confidence intervals are very small and are only shown for model slopes.
Figure 6.
Summary plots comparing each thresholds’ bootstrapped linear calibration model results. Models were built on model training samples where TCCepoch was the dependent variable and TCCthresh,seg was the independent variable. Due to the large training sample size, 95% confidence intervals are very small and are only shown for model slopes.
Figure 7.
Calibrated estimates (TCCepoch,cal), and their relative error, from models using two height thresholds for tree canopy cover across three epochs. For each epoch, the histograms show both the distribution of TCCepoch,cal (x-axis) that was sampled with the testing set of reference data and the relative error of these calibrated samples, Errthresh,seg, (the colors represent the relative error class) based on 2 m and 5 m height thresholds for canopy.
Figure 7.
Calibrated estimates (TCCepoch,cal), and their relative error, from models using two height thresholds for tree canopy cover across three epochs. For each epoch, the histograms show both the distribution of TCCepoch,cal (x-axis) that was sampled with the testing set of reference data and the relative error of these calibrated samples, Errthresh,seg, (the colors represent the relative error class) based on 2 m and 5 m height thresholds for canopy.
Figure 8.
The percent change in uncertainty, relative to pre-calibrated estimates (TCCepoch), of those from calibrated Landsat (TCCepoch,cal), using 2 m and 5 m height thresholds for canopy. The percent change values are shown with each bar.
Figure 8.
The percent change in uncertainty, relative to pre-calibrated estimates (TCCepoch), of those from calibrated Landsat (TCCepoch,cal), using 2 m and 5 m height thresholds for canopy. The percent change values are shown with each bar.
Table 1.
Summary of results from the validation of calibrated Landsat TCC (TCCepoch,cal) with reference LiDAR canopy cover estimates (TCCthresh,seg). Results from the model training on pre-calibrated Landsat TCC (TCCepoch) appear in parentheses.
Table 1.
Summary of results from the validation of calibrated Landsat TCC (TCCepoch,cal) with reference LiDAR canopy cover estimates (TCCthresh,seg). Results from the model training on pre-calibrated Landsat TCC (TCCepoch) appear in parentheses.
| Height Thresholds for Canopy | Landsat TCC Epoch | Intercept | Slope | R2 | RMSE | RMSES | RMSEU |
|---|
| 2 m | 2000 | 11.5 (16.7) | 0.81 (0.46) | 0.49 (0.51) | 29.0 (23.9) | 8.2 (18.4) | 27.8 (15.2) |
| 2005 | 10.2 (15.9) | 0.84 (0.47) | 0.54 (0.55) | 27.1 (23.1) | 7.2 (18.0) | 26.1 (14.4) |
| 2010 | 10.8 (15.6) | 0.85 (0.48) | 0.47 (0.55) | 31.1 (23.0) | 7.6 (17.8) | 30.1 (14.6) |
| 5 m | 2000 | 14.3 (22.3) | 0.79 (0.48) | 0.46 (0.42) | 28.0 (25.4) | 11.8 (19.3) | 25.4 (16.4) |
| 2005 | 13.4 (21.8) | 0.80 (0.49) | 0.49 (0.45) | 26.5 (24.7) | 11.0 (18.9) | 24.1 (15.9) |
| 2010 | 14.5 (21.7) | 0.80 (0.49) | 0.39 (0.44) | 31.5 (24.9) | 11.9 (18.8) | 29.2 (16.3) |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).