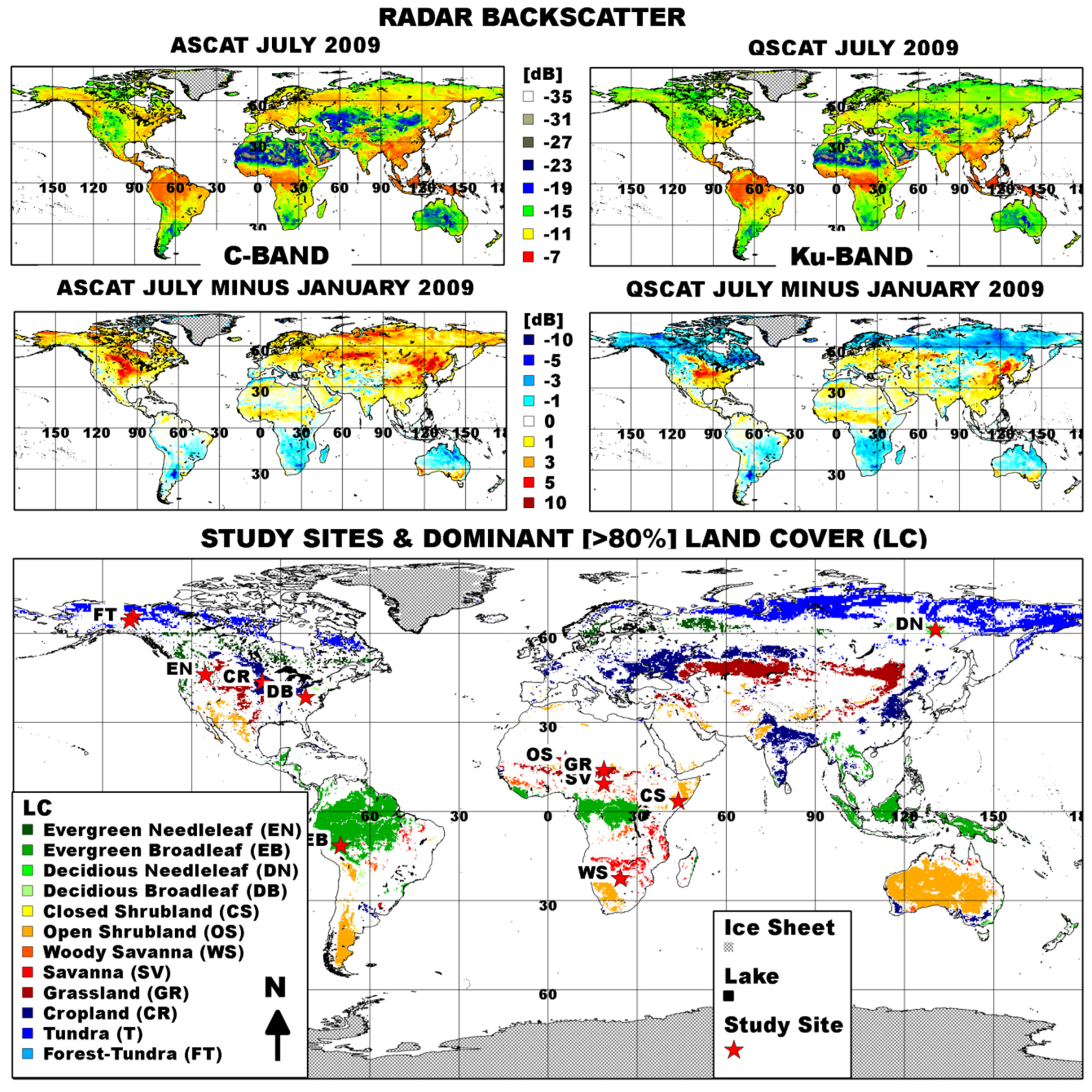
2.1. Passive and Active Microwave Satellite Data Record Construction
Tb from SSM/I and SSMI/S and σ
0 from ERS [
65], QSCAT [
66] and ASCAT [
67] were chosen to support the generation of SWAMPS over a 20+ year study period (1992–2013). We used the multi-frequency, dual-polarized SSM/I and SSMI/S Level-3
Tb observations from the National Snow & Ice Data Center [
68], binned as global and northern hemisphere Equal-Area Scalable Earth (EASE) grids at 25-km spatial resolution [
69]. The gridding procedures for these data follow the methods described in Armstrong
et al. [
68] and include the Backus-Gilbert (v1) and Inverse-Distance-Squared (v2) interpolation for respective SSM/I and SSMI/S instrument periods. Observations which use v1-gridding began in 1987 and ended in 2009; v2 covered the remainder of the study period including a 2+ year overlap period with v1.
Overlap was utilized to reduce
Tb cross-sensor differences [
68]. To do so, we constructed linear models from two years of overlapping, high-quality v1 and v2 records, separately for each frequency, polarization and overpass, appropriate to each platform, following previously developed methods [
70]. High-quality
Tb records were obtained from grid cells at least two cells away from the nearest water body and dominated (>80%) by a single forest cover as defined by the high-resolution (1-km) MODIS IGBP [
71] land cover (LC) product (MODIS LC) binned previously to the EASE-grids [
72]. v1 and v2 records that were more than 30 min apart or covered tropical forest were excluded. This approach allowed for maximizing
Tb seasonal variability while minimizing
Tb differences resulting from differences in acquisition time and method of interpolation.
Tb observations over land are largely influenced by surface temperature variations [
59,
62,
70]. To support the derivation of FW, this study employed the Microwave Polarization Difference Index (MPDI) from the 19 GHz band, defined as:
where
Tb(v) and
Tb(h) are the brightness temperatures at respective vertical (v) and horizontal (h) polarization. We employed only morning overpasses, to capture surface conditions as close to isothermal as practical. Partitioning of the polarization difference over its sum is useful because it cancels out the surface temperature component of
Tb, leaving a quantity that is largely dependent on the contributions from open water and vegetation [
61,
73]. Generally, the MPDI increases with the presence of open water bodies and decreases with increasing vegetation density.
To account for the depolarization effect that vegetation has on total MPDI and to maximize sensor sensitivity to the presence of vegetation structure and biomass dynamics in inundated areas, concurrent, high-quality σ0 observations from the ERS, QSCAT and ASCAT were acquired to solve for FW on a daily basis. We employed Level-2, VV-polarized C-band ERS, Ku-band QSCAT and C-band ASCAT and gridded these data to the EASE-grids of the Tb record using drop-in-the-bucket averaging (i.e., samples that fell within a grid cell were averaged together) with no swath averaging. σ0 coverage began in 1992 and is ongoing. The ERS and QSCAT records began in 1992 and 1999, and ended in 2000 and 2009, respectively. ASCAT covered the remainder of the study period including 1+ year of overlap with QSCAT.
A fundamental difficulty with utilizing the ERS and ASCAT for the continuous monitoring of inundated vegetation structure and biomass dynamics is additional variability in the signal caused by changes in the angle of incidence [
42,
43,
74,
75]. Following from prior results of Long and Hardin [
76], a method for deriving the normalized σ
0 coefficients at a reference incidence angle of 54°, equal to that of the QSCAT, was developed. The method is based on a simple forward model of the form:
where σ
0(θ) is backscatter acquired at incidence angle θ, α is the incidence angle corrected σ
0 in dB normalized to 54° and β is a slope factor approximating the change in σ
0 with incidence angle (θ) in dB/°. We combined a 56-day moving window approach with grid cell-wise linear regression analysis to compute time-averaged, daily α and β values by combining σ
0 measurements from each swath, overpass and all antennae regardless of look angle for all ASCAT data collected between 11 November 2008 and 31 March 2013. Time-window averaged σ
0 values were computed for four 10 degree wide incidence angle bins and aggregated to the EASE-grids using drop-in-the-bucket averaging. Since σ
0 is a measure on a logarithmic scale, it must be anti-logged prior to calculating arithmetic means. The slope factor β for each day was obtained from binned σ
0 via least-squares linear fits and the resulting slope image from the regression analysis of all grid cells was kept. Likewise, we developed a daily ASCAT climatology of the slope by averaging σ
0 from all years (2009–2012). The resulting time-averaged slope images were input to equation (2) and the VV-polarized and incidence angle normalized backscatter α at 54° for each day, swath and satellite overpass between 11th November 2008 and 31st March 2013 was computed and aggregated to the EASE-grids using drop-in-the-bucket averaging. Likewise, images of the slope obtained from averaging 4 years of ASCAT data were input to equation (2) and the VV-polarized and incidence angle corrected ERS backscatter α at 54° for each day, swath and overpass between 1st January 1992 and 31st December 2000 was computed and aggregated to the EASE-grids.
A radiometric slope correction was performed prior to the incidence angle correction to reduce the effects of incidence angle and illuminated target area on total σ
0, following from the approach of Sun
et al. [
77]. First, for each radar pulse within each EASE-grid cell, we calculated local incidence angle θ relative to slope and aspect provided by the Global Land One-km Base Elevation (GLOBE) Digital Elevation Model (DEM) of Knowles [
78] binned previously to the EASE-grids as:
where θ is the grid-based incidence angle,
is the slope angle provided by GLOBE,
is the incidence angle of the ERS, QSCAT and ASCAT scatterometers (SCAT),
is the aspect obtained from GLOBE and
is the momentary look angle of the SCAT. Second, we corrected σ
0 by relating the incidence angle of the SCAT to the local incidence angle obtained from GLOBE in Equation (3) by:
where σ
0DEM is the terrain-corrected σ
0 in dB, σ
0SCAT is σ
0 provided by the SCAT, θ is the incidence angle obtained from Equation (3) and α
SCAT is the local incidence angle of the SCAT.
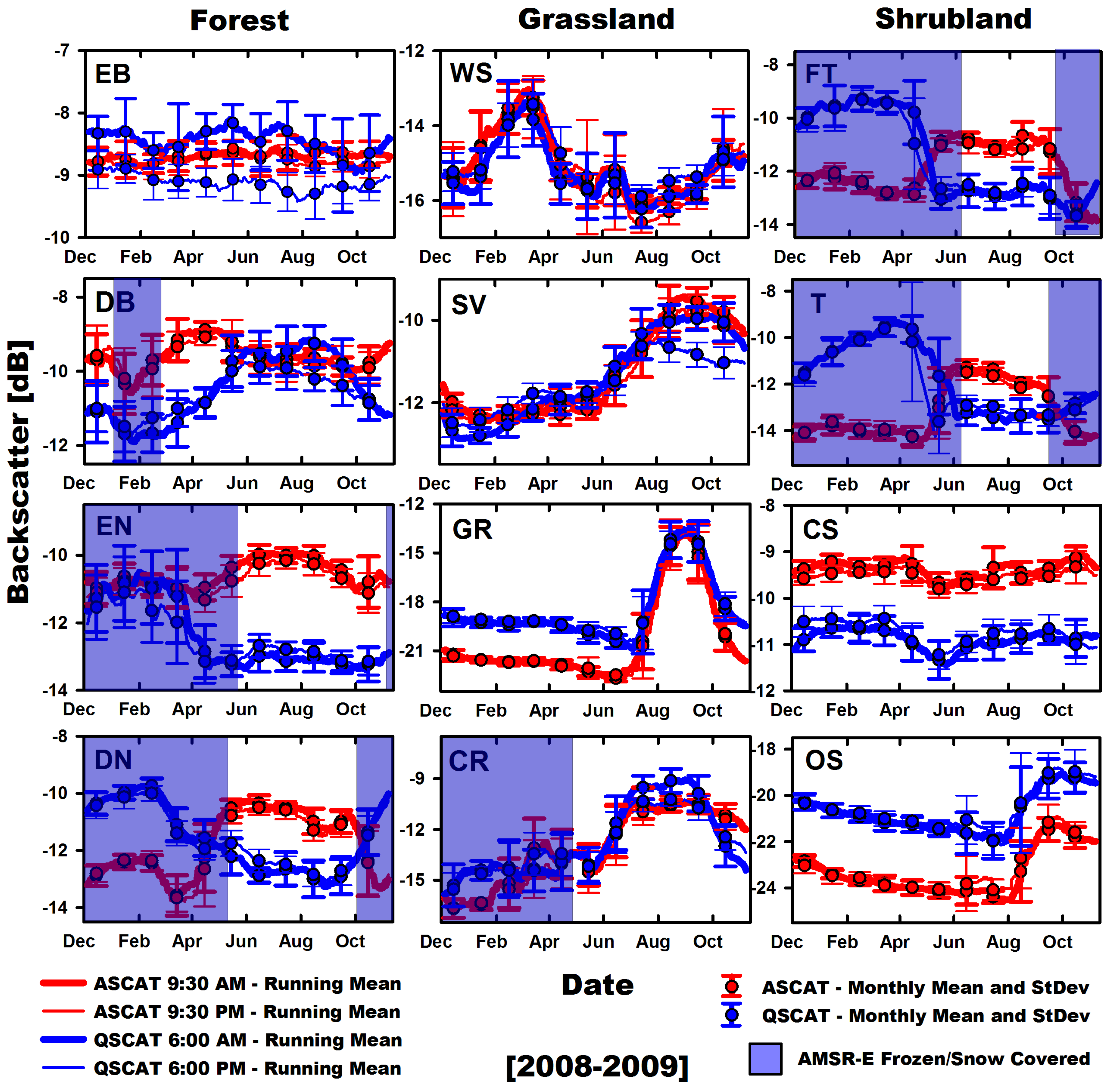
The suitability of the incidence angle and radiometric slope correction for the purpose of extending the FW record beyond the QSCAT period was evaluated next. To do so, we examined the temporal correspondence between the constant incidence angle QSCAT and the incidence angle corrected ASCAT during 1 year of overlap (November 2008–November 2009). We chose 12 vegetated and homogenous (80% classified as a single LC) evaluation sites spanning the range of MODIS LC types. Of these, six sites were identified as having seasonally frozen ground and snow cover conditions, following previously developed screening methods [
60]. To reduce the effects of weather, we aggregated daily σ
0 into 28-day moving composites including monthly means. Metrics of temporal correspondence were reported separately for screened (
i.e., seasonal frozen ground and snow cover was removed) and unscreened time series as well as for each satellite overpass to determine the orbit of maximum correspondence. Investigations on the site level were supported by grid cell-wise global calculations of Pearson’s correlation coefficients (R), excluding grid cells with ≥50% water bodies, snow/ice and urban/built-up as identified by the MODIS LC. To aid in the interpretation of spatial R patterns and to assess whether the patterns determined relate to LC and associated canopy structural differences, we stratified R based on grid cells dominated (>80%) by a single MODIS LC.
2.2. Definition of the Global SWAMPS Domains
We limited the spatial extent over which SWAMPS provides daily FW to the global land surface with <100% water bodies, snow/ice and urban/built-up as defined by the MODIS LC [
72]. This domain includes inland and coastal grid cells with FW contributions from both ocean and inland water bodies. Additionally, we screened this domain for grid cells with ≥50% water bodies to define FW in SWAMPS without costal contributions (
i.e., SWAMPS excl. coast). This additional screening eliminates a large proportion of ocean, non-ocean (e.g., large lakes) and coastal water contributions (e.g., large estuaries, river deltas and other coastal wetlands) from the SWAMPS domain and is consistent with the terrestrial focus of the global land parameter database [
58]. Seasonal snow cover and precipitating clouds over snow free surfaces can compromise FW. Screening for these conditions is thus crucial for providing accurate FW. We adopted the decision tree of Grody and Basist [
79] applied to daily (morning)
Tb records to remove grid cells contaminated by snow and frozen ground. Wet snowpacks common during winter warm periods cannot be identified with this approach [
80] and thus, if not removed from the domain, introduce erroneously high FW due to being misinterpreted as wide-spread landscape inundation. To account for this effect, we first adopted the method of Chang
et al. [
81] to estimate daily snow water equivalent (SWE) over grid cells identified by the decision tree, and second applied a 28-day moving window to SWE to conservatively remove previously unidentified grid cells of, e.g., wet, and snow. We employed the decision tree of Ferraro [
82] applied to the
Tb record to remove grid cells contaminated by precipitating clouds.
2.3. Data Record Development, Approach and Assumptions
Derivation of the SWAMPS product employs a LC-supported dynamic mixture model approach using time series satellite remote sensing radar σ0 and radiometric Tb data from a variety of sensors and wavelengths. The approach is to detect landscape inundation by identifying the temporal response of σ0 or Tb to changes in the dielectric constant of the land surface that occurs as the soil surface transitions between non-inundated and inundated conditions. The dynamic mixture model approach assumes that the large change in dielectric constant occurring between non-inundated and inundated surface conditions dominates the corresponding σ0 and Tb temporal dynamics across the non-frozen seasons, rather than other sources of temporal variability such as changes in canopy structure and biomass, atmospheric moisture variability or large precipitation events. Whether this assumption is valid for most land covers across the global domain will be examined in the results section.
To support the derivation of FW across the limits of our domain, we developed and applied a dynamic mixture model calibrated for FW detection to daily records of passive (MPDI) and active (σ
0) MW observations (
Figure 1). Construction of the mixture model involved a four step process, consisting of (1) development of a set of LC-specific models approximating seasonal biomass dynamics (
i.e., the dynamic vegetation end-member); (2) definition of a dynamic open water end-member over land using input from the Modern-Era Retrospective Analysis for Research and Application (MERRA) reanalysis of Rienecker
et al. [
83]; (3) un-mixing of the FW component given (1) and (2) and (4) construction of a consistent, global record of daily FW dynamics across multiple years.
LC-specific predictive models were developed to aid in quantifying the dynamic vegetation end-member. Input to the derivation of these models was a regression analysis applied separately to data from record periods of concurrent passive (v1 and v2) MPDI and active (ERS, QSCAT and ASCAT) σ
0 MW observations over grid cells spanning dominant MODIS LC types. MODIS LC provides a total of 17 LC classes [
71,
72]. Grid cells occupied by less than 50% of a single LC were rejected, including pixels containing any amount of water bodies, permanent wetlands and snow/ice as defined by the MODIS LC. LC classes expected to produce different MW responses when low and high-latitude regions of the same class are compared were split. This included open shrubland, woody savanna, savanna, grassland and barren land. To reduce the impact of weather, monthly climatologies from snow, ice and precipitation-screened MPDI and σ
0 observations were computed prior to the regression analysis. Monthly climatologies were generated from monthly means which were generated from daily MPDI and σ
0 observations for each record period. Screening of these data follow the methods outlined in the previous section. We used both linear and non-linear regression models to construct an optimal set of LC-specific model predictions from these data. Model performance was examined and those models which best fit the data were chosen. The resulting regression models approximate, for each LC, sub-class and record period separately, the vegetation end-member for MPDI and σ
0 regardless of the ratio of land to water within the satellites’ field of views.
Figure 1.
Flow chart of the Surface WAter Microwave Product Series (SWAMPS) surface water fraction retrieval scheme including the calibration of vegetation and open water end-members and post-product quality control.
Figure 1.
Flow chart of the Surface WAter Microwave Product Series (SWAMPS) surface water fraction retrieval scheme including the calibration of vegetation and open water end-members and post-product quality control.
Open water bodies strongly enhance sensitivity to atmospheric moisture variability when high-frequency (≥19 GHz)
Tb observations are used for FW retrieval [
84]. σ
0 of calm water is much lower than over waters roughened by wind or raindrops [
85,
86]. To solve for FW on a daily grid-by-grid cell basis, an end-member for open water that accounts for the effects of atmospheric variability on MPDI and σ
0 must be defined prior to FW retrieval. We defined this end-member by constructing regression models derived from empirical relationships between precipitation-screened MPDI and σ
0 records, and concurrent, hourly inputs of water vapor, cloud liquid water and 2 m wind speed from MERRA over open seas. Using the reanalysis as input, the models developed approximate the open water end-member for MPDI and σ
0 on land regardless of the ratio of land to water within the satellites’ field of views.
We now are able to combine the results from the regression analysis of vegetation dynamics with those from the end-member calibration of open water to quantify daily FW on a grid-by-grid cell basis within the limits of our domain. We employed a root-finding algorithm that iteratively fits a best linear solution between the open water end-member modeled independently by MERRA, the LC-specific vegetation end-member estimated from monthly MPDI and σ
0 climatologies, and daily input from the passive and active MW sensors, to obtain LC-specific and atmospherically corrected daily FW relative to end-members fully covered by water and vegetation. To obtain FW within grid cells composed of more than one MODIS LC, LC-specific FW was scaled linearly and summed according to the fractional coverage and number of LC classes within each grid cell provided by MODIS. We applied the following equation to obtain total water fraction
FWtot on a daily grid-by-grid cell basis:
where
fwlc and
fraclc denote LC-specific FW obtained from linear un-mixing, scaled by the LC-specific grid cell fraction and summed over
N land cover classes, and
fractot is the grid-based total LC fraction from MODIS, excluding contributions from water bodies, permanent wetlands and snow/ice as defined by the MODIS LC. The output of Equation (5) is the daily LC-based and atmospherically corrected total surface water fraction FW. At present, SWAMPS is available from 1992 until March 2013 consisting of daily FW record periods herein referred to as v1-ERS (01/1992–12/2000), v1-QSCAT (07/1999–04/2009) and v2-ASCAT (11/2008–03/2013).
2.4. Accuracy Assessment
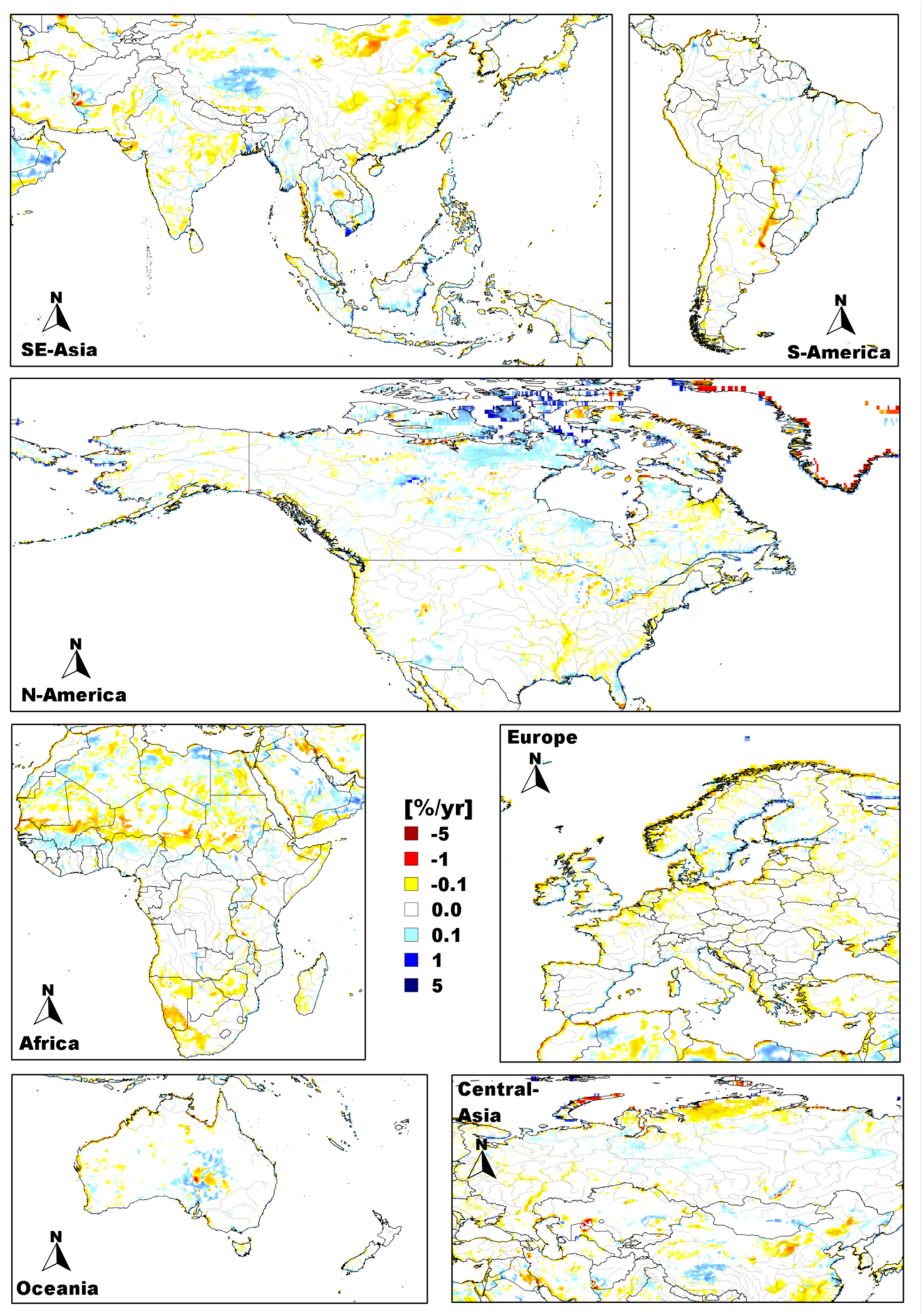
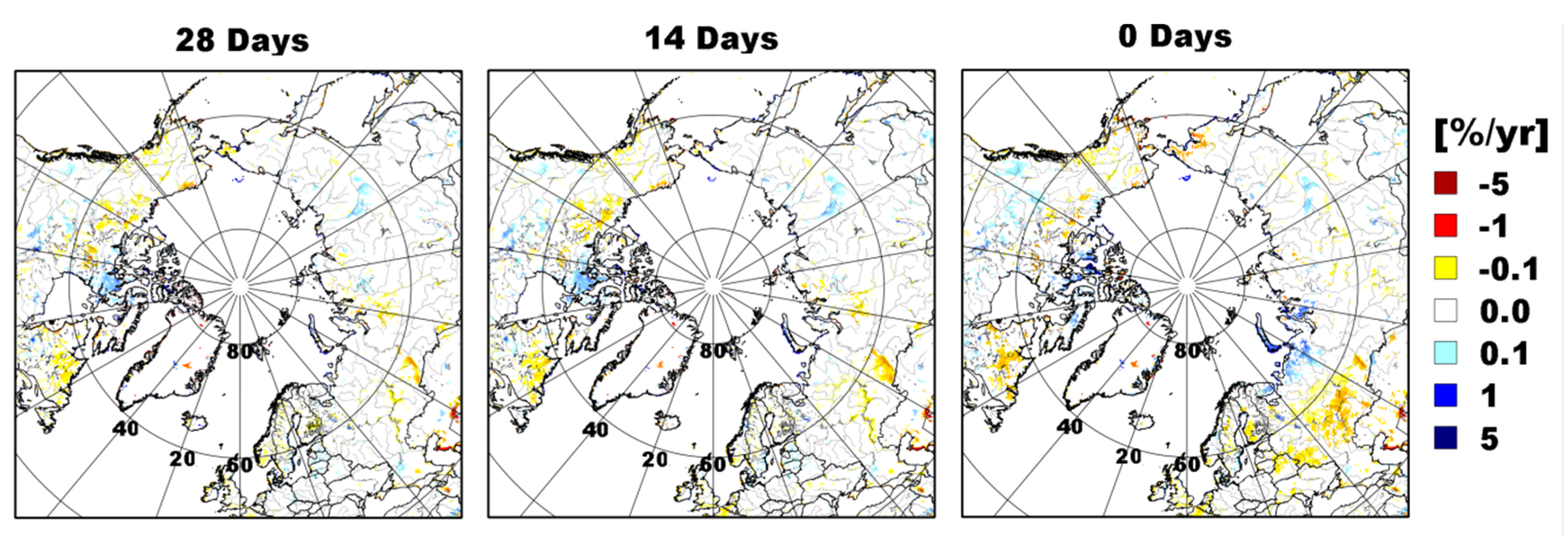
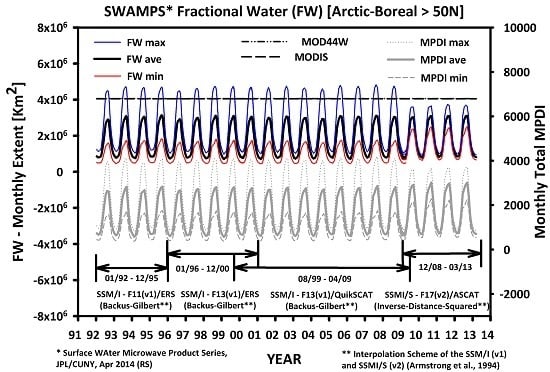
To facilitate accuracy assessment, the following temporal composites of daily FW were generated first for each record period: (1) monthly mean, minimum and maximum; (2) annual mean and average annual mean generated from (1); (3) monthly climatology generated from monthly means; and (4) the average annual maximum and minimum generated from (3). We then use these records to assess annual and seasonal FW extent and variability within the limits of our domain and the following continental regions: Arctic-Boreal (>50°N)—North America: 180°W–0°W and North Eurasia: 0°E–180°E; Tropics (30°S–30°N)—Tropical America: 180°W–25°W, Tropical Africa: 25°W–50°E and Tropical Asia: 50°E–180°E.
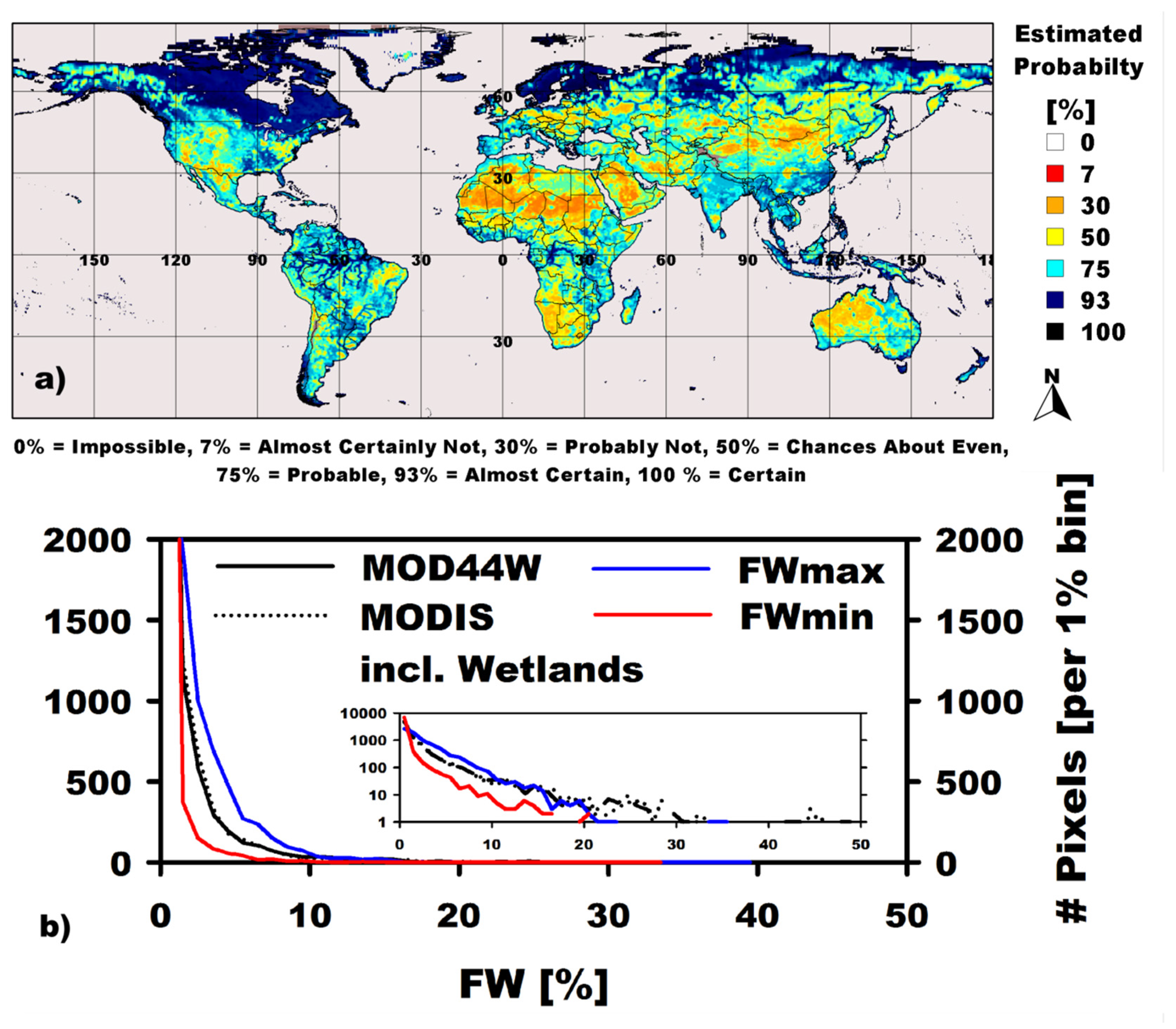
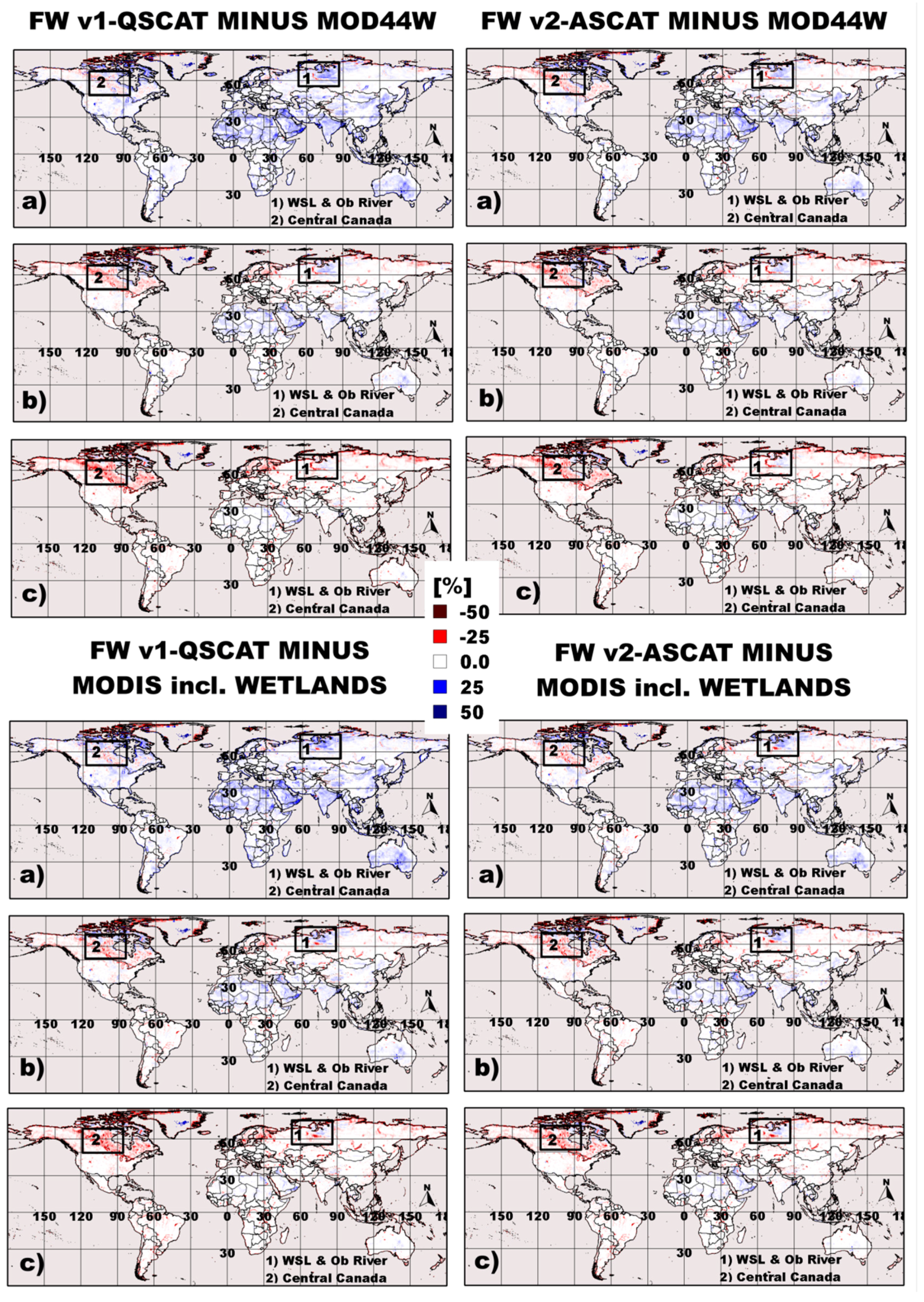
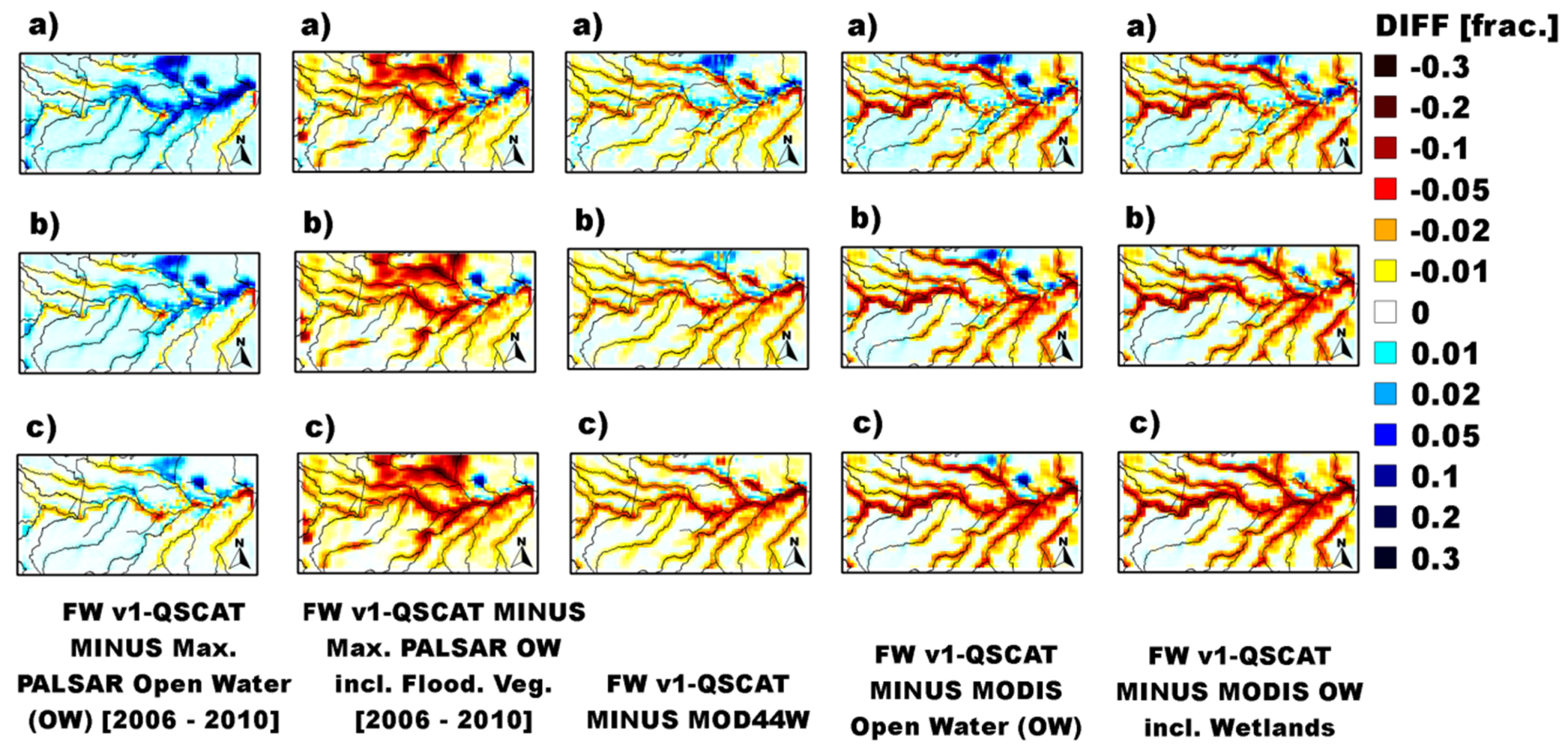
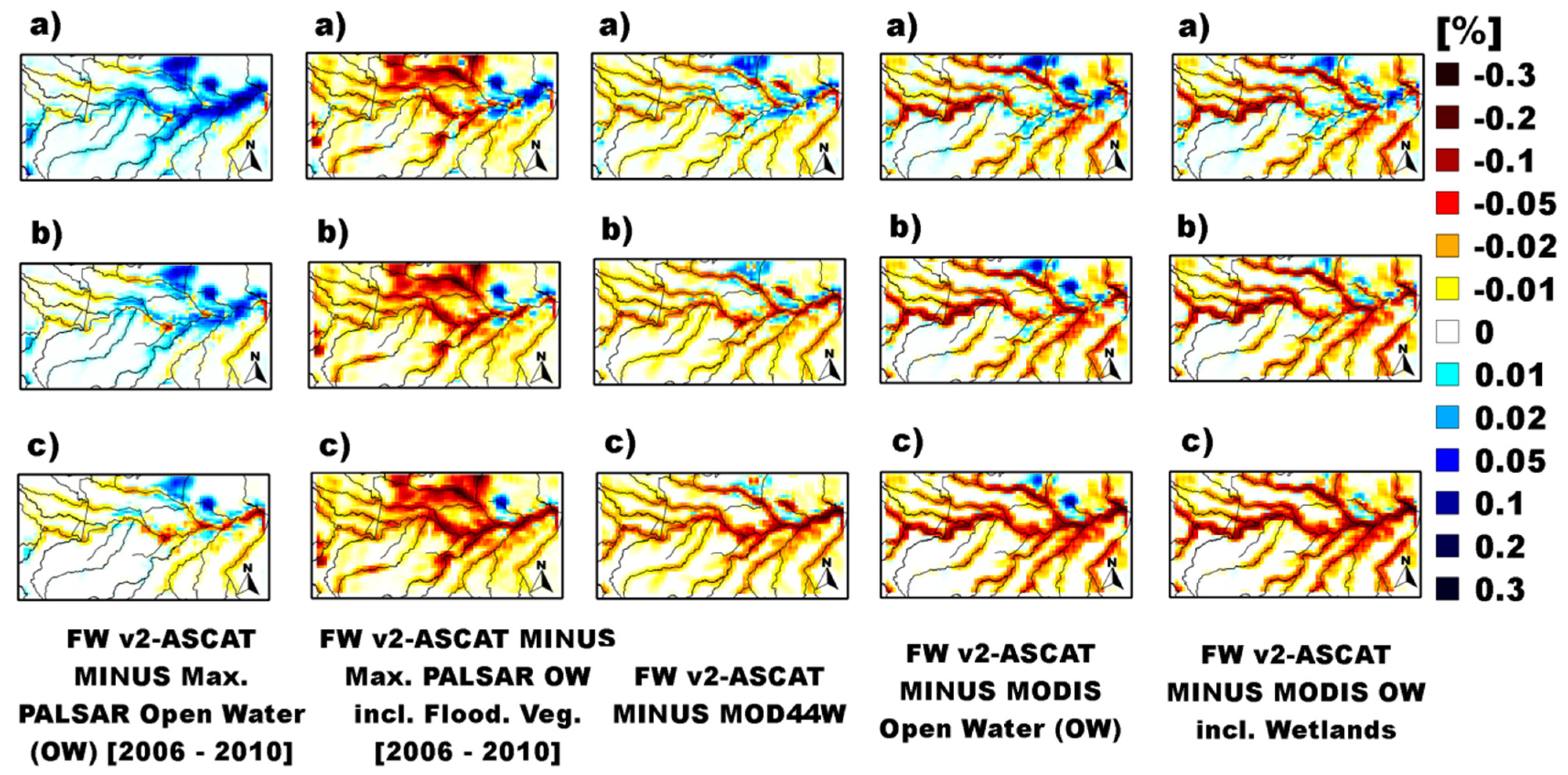
The FW composites were examined for spatial accuracy using the following independent FW products: (1) Open water (OW) bodies and permanent wetlands both from the 1-km global-scale MODIS LC product; (2) 250-m land-water mask from MODIS and the Shuttle Radar Topography Mission’s (SRTM) global-scale Water Body Dataset (MOD44W) [
87]; (3) 100-m OW and wetlands derived from the L-band Japanese Earth Resources Satellite (JERS) over the state of Alaska [
88] and (4) 100-m maximum OW and flooded forest vegetation (VEG) derived from the Advanced Land Observing Satellite (ALOS) Phased Array type L-band Synthetic Aperture Radar (PALSAR) ScanSAR over the Amazon basin [
41]. Water bodies in (1), (2) and (3) do not distinguish ocean from non-ocean water surfaces; (4) distinguishes between VEG, OW/flooded grasses and OW that was occasionally detected. It also provides an ambiguous OW class; this class was not incorporated into the comparison due to difficulty separating OW from bare ground. Maximum FW extent was generated by updating non-inundated grid cells, if in at least one image VEG or OW could be detected. Drop-in-the-bucket averaging was used to produce 25-km EASE-grids from the independent data. We applied a 3 × 3 cell (EASE-grid) weightless box-car filter to these data to account for the larger footprint size (70 × 45 km) of the 19 GHz SSM/I and SSMI/S
Tb inputs to SWAMPS. We examined the following measures of spatial correspondence: (1) coefficient of determination (R
2) to assess the percentage of spatial variability in the independent data explained by SWAMPS; (2) Mean Residual Error (MRE); and (3) Root Mean Square Error (RMSE) to provide an average bias and accuracy of SWAMPS relative to independent FW. FW from v1-ERS were not included in the comparison against these data because processing of the ERS backscatter data was still ongoing.
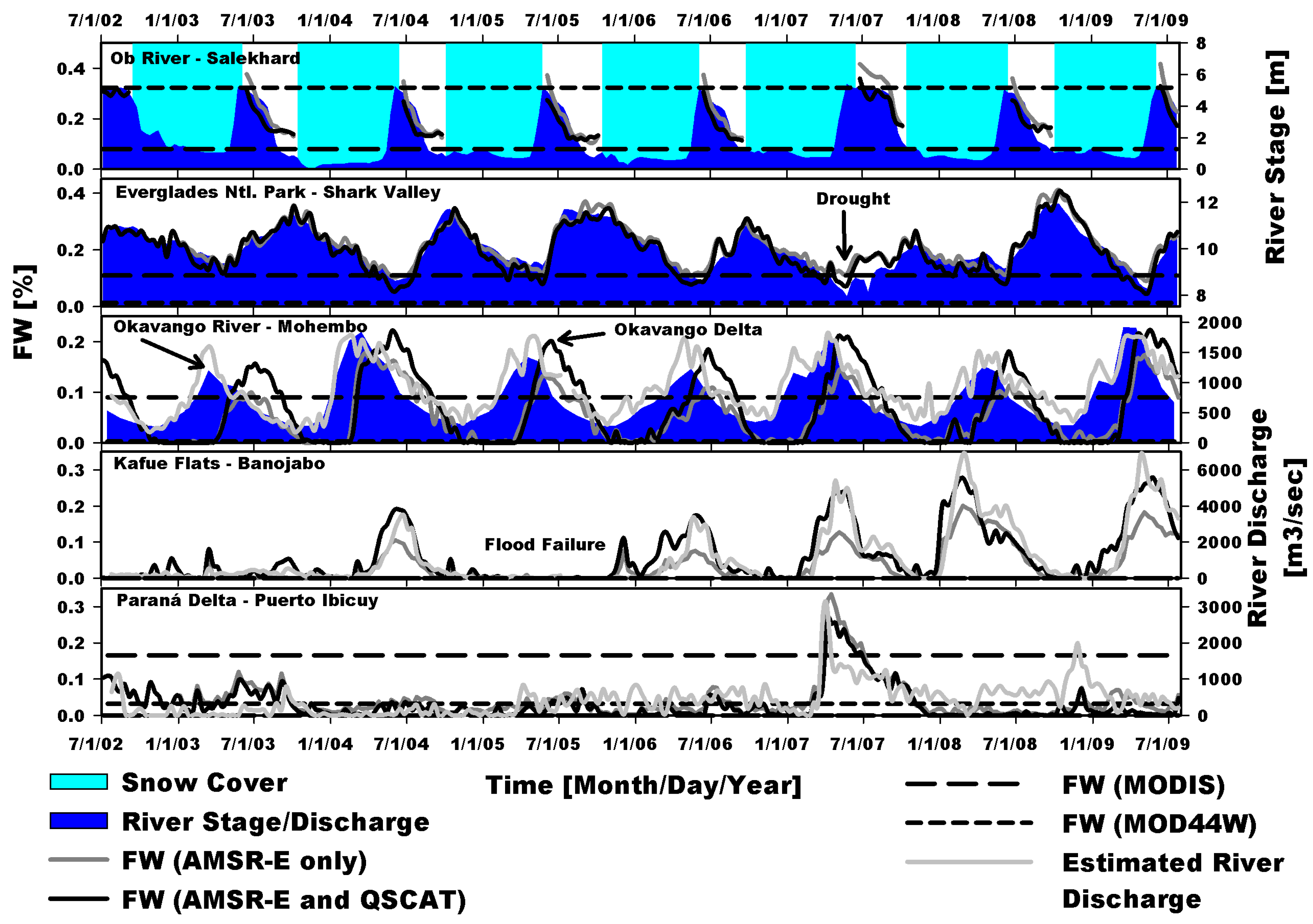
We examined the temporal accuracy of SWAMPS using concurrent precipitation (P) and river discharge (Q) records over major global river basins. Basin-averaged P was computed from the MERRA reanalysis and Q was from either WBM
plus simulations [
89] or Arctic-RIMS [
90] for the station farthest downstream. We evaluated the following measures of temporal correspondence: (1) the linear correlation coefficient (R); (2) the time-lagged (anomaly) cross-correlation coefficient (R) at maximum absolute correlation; and (3) the corresponding time-lag of the maximum (anomaly) correlation in months. Basin analyses were supported by pixel-wise calculations of R over South America (P only) and within the Amazon, Orinoco and Parana River basins (Q only) to examine lag-patterns between P, FW and Q cycles. P from MERRA was verified via P acquired from the Tropical Rainfall Measurement Mission (TRMM) multi-satellite precipitation analysis (TMPA) [
91]. Ten-day average FW records for five global wetland sites were compared against concurrent records of daily river stage height and river Q to assess the ability of the combined AMSR-E/QSCAT record, a prototype version of SWAMPS, to capture seasonal FW variations indicated by the hydrological records. Wetlands sites identified were the Ob River floodplain at Salekhard, Russia (66.53°N, 66.60°E) providing river stage height [
90], the Everglades Nat’l Park at Shark Valley, FL, USA (25.76°N, 80.77°W) providing river stage height [
92], the Okavango Delta (19.10°S, 22.55°E) providing river discharge from the delta mouth located approximately 120-km upstream at Mohembo River gauging station, Botswana [
93], the Kafue Flats at Banojabo, Zambia (15.68°S, 27.58°E) and the Paraná Delta at Puerto Ibicuy, Argentina (33.79°S, 59.19°W) providing satellite estimated river discharge [
94,
95]. FW variability for these sites was verified with coincident 10-day FW averages derived from AMSR-E [
58].
2.6. Quality Control Map
Global FW output from SWAMPS was assessed for FW accuracy relative to sensor retrievals, model results and corresponding satellite-supported P measurements generated from TRMM (supplemented by MERRA at high latitudes). We produced quality control (QC) maps from these records describing grid cell-wise static attributes of FW accuracy within the limits of our domain. Static QC attributes included (1) Tb and σ0 temporal coverage (COVER) excluding snow and precipitation events; (2) topographic variability generated from GLOBE; (3) the standard error estimates of the mixture model model predictions for each LC and (4) the plausibility of the sequence (SEQ) of seasonal inundation and precipitation events. To facilitate the first analysis, Tb and σ0 temporal gaps, including rain events and seasonal snow cover across the study domain and observation period were recorded. Areas with daily satellite coverage during the snow free season (e.g., high latitudes) and no rain events have the highest temporal coverage (COVER = 100%) while areas with limited satellite coverage and frequent rain events (e.g., tropics) have the lowest temporal coverage. Topographic variability was computed as the standard deviation of all elevation values within a 3 × 3 pixel large moving boxcar, with the lowest score (GLOBE = 0%) for areas with the highest relief variability (e.g., mountain ranges). The accuracy of the model prediction for each LC was estimated from the regression analysis of the passive and active microwave data sets. LC with large emissivity and backscatter variability not caused by seasonal biomass dynamics (e.g., barren land) receive the lowest LC score (LC = 0%). To facilitate the latter analysis, FW and P seasonal cycles were examined for temporal correspondence using phase analysis. For instance, an anti-cyclic sequence where FW decreases as P rises likely reflects modeling errors, whereas cyclic behavior tends to indicate suitable signal un-mixing and favorable FW retrievals. The resulting QC maps were linearly rescaled and aggregated to the final QC map using a weighted mean (50% SEQ, 25% LC, 15% GLOBE, 7.5% Tb and 2.5% σ0 COVER). The weights were chosen subjectively with SEQ (COVER) having the largest (smallest) expected impact on overall accuracy.
Table 1.
Relationships between Special Sensor Microwave Imager/Sounder (SSMI/S) (v2) and Special Sensor Microwave Imager (SSM/I) (v1) brightness temperatures (K × 10), during mission overlap (2007–2008), for A.M. and P.M. orbital nodes, vertical (V) and horizontal (H) polarizations, and the 19, 22, 37, and 85/91 GHz bands. Relationships are significant at a minimum 0.01 probability level.
Table 1.
Relationships between Special Sensor Microwave Imager/Sounder (SSMI/S) (v2) and Special Sensor Microwave Imager (SSM/I) (v1) brightness temperatures (K × 10), during mission overlap (2007–2008), for A.M. and P.M. orbital nodes, vertical (V) and horizontal (H) polarizations, and the 19, 22, 37, and 85/91 GHz bands. Relationships are significant at a minimum 0.01 probability level.
| Orbital Node | Polarization | 19 GHz | 22 GHz | 37 GHz | 85/91 GHz |
|---|
| [y0(1), a(2), R2(3), RMSE(4), MRE(5)] | [y0(1), a(2), R2(3), RMSE(4), MRE(5)] | [y0(1), a(2), R2(3), RMSE(4), MRE(5)] | [y0(1), a(2), R2(3), RMSE(4), MRE(5)] |
|---|
| AM | V | −85.3136, 1.0464, 0.9930, 38.5677, −36.6085 | −69.5971, 1.0342, 0.9953, 22.6536, −20.2809 | −40.2823, 1.0128, 0.9959, 12.7900, 6.8048 | 72.0668, 0.9677, 0.9890, 23.9092, 12.1443 |
| H | −49.3111, 1.0332, 0.9857, 40.8327, −36.9150 | | −33.0591, 1.0078, 0.9935, 18.9913, 14.7296 | 29.2438, 0.9834, 0.9882, 29.9569, 14.5423 |
| PM | V | 10.2076, 1.0068, 0.9923, 30.6220, −28.2329 | 11.0493, 1.0010, 0.9944, 17.0735, −13.6743 | 13.5759, 0.9894, 0.9951, 19.1385, 12.7735 | 116.9324, 0.9503, 0.9830, 25.8241, 13.7287 |
| H | 10.9150, 1.0081, 0.9844, 37.2778, −32.2804 | | 20.9808, 0.9857, 0.9924, 23.0815, 16.8249 | 83.1874, 0.9614, 0.9819, 33.1488, 18.3033 |