Automatic Orientation of Multi-Scale Terrestrial Images for 3D Reconstruction
Abstract
:1. Introduction
2. Automatic Method for 3D Point Determination
2.1. Camera Calibration
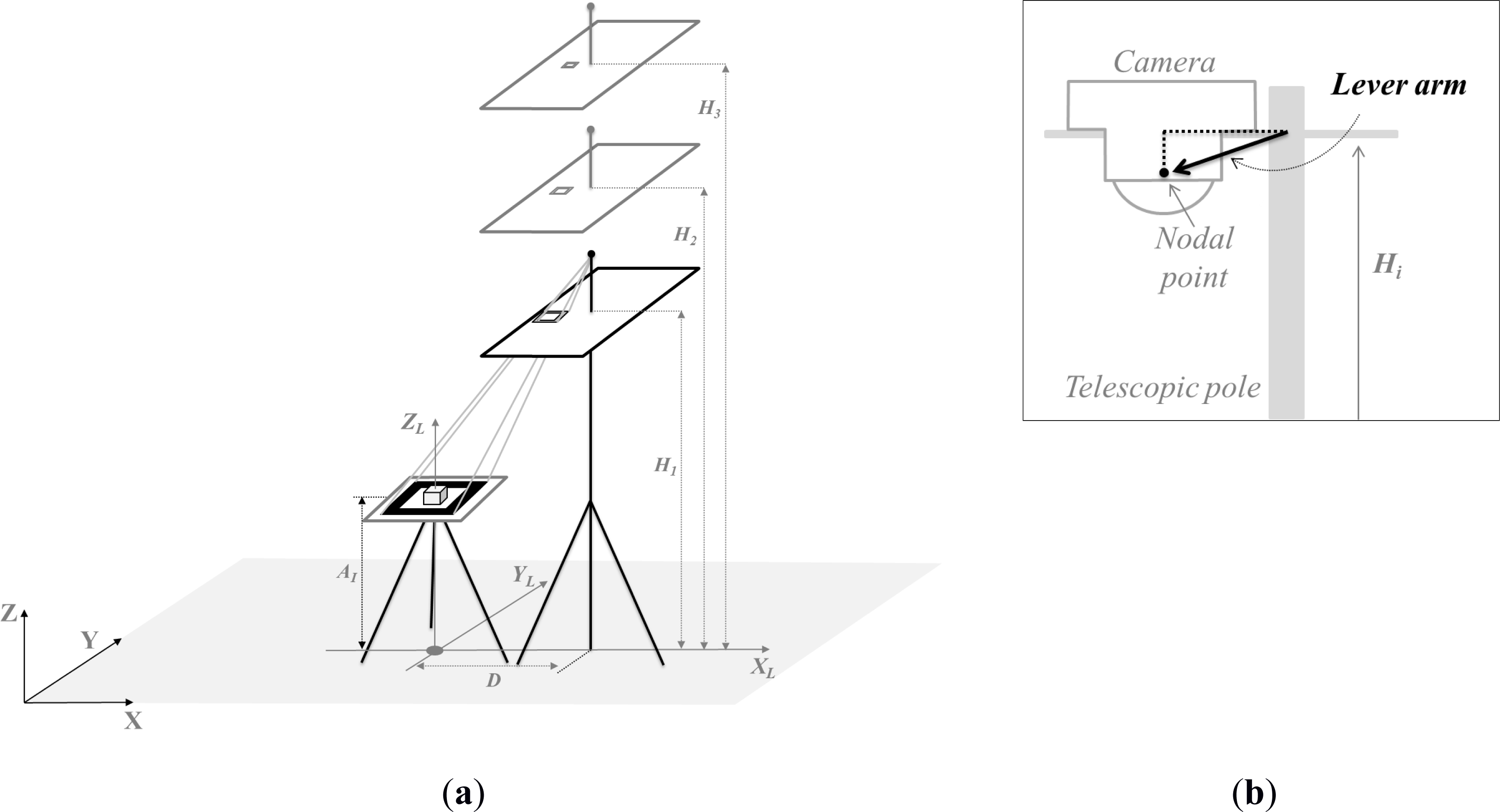
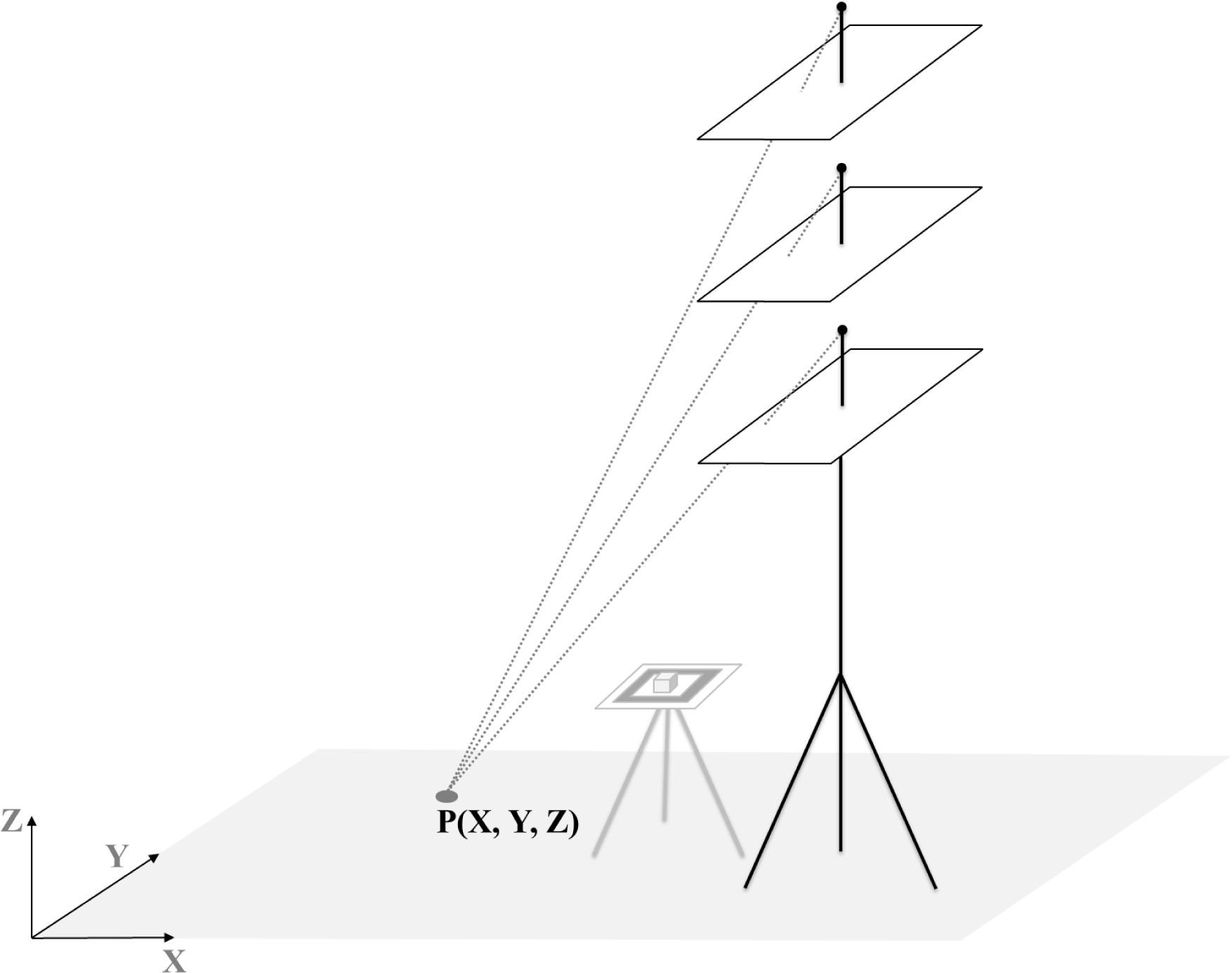
2.2. Image Acquisition
2.3. Automatic Target Detection
2.4. Generation of Multi-Scale Models
2.5. Determination of 3D Points
3. Experimental Results and Analysis
- The first trial was performed in a terrestrial calibration field mounted with ARUCO-coded targets with known terrestrial coordinates for automatic recognition. This test provided an assessment of the accuracy that can be achieved with the proposed technique based on the accurate coordinates of the targets in the calibration field.
- The second trial was applied in a typical area with distinct features to exemplify a practical application of the technique.
3.1. Camera Calibration in the Terrestrial Test Field
3.2. Experiments in the Calibration Field
- Indirect determination: The known values of the EOPs are used as approximated values in the bundle adjustment. These values are obtained from the relative positioning between the GNSS receiver and telescopic pole with the estimated heights from the graduated rule in the telescopic pole. Standard deviations of σ = 0.5 m for the (XC, YC, ZC) position and σ = 30° for the attitude were configured in the bundle adjustment, meaning that this initial value will not have any influence on the solution.
- Direct determination: The known values of the EOPs will be used as observations or weighted constraints in the bundle adjustment. These values are estimated using the distance directly measured between the GNSS receiver and telescopic pole, the heights were measured with an EDM, and the lever arm (displacement between the external lens nodal point and the platform supported by the pole; see Figure 2b) was previously estimated. The standard deviations of the camera positions were considered as σ = 10 cm in XC and YC and σ = 5 mm in ZC due to the displacements and movements involved in lifting the camera. For the attitude, the standard deviation was considered to be σ = 10°. These values likely will not have a significant role in the bundle solution.
3.3. Experiments in Areas with Distinct Features
4. Conclusions
- Occlusions can occur at the limits of these multi-scale images; however, the central area is not occluded because the receiver must be always positioned in open areas to collect GNSS signals.
- The geometry is not optimal, but it is sufficient to reconstruct the central region of the image. If a second camera station is added, the geometry can be improved but at the cost of some additional operations;
- Only small areas are reconstructed, but large enough to cover the main features of a scene.
- The image acquisition is performed while the GCP is being surveyed. There is no additional time delay to take these pictures. Only a few additional measurements are required (horizontal and vertical distance between the GNSS receiver and the camera). The time for images acquisition is compatible with the GNSS surveying period; also, the entire system can be mounted in a few minutes;
- There is no need to change the pole position as in a conventional stereo pair acquisition. The image acquisition does not add remarkable complexity into the surveying process;
- The operator can be the same surveyor that set the GNSS receiver. No expert operator is required as in the case of using an UAV;
- High-resolution terrestrial images of the GCPs (GSD less than 3 mm) can be obtained and consequently used to generate the ortho-images to serve as control chips populating an image database;
- The control panel can be positioned in any area covering distinct features. The technique does not depend on point features (which are not always available anywhere). Areas can also be used in the image matching procedures;
- The acquisition technique and multi-scale processing are original;
- There is no significant investment with materials.
Acknowledgments
Author contribution
Conflicts of Interest
References
- Dandois, J.P.; Ellis, E.C. Remote sensing of vegetation structure using computer vision. Remote Sens 2010, 2, 1157–1176. [Google Scholar]
- Wondie, M.; Schneider, W.; Melesse, A.M.; Teketay, D. Spatial and temporal land cover changes in the Simen Moutains national park, a world heritage site in northwestern Ethiopia. Remote Sens 2011, 3, 752–766. [Google Scholar]
- Nakano, K.; Chikatsu, H. Camera-variant calibration and sensor modeling for practical photogrammetry in archeological sites. Remote Sens 2011, 3, 554–569. [Google Scholar]
- Harwin, S.; Lucieer, A. Assessing the accuracy of georeferenced point clouds produced via multi-view stereopsis from unmanned aerial vehicle (UAV) imagery. Remote Sens 2012, 4, 1573–1599. [Google Scholar]
- Tommaselli, A.M.G.; Galo, M.; Moraes, M.V.A.; Marcato Junior, J.; Caldeira, C.R.T.; Lopes, R.F. Generating virtual images from oblique frames. Remote Sens 2013, 5, 1875–1893. [Google Scholar]
- Gülch, E. Automatic Control Point Measurement. In Proceedings of the Photogrammetric Week’95, Heidelberg, Germany, 11–15 November 1995; pp. 185–196.
- Heipke, C. Automation of interior, relative, and absolute orientation. ISPRS J. Photogramm. Remote Sens 1997, 52, 1–19. [Google Scholar]
- Hahn, M. Automatic Control Point Measurement. In Proceedings of the Photogrammetric Week’97, Heidelberg, Germany, 22–26 September 1997; pp. 115–126.
- Jaw, J.-J.; Wu, Y.-S. Control pacthes for automatic single photo orientation. Photogramm. Eng. Remote Sens 2006, 72, 151–157. [Google Scholar]
- Berveglieri, A.; Marcato Junior, J.; Moraes, M.V.A; Tommaselli, A.M.G. Automatic Location and Measurement of Ground Control Points Based on Vertical Terrestrial Images. In Proceedings of Remote Sensing and Photogrammetry Society Conference, London, UK, 12–14 September 2012.
- Remondino, F.; El-Hakim, S. Image-based 3D modeling: A review. Photogramm. Rec 2006, 21, 269–291. [Google Scholar]
- Barazzetti, L.; Scaioni, M.; Remondino, F. Orientation and 3D modeling from markerless terrestrial images: Combining accuracy with automation. Photogramm. Rec 2010, 25, 356–381. [Google Scholar]
- Luhmann, T; Robson, S.; Kyle, S.; Harley, I. Close Range Photogrammetry: Principles, Techniques and Applications; Whittles Publishing: Scotland, UK, 2006; p. 510. [Google Scholar]
- Brown, D.C. Close-range calibration. Photogramm. Eng 1971, 37, 855–866. [Google Scholar]
- Habib, A.F.; Morgan, M.F. Automatic calibration of low-cost digital cameras. Opt. Eng 2003, 42, 948–955. [Google Scholar]
- Schneider, D.; Schwalbe, E.; Maas, H.G. Validation of geometric models for fisheye lenses. ISPRS J. Photogramm. Remote Sens 2009, 64, 259–266. [Google Scholar]
- Freitas, V.L.S.; Tommaselli, A.M.G. An Adaptive Technique for Shadow Segmentation in High-Resolution Omnidirectional Images. In Proceedings of the IX Workshop de Visão Computacional, Rio de Janeiro, Brazil, 3–5 June 2013.
- Harris, C.; Stephens, M. A. Combined Corner and Edge Detector. In Proceedings of the 4th Alvey Vision Conference, Manchester, UK, 31 August–2 September 1988; pp. 147–151.
- Moravec, H.P. Towards Automatic Visual Obstacle Avoidance. In Proceedings of the 5th International Joint Conference on Artificial Intelligence, Cambrigde, MA, USA, 22 August 1977.
- Förstner, W. A. Feature based correspondence algorithm for image matching. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 1986, 26, 150–166. [Google Scholar]
- Schmid, C.; Mohr, R.; Bauckhage, C. Evaluation of interest point detectors. Int. J. Comput. Vis 2000, 37, 151–172. [Google Scholar]
- Jazayeri, I.; Fraser, C. Interest operators for feature based matching in close range photogrammetry. Photogramm. Rec 2010, 25, 24–41. [Google Scholar]
- Garrido-Jurado, S.; Muñoz-Salinas, R.; Madrid-Cuevas, F.J.; Marín-Jiménez, M.J. Automatic generation and detection of highly reliable fiducial markers under oclusion. Pattern Recognit 2014, 47, 2280–2292. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis 2004, 60, 91–110. [Google Scholar]
- Lingua, A.; Marenchino, D.; Nex, F. Performance analysis of the SIFT operator for automatic feature extraction and matching in photogrammetric applications. Sensors 2009, 9, 3745–3766. [Google Scholar]
- Tommaselli, A.M.G.; Polidori, L.; Hasegawa, J.K.; Camargo, P.O.; Hirao, H.; Moraes, M.V.A.; Rissate Junior, E.A.; Henrique, G.R.; Abreu, P.A.G.; Berveglieri, A.; et al. Using Vertical Panoramic Images to Record a Historic Cemetery. In Proceedings of the XXIV International CIPA Symposium, Strasbourg, France, 2–6 September 2013.
- Blachut, T.J.; Chrzanowski, A.; Saastamoinen, J.H. Map Projection Systems for Urban Areas. In Urban Surveying and Mapping; Springer-Verlag: New York, NY, USA, 1979; pp. 12–41. [Google Scholar]








| Camera model | Nikon D3100 |
| Sensor size | CMOS APS-C (23.1 × 15.4 mm) |
| Image dimension | 4608 × 3072 pixels (14.2 megapixels) |
| Pixel size | 0.005 mm |
| Nominal focal length | 8.0 mm (Bower SLY 358N) |
| Parameters | Estimated Values | Estimated Standard Deviations |
|---|---|---|
| f (mm) | 8.3794 | 0.0011 (±0.23 pixels) |
| x0 (mm) | 0.0729 | 0.0011 (±0.22 pixels) |
| y0 (mm) | 0.0019 | 0.0009 (±0.18 pixels) |
| K1 (mm−2) | 4.20 × 10−4 | 3.77 × 10−6 |
| K2 (mm−4) | 8.20 × 10−7 | 6.32 × 10−8 |
| K3 (mm−6) | −2.54 × 10−9 | 3.12 × 10−1° |
| P1 (mm−1) | 4.84 × 10−6 | 1.63 × 10−6 |
| P2 (mm−1) | −2.28 × 10−7 | 1.67 × 10−6 |
| A | 3.34 × 10−5 | 1.88 × 10−5 |
| B | −7.43 × 10−4 | 3.58 × 10−5 |
| σ naught | 0.0054 (≈1 pixel) |
| Initial Values for the EOPs | Group I (17 Tie Points) RMSE (m) | Group II (9 Tie Points) RMSE (m) | Group III (4 Tie Points) RMSE (m) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| X | Y | Z | X | Y | Z | X | Y | Z | |
| Indirect Determination | 0.019 | 0.016 | 0.023 | 0.019 | 0.018 | 0.021 | 0.034 | 0.027 | 0.029 |
| Direct Determination | 0.013 | 0.017 | 0.013 | 0.013 | 0.019 | 0.010 | 0.026 | 0.032 | 0.011 |
| Initial Values for the EOPs | Group I (17 Tie Points) RMSE (m) | Group II (9 Tie Points) RMSE (m) | Group III (4 Tie Points) RMSE (m) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| X | Y | Z | X | Y | Z | X | Y | Z | |
| Indirect Determination | 0.020 | 0.016 | 0.031 | 0.022 | 0.020 | 0.026 | 0.035 | 0.020 | 0.035 |
| Direct Determination | 0.011 | 0.017 | 0.023 | 0.011 | 0.020 | 0.018 | 0.019 | 0.025 | 0.026 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Tommaselli, A.M.G.; Berveglieri, A. Automatic Orientation of Multi-Scale Terrestrial Images for 3D Reconstruction. Remote Sens. 2014, 6, 3020-3040. https://doi.org/10.3390/rs6043020
Tommaselli AMG, Berveglieri A. Automatic Orientation of Multi-Scale Terrestrial Images for 3D Reconstruction. Remote Sensing. 2014; 6(4):3020-3040. https://doi.org/10.3390/rs6043020
Chicago/Turabian StyleTommaselli, Antonio M. G., and Adilson Berveglieri. 2014. "Automatic Orientation of Multi-Scale Terrestrial Images for 3D Reconstruction" Remote Sensing 6, no. 4: 3020-3040. https://doi.org/10.3390/rs6043020






