Comparison of Gross Primary Productivity Derived from GIMMS NDVI3g, GIMMS, and MODIS in Southeast Asia
Abstract
:1. Introduction
2. Method and Data
2.1. Models
2.1.1. GLOPEM-CEVSA
2.1.2. The MODIS Algorithm (MOD17)
2.2. Main Data for GLOPEM-CEVSA Model Input and Validations
2.2.1. Meteorological Data
2.2.2. Remotely Sensed Data
(1) GIMMS FPAR
(2) MODIS FPAR
(3) Land Cover
2.2.3. Validation and Comparison of the Derived GPPs
(1) GPP Validation Data
(2) Methods of Validation and Their Comparison
3. Results
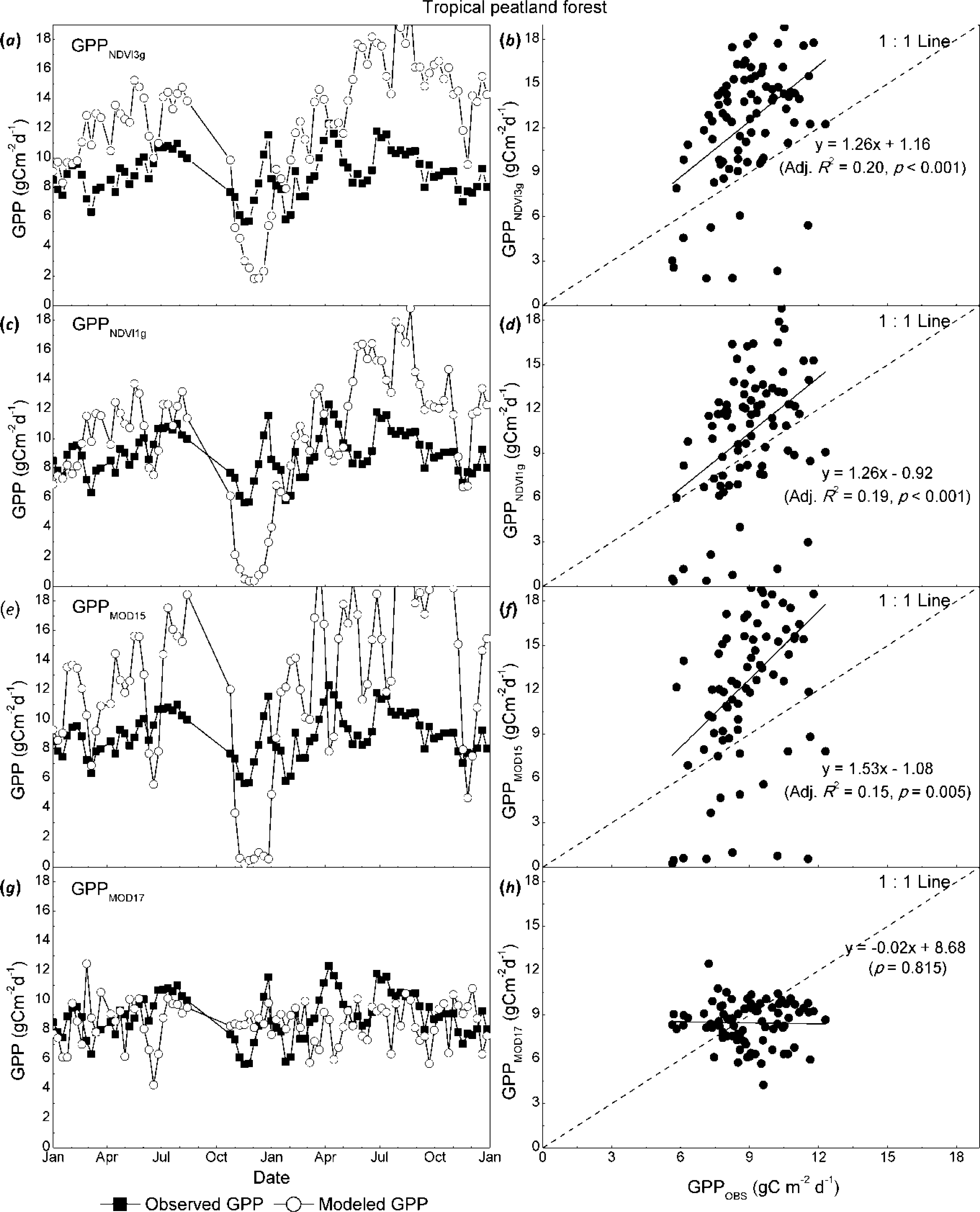
3.1. GPP Assessments on Seasonal Scale
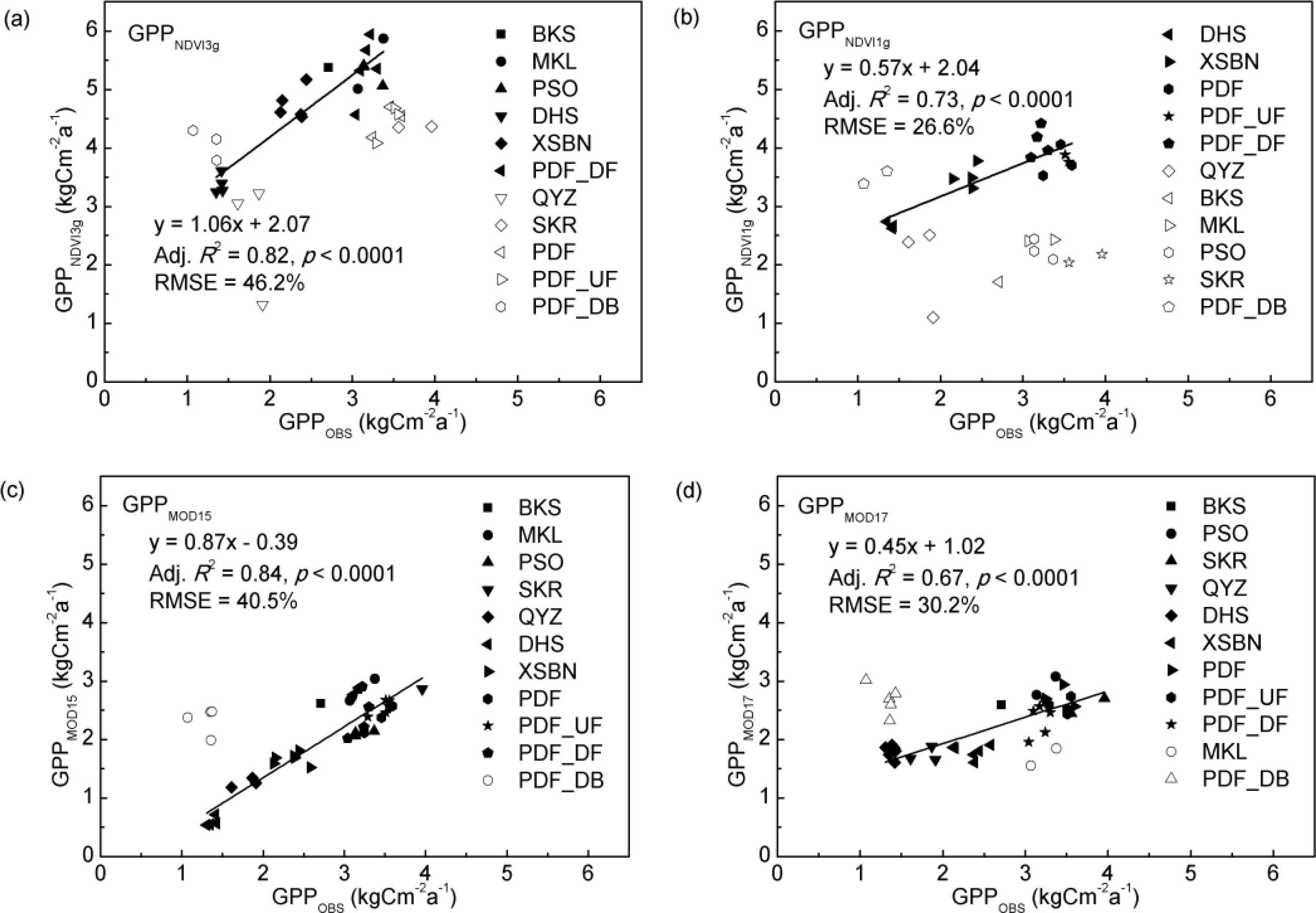
3.2. GPP Assessments on Annual Scale
3.3. Spatial and Temporal Comparison among Four GPP Results
4. Discussion
4.1. Uncertainty in GPP Modelling
4.2. Uncertainty in FPAR
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Xiao, X.; Hollinger, D.; Aber, J.; Goltz, M.; Davidson, E.A.; Zhang, Q.; Moore, B. Satellite-based modeling of gross primary production in an evergreen needleleaf forest. Remote Sens. Environ 2004, 89, 519–534. [Google Scholar]
- Gao, Q.; Li, Y.; Wan, Y.; Qin, X.; Wang, J.; Liu, Y. Dynamics of alpine grassland NPP and its response to climate change in Northern Tibet. Clim. Chang 2009, 97, 515–528. [Google Scholar]
- Beer, C.; Reichstein, M.; Tomelleri, E.; Ciais, P.; Jung, M.; Carvalhais, N.; Rodenbeck, C.; Arain, M.A.; Baldocchi, D.; Bonan, G.B.; et al. Terrestrial gross carbon dioxide uptake: Global distribution and covariation with climate. Science 2010, 329, 834–838. [Google Scholar]
- Falge, E.; Baldocchi, D.; Tenhunen, J.; Aubinet, M.; Bakwin, P.; Berbigier, P.; Bernhofer, C.; Burba, G.; Clement, R.; Davis, K.J.; et al. Seasonality of ecosystem respiration and gross primary production as derived from FLUXNET measurements. Agric. For. Meteorol 2002, 113, 53–74. [Google Scholar]
- Luo, T.; Li, W.; Zhu, H. Estimated biomass and productivity of natural vegetation on the Tibetan Plateau. Ecol. Appl 2002, 12, 980–997. [Google Scholar]
- Piao, S.; Fang, J.; He, J. Variations in vegetation net primary production in the Qinghai-Xizang Plateau, China, from 1982 to 1999. Clim. Chang 2006, 74, 253–267. [Google Scholar]
- Baldocchi, D.D. Assessing the eddy covariance technique for evaluating carbon dioxide exchange rates of ecosystems: Past, present and future. Glob. Chang. Biol 2003, 9, 479–492. [Google Scholar]
- Running, S.W.; Baldocchi, D.; Turner, D.; Gower, S.; Bakwin, P.; Hibbard, K. A global terrestrial monitoring network integrating tower fluxes, flask sampling, ecosystem modeling and EOS satellite data. Remote Sens. Environ 1999, 70, 108–127. [Google Scholar]
- Wang, J.; Liu, J.; Cao, M.; Liu, Y.; Yu, G.; Li, G.; Qi, S.; Li, K. Modelling carbon fluxes of different forests by coupling a remote-sensing model with an ecosystem process model. Int. J. Remote Sens 2011, 32, 6539–6567. [Google Scholar]
- Cao, M.; Yu, G.; Liu, J.; Li, K. Multi-scale observation and cross-scale mechanistic modeling on terrestrial ecosystem carbon cycle. Sci. China Ser. D 2005, 48, 17–32. [Google Scholar]
- Liu, J.; Chen, J.; Cihlar, J.; Park, W. A process-based boreal ecosystem productivity simulator using remote sensing inputs. Remote Sens. Environ 1997, 62, 158–175. [Google Scholar]
- Churkina, G.; Tenhunen, J.; Thornton, P.; Falge, E.M.; Elbers, J.A.; Erhard, M.; Grunwald, T.; Kowalski, A.S.; Rannik, U.; Sprinz, D. Analyzing the ecosystem carbon dynamics of four European coniferous forests using a biogeochemistry model. Ecosystems 2003, 6, 168–184. [Google Scholar]
- Law, B.E.; Waring, R.H.; Anthoni, P.M.; Aber, J.D. Measurements of gross and net ecosystem productivity and water vapour exchange of a Pinus ponderosa ecosystem, and an evaluation of two generalized models. Glob. Chang. Biol 2000, 6, 155–168. [Google Scholar]
- Churkina, G.; Running, S.W. Contrasting climatic controls on the estimated productivity of global terrestrial biomes. Ecosystems 1998, 1, 206–215. [Google Scholar]
- Turner, D.P.; Urbanski, S.; Bremer, D.; Wofsy, S.C.; Meyers, T.; Gower, S.T.; Gregory, M. A cross-biome comparison of daily light use efficiency for gross primary production. Glob. Chang. Biol 2003, 9, 383–395. [Google Scholar]
- Turner, D.P.; Ritts, W.D.; Cohen, W.B.; Gower, S.T.; Zhao, M.; Running, S.W.; Wofsy, S.C.; Urbanski, S.; Dunn, A.L.; Munger, J.W. Scaling Gross Primary Production (GPP) over boreal and deciduous forest landscapes in support of MODIS GPP product validation. Remote Sens. Environ 2003, 88, 256–270. [Google Scholar]
- Xiao, X.; Zhang, Q.; Braswell, B.; Urbanski, S.; Boles, S.; Wofsy, S.; Moore, B., III; Ojima, D. Modeling gross primary production of temperate deciduous broadleaf forest using satellite images and climate data. Remote Sens. Environ 2004, 91, 256–270. [Google Scholar]
- Xiao, X.M.; Zhang, Q.Y.; Hollinger, D.; Aber, J.; Moore, B. Modeling gross primary production of an evergreen needleleaf forest using modis and climate data. Ecol. Appl 2005, 15, 954–969. [Google Scholar]
- Behrenfeld, M.J.; Randerson, J.T.; McClain, C.R.; Feldman, G.C.; Los, S.O.; Tucker, C.J.; Falkowski, P.G.; Field, C.B.; Frouin, R.; Esaias, W.E. Biospheric primary production during an ENSO transition. Science 2001, 291, 2594–2597. [Google Scholar]
- Field, C.B.; Randerson, J.T.; Malmstrom, C.M. Global net primary production: Combining ecology and remote sensing. Remote Sens. Environ 1995, 51, 74–88. [Google Scholar]
- Potter, C.S.; Randerson, J.T.; Field, C.B.; Matson, P.A.; Vitousek, P.M.; Mooney, H.A.; Klooster, S.A. Terrestrial ecosystem production: A process model based on global satellite and surface data. Glob. Biogeochem. Cycle 1993, 7, 811–841. [Google Scholar]
- Prince, S.D.; Goward, S.N. Global primary production: A remote sensing approach. J. Biogeog 1995, 2, 815–835. [Google Scholar]
- Ruimy, A.; Saugier, B.; Dedieu, G. Methodology for the estimation of terrestrial net primary production from remotely sensed data. J. Geophys. Res.-Atmos 1994, 99, 5263–5283. [Google Scholar]
- Alton, P.; Bodin, P. A comparative study of a multilayer and a productivity (light-use) efficiency land-surface model over different temporal scales. Agric. For. Meteorol 2010, 150, 182–195. [Google Scholar]
- Zhao, M.S.; Heinsch, F.A.; Nemani, R.R.; Running, S.W. Improvements of the MODIS terrestrial gross and net primary production global data set. Remote Sens. Environ 2005, 95, 164–176. [Google Scholar]
- Yuan, W.; Liu, S.; Zhou, G.; Zhou, G.; Tieszen, L.L.; Baldocchi, D.; Bernhofer, C.; Gholz, H.; Goldstein, A.H.; Goulden, M.L.; et al. Deriving a light use efficiency model from eddy covariance flux data for predicting daily gross primary production across biomes. Agr. For. Meteorol 2007, 143, 189–207. [Google Scholar]
- Wu, C.; Munger, J.W.; Niu, Z.; Kuang, D. Comparison of multiple models for estimating gross primary production using MODIS and eddy covariance data in Harvard Forest. Remote Sens. Environ 2010, 114, 2925–2939. [Google Scholar]
- Ryu, Y.; Baldocchi, D.D.; Kobayashi, H.; Ingen, C.; Li, J.; Black, T.A.; Beringer, J.; Gorsel, E.; Knohl, A.; Law, B.E. Integration of MODIS land and atmosphere products with a coupled-process model to estimate gross primary productivity and evapotranspiration from 1 km to global scales. Glob. Biogeochem. Cycle 2011, 25. [Google Scholar] [CrossRef] [Green Version]
- Wu, C.; Chen, J.M.; Desai, A.R.; Hollinger, D.Y.; Arain, M.A.; Margolis, H.A.; Gough, C.M.; Staebler, R.M. Remote sensing of canopy light use efficiency in temperate and boreal forests of North America using MODIS imagery. Remote Sens. Environ 2012, 118, 60–72. [Google Scholar]
- Cramer, W.; Kicklighter, D.; Bondeau, A.; Iii, B.M.; Churkina, G.; Nemry, B.; Ruimy, A.; Schloss, A. Comparing global models of terrestrial net primary productivity (NPP): Overview and key results. Glob. Chang. Biol 1999, 5, 1–15. [Google Scholar]
- Zhao, G.; Wang, J.; Fan, W.; Ying, T. Vegetation net primary productivity in Northeast China in 2000–2008: Simulation and seasonal change. Chin. J. Appl. Ecol 2011, 22, 621–630. [Google Scholar]
- Wang, J.; Liu, J.; Shao, Q.; Liu, R.; Fan, J.; Chen, Z. Spatial-temporal patterns of net primary productivity for 1988–2004 based on GLOPEM-CEVSA model in the “Three-river Headwaters” region of Qinghai province, China. Chin. J. Plant Ecol 2009, 33, 254–269. [Google Scholar]
- Tucker, C.J.; Pinzon, J.E.; Brown, M.E.; Slayback, D.A.; Pak, E.W.; Mahoney, R.; Vermote, E.F.; El Saleous, N. An extended AVHRR 8-km NDVI dataset compatible with MODIS and SPOT vegetation NDVI data. Int. J. Remote Sens 2005, 26, 4485–4498. [Google Scholar]
- Sellers, P.J. Canopy reflectance, photosynthesis and transpiration. Int. J. Remote Sens 1985, 6, 1335–1372. [Google Scholar]
- Sellers, P.J.; Tucker, C.J.; Collatz, G.J.; Los, S.O.; Justice, C.O.; Dazlich, D.A.; Randall, D.A. A revised land surface parameterization (SiB2) for atmospheric GCMS. Part II: The generation of global fields of terrestrial biophysical parameters from satellite data. J. Clim 1996, 9, 706–737. [Google Scholar]
- Myneni, R.B. “Special Issue Monitoring Global Vegetation with AVHRR NDVI3g Data (1981–2011)”. Available online: https://www.mdpi.com/journal/remotesensing/special_issues/monitoring_global (accessed on 20 March 2013).
- Zeng, F.-W.; Collatz, G.J.; Pinzon, J.E.; Ivanoff, A. Evaluating and quantifying the climate-driven interannual variability in global inventory modeling and mapping studies (GIMMS) normalized difference vegetation index (NDVI3g) at global scales. Remote Sens 2013, 5, 3918–3950. [Google Scholar]
- Monteith, J.; Moss, C. Climate and the efficiency of crop production in Britain [and discussion]. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci 1977, 281, 277–294. [Google Scholar]
- Monteith, J. Solar radiation and productivity in tropical ecosystems. J. Appl. Ecol 1972, 747–766. [Google Scholar]
- Goetz, S.J.; Prince, S.D. Modelling terrestrial carbon exchange and storage: Evidence and implications of functional convergence in light-use efficiency. Adv. Ecol. Res 1999, 28, 57–92. [Google Scholar]
- Goetz, S.J.; Prince, S.D.; Small, J.; Gleason, A.C.R. Interannual variability of global terrestrial primary production: Results of a model driven with satellite observations. J. Geophys. Res 2000, 105, 20077–20091. [Google Scholar]
- Goetz, S.J.; Prince, S.D.; Goward, S.N.; Thawley, M.M.; Small, J. Satellite remote sensing of primary production: An improved production efficiency modeling approach. Ecol. Model 1999, 122, 239–255. [Google Scholar]
- Cao, M.K.; Prince, S.D.; Small, J.; Goetz, S.J. Remotely sensed interannual variations and trends in terestrial net primary productivity 1981–2000. Ecosystems 2004, 7, 233–242. [Google Scholar]
- Cao, M.; Woodward, F.I. Dynamic responses of terrestrial ecosystem carbon cycling to global climate change. Nature 1998, 393, 249–252. [Google Scholar]
- Cao, M.; Woodward, F.I. Net primary and ecosystem production and carbon stocks of terrestrial ecosystems and their response to climate change. Glob. Chang. Biol 1998, 4, 185–198. [Google Scholar]
- Cao, M.; Prince, S.; Tao, B.; Small, J.; Li, K. Regional pattern and interannual variations in global terrestrial carbon uptake in response to changes in climate and atmospheric CO2. Tellus B 2005, 57, 210–217. [Google Scholar]
- Collatz, G.; Ball, J.; Grivet, C.; Berry, J. Physiological and environmental regulation of stomatal conductance, photosynthesis and transpiration: A model that includes a laminar boundary layer. Agric. For. Meteorol 1991, 54, 107–136. [Google Scholar]
- Raich, J.W.; Rastetter, E.B.; Melillo, J.M.; Kicklighter, D.W.; Steudler, P.A.; Peterson, B.J.; Grace, A.L.; Moore, B.; Vorosmarty, C.J. Potential net primary productivity in South America: Application of a global model. Ecol. Appl 1991, 1, 399–429. [Google Scholar]
- Zhao, M.; Running, S.W. Drought-induced reduction in global terrestrial net primary production from 2000 through 2009. Science 2010, 329, 940–943. [Google Scholar]
- Zhao, M.; Running, S.W.; Nemani, R.R. Sensitivity of Moderate Resolution Imaging Spectroradiometer (MODIS) terrestrial primary production to the accuracy of meteorological reanalyses. J. Geophys. Res. Biogeosci 2006, 111. [Google Scholar] [CrossRef]
- Kanamitsu, M.; Ebisuzaki, W.; Woollen, J.; Yang, S.-K.; Hnilo, J.J.; Fiorino, M.; Potter, G.L. NCEP–DOE AMIP-II Reanalysis (R-2). Bull. Am. Meteorol. Soc 2002, 83, 1631–1643. [Google Scholar]
- Allen, R.G. Food and Agriculture Organization of the United Nations. Chapter 3: Meteorological Data. In Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; Food and Agriculture Organization of the United Nations: Rome, Italy, 1998; pp. 33–36. [Google Scholar]
- Hutchinson, M. ANUSPLIN Version 4.2; Centre for Resource and Environmental Studies, Australian National University: Canberra, Australia, 2001. [Google Scholar]
- Yatagai, A.; Kamiguchi, K.; Arakawa, O.; Hamada, A.; Yasutomi, N.; Kitoh, A. APHRODITE: Constructing a long-term daily gridded precipitation dataset for Asia based on a dense network of rain gauges. Bull. Am. Meteorol. Soc 2012, 93, 1401–1415. [Google Scholar]
- Los, S.O. Linkages between Global Vegetation and Climate: An Analysis Based on NOAA Advanced very High Resolution Radiometer Data; 016049527X; National Aeronautics and Space Administration, Goodard Space Flight Center: Greenbelt, MD, USA, 1998. [Google Scholar]
- Matlab, R.V. R2011b; The Mathworks Inc: Natick, MA, USA.
- Myneni, R.; Hoffman, S.; Knyazikhin, Y.; Privette, J.; Glassy, J.; Tian, Y.; Wang, Y.; Song, X.; Zhang, Y.; Smith, G. Global products of vegetation leaf area and fraction absorbed PAR from year one of MODIS data. Remote Sens. Environ 2002, 83, 214–231. [Google Scholar]
- Myneni, R.; Ramakrishna, R.; Nemani, R.; Running, S. Estimation of global leaf area index and absorbed PAR using radiative transfer models. IEEE Trans. Geosci. Remote Sens 1997, 35, 1380–1393. [Google Scholar]
- Knyazikhin, Y.; Martonchik, J.; Myneni, R.; Diner, D.; Running, S. Synergistic algorithm for estimating vegetation canopy leaf area index and fraction of absorbed photosynthetically active radiation from MODIS and MISR data. J. Geophys. Res 1998, 103, 32257–32276. [Google Scholar]
- Privette, J.L.; Myneni, R.B.; Knyazikhin, Y.; Mukelabai, M.; Roberts, G.; Tian, Y.; Wang, Y.; Leblanc, S.G. Early spatial and temporal validation of MODIS LAI product in the Southern Africa Kalahari. Remote Sens. Environ 2002, 83, 232–243. [Google Scholar]
- Tian, Y.; Wang, Y.; Zhang, Y.; Knyazikhin, Y.; Bogaert, J.; Myneni, R. Radiative transfer based scaling of LAI retrievals from reflectance data of different resolutions. Remote Sens. Environ 2003, 84, 143–159. [Google Scholar]
- Jönsson, P.; Eklundh, L. TIMESAT—A program for analyzing time-series of satellite sensor data. Comput. Geosci 2004, 30, 833–845. [Google Scholar]
- Eklundha, L.; Jönssonb, P. TIMESAT 3.1 Software Manual; Lund University: Lund, Sweden, 2012. [Google Scholar]
- Friedl, M.A.; McIver, D.K.; Hodges, J.C.; Zhang, X.; Muchoney, D.; Strahler, A.H.; Woodcock, C.E.; Gopal, S.; Schneider, A.; Cooper, A. Global land cover mapping from MODIS: Algorithms and early results. Remote Sens. Environ 2002, 83, 287–302. [Google Scholar]
- Liu, Y.F.; Song, X.; Yu, G.R.; Sun, X.M.; Wen, X.F.; Chen, Y.R. Seasonal variation of CO2 flux and its environmental factors in evergreen coniferous plantation. Sci. China Ser. D 2005, 48, 123–132. [Google Scholar]
- Wen, X.; Yu, G.; Sun, X.; Liu, Y. Turbulence flux measurement above the overstory of a subtropical Pinus plantation over the hilly region in Southeastern China. Sci. China Ser. D 2005, 48, 63–73. [Google Scholar]
- Yan, J.; Liu, X.; Tang, X.; Yu, G.; Zhang, L.; Chen, Q.; Li, K. Substantial amounts of carbon are sequestered during dry periods in an old-growth subtropical forest in South China. J. For. Res 2013, 18, 21–30. [Google Scholar]
- Yan, J.; Zhang, Y.; Yu, G.; Zhou, G.; Zhang, L.; Li, K.; Tan, Z.; Sha, L. Seasonal and inter-annual variations in net ecosystem exchange of two old-growth forests in Southern China. Agric. For. Meteorol 2013. [Google Scholar]
- Zhang, Y.; Tan, Z.; Song, Q.; Yu, G.; Sun, X. Respiration controls the unexpected seasonal pattern of carbon flux in an Asian tropical rain forest. Atmos. Environ 2010, 44, 3886–3893. [Google Scholar]
- Hirata, R.; Saigusa, N.; Yamamoto, S.; Ohtani, Y.; Ide, R.; Asanuma, J.; Gamo, M.; Hirano, T.; Kondo, H.; Kosugi, Y. Spatial distribution of carbon balance in forest ecosystems across East Asia. Agric. For. Meteorol 2008, 148, 761–775. [Google Scholar]
- Saigusa, N.; Yamamoto, S.; Hirata, R.; Ohtani, Y.; Ide, R.; Asanuma, J.; Gamo, M.; Hirano, T.; Kondo, H.; Kosugi, Y. Temporal and spatial variations in the seasonal patterns of CO2 flux in boreal, temperate, and tropical forests in East Asia. Agric. For. Meteorol 2008, 148, 700–713. [Google Scholar]
- Yamamoto, S.; Saigusa, N.; Murayama, S.; Gamo, M.; Ohtani, Y.; Kosugi, Y.; Tani, M. Synthetic Analysis of the CO2 Fluxes at Various Forests in East Asia. In Plant Responses to Air Pollution and Global Change; Omasa, K., Nouchi, I., Kok, L., Eds.; Springer: Tokyo, Japan, 2005; pp. 215–225. [Google Scholar]
- Hirano, T.; Segah, H.; Kusin, K.; Limin, S.; Takahashi, H.; Osaki, M. Effects of disturbances on the carbon balance of tropical peat swamp forests. Glob. Chang. Biol 2012, 18, 3410–3422. [Google Scholar]
- Hirano, T.; Kusin, K.; Limin, S.; Osaki, M. Carbon dioxide emissions through oxidative peat decomposition on a burnt tropical peatland. Glob. Chang. Biol 2013, 20, 555–565. [Google Scholar]
- Song, X.; Yu, G.; Liu, Y.; Sun, X.; Ren, C.; Wen, X. Comparison of flux measurement by open-path and close-path eddy covariance systems. Sci. China Ser. D 2005, 48, 174–184. [Google Scholar]
- Song, X.; Liu, Y.; Xu, X.; Yu, G.; Wen, X. Comparison study on carbon dioxide, water and heat fluxes of the forest ecosystem in red earth hilly zone over winter and spring. Resour. Sci 2004, 26, 96–104. [Google Scholar]
- Yang, F. Influences of Land Use on Terrestrial Carbon Cycles in Red Soil Hilly Area of South China: Case Research at Qianyanzhou Experimental Station; Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences: Beijing, China, 2005. [Google Scholar]
- Li, Z.Q.; Yu, G.R.; Wen, X.F.; Zhang, L.M.; Ren, C.Y.; Fu, Y.L. Energy balance closure at ChinaFlux sites. Sci. China Ser. D 2005, 48, 151–162. [Google Scholar]
- Yu, G.R.; Wen, X.F.; Li, Q.K.; Zhang, L.M.; Ren, C.Y.; Liu, Y.F.; Guan, D.X. Season pattern and response character to environment of sub-tropic and temperature forest ecosystem respiration in China. Sci. China Ser. D 2005, 48, 93–105. [Google Scholar]
- Hirano, T.; Segah, H.; Harada, T.; Limin, S.; June, T.; Hirata, R.; Osaki, M. Carbon dioxide balance of a tropical peat swamp forest in Kalimantan, Indonesia. Glob. Chang. Biol 2007, 13, 412–425. [Google Scholar]
- Fensholt, R.; Proud, S.R. Evaluation of Earth Observation based global long term vegetation trends—Comparing GIMMS and MODIS global NDVI time series. Remote Sens. Environ 2012, 119, 131–147. [Google Scholar]
- Gibson, L.; Lynam, A.J.; Bradshaw, C.J.A.; He, F.; Bickford, D.P.; Woodruff, D.S.; Bumrungsri, S.; Laurance, W.F. Near-complete extinction of native small mammal fauna 25 years after forest fragmentation. Science 2013, 341, 1508–1510. [Google Scholar]
- Chen, J.M.; Mo, G.; Pisek, J.; Liu, J.; Deng, F.; Ishizawa, M.; Chan, D. Effects of foliage clumping on the estimation of global terrestrial gross primary productivity. Glob. Biogeochem. Cycle 2012, 26. [Google Scholar] [CrossRef]
- Zhu, Z.; Bi, J.; Pan, Y.; Ganguly, S.; Anav, A.; Xu, L.; Samanta, A.; Piao, S.; Nemani, R.; Myneni, R. Global data sets of vegetation leaf area index (LAI)3g and fraction of photosynthetically active radiation (FPAR)3g derived from global inventory modeling and mapping studies (GIMMS) normalized difference vegetation index (NDVI3g) for the period 1981 to 2011. Remote Sens 2013, 5, 927–948. [Google Scholar]
- Turner, D.P.; Ritts, W.D.; Cohen, W.B.; Gower, S.T.; Running, S.W.; Zhao, M.S.; Costa, M.H.; Kirschbaum, A.A.; Ham, J.M.; Saleska, S.R.; et al. Evaluation of MODIS NPP and GPP products across multiple biomes. Remote Sens. Environ 2006, 102, 282–292. [Google Scholar]
- Serbin, S.P.; Ahl, D.E.; Gower, S.T. Spatial and temporal validation of the MODIS LAI and FPAR products across a boreal forest wildfire chronosequence. Remote Sens. Environ 2013, 133, 71–84. [Google Scholar]
- Eklundha, L.; Jönssonb, P. Timesat 3.0 Software Manual; Lund University: Lund, Sweden, 2010. [Google Scholar]
- Hird, J.N.; McDermid, G.J. Noise reduction of NDVI time series: An empirical comparison of selected techniques. Remote Sens. Environ 2009, 113, 248–258. [Google Scholar]
- Schubert, P.; Lagergren, F.; Aurela, M.; Christensen, T.; Grelle, A.; Heliasz, M.; Klemedtsson, L.; Lindroth, A.; Pilegaard, K.; Vesala, T.; et al. Modeling GPP in the Nordic forest landscape with MODIS time series data—Comparison with the MODIS GPP product. Remote Sens. Environ 2012, 126, 136–147. [Google Scholar]
- Huete, A.R.; Restrepo-Coupe, N.; Ratana, P.; Didan, K.; Saleska, S.R.; Ichii, K.; Panuthai, S.; Gamo, M. Multiple site tower flux and remote sensing comparisons of tropical forest dynamics in Monsoon Asia. Agric. For. Meteorol 2008, 148, 748–760. [Google Scholar]
Appendix Potential Light Use Efficiency

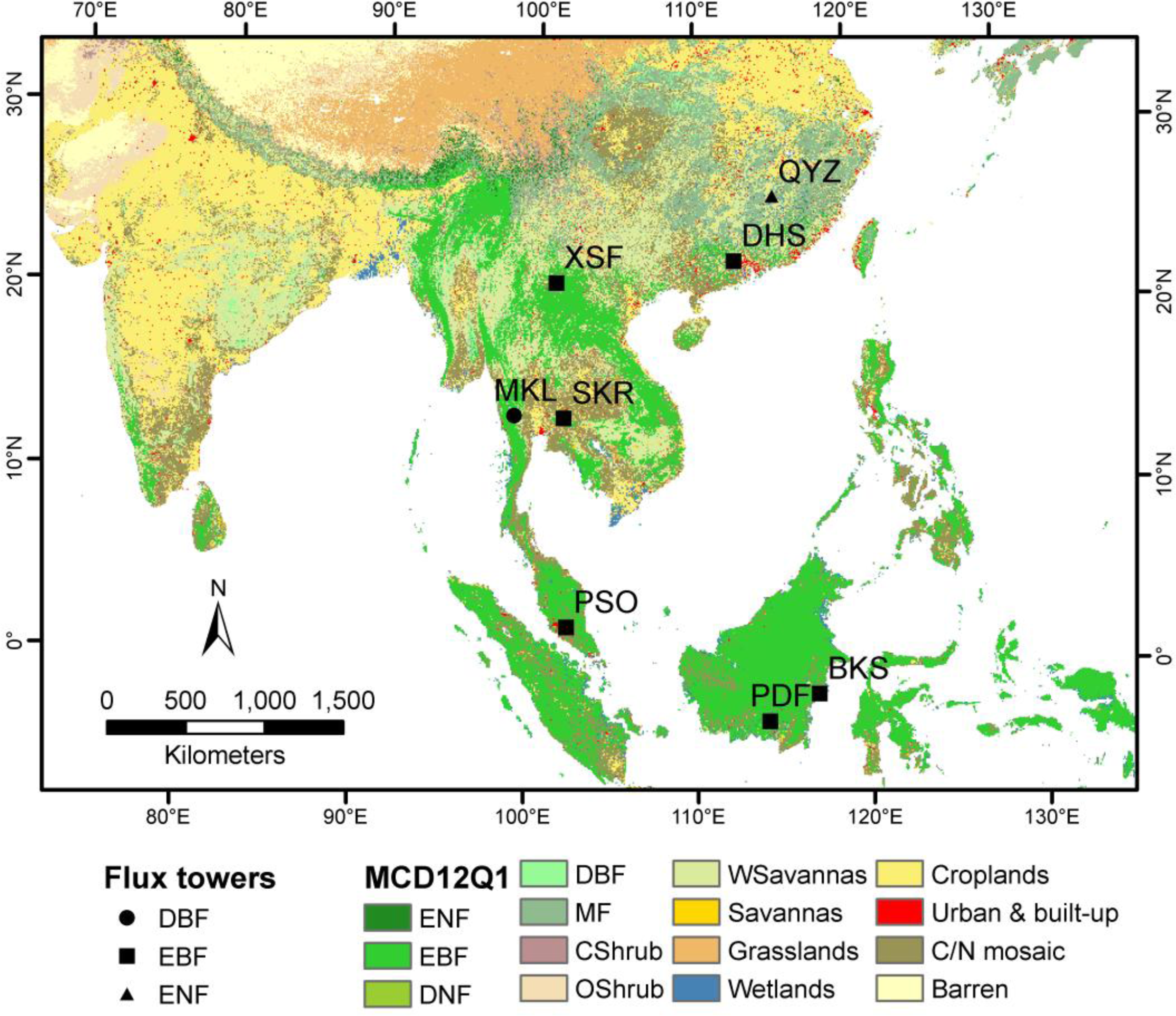



| Site name (Site Code), Country | Latitude and Longitude (°) | Elevation (m) | Forest Type | Annual Mean T (°C) | Annual Precipitation (mm) | Period | References |
|---|---|---|---|---|---|---|---|
| Qianyanzhou (QYZ), China | 26.73, 115.07 | 102 | Subtropical evergreen conifer plantation | 18 | 1485 | 2003–2005 | [65,66] |
| Dinghushan (DHS), China | 23.17, 112.53 | 100–700 | Subtropical evergreen broadleaf forest | 21 | 1700 | 2003–2009 | [67,68] |
| Xishuangbanna (XSF), China | 21.93, 101.27 | 750 | Tropical rain forest | 22 | 1487 | 2003–2008 | [69] |
| Mae Klong (MKL), Thailand | 14.57, 98.83 | 160 | Tropical seasonal deciduous forest | 25 | 1200 | 2003–2004 | [70,71] |
| Sakaerat (SKR), Thailand | 14.48, 101.90 | 535 | Tropical dry evergreen forest | 24 | 1500 | 2002–2003 | [70,71] |
| Pasoh Forest Reserve (PSO), Malaysia | 2.97, 102.30 | 75–150 | Tropical rain forest | 26 | 1700 | 2003–2005 | [70,71] |
| Bukit Soeharto (BKS), Indonesia | −0.86, 117.04 | 20 | Tropical secondary forest | 27 | 3300 | 2002 | [70,72] |
| Palangkaraya drained forest (PDF), Indonesia | −2.35, 114.03 | 30 | Tropical peat swamp forest | 26 | 2540 | 2004–2008 | [70,73,74] |
| Period | Subtropical Evergreen Needleleaf Forest (QYZ) | Tropical Peat Swamp Forest (PDF) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| GPPNDVI3g | GPPNDVI1g | GPPMOD15 | GPPMOD17 | GPPOBS | GPPNDVI3g | GPPNDVI1g | GPPMOD15 | GPPMOD17 | GPPOBS | |
| Whole Year (gC·m−2·a−1) | ||||||||||
| 2002 | 1803.1 | 4365.3 | 3350.4 | 2176.6 | 3122.6 | 3246.1 | ||||
| 2003 | 1430.7 | 1080.8 | 1362.6 | 1674.2 | 1610.4 | 4785.2 | 4656.2 | 2487.7 | 3053.4 | 3460.6 |
| 2004 | 1453.7 | 1319.8 | 1606.9 | 1884.6 | 1867.4 | 4786.3 | 4294.8 | 2447.7 | 3166.0 | 3593.8 |
| 2005 | 1319.6 | 1098.2 | 1259.3 | 1653.4 | 1912.0 | 4632.4 | 4023.8 | 2534.2 | 2711.3 | |
| May–October (gC·m−2 in 6 months) | ||||||||||
| 2002 | 1180.2 | 2221.6 | 1517.7 | 939.1 | 1575.0 | 1652.3 | ||||
| 2003 | 1091.7 | 862.6 | 1039.4 | 1042.9 | 1068.5 | 2501.3 | 2410.5 | 1333.0 | 1586.6 | 1806.9 |
| 2004 | 1151.0 | 1058.5 | 1211.1 | 1237.4 | 1294.5 | 2451.0 | 2183.2 | 1358.8 | 1698.9 | 1848.3 |
| 2005 | 1130.6 | 935.0 | 1022.2 | 1188.6 | 1340.9 | 2243.7 | 1954.3 | 1366.6 | 1423.3 | |
| November–April (gC·m−2 in 6 months) | ||||||||||
| 2002 | 623.3 | 2143.6 | 1832.6 | 1237.5 | 1547.4 | 1593.8 | ||||
| 2003 | 339.0 | 218.1 | 323.2 | 631.4 | 541.9 | 2283.8 | 2245.7 | 1154.7 | 1467.1 | 1653.7 |
| 2004 | 302.6 | 261.3 | 395.8 | 647.2 | 572.9 | 2335.2 | 2111.6 | 1088.9 | 1467.0 | 1745.5 |
| 2005 | 188.9 | 163.2 | 237.1 | 464.9 | 571.1 | 2388.7 | 2069.4 | 1167.7 | 1287.8 | |
| Modeled GPP | Intercept | Slope | Statistics | RMSE (%) | Sample Number | |||
|---|---|---|---|---|---|---|---|---|
| Value | Error | Value | Error | Adj. R2 | p | |||
| All data | ||||||||
| GPPNDVI3g | 3.10 | 0.33 | 0.53 | 0.12 | 0.35 | 0.00 | 72.8 | 38 |
| GPPNDVI1g | 3.10 | 0.52 | −0.06 | 0.18 | −0.03 | 0.74 | 37.9 | 33 |
| GPPMOD15 | 0.53 | 0.25 | 0.57 | 0.09 | 0.49 | 0.00 | 32.6 | 43 |
| GPPMOD17 | 1.76 | 0.22 | 0.23 | 0.08 | 0.16 | 0.00 | 34.1 | 43 |
| Exclude PDF-DB | ||||||||
| GPPNDVI3g | 2.84 | 0.41 | 0.61 | 0.14 | 0.35 | 0.00 | 66.2 | 35 |
| GPPNDVI1g | 2.79 | 0.63 | 0.04 | 0.21 | −0.03 | 0.87 | 32.1 | 31 |
| GPPMOD15 | −0.42 | 0.17 | 0.87 | 0.06 | 0.85 | 0.00 | 29.8 | 39 |
| GPPMOD17 | 1.03 | 0.22 | 0.45 | 0.07 | 0.51 | 0.00 | 28.0 | 38 |
| Best-Fitting | ||||||||
| GPPNDVI3g | 2.07 | 0.30 | 1.06 | 0.11 | 0.82 | 0.00 | 46.2 | 19 |
| GPPNDVI1g | 2.04 | 0.25 | 0.57 | 0.09 | 0.73 | 0.00 | 26.6 | 14 |
| GPPMOD15 | −0.42 | 0.17 | 0.87 | 0.06 | 0.85 | 0.00 | 29.8 | 39 |
| GPPMOD17 | 1.02 | 0.15 | 0.45 | 0.05 | 0.67 | 0.00 | 30.2 | 33 |
| Vegetation Type | GPPNDVI3g (kgC·m−2·a−1) | GPPNDVI1g (kgC·m−2·a−1) | GPPMOD15 (kgC·m−2·a−1) | GPPMOD17 (kgC·m−2·a−1) | Vegetation Area % | Total GPPNDVI3g (Pg·C·a−1) |
|---|---|---|---|---|---|---|
| Forest | 2.12 ± 0.06 | 1.79 ± 0.03 | 2.08 ± 0.09 | 2.20 ± 0.06 | 29.8 | 8.78 |
| ENF | 1.14 ± 0.04 | 0.84 ± 0.03 | 0.91 ± 0.06 | 1.03 ± 0.05 | 4.2 * | 0.20 |
| DNF | 1.41 ± 0.04 | 1.01 ± 0.01 | 1.18 ± 0.07 | 1.49 ± 0.05 | 0.1 * | 0.00 |
| MF | 1.69 ± 0.05 | 1.31 ± 0.02 | 1.55 ± 0.06 | 1.43 ± 0.04 | 21.9 * | 1.53 |
| EBF | 2.33 ± 0.07 | 2.02 ± 0.04 | 2.35 ± 0.10 | 2.57 ± 0.07 | 68.6 * | 6.63 |
| DBF | 1.84 ± 0.04 | 1.53 ± 0.01 | 1.73 ± 0.06 | 1.53 ± 0.04 | 5.3 * | 0.41 |
| Crop | 1.51 ± 0.02 | 1.28 ± 0.01 | 1.21 ± 0.04 | 1.10 ± 0.03 | 30.8 | 6.46 |
| Grass | 1.28 ± 0.03 | 1.00 ± 0.01 | 1.00 ± 0.04 | 1.01 ± 0.03 | 23.8 | 4.26 |
| Shrub | 0.64 ± 0.02 | 0.54 ± 0.02 | 0.46 ± 0.03 | 0.46 ± 0.03 | 7.4 | 0.66 |
| Barren | 0.08 ± 0.01 | 0.12 ± 0.01 | 0.06 ± 0.00 | 0.13 ± 0.01 | 8.2 | 0.09 |
| Total | 1.45 ± 0.03 | 1.21 ± 0.02 | 1.27 ± 0.05 | 1.28 ± 0.04 | 100 | 20.24 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Wang, J.; Dong, J.; Liu, J.; Huang, M.; Li, G.; Running, S.W.; Smith, W.K.; Harris, W.; Saigusa, N.; Kondo, H.; et al. Comparison of Gross Primary Productivity Derived from GIMMS NDVI3g, GIMMS, and MODIS in Southeast Asia. Remote Sens. 2014, 6, 2108-2133. https://doi.org/10.3390/rs6032108
Wang J, Dong J, Liu J, Huang M, Li G, Running SW, Smith WK, Harris W, Saigusa N, Kondo H, et al. Comparison of Gross Primary Productivity Derived from GIMMS NDVI3g, GIMMS, and MODIS in Southeast Asia. Remote Sensing. 2014; 6(3):2108-2133. https://doi.org/10.3390/rs6032108
Chicago/Turabian StyleWang, Junbang, Jingwei Dong, Jiyuan Liu, Mei Huang, Guicai Li, Steven W. Running, W. Kolby Smith, Warwick Harris, Nobuko Saigusa, Hiroaki Kondo, and et al. 2014. "Comparison of Gross Primary Productivity Derived from GIMMS NDVI3g, GIMMS, and MODIS in Southeast Asia" Remote Sensing 6, no. 3: 2108-2133. https://doi.org/10.3390/rs6032108







