Empirical and Physical Estimation of Canopy Water Content from CHRIS/PROBA Data
Abstract
:1. Introduction
2. Study Area and Data
2.1. Study Area
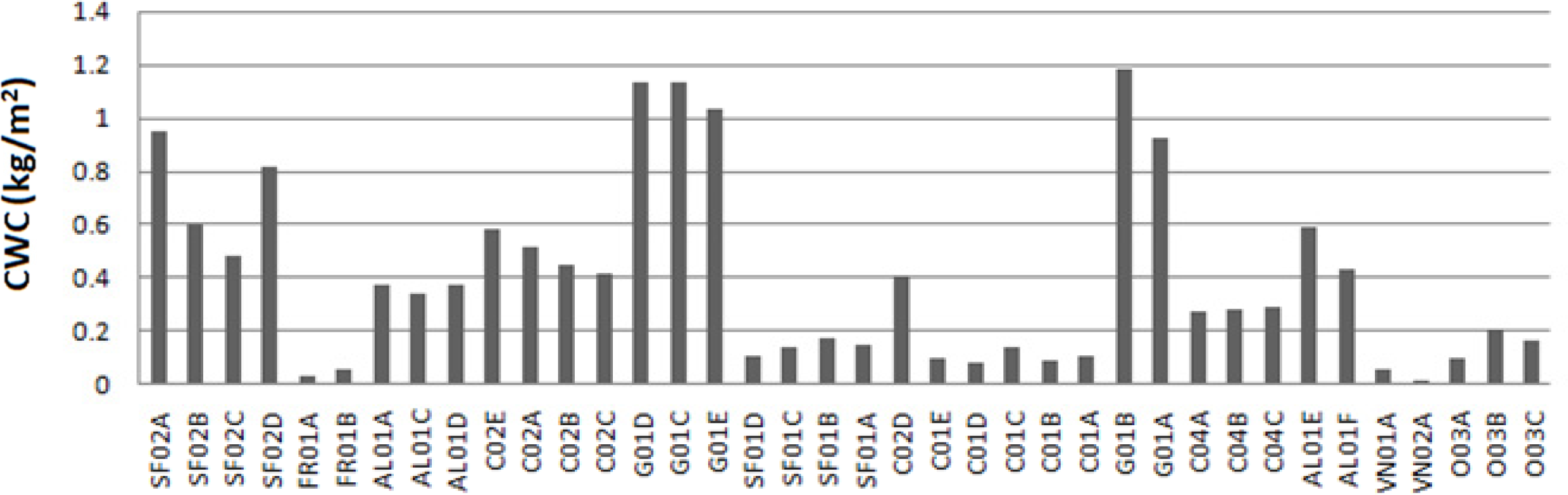
2.2. Field Campaign
2.3. Satellite Data
3. Canopy Water Content Modeling and Retrieval Approaches
3.1. PROSAIL Model
3.2. Spectral Sensitivity Analysis and Band Selection
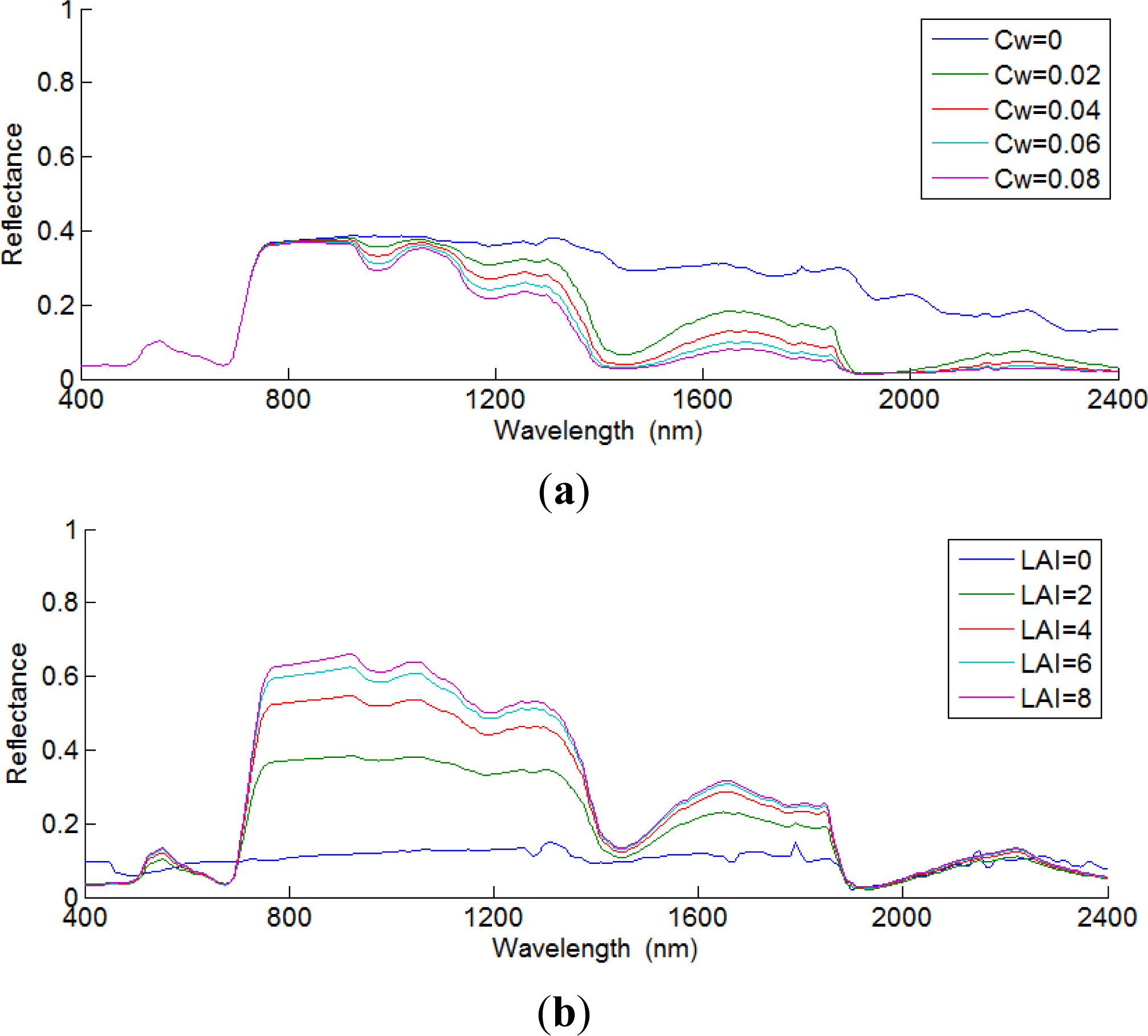
- The PROSAIL model was run in forward mode and the canopy reflectance was computed by fixing the different parameters to their mean values (Table 1) and varying the two components of CWC, i.e., leaf water content, Cw, and LAI, between their ranges of variation in the study area. The sensitivity of canopy reflectance to Cw and LAI variations in the optical spectra (400–2,400 nm) is illustrated in Figure 3. The maximum sensitivity to Cw (Figure 3a) is observed in the near infrared (NIR) and middle infrared with water absorption features centered around 970 nm, 1,200 nm, 1,450 nm and 1,950 nm [24]. Only the spectral information around 970 nm can be exploited for the estimation of Cw from CHRIS data due to the limited spectral range of the sensor (405–1,005 nm). The last four spectral bands (from band b59 to b62) of CHRIS ranging from 960 to 1,005 nm appear to be the optimal spectral domain for Cw retrieval. In the case of LAI (Figure 3b), the sensitivity analysis confirms that red (bands b21–b25 ranging from 627 to 677 nm) and NIR (bands b41–b52 ranging from 773 to 891 nm) are the domains of major interest for the estimation of LAI. Several studies have demonstrated that the combination of two bands in NIR (high sensitivity to LAI) and red (used as a reference band to minimize the influence of soil background) spectral domains is optimal for LAI retrieval [28]. An additional band in the green region (bands b11–b14 ranging from 526 to 566 nm) provides complementary information and a wider range of reflectance sensitivity to LAI (Figure 3b).
- A coefficient of variability (CV), defined here as the ratio between the standard deviation of reflectance measurements and their mean value expressed in percentage, was computed over a homogeneous surface as an indicator of the stability of reflectance measurements to signal noise. Results (Figure 4) show that first CHRIS bands located in the blue spectral domain are significantly affected by residual atmospheric effects (non-physical negative values of reflectances and high CVs). Residual noise also affects the CHRIS bands in the red domain.
3.3. Neural Network Inversion Approach
- The architecture of the networks was made of one input layer with as much neurons as the number of inputs. The number of hidden layers and the number of neurons per layer was empirically defined by selecting the optimal values. Based on a comparison of different activation functions in literature [28,45,46] three combinations were tested by considering hyperbolic tangent in hidden layers, and hyperbolic tangent, linear or saturated linear in the output layer.
- The training process consists in adjusting the networks coefficients by minimizing a cost function using a back propagation algorithm [47]. The selected cost function was here defined as the root mean square error between the targeted variable in the simulation dataset and the network output. The Levenberg-Marquardt minimization algorithm was used because of its efficient convergence performance. For generating the training dataset, truncated Gaussian distributions that mimic the actual distribution of the radiative transfer model input variables based on prior knowledge of the study area (Table 1) were considered. Verger et al. [28] demonstrated that for neural networks training such Gaussian distributions of model parameters performs better than uniform distributions for which no prior information is exploited. Including moderate uncertainties in the reflectance simulations used in the training process improves the flexibility of the neural networks in cases where simulations slightly depart from observations [28]. Three different Gaussian-white noise levels (2, 4 and 6%) were added to the simulated reflectances in order to include instrumental noise and radiometric and atmospheric uncertainties.
- The training datasets were randomly split into three subsets [44]: one half of the simulated cases were used to train the network, one fourth to avoid over-specializations during the training process and one fourth to test the performance of the network and select the solution. The solution was finally extracted by training 10 parallel networks to select the one providing the best performance over the test dataset.
3.4. Look up Table Inversion Approach
3.5. Empirical Transfer Function Approach
4. Results
4.1. Optimal Modalities of Neural Network Inversion
4.2. Optimal Modalities of Look up Table Inversion
4.3. Optimal Modalities of Empirical Approach
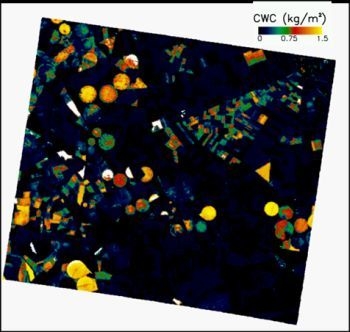
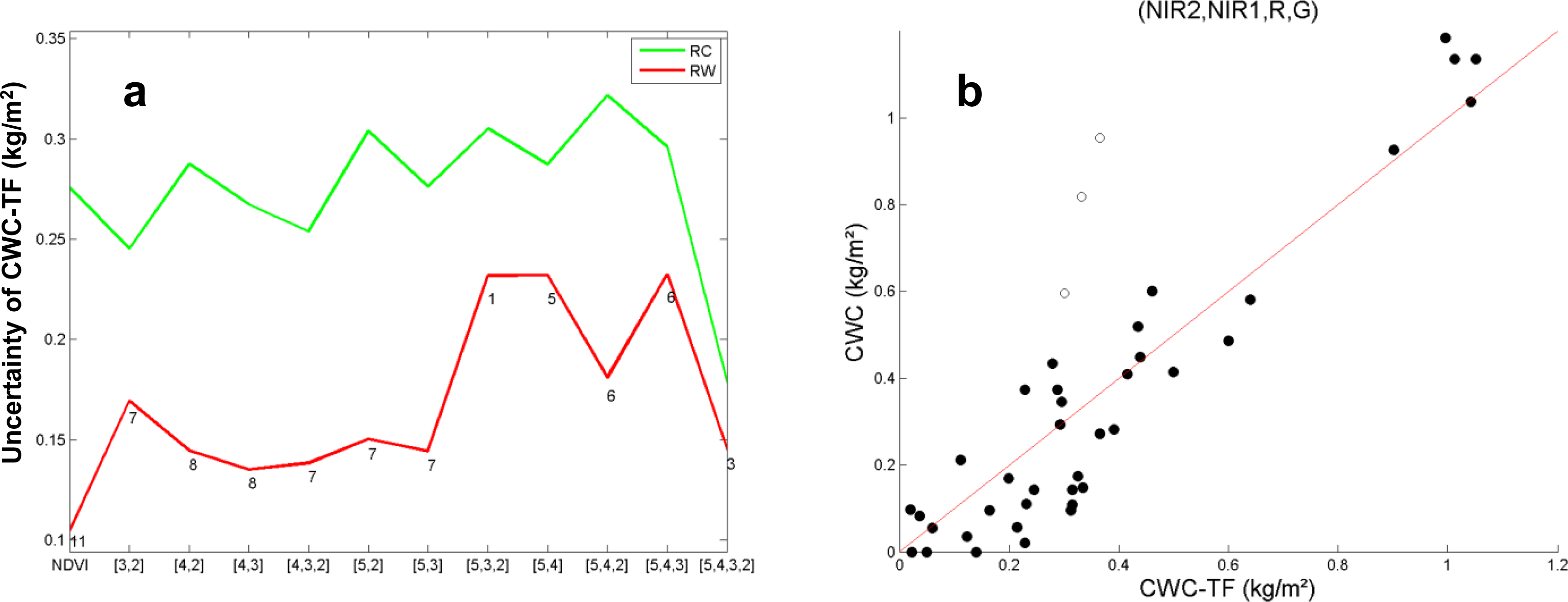
4.4. Comparison of Empirical and Physical Approaches
5. Discussion
6. Conclusions
Acknowledgments
Conflict of Interest
References
- Tucker, C.J. Remote sensing of leaf water content in the near infrared. Remote Sens. Environ 1980, 10, 23–32. [Google Scholar]
- Chuvieco, E.; Riaño, D.; Aguado, I.; Cocero, D. Estimation of fuel moisture content from multitemporal analysis of Landsat Thematic Mapper reflectance data: Applications in fire danger assessment. Int. J. Remote Sens 2002, 23, 2145–2162. [Google Scholar]
- Yebra, M.; Dennison, P.E.; Chuvieco, E.; Riaño, D.; Zylstra, P.; Hunt, E.R., Jr; Danson, F.M.; Qi, Y.; Jurdao, S. A global review of remote sensing of live fuel moisture content for fire danger assessment: Moving towards operational products. Remote Sens. Environ 2013, 136, 455–468. [Google Scholar]
- Yilmaz, M.T.; Hunt, E.R., Jr; Jackson, T.J. Remote sensing of vegetation water content from equivalent water thickness using satellite imagery. Remote Sens. Environ 2008, 112, 2514–2522. [Google Scholar]
- Yilmaz, M.T.; Hunt, E.R., Jr; Goins, L.D.; Ustin, S.L.; Vanderbilt, V.C.; Jackson, T.J. Vegetation water content during SMEX04 from ground data and Landsat 5 Thematic Mapper imagery. Remote Sens. Environ 2008, 112, 350–362. [Google Scholar]
- Curran, P.J. Remote sensing of foliar chemistry. Remote Sens. Environ 1989, 30, 71–278. [Google Scholar]
- Clevers, J.G.P.W.; Kooistra, L.; Schaepman, M.E. Estimating canopy water content using hyperspectral remote sensing data. Int. J. Appl. Earth Obs. Geoinf 2010, 12, 119–125. [Google Scholar]
- Clevers, J.G.P.W.; Kooistra, L.; Schaepman, M.E. Using spectral information from the NIR water absorption features for the retrieval of canopy water content. Int. J. Appl. Earth Obs. Geoinf 2008, 10, 388–397. [Google Scholar]
- Peñuelas, J.; Filella, I.; Biel, C.; Serrano, L.; Save, R. The reflectance at the 950–970 nm region as an indicator of plant water status. Int. J. Remote Sens 1993, 14, 1887–1905. [Google Scholar]
- Roberts, D.A.; Green, R.O.; Adams, J.B. Temporal and Spatial patterns in vegetation and atmospheric properties from AVIRIS. Remote Sens. Environ 1997, 62, 223–240. [Google Scholar]
- Green, R.O.; Conel, J.E.; Roberts, D.A. Estimation of aerosol optical depth, pressure elevation, water vapor, and calculation of apparent surface reflectance from radiance measured by the airborne visible/infrared imaging spectrometer (AVIRIS) using a radiative transfer code. Proc. SPIE 1993. [Google Scholar] [CrossRef]
- Cheng, Y.-B.; Ustin, S.L.; Riaño, D.; Vanderbilt, V.C. Water content estimation from hyperspectral images and MODIS indexes in Southeastern Arizona. Remote Sens. Environ 2008, 112, 363–374. [Google Scholar]
- Stagakis, S.; Markos, N.; Sykioti, O.; Kyparissis, A. Monitoring canopy biophysical and biochemical parameters in ecosystem scale using satellite hyperspectral imagery: An application on a Phlomis fruticosa Mediterranean ecosystem using multiangular CHRIS/PROBA observations. Remote Sens. Environ 2010, 114, 977–994. [Google Scholar]
- Sykioti, O.; Paronis, D.; Stagakis, S.; Kyparissis, A. Band depth analysis of CHRIS/PROBA data for the study of a Mediterranean natural ecosystem. Correlations with leaf optical properties and ecophysiological parameters. Remote Sens. Environ 2011, 115, 752–766. [Google Scholar]
- Ceccato, P.; Flasse, S.; Tarantola, S.; Jacquemoud, S.; Grégoire, J.M. Detecting vegetation leaf water content using reflectance in the optical domain. Remote Sens. Environ. 2001, 77. [Google Scholar]
- Combal, B.; Baret, F.; Weiss, M. Improving canopy variables estimation from remote sensing data by exploiting ancillary information. Case study on sugar beet canopies. Agronomie 2002, 22, 205–215. [Google Scholar]
- Anderson, M.C.; Neale, C.M.U.; Li, F.; Norma, J.M.; Kustas, W.P.; Jayanthi, H.; Chavez, J. Upscaling ground observations of vegetation water content, canopy height, and leaf area index during SMEX02 using aircraft and Landsat imagery. Remote Sens. Environ 2004, 92, 447–464. [Google Scholar]
- Zarco-Tejada, P.J.; Rueda, C.A.; Ustin, S.L. Water content estimation in vegetation with MODIS reflectance data and model inversion methods. Remote Sens. Environ 2003, 85, 109–124. [Google Scholar]
- Fernandes, R. Valse2 Algorithm Theorical Basis Document (ATBD) for Canopy Water Content: Normalized Difference Water Index; Report for ESA contract AO/1–6958/11/NL/BJ; CCRS: Ottawa, ON, Canada, 2012; p. 50. [Google Scholar]
- Ceccato, P.; Gobron, N.; Flasse, S.; Pinty, B.; Tarantola, S. Designing a spectral index to estimate vegetation water content from remote sensing data: Part 1 Theoretical approach. Remote Sens. Environ 2002, 82, 188–197. [Google Scholar]
- Colombo, R.; Meroni, M.; Marchesi, A.; Busetto, L.; Rossini, M.; Giardino, C.; Panigada, C. Estimation of leaf and canopy water content in poplar plantations by means of hyperspectral indices and inverse modeling. Remote Sens. Environ 2008, 112, 1820–1834. [Google Scholar]
- Yebra, M.; Chuvieco, M.; Riaño, D. Estimation of live fuel moisture content from MODIS images for fire risk assessment. Agric. For. Meteorol 2008, 148, 523–536. [Google Scholar]
- Dorigo, W.; Richter, R.; Baret, F.; Bamler, R.; Wagner, W. Enhanced automated canopy characterization from hyperspectral data by a novel two step radiative transfer model inversion approach. Remote Sens 2009, 1, 1139–1170. [Google Scholar]
- Rubio, M.A.; Riaño, D.; Cheng, Y.B.; Ustin, S.L. Estimation of Canopy Water Content from MODIS Using Artificial Neural Networks Trained with Radiative Transfer Models. Proceedings of 6th Annual Meeting of the European Meteorological Society & 6th European Conference on Applied Climatology, Ljubljana, Slovenia, 4–8 September 2006.
- Trombetti, M.; Riano, D.; Rubio, M.A.; Cheng, Y.B.; Ustin, S.L. Multi-temporal vegetation canopy water content retrieval and interpretation using artificial neural networks for the continental USA. Remote Sens. Environ 2008, 112, 203–215. [Google Scholar]
- Baret, F.; Buis, S. Estimating Canopy Characteristics from Remote Sensing Observations. Review of Methods and Associated Problems. In Advances in Land Remote Sensing: System, Modeling, Inversion and Application; Liang, S., Ed.; Springer: Heidelberg, Germany, 2007; pp. 171–200. [Google Scholar]
- Mas, J.F.; Flores, J.J. The application of artificial neural networks to the analysis of remotely sensed data. Int. J. Remote Sens 2008, 29, 617–663. [Google Scholar]
- Verger, A.; Baret, F.; Camacho de Coca, F. Optimal modalities for radiative transfer-neural network estimation of canopy biophysical characteristics: Evaluation over an agricultural area with CHRIS/PROBA observations. Remote Sens. Environ 2011, 115, 415–426. [Google Scholar]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. PROSPECT + SAIL models: A review of use for vegetation characterization. Remote Sens. Environ 2009, 113, S56–S66. [Google Scholar]
- Brockmann, C. Sentinel-3 Experimental Campaign (SEN3EXP) Final Report. ESA Contract 22661/09/I-LG; ESA Publications Division: Noordwijk, The Netherlands, 2011; p. 294. [Google Scholar]
- Martinez, B.; Camacho, F.; García-Haro, F.J. Estimación de parámetros biofísicos de vegetación utilizando el método de la cámara hemisférica. Revista Española de Teledetección 2006, 26, 5–17. [Google Scholar]
- CAN-EYE Website. Available online: http://www4.paca.inra.fr/can-eye (accessed on 31 July 2013).
- Camacho, F.; Giner, M.; Delegido, J.; Vergara, C. Ground Measurement Acquisition Report: Vegetation Parameters; Barrax site, 20–24, June 2009; SEN3EXP Internal Report; SEN3EXP: Valencia, Spain, 2009; p. 22. [Google Scholar]
- Alonso, L.; Moreno, J. Advances and Limitations in A Parametric Geometric Correction of Chris/Proba Data. Proceedings of Third CHRIS/Proba Workshop, ESRIN, Frascati, Italy, 21–23 March 2005; pp. 7–14.
- Moreno, J.F.; Melia, J. An optimum interpolation method applied to the resampling of NOAA AVHRR data. IEEE Trans. Geosci. Remote Sens 1994, 32, 131–151. [Google Scholar]
- BEAM Website. Available online: http://www.brockmann-consult.de/cms/web/beam (accessed on 31 July 2013).
- Jacquemoud, S.; Baret, F. PROSPECT: A model of leaf optical properties spectra. Remote Sens. Environ 1990, 34, 75–91. [Google Scholar]
- Verhoef, W. Light scattering by leaf layers with application to canopy reflectance modeling: The SAIL model. Remote Sens. Environ 1984, 16, 125–141. [Google Scholar]
- Verhoef, W. Earth observation modeling based on layer scattering matrices. Remote Sens. Environ 1985, 17, 165–178. [Google Scholar]
- Kuusk, A. The hot spot effect of a uniform vegetative cover. Remote Sens. Environ 1985, 3, 645–658. [Google Scholar]
- Liu, W.; Baret, F.; Gu, X.F.; Zhang, B.; Tong, Q.; Zhang, L. Evaluation of methods for soil surface moisture estimation from reflectance data. Int. J. Remote Sens 2003, 24, 2069–2083. [Google Scholar]
- Richter, K.; Hank, T.B.; Vuolo, F.; Mauser, W.; D’Urso, G. Optimal exploitation of the Sentinel-2 spectral capabilities for crop leaf area index mapping. Remote Sens 2012, 4, 561–582. [Google Scholar]
- Bacour, C.; Baret, F.; Béal, D.; Weiss, M.; Pavageau, K. Neural network estimation of LAI, fAPAR, fCover and LAIxCab, from top of canopy MERIS reflectance data: Principles and validation. Remote Sens. Environ 2006, 105, 313–325. [Google Scholar]
- Baret, F.; Hagolle, O.; Geiger, B.; Bicheron, P.; Miras, B.; Huc, M.; Berthelot, B.; Weiss, M.; Samain, O.; Roujean, J.L.; et al. LAI, fAPAR and fCover CYCLOPES global products derived from VEGETATION. Part 1: Principles of the algorithm. Remote Sens. Environ 2007, 110, 275–286. [Google Scholar]
- Vohland, M.; Mader, S. Numerical Minimisation and Artificial Neural Networks: Two Different Approaches to Retrieve Parameters from a Canopy Reflectance Model. Proceedings of 5th EARSeL Workshop on Imaging Spectroscopy, Bruges, Belgium, 23–25 April 2007.
- Demuth, H.; Beale, M. Neural Network Toolbox User’s Guide; MathWorks: Natick, MA, USA, 1998. [Google Scholar]
- Atkinson, P.M.; Tatnall, A.R.L. Neural network in remote sensing. Int. J. Remote Sens 1997, 18, 699–709. [Google Scholar]
- Morisette, J.; Baret, F.; Privette, J.L.; Myneni, R.B.; Nickeson, J.; Garrigues, S.; Shabanov, N.; Weiss, M.; Fernandes, R.; Leblanc, S.; et al. Validation of global moderate resolution LAI Products: A framework proposed within the CEOS Land Product Validation subgroup. IEEE Trans. Geosci. Remote Sens 2006, 44, 1804–1817. [Google Scholar]
- Martínez, B.; García-Haro, F.J.; Camacho-de Coca, F. Derivation of high-resolution leaf area index maps in support of validation activities: Application to the cropland Barrax site. Agric. For. Meteorol 2009, 149, 130–145. [Google Scholar]
- Ronchetti, E.; Field, C.; Blanchard, W. Robust linear model selection by cross-validation. J. Am. Stat. Assoc 1997, 92, 1017–1023. [Google Scholar]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W.; Harlan, J.C. Monitoring the Vernal Advancement of Retrogradation of Natural Vegetation; NASA/GSFC: Greenbelt, MD, USA, 1974; p. 371. [Google Scholar]
- Chuvieco, E.; Cocero, D.; Riaño, D.; Martin, P.; Martínez-Vega, J.; de la Riva, J.; Pérez, F. Combining NDVI and surface temperature for the estimation of live fuel moisture content in forest fire danger rating. Remote Sens. Environ 2004, 92, 322–331. [Google Scholar]
- Cheng, T.; Riaño, D.; Koltunov, A.; Whiting, M.L.; Ustin, S.L.; Rodriguez, J. Detection of diurnal variation in orchard canopy water content using MODIS/ASTER airborne simulator (MASTER) data. Remote Sens. Environ 2013, 132, 1–12. [Google Scholar]
- Baghzouz, M.; Devitt, D.A.; Fenstermaker, L.F.; Young, M.H. Monitoring vegetation phenological cycles in two different semi-arid environmental settings using a ground-based NDVI system: A potential approach to improve satellite data interpretation. Remote Sens 2010, 2, 990–1013. [Google Scholar]
- Sobrino, J.A.; Franch, B.; Mattar, C.; Jiménez-Muñoz, J.C.; Corbari, C. A method to estimate soil moisture from Airborne Hyperspectral Scanner (AHS) and ASTER data: Application to SEN2FLEX and SEN3EXP campaigns. Remote Sens. Environ 2012, 117, 415–428. [Google Scholar]
- Atzberger, C.; Richter, K. Spatially constrained inversion of radiative transfer models for improved LAI mapping from future Sentinel-2 imagery. Remote Sens. Environ 2012, 120, 208–218. [Google Scholar]



| Model Variables | N class | Min | Max | Mean | Std. Dev. | |
|---|---|---|---|---|---|---|
| Leaf | N | 4 | 1.0 | 2.5 | 1.5 | 1.0 |
| Cab (μg/cm2) | 4 | 20 | 50 | 33 | 5 | |
| Cw (g/cm2) | 4 | 0 | 0.08 | 0.03 | 0.02 | |
| Cm (g/cm2) | 4 | 0.003 | 0.02 | 0.01 | 0.003 | |
| Canopy | LAI (m2/m2) | 6 | 0 | 8 | 2 | 2 |
| ALA (°) | 4 | 30 | 80 | 50 | 10 | |
| Hot | 1 | 0.001 | 1 | 0.1 | 0.3 | |
| Soil | Bs | 4 | 0.7 | 2.3 | 1.4 | 0.3 |
| Min | Mean | |||
|---|---|---|---|---|
| Noise level | No noise | 0.17 | 0.19 | |
| 2% | 0.21 | 0.23 | ||
| 4% | 0.16 | 0.19 | ||
| 6% | 0.17 | 0.19 | ||
| Architecture | 1 hidden layer | 2 | 0.16 | 0.20 |
| 5 | 0.16 | 0.19 | ||
| 8 | 0.23 | 0.25 | ||
| 11 | 0.22 | 0.24 | ||
| 2 hidden layers | 5-2 | 0.18 | 0.19 | |
| 8-5 | 0.20 | 0.21 | ||
| Activation functions | Tang-Tang | 0.16 | 0.19 | |
| Tang-Lin | 0.21 | 0.23 | ||
| Tang-Slin | 0.20 | 0.22 | ||
| Number of Simulations | ||||
|---|---|---|---|---|
| 600 | 3,600 | 7,200 | ||
| Distribution functions | Uniform | 0.32 | 0.25 | 0.25 |
| Gaussian | 0.25 | 0.22 | 0.24 | |
| Ground Measurements | ETF Map | |||||||
|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | Bias | S | R2 | RMSE | Bias | S | |
| ETF | 0.89 | 0.16 | 0.02 | 0.15 | − | − | − | − |
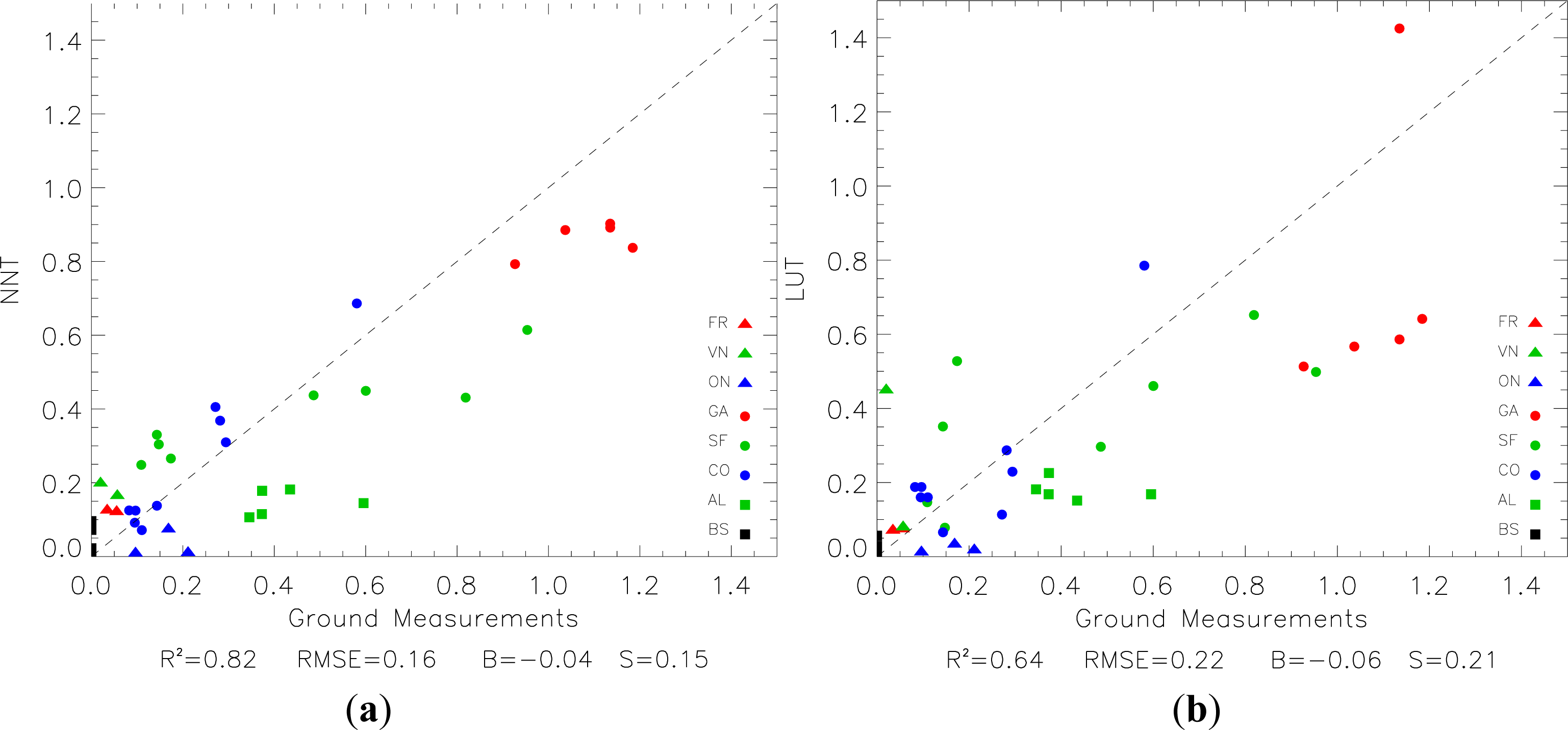
| NNT | 0.82 | 0.16 | −0.04 | 0.15 | 0.92 | 0.14 | −0.05 | 0.13 |
| LUT | 0.64 | 0.22 | −0.06 | 0.21 | 0.89 | 0.16 | −0.01 | 0.15 |
© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Cernicharo, J.; Verger, A.; Camacho, F. Empirical and Physical Estimation of Canopy Water Content from CHRIS/PROBA Data. Remote Sens. 2013, 5, 5265-5284. https://doi.org/10.3390/rs5105265
Cernicharo J, Verger A, Camacho F. Empirical and Physical Estimation of Canopy Water Content from CHRIS/PROBA Data. Remote Sensing. 2013; 5(10):5265-5284. https://doi.org/10.3390/rs5105265
Chicago/Turabian StyleCernicharo, Jesus, Aleixandre Verger, and Fernando Camacho. 2013. "Empirical and Physical Estimation of Canopy Water Content from CHRIS/PROBA Data" Remote Sensing 5, no. 10: 5265-5284. https://doi.org/10.3390/rs5105265